tops is

1.

Южный федеральный университет
Кафедра синергетики и процессов управления
Презентация к практическим занятиям
по дисциплине
«Теория систем и системный анализ»
тема:
«Использование метода TOPSIS для
группового принятия решения»

2.

ОПИСАНИЕ МЕТОДА
Достоинства и широкое использование метода TOPSIS обусловили его развитие и применение не только
для многокритериальных задач с четкими и нечеткими значениями, но и для группового принятия решения
(group decision making), т.е. многокритериальных задач, в которых матрицы оценок (решений) альтернатив
представлены не одним, а несколькими ЛПР или экспертами, образующими группу принятия решения –
ГПР, и возникает необходимость рационального выбора эффективного решения с учетом агрегирования
оценок всех членов ГПР.
Описание представленного здесь варианта метода G-TOPSIS базируется на статье
«Shih H.-S. , Shyur H.-J., Lee E.S. An extension of TOPSIS for group decision making // Mathematical and
Computer Modelling. – 2007. – Vol. 45. – P. 801-813».
2

3.

ПОСТАНОВКА ЗАДАЧИ
Пусть имеется n альтернатив (Xi) и m критериев (Kj), а также K членов ГПР.
Тогда имеем k=1,2,…, K матриц оценок (решений) для каждого члена ГПР, в
которой ukij оценка (полезность) i-той альтернативы по j-тому критерию в матрице
оценок k-го члена ГПР. В результате имеем
U u ij
k
k
n m
K1
K2
…
Km
X1
uk11
uk12
…
uk1m
X2
uk21
uk22
…
uk2m
…
…
…
…
…
Xn
ukn1
ukn2
…
uknm
3

4.

ПОСТАНОВКА ЗАДАЧИ
Пусть J множество критериев, которые необходимо максимизировать.
Пусть J' множество критериев, которые необходимо минимизировать.
Также как и для базового метода TOPSIS веса важности критериев
wkj для k-го
члена ГПР являются входными данными, т.е. должны быть предварительно
определены, при этом для каждого члена ГПР также должно выполняться условие
m
нормировки wkj 1 .
j 1
4

5.

АЛГОРИТМ G-TOPSIS
Шаг 1. Построение нормированной матрицы решений для каждого k-го члена
ГПР
Исходную матрицу решений U uij
k
k
n m
преобразовываем
в
нормированную
в соответствии с выражением:
матрицу Rk rijk
n m
rijk
uijk
n
i 1
.
k 2
uij
5

6.

Шаг 2. Построение идеального и неприемлемого решения для каждого k-го
члена ГПР
Идеальное решение:
где
A
k*
,
vkj * max rijk , j J ;min rijk , j J ' .
i
i
k'
Неприемлемое решение: A
где
k* k*
k*
v1 , v2 ,....., vm
k'
vj
k' k'
k'
v1 , v2 ,....., vm
,
min , j J ;max , j J ' .
i
k
rij
i
k
rij
6

7.

Шаг 3. Вычисление расстояния до идеального и неприемлемого решения для
каждого k-го члена ГПР
1
2
m
2
k*
k
k*
k
S
w
v
r
Расстояние до идеального решения для i-й альтернативы:
j j
i
ij
j 1
1
2
m
2
k
k'
k
Расстояние до неприемлемого решения для i-й альтернативы : S k '
w
v
r
j j ij
i
j 1
k* k '
v j , v j элементы векторов идеального и неприемлемого решения, соответственно.
7

8.

Шаг 4. Вычисление агрегированного расстояния до идеального
неприемлемого решения для ГПР в целом по каждой альтернативе
Расстояние до идеального решения для i-й альтернативы:
*
Si
K
k 1
1/ K
k*
Si
1/ K
k'
Расстояние до неприемлемого решения для i-й альтернативы : Si Si
k 1
'
и
K

9.

Шаг 5. Вычисление относительной приближенности к идеальному решению
*
Сi
'
Si
*
,
0
С
*
'
i 1.
Si Si
Шаг 6. Ранжирование альтернатив в соответствии со значениями, полученными на
Шаге 5
Наилучшей (компромиссной/эффективной) считается альтернатива со значением Сi* ,
ближайшим к единице.
9

10.

Пример 1
ГПР из 3 экспертов (K=3) выбирает один из 3 вариантов автомобилей (n=3): Audi, Mazda,
Toyota. Каждый автомобиль оценивается по трем показателям (m=3): Расход топлива,
Надежность, Цена. По результатам экспертизы каждый из экспертов выставил следующие
баллы от 1 до 9, представленные в матрице решений эксперта. При этом при оценивании
было принято, что для максимизируемых критериев чем выше балл, тем предпочтительнее
значение, для минимизируемых – чем ниже балл тем предпочтительнее.
J = {Надежность}.
J' = {Цена, Расход топлива}.
Эксперт 1:
Весовые коэффициенты критериев w11 0.4; w12 0.25; w31 0.35
Надежность
Цена
Расход топлива
Audi
6
9
6
Mazda
4
7
4
Toyota
7
8
8

11.

Эксперт 2:
Весовые коэффициенты критериев w1 0.3; w2 0.2; w3 0.5
2
2
2
Надежность
Цена
Расход топлива
Audi
9
8
7
Mazda
7
6
8
Toyota
8
7
4
Эксперт 3:
Весовые коэффициенты критериев w13 0.25; w23 0.45; w33 0.3
Надежность
Цена
Расход топлива
Audi
7
8
6
Mazda
5
7
4
Toyota
6
6
5

12.

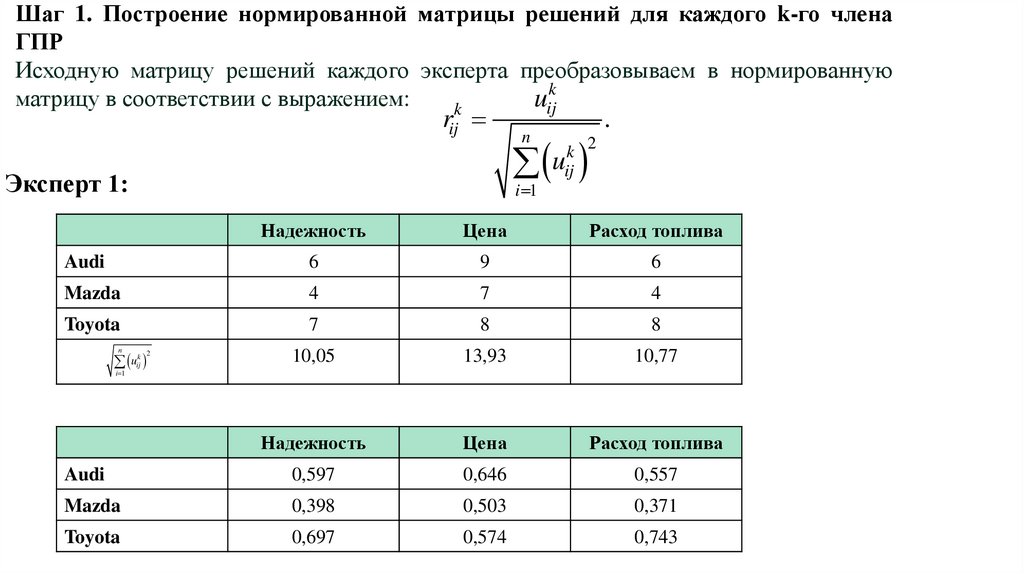
Шаг 1. Построение нормированной матрицы решений для каждого k-го члена
ГПР
Исходную матрицу решений каждого эксперта преобразовываем в нормированную
k
матрицу в соответствии с выражением:
u
ij
k
rij
Эксперт 1:
n
i 1
.
k 2
uij
Надежность
Цена
Расход топлива
Audi
6
9
6
Mazda
4
7
4
Toyota
7
8
8
10,05
13,93
10,77
Надежность
Цена
Расход топлива
Audi
0,597
0,646
0,557
Mazda
0,398
0,503
0,371
Toyota
0,697
0,574
0,743
uijk
n
2
i 1

13.

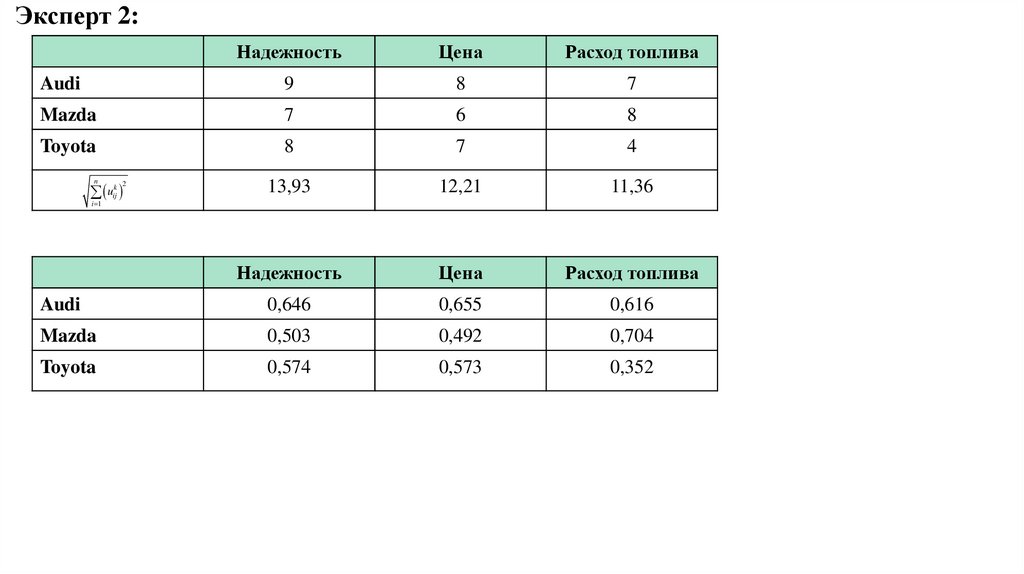
Эксперт 2:
Надежность
Цена
Расход топлива
Audi
9
8
7
Mazda
7
6
8
Toyota
8
7
4
13,93
12,21
11,36
Надежность
Цена
Расход топлива
Audi
0,646
0,655
0,616
Mazda
0,503
0,492
0,704
Toyota
0,574
0,573
0,352
uijk
n
2
i 1

14.

Эксперт 3:
Надежность
Цена
Расход топлива
Audi
7
8
6
Mazda
5
7
4
Toyota
6
6
5
10,49
12,21
8,77
Надежность
Цена
Расход топлива
Audi
0,667
0,655
0,684
Mazda
0,477
0,573
0,456
Toyota
0,572
0,492
0,570
uijk
n
2
i 1

15.

Шаг 2. Построение идеального и неприемлемого решения для каждого k-го
члена ГПР
k'
k' k'
k'
Неприемлемое решение: A v1 , v2 ,....., vn ,
k*
k
rijk , j J ' .
где v j max rij , j J ;min
i
где vkj ' min rijk , j J ;max rijk , j J ' .
Идеальное решение: Ak* v1k* , v2k* ,....., vnk* ,
i
Эксперт 1:
i
i
max
min
min
Надежность
Цена
Расход топлива
Audi
0,597
0,646
0,557
Mazda
0,398
0,503
0,371
Toyota
0,697
0,574
0,743
A1* 0.697;0.503;0.371
A1' 0.398;0.646;0.743

16.

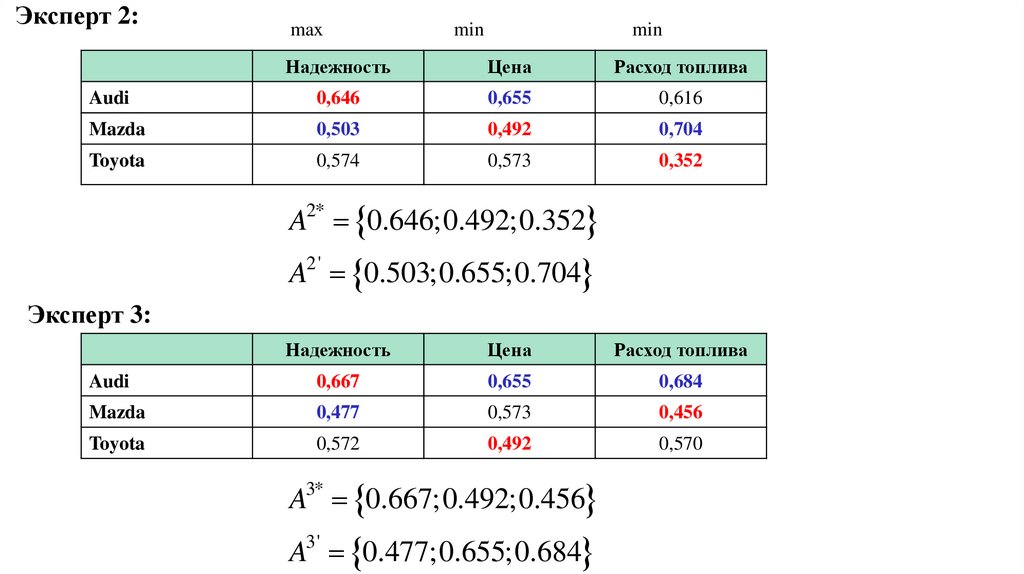
Эксперт 2:
max
min
min
Надежность
Цена
Расход топлива
Audi
0,646
0,655
0,616
Mazda
0,503
0,492
0,704
Toyota
0,574
0,573
0,352
A 0.646;0.492;0.352
2*
A2' 0.503;0.655;0.704
Эксперт 3:
Надежность
Цена
Расход топлива
Audi
0,667
0,655
0,684
Mazda
0,477
0,573
0,456
Toyota
0,572
0,492
0,570
A3* 0.667;0.492;0.456
A3' 0.477;0.655;0.684

17.

Шаг 3. Вычисление расстояния до идеального и неприемлемого решения для
каждого k-го члена ГПР
1
2
m
2
k
k*
k
Расстояние до идеального решения для i-й альтернативы: S k *
wj v j rij
i
j 1
1
2
m
2
Расстояние до неприемлемого решения для i-й альтернативы :
Sik ' wkj vkj ' rijk
j 1
w1 0.4; w1 0.25; w1 0.35
Эксперт 1:
2
3
Надежность
Цена
Расход
топлива
1*
Si
1'
Si
Audi
0,597
0,646
0,557
0,146
0,167
Mazda
0,398
0,503
0,371
0,189
0,231
Toyota
0,697
0,574
0,743
0,223
0,192
S11* 0.4
S11' 0.4
1
A1* 0.697;0.503;0.371
A1' 0.398;0.646;0.743
0.697 0.597 0.25 0.503 0.646 0.35 0.371 0.557
2
2
2
1
1
2
0.146
0.398 0.597 0.25 0.646 0.646 0.35 0.743 0.557 2 0.167
2
2
2

18.

Эксперт 2:
w12 0.3; w22 0.2; w32 0.5
Надежность
Цена
Расход
топлива
Si2*
Si2'
Audi
0,646
0,655
0,616
0,201
0,100
Mazda
0,503
0,492
0,704
0,261
0,073
Toyota
0,574
0,573
0,352
0,054
0,255
Эксперт 3:
w13 0.25; w23 0.45; w33 0.3
Надежность
Цена
Расход
топлива
3*
Si
3'
Si
Audi
0,667
0,655
0,684
0,166
0,095
Mazda
0,477
0,573
0,456
0,110
0,136
Toyota
0,572
0,492
0,570
0,079
0,135

19.

Шаг 4. Вычисление агрегированного расстояния до идеального
неприемлемого решения для ГПР в целом по каждой альтернативе
1/ K
Si* Sik*
k 1
K
Расстояние до идеального решения для i-й альтернативы:
и
1/ K
Расстояние до неприемлемого решения для i-й альтернативы : Si ' Sik '
k 1
Si1*
Si1'
Si2*
Si2'
Si3*
Si3'
0,146
0,167
0,201
0,100
0,166
0,095
0,189
0,231
0,261
0,073
0,110
0,136
0,223
0,192
0,054
0,255
0,079
0,135
S1* 3 0.146 0.201 0.166 0.169
i
Si*
Si '
S1 0.167 0.1 0.095 0.117
1
0,169
0,117
2
0,179
0,132
3
0,098
0,188
'
3
K

20.

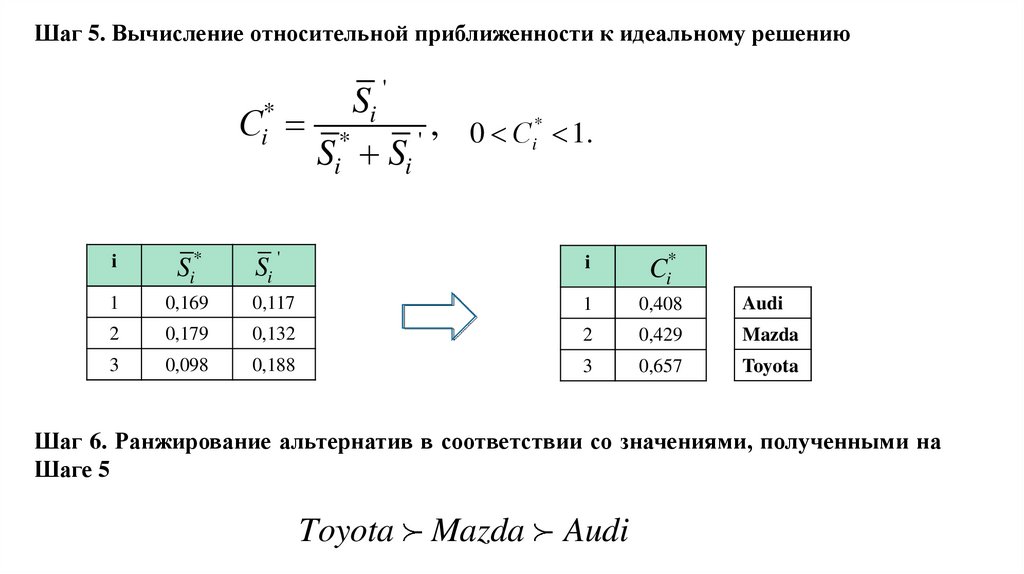
Шаг 5. Вычисление относительной приближенности к идеальному решению
*
Сi
'
Si
*
,
0
С
*
'
i 1.
Si Si
i
Si*
Si '
i
Ci*
1
0,169
0,117
1
0,408
Audi
2
0,179
0,132
2
0,429
Mazda
3
0,098
0,188
3
0,657
Toyota
Шаг 6. Ранжирование альтернатив в соответствии со значениями, полученными на
Шаге 5
Toyota
Mazda
Audi

21.

Задание для самостоятельной работы
В сентябре 2019 г. был проведен бизнес-пикник «Взаимодействие бизнеса и вуза ИКТИБ ЮФУ».
Одной из целевых проблем встречи было обсуждение вопроса «Как студенту совмещать учебу и работу, чтобы
это приносило пользу всем заинтересованным сторонам?»
Были сделаны следующие предложения (альтернативы):
В1 обеспечить студенту гибкий учебный график (свободное посещение занятий)
В2 формировать индивидуальную траекторию обучения студента (индивидуальный учебный план, свободный набор вариативных
дисциплин)
В3 представитель компании из лица преподавателей вуза координирует обучение студента и содержание дисциплин
В4 рабочий проект в компании представляется как ВКР и компания участвует в фактическом подтверждении итоговых уровней
сформированности компетенций образовательной программы
Критерии оценки альтернатив:
К1 заинтересованность студентов
К2 заинтересованность компании
К3 заинтересованность вуза
К4 уровень затрат (трудовых, финансовых, временных и др.) вуза для реализации альтернативы
К5 уровень затрат (трудовых, финансовых, временных и др.) компании для реализации альтернативы
К6 вероятность успешной реализации для всех заинтересованных сторон
К7 вероятность неудачной реализации альтернативы
Группа разбивается на подгруппы по 3-4 человека. Подгруппа определяет шкалу оценок по критериям, а
каждый из членов подгруппы выступает как эксперт и формирует свою уникальную матрицу оценок и веса
важности критериев. Подгруппе необходимо определить эффективное решение методом G-TOPSIS.
Задание выполнить в Excel (шаги 1-3 метода выполняются индивидуально в отдельном файле, шаги 4-6 в
объединенном файле.)