phpM9fU8o_teorema-Falesa

1. Теорема Фалеса

2.

Фале́с (640/624 — 548/545 до н. э.) —
древнегреческий философ и математик
из Милета (Малая Азия).

3.

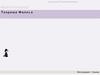
Задача 1
Доказать, что отрезок, соединяющий середины
боковых сторон трапеции, параллелен
основаниям трапеции
Доказательство:

4.

Задача 1
Доказать, что отрезок, соединяющий середины
боковых сторон трапеции, параллелен
основаниям трапеции
Доказательство:
Пусть К–середина АВ.
Проведем KL || BC ||AD.
Тогда по теореме Фалеса L –середина CD
Докажем, что КL- единственный.
Через точки К и L можно провести только одну
прямую(аксиома), т.е. отрезок, соединяющий
середины боковых сторон трапеции ABCD
параллелен основаниям. ч.т.д.

5.

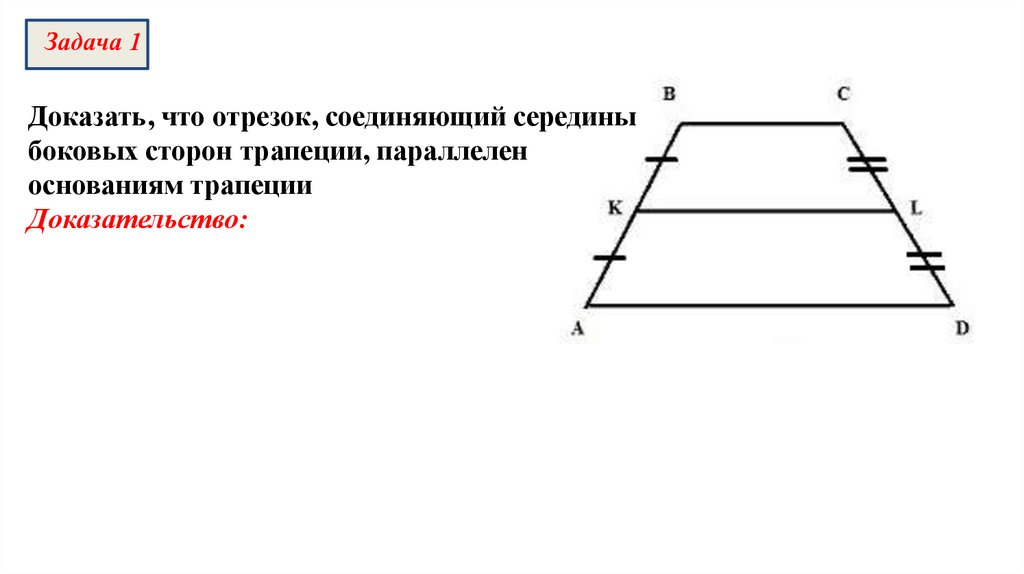
Задача 2
Дано: МК || ВЕ ||СD, AD=16 см, ВС=8 см
Найти:АК
в
C
M
A
D
K
E

6.

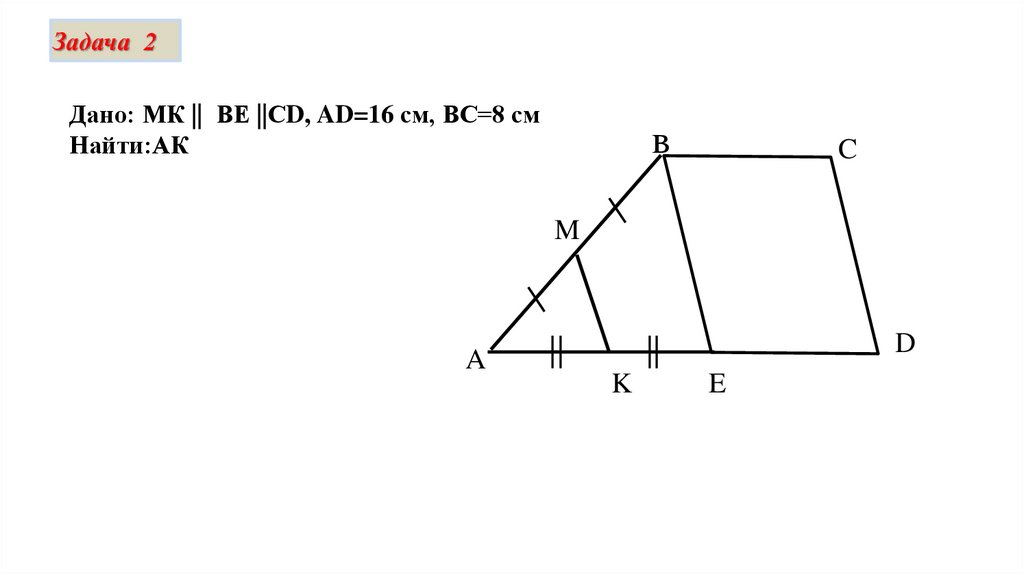
Задача 2
Дано: МК || ВЕ ||СD, AD=16 см, ВС=8 см
Найти:АК
Решение:
По теореме Фалеса АК=КЕ, т.к.
АМ=МВ и МК || ВЕ
ВС=ЕD, т.к. BCDЕпараллелограмм по определению
АК=0.5∙АЕ= 0.5∙(АD- ЕD)=
= 0.5∙(16-8)=4 см
Ответ: 4 см
в
C
M
A
D
K
E

7.

Следствие
Прямая, проведенная через середину стороны
треугольника параллельно другой его стороне, делит
третью сторону пополам
Дано: ∆ АВС, ВМ=МА, М € АВ, MN || АС
Доказать: BN=NC
Доказательство:

8.

Следствие
Прямая, проведенная через середину стороны
треугольника параллельно другой его стороне, делит
третью сторону пополам
Дано: ∆ АВС, ВМ=МА, М € АВ, MN || АС
Доказать: BN=NC
Доказательство:
По теореме Фалеса для угла В имеем
BN=NC ч.т.д.

9.

Деление отрезка на равные части
AC1=C1D1=D1E1=E1B
А
C1
C
D
Пусть отрезок АВ требуется разделить например на 4 равных
части.
• Для этого из любого конца отрезка (из точки А) проведем под
острым углом к отрезку прямую линию АM,
• на которой от точки А измерительным циркулем
откладываем 4 равных отрезка произвольной величины.
• Точку F соединяем с точкой В (концом данного отрезка)
прямой.
• Из точек C, D, E проведем ряд прямых параллельных прямой
FB, которые пересекая отрезок АВ разделят его на 4 равных
части.
D1
E
В
E1
F
M

10.

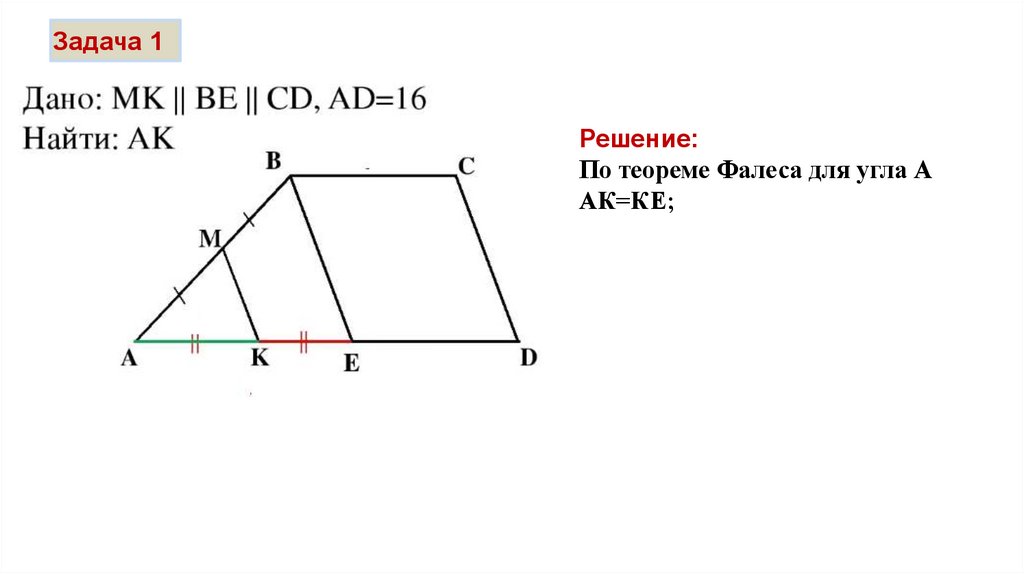
Задача 1
Решение:
По теореме Фалеса для угла А
АК=КЕ;

11.

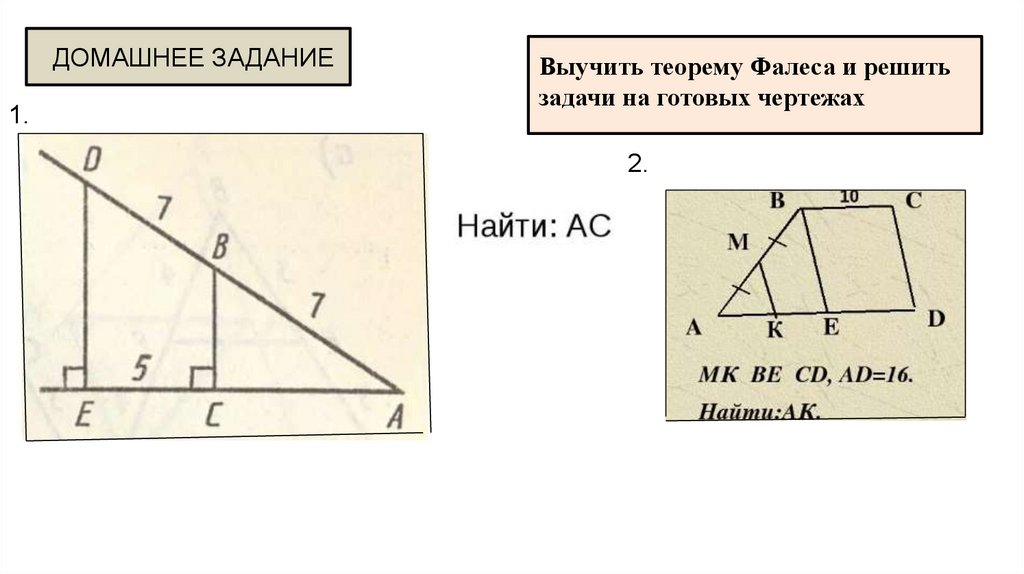
ДОМАШНЕЕ ЗАДАНИЕ
1.
Выучить теорему Фалеса и решить
задачи на готовых чертежах
2.

12. Интересные факты

Теорема Фалеса до сих пор используется в морской
навигации в качестве правила о том, что столкновение
судов, двигающихся с постоянной скоростью,
неизбежно, если сохраняется курс судов друг на друга.