Similar presentations:
«Теорема Фалеса» 8 класс. Урок №9 по геометрии
1. Теорема Фалеса
Урок №9 по геометрии в 8классе
Учитель: Федорова Т.Ф.
2009-2010 уч. год.
5klass.net
2. Цели урока:
• Рассмотреть теорему Фалеса изакрепить ее в процессе решения
задач.
Совершенствовать навыки решения
задач на применение свойств
равнобедренной трапеции, ее
признаков, а также на применение
знаний по теме « Трапеция»
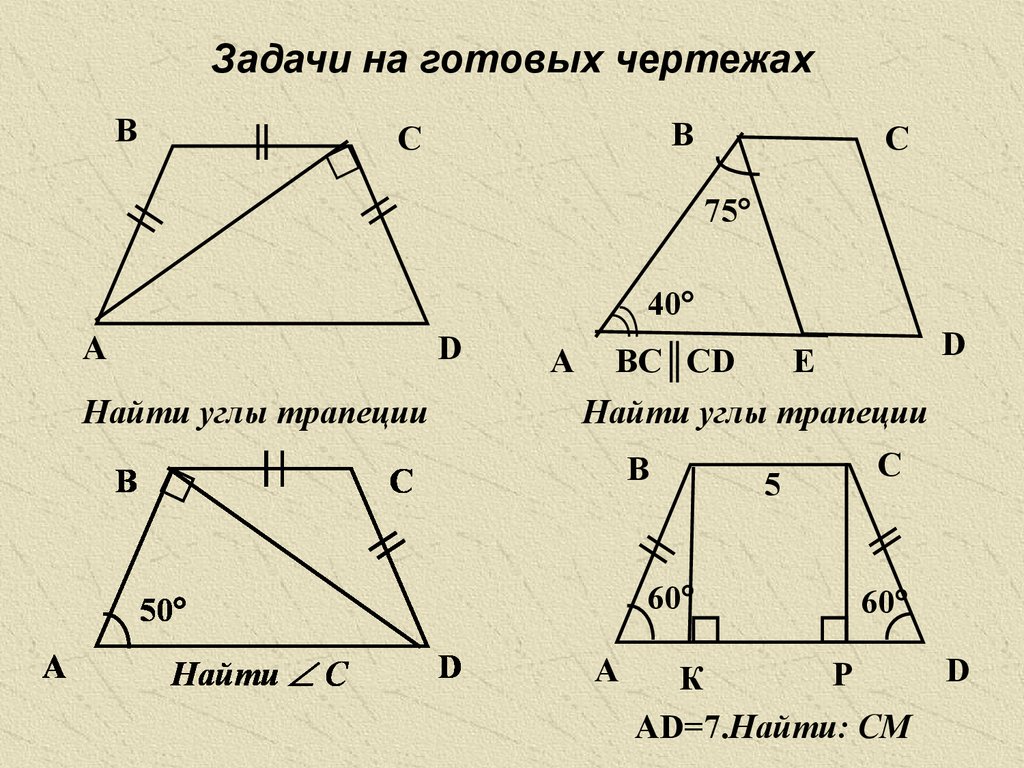
3. Задачи на готовых чертежах
ВВ
С
С
75
40
А
D
Найти углы трапеции
В
А
BC║CD
Е
Найти углы трапеции
В
С
60
50
А
Найти С
D
А
5
D
С
60
Р
К
AD=7.Найти: СМ
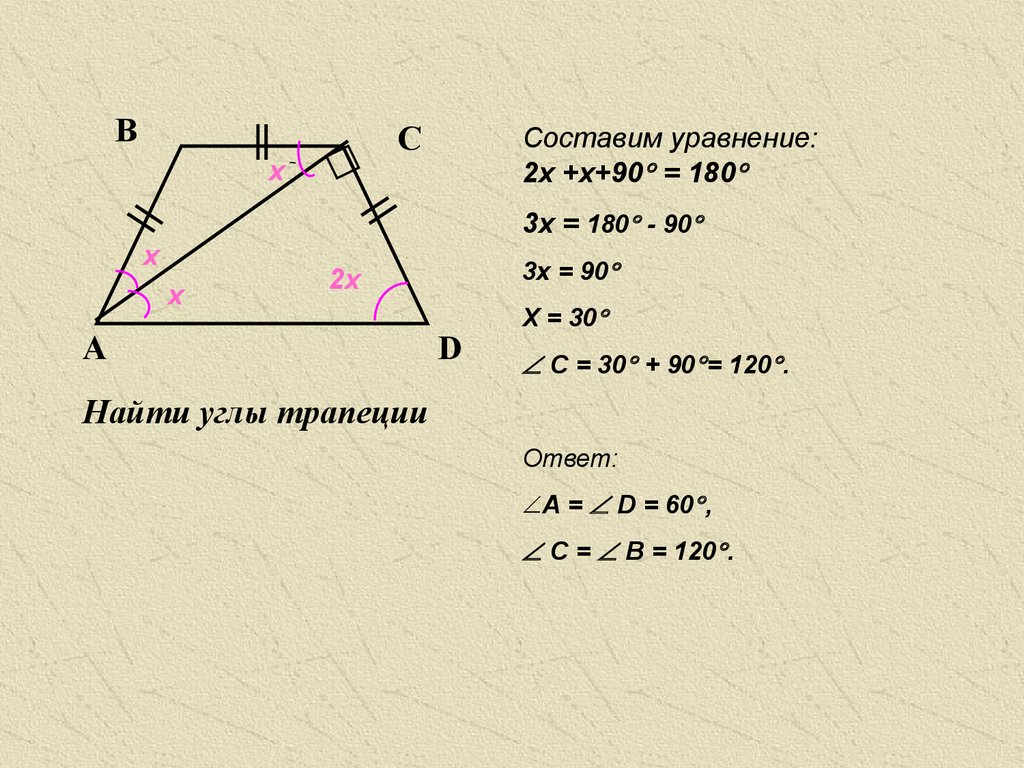
D
4.
ВС
х
Составим уравнение:
2х +х+90 = 180
3х = 180 - 90
х
х
3х = 90
2х
А
D
Х = 30
C = 30 + 90 = 120 .
Найти углы трапеции
Ответ:
А = D = 60 ,
C = B = 120 .
5. Ответы к задачам
1. A = D = 60 , B = C =120 .
2. A=40 , D=65 , C=115 , B=140 .
3. C = 100 .
4. CM =2.
6.
Фалес Милетский624-547г.г. до н.э.
Великий учёный Фалес
Милетский основал одну из
прекраснейших наукгеометрию. Известно, что
Фалес Милетский имел титул
одного из семи мудрецов
Греции, что он был поистине
первым философом, первым
математиком, астрономом и
вообще первым по всем наукам
в Греции. Короче: он был то
же для Греции, что Ломоносов
для России.
Карьеру он начинал как купец и ещё в
молодости попал в Египет. В Египте
Фалес застрял на много лет, изучая
науки в Фивах и Мемфисе.
Считается, что геометрию и
астрономию в Грецию привёз он.
Фалес- математик. Он измерил по
тени высоту пирамиды; установил,
что окружность диаметром
делится пополам, что углы при
основании равнобедренного
треугольника равны. Ему же
принадлежит теорема, что
вписанный угол, опирающийся на
диаметр окружности- прямой
7.
8.
До наших дней дошли изречения Фалеса, вот некоторые из них:9.
.10.
11.
12.
Фалес известен как геометр. Ему приписывают открытие и доказательстворяда теорем: о делении круга диаметром пополам, о равенстве углов при
основании равнобедренного треугольника, о равенстве вертикальных
углов, один из признаков равенства прямоугольных треугольников и
другие. Он открыл любопытный способ определения расстояния от берега
до видимого корабля.
Столь же остроумно Фалес предложил измерять высоту предметов. Став недалеко
от предмета, надо дождаться пока тень человека не сделается равной его росту.
Измерив тогда длину тени предмета, можно заключить, что она равно длине
предмета. Говорят, что таким способом он измерял высоту египетских пирамид.
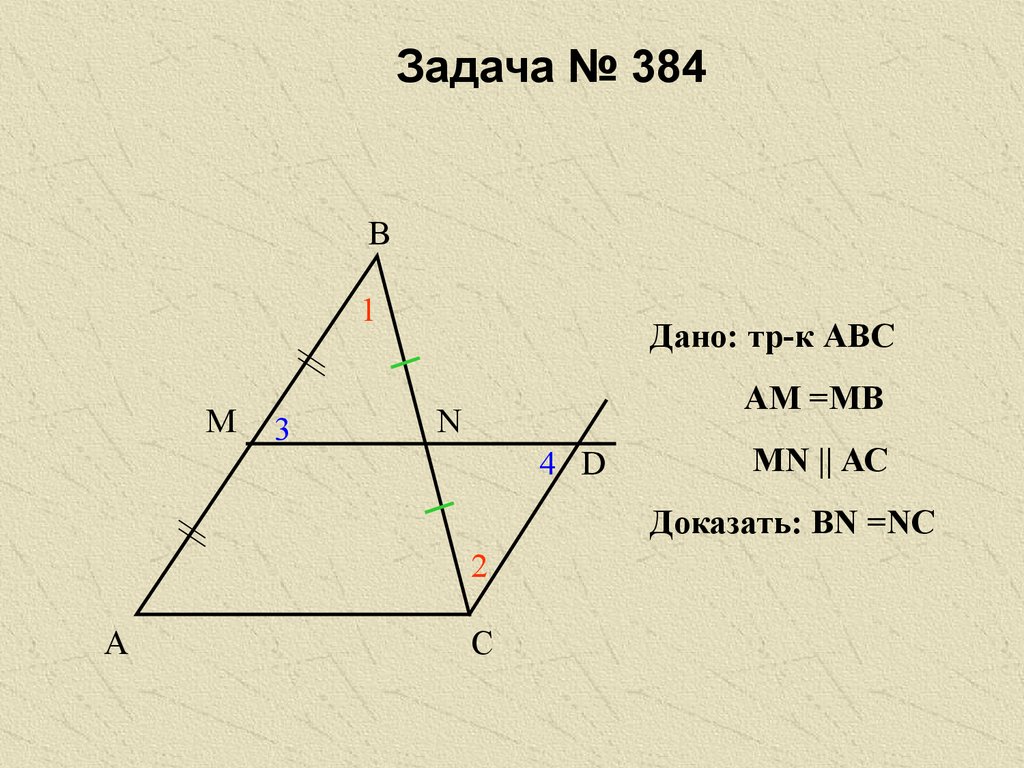
13. Задача № 384
В1
М
3
Дано: тр-к АВС
АМ =МВ
N
4 D
МN || АС
Доказать: ВN =NC
2
А
С
14.
Теорема: если параллельные прямые, пересекающие стороныугла, отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Дано: угол, параллельные прямые
пересекают стороны угла, А1А2=А2А3
В2
F
Доказать: В1В2=В2В3
В3
Доказательство.
E
1. Проведём через точку В2 прямую ЕF,
параллельную прямой А1А3.
В1
А1
А2
А3
2. По свойству параллелограмма
А1А2=FВ2, А2А3=В2Е.
3. Так как А1А2=А2А3, то FВ2=В2Е
4. Треугольники В2В1F и В2В3Е равны по
второму признаку ( у них В2F=В2Е по
доказанному. Углы при вершине В2
равны как вертикальные, а углы
В2FВ3равны как внутренние накрест
лежащие при параллельных А1В1 и А3В3
и секущей ЕF.)
5. Из равенства треугольников следует
15.
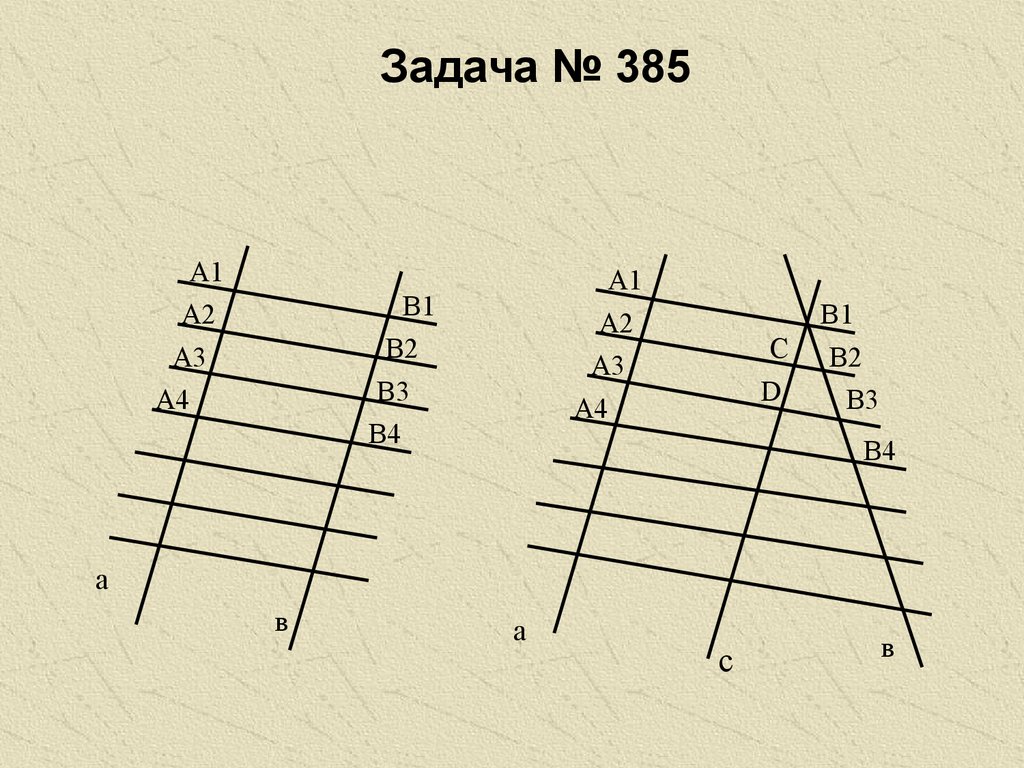
16. Задача № 385
А1А2
А3
А4
А1
А2
А3
А4
В1
В2
В3
В4
С
D
В1
В2
В3
В4
а
в
а
с
в
17.
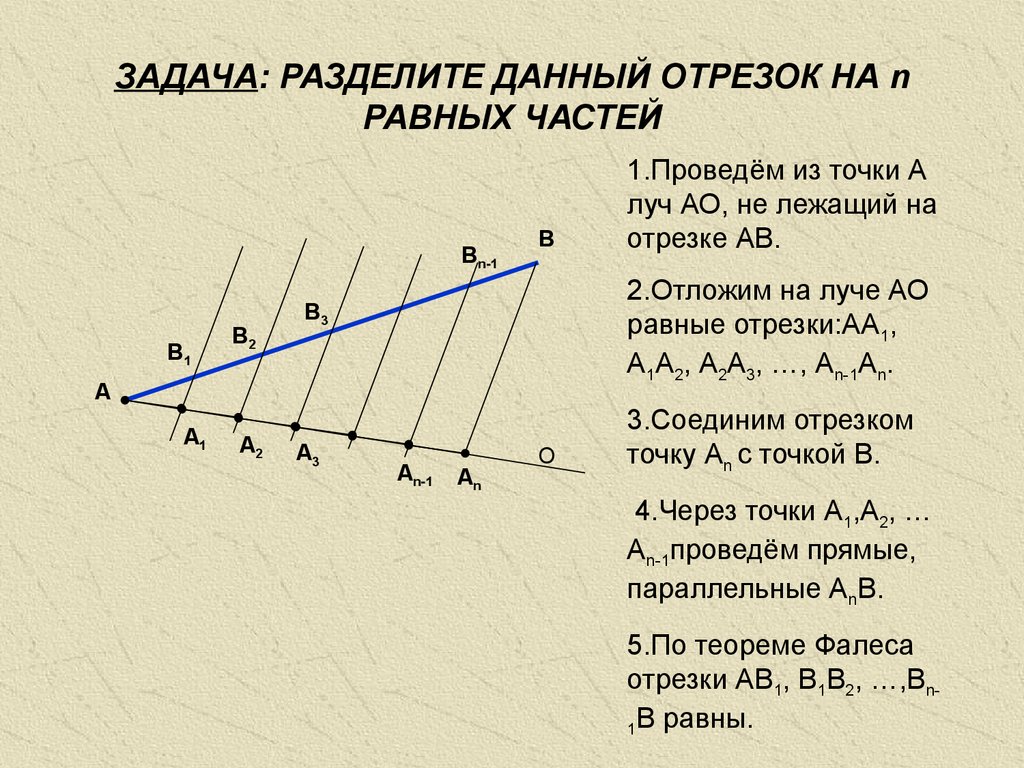
ЗАДАЧА: РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА nРАВНЫХ ЧАСТЕЙ
Вn-1
В1
В2
В
2.Отложим на луче АО
равные отрезки:АА1,
А1А2, А2А3, …, Аn-1Аn.
В3
А
А1
А2
А3
1.Проведём из точки А
луч АО, не лежащий на
отрезке АВ.
Аn-1
Аn
О
3.Соединим отрезком
точку Аn с точкой В.
4.Через точки А1,А2, …
Аn-1проведём прямые,
параллельные АnВ.
5.По теореме Фалеса
отрезки АВ1, В1В2, …,Вn1В равны.
18. Задачи на готовых чертежах
BЗадачи на готовых чертежах
A
A1 A2 A3 A4
F
E
B1
5
4
12
A
C
EF║AC. Найти:РАВС
В
B3
B4
АВ4=20. Найти:В2В3.
С
10
В
С
М
N
М
B2
O
А
Доказать:АО = СО
D
А
К
Е
МК║ВЕ║СD, AD=16.
Найти:АК.
D
19. Задача №386
• Докажите, что отрезок, соединяющий серединыбоковых сторон трапеции, параллелен
основаниям трапеции.
В
M
А
С
N
D
20. Задача № 393 б)
d1d2
Дано:d1-диагональАС
d2- диагональ ВD
а- угол между диагоналями
a
Построить:
АВСD
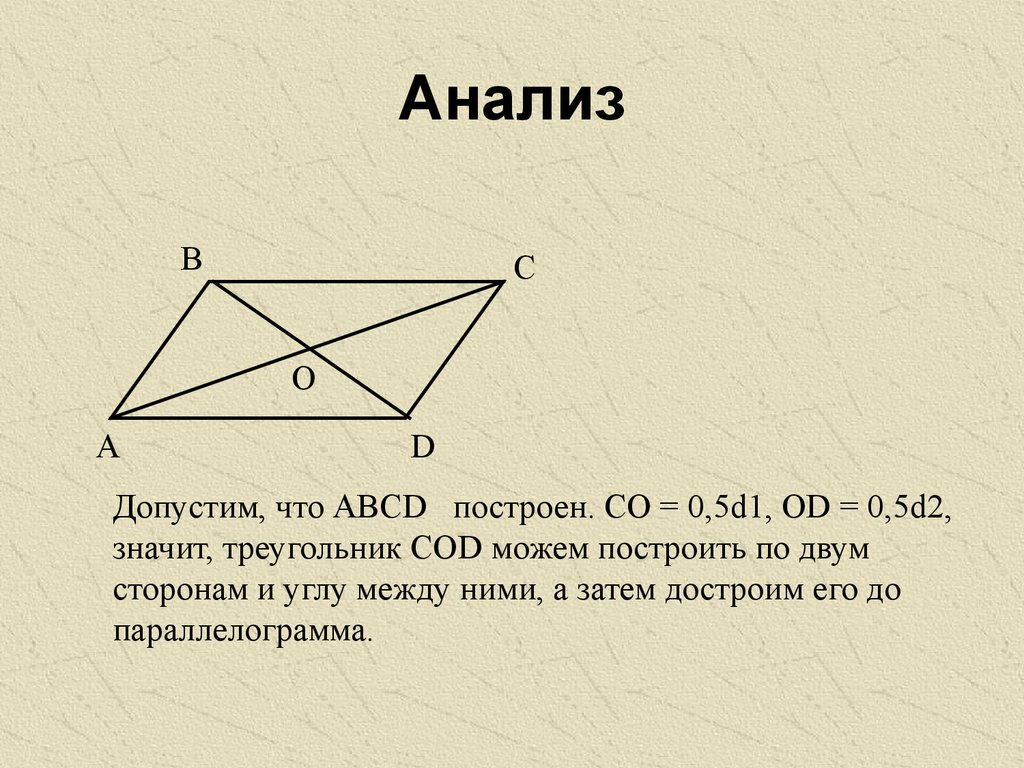
21. Анализ
ВС
О
А
D
Допустим, что АВСD построен. СО = 0,5d1, ОD = 0,5d2,
значит, треугольник СОD можем построить по двум
сторонам и углу между ними, а затем достроим его до
параллелограмма.
22. Доказательство
В четырёхугольнике АВСD диагонали точкойпересечения делятся пополам, значит АВСDпараллелограмм. АС=d1, ВD = d2 ,
угол СОD=a, значит АВСD – искомый
параллелограмм.
23. Исследование
Задача имеет одно решение и всегда возможна.24. Домашнее задание
Задачи № 391, № 392Дополнительная задача:
В равнобедренной трапеции острый
угол равен 60 . Докажите, что меньшее
основание равно разности большего
основания и боковой стороны.


















 mathematics
mathematics








