Similar presentations:
Теорема Фалеса
1.
2.
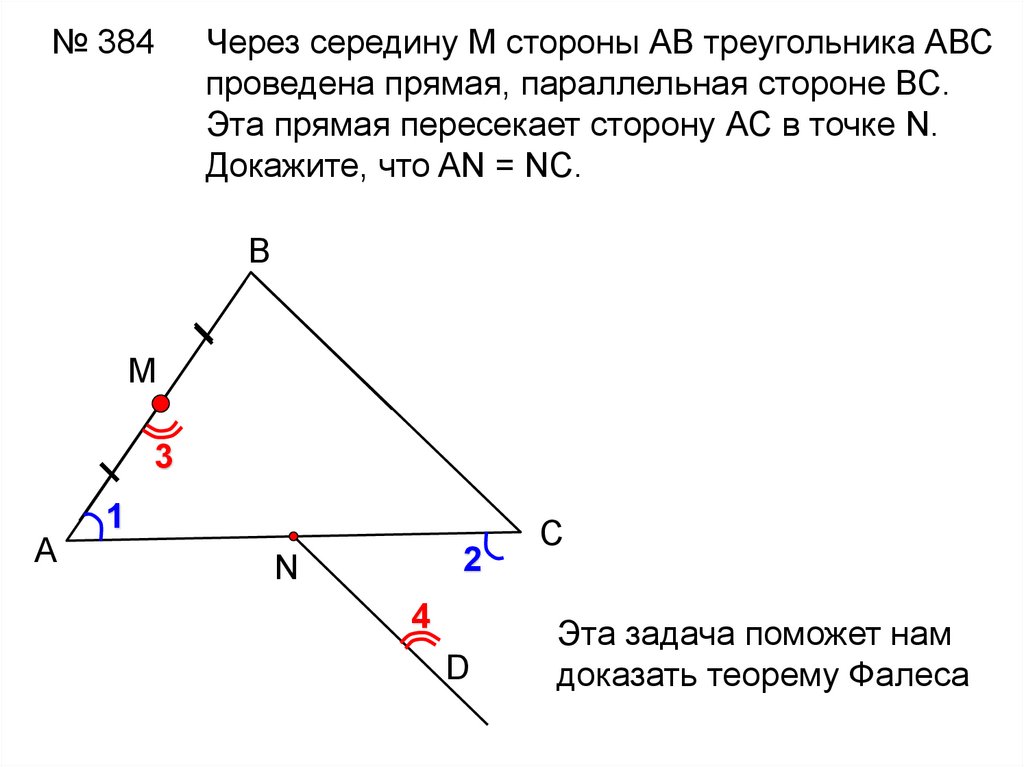
№ 384Через середину М стороны АВ треугольника АВС
проведена прямая, параллельная стороне ВС.
Эта прямая пересекает сторону АС в точке N.
Докажите, что AN = NC.
В
М
3
А
1
2
N
4
D
С
Эта задача поможет нам
доказать теорему Фалеса
3.
Фалес МилетскийДревнегреческий ученый
(ок. 625 – 547 гг. до н. э.)
Если на одной из двух прямых
отложить последовательно
несколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то они
отсекут на второй прямой равные между собой отрезки.
4.
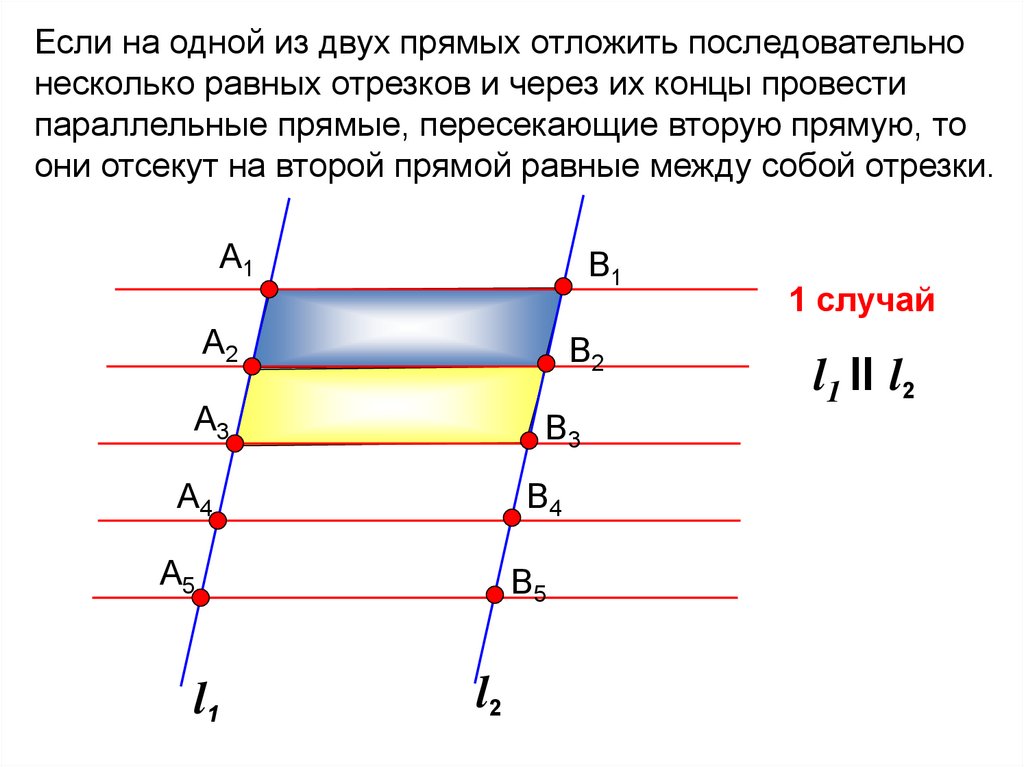
Если на одной из двух прямых отложить последовательнонесколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то
они отсекут на второй прямой равные между собой отрезки.
А1
В1
А2
В2
А3
В3
А4
В4
А5
В5
l1
l2
1 случай
l1 II l2
5.
А1В1
А2
В2
А3
В3
А4
В4
А5
В5
l1
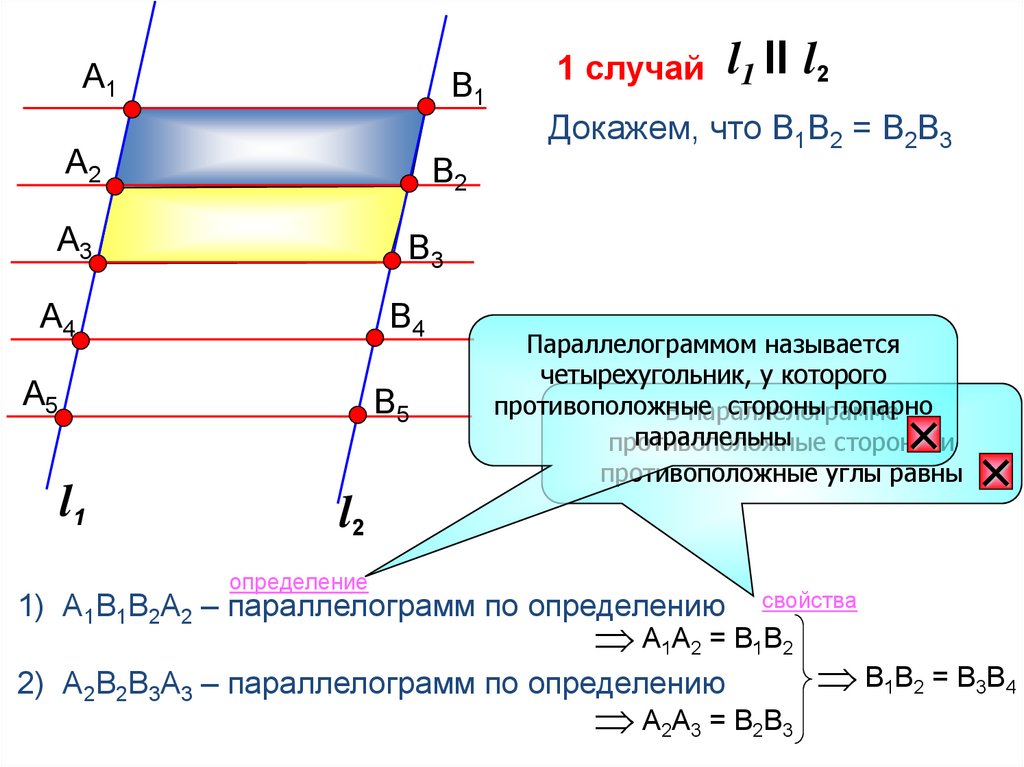
1 случай l1 II l2
Докажем, что В1В2 = В2В3
Параллелограммом называется
четырехугольник, у которого
противоположные
стороны попарно
В параллелограмме
параллельны
противоположные
стороны и
противоположные углы равны
l2
определение
1) А1В1В2А2 – параллелограмм по определению
свойства
А1А2 = В1В2
2) А2В2В3А3 – параллелограмм по определению
А2А3 = В2В3
В1В2 = В3В4
6.
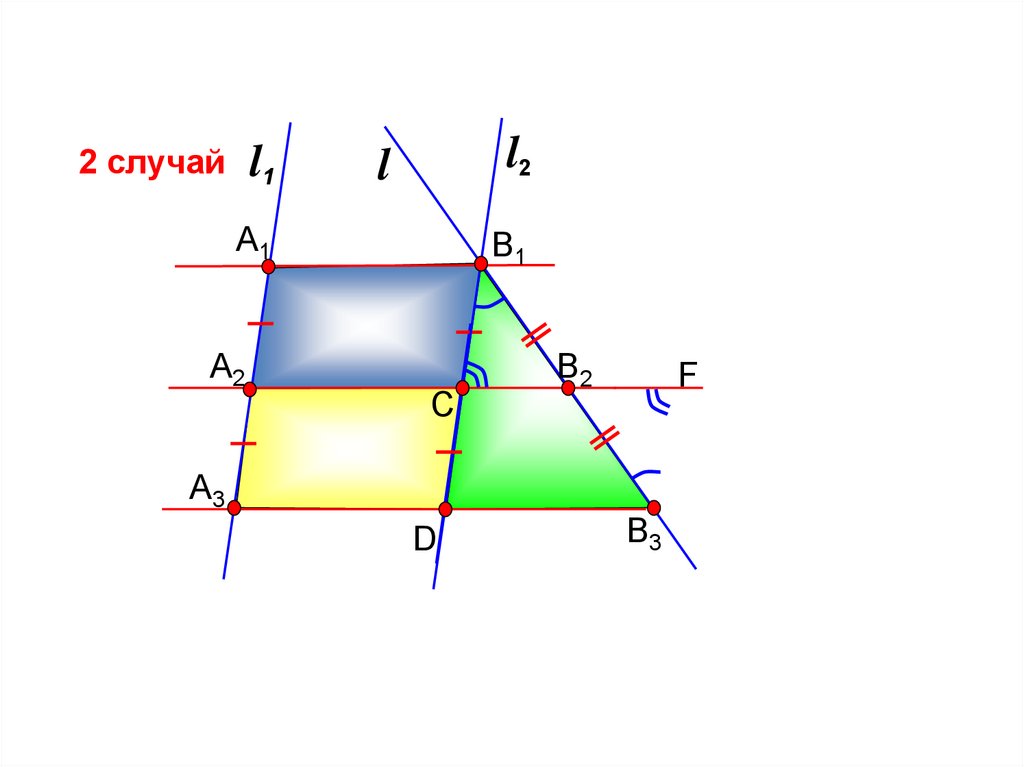
2 случай l1l2
l
А1
А2
В1
С
А3
D
В2
F
В3
7.
l1l
А1
А2
С
А3
D
l1 II l
l2
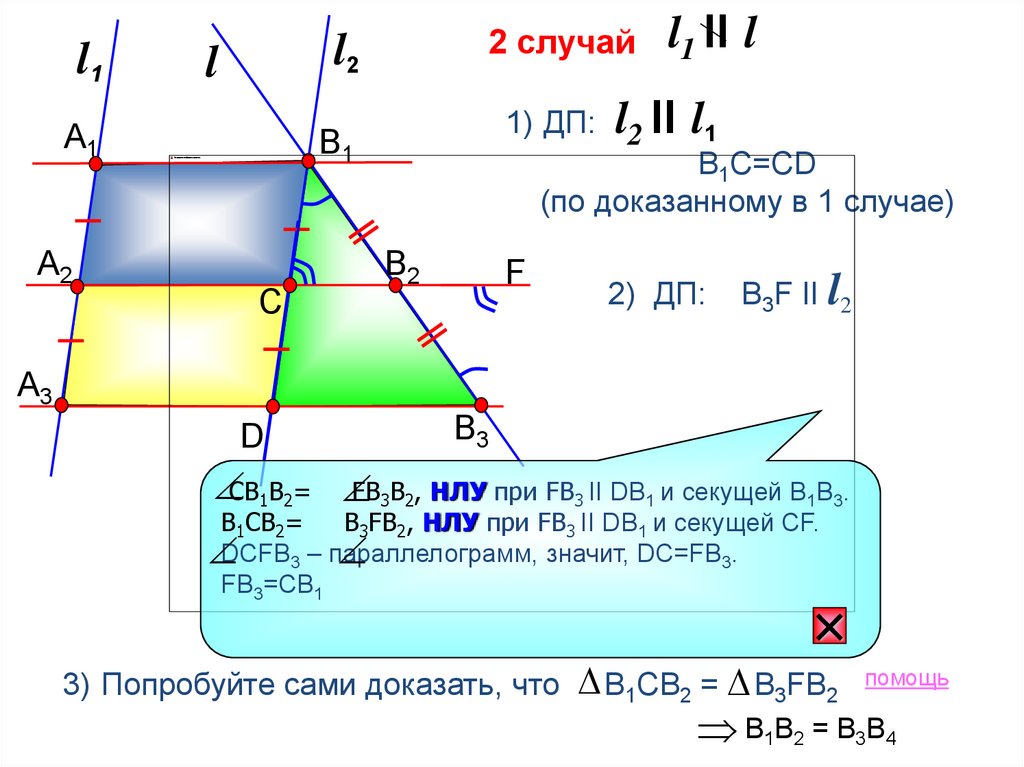
2 случай
В1
1) ДП: l2 II l1
B1C=CD
(по доказанному в 1 случае)
В2
F
2) ДП:
B3F II l2
В3
СВ1В2=
FB3B2, НЛУ при FB3 II DB1 и секущей В1В3.
В1СВ2=
B3FB2, НЛУ при FB3 II DB1 и секущей СF.
значит, DC=FB3.
DCFВ3 – параллелограмм,
FB3=CB1
3) Попробуйте сами доказать, что В1СВ2 = В3FB2
помощь
В1В2 = В3В4
8.
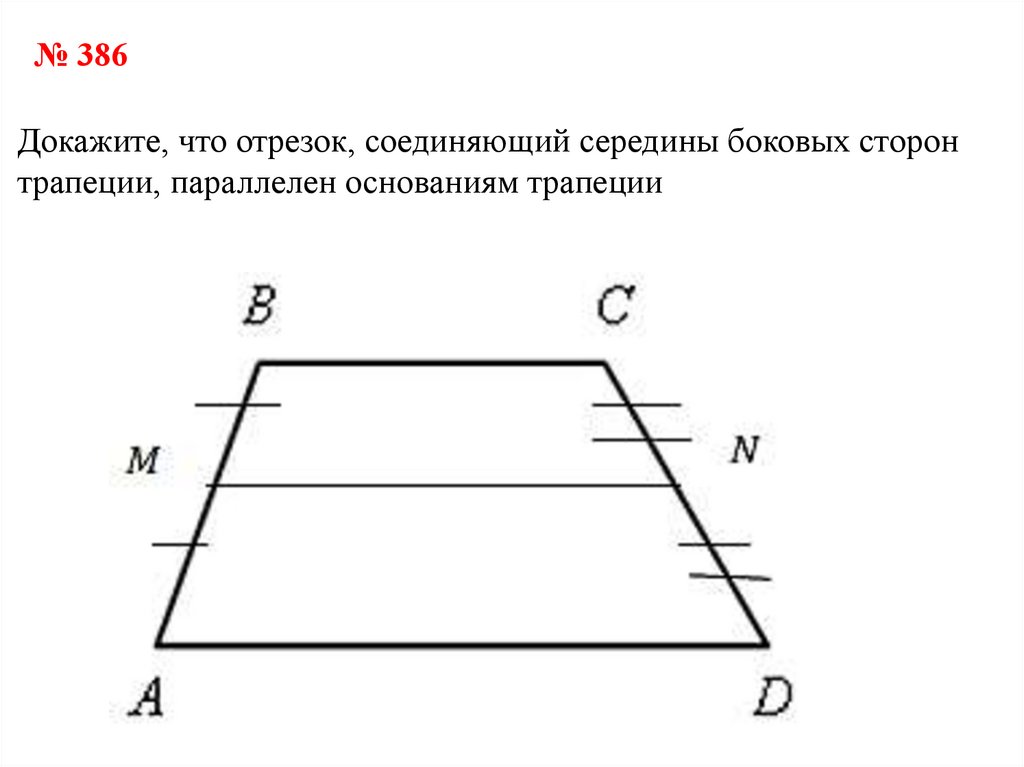
№ 386Докажите, что отрезок, соединяющий середины боковых сторон
трапеции, параллелен основаниям трапеции
9.
ЕМ
М1
М3
М2
М4
К
К1
К2
К3
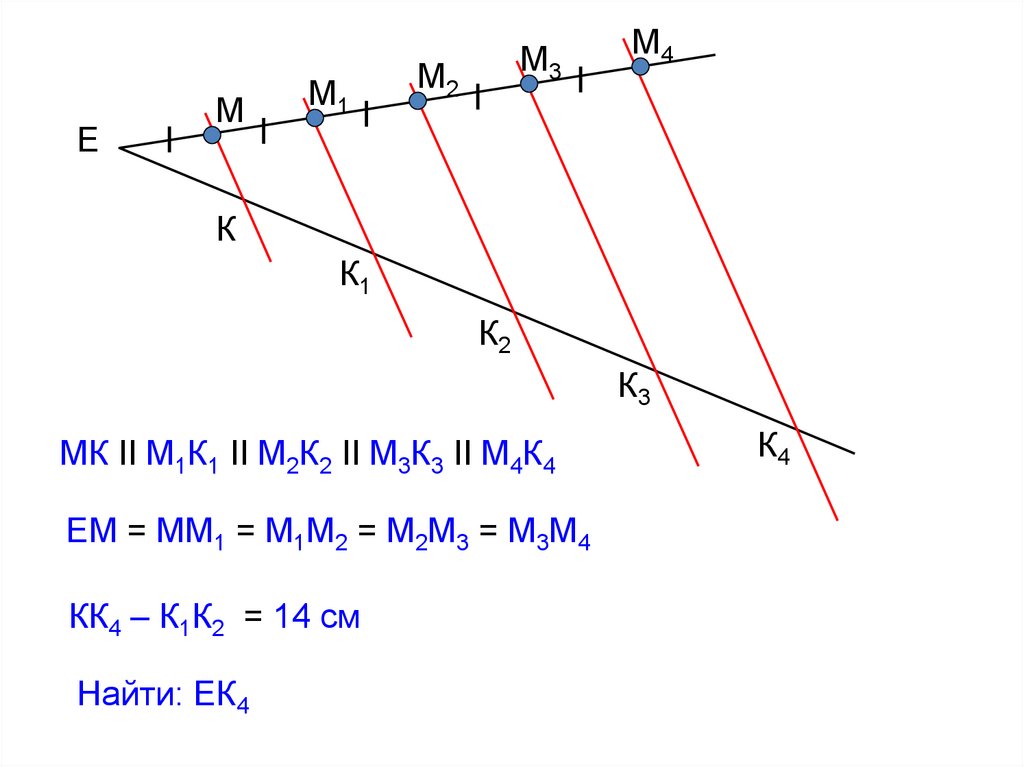
МК II М1К1 II М2К2 II М3К3 II М4К4
ЕМ = ММ1 = М1М2 = М2М3 = М3М4
КК4 – К1К2 = 14 см
Найти: ЕК4
К4
10.
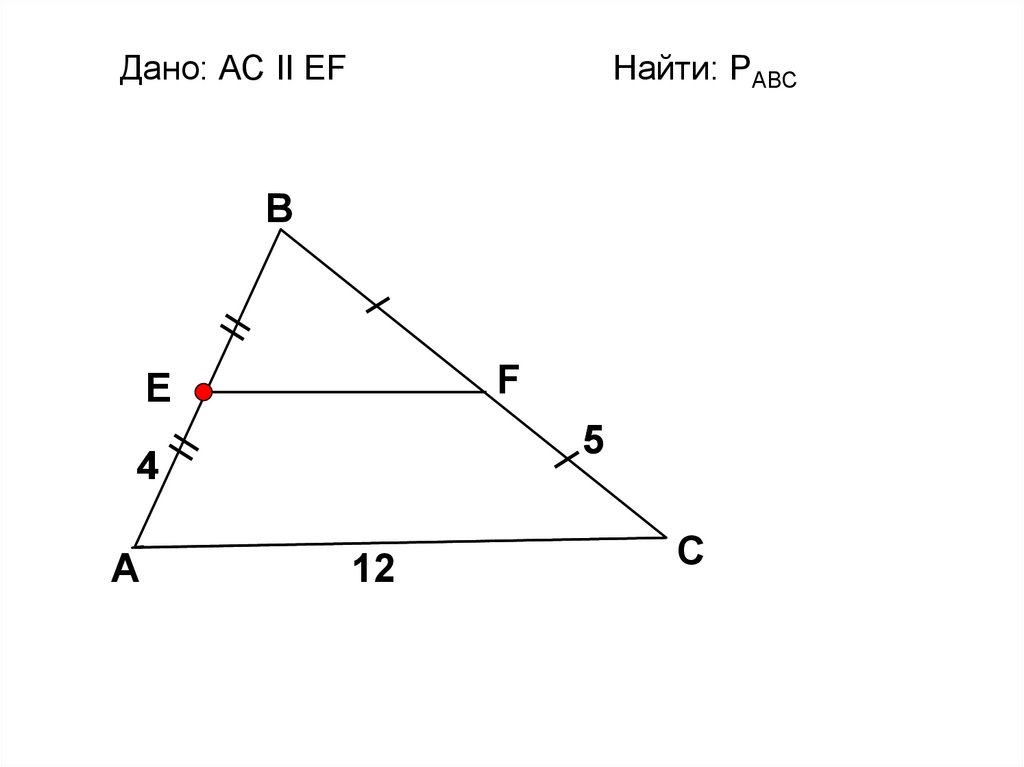
Дано: АС II EFНайти: PАВС
B
F
E
5
4
A
12
C
11.
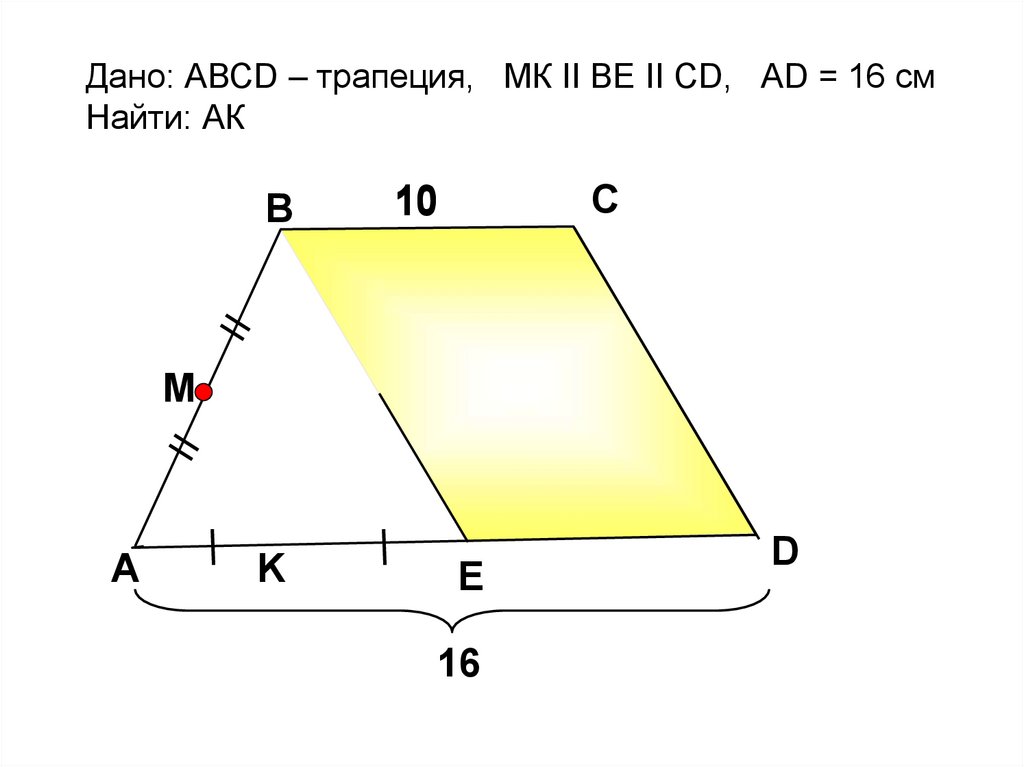
Дано: АВСD – трапеция, МК II ВE II СD, АD = 16 cмНайти: АК
B
10
C
M
A
K
E
16
D
12.
Дана трапеция MPOK с основаниями МK и ОР.1) Найти углы трапеции, если М = 72°, О = 105°.
2) Найти ОРK и РОМ, если ОМK = 38°, РKM
= 48°.
3) Углы МKN (N – точка пересечения диагоналей
трапеции), если ОРK = 72°, РОМ = 48°.



 mathematics
mathematics








