Similar presentations:
Определение истинности составного высказывания
1.
Определениеистинности
составного
высказывания
В математической логике, определение истинности составного
высказывания - это ключевой навык. Это позволяет нам анализировать
и понимать сложность логических выражений.
2.
Что такое составноевысказывание?
Составное высказывание - это предложение, которое объединяет
несколько простых высказываний с помощью логических операций.
Простые высказывания
Логические операции
Связывают простые
Эти высказывания могут быть
высказывания, образуя
истинными или ложными.
сложные.
3.
Основные логические операцииИспользуются для построения составных высказываний.
Конъюнкция (И)
Истинна, если оба высказывания истинны.
Дизъюнкция (ИЛИ)
Истинна, если хотя бы одно высказывание истинно.
Отрицание (НЕ)
Меняет истинность высказывания на противоположную.
4.
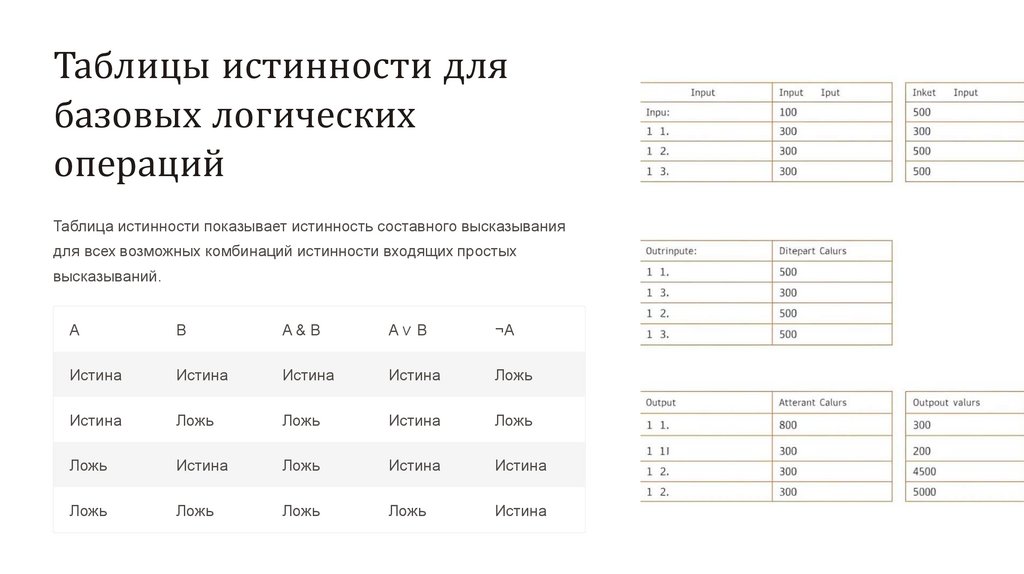
Таблицы истинности длябазовых логических
операций
Таблица истинности показывает истинность составного высказывания
для всех возможных комбинаций истинности входящих простых
высказываний.
A
B
A& B
A∨ B
¬A
Истина
Истина
Истина
Истина
Ложь
Истина
Ложь
Ложь
Истина
Ложь
Ложь
Истина
Ложь
Истина
Истина
Ложь
Ложь
Ложь
Ложь
Истина
5.
Правила определения истинности длясоставных высказываний
Используя таблицы истинности для базовых логических операций, можно определить истинность
сложных составных высказываний.
1
Шаг 1: Разбить высказывание на простые.
Идентиф ицировать простые высказывания и логические операции.
2
Шаг 2: Определить истинность простых высказываний.
Установить, истинны или ложны простые высказывания.
3
Шаг 3: Применить таблицы истинности.
Определить истинность каждой логической операции, следуя таблицам.
4
Шаг 4: Определить истинность всего составного высказывания.
Проследить последовательность операций до определения итоговой истинности.
6.
Примеры составныхвысказываний
Разберем несколько примеров, чтобы понять процесс определения истинности.
«Дождь идет, и светит солнце»
Это конъюнкция. Истинна только если оба высказывания истинны.
«Я люблю кошек или собак»
Это дизъюнкция. Истинна, если хотя бы одно высказывание истинно.
«Неправда, что сегодня понедельник»
Это отрицание. Истинна, если исходное высказывание ложно.
7.
Практика: определениеистинности составных
высказываний
Попробуйте сами определить истинность составных высказываний с
помощью таблиц истинности.
1
3
Пример 1:
2
Пример 2:
«Сегодня вторник, и я иду
«У меня есть машина, но я
на работу».
не умею водить».
Пример 3:
«Неверно, что я не люблю шоколад».
8.
Разбор сложных случаевИногда составные высказывания могут быть очень сложными, с множеством вложенных логических операций.
Скобки
Иерархия операций
Логические эквивалентности
Скобки определяют порядок
Некоторые операции имеют
вычисления логических операций.
приоритет над другими (например,
Используя законы логики, можно
отрицание).
упростить сложные выражения.
9.
Вывод: принципыопределения истинности
Определение истинности составных высказываний требует
систематического подхода и знания логических законов.
Понимание базовых
операций
Применение таблиц
истинности
Конъюнкция, дизъюнкция,
Для определения истинности
отрицание.
составных высказываний.
Разбор сложных случаев
Использование скобок, иерархии операций.







 informatics
informatics








