5-тәжірибелік сабақ ИГ1 5кр

1.

5-тәжірибелік сабақ
Қисықтар мен беттер

2.

Қисық- нүктелердің бірпараметрлік жиыны. Сызба геометрияда қисық сызық
кеңістікте үздіксіз қозғалатын нүктенің траекториясы ретінде қарастырылады.
Қисықтарды жазықтық және кеңістік қисықтары деп екі топқа бөледі.
Барлық нүктелері бір жазықтықта жататын қисықтарды жазықтық қисықтары
(эллипс, парабола, гипербола және т.б.) деп атайды. Барлық нүктелері бір
жазықтықта жатпайтын қисықтарды кеңістік (цилиндрлік, конустық бұрама
сызықтар және т.б.) қисықтары деп атайды.
Сызбада қисықтың жазық немесе
кеңістік екенін қалай анықтауға
болады?
Жазық қисықтың кез-келген
екі хордасы қиылысатын
түзулер болады, ал кеңістік
қисығында олар айқас
болады.
Суреттегі мысалда қисық
кеңістік болып табылады.
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]
21
m1
31
11
41
x12
12
42
22
m2
32

3.

•Қисық аналитикалық жолмен, яғни алгебралық (эллипс, парабола,
гипербола және т.б.) немесе трансценденттік (синусоида және т.б.)
теңдеумен берілуі мүмкін. Кейбір сызықтар тек қана графикалық жолмен
беріледі, мысалы, топографиялық картадағы горизонтальдар.
•Алгебралық қисықтың теңдеуінің дәрежесі қисықтың ретін анықтайды.
Алгебралық қисықтың ретi оның түзумен (кеңiстiк қисығы үшiн жазықтықпен)
қиылысу нүктелерiнiң санымен анықталады.
2
1
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]

4.

Қисықтың қасиеттері
•1) егер нүкте қисық сызықта жатса, онда оның проекциялары да қисық сызықтың
аттас проекцияларына тиісті болады;
•2) қисық сызықтың жанамасы осы қисық сызықтың проекциясының жанамасына
проекцияланады (егер проекциялау бағыты мен жанама параллель болмаса).
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]

5.

2-ші реттік қисық сызықтар
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]

6.

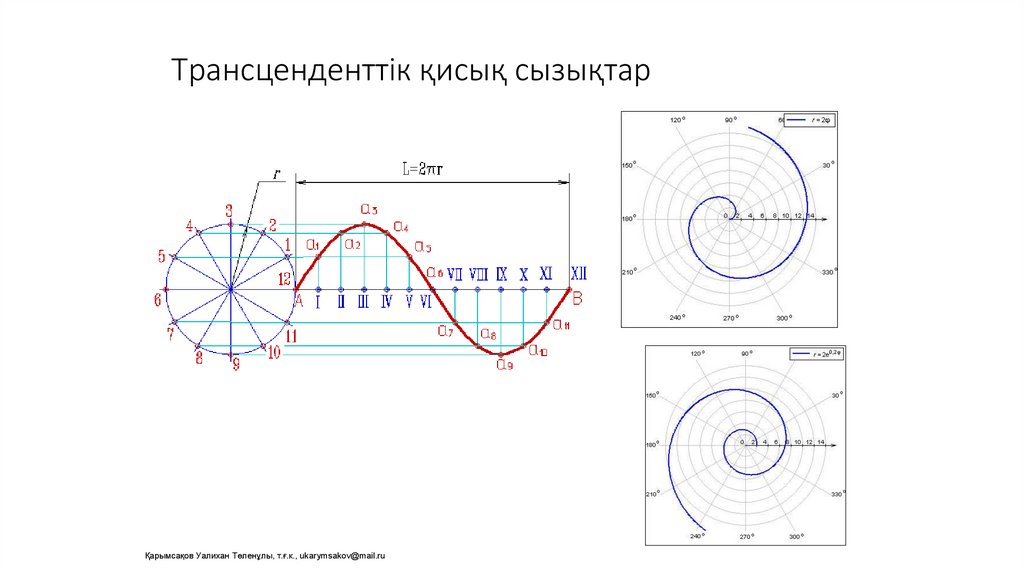
Трансценденттік қисық сызықтар
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]

7.

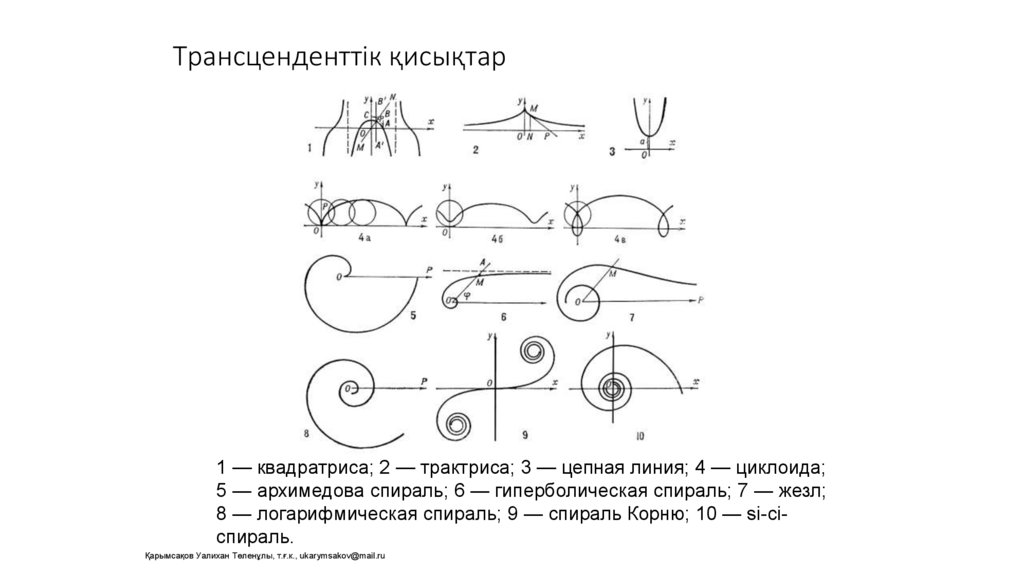
Трансценденттік қисықтар
1 — квадратриса; 2 — трактриса; 3 — цепная линия; 4 — циклоида;
5 — архимедова спираль; 6 — гиперболическая спираль; 7 — жезл;
8 — логарифмическая спираль; 9 — спираль Корню; 10 — si-cicпираль.
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]

8.

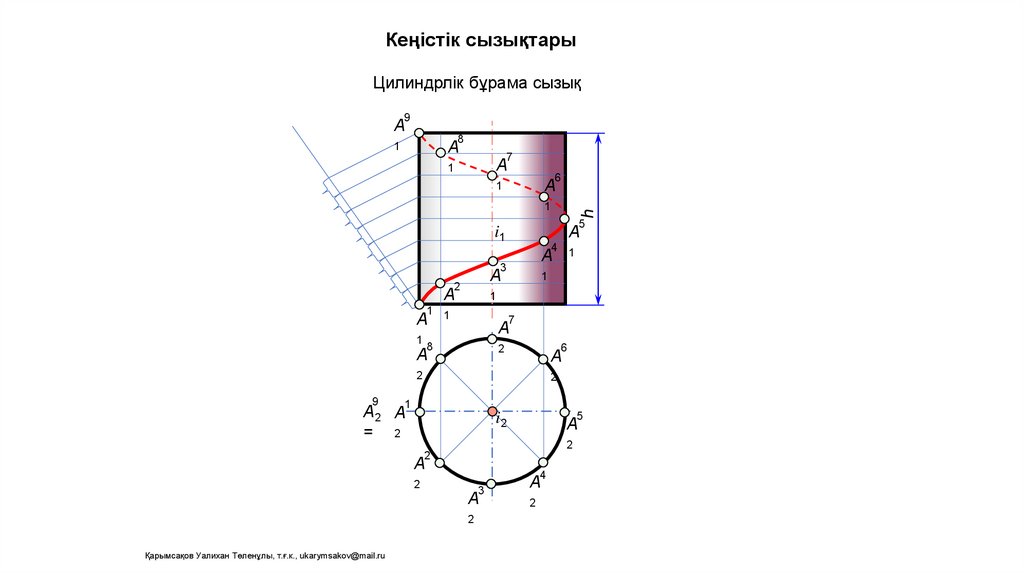
Кеңістік сызықтары
Цилиндрлік бұрама сызық
9
A
8
A
1
7
A
1
6
A
1
5
A
i1
4 1
A
3
A
2
A
1
1
1
A 1
1
7
A
8
6
2
A
A
2
9
2
1
A2 A
= 2
5
i2
A
2
2
A
4
2
3
A
2
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]
h
1
A
2

9.

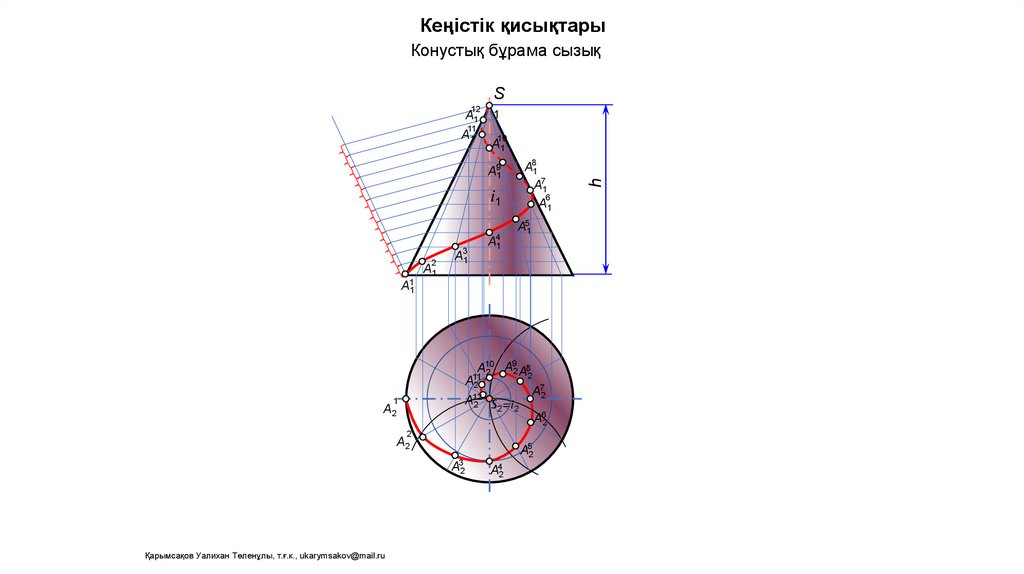
Кеңістік қисықтары
Конустық бұрама сызық
S
1
10
A1
A91
i1
2
A1
A31
A41
A81
A71
6
A1
A51
A11
A92 A8
A10
2
2
A11
2
A72
A12
2
S2=i2
A62
1
A2
2
A2
A52
A32
Қарымсақов Уалихан Төленұлы, т.ғ.к., [email protected]
A42
h
12
A1
11
A1

10.

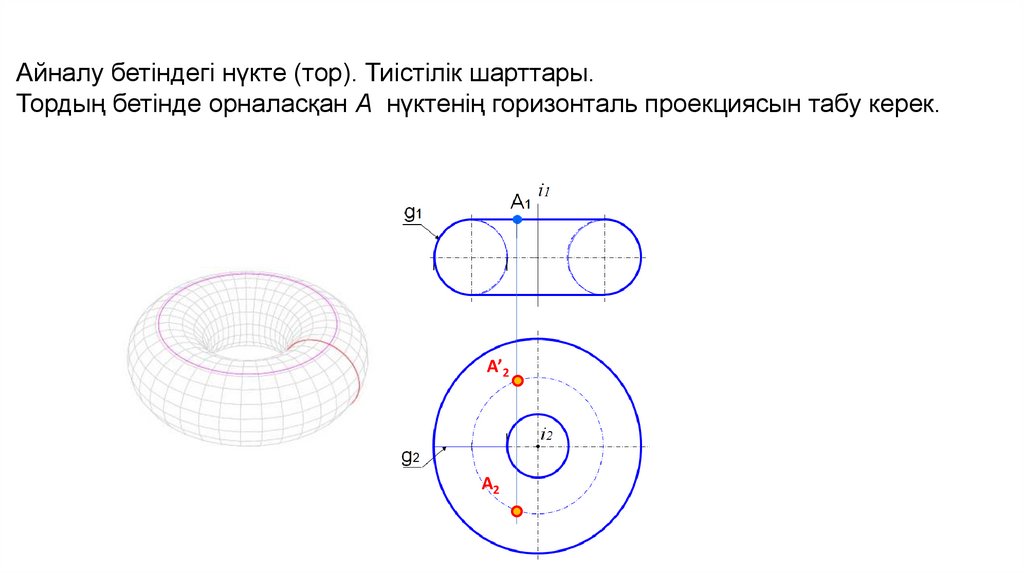
Айналу бетіндегі нүкте (тор). Тиістілік шарттары.
Тордың бетінде орналасқан А нүктенің горизонталь проекциясын табу керек.
А’2
А2

11.

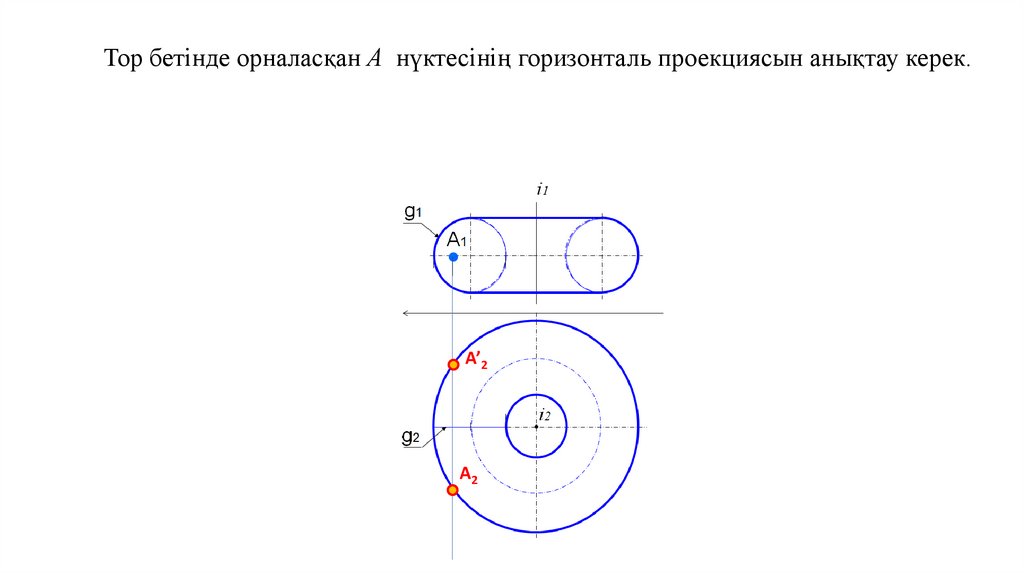
Тор бетінде орналасқан А нүктесінің горизонталь проекциясын анықтау керек.
А’2
А2

12.

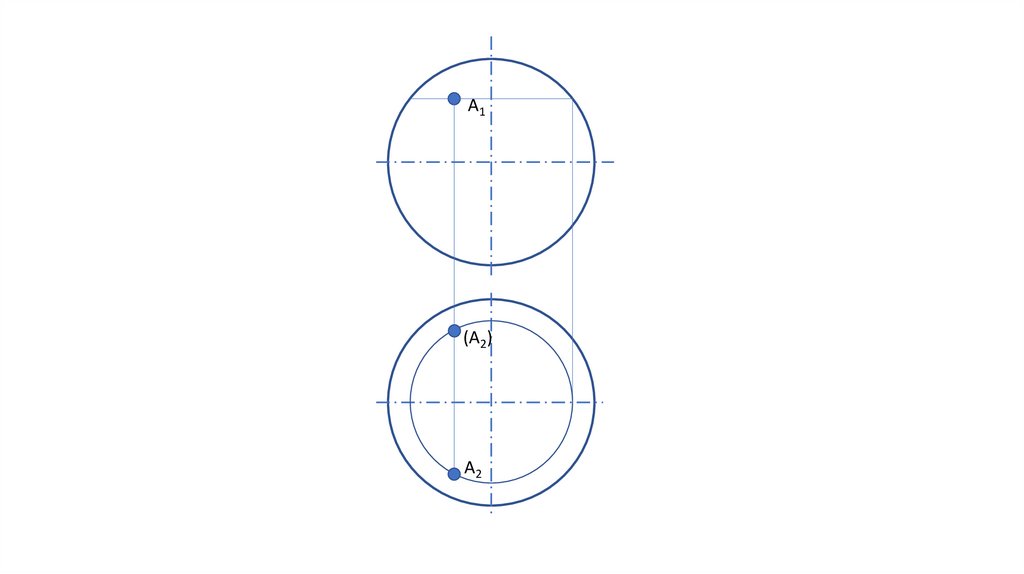
А1
(А2)
А2

13.

(О,С) сферасының фронталь және профиль проекциясын
салу керек. Мұндағы О – сфера центрі, С – сфера бетіндегі
нүкте.
О1
С0
О3
С1
С3
A1
Δ

14.

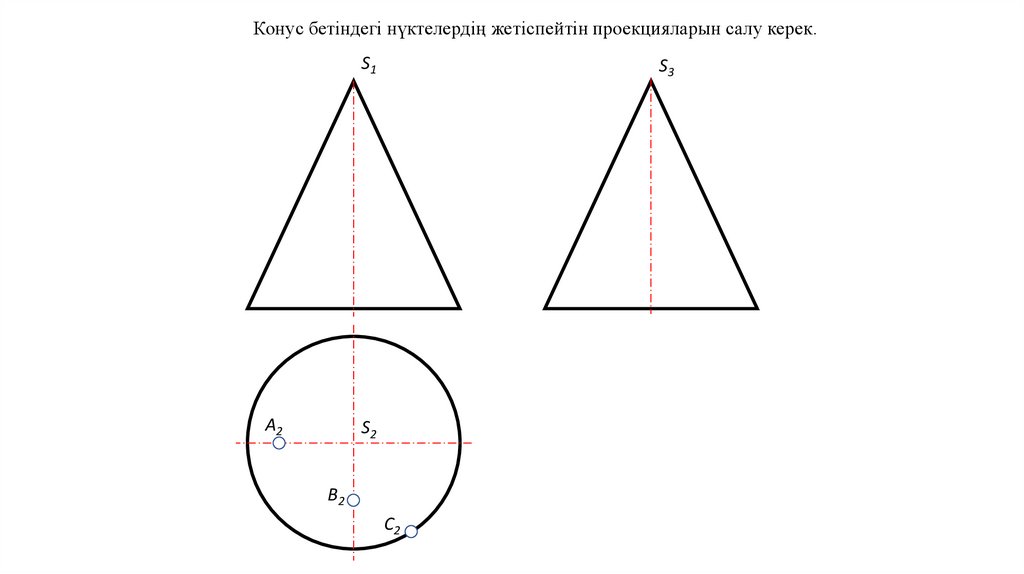
Конус бетіндегі нүктелердің жетіспейтін проекцияларын салу керек.
S1
S3
A1
B1
C1
11
21
(C2)
(22)
(B2)
S2
12
A2
B2
C2
22

15.

Конус бетіндегі нүктелердің жетіспейтін проекцияларын салу керек.
S1
A2
S3
S2
B2
C2