10_Построение сечений

1.

Построить сечение многогранника
плоскостью – это значит указать точки
пересечения секущей плоскости с
ребрами многогранника и соединить эти
точки отрезками, принадлежащими
граням многогранника.
Для построения сечения многогранника
плоскостью нужно в плоскости каждой
грани указать 2 точки, принадлежащие
сечению, соединить их прямой и найти
точки пересечения этой прямой с
ребрами многогранника.

2.

Урок-презентация.

3.

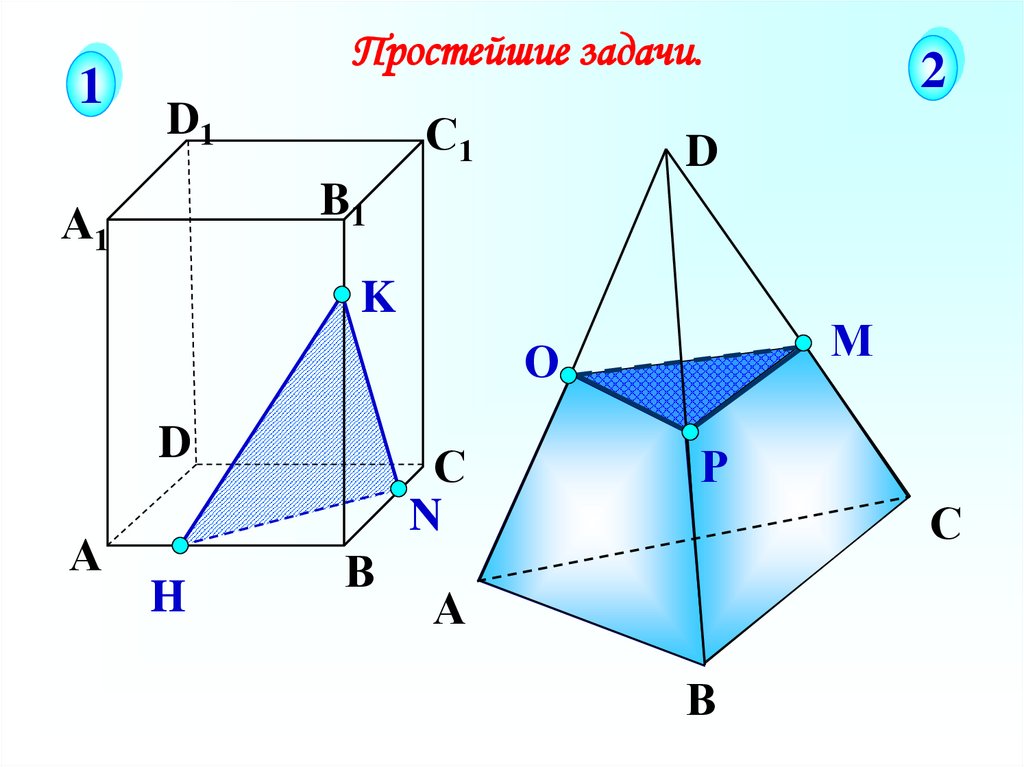
1
Простейшие задачи.
D1
С1
D
B1
А1
K
М
О
D
А
2
H
С
N
В
Р
С
А
В

4.

D
3
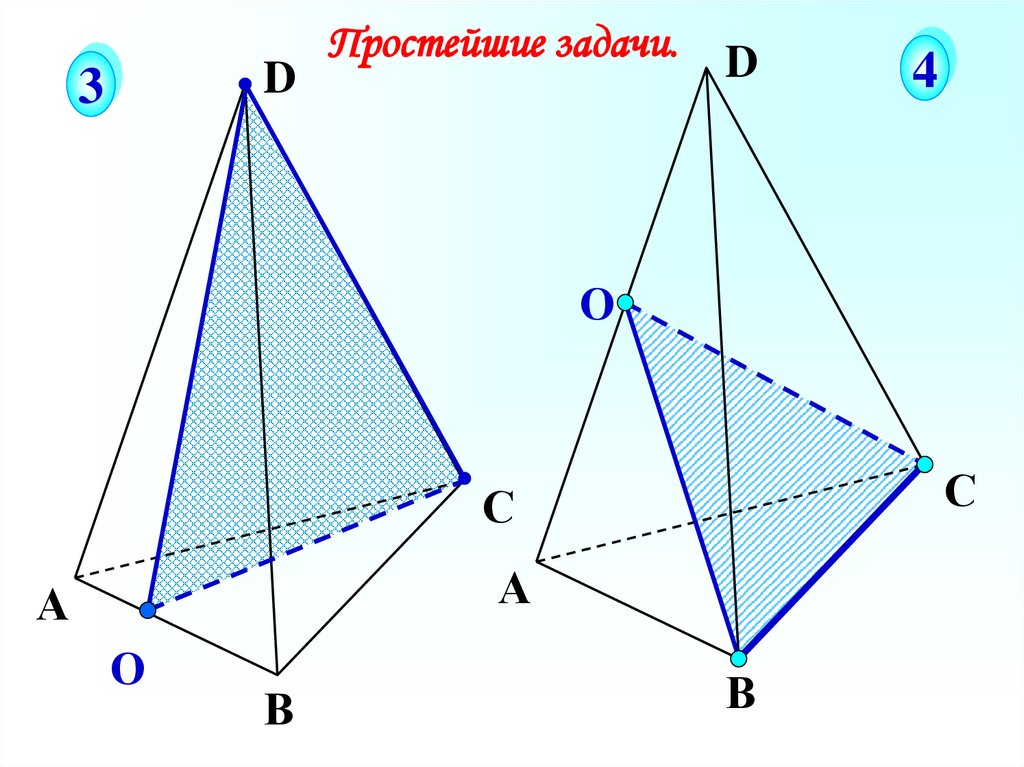
Простейшие задачи.
D
4
О
С
С
А
А
О
В
В

5.

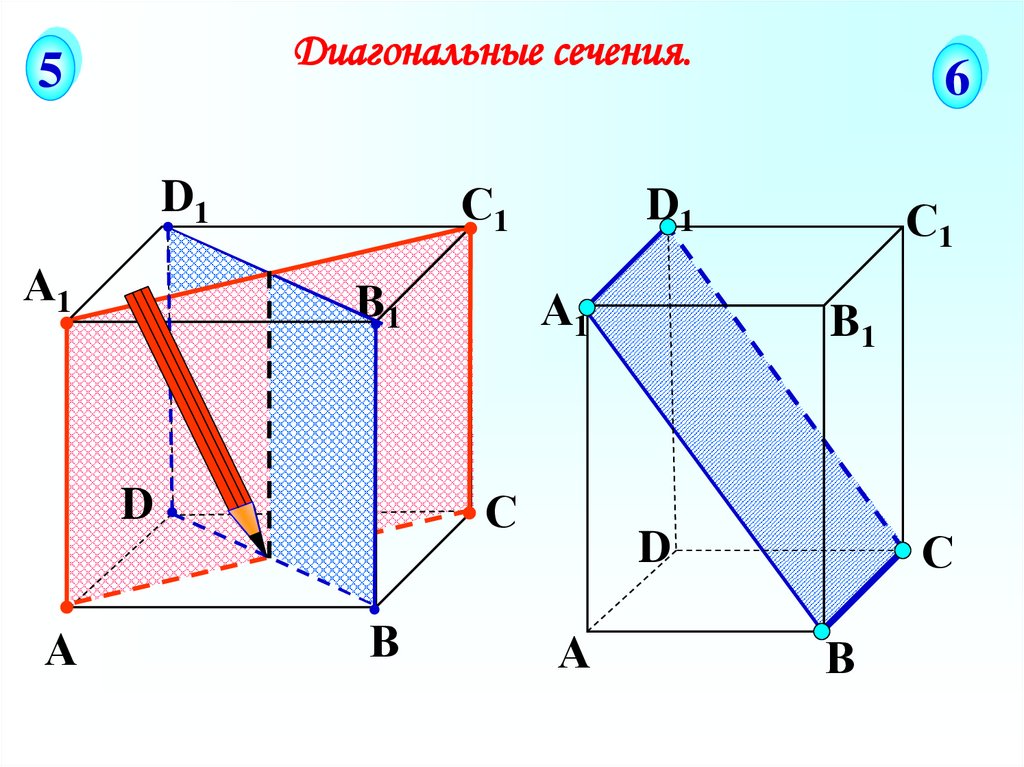
Диагональные сечения.
5
С1
D1
А1
С
D
А
D1
А1
B1
В
6
С1
B1
С
D
А
В

6.

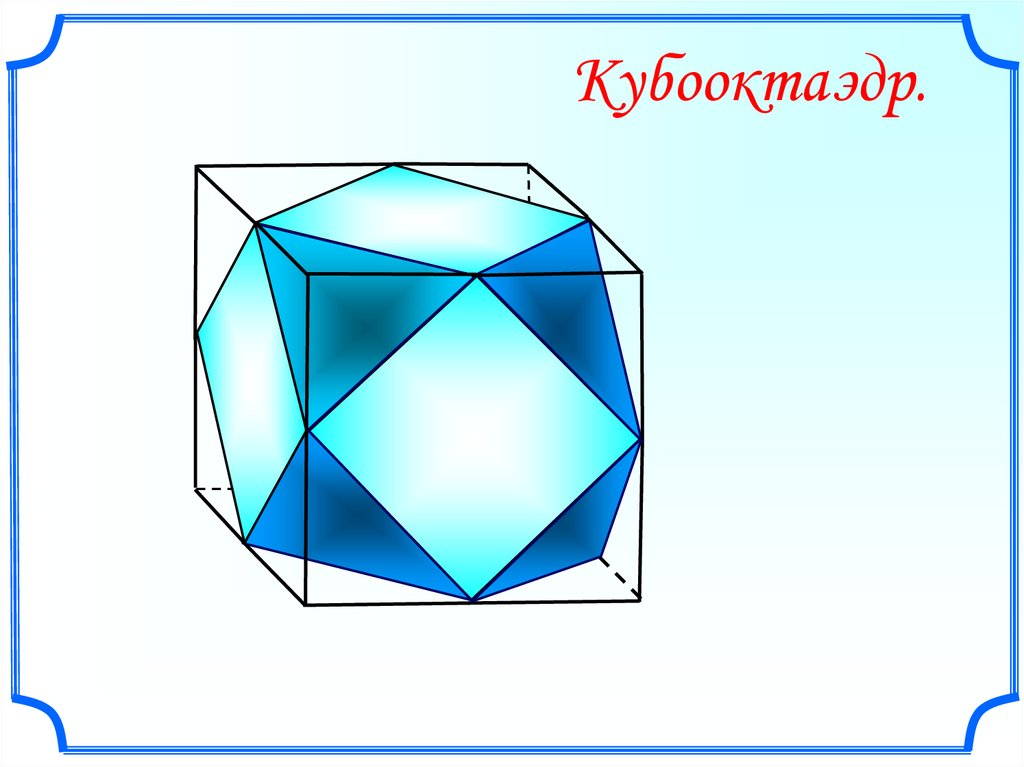
Кубооктаэдр.

7.

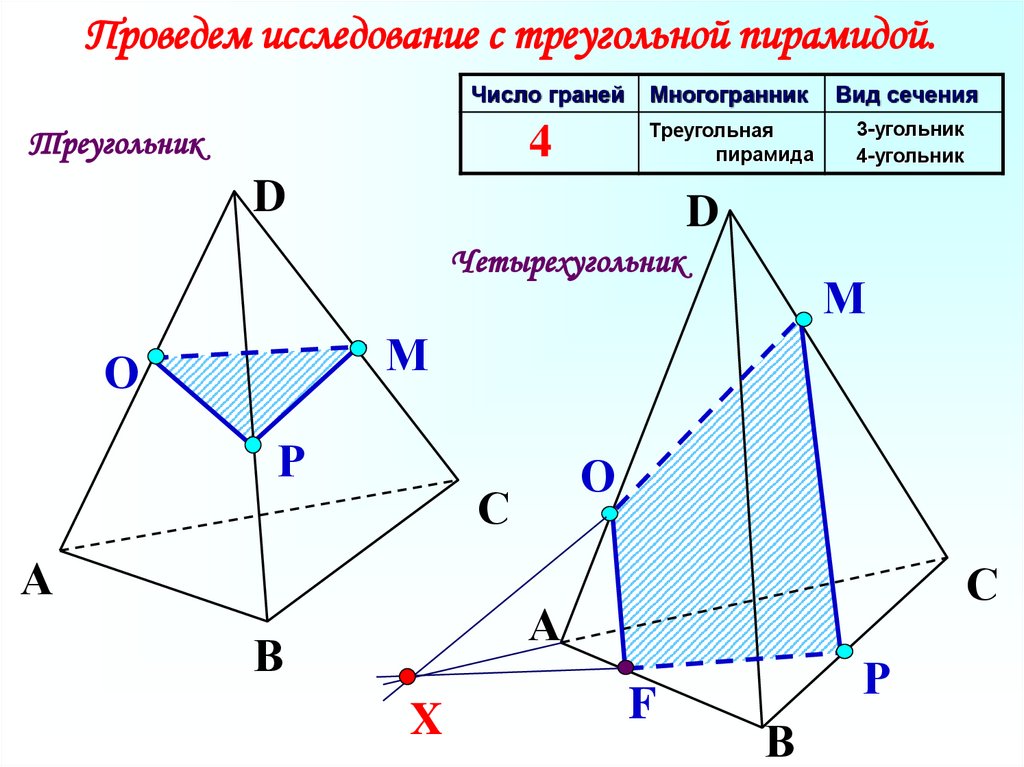
Проведем исследование с треугольной пирамидой.
Число граней
Многогранник
Вид сечения
4
Треугольная
пирамида
3-угольник
4-угольник
Треугольник
D
D
Четырехугольник
М
М
О
Р
О
С
А
С
А
В
X
F
Р
В

8.

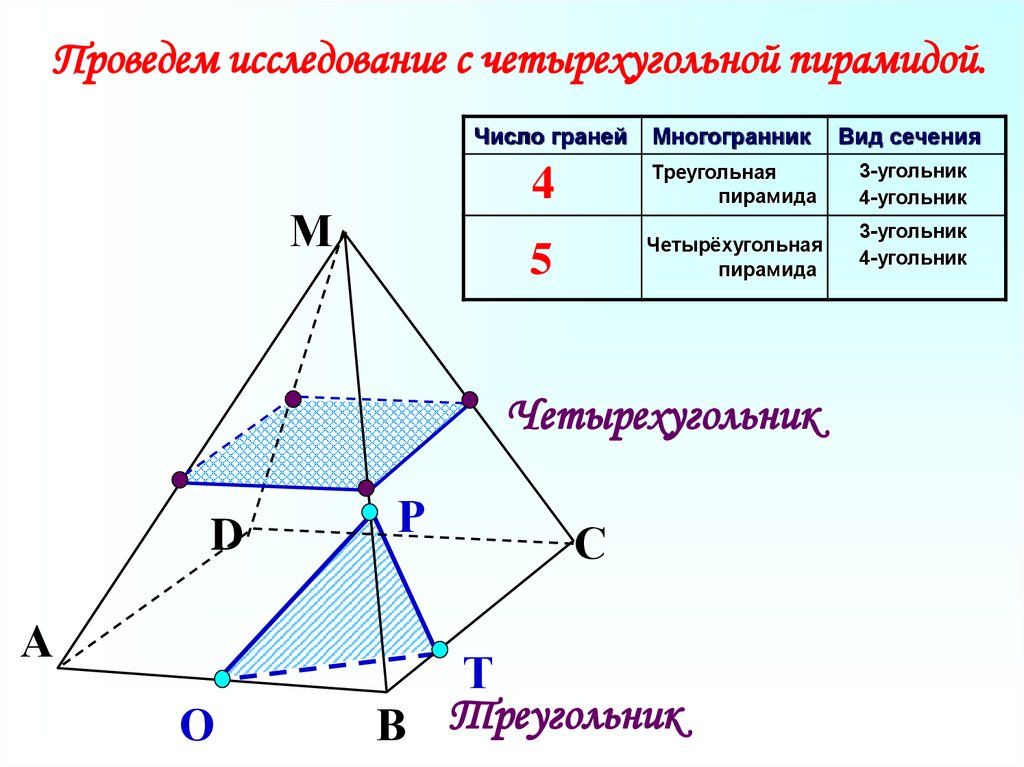
Проведем исследование с четырехугольной пирамидой.
М
Число граней
Многогранник
Вид сечения
4
Треугольная
пирамида
3-угольник
4-угольник
5
Четырёхугольная
пирамида
Четырехугольник
D
Р
О
Т
В Треугольник
А
С
3-угольник
4-угольник

9.

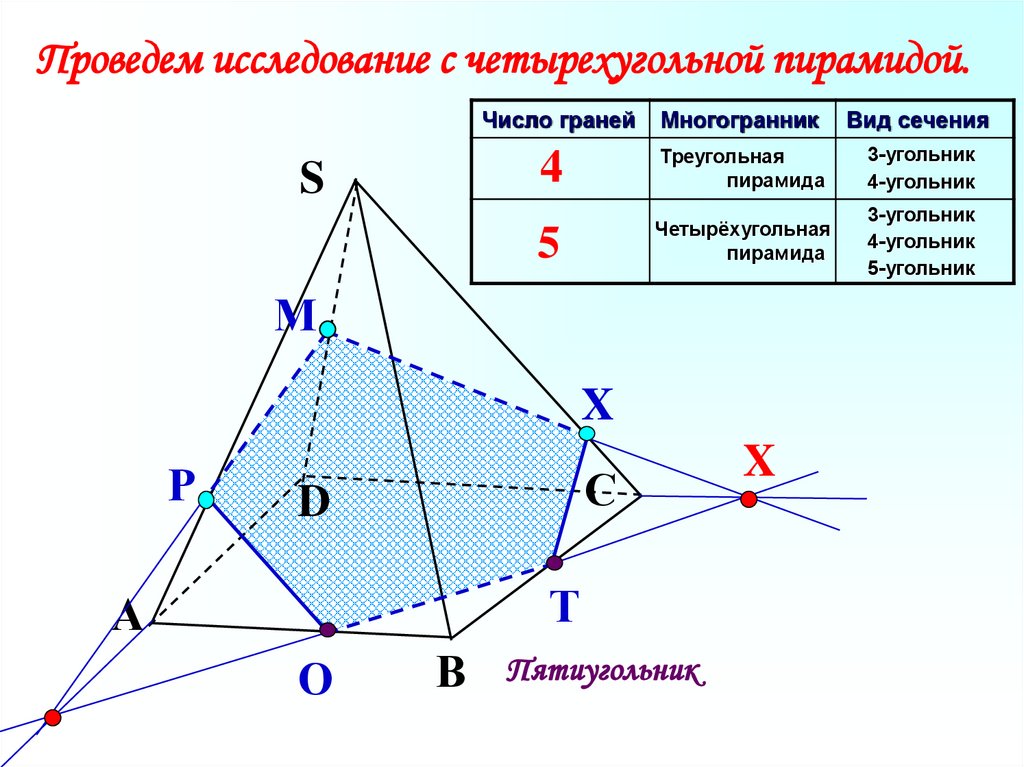
Проведем исследование с четырехугольной пирамидой.
S
Число граней
Многогранник
Вид сечения
4
Треугольная
пирамида
3-угольник
4-угольник
5
Четырёхугольная
пирамида
3-угольник
4-угольник
5-угольник
М
X
Р
С
D
Т
А
О
В
Пятиугольник
X

10.

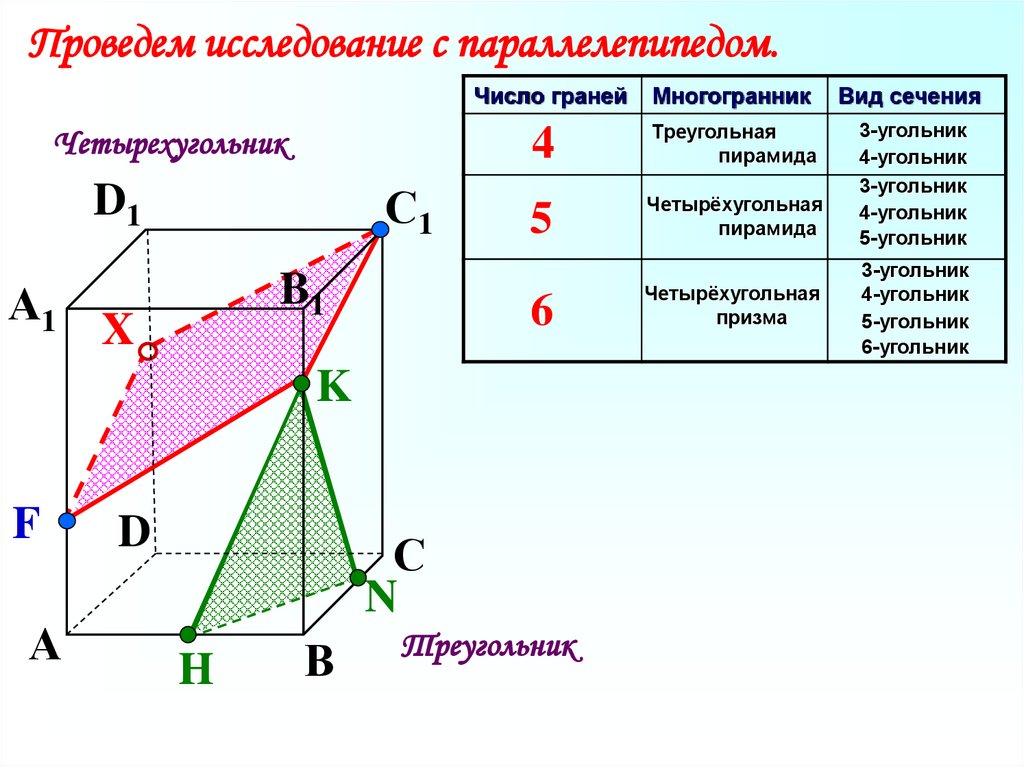
Проведем исследование с параллелепипедом.
Четырехугольник
С1
D1
А1
B1
X
Число граней
Многогранник
Вид сечения
4
Треугольная
пирамида
5
Четырёхугольная
пирамида
3-угольник
4-угольник
3-угольник
4-угольник
5-угольник
6
K
F
А
D
С
N
H
В
Треугольник
Четырёхугольная
призма
3-угольник
4-угольник
5-угольник
6-угольник

11.

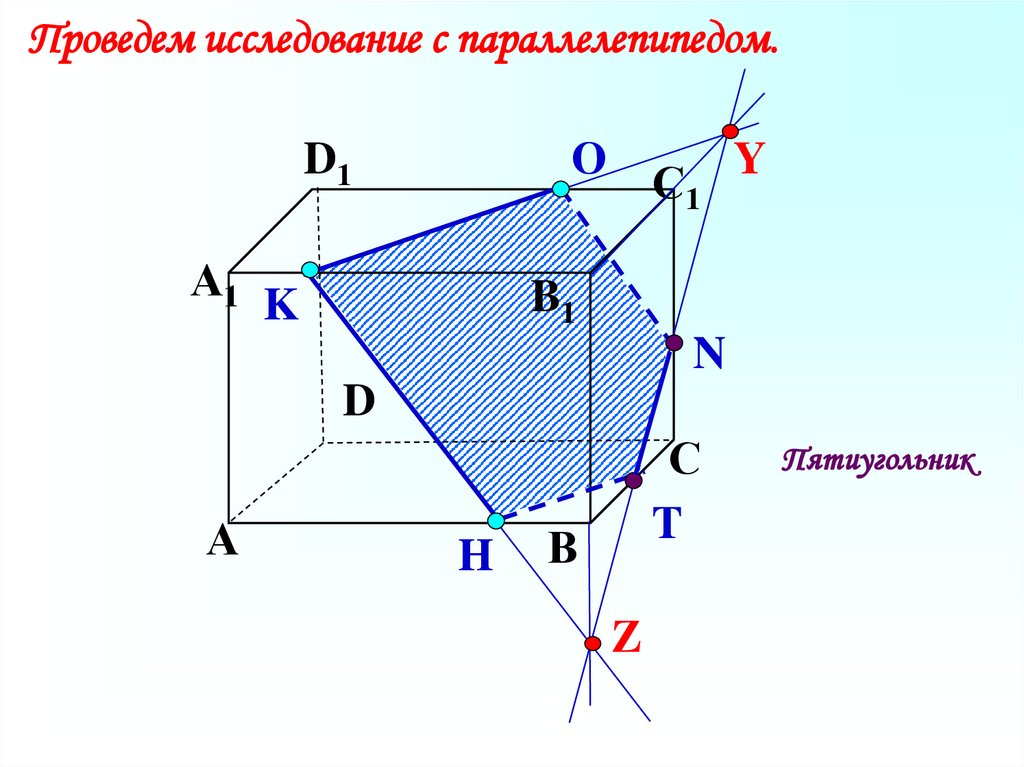
Проведем исследование с параллелепипедом.
О
D1
А1
С1
Y
B1
K
N
D
А
H
С
T
В
Z
Пятиугольник

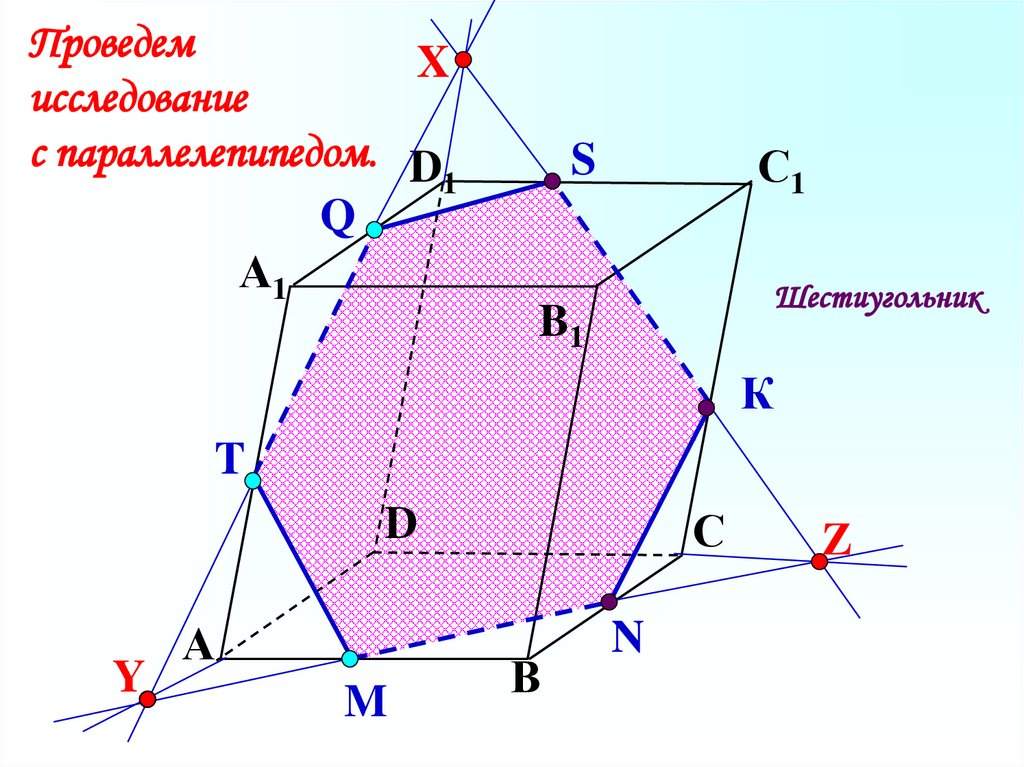
12.

Проведем
X
исследование
с параллелепипедом. D
1
Q
А1
С1
S
Шестиугольник
B1
К
T
С
D
Y
А
M
В
N
Z

13.

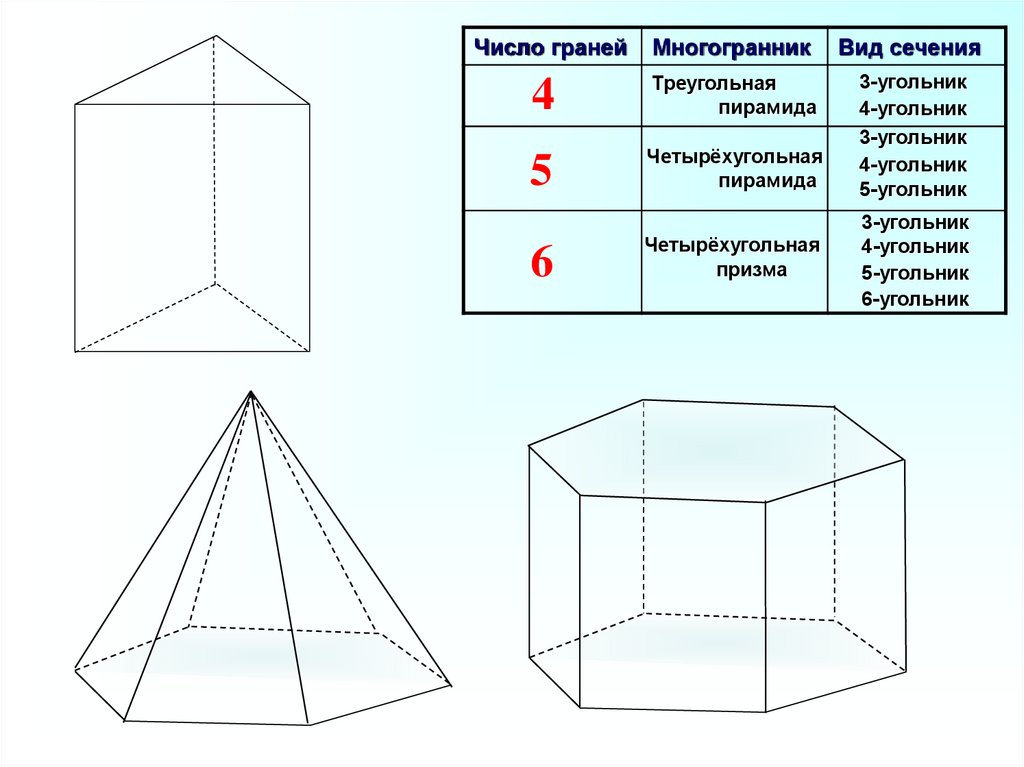
Число граней
Многогранник
Вид сечения
4
Треугольная
пирамида
5
Четырёхугольная
пирамида
3-угольник
4-угольник
3-угольник
4-угольник
5-угольник
6
Четырёхугольная
призма
3-угольник
4-угольник
5-угольник
6-угольник

14.

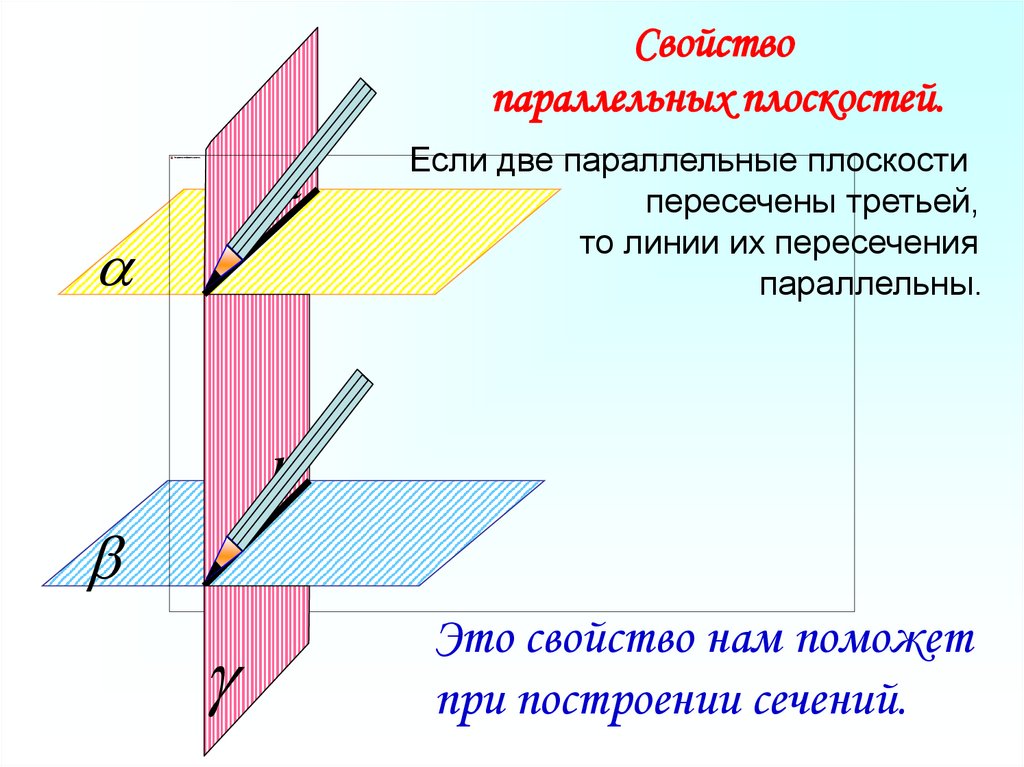
Свойство
параллельных плоскостей.
а
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
b
Это свойство нам поможет
при построении сечений.

15.

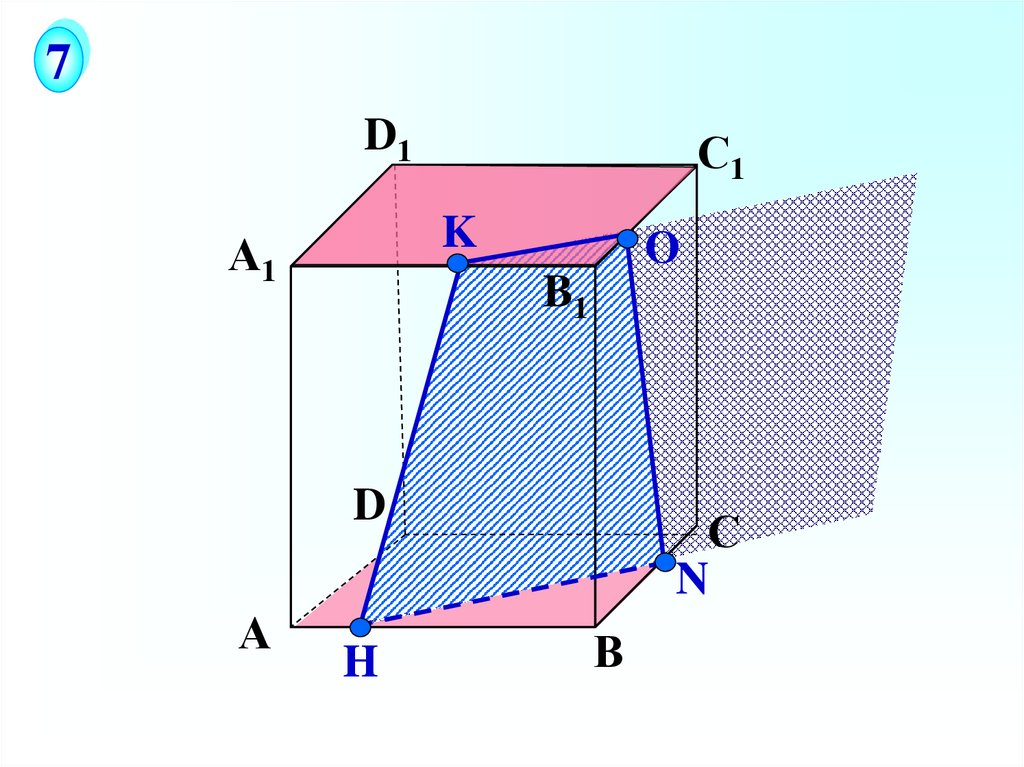
7
D1
С1
K
А1
О
B1
D
А
H
С
N
В

16.

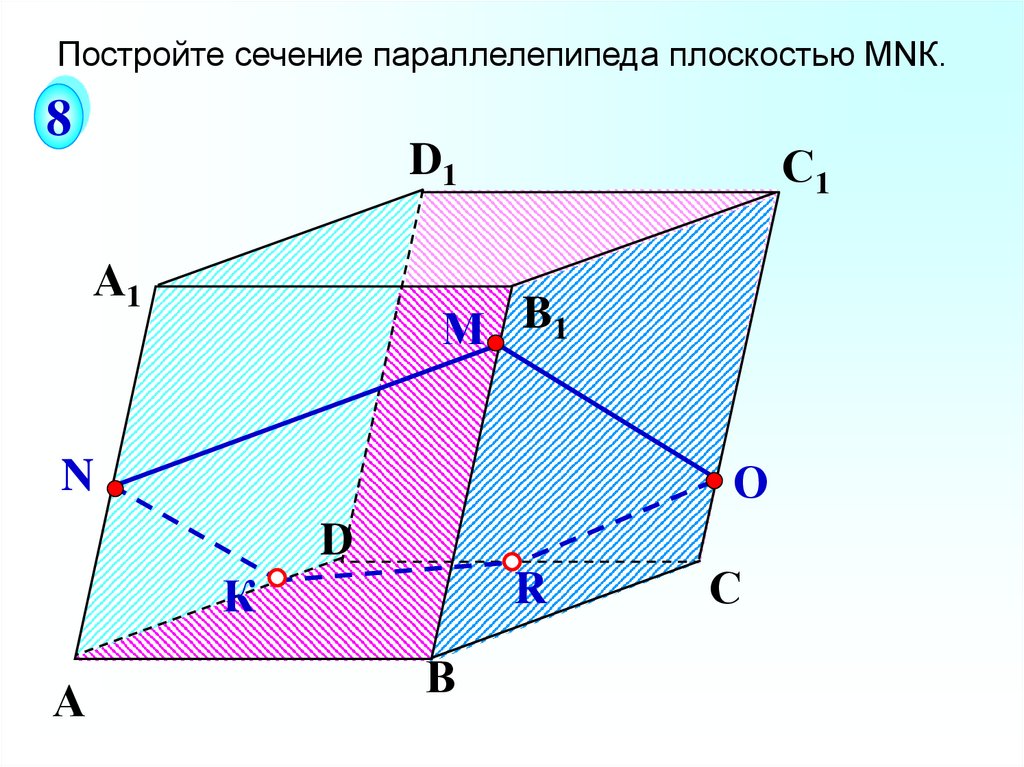
Постройте сечение параллелепипеда плоскостью МNК.
8
С1
D1
А1
М B1
О
N
D
К
А
R
В
С

17.

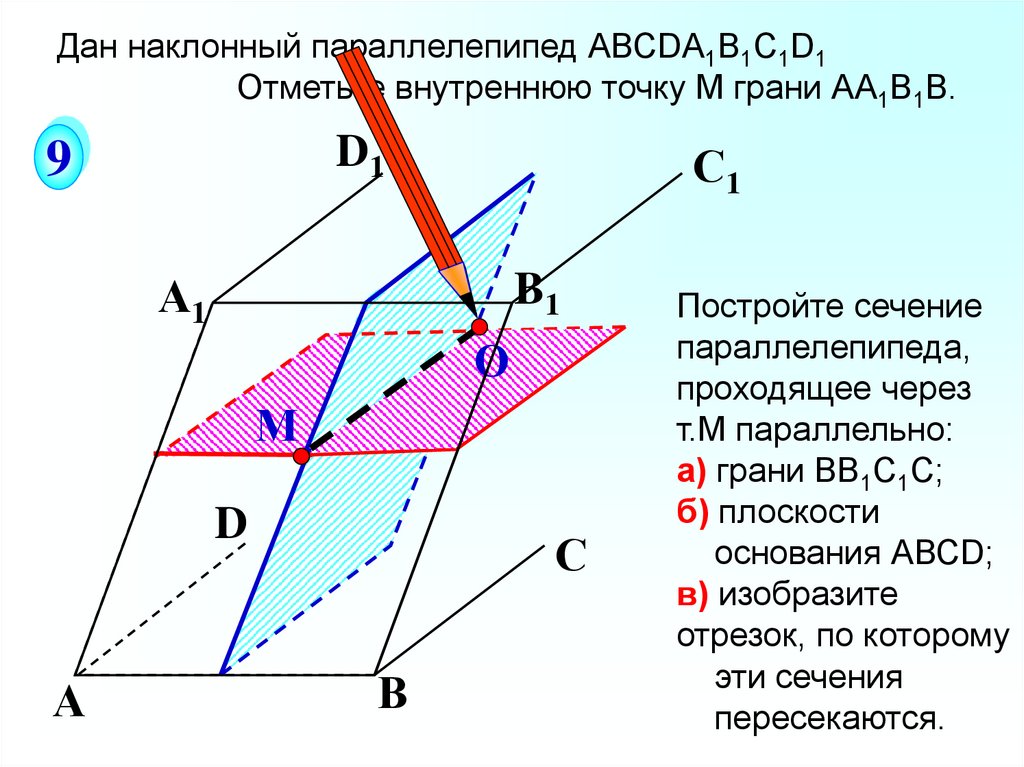
Дан наклонный параллелепипед АВСDА1В1С1D1
Отметьте внутреннюю точку M грани АА1В1В.
D1
9
С1
А1
B1
О
М
D
А
С
В
Постройте сечение
параллелепипеда,
проходящее через
т.М параллельно:
а) грани ВВ1С1С;
б) плоскости
основания АВСD;
в) изобразите
отрезок, по которому
эти сечения
пересекаются.

18.

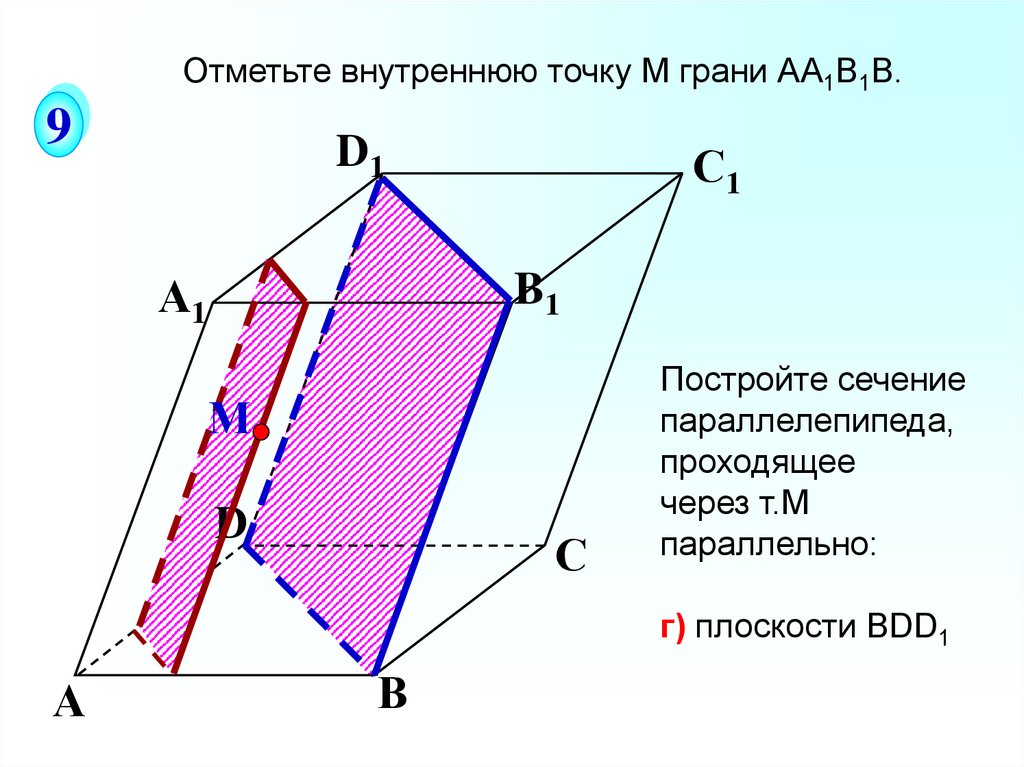
Отметьте внутреннюю точку M грани АА1В1В.
9
D1
А1
С1
B1
М
D
С
Постройте сечение
параллелепипеда,
проходящее
через т.М
параллельно:
г) плоскости ВDD1
А
В

19.

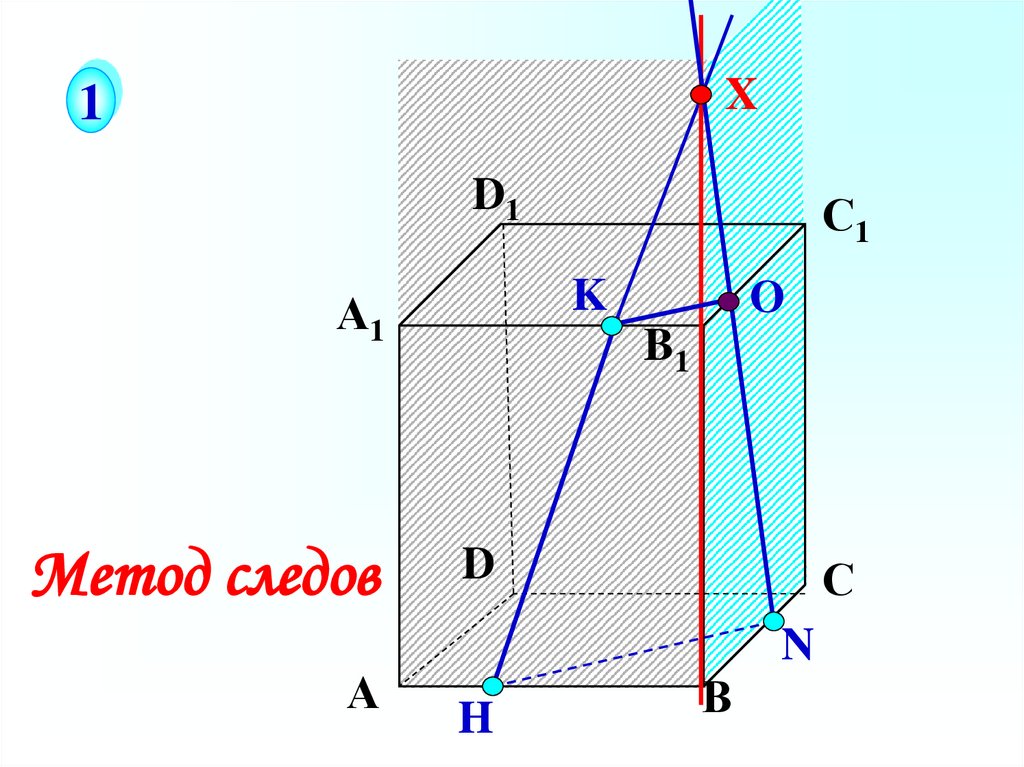
Метод следов

20.

Для любознательных
Многие художники, искажая законы перспективы,
рисуют необычные картины. Кстати, эти рисунки очень
популярны среди математиков. В сети Internet можно
найти множество сайтов, где публикуются эти
невозможные объекты.
Популярные художники Морис Эшер, Оскар
Реутерсвард, Жос де Мей и другие, удивляли своими
картинами математиков.
http://www.im-possible.info/english/art/mey/mey2.html
http://alone.sammit.kiev.ua/moremind/illusion/index.html
http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html

21.

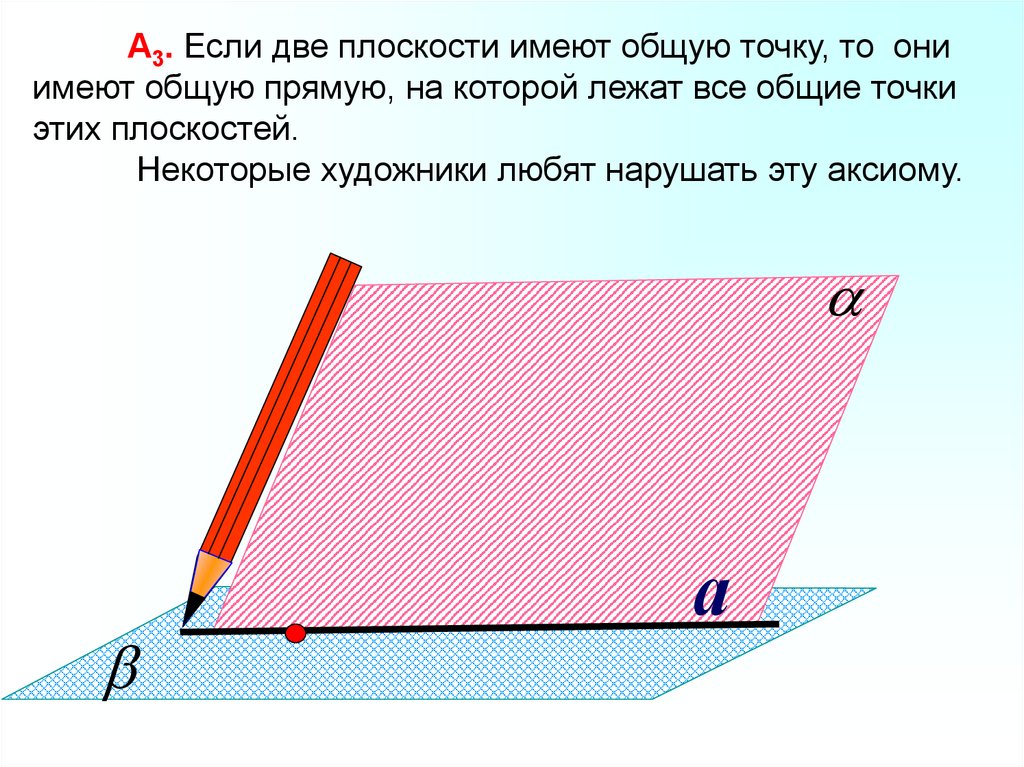
А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие точки
этих плоскостей.
Некоторые художники любят нарушать эту аксиому.
а

22.

"Такое может нарисовать только тот, кто делает
дизайн, не зная перспективы..."
Жос де Мей

23.

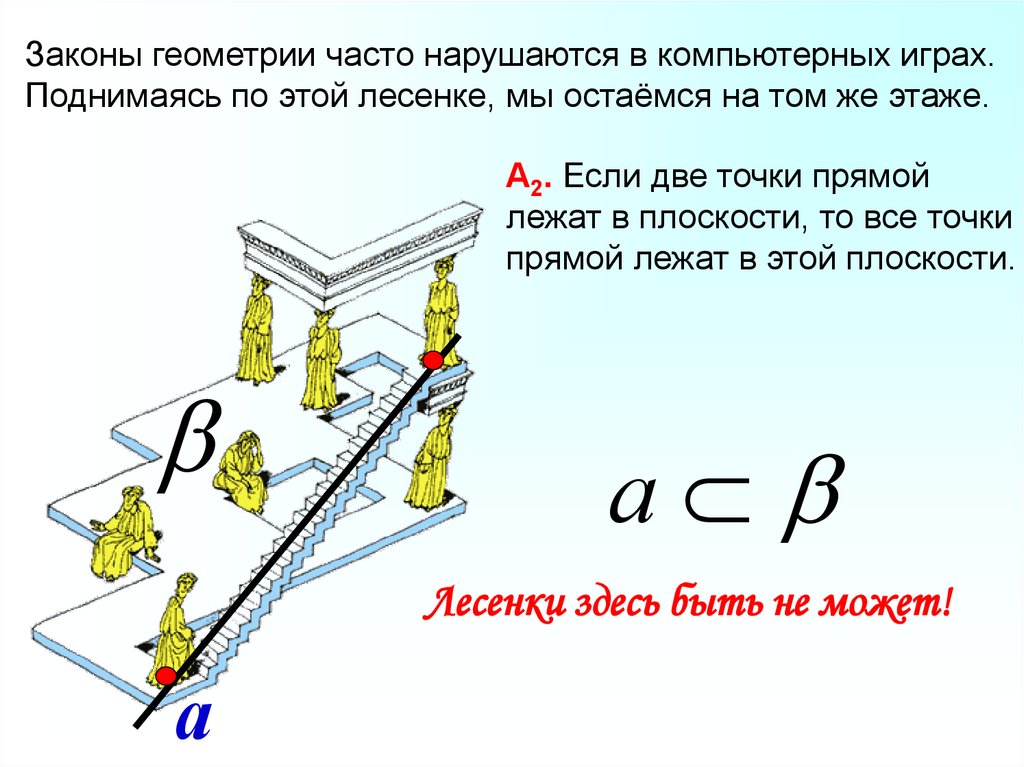
Законы геометрии часто нарушаются в компьютерных играх.
Поднимаясь по этой лесенке, мы остаёмся на том же этаже.
А2. Если две точки прямой
лежат в плоскости, то все точки
прямой лежат в этой плоскости.
а
Лесенки здесь быть не может!
а

24.

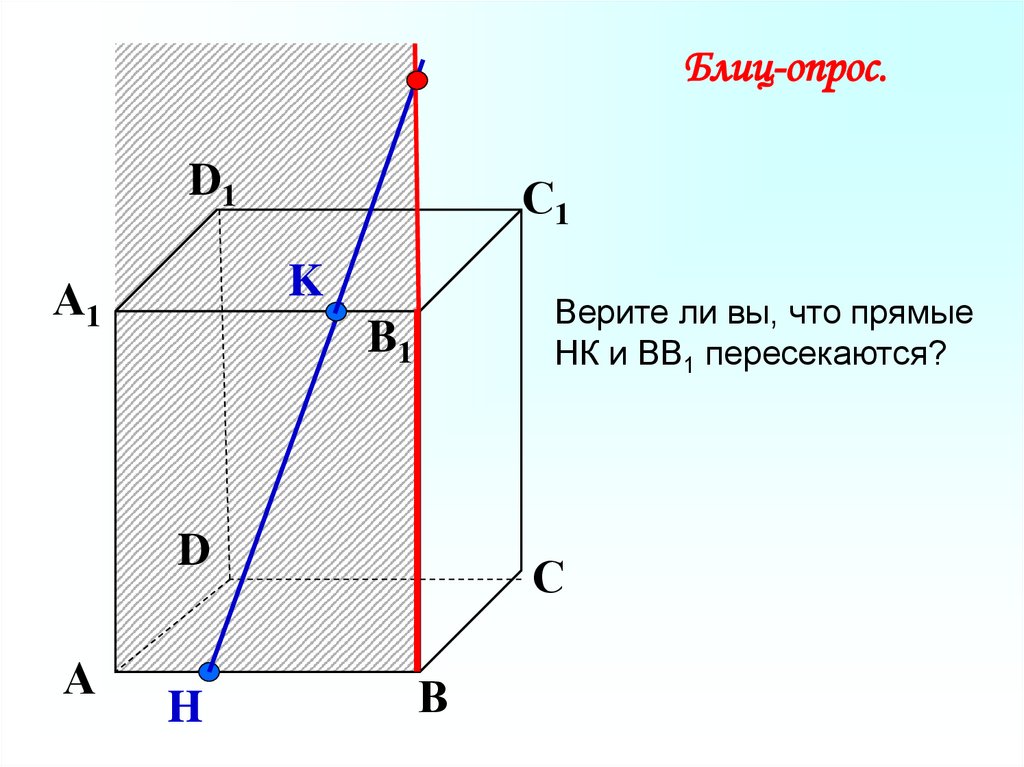
Блиц-опрос.
D1
С1
K
А1
Верите ли вы, что прямые
НК и ВВ1 пересекаются?
B1
D
А
H
С
В

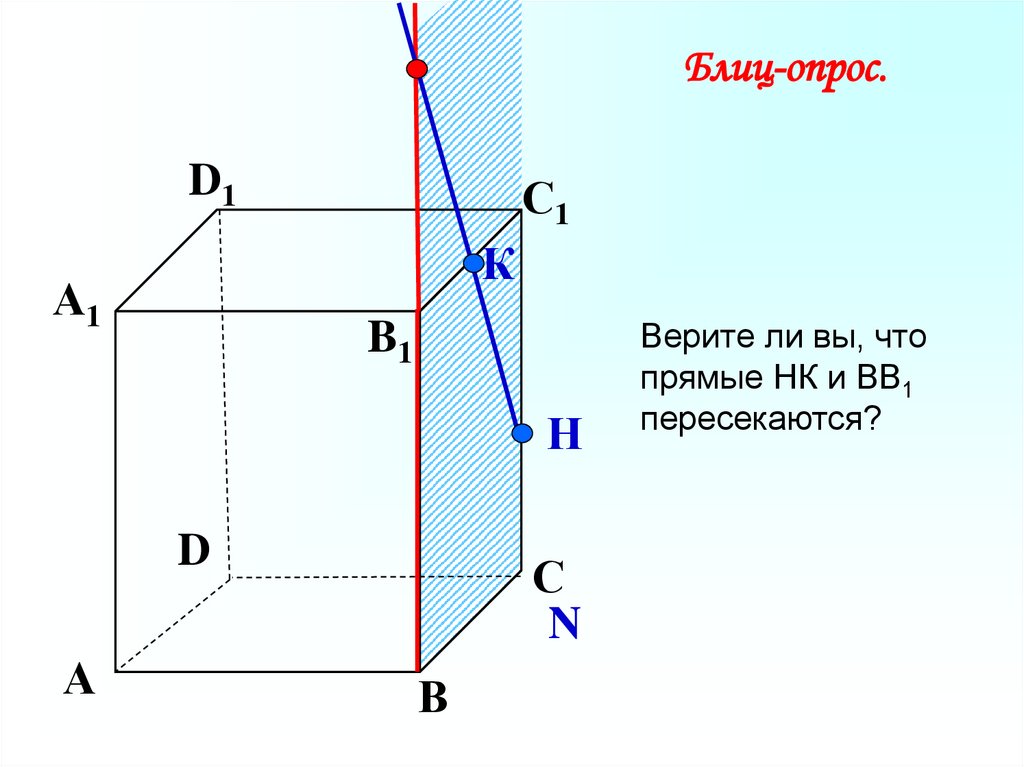
25.

Блиц-опрос.
D1
С1
К
А1
B1
Н
D
А
С
N
В
Верите ли вы, что
прямые НК и ВВ1
пересекаются?

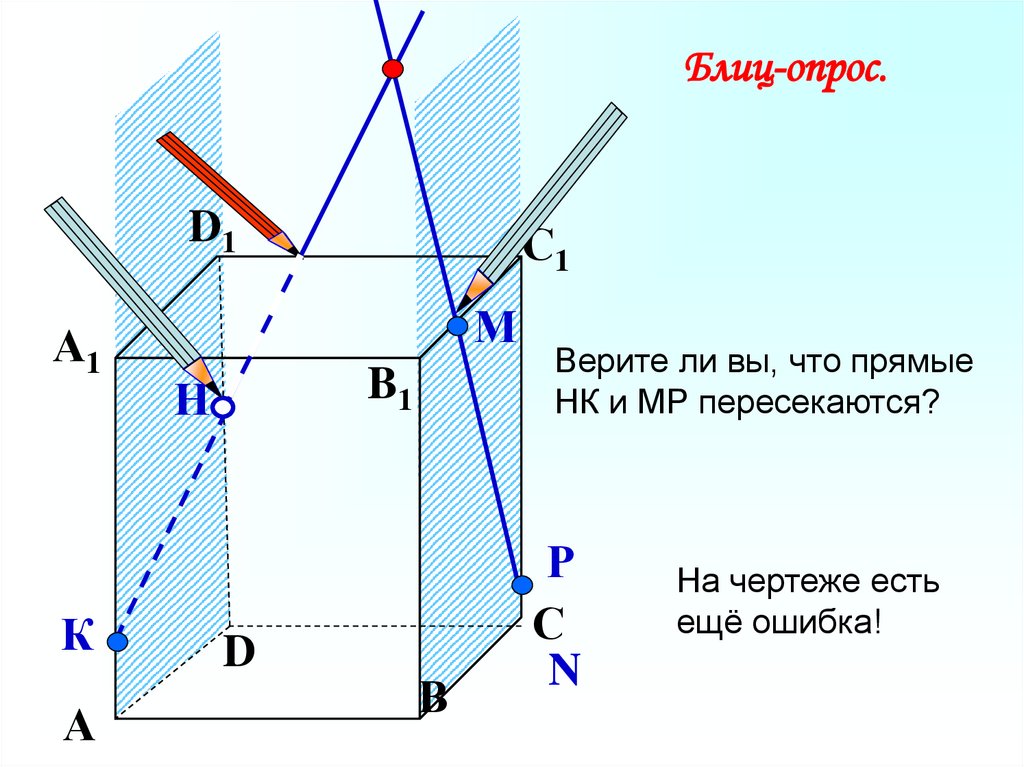
26.

Блиц-опрос.
D1
А1
К
А
С1
М
B1
Н
D
В
Верите ли вы, что прямые
НК и МР пересекаются?
Р
С
N
На чертеже есть
ещё ошибка!

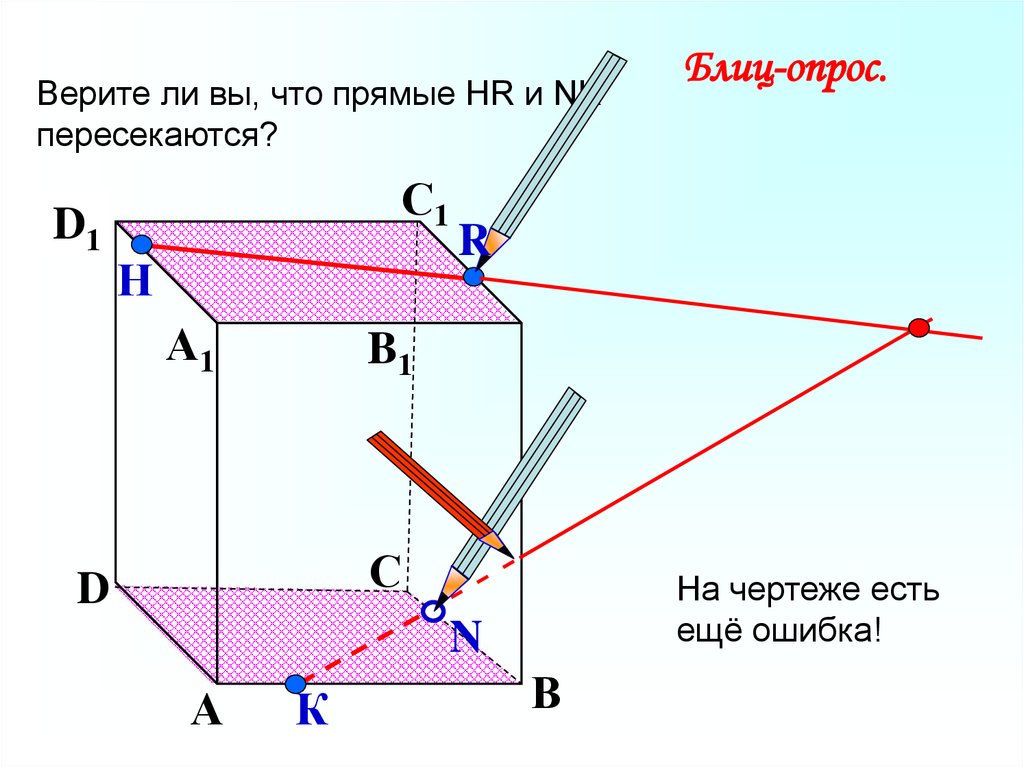
27.

Верите ли вы, что прямые НR и NK
пересекаются?
D1
С1
Н
А1
R
B1
С
D
На чертеже есть
ещё ошибка!
N
А
Блиц-опрос.
К
В

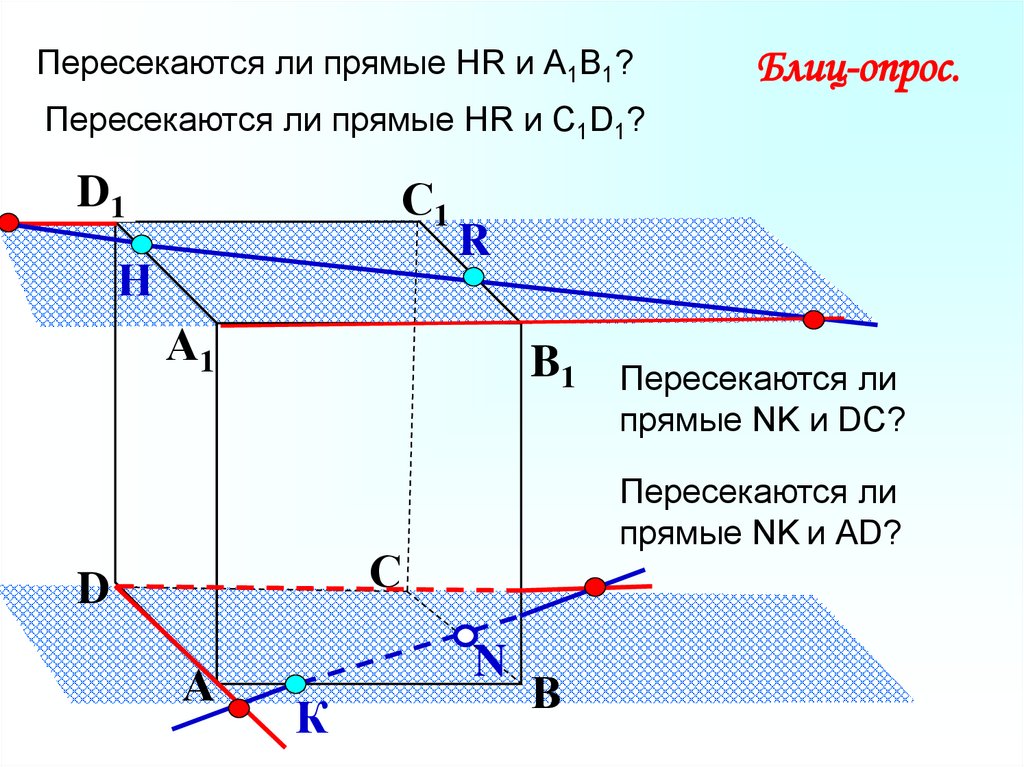
28.

Пересекаются ли прямые НR и А1В1?
Блиц-опрос.
Пересекаются ли прямые НR и С1D1?
С1
D1
Н
R
А1
B1
Пересекаются ли
прямые NK и АD?
С
D
А
N
К
Пересекаются ли
прямые NK и DC?
В

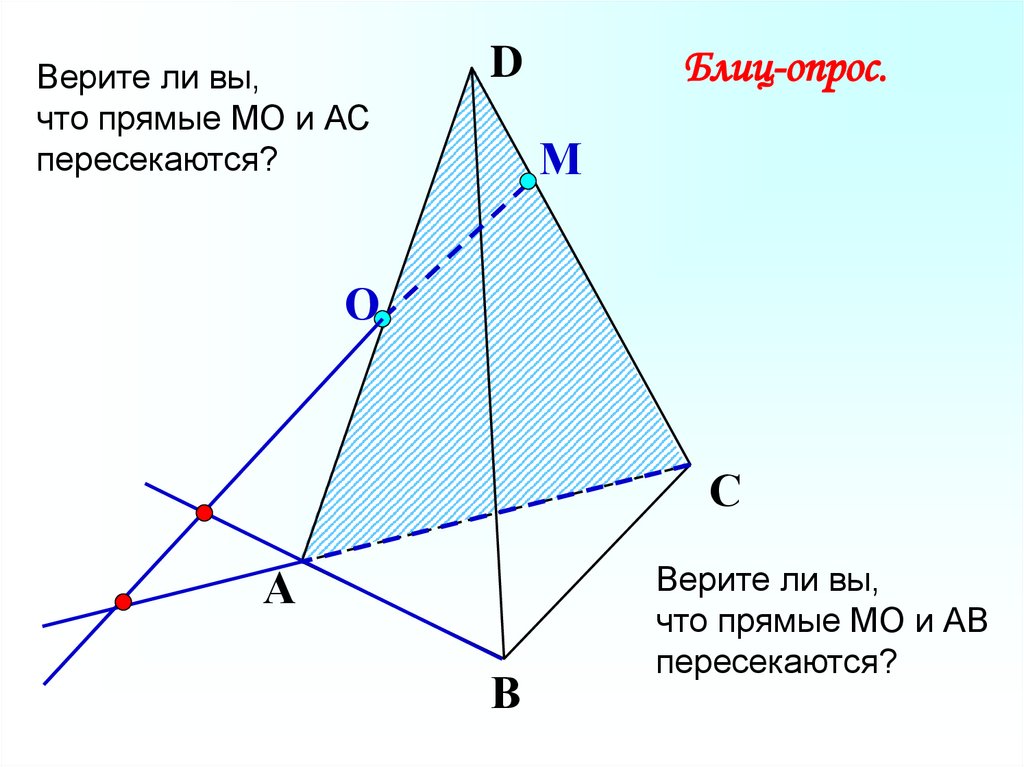
29.

Верите ли вы,
что прямые МО и АС
пересекаются?
Блиц-опрос.
D
М
О
С
А
В
Верите ли вы,
что прямые МО и АВ
пересекаются?

30.

X
1
D1
А
О
K
А1
Метод следов
С1
B1
D
С
N
H
В

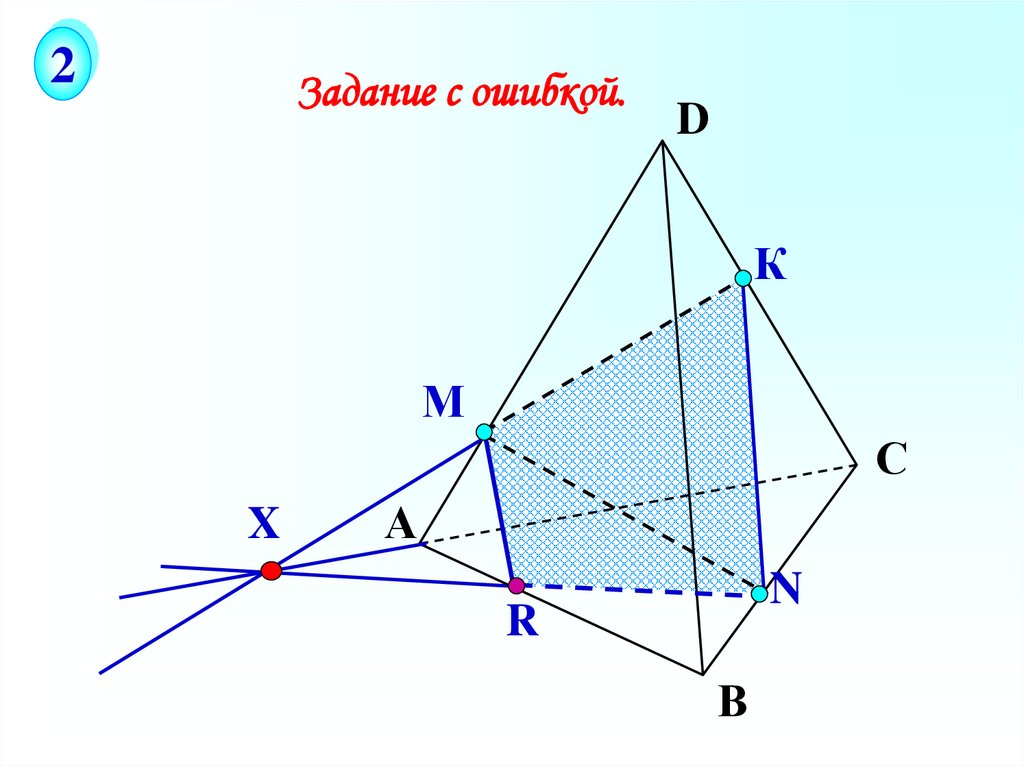
31.

2
Задание с ошибкой.
D
К
М
С
X
А
N
R
В

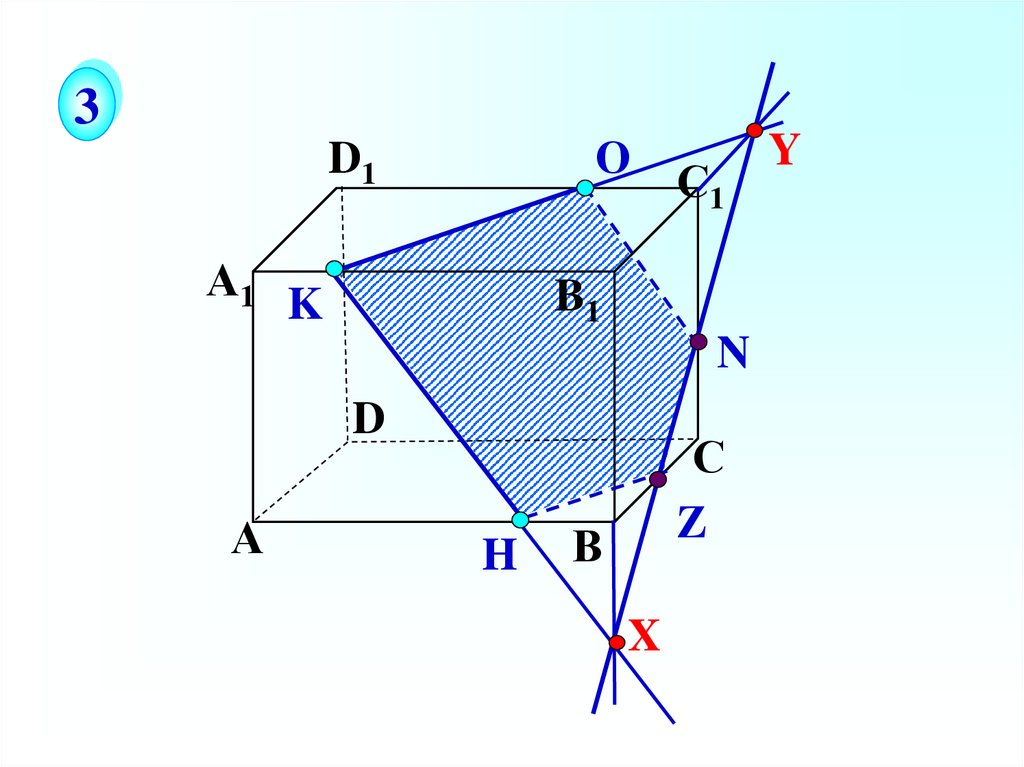
32.

3
О
D1
А1
С1
B1
K
N
D
А
H
С
Z
В
X
Y

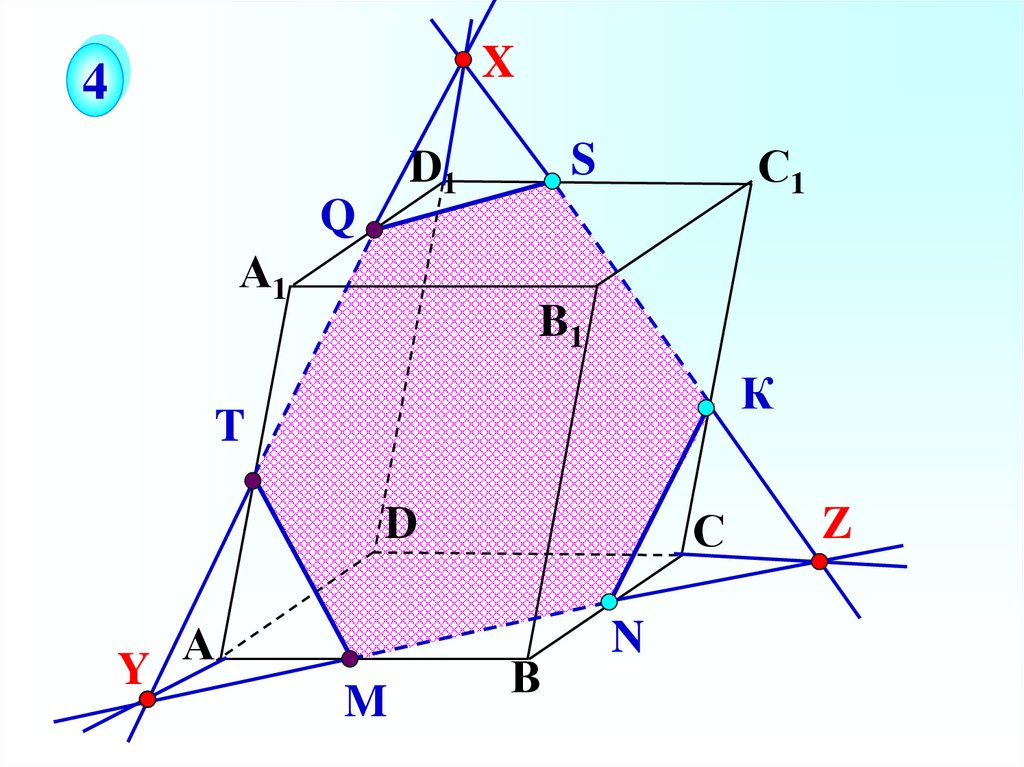
33.

X
4
Q
А1
С1
S
D1
B1
К
T
С
D
Y
А
M
В
N
Z

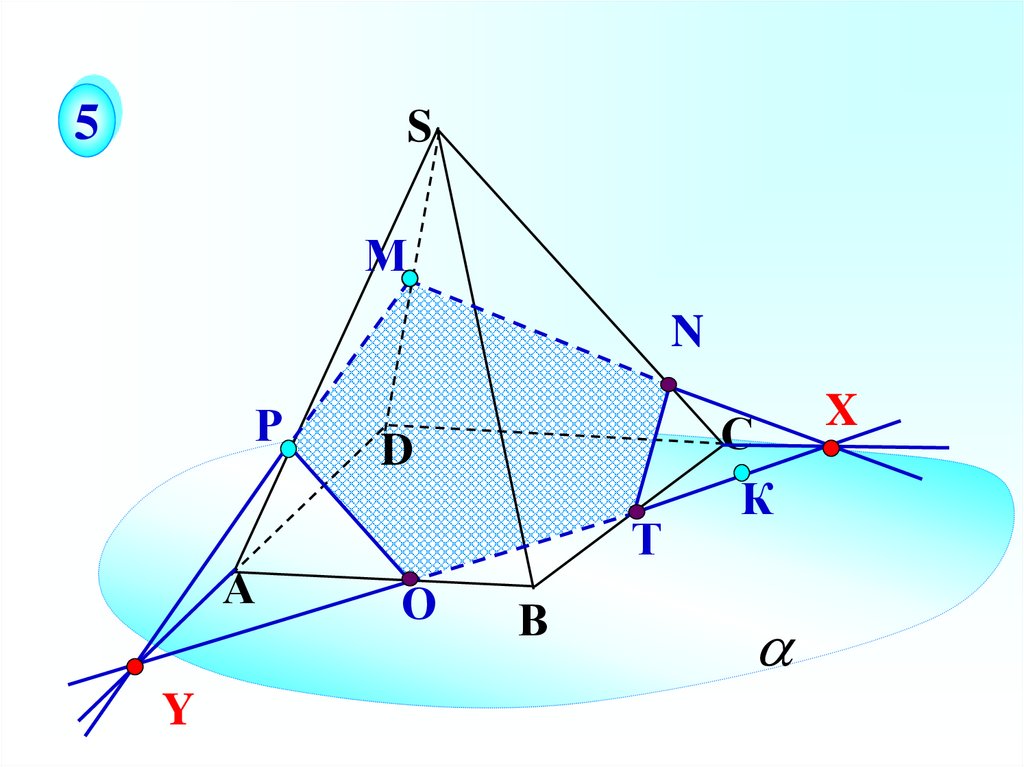
34.

5
S
М
N
Р
А
Y
D
Т
О
В
С
К
X

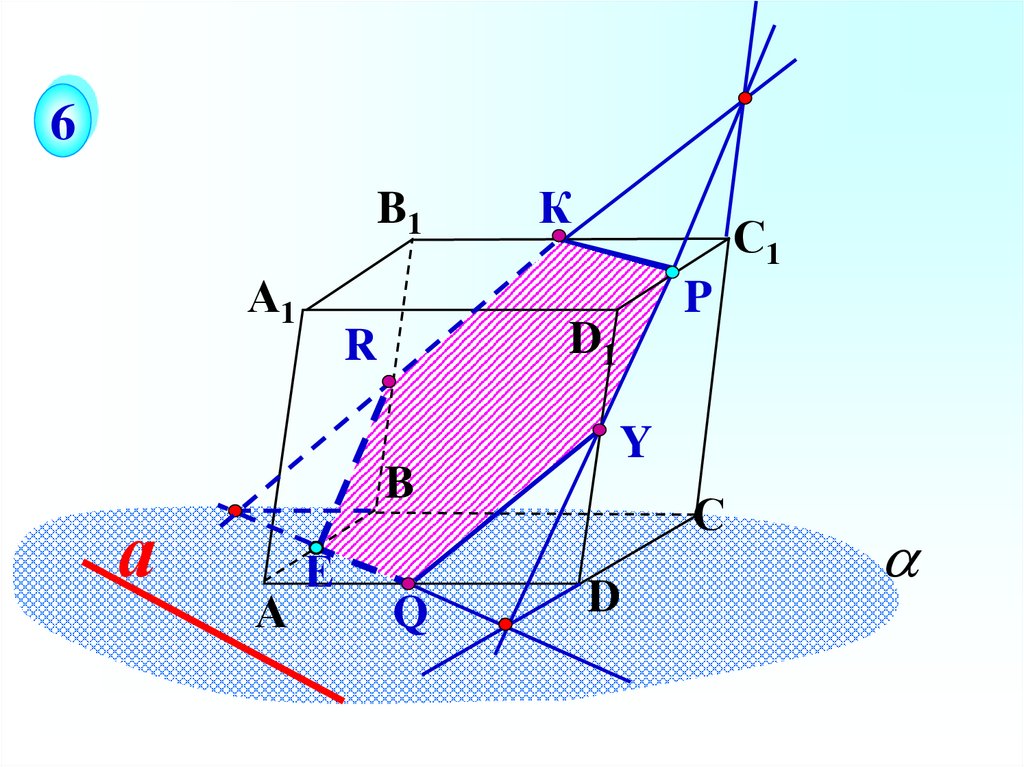
35.

6
B1
А1
А
С1
P
D1
R
B
а
К
Е
Q
Y
С
D