Similar presentations:
Движение тела брошенного под углом к горизонту
1. Движение тела брошенного под углом к горизонту.
Приложение 1Движение тела
брошенного под
углом к горизонту.
2.
Лыжникдвижется при
прыжке с
трамплина
Струя воды
движется из
брандспойта
Движения
артиллерийских
снарядов
3.
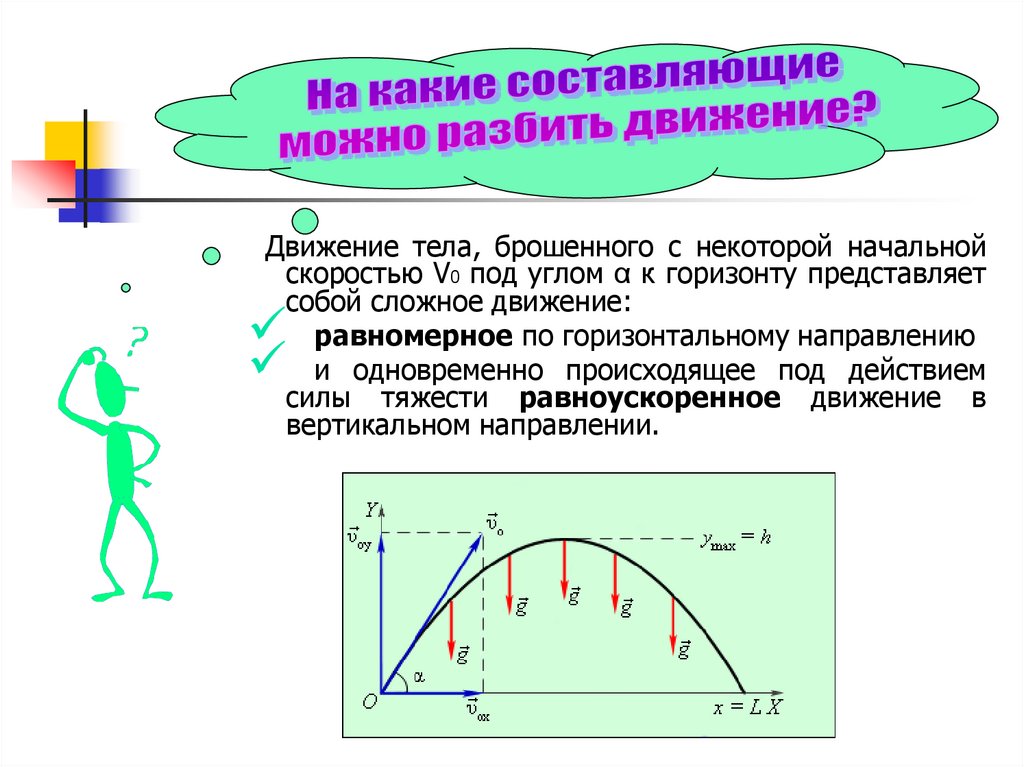
Движение тела, брошенного с некоторой начальнойскоростью V0 под углом α к горизонту представляет
собой сложное движение:
равномерное по горизонтальному направлению
и одновременно происходящее под действием
силы тяжести равноускоренное движение в
вертикальном направлении.
4.
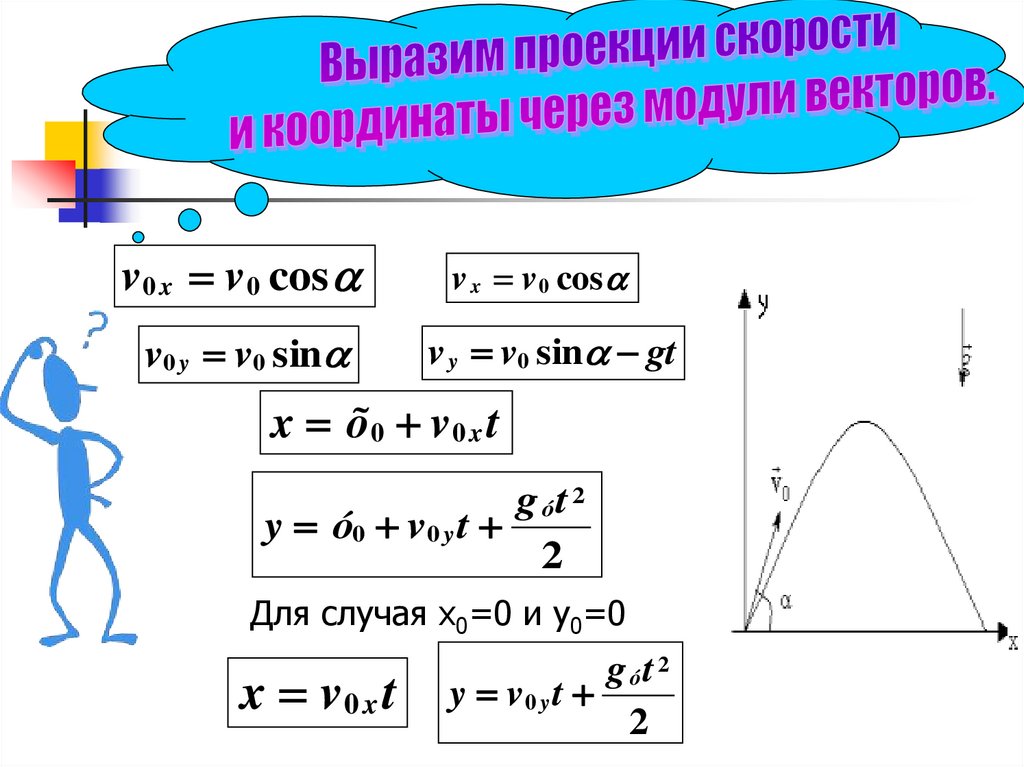
v 0 x v 0 cosv0 y v0 sin
v x v 0 cos
v y v0 sin gt
x õ0 v 0 x t
g ót 2
y ó0 v0 y t
2
Для случая х0=0 и y0=0
x v0 x t
g ót 2
y v0 y t
2
v0 y v0 sin
5.
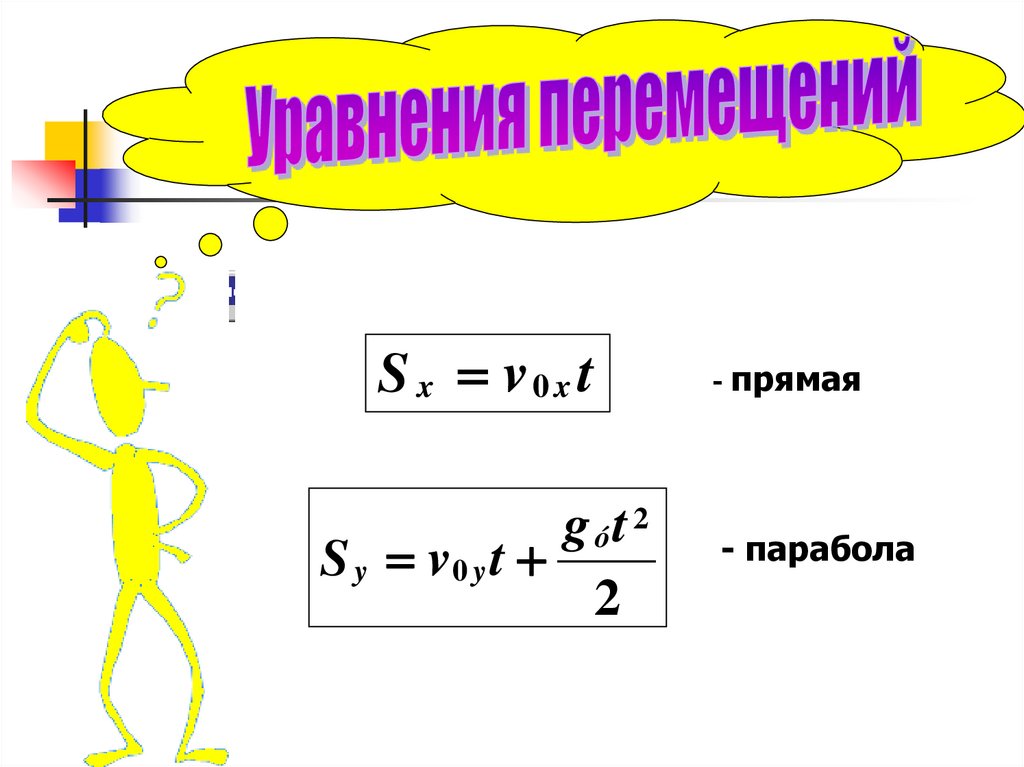
S x v0x tg ót 2
S y v0 y t
2
- прямая
- парабола
6.
v 0 x v 0 cosv0 y v0 sin
g ót 2
y v0 y t
2
x v0 x t
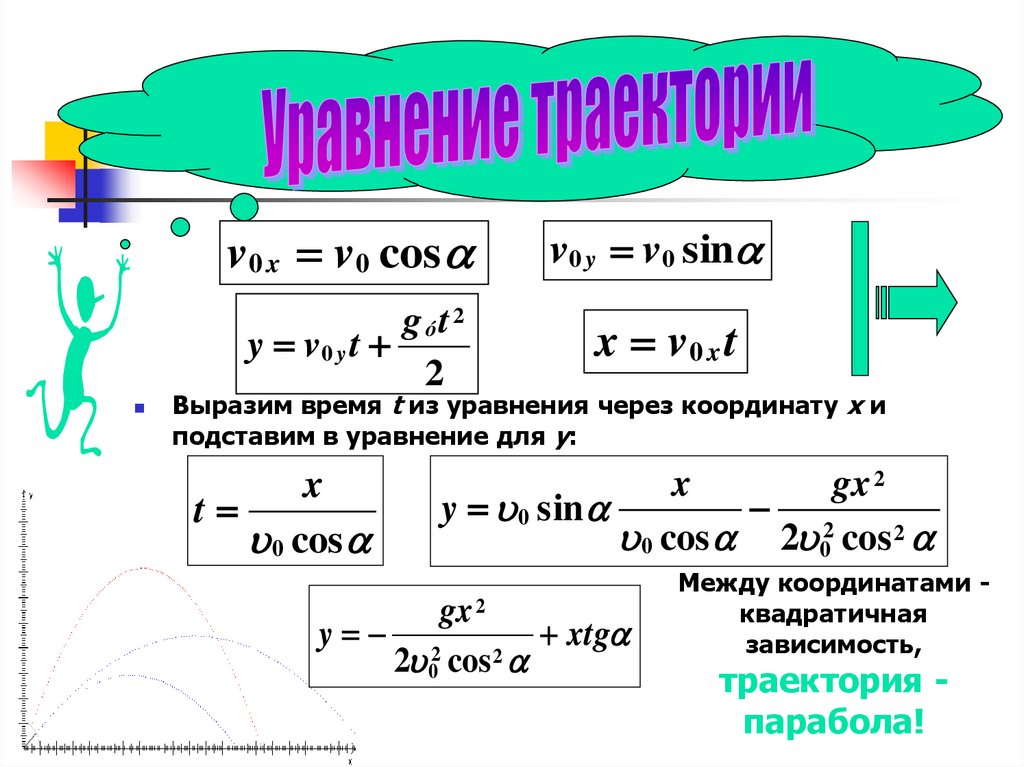
Выразим время t из уравнения через координату x и
подставим в уравнение для y:
x
t
0 cos
x
gx 2
y 0 sin
2
0 cos 2 0 cos 2
gx 2
y 2
xtg
2
2 0 cos
Между координатами квадратичная
зависимость,
траектория парабола!
7.
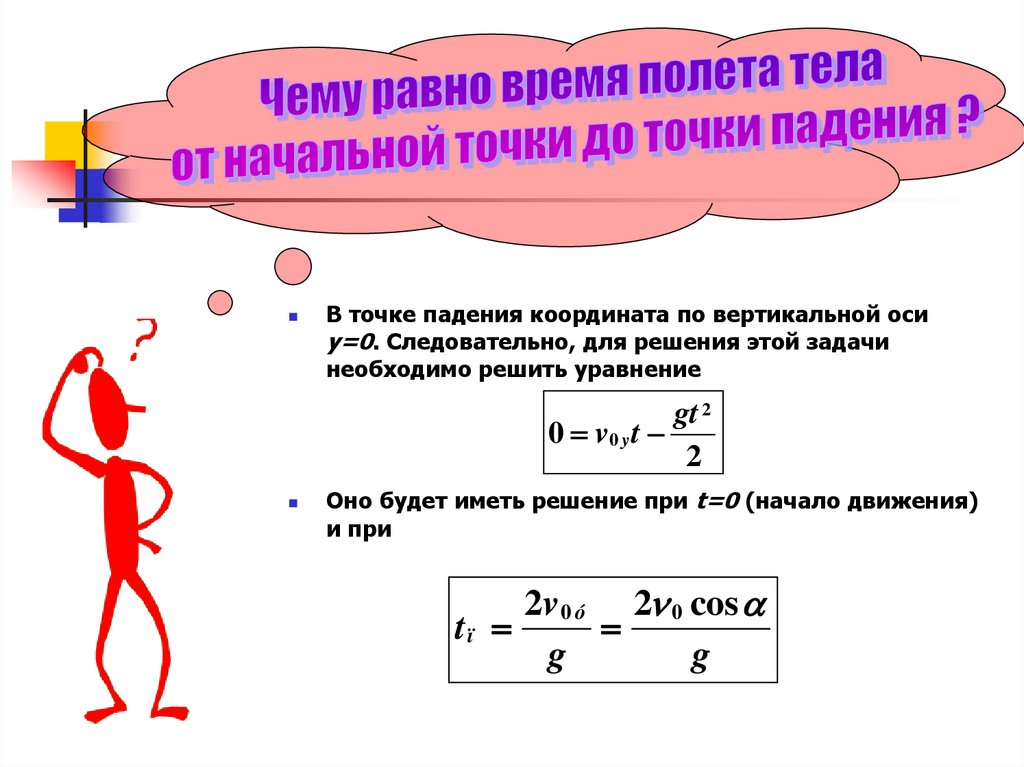
В точке падения координата по вертикальной осиу=0. Следовательно, для решения этой задачи
необходимо решить уравнение
gt 2
0 v0 y t
2
Оно будет иметь решение при t=0 (начало движения)
и при
2v 0 ó 2 0 cos
tï
g
g
8.
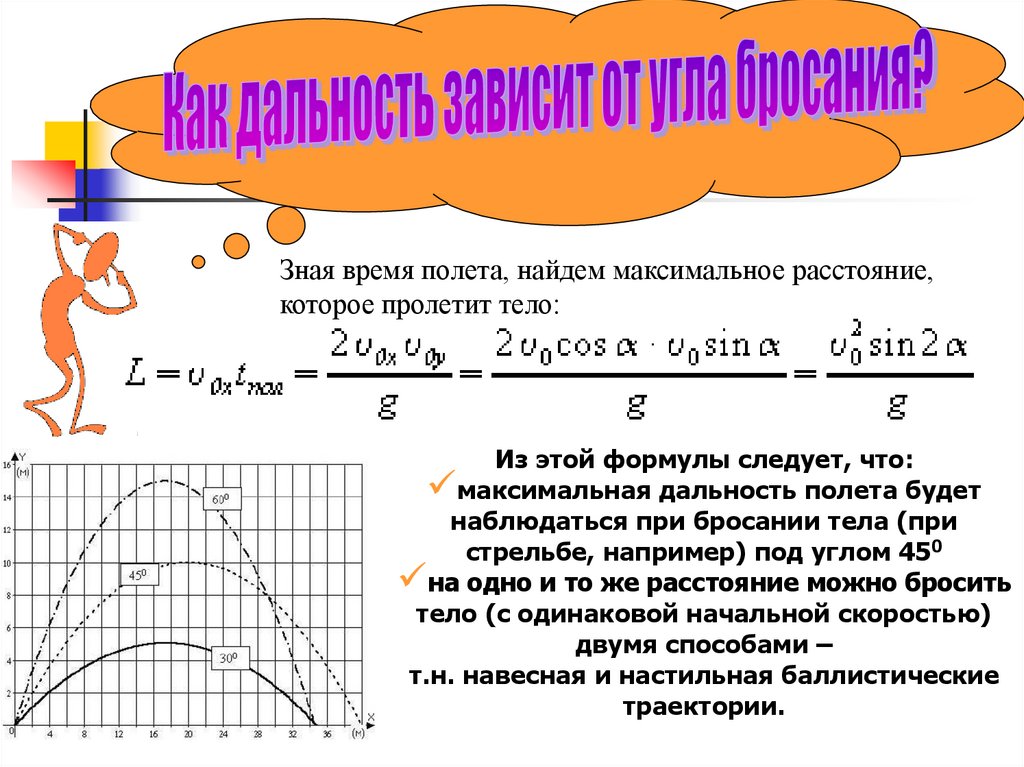
Зная время полета, найдем максимальное расстояние,которое пролетит тело:
Из этой формулы следует, что:
максимальная дальность полета будет
наблюдаться при бросании тела (при
стрельбе, например) под углом 450
на одно и то же расстояние можно бросить
тело (с одинаковой начальной скоростью)
двумя способами –
т.н. навесная и настильная баллистические
траектории.
9.
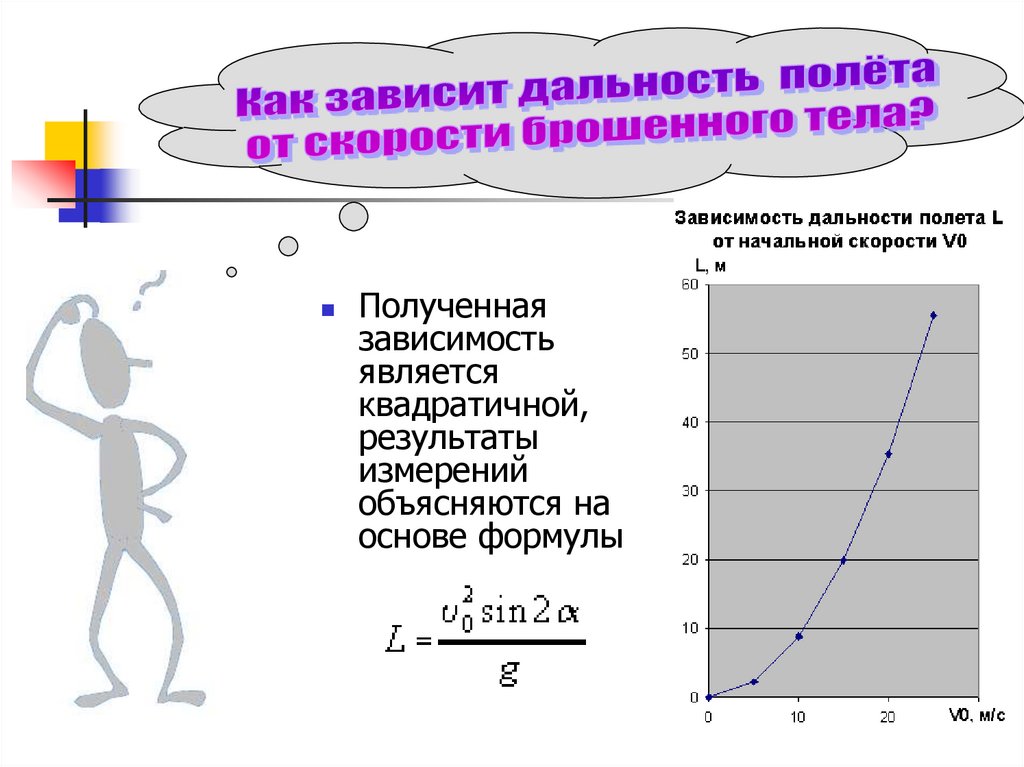
Полученнаязависимость
является
квадратичной,
результаты
измерений
объясняются на
основе формулы
10.
Используя то, что парабола - это симметричная кривая,найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно:
Тогда:
11.
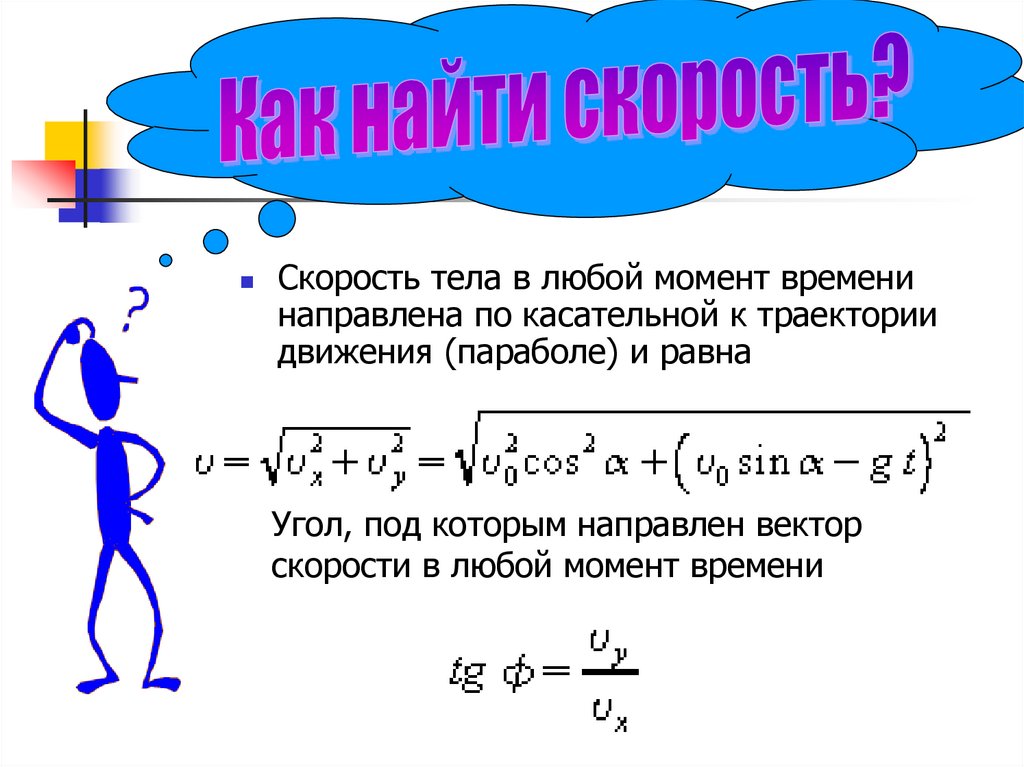
Скорость тела в любой момент временинаправлена по касательной к траектории
движения (параболе) и равна
Угол, под которым направлен вектор
скорости в любой момент времени
12.
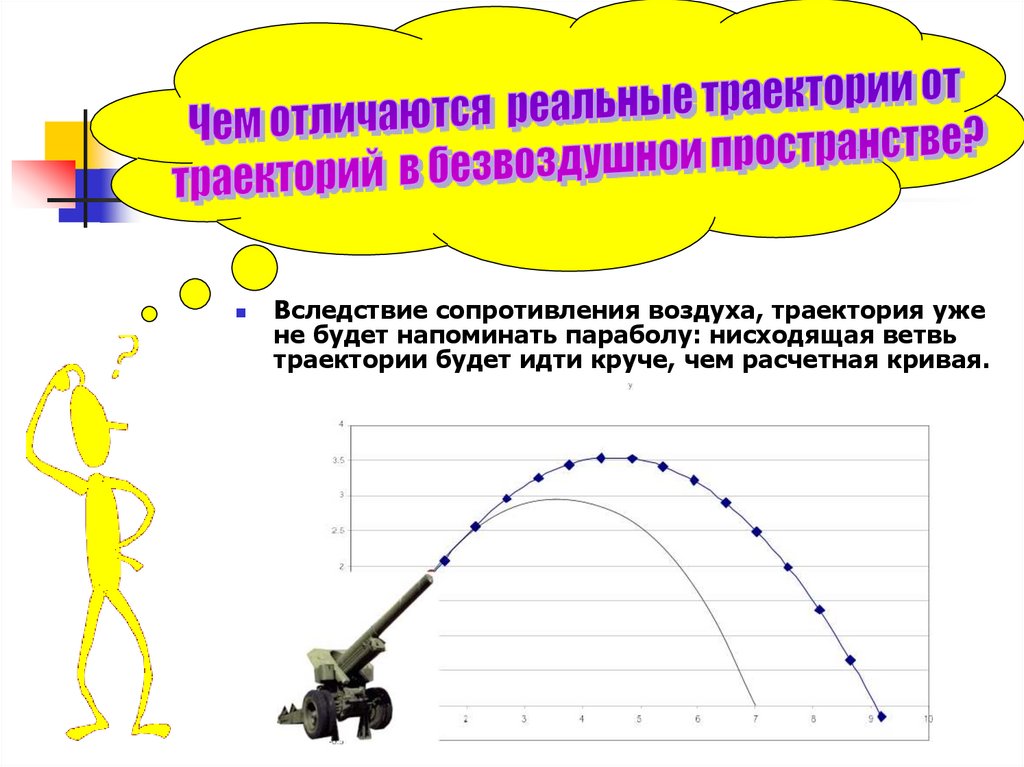
Вследствие сопротивления воздуха, траектория ужене будет напоминать параболу: нисходящая ветвь
траектории будет идти круче, чем расчетная кривая.


 physics
physics








