Similar presentations:
Движение тела брошенного под углом к горизонту. Повторение, решение задач (10 класс)
1. Движение тела брошенного под углом к горизонту
Повторение, решение задач10 класс
2. Движение тела под действием силы тяжести.
Задача. Решить основную задачу механики длятела брошенного с начальной скоростью v0 под
углом к горизонту α
Дано:
v0
α
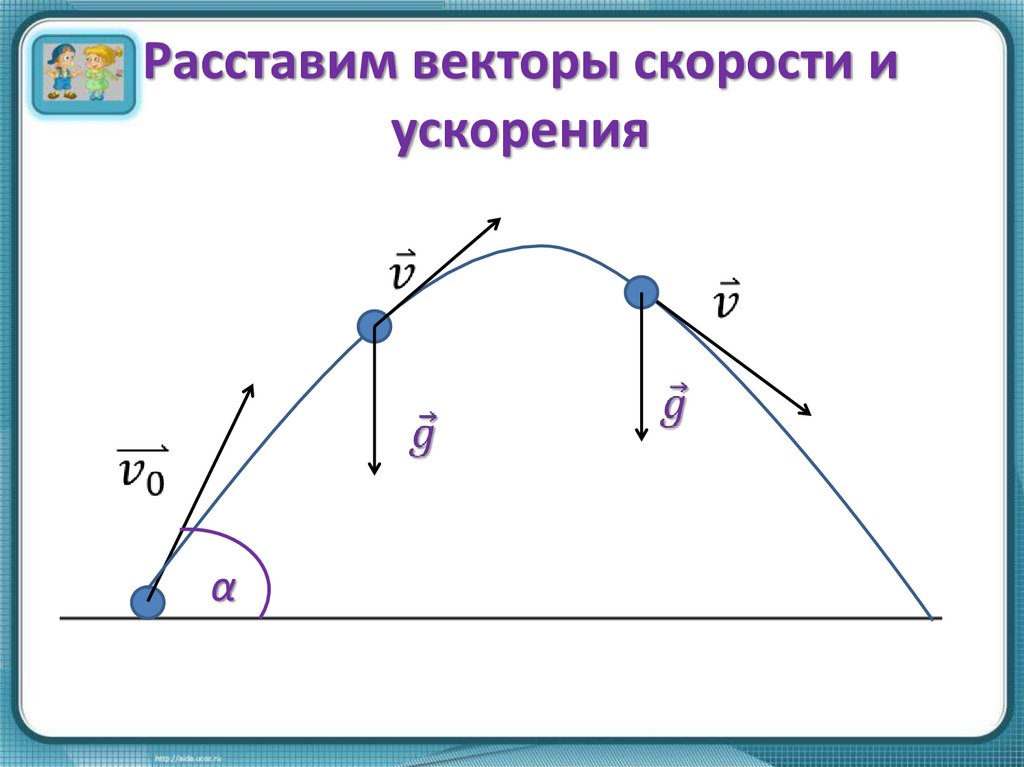
3. Расставим векторы скорости и ускорения
α4. Решение задачи.
Так как тело движется с ускорением свободногопадения, то искать решение будем исходя из
уравнения равноускоренного движения.
Почему для описания движения тела брошенного
под углом к горизонту нужно два уравнения?
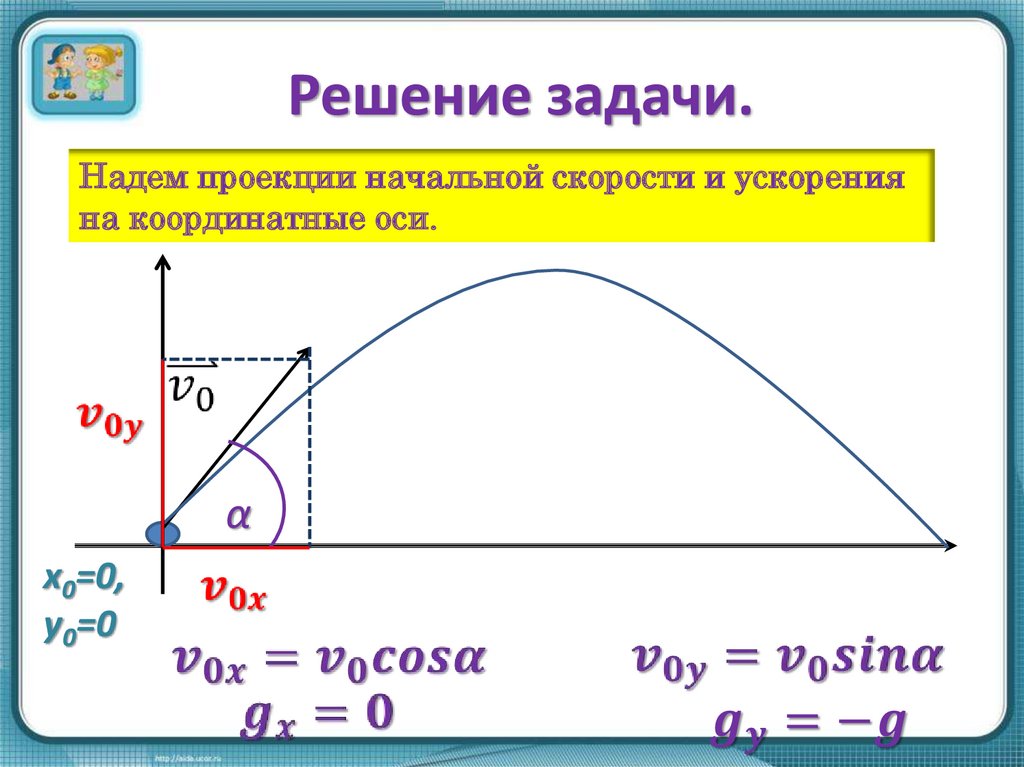
5. Решение задачи.
Надем проекции начальной скорости и ускоренияна координатные оси.
α
x0=0,
y0=0
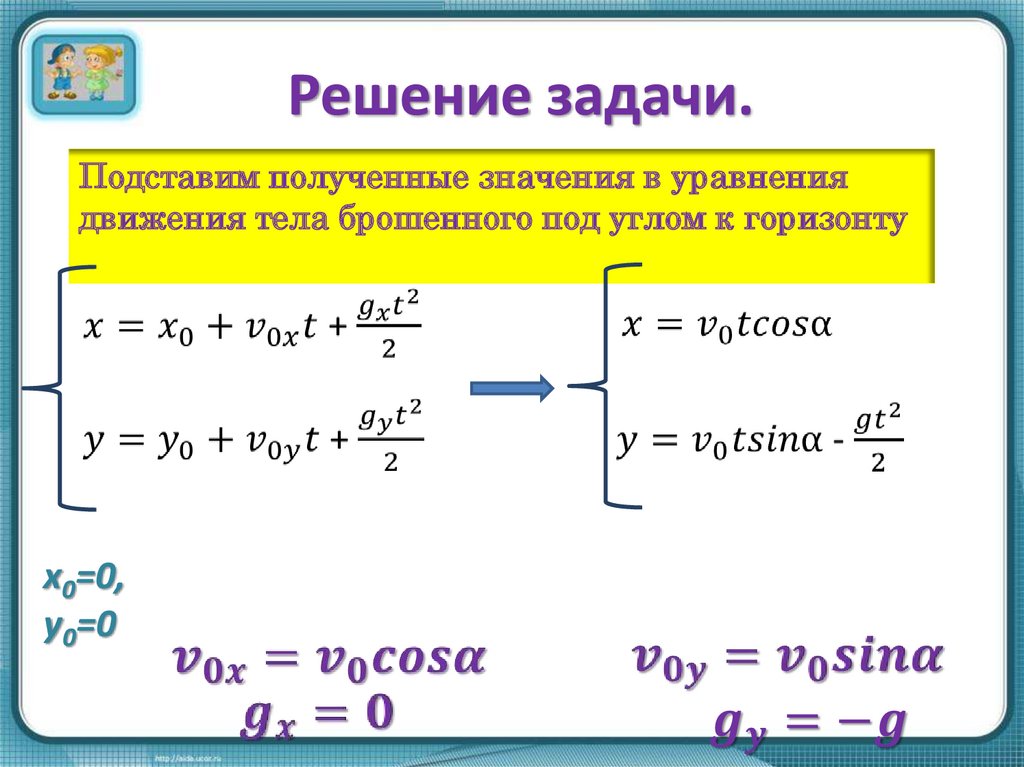
6. Решение задачи.
Подставим полученные значения в уравнениядвижения тела брошенного под углом к горизонту
x0=0,
y0=0
7.
Время подъёма tпод(до точки А).1.Vy=V0 *sinα-gt
2.В точке А проекция скорости Vу на ось ОУ равна нулю при
t=tпод : Vу=0 =>
3. 0=Vо*sinα-gtпод =>
4.gtпод =Vо*sinα =>
5.tпод =Vо*sinα/g
Vo sin
tпод
g
8.
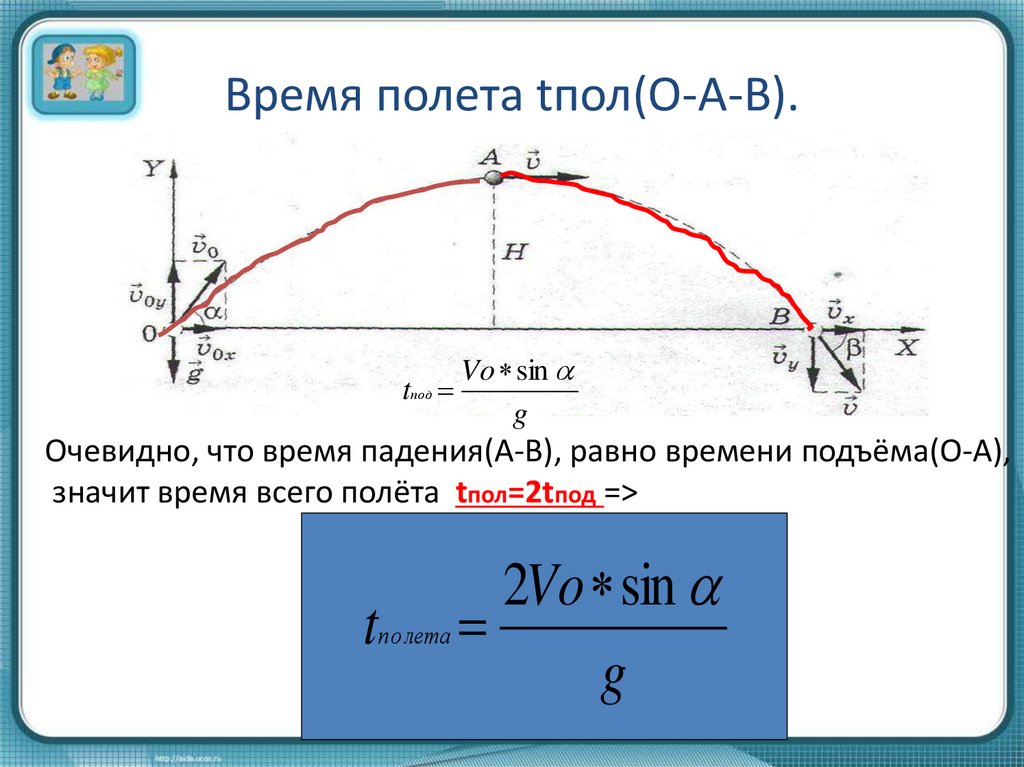
Время полета tпол(О-А-В).Vo sin
tпод
g
Очевидно, что время падения(А-В), равно времени подъёма(О-А),
значит время всего полёта tпол=2tпод =>
2Vo sin
tполета
g
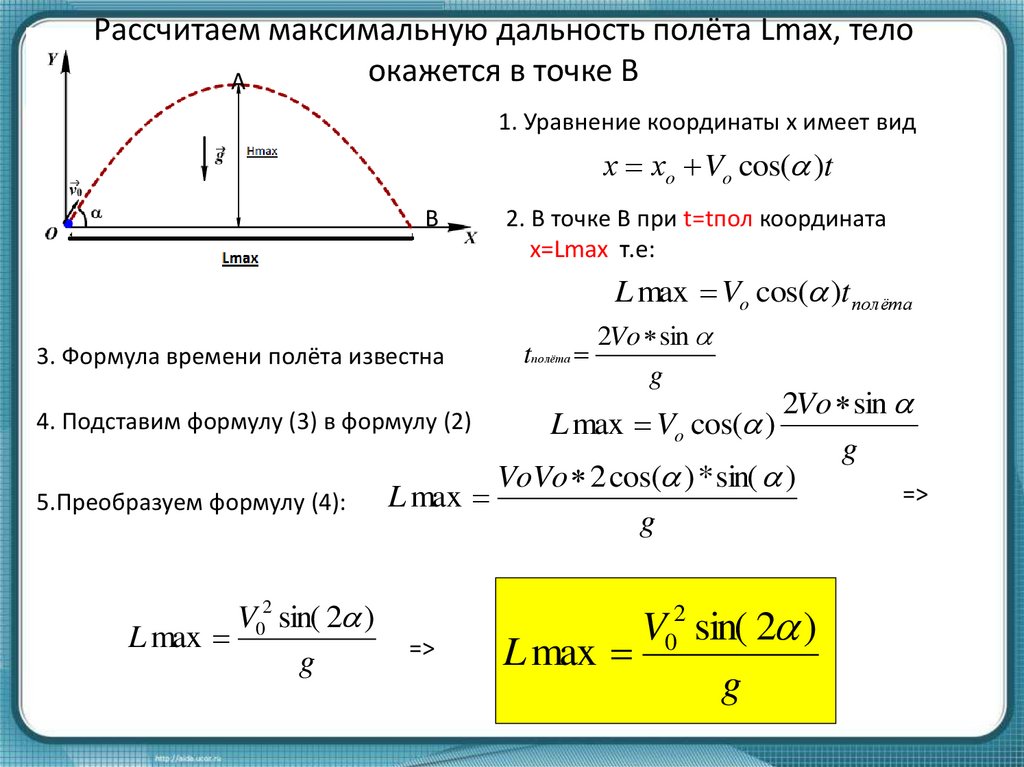
9. Рассчитаем максимальную дальность полёта Lmax, тело окажется в точке В
А1. Уравнение координаты х имеет вид
х хo Vo cos( )t
В
2. В точке В при t=tпол координата
х=Lmax т.е:
L max Vo cos( )tполёта
3. Формула времени полёта известна
tполёта
2Vo sin
g
2Vo sin
L max Vo cos( )
g
VoVo 2 cos( ) * sin( )
=>
L max
g
4. Подставим формулу (3) в формулу (2)
5.Преобразуем формулу (4):
V02 sin( 2 )
L max
g
=>
V02 sin( 2 )
L max
g
10. Рассчитаем максимальную высоту подъёма Нmax
А1. Уравнение координаты у имеет вид
gt 2
у уo Vo sin( )t
2
В
2. В точке А при t=tпод координата
у=Нmax т.е:
2
Н max
tпод
3. Формула времени подъёма известна
Н max
V 2o sin 2 V 2o sin 2
g
2g
Н max
Vo sin
g
Vo sin
g
V 2 o sin 2
g
V 2 o sin 2
g2
=>
g
2
4. Подставим формулу (3) в формулу (2)
5.Преобразуем формулу (4):
gtпод
Vo sin( )tпод
2
Н max Vo sin( )
=>
Н
max
2
2
V o sin
2g
g(
Vo sin 2
)
g
2
11. Задачи
12. Из окна дома с высоты 19,6 м горизонтально брошена монета со скоростью 5 м/с. Пренебрегая сопротивлением воздуха, найдите,
через какойпромежуток времени монета упадет на Землю На
каком расстоянии по горизонтали от дома находится
точка падения?
13.
14.
ответ:15.
• 2. Используя условие задачи 1, найдитескорость падения монеты и угол, который
образует вектор скорости с горизонтом в
точке падения
16.
17.
ответ:18. 3. Длина скачка блохи на столе, прыгающей под углом 45° к горизонту, равна 20 см. Во сколько раз высота ее подъема над столом
превышает еесобственную длину, составляющую 0,4 мм?
• рисунок.
19.
ответ:
20. Мяч, брошенный под углом 45° к горизонту, упруго отскочив от вертикальной стены, расположенной на расстоянии L от точки
Мяч, брошенный под углом 45° к горизонту, упругоотскочив от вертикальной стены, расположенной на
расстоянии L от точки бросания, ударяется о Землю на
расстоянии l от стены С какой начальной скоростью был
брошен мяч?
21.
4.• при абсолютно упругом ударе мяча о стенку
модуль его скорости не изменяется, а угол
падения равен углу отражения.
реальная траектория мяча является зеркальным
отражением той траектории, по которой мяч
летел бы в отсутствии стенки.
тогда из рисунка видно, что дальность полета
мяча
22.
23.
Домашнее задание§ 16, Упр.4 (2, 3),
(Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский Физика).
Спасибо за работу!
24. Использованные материалы:
• http://davay5.com/z.php?book=myakishevbuhovcev_10_klass• http://davay5.com/z.php?book=kasyanov_10_
klass
• http://davay5.com/z.php?book=rymkevich_10
_klass


















 physics
physics








