Similar presentations:
Удвоение медианы. Центральная симметрия
1.
Доброе утро, уважаемые восьмиклассники:•Перед началом работы ознакомьтесь с рекомендациями по
организации работы на уроке.
•Познакомьтесь с теоретическим материалом по теме урока. При
наличии вопросов по теоретическому материалу запиши их в тетрадь,
чтобы потом задать их учителю.
•Познакомьтесь с представленной в уроке презентацией.
Проанализируйте содержание слайдов. Если есть вопросы, запишите
их в рабочую тетрадь.
•Не торопясь, выполните тренировочные упражнения или
практическую работу, согласно заданию. Отметьте задания, при
выполнении которых возникли затруднения, чтобы впоследствии
проконсультироваться с учителем.
•Для закрепления пройденного материала выполнить тесты (при их
наличии) в конце урока.
•Сделайте перерыв по окончании урока (чайная пауза, физическая
разминка, уборка по дому). Переходите к следующему уроку.
2.
Безопасность прежде всего!•Доброе утро. В период дистанционного обучения вам приходится
очень много времени проводить в одиночестве дома. Самое
главное, чтоб ваше пребывание дома было максимально
безопасным!
Рекомендуем
познакомиться
с
правилами
безопасности при нахождении дома. Обратите внимание на
телефоны экстренных служб. Берегите себя!!!
•http://гимназия1.рф/o-gimnazii-1/informaciya-dlyapostupayushhix/pravila-bezopasnosti-doma/
3.
Запишите в тетради:15.10.2024
Удвоение медианы.
Центральная симметрия.
4.
План работы на уроке:1.Изучи материал в презентации (слайд 6-19) или
прочитай в учебнике п. 48 стр. 110-111.
2.Выполни упражнение (слайд 20)
3.Направить выполненное задание (фото,
скан, документ) можно посредством
личных сообщений
в VK-мессенждере,
в ЭКЖ (Гимадиева Анна Михайловна)
Viber, WhatsApp (89821938281)
Жду работы 15.09.2024 до 21.00
Желаю удачи! У тебя все получится!
5.
Сегодня мы познакомимся с методомудвоения медианы, узнаем определение
центральной симметрии.
6.
Рассмотрим треугольник ABC, в котором проведена медиана BM.В
А
М
С
7.
Удвоим эту медиану, т.е. проведем отрезок MD: MD=BM.В
А
М
D
С
8.
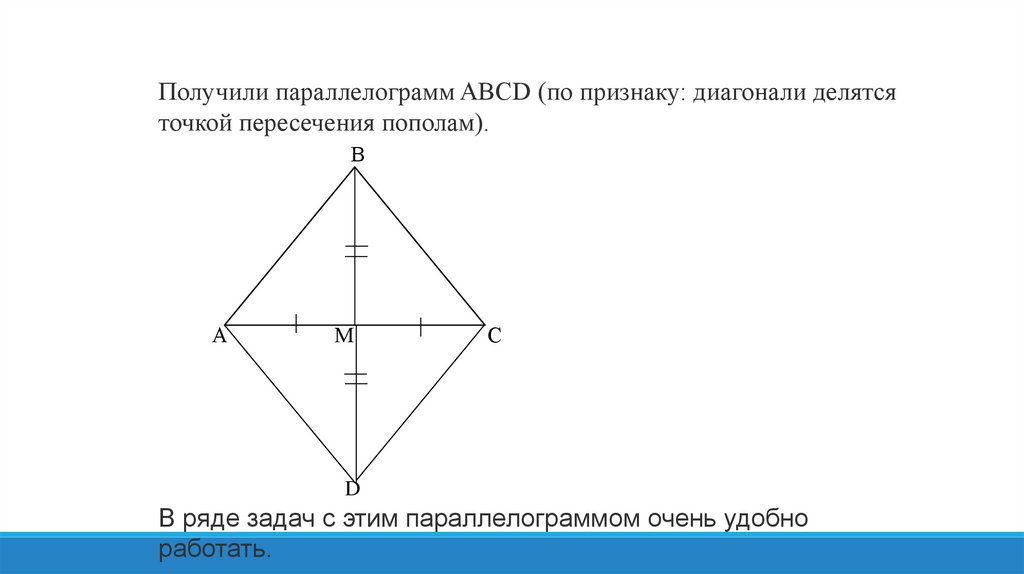
Получили параллелограмм ABCD (по признаку: диагонали делятсяточкой пересечения пополам).
В
А
М
С
D
В ряде задач с этим параллелограммом очень удобно
работать.
9.
Теорема: Если в треугольнике медиана совпадает с высотой, тоэтот треугольник равнобедренный.
В
А
М
Доказательство:
Рассмотрим треугольник ABC, в котором
проведена медиана BM, которая совпадает с
высотой. Продлим медиану: MD=BM.
Четырехугольник ABCD – параллелограмм
(AM=MC, т.к. BM – медиана, BM=MD (по
С построению)).
С другой стороны, у него перпендикулярны
диагонали. => ABCD – ромб => AB=BC, т.е.
треугольник ABC – равнобедренный. Что и
требовалось доказать.
D
10.
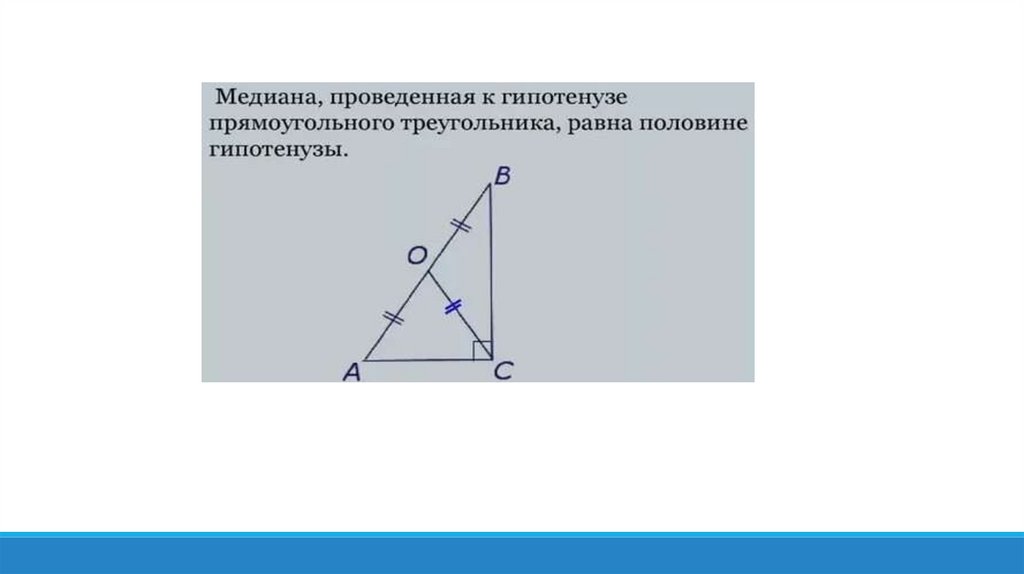
Теорема: Медиана в прямоугольном треугольнике равна половине егогипотенузы.
В
А
Доказательство:
С
M
Удвоив медиану ВМ, продлив её за точку М.
АВСD – параллелограмм (по признаку).
C другой стороны, в этом параллелограмме ∠В = 90°,
следовательно АВСD – прямоугольник.
Значит СМ = АМ = ВМ = МD.
1
АМ = АС.
2
D
11.
12.
Cделаем вывод:Если в задаче дана медиана, то очень часто полезно ее удвоить, чтобы
свести задачу к параллелограмму, ромбу или прямоугольнику, с
помощью чего можно решать ряд задач.
13.
14.
15.
Центральная симметрияТеперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
На картинках центральная симметрия: точка O здесь — центр симметрии.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду.
Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
16.
Давайте разберемся, как построить центральнуюсимметрию и рассмотрим алгоритм построения
фигур с центральной симметрией.
17.
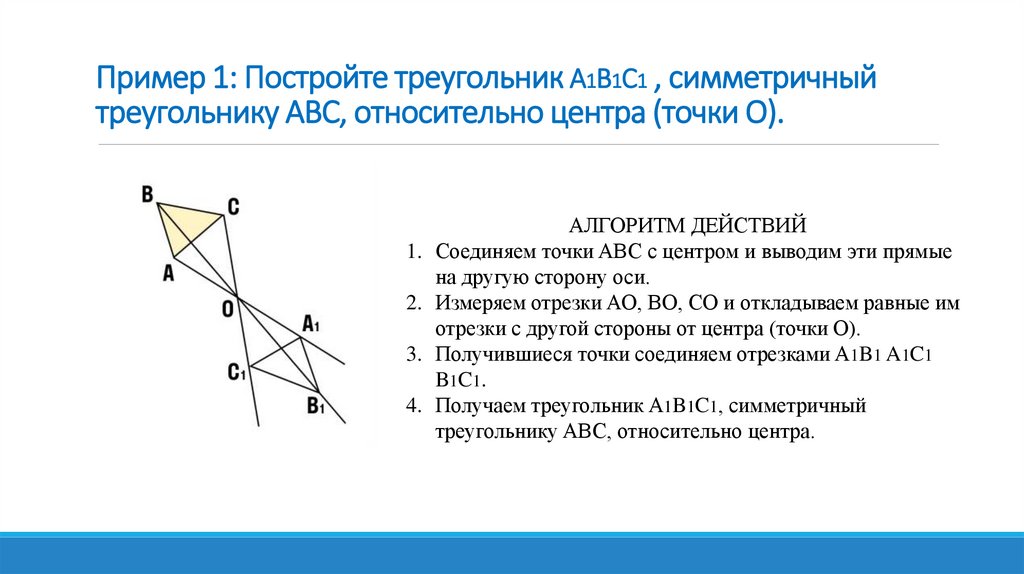
Пример 1: Постройте треугольник A1B1C1 , симметричныйтреугольнику ABC, относительно центра (точки О).
АЛГОРИТМ ДЕЙСТВИЙ
1. Соединяем точки ABC c центром и выводим эти прямые
на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им
отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A1B1 A1C1
B1C1.
4. Получаем треугольник A1B1C1, симметричный
треугольнику ABC, относительно центра.
18.
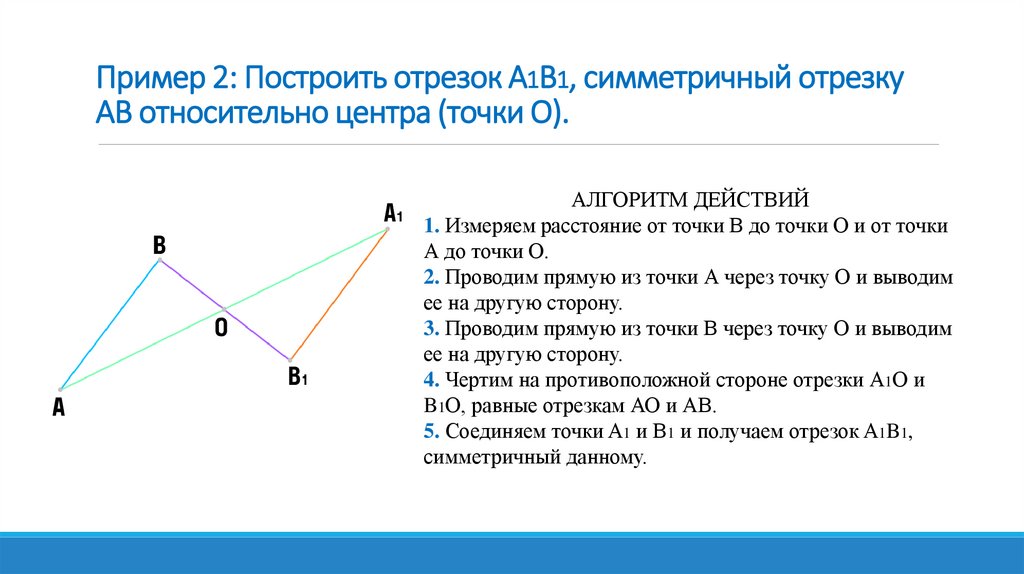
Пример 2: Построить отрезок A1B1, симметричный отрезкуAB относительно центра (точки О).
АЛГОРИТМ ДЕЙСТВИЙ
1. Измеряем расстояние от точки B до точки О и от точки
А до точки О.
2. Проводим прямую из точки А через точку О и выводим
ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим
ее на другую сторону.
4. Чертим на противоположной стороне отрезки А1О и
B1О, равные отрезкам АО и АB.
5. Соединяем точки A1 и B1 и получаем отрезок A1B1,
симметричный данному.
19.
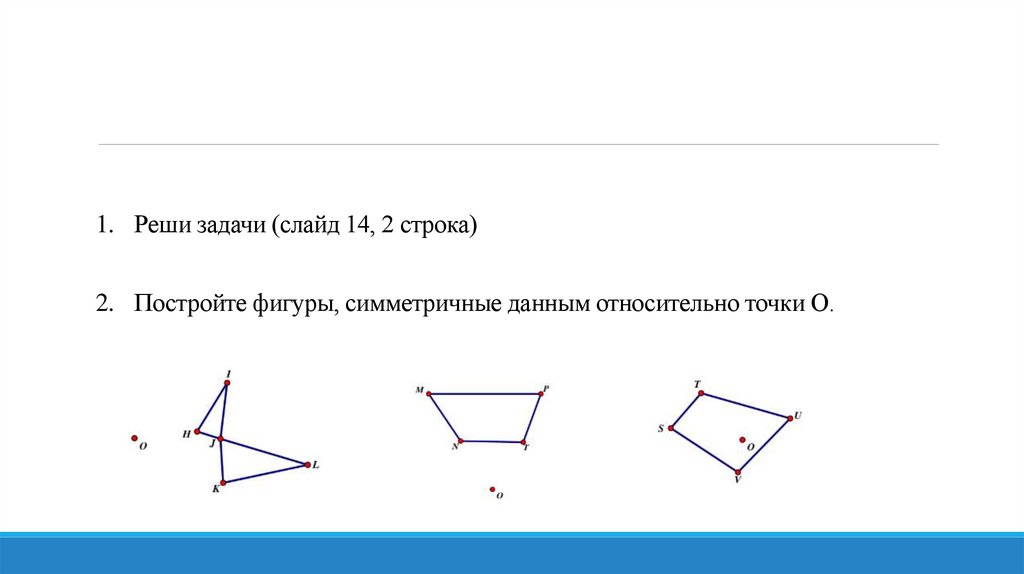
1. Реши задачи (слайд 14, 2 строка)2. Постройте фигуры, симметричные данным относительно точки О.














 mathematics
mathematics