Similar presentations:
Удвоение медианы. Центральная симметрия (8 класс)
1.
Геометрия8 класс
Тема: Удвоение медианы.
Центральная симметрия.
2.
Сегодня мы познакомимся с методомудвоения медианы, узнаем определение
центральной симметрии.
3.
ВСПОМНИ!Что называют трапецией?
Четырёхугольник, две стороны которого параллельны, а две другие не
параллельны, называется трапецией.
• Что называют основанием трапеции, а какие стороны называют
боковыми?
Параллельные стороны называются основаниями трапеции, непараллельные
стороны – боковыми сторонами.
• Какую трапецию называют прямоугольной?
Если один из углов трапеции прямой, то она называется прямоугольной.
• Какую трапецию называют равнобокой?
Если боковые стороны трапеции равны, то она называется равнобедренной
трапецией (равнобокой).
4.
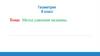
Рассмотрим треугольник ABC, в котором проведена медиана BM.В
А
М
С
5.
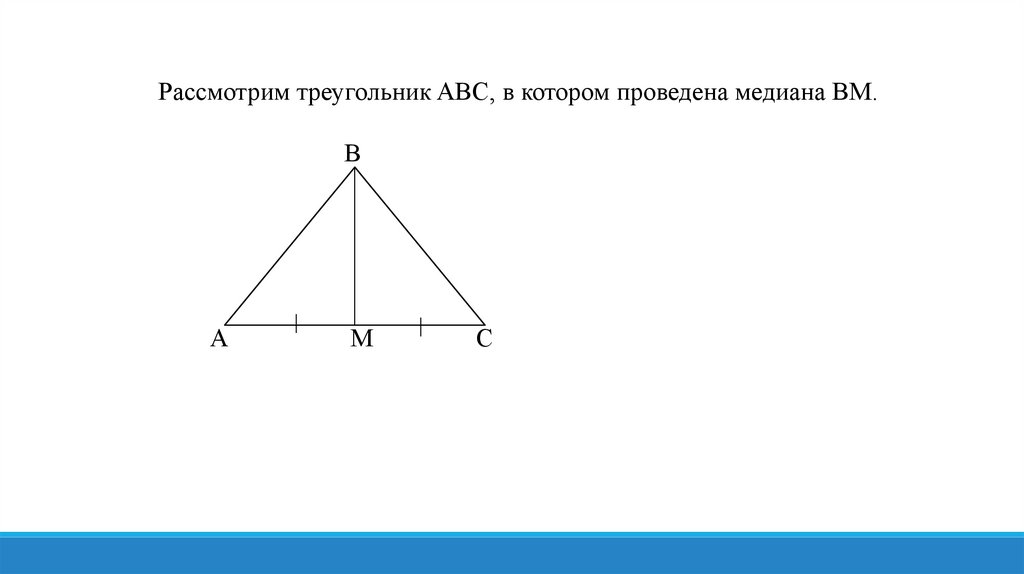
Удвоим эту медиану, т.е. проведем отрезок MD: MD=BM.В
А
М
D
С
6.
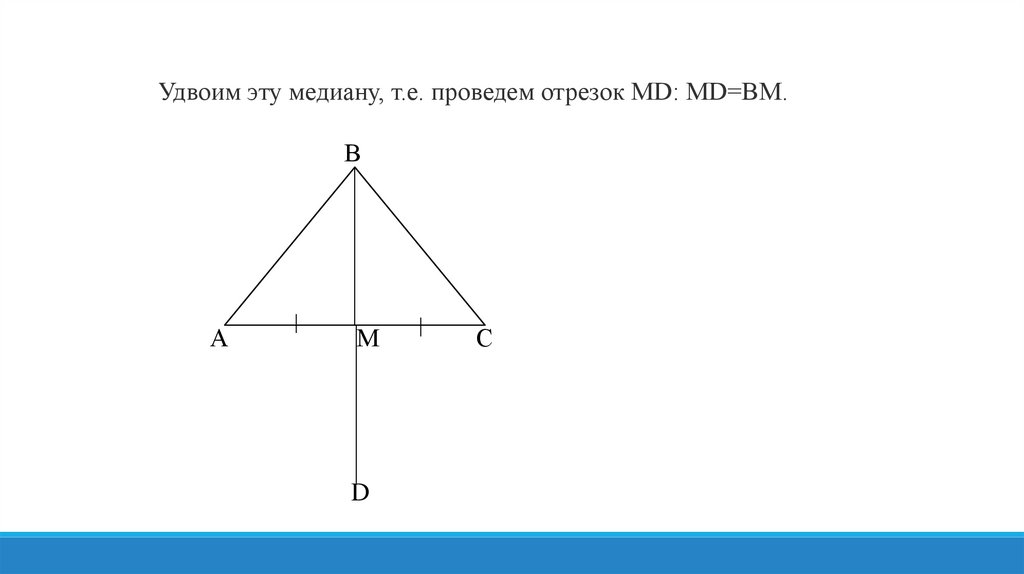
Получили параллелограмм ABCD (по признаку: диагонали делятсяточкой пересечения пополам).
В
А
М
С
D
В ряде задач с этим параллелограммом очень удобно
работать.
7.
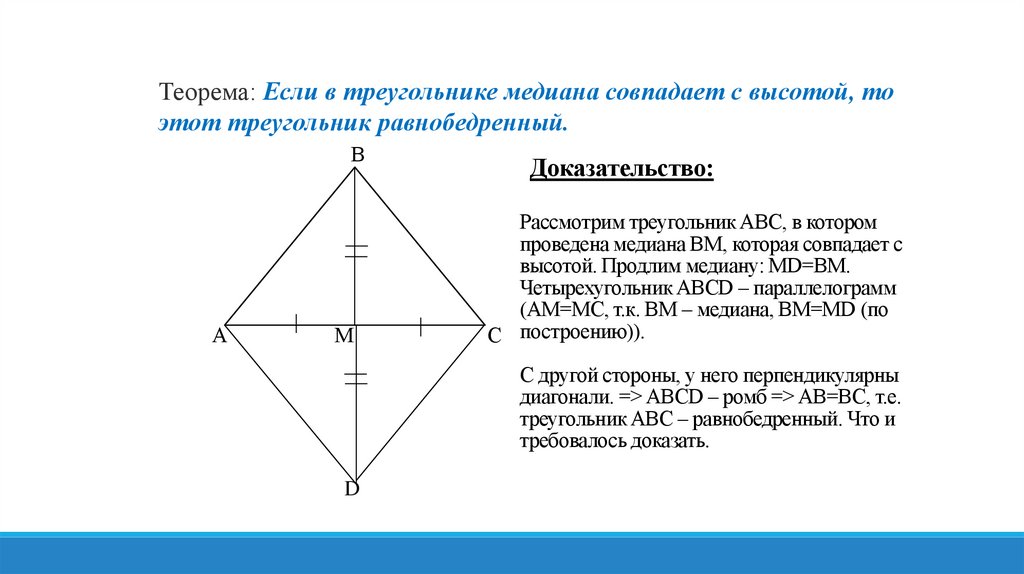
Теорема: Если в треугольнике медиана совпадает с высотой, тоэтот треугольник равнобедренный.
В
А
М
Доказательство:
Рассмотрим треугольник ABC, в котором
проведена медиана BM, которая совпадает с
высотой. Продлим медиану: MD=BM.
Четырехугольник ABCD – параллелограмм
(AM=MC, т.к. BM – медиана, BM=MD (по
С построению)).
С другой стороны, у него перпендикулярны
диагонали. => ABCD – ромб => AB=BC, т.е.
треугольник ABC – равнобедренный. Что и
требовалось доказать.
D
8.
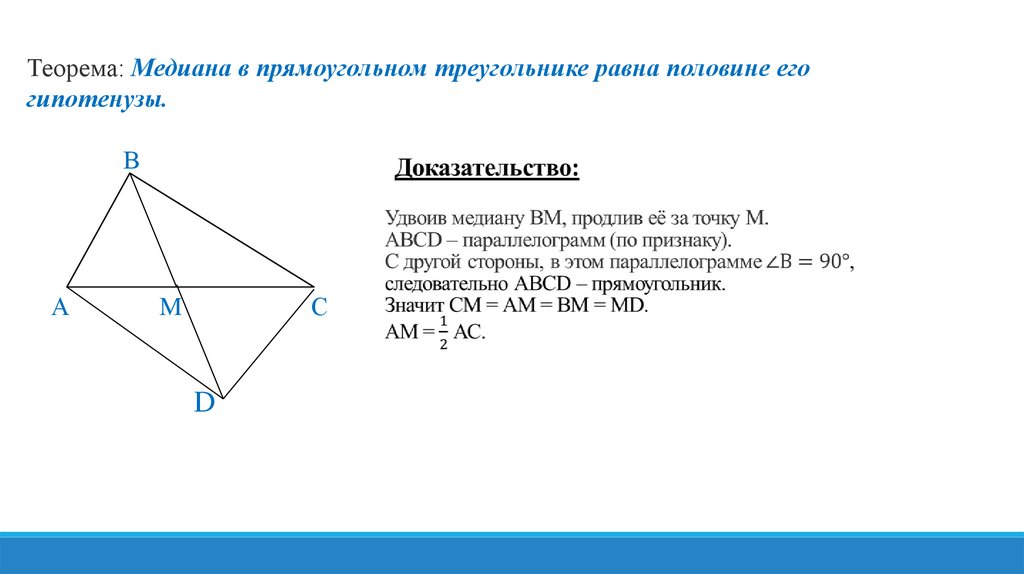
Теорема: Медиана в прямоугольном треугольнике равна половине егогипотенузы.
В
А
С
M
D
9.
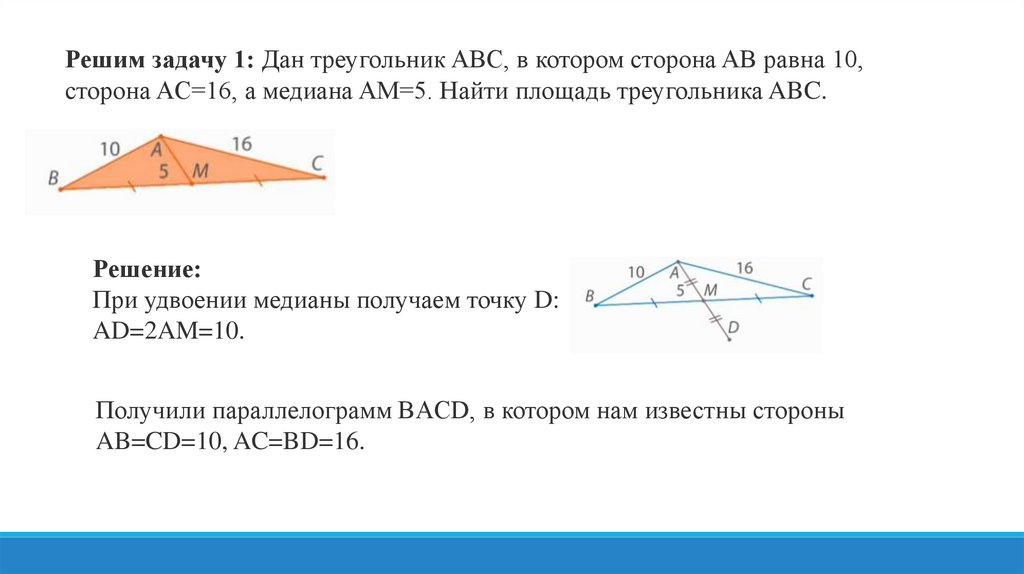
Решим задачу 1: Дан треугольник ABC, в котором сторона AB равна 10,сторона AC=16, а медиана AM=5. Найти площадь треугольника ABC.
Решение:
При удвоении медианы получаем точку D:
AD=2AM=10.
Получили параллелограмм BACD, в котором нам известны стороны
AB=CD=10, AC=BD=16.
10.
Продолжение решения задачи 111.
Cделаем вывод:Если в задаче дана медиана, то очень часто полезно ее удвоить, чтобы
свести задачу к параллелограмму, ромбу или прямоугольнику, с
помощью чего можно решать ряд задач.
12.
Центральная симметрияТеперь поговорим о центральной симметрии — вот ее определение:
Центральной симметрией называется симметрия относительно точки.
На картинках центральная симметрия: точка O здесь — центр симметрии.
Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду.
Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.
13.
Давайте разберемся, как построить центральнуюсимметрию и рассмотрим алгоритм построения
фигур с центральной симметрией.
14.
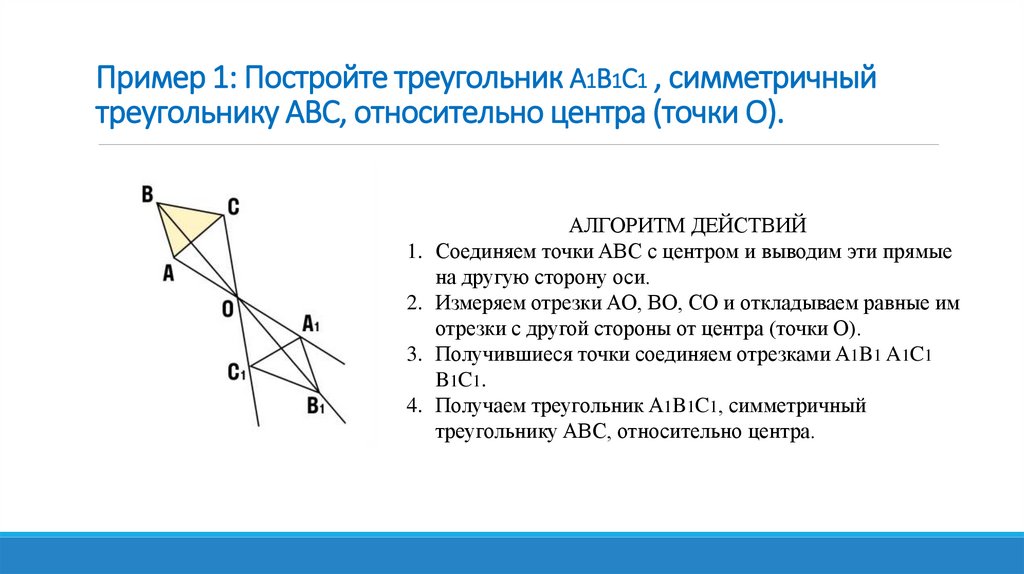
Пример 1: Постройте треугольник A1B1C1 , симметричныйтреугольнику ABC, относительно центра (точки О).
АЛГОРИТМ ДЕЙСТВИЙ
1. Соединяем точки ABC c центром и выводим эти прямые
на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им
отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A1B1 A1C1
B1C1.
4. Получаем треугольник A1B1C1, симметричный
треугольнику ABC, относительно центра.
15.
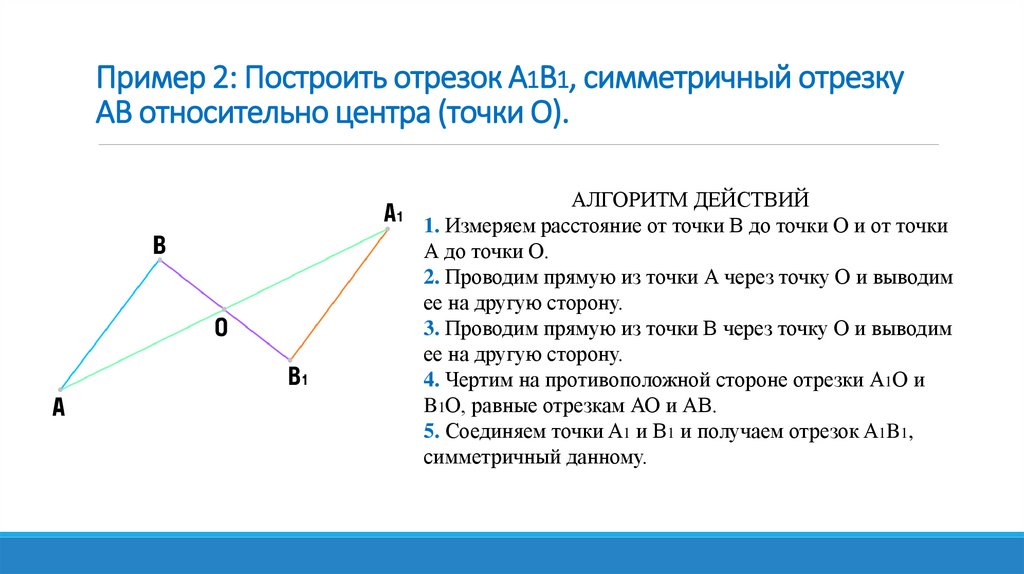
Пример 2: Построить отрезок A1B1, симметричный отрезкуAB относительно центра (точки О).
АЛГОРИТМ ДЕЙСТВИЙ
1. Измеряем расстояние от точки B до точки О и от точки
А до точки О.
2. Проводим прямую из точки А через точку О и выводим
ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим
ее на другую сторону.
4. Чертим на противоположной стороне отрезки А1О и
B1О, равные отрезкам АО и АB.
5. Соединяем точки A1 и B1 и получаем отрезок A1B1,
симметричный данному.
16.
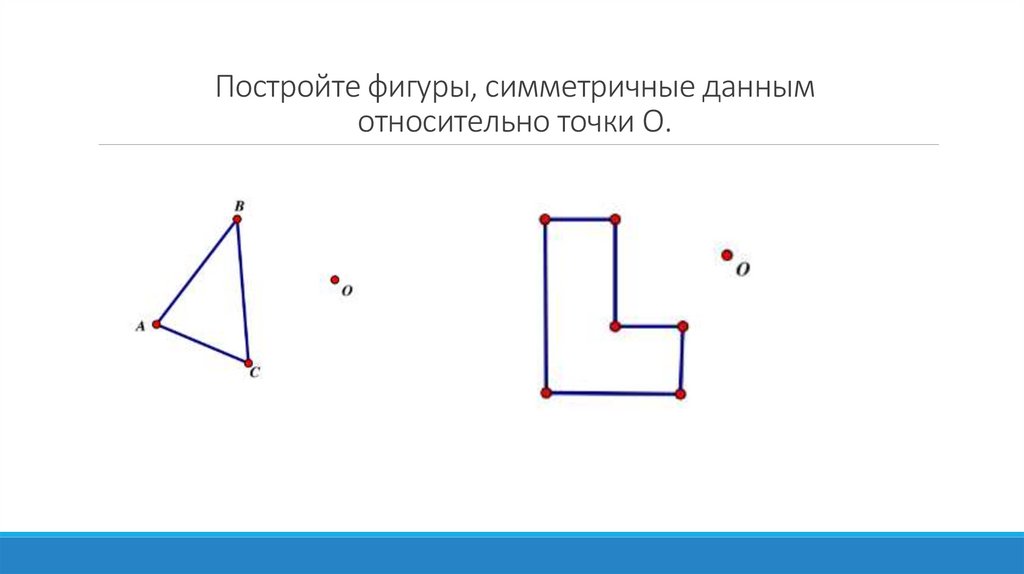
Задачи для классной работы:17.
Постройте фигуры, симметричные даннымотносительно точки О.








 mathematics
mathematics