Метод удвоения медианы

1.

Метод
удвоения
медианы

2.

Рассмотрим треугольник ABC, в котором проведена
медиана BM.

3.

Удвоим эту медиану, т.е. проведем отрезок MD:
MD=BM.

4.

Получили параллелограмм ABCD (по признаку:
диагонали делятся точкой пересечения пополам).
В ряде задач с этим параллелограммом очень удобно работать.

5.

Теорема: Если в треугольнике медиана совпадает с
высотой, то этот треугольник равнобедренный.
Доказательство:
Рассмотрим треугольник ABC, в
котором проведена медиана BM,
которая совпадает с высотой.
Продлим медиану: MD=BM.
Четырехугольник ABCD –
параллелограмм (AM=MC, т.к.
BM – медиана, BM=MD (по
построению)).
С другой стороны, у него
перпендикулярны диагонали. =>
ABCD – ромб => AB=BC, т.е.
треугольник ABC –
равнобедренный. Что и
требовалось доказать.

6.

Теорема: Медиана в прямоугольном
треугольнике равна половине его гипотенузы.
Доказательство:
Удвоив медиану ВМ, продлив её
за точку М.
АВСD – параллелограмм (по
признаку).
C другой стороны, в этом
параллелограмме ∠В = 90°,
следовательно АВСD –
прямоугольник.
Значит СМ = АМ = ВМ = МD.
1
ВМ = АС.
2

7.

Дан треугольник ABC, в котором сторона AB равна 10,
сторона AC=16, а медиана AM=5. Найти площадь
треугольника ABC.
Решение:
При удвоении медианы
получаем точку D:
AD=2AM=10.
Получили параллелограмм BACD, в котором нам
известны стороны AB=CD=10, AC=BD=16.

8.

Рассмотрим треугольник BAD.
В этом треугольнике мы знаем все 3 стороны: 10, 10, 16.
Получился равнобедренный
треугольник.
Проведём высоту АН.
По теореме Пифагора АН = 6.
1
1
SBAD= · BD · AH = · 16 · 6 = 48.
2
2
SABCD= 2· SABD= 2· SABC
SABC = SABD= 48.

9.

ВЫВОД!!!
Если в задаче дана медиана, то очень
часто полезно ее удвоить, чтобы свести
задачу к параллелограмму, ромбу или
прямоугольнику, с помощью чего можно
решать ряд задач.

10.

Осевая и
центральная
симметрия

11.

Слово «симметрия» греческое ( συμμετρία), оно
означает “соразмерность, пропорциональность,
одинаковость в расположении частей”,
неизменность при каких-либо преобразованиях.
Симметрия является той идеей,
с помощью которой человек
веками пытается объяснить и
создать порядок, красоту и
совершенство.
Герман Вейль.

12.

А
а
О
А1
Две точки А и А1 называются
симметричными относительно прямой а,
если эта прямая проходит через середину
отрезка АА1 и перпендикулярна к нему
а – ось симметрии

13.

Осевая симметрия (алгоритм построения)
1) Проведём через точку А
прямую АO,перпендикулярную
оси симметрии a.
2) С помощью циркуля отложим на
прямой АO отрезок OА1, равный
отрезку OА.
А1
А
а

14.

Являются ли данные точки
симметричными ?
М
b
m
а
D
М1
Рисунок 1
С
Рисунок 2
В1
B
Рисунок 3

15.

А
В
АВСD - квадрат
а
D
С
Фигура называется симметричной
относительно прямой а, если для каждой
точки фигуры симметричная ей точка
относительно прямой а также принадлежит
этой фигуре

16.

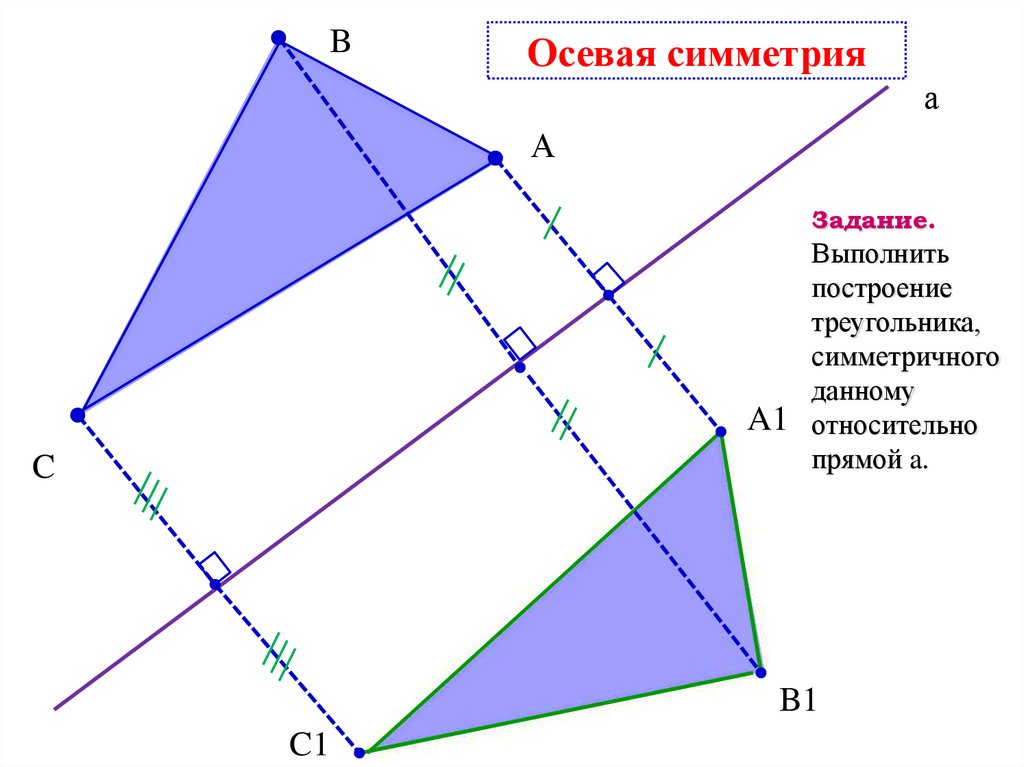
B
Осевая симметрия
а
А
Задание.
Выполнить
построение
треугольника,
симметричного
данному
A1 относительно
прямой a.
C
B1
C1

17.

Геометрические фигуры,
обладающие осевой симметрией

18.

Фигуры, обладающие осевой
симметрией

19.

Сколько осей
симметрии имеет:
- Отрезок
- Прямая
А
В
одна
- Луч
а
множество
О
Е
Ни одной

20.

А
О
А1
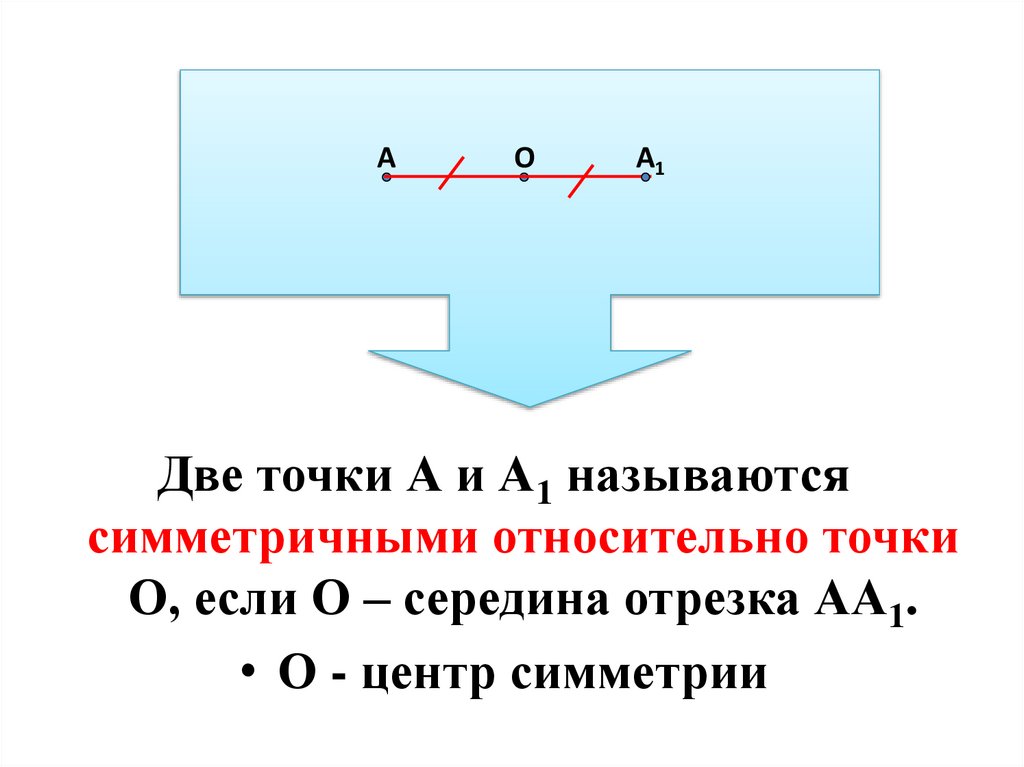
Две точки А и А1 называются
симметричными относительно точки
О, если О – середина отрезка АА1.
• О - центр симметрии

21.

Центральная симметрия (алгоритм построения)
Отметим на листе бумаги
произвольные точки O и A.
Проведём через точки прямую
OA.
А1
О
На этой прямой
отложим от точки O
отрезок OA1, равный
отрезку AO, но по
другую сторону от
точки O.
А
Точка А симметрична точке А1 относительно точки О.
О - центр симметрии.

22.

В
С
О
А
Д
Фигура называется симметричной
относительно точки О, если для каждой
точки фигуры симметричная ей точка
относительно О также принадлежит этой

23.

Центральная симметрия
В
Задание.
А
Выполнить построение
треугольника, симметричного
данному, относительно точки
O.
О
С1
С
А1
В1

24.

Задание .
Выполнить построение трапеции, симметричной данной,
относительно точки O.
B
C
1) Проведём от вершин трапеции через
точку O лучи AO, BO, CO, DO.
D
A
O
2)
Построим
на
лучах
точки,
симметричные вершинам трапеции,
относительно точки O.
3) Соединим полученные точки.
A1
D1
C1
B1

25.

Являются ли точки симметричными
относительно данной точки
А1
М
С
О
М1
А
В1
В
Рисунок 1
О
Рисунок 3
Рисунок 2

26.

Задание.
Выполнить
построение прямоугольника,
симметричного
данному
относительно
прямой a.
C
D1
a
C1
D
B
B1
A
A1
1) Проведём от вершин прямоугольника прямые, перпендикулярные
данной прямой a.
2) Построим точки, симметричные вершинам прямоугольника.
3) Соединим полученные точки.

27.

Геометрические фигуры, обладающие
центральной симметрией
О
О
О
О

28.

Фигуры, обладающие центральной
симметрией

29.

Имеют ли центр симметрии:
- Отрезок
- Прямая
О
один
О
О1
О2
множество
- Луч
Ни одного

30.

Фигуры,
обладающие
1
центральной симметрией
Фигуры, обладающие осевой
симметрией
2, 4, 6, 8, 9, 11, 13, 15
1, 3, 4, 6, 7, 8, 9, 10, 1, 4, 6, 8, 9, 11, 13, 15
2
Фигуры, имеющие обе
симметрии
3