Построение сечений многогранников

1.

2.

"Те, кто влюбляются в
практику без теории,
уподобляются
мореплавателю,
садящемуся на корабль
без руля и компаса и
потому
никогда
не
знающему,
куда
он
плывет".
Леонардо да Винчи

3.

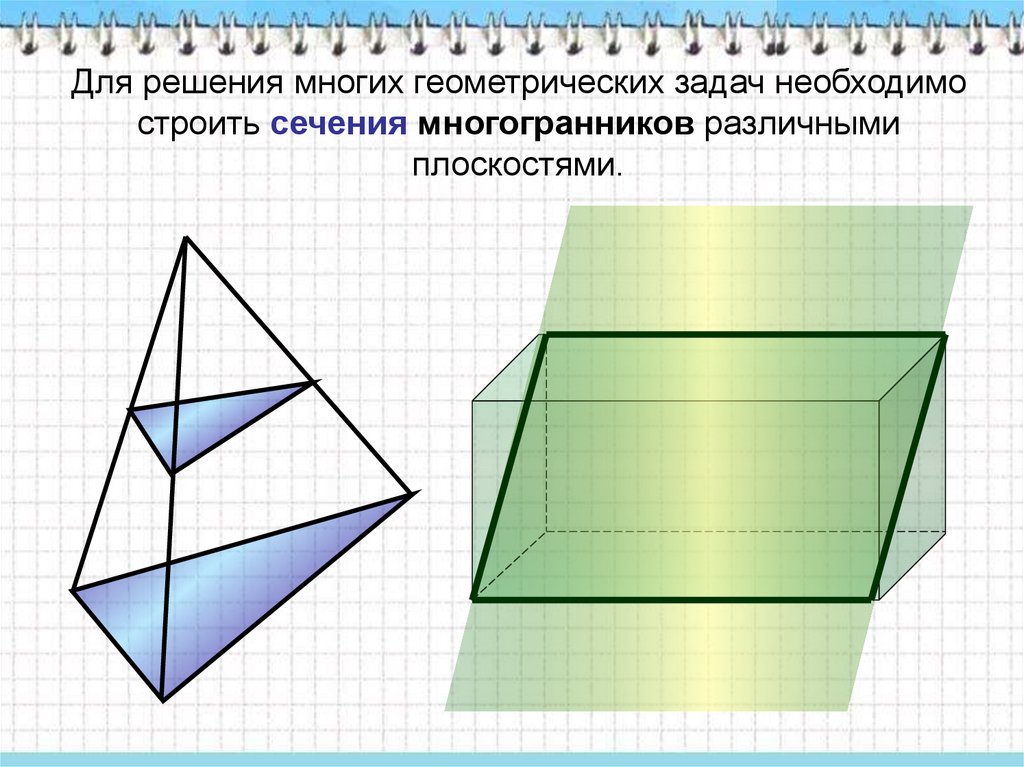
Для решения многих геометрических задач необходимо
строить сечения многогранников различными
плоскостями.

4.

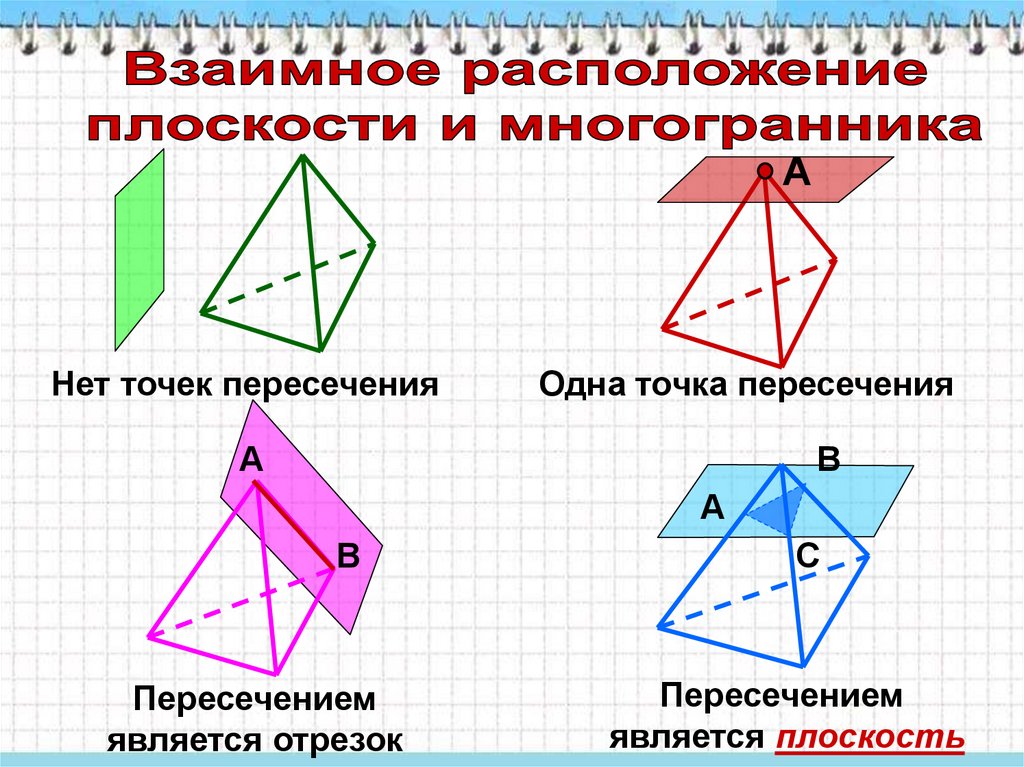
А
Нет точек пересечения
Одна точка пересечения
А
В
А
В
Пересечением
является отрезок
С
Пересечением
является плоскость

5.

Любая плоскость, пересекающая поверхность
многогранника, является секущей плоскостью
Секущей плоскостью параллелепипеда
(тетраэдра) называется любая плоскость,
по обе стороны от которой имеются точки
данного параллелепипеда (тетраэдра).
L

6.

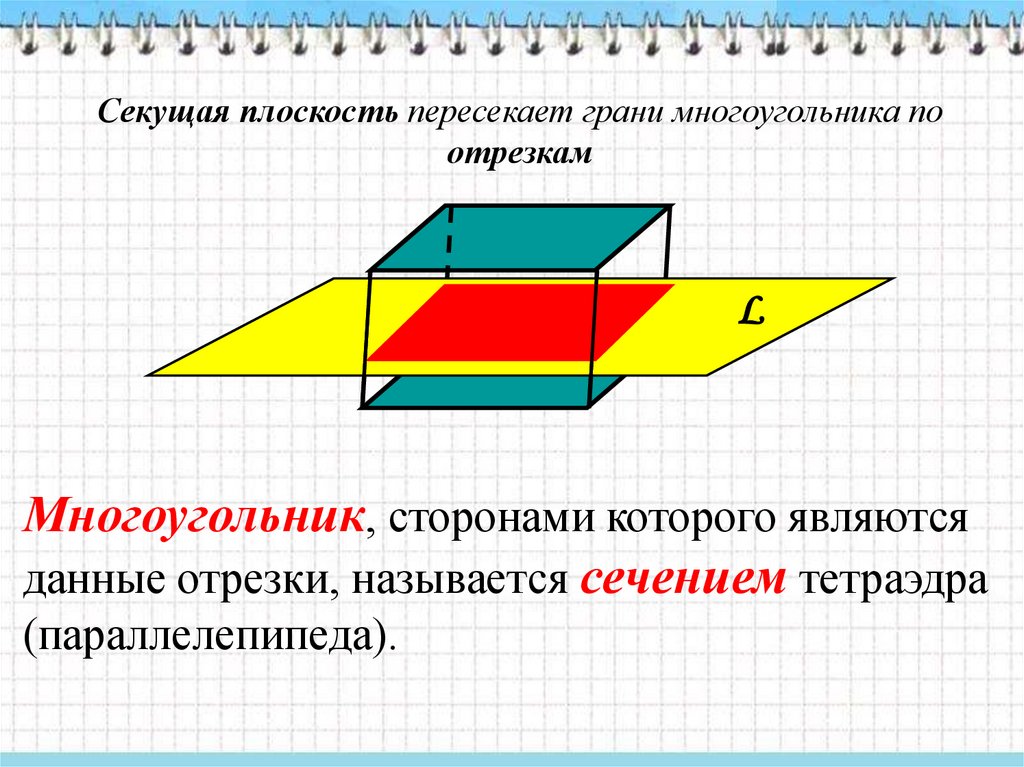
Секущая плоскость пересекает грани многоугольника по
отрезкам
L
Многоугольник, сторонами которого являются
данные отрезки, называется сечением тетраэдра
(параллелепипеда).

7.

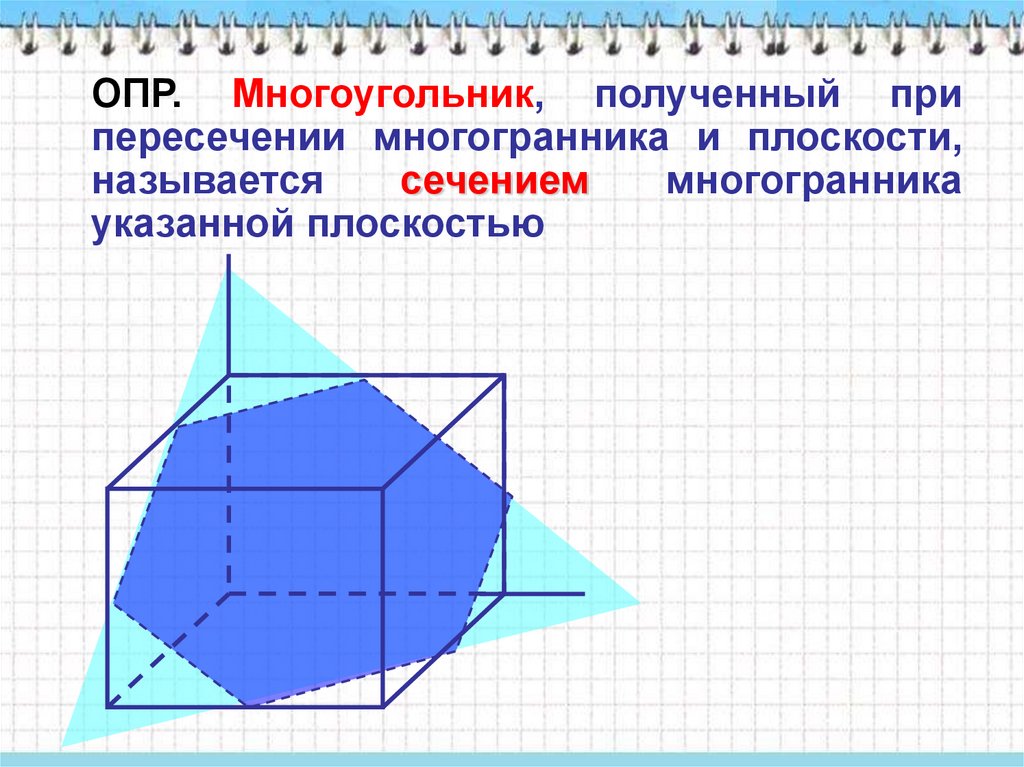
ОПР. Многоугольник, полученный при
пересечении многогранника и плоскости,
называется
сечением
многогранника
указанной плоскостью

8.

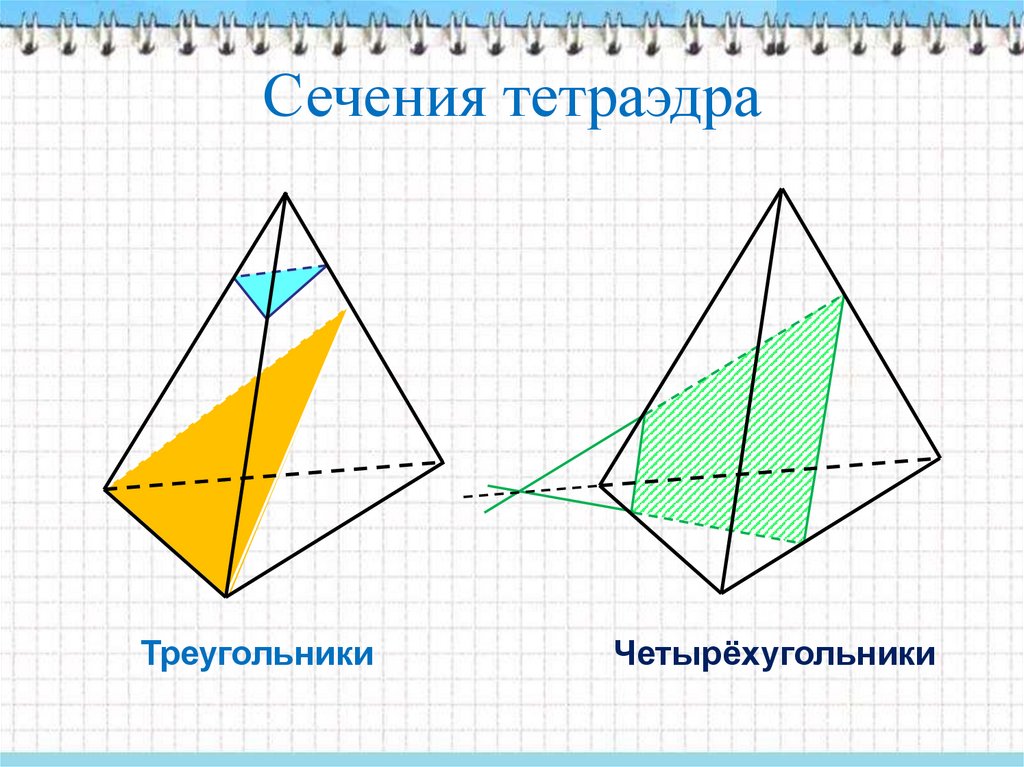
Сечения тетраэдра
Треугольники
Четырёхугольники

9.

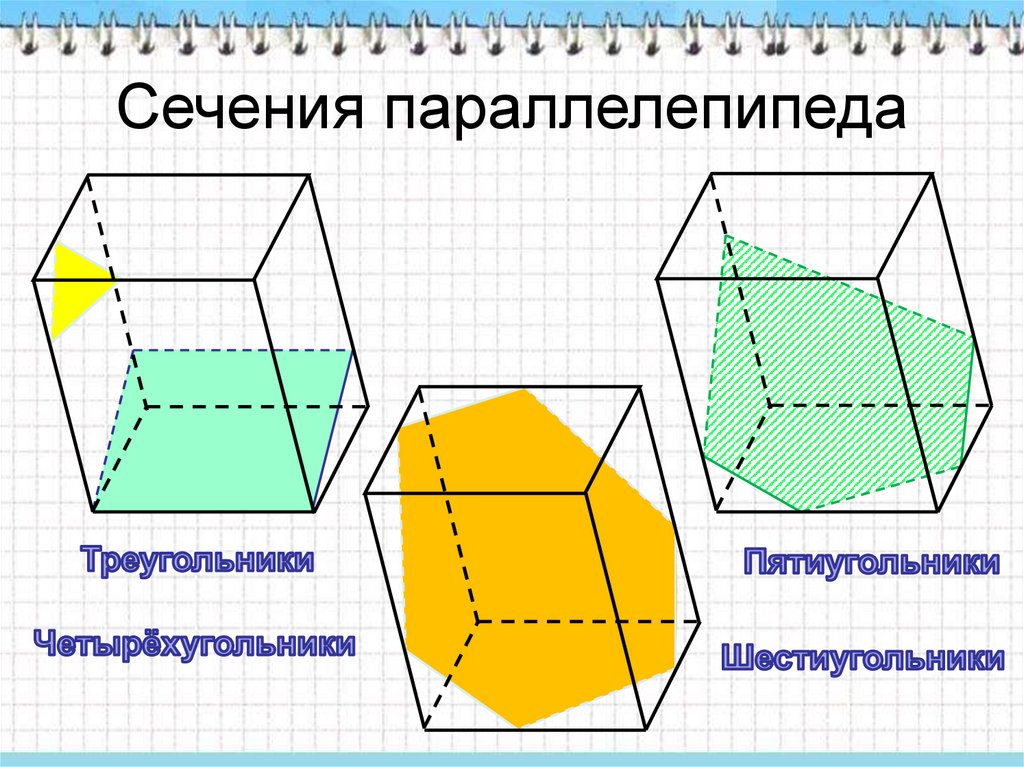
Сечения параллелепипеда

10.

Для построения сечения нужно построить точки
пересечения секущей плоскости с ребрами и
соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
параллельные
грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку.
Для этого необходимо найти точки пересечения уже
построенных прямых с другими прямыми, лежащими
в тех же гранях.

11.

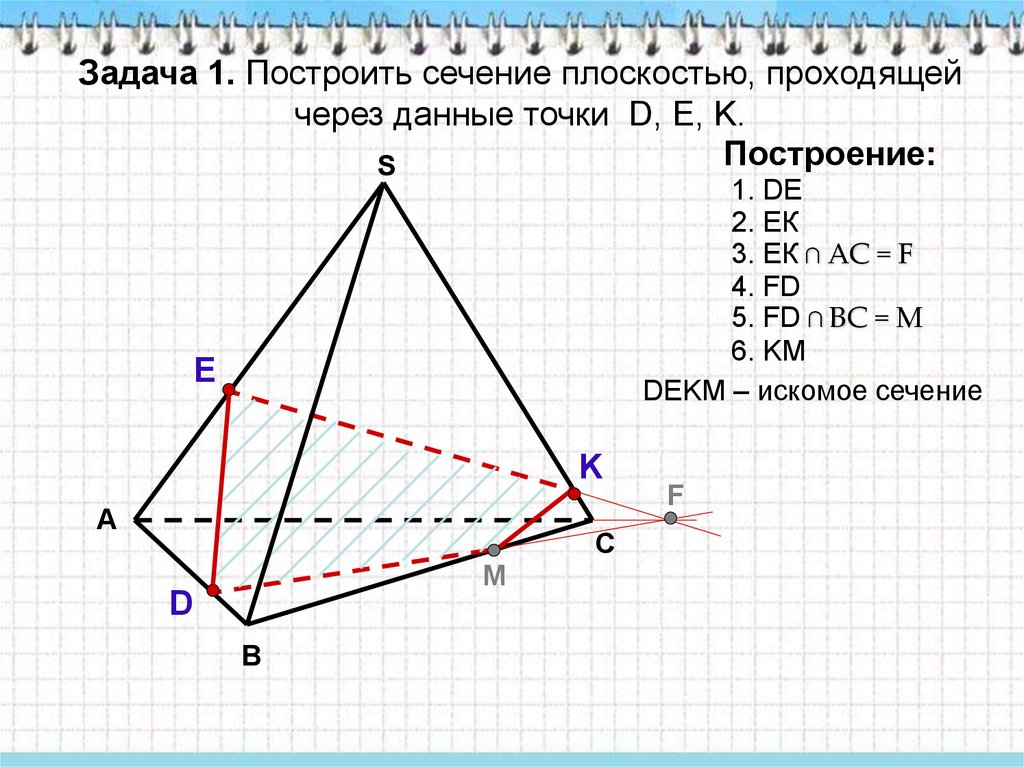
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

12.

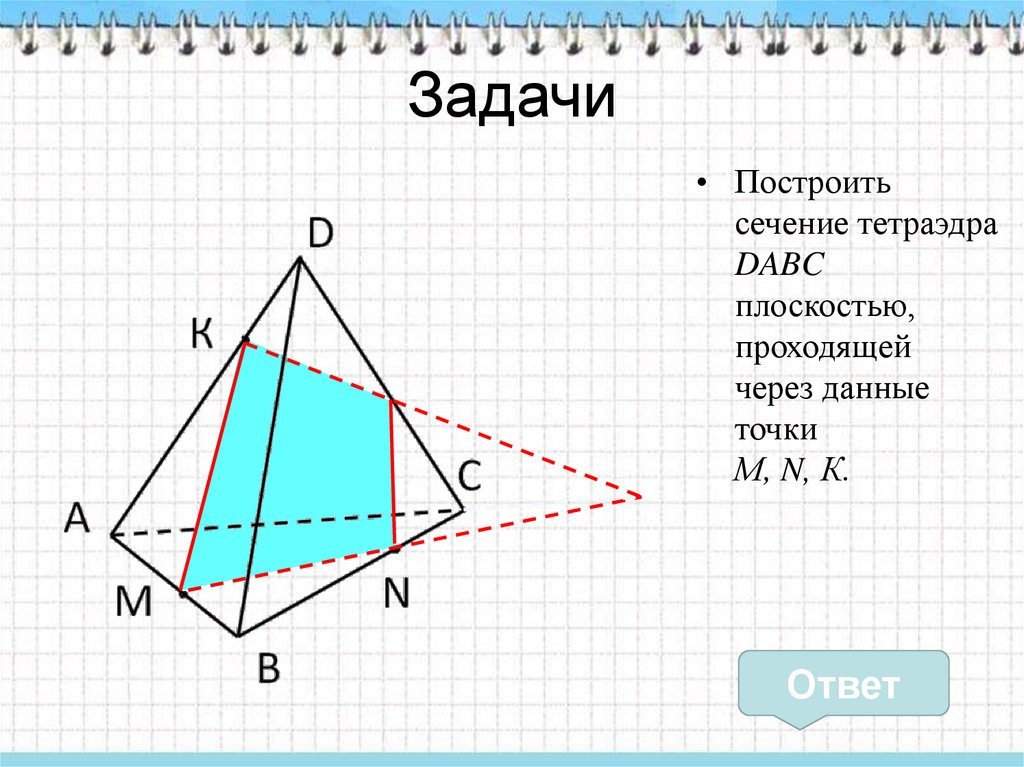
Задачи
• Построить
сечение тетраэдра
DABC
плоскостью,
проходящей
через данные
точки
М, N, К.
Ответ

13.

M
P
M
N
P
M
N
N
P
N
M
N
M
P
N
P
P
M

14.

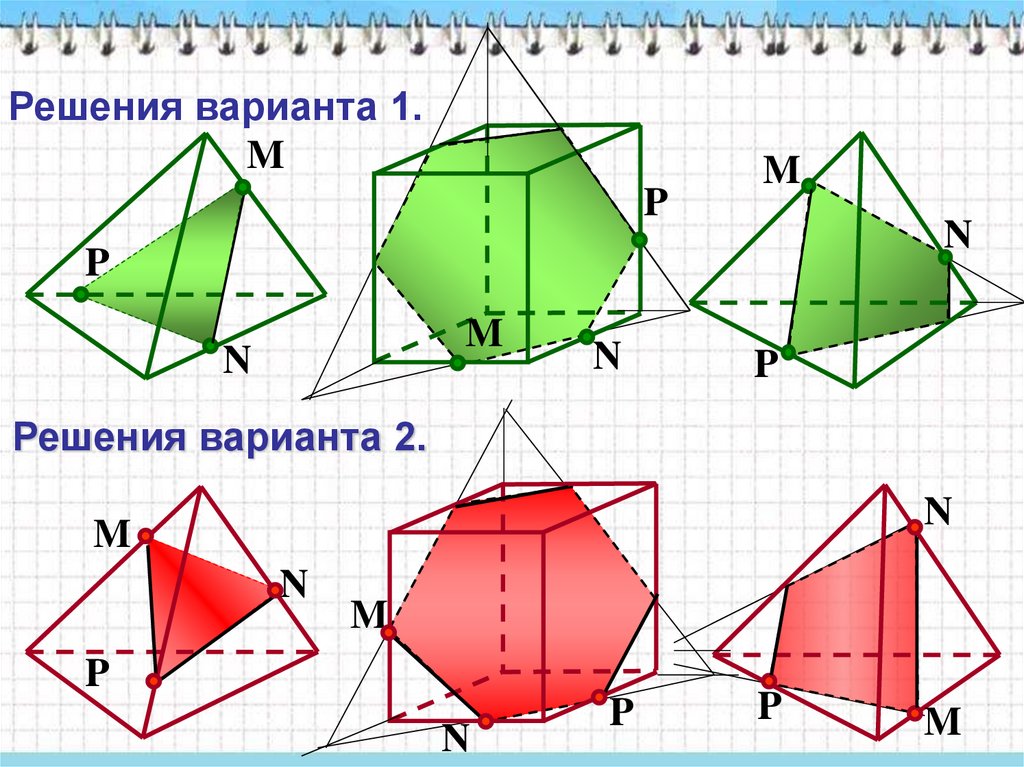
Решения варианта 1.
M
P
M
N
P
M
N
N
P
Решения варианта 2.
N
M
N
M
P
N
P
P
M