Прямоугольник. Ромб, квадрат. Решение задач

1.

Г-8
У-4

2.

Цели учебного занятия:
• Ввести определения прямоугольника,
ромба, квадрата как частных видов
параллелограмма, изучить их
свойства и признаки, закрепить
полученные знания при решении
задач.
•Повторить, обобщить, систематизировать
знания учащихся о параллелограммах.

3.

•Прямоугольник
•Ромб
•Квадрат
•Решение задач

4.

ПРЯМОУГОЛЬНИК
Прямоугольник – это
параллелограмм, у которого
все углы прямые.

5.

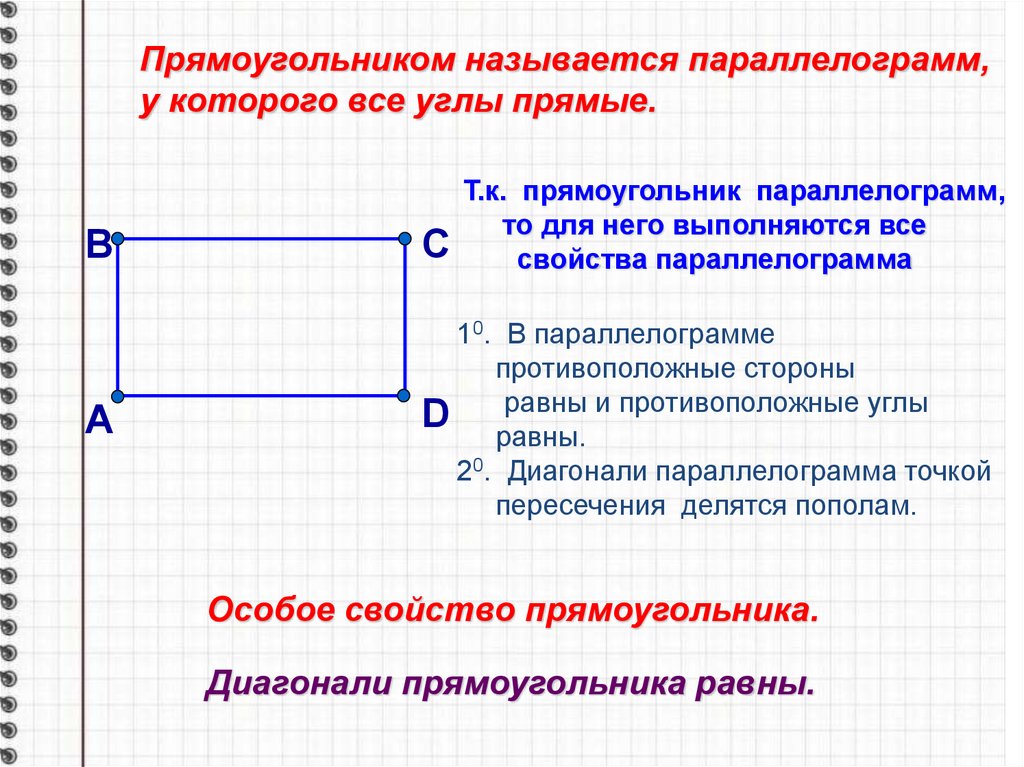
Прямоугольником называется параллелограмм,
у которого все углы прямые.
В
А
Т.к. прямоугольник параллелограмм,
то для него выполняются все
С
свойства параллелограмма
10. В параллелограмме
противоположные стороны
равны и противоположные углы
D равны.
20. Диагонали параллелограмма точкой
пересечения делятся пополам.
Особое свойство прямоугольника.
Диагонали прямоугольника равны.

6.

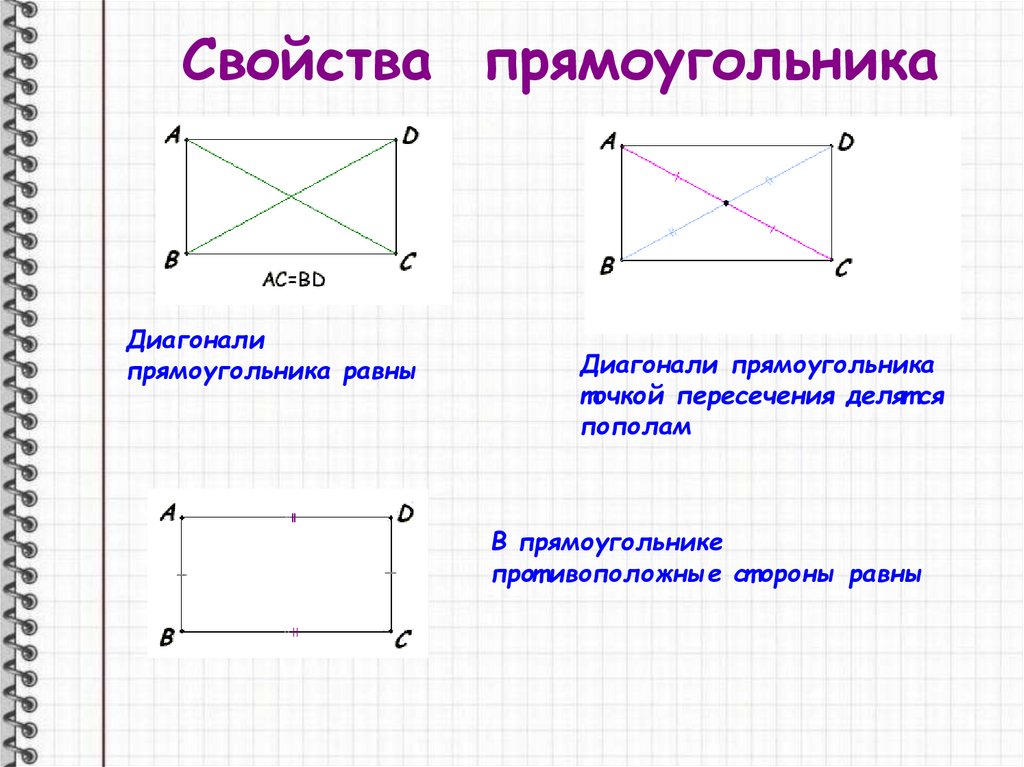
Свойства прямоугольника
Диагонали
прямоугольника равны
Диагонали прямоугольника
точкой пересечения делят ся
пополам
В прямоугольнике
прот ивоположные ст ороны равны

7.

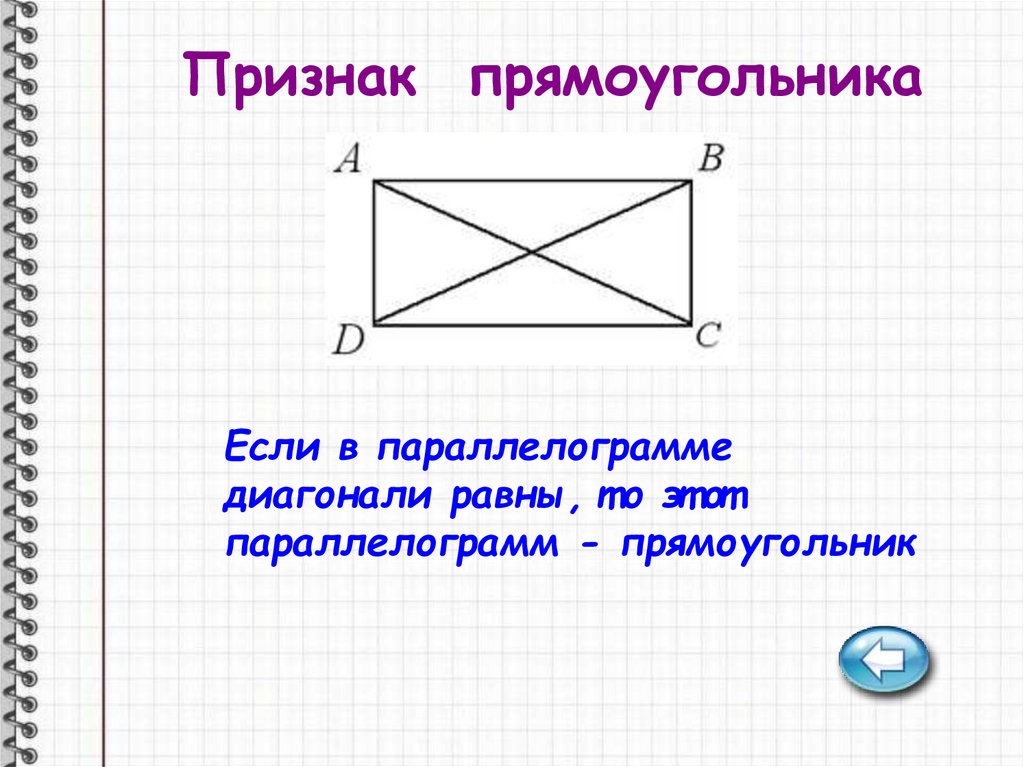
Признак прямоугольника
Если в параллелограмме
диагонали равны, т о эт от
параллелограмм - прямоугольник

8.

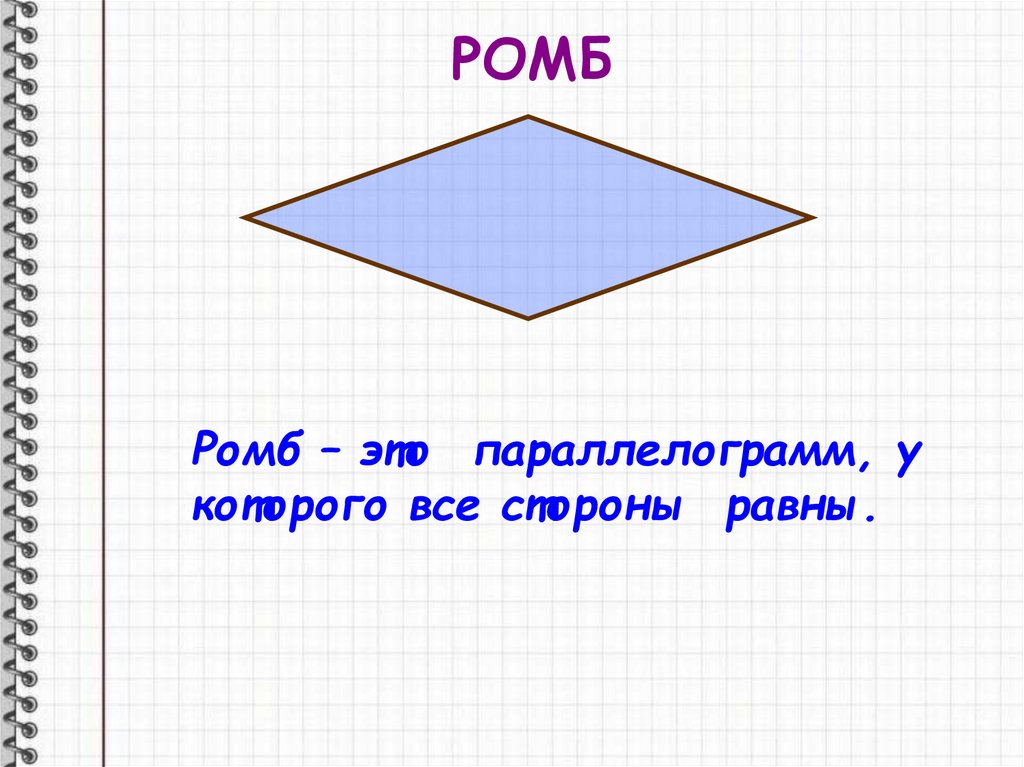
РОМБ
Ромб – это параллелограмм, у
которого все стороны равны.

9.

Слово ромб
произошло от
греческого слова
rombos – “бубен”.
Впервые термин
употребляется у
древнегреческих
учёных Герона и
Паппа
Александрийского

10.

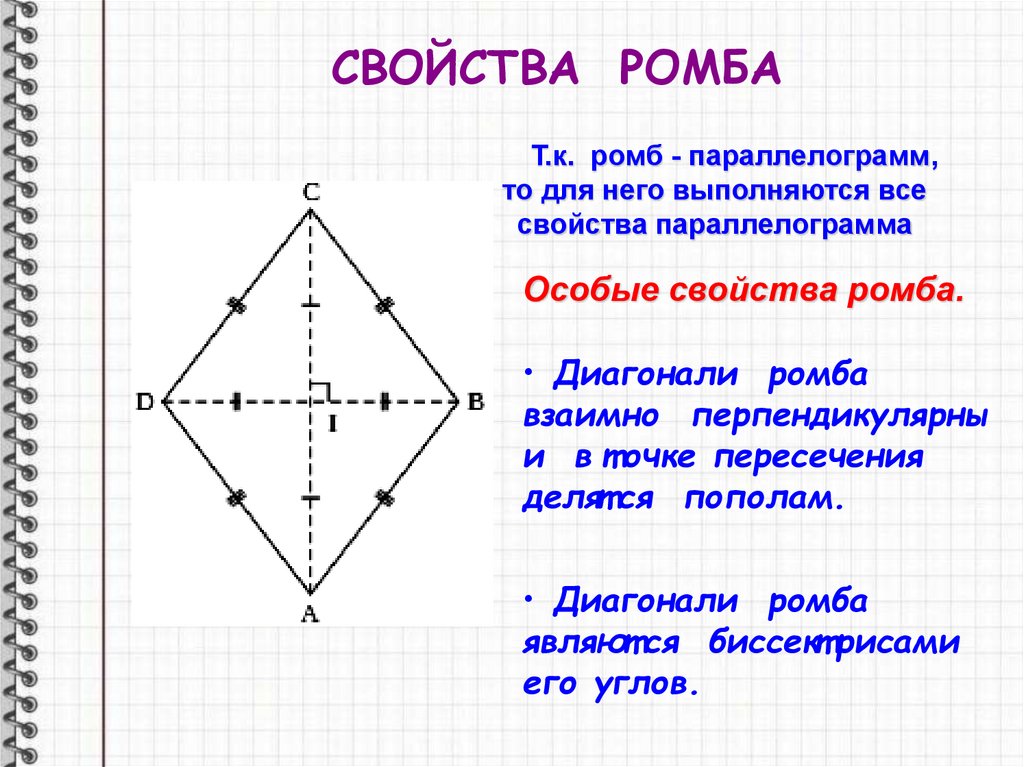
СВОЙСТВА РОМБА
Т.к. ромб - параллелограмм,
то для него выполняются все
свойства параллелограмма
Особые свойства ромба.
• Диагонали ромба
взаимно перпендикулярны
и в т очке пересечения
делят ся пополам.
• Диагонали ромба
являют ся биссект рисами
его углов.

11.

ПРИЗНАК
РОМБА
Если у параллелограмма диагонали
взаимно перпендикулярны, то этот
параллелограмм является ромбом.

12.

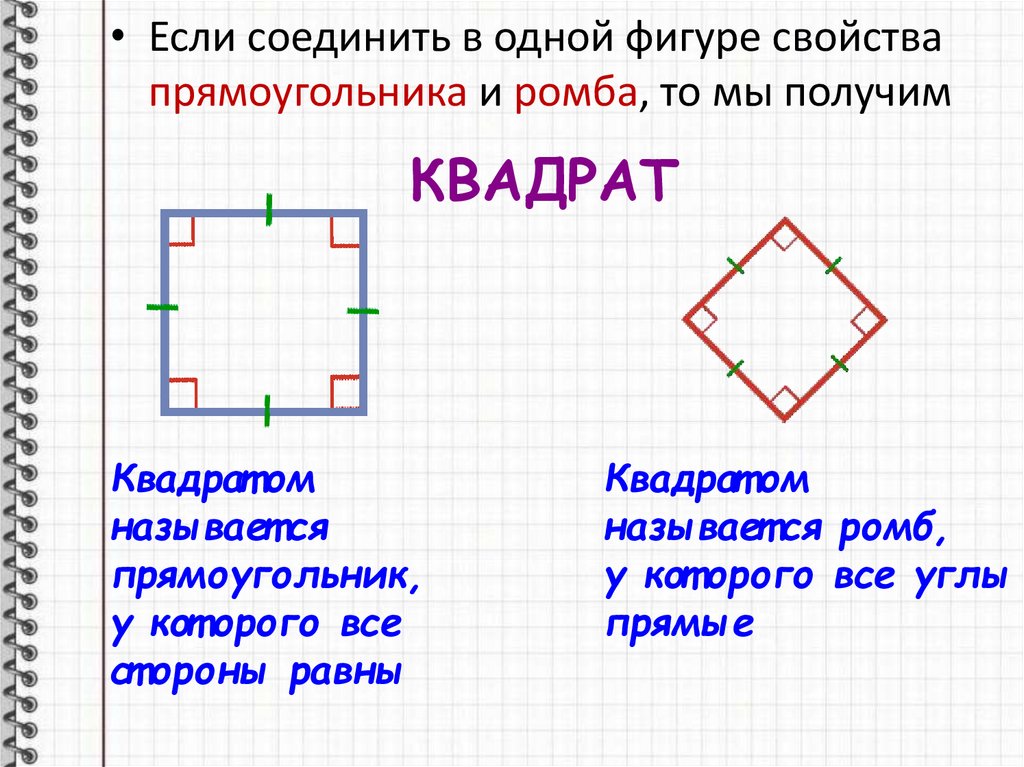
• Если соединить в одной фигуре свойства
прямоугольника и ромба, то мы получим
КВАДРАТ
Квадрат ом
называет ся
прямоугольник,
у кот орого все
ст ороны равны
Квадрат ом
называет ся ромб,
у кот орого все углы
прямые

13.

Слово квадрат
Квадратом
произошло от
также называют
латинского слова возведение
quadratus –
в степень 2
“четырехугольный”
(от guattuor χ²
“четыре”).
3²
5²
Y²

14.

СВОЙСТВА КВАДРАТА
Т.к. квадрат - параллелограмм,
то для него выполняются все
свойства параллелограмма
Особые свойства квадрата.
Все углы квадрат а прямые.
Диагонали квадрат а равны.
Диагонали квадрат а взаимно
перпендикулярны, т очкой пересечения
делят ся пополам.
Диагонали квадрат а делят углы
квадрат а пополам.

15.

Признаки квадрата
* Если в параллелограмме диагонали
перпендикулярны и равны, т о эт от
параллелограмм – квадрат
* Если в прямоугольнике диагонали
перпендикулярны, т о эт от прямоугольник –
квадрат
* Если в ромбе диагонали равны, т о
эт от ромб - квадрат

16.

Перенести схему в тетрадь и заполнить ее
опираясь на изложенный выше материал
(определения и свойства)
Для удобства дальнейшей работы со схемой, можно
использовать различные цвета
На следующем уроке в классе проверим
качество ее заполнения

17.

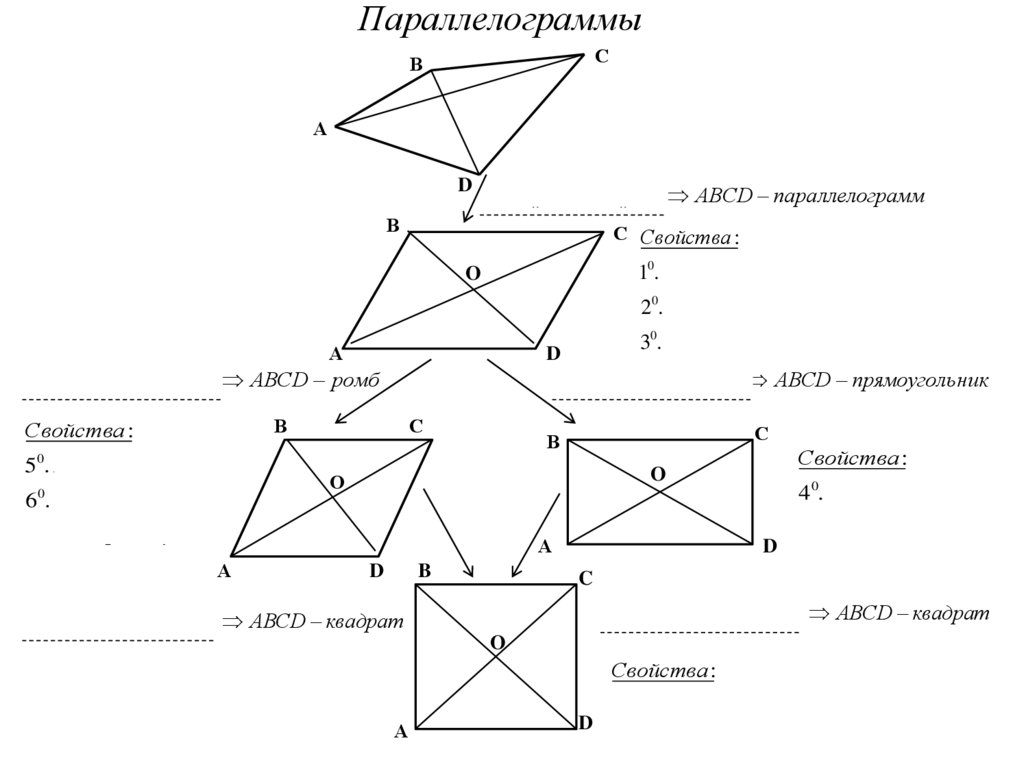
Параллелограммы
С
В
А
D
АВ || DС , ВС || AD АВСD параллелограмм
В
С Свойства :
10. АО АС; ВО ОD
O
2 0. А C ; В D
А
D
АВ DС ВС AD АВСD ромб
А В С D АВСD прямоуголь ник
В
Свойства :
50. АС ВD ;
30. АВ DС ; ВС АD
С
С
В
О
6 . АС и ВD
биссектрисы углов
0
А
А
Свойства :
O
D
B
40. АС ВD
D
C
АВ DС ВС AD АВСD квадрат
А В С D АВСD квадрат
O
Свойства :
А
D
10 , 20 , 30 , 40 , 50 , 60

18.

1 Решите задачи в тетради:
8
16
Дано : АВСD прямоуголь ник
Найти : СОD
Ответ : 60
0

19.

Решите
задачи
в
тетради:
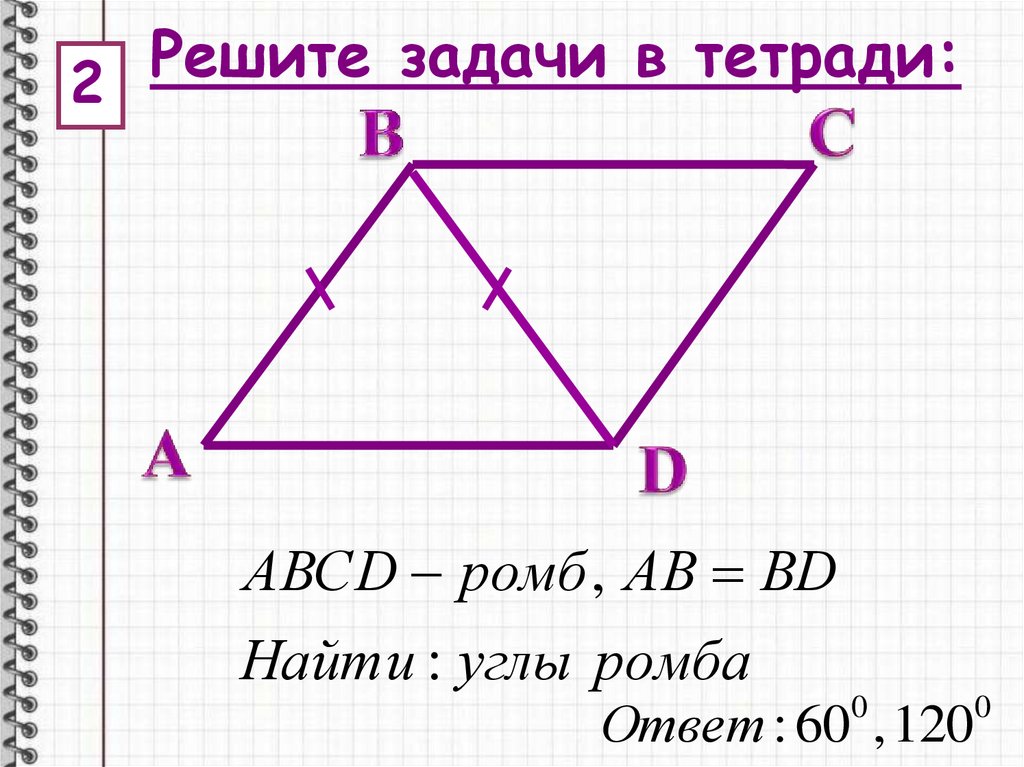
2
АВСD ромб , АВ ВD
Найти : углы ромба
Ответ : 60 , 120
0
0

20.

Домашнее задание
- Выполнить конспект по презентации,
- Выучить все определения, свойства и признаки
фигур, подготовиться к математическому
диктанту по теории.
- На выбор можно решить любые две задачи.
Задача 1.
Диагонали прямоугольника АВСD пересекаются в
точке О, АВО = 36 . Найдите АОD.
Задача 2.
Найдите периметр ромба ABCD, если В = 120 ,
а BD=8 см.
Задача 3.
Периметр ромба ABCD равен 16 см. Высота,
опущенная к стороне AD из вершины B, равна
2 см. Найдите углы ромба.

21.

Улыбнись, но запомни!!!!
Как только бросили нам клич
Мы все тут тотчас собрались.
Я - параллелограмм
Важнее всех фигур,
Я всех их свойствами своими наделил.
Но их достоинств я не смею умалить
Ведь место в геометрии есть и для них.
Хоть стороны мои попарно и равны и
параллельны,
Всёж я в печали, что не равны мои диагонали,
Да и углы они не делят пополам.

22.

• А я - особый параллелограмм,
Все стороны мои наклонены,
Да и к тому же все равны.
• Меня за это ромбом величают,
Геометрической фигурой называют
Диагонали под прямым углом пройдут,
Они же тотчас пополам углы разделят
На части равные фигуру разобьют.

23.

• А я - прямоугольник,
В отличии от всех
Все стороны свои держу я строго,
Две - чуть поменьше, ну а две - побольше,
Которые напротив - те равны,
А те, что смежные - углом прямым скрепляю,
И преимущество имею перед вами:
Ведь все ж равны мои диагонали.

24.

• Рекомендуюсь: я квадрат.
Любую площадь я замерить рад.
С глубокой древности я - мера площадей,
Она в квадрате стороны моей.
Имею я четыре стороны.
И все они между собой равны.
Но у меня притом равны диагонали,
Углы они мне делят пополам,
На части равные разбит я ими сам.
Вобрав все важное в себя,
Фигурой знатной стал и я.

25.

• А я фигура не похожая на всех.
Хоть я и не параллелограмм,
Но среди них мне место есть
Ведь у меня же параллельны основания,
Бывают стороны равны, диагонали,
Ещё углы при основании,
Трапецией зовусь я с давних пор
Поэтому я влезла в этот спор.