Similar presentations:
Чотирикутник та його елементи
1.
Тема:Чотирикутник
та його
елементи.
2.
Означеннячотирикутника
Чотирикутником називається фігура, що складається з
чотирьох точок, кожні три з яких не лежать на даній прямій і
чотирьох відрізків, які послідовно сполучають ці точки.
3.
Елементи чотирикутникаВ
А
D
С
• Точки А, В, С, D – вершини
чотирикутника
• Відрізки АВ, ВС, CD, DA – сторони
чотирикутника
• Відрізки
AC,
DB
–
діагоналі
чотирикутника
• Для позначення чотирикутника всі його вершини необхідно
назвати послідовно, по одному разу кожну вершину.
Наприклад: ABCD, BCDA, CDAB, DABC
4.
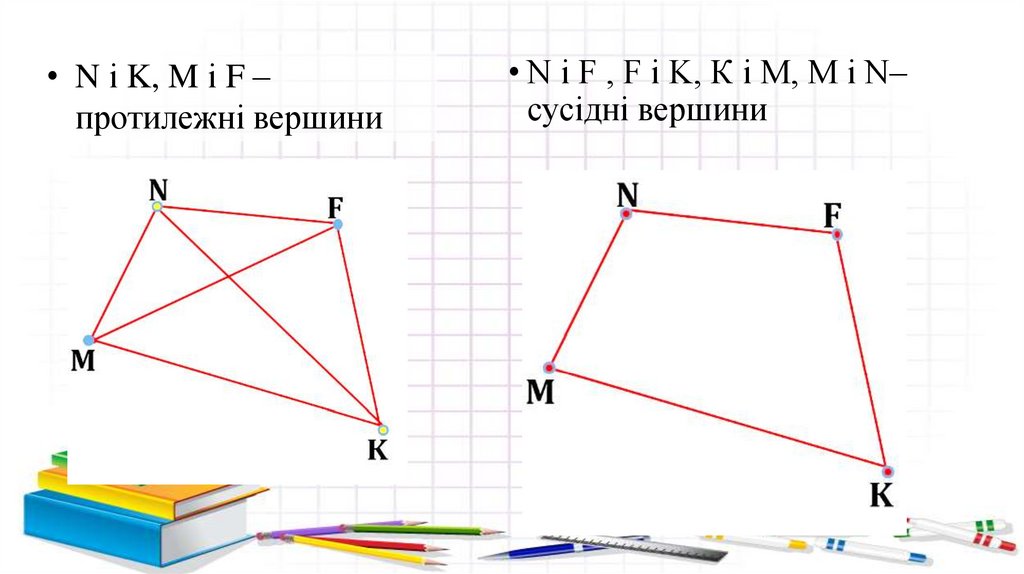
• N і K, M і F –протилежні вершини
• N і F , F і K, К і M, М і N–
сусідні вершини
5.
• NF і МК, МN і FК –протилежні cторони
• MN і NF, NF і FK, FK і КM,
KM і MN– сусідні сторони
6.
Опуклий і неопуклийчотирикутники
Чотирикутник називається опуклим,
якщо він лежить в одній площині
(разом із прямою, що її обмежує)
відносно будь-якої прямої, що містить
сторону цього чотирикутника
Неопуклий чотирикутник
7.
• Термін «діагональ» походить відгрецького слова diagonios, що
означає «той що йде від кута до
кута»
• MF і NK – діагоналі
8.
Периметр чотирикутникаВ
А
D
• Периметр чотирикутника
дорівнює сумі всіх його сторін
С
РАВСD AB BC CD AD
9.
Теорема (про суму кутівчотирикутника)
В
А
Сума кутів чотирикутника
дорівнює 360
D
С
А В С D 360
10.
11.
Тема:Паралелограм. Властивості
паралелограма.
12.
СВ
D
A
АВ || CD
Паралелограмом називають
чотирикутник,
протилежні
сторони
якого
попарно
паралельні.
BC || AD
Термін «паралелограм» походить від грецьких слів «паралелос» –
той, що йде поруч, паралельний, і «грамма» - лінія.
13.
14.
Властивості паралелограмаA
B
ABCD –
паралелограм,
AB || CD, АD || BC,
D
C
АВ = СD, AD = DC.
У паралелограма протилежні
сторони попарно паралельні.
У паралелограма протилежні
сторони попарно рівні.
15.
Властивості паралелограмаB
C
ABCD – паралелограм,
B = D, A = C.
A
D
У паралелограма протилежні
кути рівні.
16.
Властивості паралелограмаB
C
ABCD –паралелограм,
А + В = В + C =
= С + D = A + D = 180°.
A
D
Cума кутів, прилеглих до однієї
сторони паралелограма, дорівнює
180°.
17.
Властивості паралелограмаB
C
паралелограм,
O
A
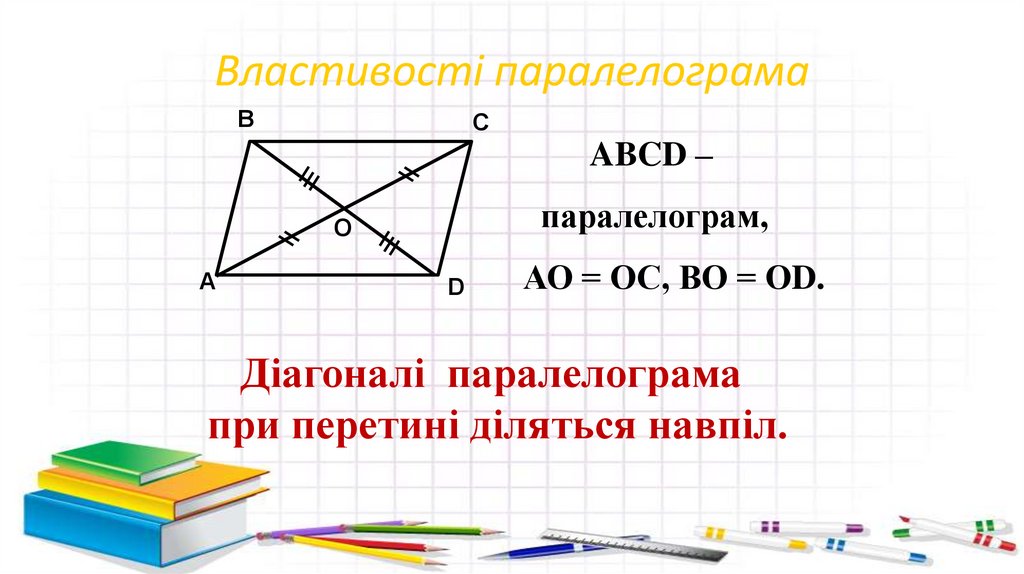
ABCD –
D
АО = ОС, ВО = ОD.
Діагоналі паралелограма
при перетині діляться навпіл.
18.
19.
20.
ВИСОТА ПАРАЛЕЛОГРАМАВисота паралелограма — це перпендикуляр, проведений з
вершини цього паралелограма на протилежну сторону.
21.
Властивості висот паралелограмаC
B
H
A
D
K
M
B
C
A
D
N
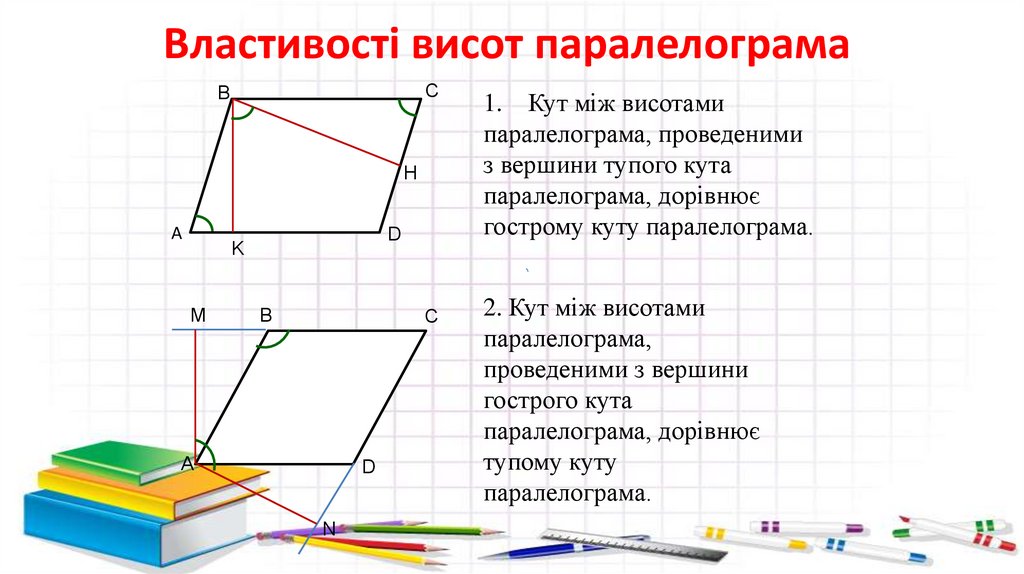
1. Кут між висотами
паралелограма, проведеними
з вершини тупого кута
паралелограма, дорівнює
гострому куту паралелограма.
2. Кут між висотами
паралелограма,
проведеними з вершини
гострого кута
паралелограма, дорівнює
тупому куту
паралелограма.
22.
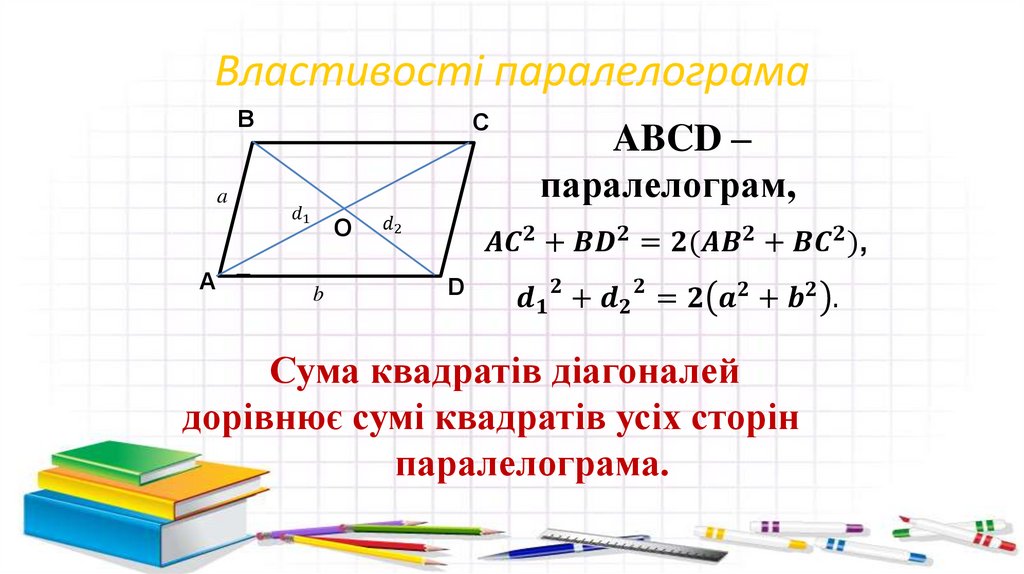
Властивості паралелограмаC
B
ABCD – паралелограм;
A
D
∆ АВD = ∆CDB.
Кожна діагональ паралелограма ділить
його на два рівних трикутники.
Доведення
Нехай ABCD – даний паралелограм, BD – діагональ
паралелограма.
Розглянемо трикутники ABD і CDB. У них AB=CD, AD=BC, як
протилежні сторони паралелограма, BD – спільна сторона. Отже,
ці трикутники рівні за третьою ознакою рівності трикутників.
23.
Властивості паралелограмаB
a
A
C





















 mathematics
mathematics








