Similar presentations:
Паралелограм і його властивості
1.
2.
ВA
АВ || CD
С
D
BC || AD
Паралелограмом
називають
чотирикутник,
протилежні сторони
якого
попарно
паралельні.
3.
BC Теорема 1.
Якщо діагоналі
чотирикутника перетинаються та
діляться точкою перетину навпіл, то
цей чотирикутник – паралелограм.
O
A
D
4.
Теорема 2. Якщо в чотирикутнику кожні дві протилежністорони рівні, то цей чотирикутник – паралелограм.
Теорема 3. Якщо дві протилежні сторони чотирикутника
паралельні і рівні, то цей чотирикутник – паралелограм.
Теорема 4. Якщо протилежні кути чотирикутника
попарно рівні, то цей чотирикутник – паралелограм.
Теорема 5. Якщо сума кутів, прилеглих до будь якої
сторони чотирикутника, дорівнює 180о , то цей
чотирикутник – паралелограм.
5.
AB
ABCD –
паралелограм,
AB || CD, АD || BC,
D
C
АВ = СD, AD = DC.
У паралелограма протилежні
сторони попарно паралельні.
У паралелограма протилежні
сторони попарно рівні.
6.
BC
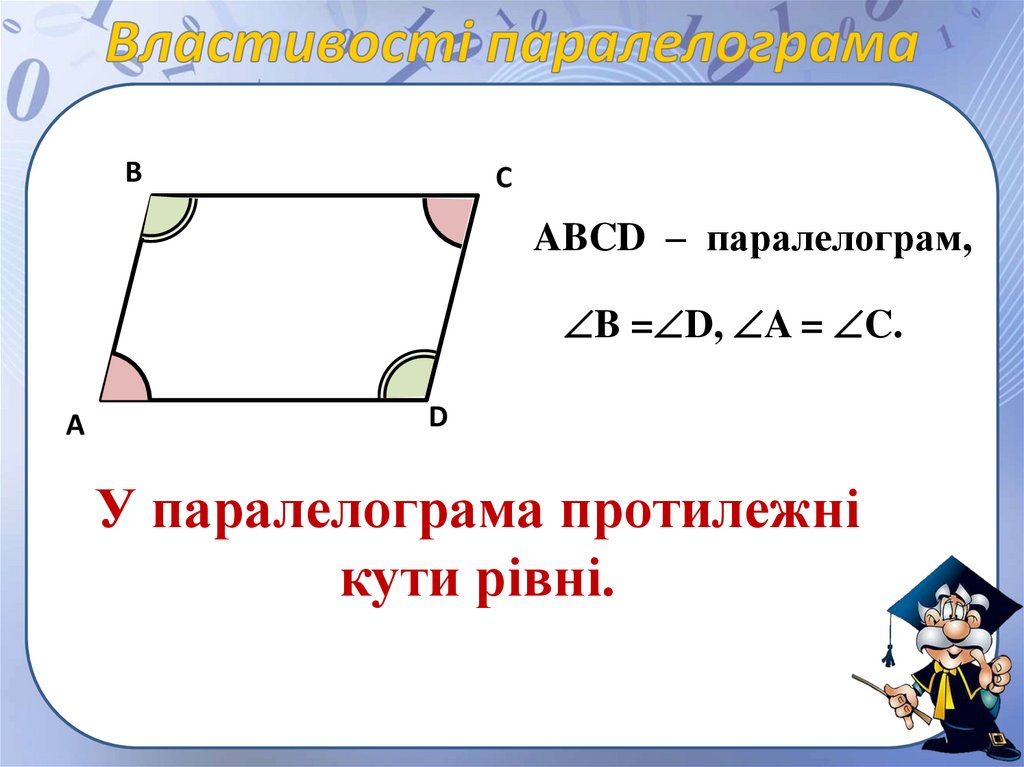
ABCD – паралелограм,
B = D, A = C.
A
D
У паралелограма протилежні
кути рівні.
7.
BC
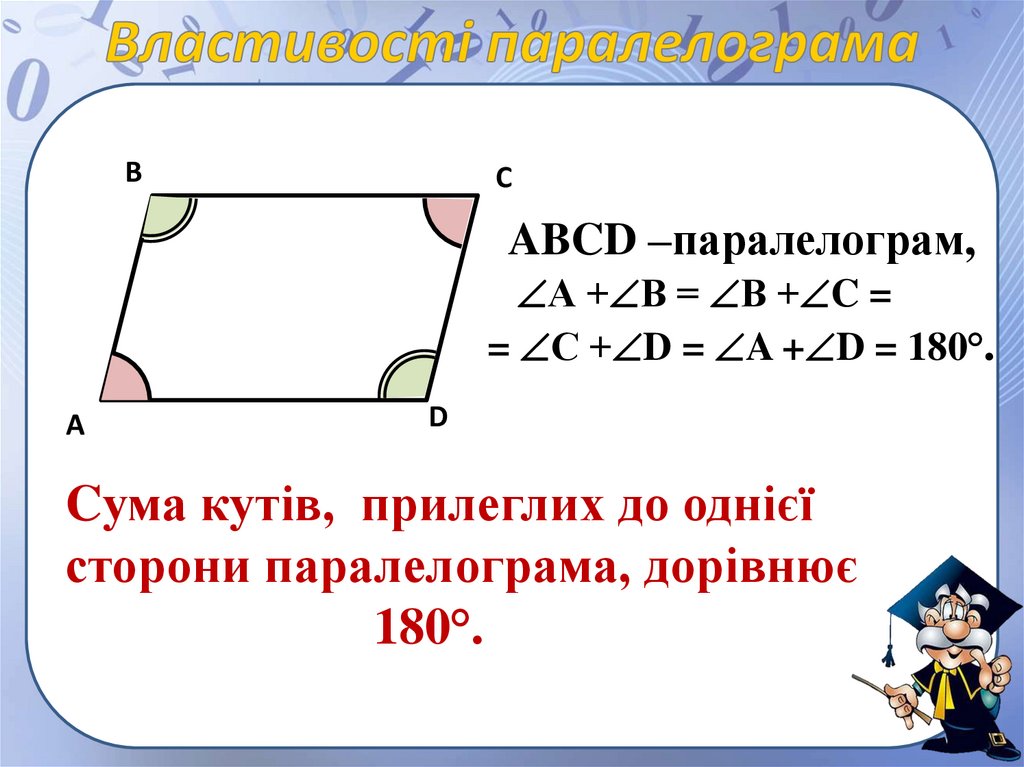
ABCD –паралелограм,
А + В = В + C =
= С + D = A + D = 180°.
A
D
Cума кутів, прилеглих до однієї
сторони паралелограма, дорівнює
180°.
8.
BC
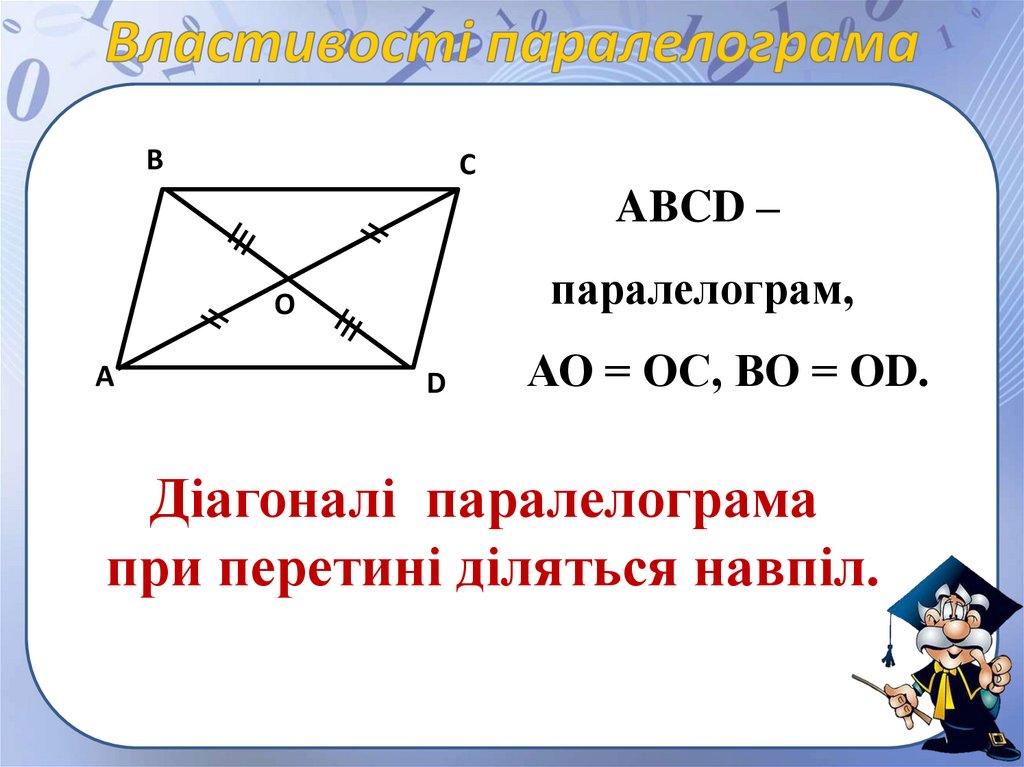
паралелограм,
O
A
ABCD –
D
АО = ОС, ВО = ОD.
Діагоналі паралелограма
при перетині діляться навпіл.





 mathematics
mathematics








