Аналитическая геометрия на плоскости и в пространстве

1.

АКАДЕМИЯ ГРАЖДАНСКОЙ АВИАЦИИ
кафедра «Общеобразовательные дисциплины
Лекция №3
ТЕМА 3. Аналитическая геометрия на плоскости и
в пространстве
Ассоцированный профессор кафедры
«Общеобразовательных дисциплин»
к.ф.-м.н.- Сегизбаева Р.У.
АЛМАТЫ -2023

2.

Лекция №3
ТЕМА3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ И В
ПРОСТРАНСТВЕ
1. Простые геометрические конструкции.
Тригонометрические соотношения. Применение
таблиц. Декартова и полярная системы координат.
2. Понятие об уравнении линии на плоскости.
Различные формы задания уравнения прямой линии
на плоскости. Взаимное расположение двух прямых.
Условие параллельности и перпендикулярности.
Понятие об уравнении поверхности и линии в
пространстве.

3.

Основные вопросы.
1. Понятие об уравнении линии на плоскости.
Различные формы задания уравнения прямой
линии на плоскости.
2. Взаимное расположение двух прямых. Условие
параллельности и перпендикулярности.
Понятие об уравнении поверхности и линии в
пространстве.
3. Различные формы задания уравнения плоскости.
Угол между плоскостями, условие параллельности и
перпендикулярности двух плоскостей.
4. Прямая линия в пространстве.

4.

Основная литература
1
Методические
указания по
выполнению
практических
работ по
дисциплине Высш
ая математика:
Методический
указания / Сост.
Сейдилдаева
А.К.Высшей
математике 1:
Методический
указания по
выполнению
практических
работ /
Высшая математи
ка: Методический
указания по
выполнению
практических
работ.
Туганбаев, А.А.
Высшая математи
ка.
Дифференциальн
ые
уравнения [Текст]
: Учебник /
2
3
4
5
A collection of
Mathematical
Tasks
Авторы
экземпляр
Издат-о
Год
изд
библиотек
е
Наимнование
На
кафедре
№
п/п
Количество
страниц
1.
Сейдилдаева
А.К.
Алматы:
Академия
гражданско
й авиации,
2021.
- 149
с.
1
1
Сост.
Р.У.
Сегизбаева.-
Алматы:
РИО,
2021.
150
1
1
Сост.
А.К.
Сейдилдаева,
Р.У.
Сегизбаева.-
Алматы:
РИО,
2021
160
1
1
А.А. Туганбаев.
М.:
ФЛИНТА,
2021.
- 152
с.
1
1
134
10
Makhmedjanov.,
Dildabek
Almaty:
Qazaq
university
2019
134
c.

5.

6
Высшая математи
ка в упражнениях
и задачах [Текст]:
Учебное пособие
для вузов /,..
Данко, П.Е. 7-е
изд., исправл.-
7
Высшая
математика в
упражнениях и
задачах [Текст]:
Учебное пособие
для вузов / П.Е.
Данко.- 7-е изд.,
исправл.
Высшая математи
ка. Руководство к
решению задач
Ч.2 [Текст]:
Учебное пособие /
Гомонов, С.А.
Математика.
Линейная
алгебра [Текст]:
Учебносправочное
пособие.
Высшая математи
ка в вопросах и
ответах [Текст]:
Учебное пособие
Данко, П.Е.
8
9
10
М.:
Издательств
о АСТ: Мир
и
Образовани
е
М.:
Издательств
о АСТ: Мир
и
Образовани
е,
2016
- 816
с
2015
816 с
1
3
Лунгу,
К.Н.,
Е.В. Макаров.
.М.:
ФИЗМАТЛ
ИТ,
2015
- 384
с.
-
1
С.А. Гомонов,
К.М. Расулов;
Под ред. К.М.
Расулова
.М.:
ФОРУМ,
/ 2015
- 144
с.
-
2
Крицков, Л.В.;
под ред.: В.А.
Ильина
М.:
Проспект
/.-,
2015
.176
с.
-
1
1

6.

11
Высшая математи
ка в упражнениях
и задачах [Текст]:
Учебное пособие
для вузов /
Данко, П.Е..-
12
Обыкновенные ди
фференциальные
уравнения [Элект
ронный ресурс] /
Жанбусинова
Б.Х., Рамазанов
М.И., Петерс
С.Н.Ильин В.А.,
Куркина А.В.
Высшая математи
ка [Текст]
Дифференциалды
қ теңдеулер
курсы.
Жоғары математи
ка есептер
жинағы. 3
бөлім [Текст]:
Құраст.:
Сызықты алгебра
және векторлық
алгебра
элементері.
Аналитикалық
геометрия
элементтері.
Жоғары
матемтика
есептер жинағы. 1
бөлім [Текст] /
Жанбусинова
Б.Х., Рамазанов
М.И.,
Петерс
С.Н
13
14
15
7-е
изд.,
исправл.М.:
Издательств
о АСТ: Мир
и
Образовани
е,.
Караганда,
2015
/ Куркина А.В.
Ильин В.А.- 3-е
изд., перераб. и
дополн.
Байбазаров
М.Б.,
Джумадиллаев
С.А.
М.:
Проспект,
2015.-
608с
.
Алматы:
Азаматтық
авиация
академиясы,
2015.
-103
б.
289
Байбазаров
М.Б.,
Джумадиллаев
С.А.
Алматы:
Азаматтық
авиация
академиясы,
2015.-
85 б.
290
- 816
с.
-
2015.
2
1
-
1

7.

18
Жоғары
математика 1
оқулық
19
Higher
mathematics:
textbook
20
Methodological
guidelines for the
implementation of
practical work
in the discipline
HIGHER
MATHEMATICS
1
Байбазаров
М.Б.,
Джумадиллаев
С.А.
Алматы:
Азаматтық
авиация
академиясы,
2015.-
166
б.
Байбазаров
М.Б.,
Джумадиллаев
С.А.-
Алматы:
Азаматтық
авиация
академиясы,
2015.-
166
б.
2023
338
2023
333
5
5
2024,
май
Acad
emy
Civil
avaia
tion
5
5
Сейдилдаева
А.К.
Сегизбаева Р.У.
Джумадиллаев
С.А.
R.U.
Segizbayeva,
A.K.
Seidildayeva,
R.K. Anayatova
R.U.
Segizbayeva,
A.K.
Seidildayeva,
ТОО
«АDAL
KITAP»
,
ISBN
978601-720041-1
Almaty,
ADAL
KITAP
Almaty,
Academy
Civil
avaiation
296
5
17
Еселі және қисық
сызықты
интегралдар.
Беттік
интегралдар.
Қатарлар.
Жоғары математи
ка есептер
жинағы. 4
бөлім [Текст] /
Құраст.:
Математикалық
анализ негіздері.
Жоғары математи
ка есептер
жинағы. 2
бөлім [Текст] /
Құраст.:
5
16

8.

Аналитическая
геометрия на
плоскости и в
пространстве
1. Простейшие задачи аналитической геометрии
https://www.youtube.com/watch?v=sdpkQaLqbvg
2. Уравнение прямой с угловым коэффициентом
https://www.youtube.com/watch?v=ALmtmx-1VY8
3. Угол между прямыми https://www.youtube.com/watch?v=lOxMwy7Z6hI
4. Уравнение прямой, проходящей через две точки
https://www.youtube.com/watch?v=wqjVIX39cuM
1. Общее уравнение прямой
https://www.youtube.com/watch?v=Pdqqlvx0OX8
2. Параметрические уравнения прямой
https://www.youtube.com/watch?v=1BmfcwFOyps
3. Нормальное уравнение прямой https://www.youtube.com/watch?v=zbnFLx-bwE
4. Расстояние от точки до прямой
https://www.youtube.com/watch?v=RSK8alwClyE
5. Общее уравнение плоскости
https://www.youtube.com/watch?v=abPfMUU4l1E
https://www.youtube.com/watch?v=aG5Q_XoIoE0

9.

Введение
Рассмотрим произвольную точку М плоскости Оху. Вектор
ОМ называется радиусом-вектором точки М.
Координатами точки М в системе координат Оху
называются координаты радиус-вектора ОМ. Если ОМ=(х,у),
то координаты точки М записывают так: М(х,у),
число х называется абциссой точки М,
а у – ординатой точки М.

10.

11.

Определение расстояния между
двумя точками.
Расстояние d между двумя точками
М1(x1,y1) и М2(x2,y2) на плоскости
вычисляется по формуле
d ( x2 x1 ) ( y2 y1 )
2
2

12.

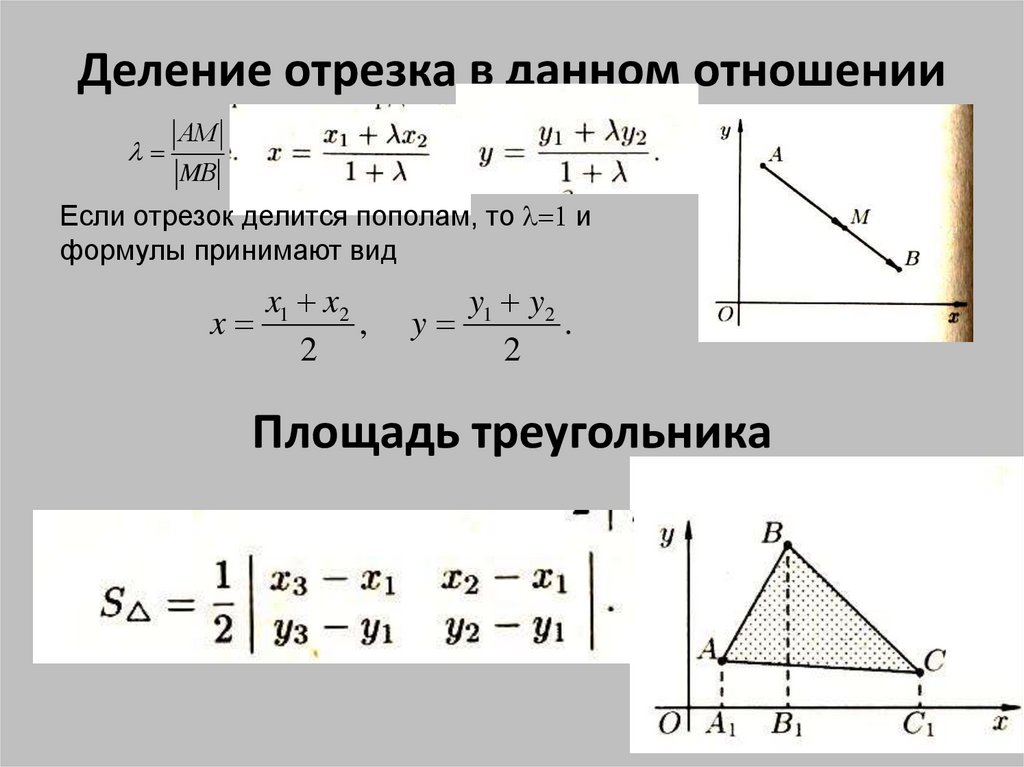
Деление отрезка в данном отношении
АM
MВ
Если отрезок делится пополам, то и
формулы принимают вид
x1 x2
x
,
2
y1 y2
y
.
2
Площадь треугольника

13.

n
Определение
Уравнением линии на плоскости называется такое
уравнение F(x, у) = 0, которому удовлетворяют
координаты каждой точки, лежащей на этой
линии, и не удовлетворяют координаты, никакой
точки, не лежащей на ней.
Такое определение дает основу методам
аналитической геометрии, которые заключаются
в том, что рассматриваемые линии исследуются
при помощи анализа их уравнений.
Пример.
– уравнение параболы.
– уравнение окружности.

14.

10. Уравнение прямой проходящей через данную
точку с заданным нормальным вектором.
Пусть на плоскости Оху задана точка
М0(х0; у0) и ненулевой вектор n = А; В ,
перпендикулярный данной прямой. Любой
вектор, перпендикулярный данной прямой
называется нормальным вектором этой прямой.

15.

20. Общее уравнение прямой и его частные случаи.
Запишем уравнение А(х – х0) + В(у - у0) = 0
в виде Ах + Ву + С = 0, где С = -Ах0 – Ву0.
Уравнение Ах + Ву + С = 0
называется общим уравнением прямой,
полученное уравнение является уравнением
первой степени с двумя переменными х и у.
Таким образом, всякая прямая на плоскости
в прямоугольной системе координат
определяется уравнением первой степени
относительно х и у.

16.

17.

30.
Уравнение
прямой
с
угловым
коэффициентом и начальной ординатой.
Пусть на плоскости Оху задана прямая l не
параллельная оси Оу и которая отсекает на оси Оу
отрезок b, считая от начала координат. Тогда
уравнение y kx b называется уравнением
прямой с угловым коэффициентом и начальной
ординатой.
– угловой коэффициент
прямой, b – начальная ордината, отрезок,
отсекаемый прямой по оси ординат, считая от
начала координат.

18.

40. Уравнение прямой, проходящей через
данную точку М1(x1;y1) параллельно данной
прямой y=kx+b:
y-y1=k·(x-x1)

19.

50. Уравнение прямой, проходящей через данную
точку параллельно данному вектору.

20.

60. Уравнение прямой в отрезках

21.

2. Взаимное расположение двух прямых. Угол
между прямыми. Условие параллельности и
перпендикулярности двух прямых.
Пусть две прямые l1 и l2 заданы уравнениями
Если прямые пересекаются, то существует общая
точка этих прямых, координаты которой
удовлетворяют каждому из уравнений.
Следовательно, для нахождения точки
пересечения двух прямых нужно решить систему
уравнений

22.

При решении системы (2) возможны три случая:

23.

24.

3. Расстояние от точки до прямой.

25.

Тема: «Плоскость и прямая в
пространстве»
Определение.
Уравнением поверхности в пространстве
называется такое уравнение F(x, у, z) = 0,
которому удовлетворяют координаты каждой
точки, лежащей на этой поверхности, и не
удовлетворяют координаты никакой точки,
не лежащей на ней.

26.

10. Уравнение плоскости,
проходящей через данную точку с
заданным нормальным вектором.

27.

28.

29.

2. Прямая линия в пространстве
Всякая линия в пространстве определяется как линия
пересечения двух поверхностей, задаваемых своими
уравнениями. В частности, прямая линия l определяется
совместным заданием двух уравнений первой степени:
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0

30.

31.

Выражая текущие координаты прямой через
параметр t, получим параметрические уравнения
прямой:
x x0 mt,
y y0 nt ,
z z pt.
0