Similar presentations:
Вычисление пределов функции
1.
14.09.2024Вычисление пределов функции.
2.
Определение предела. Число b – пределфункции f(x) при x стремящемся к a, если для
каждого положительного числа e можно
указать такое положительной число d, что
для всех x, отличных от a и
удовлетворяющих неравенству |x-a|<d,
имеет место неравенство |f(x)-b|<d.
Если b есть предел
функции f(x) при x стремящемся к a, то
записывают это так:
Функция f(x) непрерывна в точке a, если
3.
Основные теоремы о пределах:ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен
сумме пределов этих функций , то есть
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся
к a равен произведению пределов этих функций, то есть
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен
частному пределов, если предел знаменателя отличен от нуля, то есть
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел
числителя конечен и отличен от нуля.
4.
Вычислить пределы:5
1) lim
x 2 2 x 8
2
3x 2 x
3) lim 2
x 0 2 x 5 x
x
3) lim
x 0 5 x 5 x
2) lim x x 5
x 3
3
4) lim x 2 x 15
2
x 3
x 9
2
3) lim 2 x 2 x
x 0
5x
5.
Вычислить пределы:4
1. lim
x 0 x 2
2. lim 3 x 4 2
x 0
5
3. lim
x 3 x 7
x 2 4 x 3
4. lim
x 2
x 2
4 x
5. lim
x 16 16 x
6.
Предел на бесконечности:Число А называется пределом функции
y=f(x) на бесконечности (или при х,
стремящимся к бесконечности), если для
всех достаточно больших по модулю
значений аргумента х соответствующие
значения функции f(x) сколь угодно мало
отличаются от числа А.
7.
1.5
lim
x 4 x 1
x 4 2x 2 3
2. lim
3x 3 5
x
3.
lim x 3x
3
2
x
2 3
5
2
lim
x x
x
3x
5. lim
x x 2
4.
x5 x6
6. lim 3
4
x x x
8.
Задание на домВычислите пределы:
x 1
1. lim
x 1 x 1
3
x 7 x 10
2. lim 2
x 5 x 9 x 20
2
3.
lim
x 0
x 1 1
x






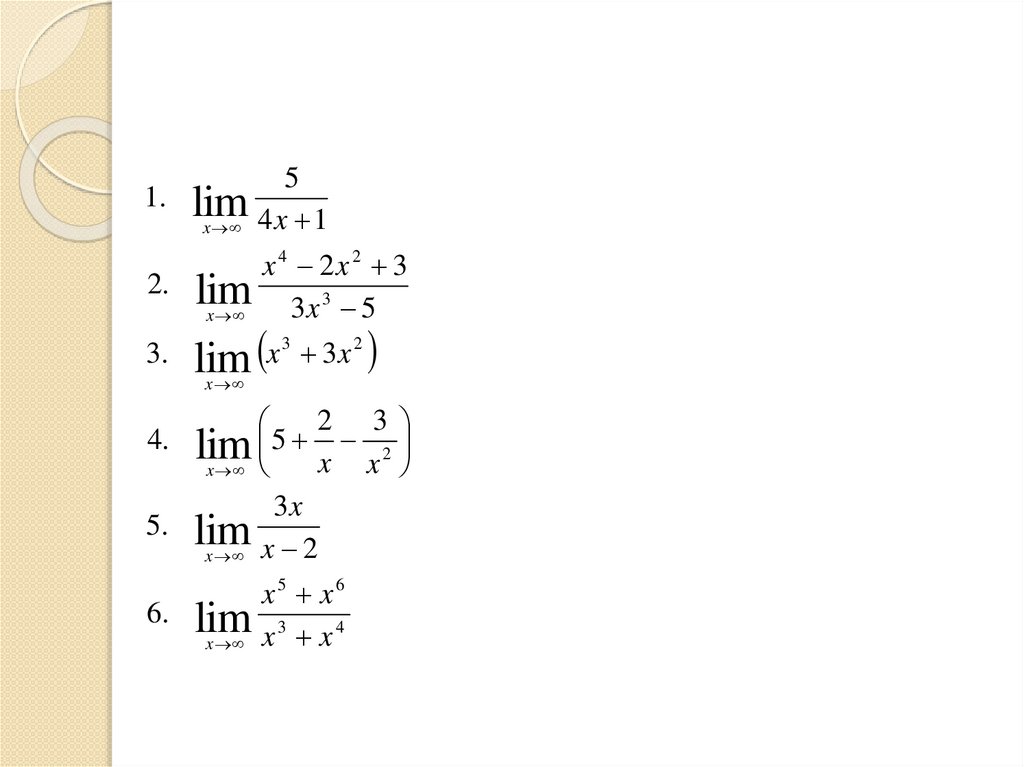

 mathematics
mathematics








