Similar presentations:
Матрицы и определители. Лекция 1
1.
ЛЕКЦИЯ 1Матрицы и
определители
2.
КВАНТОРЫ, ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ] – пусть; ( ) – и;
– или;
– не;
– для любого, для всех;
: – такой, что;
– существует;
! – единственный;
– стремится;
– следует,
следовательно;
– тогда и только тогда;
– сумма;
– произведение;
– знак объединения;
– знак пересечения;
3.
1. Матрицы4.
Термин «матрица»ввел английский математик
Джеймс Джозеф Сильвестр.
1814–1897
«Математика – музыка разума».
Джеймс Джозеф Сильвестр
5.
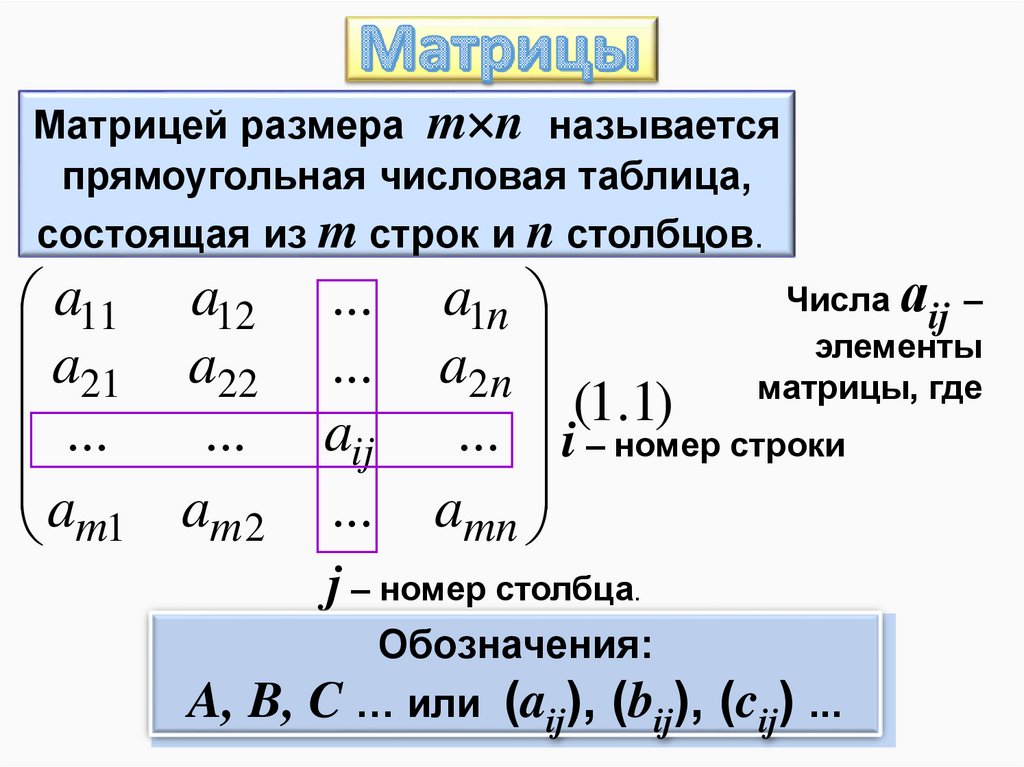
Матрицей размера m n называетсяпрямоугольная числовая таблица,
состоящая из m строк и n столбцов.
a11 a12
a
a22
21
...
...
a
m1 am 2
...
...
aij
...
Числа аij –
a1n
элементы
a2 n
(1.1) матрицы, где
... i – номер строки
amn
j – номер столбца.
Обозначения:
A, B, C … или (aij), (bij), (cij) ...
6.
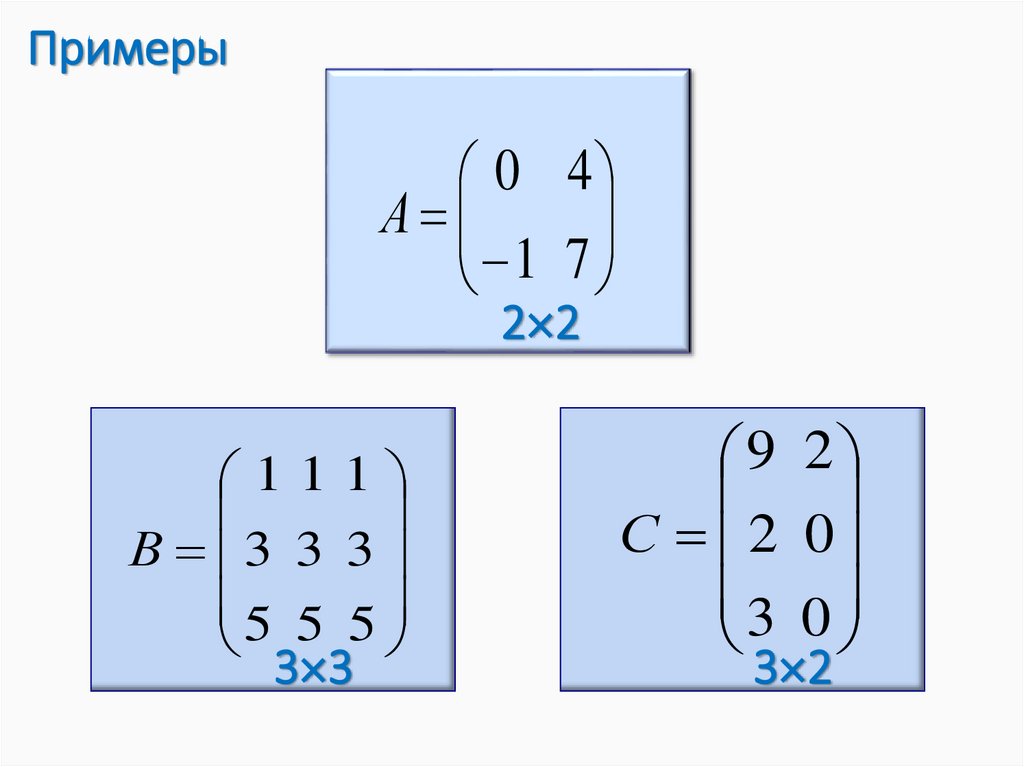
Примеры0 4
А
1 7
2 2
111
В 3 3 3
5 5 5
3 3
9 2
С 2 0
3 0
3 2
7.
1.1. Виды матриц8.
1. Прямоугольная матрицаМатрица, в которой число строк не равно числу
столбцов, называется прямоугольной.
0 1 2
A2 х 3
1 7 0
9.
2. Матрица-строка и матрица-столбецМатрица-строка (1 n)
A a1 a2 ... an
Матрица-столбец (n 1)
b1
b
B 2
...
bn
10.
3. Нулевая матрицаМатрица, все элементы которой
равны нулю, называется нулевой.
Обозначается буквой О.
Нулевая
0 ... 0
Оmxn ... ... ...
0 ... 0
11.
4. Квадратная матрица (m=n)a11
a 21
A
....
a
n1
a12
a 22
....
an2
.... a1n
.... a 2 n
(1.2)
..... .....
..... a nn
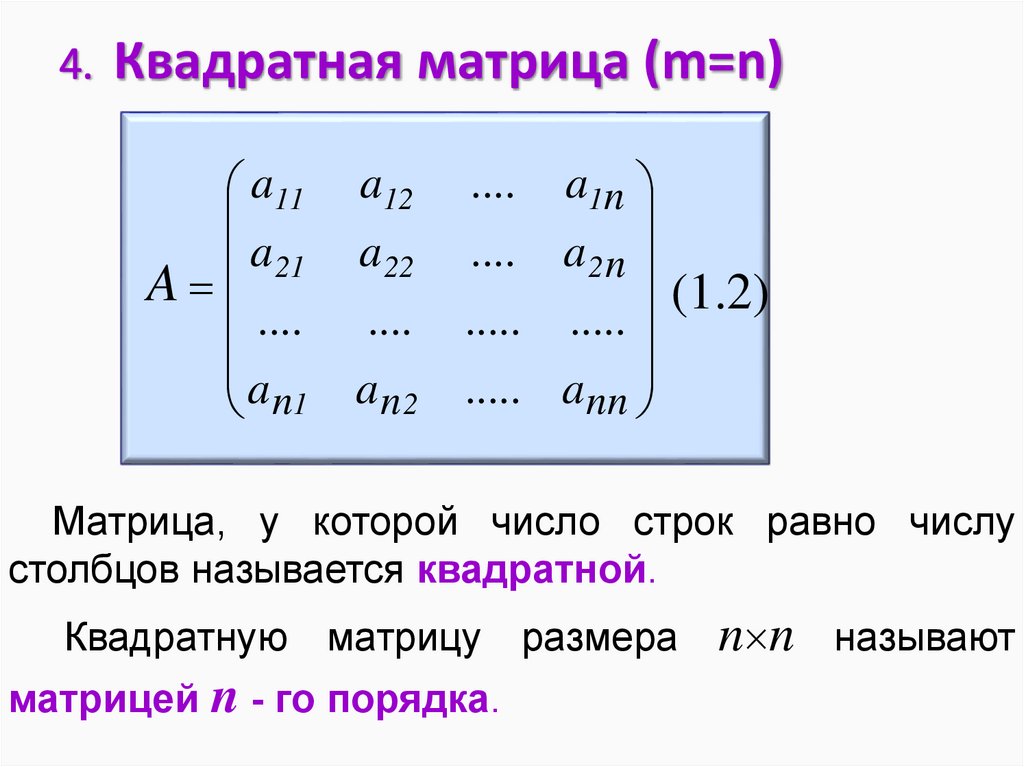
Матрица, у которой число строк равно числу
столбцов называется квадратной.
Квадратную матрицу размера
матрицей n - го порядка.
n n
называют
12.
ПримерыКвадратные матрицы
5 11
А 2 4 2
3 1 3
3-го порядка
7 2
B
1 5
2-го порядка
13.
5. Диагональная матрицаa11 0 0 ... 0 0... 0
a
11 0 a 0 ... 0
А 0 0 a22 022 ...a 0... 0diag
(1. 3a
) 11, a22,..., ann .
33
... ... ... ... ... ... ...... ...
0 0 0 0 ... 0 a ... a
nn nn
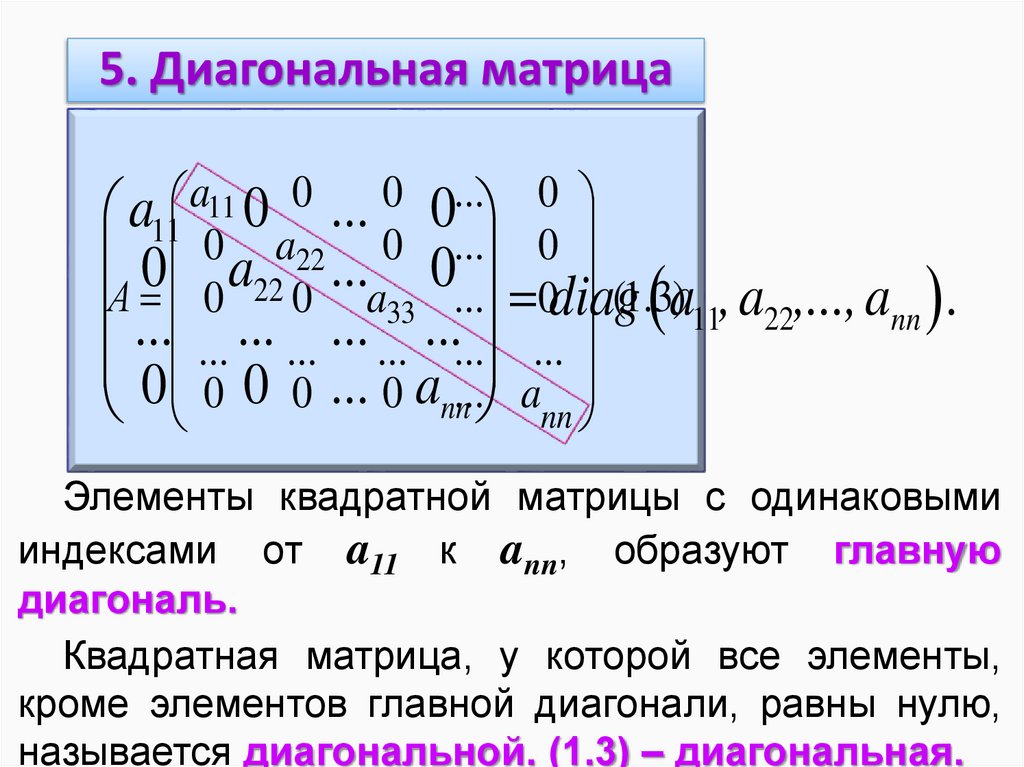
Элементы квадратной матрицы с одинаковыми
индексами от a11 к ann, образуют главную
диагональ.
Квадратная матрица, у которой все элементы,
кроме элементов главной диагонали, равны нулю,
называется диагональной. (1.3) – диагональная.
14.
Примеры1 0 0
А 0 3 0
0 0 5
7 0
B
0 5
Диагональная матрица 3-го порядка Диагональная матрица 2-го порядка
15.
6. Единичная матрицаДиагональная матрица, у которой каждый элемент
главной диагонали равен единице,
называется единичной.
Обозначается буквой Е или I.
16.
10
Е2 diag 1, 1 0 1
Еn diag 1, 1, ...,1
1 0 0
Е3 diag 1, 1, 1 0 1 0
0 0 1
16
17.
7. Треугольная матрицаКвадратная матрица называется треугольной, если
все элементы, расположенные по одну сторону от
главной диагонали, равны нулю.
Примеры
верхнетреугольная
нижнетреугольная
111
А 0 3 3
0 0 5
7
B
1
0
5
18.
8. Транспонированная матрицаМатрица, полученная из данной заменой каждой
её строки столбцом с тем же номером, называется
матрицей транспонированной к данной.
Обозначается AT.
Пример
0 3
А 1 4
2 5
0
1
2
А 3 4 5
T
(АТ)Т=А
19.
9. Симметрическая матрица• Если AT = A то матрица A называется симметрической.
Пример
1
2
3
1 2 3
Т
С 2 3 0 С 2 3 0 C
3 0 5
3 0 5
20.
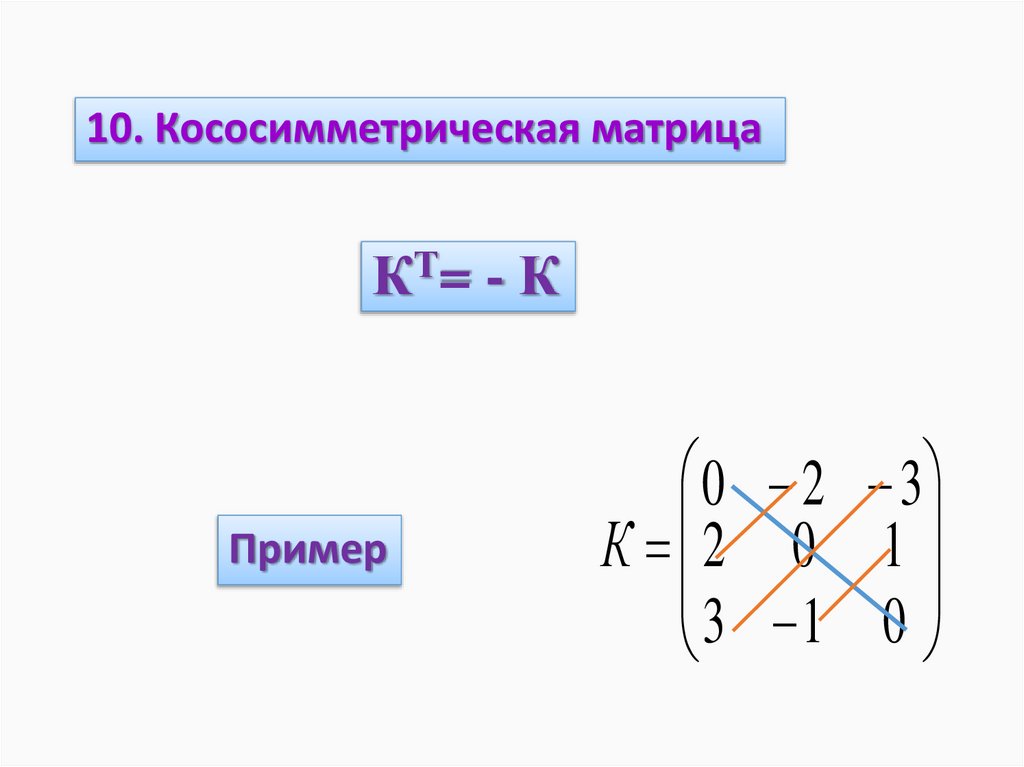
10. Кососимметрическая матрицаКТ= - К
Пример
0 2 3
К 2 0 1
3 1 0
21.
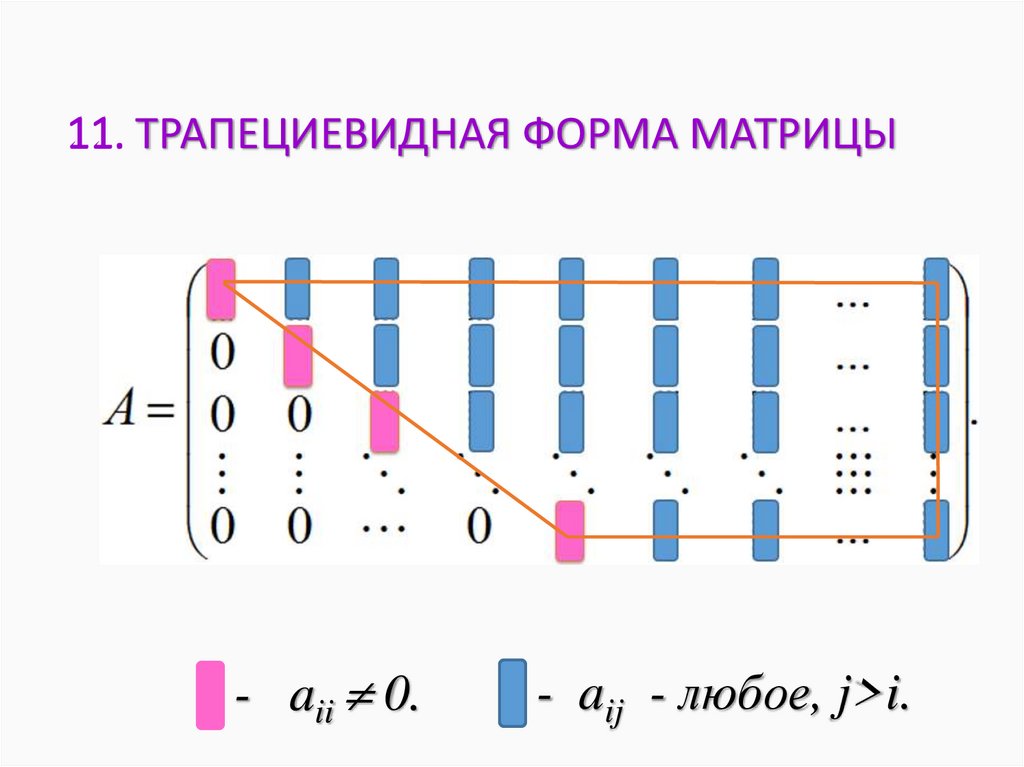
11. ТРАПЕЦИЕВИДНАЯ ФОРМА МАТРИЦЫ- aii 0.
- aij - любое, j>i.
22.
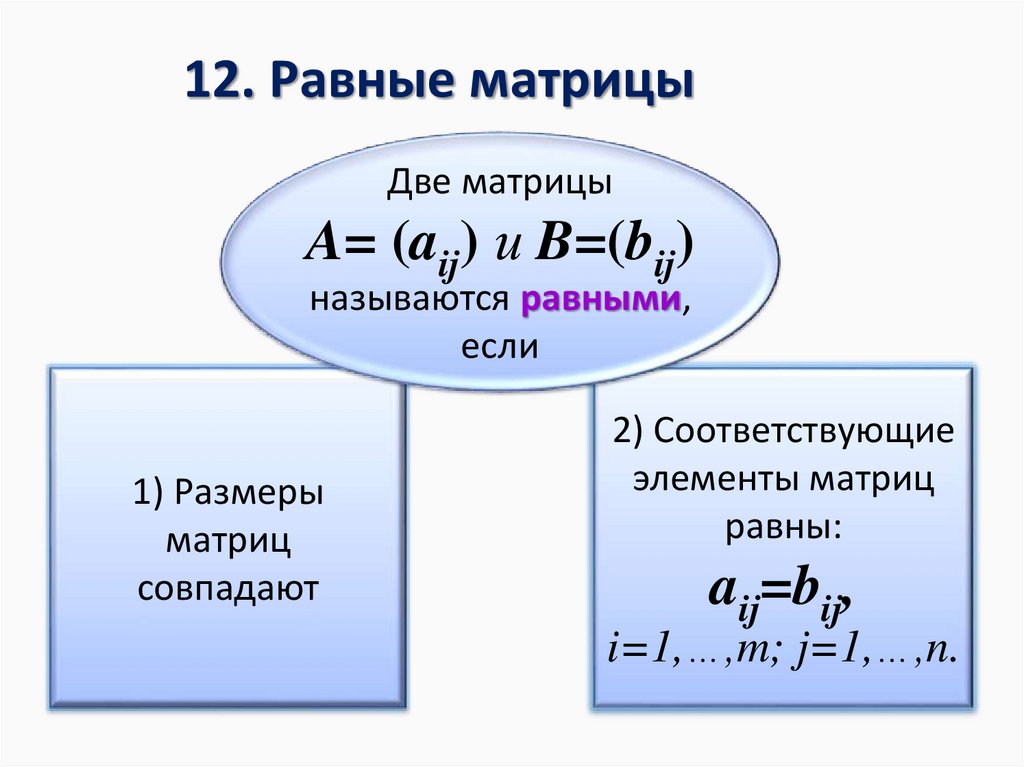
12. Равные матрицыДве матрицы
A= (aij) и B=(bij)
называются равными,
если
1) Размеры
матриц
совпадают
2) Соответствующие
элементы матриц
равны:
aij=bij,
i=1,…,m; j=1,…,n.
23.
1.2. Операции над матрицами24.
Сумма матрицСложение и вычитание матриц возможно, если
эти матрицы имеют одинаковый размер.
Суммой матриц A=(aij) и B=(bij)
размера m n называется матрица C=(cij) размера m n,
каждый элемент которой равен сумме соответствующих
элементов матриц A и B.
cij aij bij , ( i 1 , m ; j 1 , n )
25.
Сумма матрицПример
2 3 4 5 2 4 3 5 6 2
A B
1 0 2 8 1 2 0 8 1 8
26.
ПримерНайти разность матриц
33
0 2
A 1 0 и B 3 1 .
1 2
2 2
3 3 0 2 3 0 3 2 3 1
A B 1 0 3 1 1 3 0 1 4 1 .
1 2 2 2 1 2 2 2 1 0
27.
Умножение матрицы на числоПроизведением матрицы A=(aij) и числа
называется матрица того же размера,
элементы которой равны aij.
2
1 2 3
А 0 0 4 2 А 0
0 0 5
0
4 6
0 8 .
0 10
28.
Свойства суммы матриц иумножения матрицы на число
29.
Пусть A, B, C, О ─ матрицыодного размера, а , , - числа.
1. Коммутативность суммы матриц
A B B A
30.
2. Ассоциативность сложения матриц( A B) C A ( B C )
31.
3. Дистрибутивность( A B) A B
число.
A A A , , - числа.
32.
4.А+О=А
О – нулевая матрица, того же размера, что и А.
33.
Произведение матриц34.
Умножение матриц выполнимо, если числостолбцов первой матрицы равно числу
строк второй.
35.
Умножениестроки на столбец
b1
b2
A a1, a2 , , an , B .
b
n
AB a1b1 a2b2 anbn .
Пример
1
A 3 , 1 , 4 , B 0 .
3
AB 3 1 1 0 4 3 15.
36.
Умножение матрицы на столбецКаждая строка матрицы скалярно
умножается на столбец
3 1 2 8 3 8 1 7 2 2 21
4 2 0 7 4 8 2 7 0 2 46
5 6 1 2 5 8 6 7 1 2 4
37.
Произведением матриц A=(aij) (размера m p)B=(bij) (размера p n) называется матрица
C=(cij) (размера m n), элементы cij которой
вычисляются как скалярное произведение i – й
строки матрицы A и j – го столбца матрицы B.
и
Умножение матриц
b1 j
b2 j
a a a
i1 i 2
ip
b
pj
.
cij
38.
Пример2 6 1 2 0
Найти произведение матриц
.
1 2 0 1 3
2 2 6 ( 1)
2 0 6 3
2 1 6 0
1 1 ( 2) 0 1 2 ( 2) ( 1) 1 0 ( 2) 3
2 2 18
1 4 6
39.
A B B AВообще говоря, если произведения АВ и ВА существуют, то АВ ВА.
Если АВ=ВА, то такие матрицы называются перестановочными.
Пример.
39
40.
УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ7 5
7 2
7
0 2 5 3 0 2
0
5
4
4 2 4 5
14 35 21
0
0
0
8 20 12
7 3
0 3
4 3
41.
При условии, что операции в обеих частяхравенств выполнимы, справедливы
следующие свойства.
Свойства произведения матриц
1. А · О = О;
2. А · Е = А;
3. А · В ≠ В · А;
4. α (АВ) = (αА) · В = А · (αВ);
5. АВС = (АВ) · С = А · (ВС);
6. А (В + С) = АВ + АС;
7. (А · В)Т =ВТ · АТ.
42.
2. Определители43.
Вильгельм ГотфридЛейбниц
(1646-1716) — саксонский
философ, логик, математик,
механик, физик, юрист,
историк, дипломат,
изобретатель и языковед.
Понятие «определитель»
принадлежит Г. Лейбницу
(1678).
44.
Определитель (детерминант) –числовая характеристика квадратной матрицы.
Обозначения определителя матрицы А:
|A|, det A, .
45.
Невырожденная матрица• Квадратная матрица А называется
невырожденной, если её определитель
det А 0.
• В противном случае (det А = 0) матрица
А называется вырожденной.
46.
Квадратной матрице А порядка n можно сопоставитьчисло det A, называемое ее определителем, следующим
образом:
1. n = 1. А = (a1); det A = a1
2. n = 2.
a11
| A |
a21
a12
a11 a22 a12 a21
a22
• Вычисление определителя 2-го порядка
иллюстрируется схемой:
Пример.
47.
3. n = 3.Для вычислении определителя 3-го порядка используют
правило треугольников (Саррюса).
a11a12 a13
det A a21a22 a23 a11a22 a33 a12 a23a31
a31a32 a33
a13a21a32 a31a22 a13 a32 a23a11 a33a21a12
48.
**
*
*
*
*
* *
* *
* *
*
*
*
*
*
*
49.
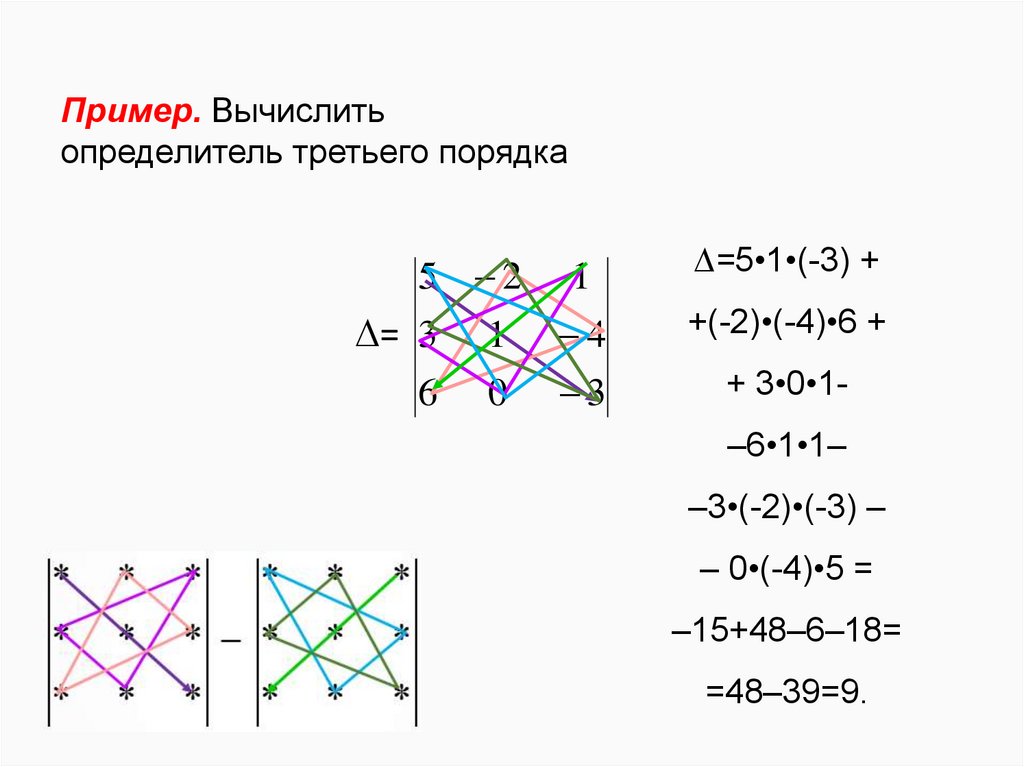
Пример. Вычислитьопределитель третьего порядка
5 2 1
= 3 1 4
6 0 3
=5•1•(-3) +
+(-2)•(-4)•6 +
+ 3•0•1–6•1•1–
–3•(-2)•(-3) –
– 0•(-4)•5 =
–15+48–6–18=
=48–39=9.
50.
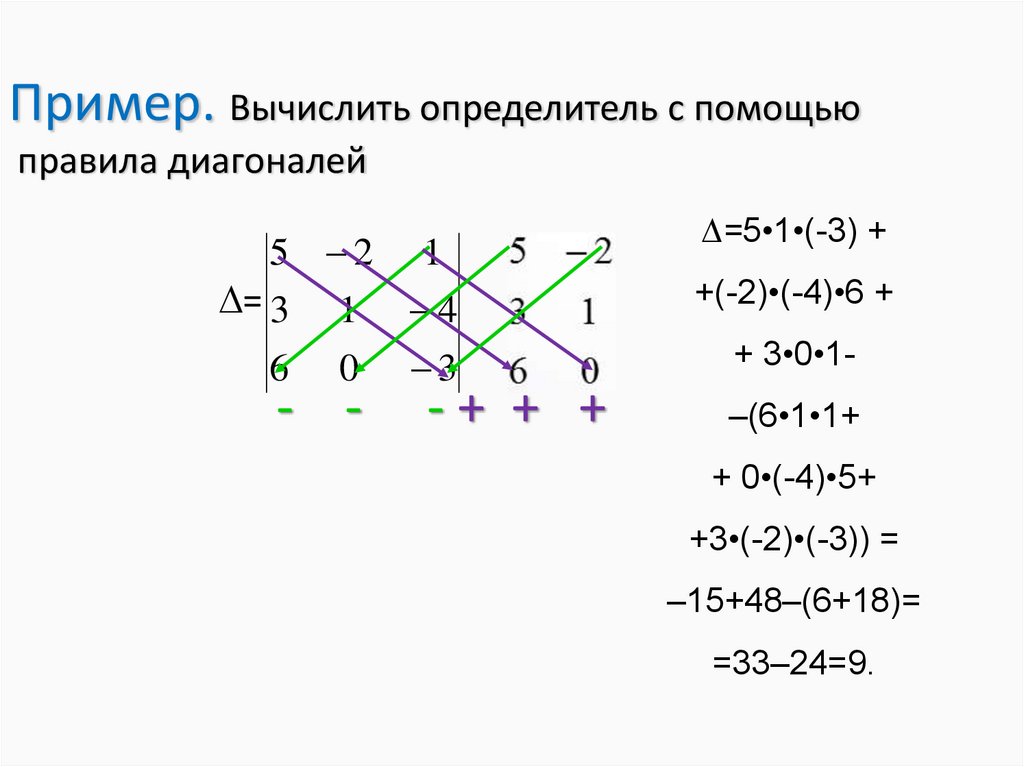
Пример. Вычислить определитель с помощьюправила диагоналей
5 2 1
= 3 1 4
6 0 3
- -
-+ + +
=5•1•(-3) +
+(-2)•(-4)•6 +
+ 3•0•1–(6•1•1+
+ 0•(-4)•5+
+3•(-2)•(-3)) =
–15+48–(6+18)=
=33–24=9.
51.
Определитель произвольнойтреугольной матрицы равен
произведению элементов главной
диагонали
52.
Минор элемента аi j• Минором некоторого элемента aij квадратной матрицы
А n-го порядка называется определитель n –1-го
порядка матрицы, полученной из исходной путем
вычеркивания из А строки и столбца, на пересечении
которых находится выбранный элемент aij , минор
обозначается Мij.
3
7
А 0
5
2
3
5
7
5
4
6
9
a23=4
1
2
2
4
3 2 1
M23 0 5 2 60 20 0 250 0 42 13
5 7 4
M31=5
M14=11
53.
Алгебраическое дополнение Aik• Алгебраическим дополнением элемента aik
квадратной матрицы А называется число Аik :
Для предыдущего примера:
А23= –М23= –13
А31= М31= 5
А14= –М14= –11
54.
ФОРМУЛА ЛАПЛАСАТеорема. Определитель матрицы равен сумме
произведений элементов любого ее ряда на
соответствующие им алгебраические a11 a12 a13
дополнения.
a21 a22 a23
a
Разложение определителя по 31
a32
a33
элементам первой строки:
det A a 11 A11 a 12 A12 a 13 A13 .
Пьер-Симо́н, маркиз де
Лапла́с (1749 - 1827) —
французский математик,
механик, физик и астроном
55.
2 1 14 3
1 1
2 4 3 2
2
17 12
17 12
11 17 12
1 1
11
2( 48 51) 2(12 17) 11(3 4)
4 3
6 10 11 5.
4 1
3 5
2 3
5 0
0 3
4 1
3
2 4
4 1
1 3
2 2 3 1 2 5
5
0 1
3
1
2
3
5 0 5
0 5
2(5 10 5 ( 14)) 2(50 70) 2 120 240
56.
ПРАВИЛО ЧУЖИХ ДОПОЛНЕНИЙ• Сумма произведений элементов любого
ряда кв. матрицы на алгебраические
дополнения соответствующих элементов
другого ее параллельного ряда равна нулю.
57.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ1. Транспонирование матрицы не меняет значения ее
определителя.
det A det A
T
3 5 6 3 4 5
4 2 1 5 2 3
5 3 2 6 1 2
58.
Свойства определителей2. При перестановке двух параллельных рядов определитель
меняет знак.
3. Если соответствующие элементы двух параллельных рядов
равны или пропорциональны, то определитель равен 0.
4. Общий множитель элементов какого-либо ряда можно
вынести за знак определителя.
5. Определитель не изменится, если к элементам одного ряда
прибавить соответствующие элементы параллельного ряда,
умноженные на одно и то же число.
6. Определитель матрицы, содержащей целый ряд из нулей,
равен нулю.
7. det Е 1
8. det( A B ) det A det B
59.
9. Если элементы какой-либо ряда квадратной матрицыА состоят из двух слагаемых, то определитель А равен
сумме определителей двух матриц, различающихся
между собой только элементами этого ряда, бывшими
ранее отдельными слагаемыми.
а11
а11
а 21
а 21
а31
а31
а12
а 22
а32
а13
а11
а 23 а 21
а33 а31
а12
а 22
а32
а13 а11
а 23 а 21
а33 а31
а12
а 22
а32
а13
а 23 .
а33
60.
«А математику уже затем учитьследует, что она ум в порядок
приводит».
М. В. Ломоносов
Спасибо за внимание!











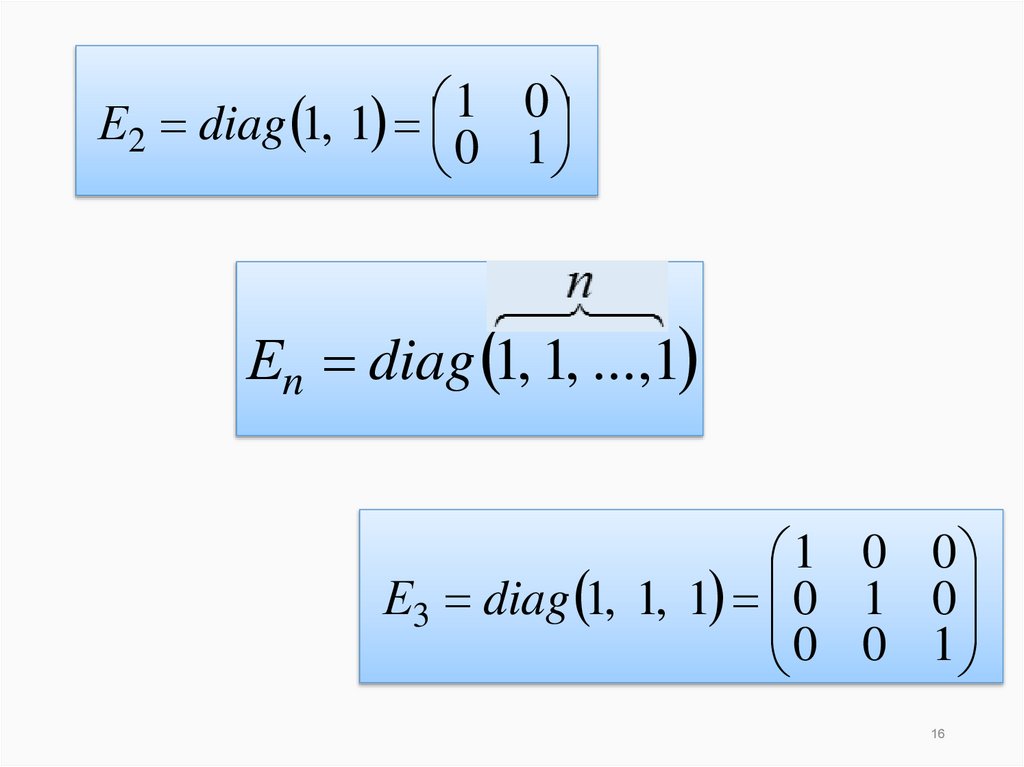




















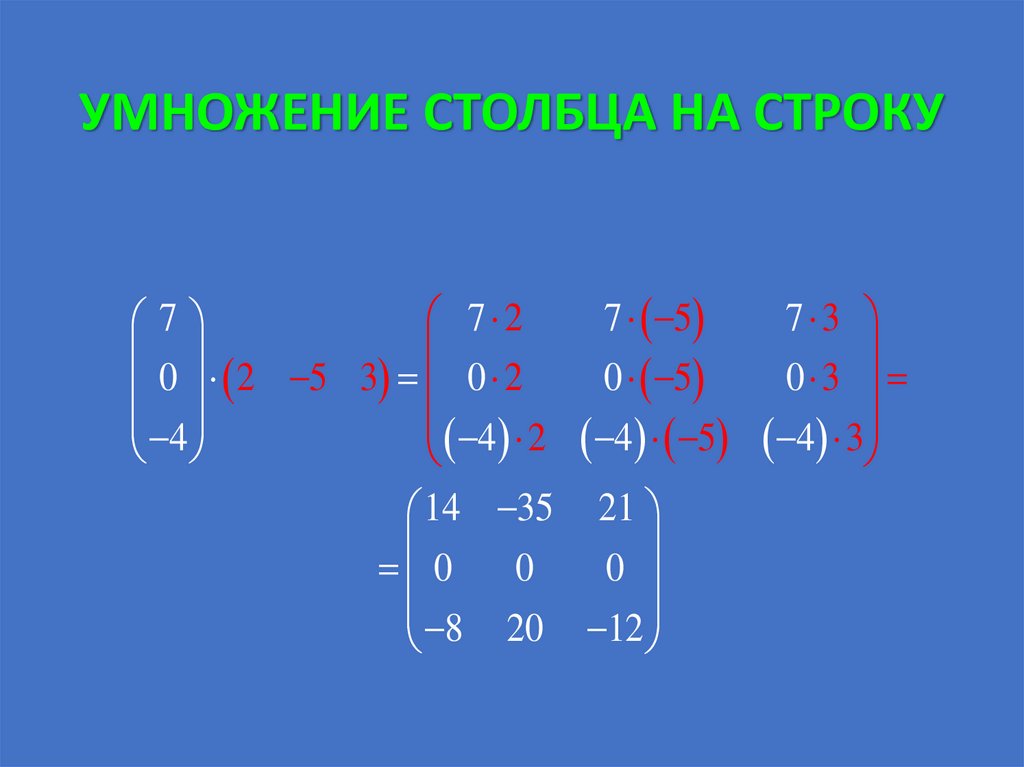







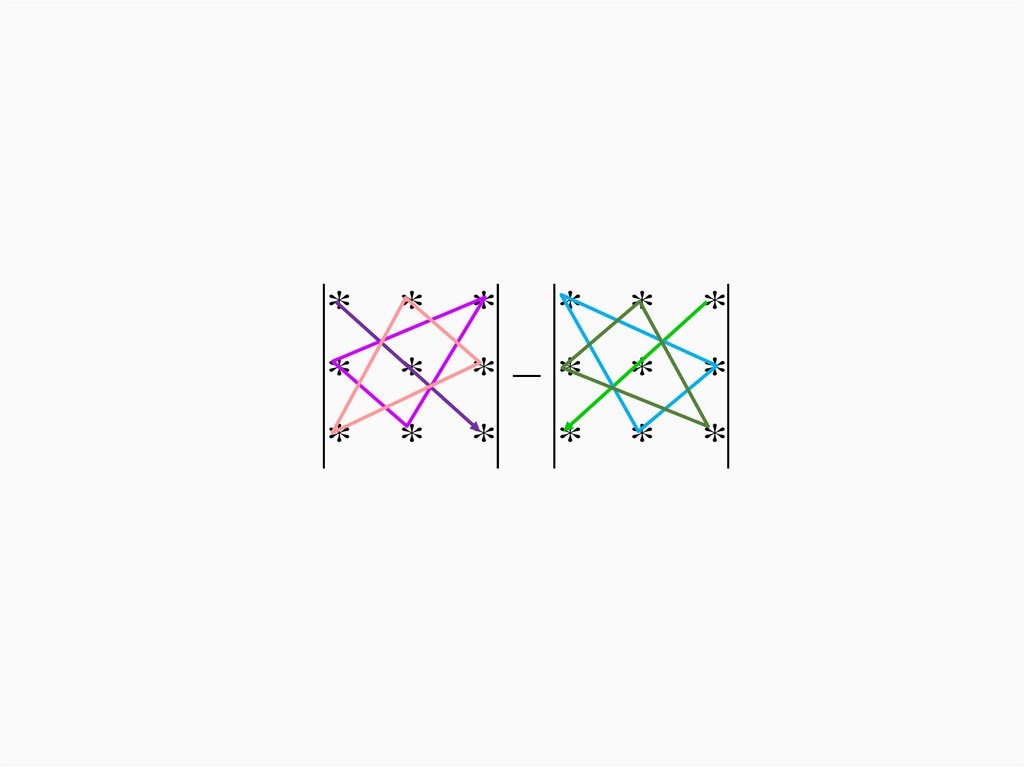




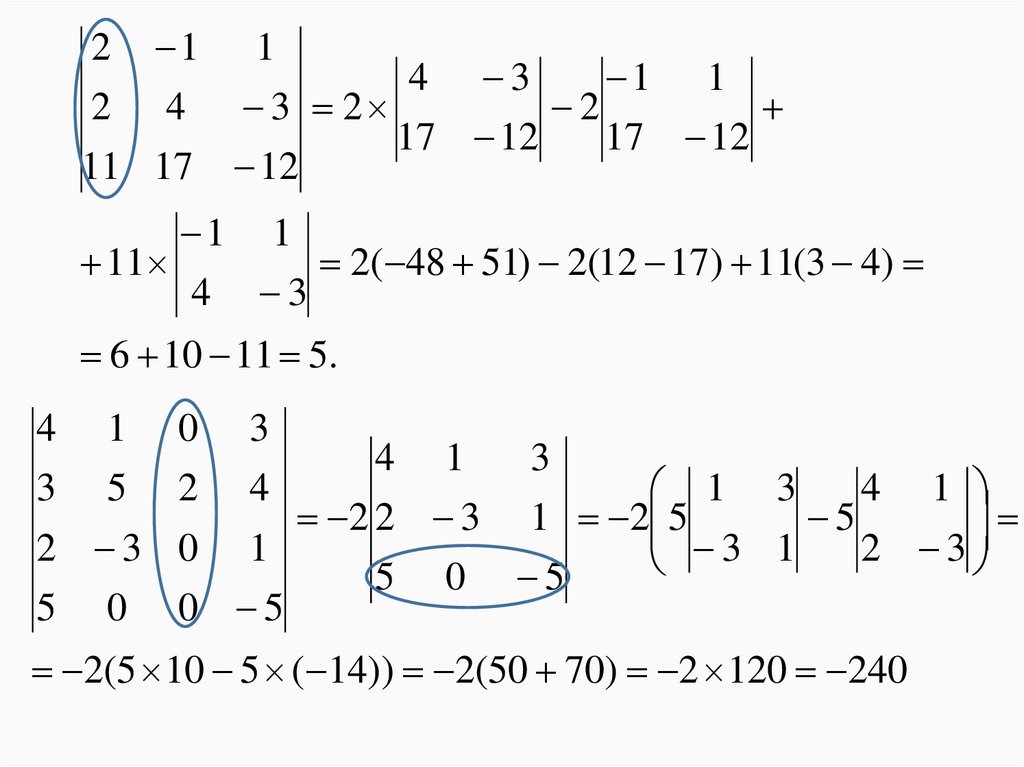





 mathematics
mathematics








