Similar presentations:
Событие. Элементарное событие
1.
Событие• Элементарное событие.
• Событие как множество.
• Невозможное событие.
• Достоверное событие.
• Несовместные события.
• Полная группа событий.
1
2.
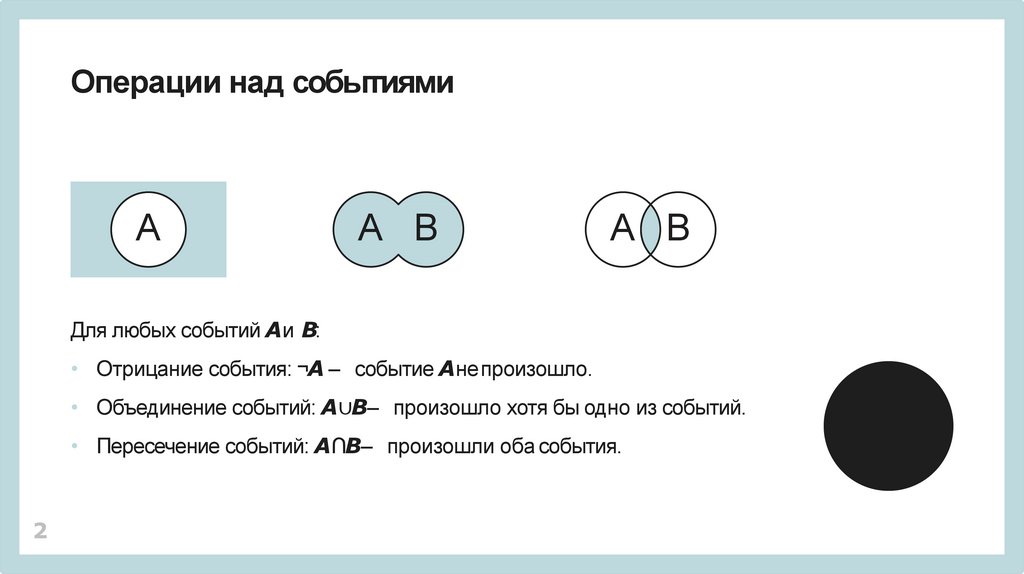
Операции над событиямиА
А B
А B
Для любых событий Aи B:
• Отрицание события: ¬A – событие Aнепроизошло.
• Объединение событий: A∪B– произошло хотя бы одно из событий.
• Пересечение событий: A∩B– произошли оба события.
2
3.
Вероятность• Мера возможности наступления события.
• Для достоверного события вероятность 1.
• Для невозможного события вероятность 0.
• Вероятность события Aобозначим P(A).
3
4.
Вероятность отрицания события«A или ¬A» – всегда достоверное событие.
• Следовательно, P(A)+P(¬A)=1
• Следовательно,
P(¬A)=1 −P(A)
4
5.
Вероятность пересечения событий• Для независимых событий:
P(A∩B)=P(A)•P(B)
• В общем случае:
P(A∩ B) =P(A)•P(B|A)
P(A∩ B) =P(B)•P(A|B)
5
6.
Условная вероятность• P(B|A)– вероятность наступления событияB
при условии A:
P(A
∩B
)
P(B|A)=
P(A)
• Для независимых событий:
P(A)•P(B)
P(B|A)=
=P(B)
P(А)
6
7.
Вероятность объединения событий• Для несовместных событий:
P(A∪B)=P(A)+P(B)
• Для полной группы событий:
P(A1)+P(A2)+… +P(An)=1
• В общем случае:
P(A∪B)=P(A)+P(B)−P(A∩B)
7
8.
Принцип включения-исключения для вероятностейФормула вероятности объединения для произвольного числа событий:
n
n
n
(⋃A)=∑P(A) − ∑ P(A ∩A ) + ∑ P(A ∩A ∩A ) + ... + (−1) ∙ P(⋂A)
P
i
i =1
8
i
i =1
i
1 ≤i <j≤n
i
j
1≤i <j <k≤n
j
k
n−1
i
i =1
9.
Формула полной вероятностиДля полной группы событий A1, A2, ..., Anи события B:
n
1=
n
∑ P(A|B)= ∑
i =1
i
P(Ai∩B)
P(B)
i =1
n
=
P(B|Ai)∙ P(A)
i
∑
P(B)
i =1
Формула полной вероятности:
n
∑P(A)∙P(B|A)
P(B)=
i
i =1
9
i
10.
Формула БайесаИспользуем равенства P(A⋂B) =P(A) ∙P(B|A) и P(A⋂B)=P(B)∙P(A|B)
• Формула Байеса:
P(A)∙P(B|A)
P(A|B)=
P(B)
• С учетом формулы полной вероятности для полной группы событий {Ai }:
P(Aj|B)=
10
∑
P(Aj)∙P(B|Aj)
n
P(Ai)∙P(B|Ai)
i =1
11.
Классическоеопределение вероятности
P(A)=
благоприятные исходы
равновероятные события
• Опирается на комбинаторные методы.
• Подходит для идеальных условий.
11
12.
Геометрическая вероятностьP(A)=
Мера (A)
Мера (Ω)
• Когда невозможно вычислить количество
элементарных событий.
12
13.
Статистическая вероятностьP(A)=
благоприятные исходы
проведенные эксперименты
• Приближается к реальной вероятости
при росте числа экспериментов.
13
14.
Байесовская вероятностьP(Aj|B)=
∑
P(Aj)∙P(B|Aj)
n
P(Ai)∙P(B|Ai)
i =1
• Степень уверенности.
• Пересчет при поступлении дополнительной информации.
14
15.
Пример: условия• Коллекция документов:
– 95% документов типа R;
– 5% документов типа Q.
• Алгоритм клас ификации ошибается в 1% случаев.
• Какова вероятность, что ответ Q окажется верным?
15
16.
Пример: решение• Пусть событие AX– выбран документ типаX.
• Событие BX– алгоритм выдал ответ X.
• Применим формулу Байеса:
P(AQ|BQ)=
P(AQ|BQ)=
16
P(AQ)∙P(BQ|AQ)
P(AQ)∙ P(BQ|AQ)+P(AR)∙P(BQ|AR)
0.05 ∙ 0.99
0.05 ∙ 0.99 +0.95 ∙ 0.01
≈0.83898
17.
Вероятностное пространство• Множество элементарных событий.
• σ-алгебра событий.
• Вероятностная мера на множестве
элементарных событий.
17
18.
Случайная величина• Неизвестное числовое значение –
результат случайного эксперимента.
• Отображение из множества элементарных
событий в вещественные числа:
X: Ω →
• Для количественных и качественных
характеристик события.
18
19.
Дискретные и непрерывные• Дискретные: изолированные значения.
Конечное или счетное множество значений.
• Непрерывные: произвольные значения
из некоторого интервала.
Несчетное множество значений.
19
20.
Независимые случайные величиныСобытия независимы, если P(A∩B)=P(A)•P(B)
Случайные величины X1и X2независимы, если
• независимы события «X1=a»и «X2=b»
• то есть, ∀a, b∈
:
P((X1=a)∩(X2=b))=P(X1=a)•P(X2=b)
20
21.
Характеристики случайной величины• Распределение вероятностей.
• Математическое ожидание.
• Дисперсия.
• Среднеквадратичное отклонение.
21
22.
Распределение• Вероятность P(X=a)– общая вероятность всех ω:
X(ω)=a
• Функция распределения:
FX(a)=P(X≤a)
Свойства:
• 0≤FX(x)≤1,
• FX– неубывающая,
• P(a<X≤b)=FX(b)−FX(a)
22
23.
Плотность распределения• Скорость изменения вероятности.
• Для непрерывной случайной величины, производная функции распределения:
f (x) =F’(x)
Свойства:
a
• P(a<X<b)=∫ f(x)dx
b
• f(x)≥0
+∞
−∞
• ∫ f(x)=1
a
−∞
• F(a) =∫ f(x)dx
23
24.
Математическое ожиданиеОбозначают E[X],M[X],µ
• Для дискретной случайной величины:
n
∑x ∙p
E[X]=
i
i
или
i =1
∞
∑x ∙p
E[X]=
i =1
• Для непрерывной случайной величины:
+∞
∫−∞x∙ f(x)∙ dx
E[X]=
24
i
i
25.
Свойства математического ожидания• E[C]=C
• E[C•X]=C •E[X]
• E[X+Y]=E[X]+E[Y]
• Для независимых Xи Y:
E[X∙ Y]=E[X]∙E[Y]
25
26.
ДисперсияМатематческое ожидание квадрата отклонения, обозначают Var(X),D[X],σ2
Var(X)=E[(X −E[X])2]
• Для дискретной случайной величины:
∞
n
∑
Var(X)=
pi∙ (xi−E[X])2
∑
или Var(X)=
i =1
i =1
• Для непрерывной случайной величины:
+∞
∫−∞(x−E[X]) ∙f(x)dx
Var(X)=
26
pi∙ (xi−E[X])2
2
27.
Свойства дисперсии• Var(X)=E[X2]−E[X]2
• Var(X)≥0
• Var(C)=0
• Var(C•X)=C2•Var(X)
• Var(X±Y)=Var(X)+Var(Y)
27
28.
Среднеквадратичное отклонение• Var(X)=σ2,
• σ =√Var(X)=√E[(X−E[X])2]
Единицы измерения случайной величины.
28
29.
Закон больших чиселПри достаточно большом числе испытаний
среднее арифметическое реализовавшихся значений
случайной величины с фиксированным распределением
будет приближаться к математическому ожиданию
для этого распределения.
29
30.
Примеры распределенийслучайных величин
• Распределения дискретных случайных величин.
• Распределения непрерывных случайных величин.
30
31.
Биномиальное распределениеИспытания с двумя исходами.
Вероятность успеха p и неудачи q =1−p.
• X=k – ровно k удач из n испытаний.
• Формула Бернулли:
Pn(k)=Cnk •pk•qn−k
• Математическое ожидание: E[X]=n•p
• Дисперсия: Var(X)=n •p •q
31
32.
Геометрическое распределениеИспытания с двумя исходами.
Вероятность успеха p и неудачи q =1−p.
• X=k – первая удача в k-том испытании.
P(X=k)=qk−1∙p
• P(1),P(2),P(3),... – геометрическая прогрессия.
1
• Математическое ожидание: E[X]= p
q
• Дисперсия: Var(X)= 2
p
32
33.
Гипергеометрическое распределениеKиз Nпредметов особенные, выбираем n преметов из N.
• X=k – выбрано ровно k особенных предметов.
−k
CKk ∙ CNn−K
P(X=k)=
CNn
• Математическое ожидание: E[X]=n ∙K
N
• Дисперсия: Var(X)=n ∙ K∙ (1− K)∙ N−n
N
N
N−1
33
34.
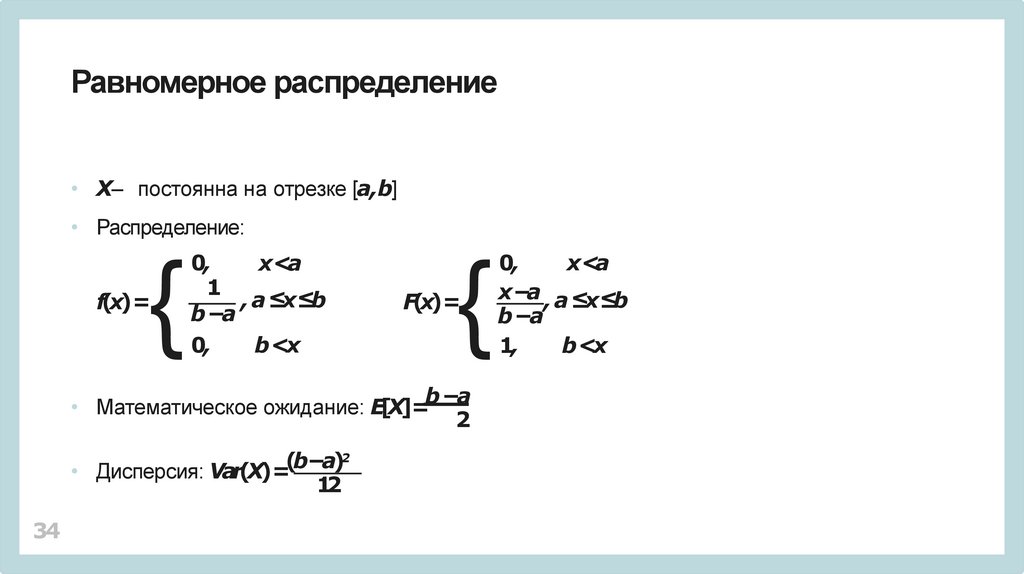
Равномерное распределение• X– постоянна на отрезке [a,b]
• Распределение:
{
f(x)=
0,
x<a
1
, a ≤x≤b
b −a
0,
b <x
{
F(x)=
b −a
• Математическое ожидание: E[X]=
2
2
(
b
−a)
• Дисперсия: Var(X)=
12
34
0,
x<a
x−a , a ≤x≤b
b −a
1,
b <x
35.
Показательное распределение• Xхарактеризует время между повторяющимися случайными событиями.
• Является непрерывным аналогом геометрического распределения.
• Распределение:
f(x)=
{
0,
F(x)=
λ•e−λx, x≥0
1
• Математическое ожидание: E[X]=
1
• Дисперсия: Var(X)= 2
λ
35
{
x<0
λ
0,
x<0
1−e−λx, x≥0
36.
Распределение Гаусса• Относится ко многим физическим
и социальным величинам.
• Нормальное распределение:
1
f(x)=
e
σ√2∏
(x−µ)2
2σ2
x
1
F(x)=
∫−∞e
σ√2∏
• Математическое ожидание: E[X]=µ
• Дисперсия: Var(X)=σ2
36
(t−µ)2
2σ2
dt
37.
Стандартное нормальноераспределение
• Нормальное распределение при µ=0, σ =1
x2
1
φ(x)=
e 2
√2∏
1
x
−
μ
φ
• f(x)=
σ
σ
x
−
μ
• F(x)=Φ
σ
(
(
t2
x
1
Φ(x)=
∫−∞ e 2dt
√2∏
)
)
µ– коэффициент смещения,
σ – коэффициент масштабирования.
37
38.
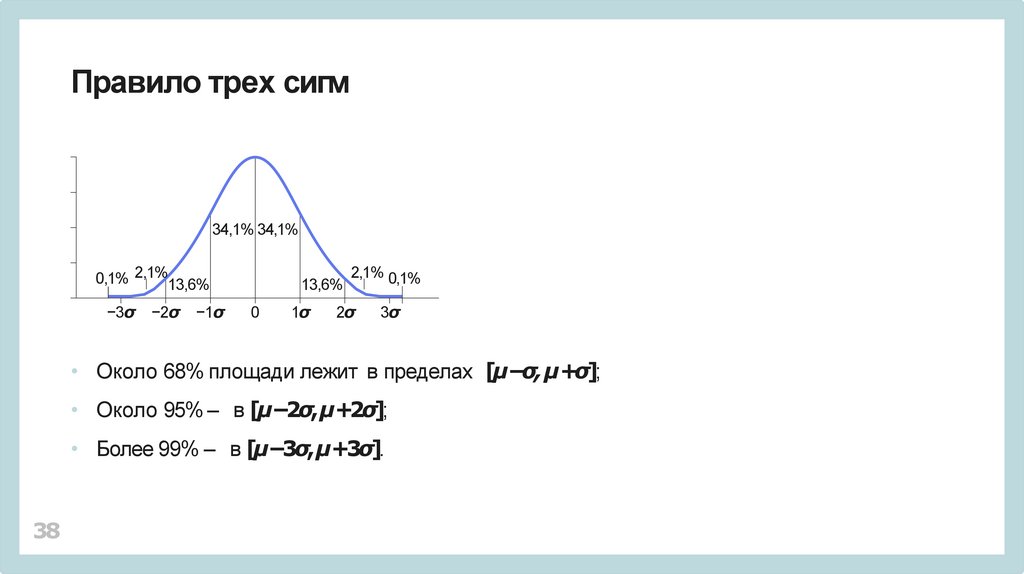
Правило трех сигм34,1% 34,1%
0,1% 2,1%13,6%
−3σ
−2σ
−1σ
13,6%
0
1σ
2,1% 0,1%
2σ
3σ
• Около 68% площади лежит в пределах [µ−σ, µ+σ];
• Около 95% – в [µ−2σ, µ+2σ];
• Более 99% – в [µ−3σ, µ+3σ].
38
39.
Центральная предельная теоремаЕсли случайная величина Xпредставляет собой сумму
достаточно большого числа независимых случайных
величин, влияние каждой из которых на всю сумму мало,
то Xимеет распределение, близкое к нормальному.
39
40.
Задачи статистикиИмеется случайная величина доступная через наблюдения.
• Собирать данные.
• Структурировать.
• Представлять.
• Анализировать параметры.
• Предсказывать будущее поведение.
40
41.
Генеральная совокупность и выборка• Генеральная совокупность – точное поведение
в прошлом и будущем.
• Выборка – отдельная группа наблюдений
Пример:
• Поведение покупателей в магазине.
• Выборка – статистика посещений и покупок
группы людей за определенный период.
41
42.
Выборка как случайная величина• Каждое наблюдение как случайная величина.
• Выборка – набор случайных величин заданной длины.
• Среднее по выборке.
42
43.
Точечная оценкаи доверительный интервал
• Точечная оценка.
• Доверительный интервал для оценивания величины X
и вероятности p:
[a,b]: P(a≤X≤b)=p
• Искомая величина лежит в интервале [a,b]
с заданной вероятностью.
43
44.
Квантиль• α-квантиль – это такое xα, что
P(X ≤xα)≥α и P(X≥xα)≥1−α
• Пропорциональная α доля выборки лежит не выше xα,
• k-тая q-вантиль – это kq-квантиль.
Например, перцентиль –
1 -квантиль,
100
95-тая перцентиль – 0.95-квантиль.
44
45.
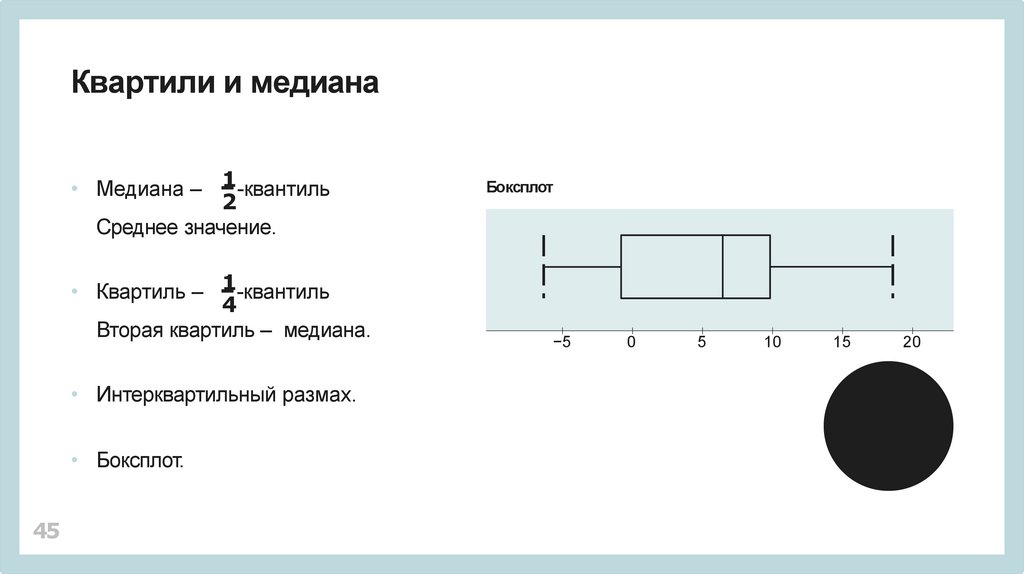
Квартили и медиана1
• Медиана –
-квантиль
2
Среднее значение.
• Квартиль – 1-квантиль
4
Вторая квартиль – медиана.
• Интерквартильный размах.
• Боксплот.
45
Боксплот
−5
0
5
10
15
20
46.
Корреляция• Свойство быть зависимыми.
• Закономерная зависимость между изменениями
нескольких случайных величин.
• Причина и следствие?
• Отсутствие корреляции и зависимость.
46
47.
Ковариация• Мера линейной зависимости.
• Математическое ожидание произведения отклонений:
cov(X, Y)=E[(X−E[X])•(Y−E[Y])]
• Положительная и отрицательная корреляция.
47
48.
Свойства ковариации• cov(X, Y)=E[X•Y]−E[X]•E[Y]
• cov(X, X)=Var(X)
• |cov(X,Y)|≤√Var(X)•Var(Y)
• Для независимых случайных величин: cov(X,Y)=0,
обратное неверно.
• Единицы измерения.
48
49.
Коэффициент корреляцииКоэффициент корреляции Пирсона:
ρX,Y =
cov(X,Y)
σX∙σY
=
E[(X−E[X])∙ (Y−E[Y])]
√E[(X−E[X])2]∙ E[(Y−E[Y])2]
• −1≤ρX,Y≤1
• Единицы измерения.
• 0для независимых величин.
• Положительная и отрицательная корреляция.
49
50.
Выбросы• Наблюдение, которое сильно выбивается.
• Влияние на оценки.
• Робастные методы.
50
51.
Ресемплинг• Генерация псевдовыборок –
создание дополнительных наборов
из имеющихся наблюдений.
• Имитация тестирования на генеральной совокупности.
51
52.
Метод складного ножа• Оценка статистических характеристик.
• Генерация выборок исключением одного элемента.
• n выборок размера n −1.
52
53.
Метод перекрестной проверки• Выборка делится на k частей.
• k −1часть используется для обучения.
• Одна часть – дляпроверки.
53
54.
Бутстрэп• Случайная генерация из имеющейся выборки:
выборки с повторениями.
• Не уменьшает число наблюдений на выборку.
54
55.
Используемые обозначения• det – определитель,
• rank – ранг,
• ||A||– евклидованорма:
=√∑[элементывектора (матрицы)]2
• .Т– транспонирование,
• .−1– обращение,
• E– единичная матрица,
• A[j]– j-й столбец матрицы A.
55
56.
Собственные числа и собственные векторы матрицыA: =
a11 a12 … a1n
a21 a22 … a2n
… …
…
an1 an2 … ann
Вектор-столбец X=[x1,x2, … , xn]Т– собственный вектор матрицы,
принадлежащий собственному числу λ если AX=λXи ∃xj≠0.
56
57.
Собственные числа и собственные векторы матрицыA: =
a11 a12 … a1n
a21 a22 … a2n
… …
…
an1 an2 … ann
Вектор-столбец X=[x1,x2, … , xn]Т– собственный вектор матрицы,
принадлежащий собственному числу λ если AX=λXи ∃xj≠0.
Система л. у. относительно x1, x2, … ,xn:
57
a11−λ
a21
a12
a22−λ
a1n
a2n
x1
x2
an1
an2
ann−λ
xn
=
0
0
0
58.
Характеристический полиномdet(A −λE)=0
58
59.
Характеристический полиномdet(A −λE) =0
Не обязательно собственные числа будут вещественными.
59
60.
Характеристический полиномdet(A −λE)=0
Не обязательно собственные числа будут вещественными.
Но для симметричной матрицы A =AТбудут!
60
собственны
е числа
λ1
λ2
…
λn вещественны
собственны
е векторы
Ӿ1
Ӿ2
…
Ӿn попарно ортогональны
61.
Ортогональная матрицаӾj=[x1,x2, …, xn]Т, Ӿk=[y1, y2, …, yn]Т
(Ӿj, Ӿk): =x1y1+x2y2 +… +xnyn=0
61
при j ≠ k
62.
Ортогональная матрицаӾj=[x1,x2, …, xn]Т, Ӿk=[y1, y2, …, yn]Т
(Ӿj, Ӿk): =x1y1+x2y2 +… +xnyn=0
при j ≠ k
А можно еще и нормировать:
||Ӿ|j|:2=(Ӿ, Ӿj )=jx
62
2
1
+x22 +… +x2n =1
63.
Ортогональная матрицаӾj=[x1,x2, …, xn]Т, Ӿk=[y1, y2, …, yn]Т
(Ӿj, Ӿk): =x1y1+x2y2 +… +xnyn=0
при j ≠ k
А можно еще и нормировать:
||Ӿ|j|:2=(Ӿ, Ӿj )=jx
2
1
+x22 +… +x2n =1
AӾ1=λ1Ӿ1, AӾ2=λ2Ӿ2, …, AӾn=λnӾn
A[Ӿ1|Ӿ2|…| Ӿn]=[Ӿ1|Ӿ2|…| Ӿn]
63
λ1
0
0
λ2
0
0
0
0
λn
64.
Симметричнаяи ортогональная матрицы
Ортогональная матрица P:=[P[1]|P[2]|… |P[n]]:
P • P Т= P Т• P = E
P −1 = P Т
64
65.
Симметричнаяи ортогональная матрицы
Ортогональная матрица P:=[P[1]|P[2]|… |P[n]]:
P • P Т= P Т• P = E
P −1 = P Т
симметричная
матрица
65
=P
диагональная
матрица
• PТ
66.
Симметричнаяи ортогональная матрицы
Ортогональная матрица P:=[P[1]|P[2]|… |P[n]]:
P • P Т= P Т• P = E
P −1 = P Т
симметричная
матрица
=P
диагональная
матрица
Т +… +λ P
Т
+
λ
P
•P
•P
A=λ1P[1] •P
[n]
2 [2]
[2]
n [n]
Т
[1]
66
• PТ
67.
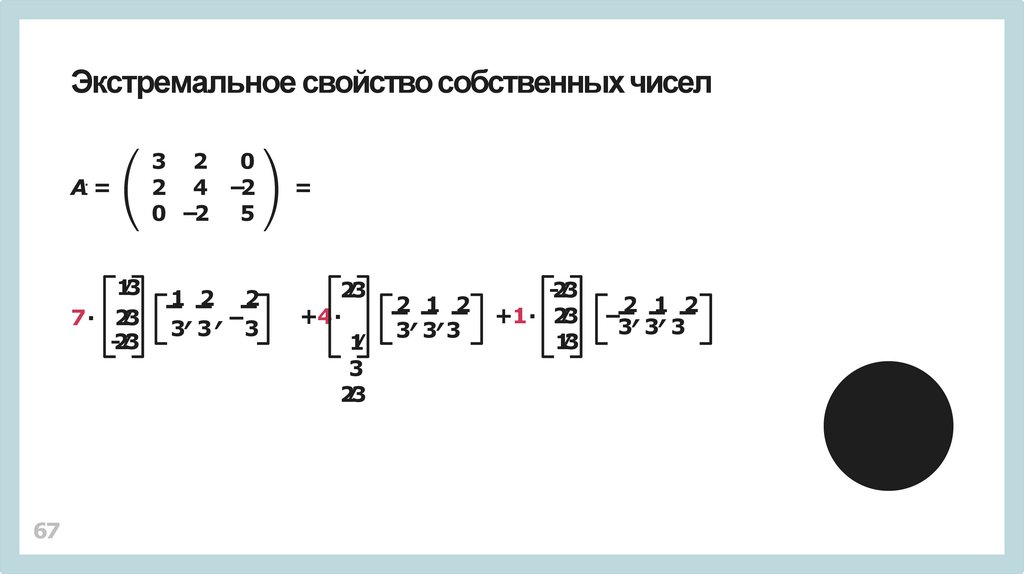
Экстремальное свойство собственныхчисел67
A: =
3 2 0
2 4 −2
0 −2 5
1⁄3
7∙ 2⁄3
-2⁄3
1 2 2
, ,−
3 3 3
=
2⁄3
+4∙
1⁄
3
2⁄3
2 1 2
, ,
3 33
-2⁄3
+1∙ 2⁄3
1⁄3
2 1 2
− , ,
3 3 3
68.
Экстремальное свойство собственныхчиселA: =
3 2 0
2 4 −2
0 −2 5
1⁄3
7∙ 2⁄3
-2⁄3
1 2 2
, ,−
3 3 3
=
2⁄3
-2⁄3
2 1 2
2 1 2
+1∙ 2⁄3 − , ,
+4∙
, ,
3 3 3
3 33
1⁄3
1⁄
3
2⁄3
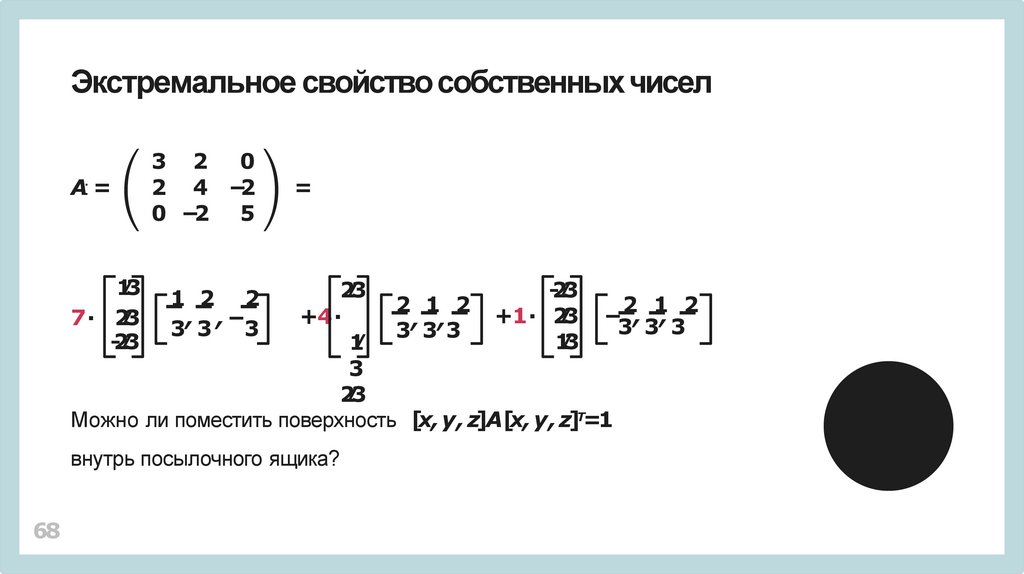
Можно ли поместить поверхность [x, y , z]A[x, y , z]Т=1
внутрь посылочного ящика?
68
69.
Экстремальное свойство собственныхчиселA: =
3 2 0
2 4 −2
0 −2 5
1⁄3
7∙ 2⁄3
-2⁄3
1 2 2
, ,−
3 3 3
=
2⁄3
-2⁄3
2 1 2
2 1 2
+1∙ 2⁄3 − , ,
+4∙
, ,
3 3 3
3 33
1⁄3
1⁄
3
2⁄3
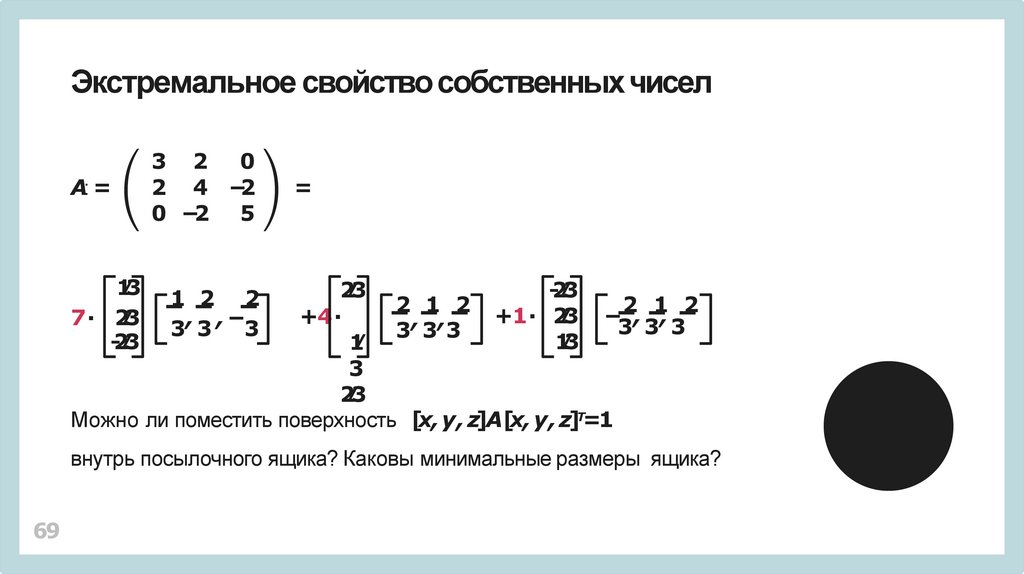
Можно ли поместить поверхность [x, y , z]A[x, y , z]Т=1
внутрь посылочного ящика? Каковы минимальные размеры ящика?
69
70.
Экстремальное свойство собственныхчисел(x;y;z)A
7
70
x
y
z
=1
1 1 2
x+ y − z
3
3
3
2
+4
2 1 2
x+ y + z
3
3
3
2
+1
2 2 1
− x+ y− z
3
3
3
2
=1
71.
Экстремальное свойство собственныхчисел(x;y;z)A
7
x
y
z
=1
1 1 2
x+ y − z
3
3
3
7X 2+4Y2+1Z 2=1
71
2
+4
2 1 2
x+ y + z
3
3
3
2
+1
2 2 1
− x+ y− z
3
3
3
2
=1
72.
Экстремальное свойство собственныхчисел(x;y;z)A
7
x
y
z
=1
1 1 2
x+ y − z
3
3
3
2
+4
2 1 2
x+ y + z
3
3
3
2
+1
2 2 1
− x+ y− z
3
3
3
2
=1
7X 2+4Y2+1Z 2 =1
… и переход к новым переменным не меняет расстояний между точками!
72
73.
Экстремальное свойство собственныхчиселЭллипсоид в
n
XТAX =1
«шире всего» в направлении его оси, соответствующей
минимальному собственному числу матрицы A,
73
74.
Экстремальное свойство собственныхчиселЭллипсоид в
n
XТAX =1
«шире всего» в направлении его оси, соответствующей
минимальному собственному числу матрицы A,
размеры минимального ящика (длина, ширина, высота …) –
2
2
2
,
, …,
,
√λ1 √λ2
√λn
74
75.
Экстремальное свойство собственныхчиселЭллипсоид в
n
XТAX =1
«шире всего» в направлении его оси, соответствующей
минимальному собственному числу матрицы A,
размеры минимального ящика (длина, ширина, высота …) –
2
2
2
,
, …,
,
√λ1 √λ2
√λn
а ориентировать ребра ящика надо по собственным векторам
Ӿ1,
75
Ӿ2,
…,
Ӿn
76.
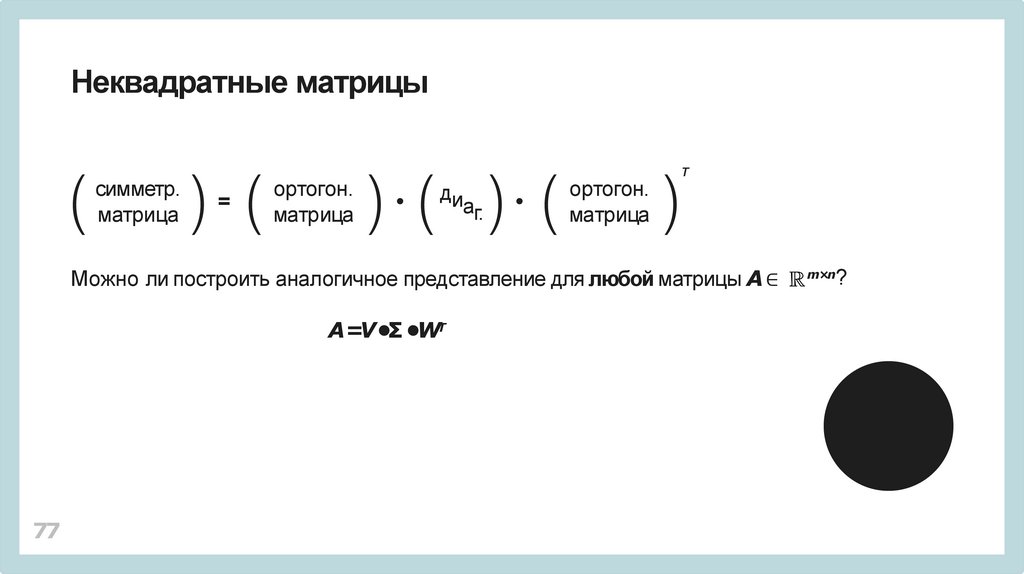
Неквадратные матрицысимметр.
матрица
=
ортогон.
матрица
ди
аг.
ортогон.
матрица
Т
Можно ли построить аналогичное представление для любой матрицы A ∈
76
m×n
?
77.
Неквадратные матрицысимметр.
матрица
=
ортогон.
матрица
ди
аг.
ортогон.
матрица
Т
Можно ли построить аналогичное представление для любой матрицы A ∈
A=V •Σ •WТ
77
m×n
?
78.
Неквадратные матрицысимметр.
матрица
ортогон.
матрица
=
ди
аг.
ортогон.
матрица
Т
Можно ли построить аналогичное представление для любой матрицы A ∈
A=V •Σ •WТ
Матрицы V ∈
и W∈
m×m
n ×n
– ортогональные.
Элементы Σ =[σij]все равны 0если i ≠j.
78
m×n
?
79.
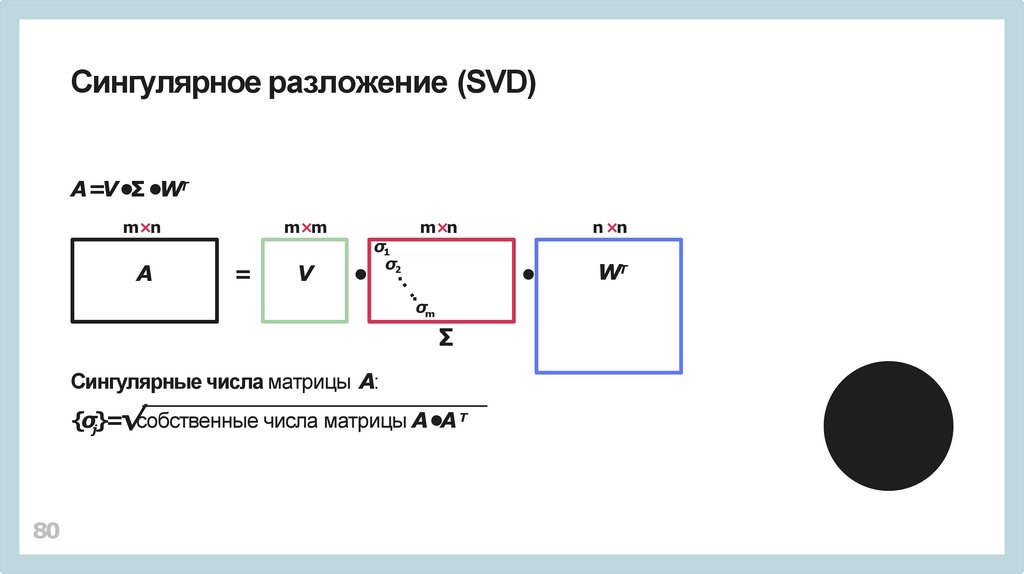
Сингулярное разложение (SVD)A=V •Σ •WТ
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
79
n ×n
WT
80.
Сингулярное разложение (SVD)A=V •Σ •WТ
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
Сингулярные числа матрицы A:
{σj}=√собственные числа матрицы A•A Т
80
n ×n
WT
81.
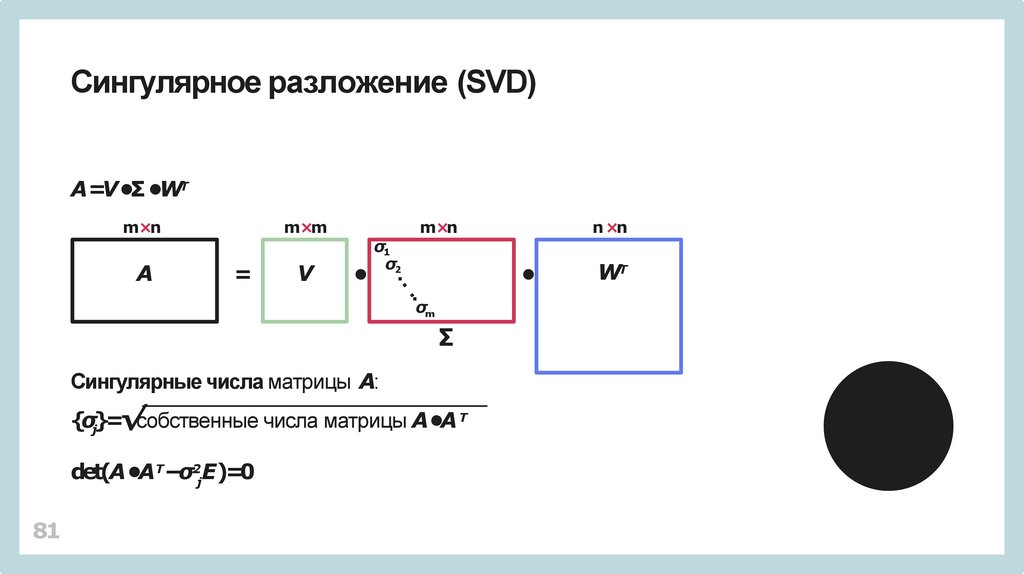
Сингулярное разложение (SVD)A=V •Σ •WТ
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
Сингулярные числа матрицы A:
{σj}=√собственные числа матрицы A•A Т
det(A •AТ−σ2jE)=0
81
n ×n
WT
82.
Сингулярные числа и векторыσ1>0, σ2>0, . . . , σr>0при r: =rank(A)
Сингулярные векторы матрицы A
82
V[j ]– левый
A•AТV[j ]=σ 2V[j]
W[j ]– правый
AТ AW[j ]=σ 2W[j]
j
j
83.
Сингулярные числа и векторыσ1>0, σ2>0, . . . , σr>0при r: =rank(A)
Сингулярные векторы матрицы A
V[j ]– левый
A•AТV[j ]=σ 2V[j]
W[j ]– правый
AТ AW[j ]=σ 2W[j]
j
j
A•W[j ]=σjV[j ], AТV[j ]=σjW[j]
83
84.
Сингулярное разложение: приближение матрицыПусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
84
85.
Сингулярное разложение: приближение матрицыПусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
85
86.
Сингулярное разложение: приближение матрицыПусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
Основной «взнос» в сумму производится за счет множителей σj.
большие
σ1,…, σk, σk+1, …, σr
малые
86
87.
Сингулярное разложение: приближение матрицыПусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
Основной «взнос» в сумму производится за счет множителей σj.
большие
σ1,…, σk,σk+1, …, σr
малые
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
87
88.
Сингулярное разложение:приближение матрицы
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
Ошибка приближения (норма – евклидова):
||A−A|k|=√σ
88
2
k +1
+… +σ2r
89.
Сингулярное разложение:приближение матрицы
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
Ошибка приближения (норма – евклидова):
||A−A|k|=√σ
2
k +1
+… +σ2r
Матрица Ak– наилучшее приближение матрицы A
во множестве матриц ранга k.
89
90.
Сингулярное разложение:основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
90
91.
Сингулярное разложение:основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
91
92.
Сингулярное разложение:основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
• Всегда ли это работает?
92
93.
Сингулярное разложение:основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
• Всегда ли это работает?
• Откуда взялась матрица A •AТ?!
93
94.
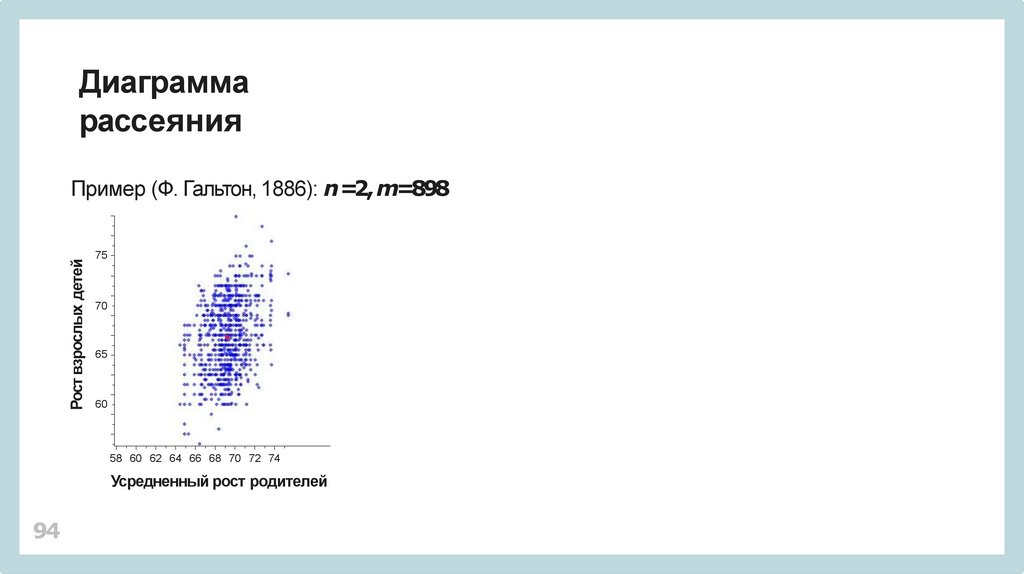
Диаграммарассеяния
Рост взрослых детей
Пример (Ф. Гальтон, 1886): n =2, m=898
75
70
65
60
58 60 62 64 66 68 70 72 74
Усредненный рост родителей
94
95.
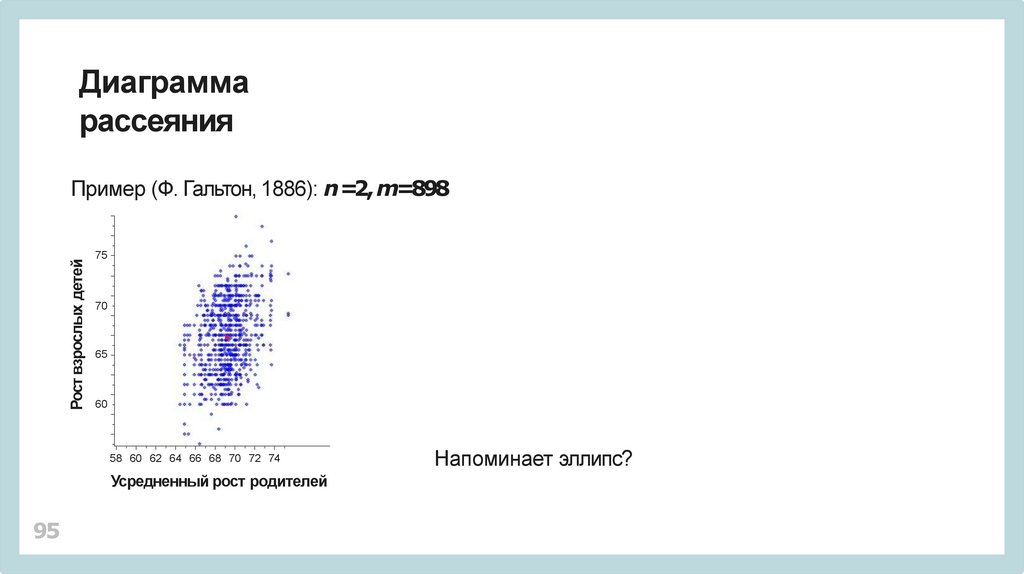
Диаграммарассеяния
Рост взрослых детей
Пример (Ф. Гальтон, 1886): n =2, m=898
75
70
65
60
58 60 62 64 66 68 70 72 74
Усредненный рост родителей
95
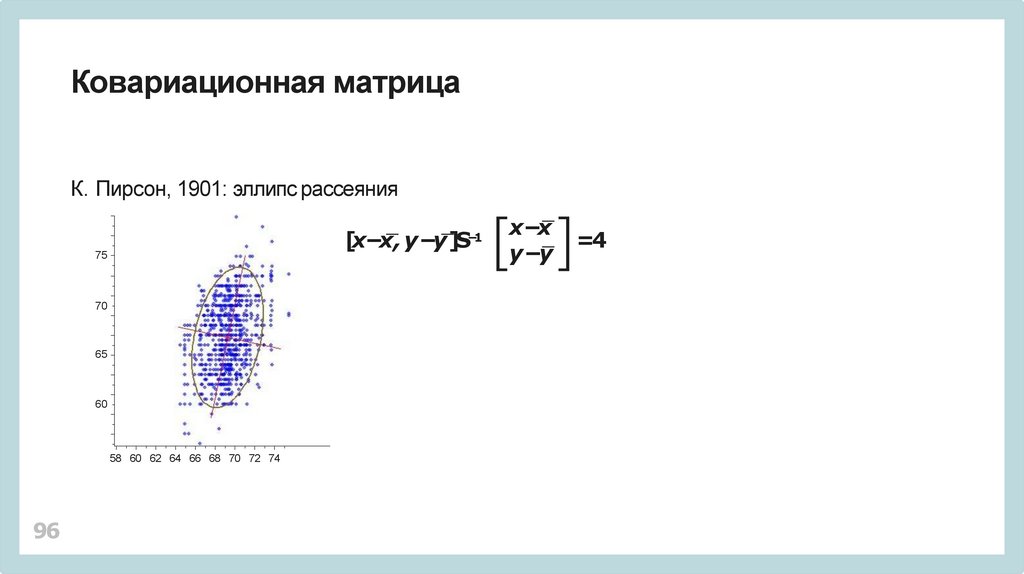
Напоминает эллипс?
96.
Ковариационная матрицаК. Пирсон, 1901: эллипс рассеяния
[x−x, y −y]S
−1
75
70
65
60
58 60 62 64 66 68 70 72 74
96
x−x
y −y
=4
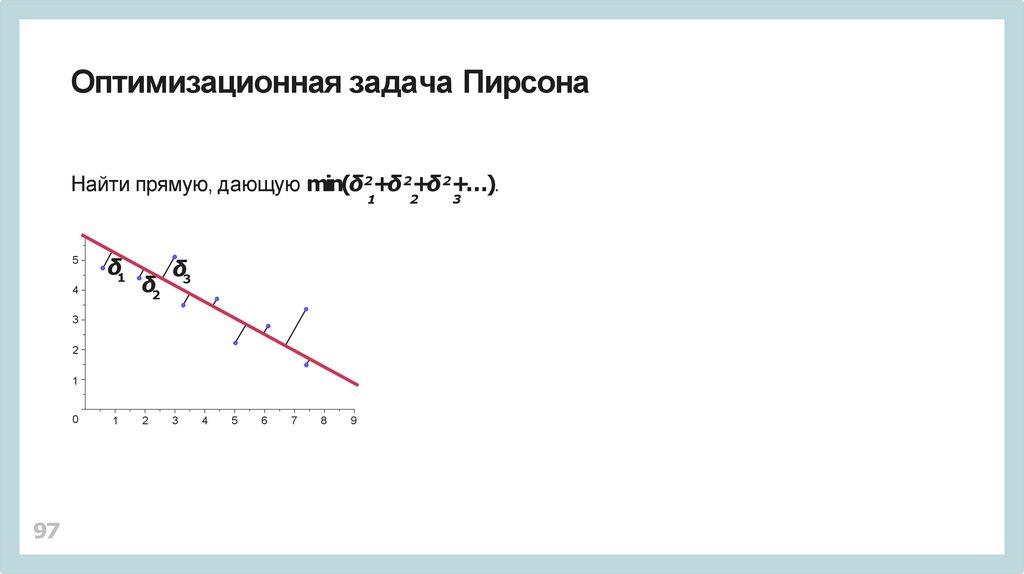
97.
Оптимизационная задача ПирсонаНайти прямую, дающую min(δ2+δ 2+δ 2+…).
1
5
δ1
4
δ2
δ3
3
2
1
0
97
1
2
3
4
5
6
7
8
9
2
3
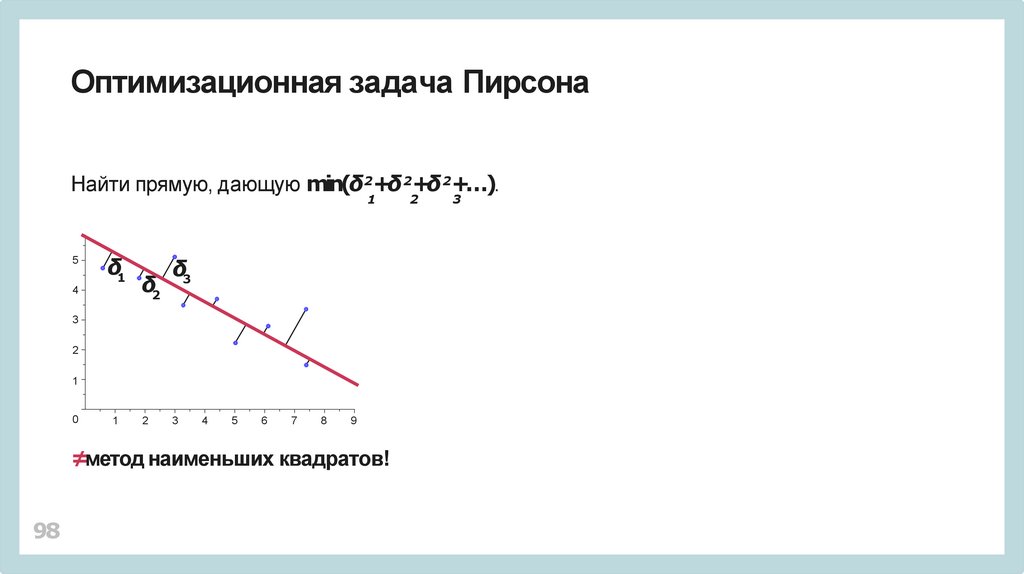
98.
Оптимизационная задача ПирсонаНайти прямую, дающую min(δ2+δ 2+δ 2+…).
1
5
δ1
4
δ2
δ3
3
2
1
0
1
2
3
4
5
6
7
8
9
≠метод наименьших квадратов!
98
2
3
99.
Ковариационная матрицаЦентрируем данные:
F :=
99
x1−x
y1−y
x2−x
y2−y
… xm−x
… ym−y
Т
100.
Ковариационная матрицаЦентрируем данные:
F :=
x1−x
y1−y
x2−x
y2−y
Ковариационная матрица
1 Т
S: = F F
m
100
… xm−x
… ym−y
Т
101.
Ковариационная матрицаЦентрируем данные:
F :=
x1−x
y1−y
x2−x
y2−y
… xm−x
… ym−y
Т
Ковариационная матрица
1 Т
S: = F F
m
Вдоль какого направления эллипс шире всего?
101
102.
Ковариационная матрица: геометрияЭллипс рассеяния
102
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
103.
Ковариационная матрица: геометрияЭллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ2?Эллипс →отрезок прямой.
103
104.
Ковариационная матрица: геометрияЭллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ2?Эллипс →отрезок прямой.
Гипотеза: закон связи между xи y – линейный,
а рассеяние вызвано ошибками наблюдений.
104
105.
Ковариационная матрица: геометрияЭллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ2?Эллипс →отрезок прямой.
Гипотеза: закон связи между xи y – линейный,
а рассеяние вызвано ошибками наблюдений.
Вместо эллипса достаточно рассматривать его проекцию.
105
106.
Метод главных компонентДанные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
106
[n]
107.
Метод главных компонентДанные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
малые
107
[n]
108.
Метод главных компонентДанные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
k
S≈S=
k
108
малые
∑
j =1
λjP[j] ∙P[Тj]
[n]
109.
Метод главных компонентДанные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
[n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
малые
k
S≈S=
k
∑
λj P[j ]∙P [Тj]
j =1
Эллипсоид рассеяния адекватно оценивается своей «тенью»,
т.е. проекцией на плоскость с направляющими векторами {P[j]}jk=1.
109
110.
Сингулярное разложение: распознавание фотографийОблако данных может состоять из нескольких «эллипсоидов».
110
111.
Сингулярное разложение: распознавание фотографийОблако данных может состоять из нескольких «эллипсоидов».
Сингулярное разложение часто срабатывает.
Пример: 10 человек, 80 оцифрованных и векторизованных фотографий,
10 000 пикселей каждая. Сингулярное разложение матрицы данных F∈ 80×10000
80
∑
F=
j =1
σj V[j ]WТ]
[j
Что произойдет, если оставим только 9 первых слагаемых?
F[Тj] ≈αj 1W[1]+αj2WТ[2] +… +αj 9W[Т9]
111
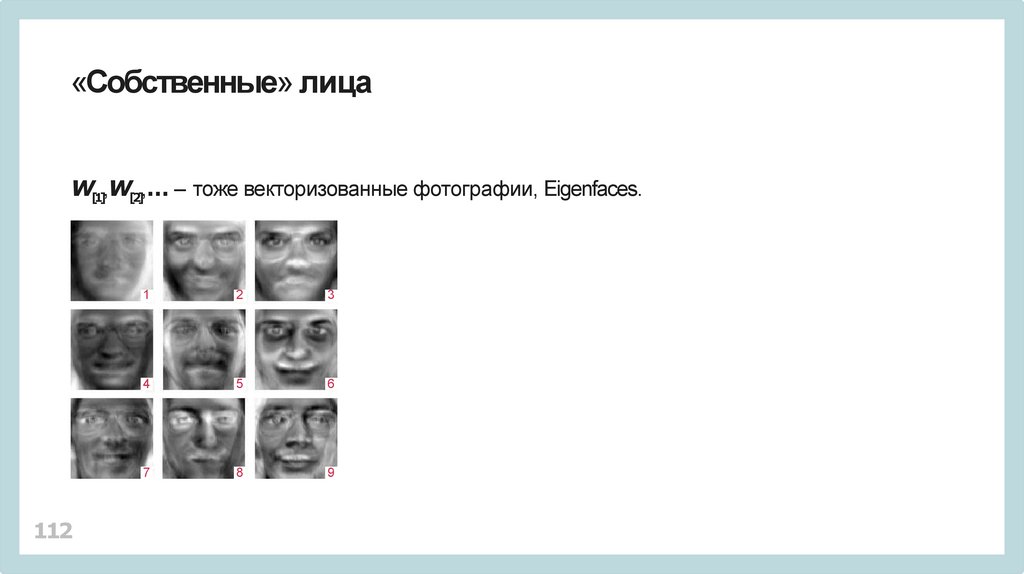
112.
«Собственные» лицаW[1],W[2],… – тоже векторизованные фотографии, Eigenfaces.
112
1
2
3
4
5
6
7
8
9
113.
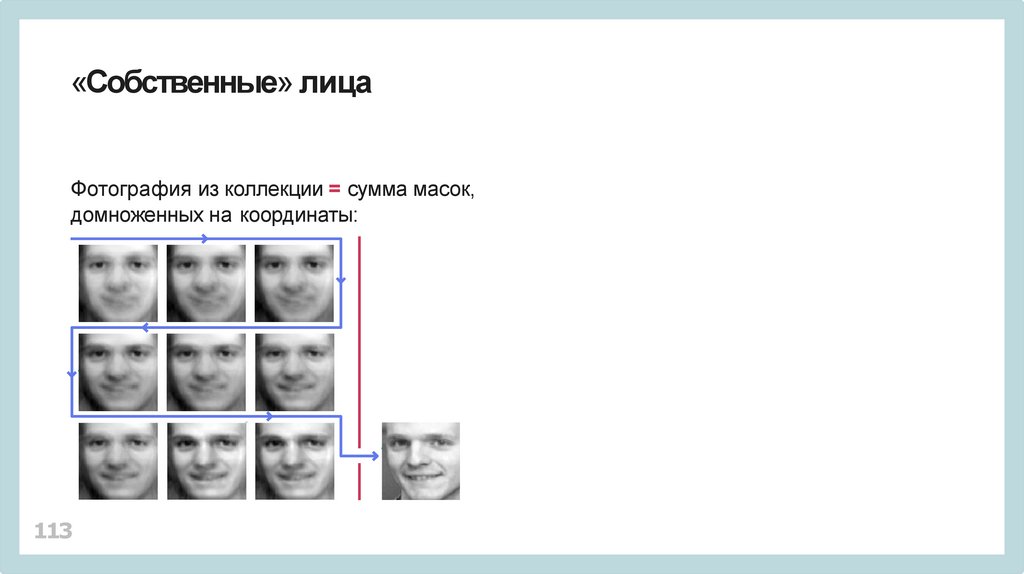
«Собственные» лицаФотография из коллекции = сумма масок,
домноженных на координаты:
113
114.
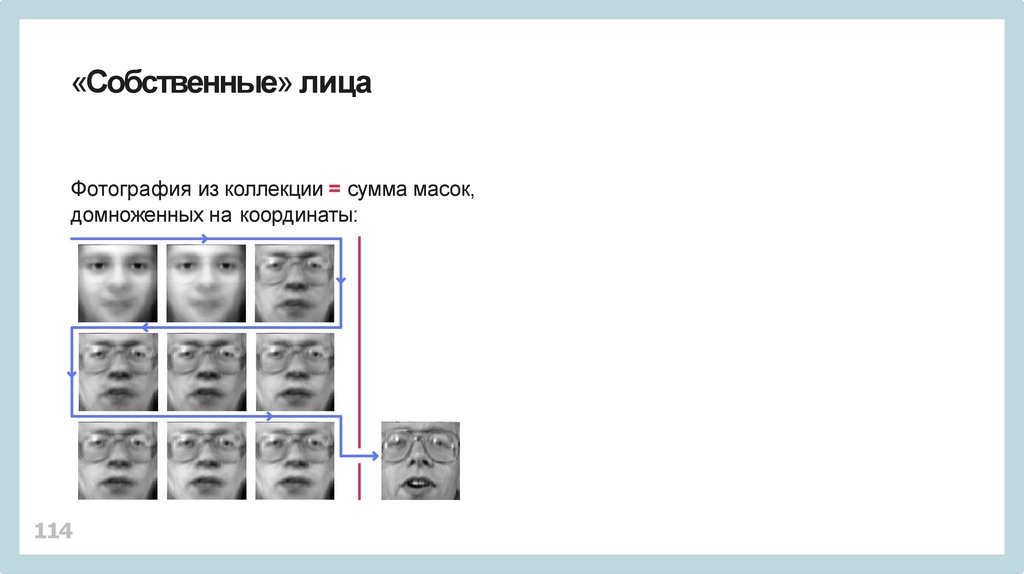
«Собственные» лицаФотография из коллекции = сумма масок,
домноженных на координаты:
114
115.
«Собственные» лицаТестовая фотография = сумма «масок»,
домноженных на координаты.
115
116.
«Собственные» лицаТестовая фотография = сумма «масок»,
домноженных на координаты.
Чья фотография? – Сравните векторы координат.
116
117.
Вычислительные аспекты сингулярного разложенияСингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
117
118.
Вычислительные аспекты сингулярного разложенияСингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
118
119.
Вычислительные аспекты сингулярного разложенияСингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
Существуют методы, позволяющие строить сингулярное разложение
матрицы A последовательным вычислением первого слагаемого
Т
σV
W
,
1 [1] [1]
119
120.
Вычислительные аспекты сингулярного разложенияСингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
Существуют методы, позволяющие строить сингулярное разложение
матрицы A последовательным вычислением первого слагаемого
Т
σV
W
,
1 [1] [1]
потом первого слагаемого разложения
Т
A− σV
W
и т.д.
1 [1] [1]
120






































































































 mathematics
mathematics








