Первообразная и интеграл

1. Первообразная И Интеграл.

Теория И Приложения.

2. Первообразная и интеграл

Сведения из истории
Первообразная
Неопределенный интеграл.Правила
интегрирования
Определенный интеграл.
Криволинейная трапеция.
Геометрический смысл
Спектры применения интеграла

3.

Создатели интегрального исчисления
Формула Ньютона-Лейбница
Для непрерывной функции
b
f ( x)dx F (b) F (a)
a
где, F(x) -первообразная функции f(x)
Исаак
Ньютон
(1643-1727)
Английский
математик
и физик
Готфрид Лейбниц
(1646-1716)
Немецкий философ и
математик

4.

Сенсация!
В ноябре 1613 года королевский математик и
астролог
австрийского двора И.Кеплер праздновал
свадьбу.
Готовясь к ней он приобрел несколько бочек
виноградного вина .При покупке Кеплер был
поражен тем, что продавец определял
вместимость бочки, производя одноединственное действие –измеряя расстояние от
наливного отверстия до точки днища. Ведь
такое измерение не учитывало форму бочки!
Размышляя над этой задачей , он нашел
формулы не только для объема бочек, но и для
объема самых различных тел: лимона, яблока,
айвы и даже турецкой чалмы. А вы знаете в чем
тут дело?
?!

5.

Найдем объем поданного к столу лимона.
Разрезав его на мелкие ломтики , ровно
обрезав край каждого ломтика, можно
легко превратить его в цилиндр, объем
которого легко посчитать. Прикладывая
друг к другу эти цилиндры , мы получим
ступенчатое тело. Его объем равен сумме
объемов цилиндров. Если ломтики очень
маленькие, то объем ступенчатого тела
мало отличается от объема лимона.
? !
Объемы каких тел изображенных
на рисунке можно вычислить
аналогично?

6.

•Функция F(x) называется первообразной для функции
f(x) на данном промежутке, если для любого х из этого промежутка
F '(x)=f(x)
Пример. Первообразной для функции f(x)=x на всей числовой оси
является F(x)=x2/2, поскольку ( х2/2)'=x
•Если F(x)-первообразная функции f(x), то и функция F(x)+C,где
С –произвольная постоянная, также является первообразной
функции f(x)
у
Геометрическая
интерпретация
х

7.

Совокупность всех первообразных данной
функции f(x) называется ее
неопределенным интегралом и
обозначается f ( x)dx
f ( x)dx F ( x) C
где С –произвольная постоянная.
cf ( x)dx c f ( x)dx,c const
( f ( x) g ( x))dx f ( x)dx g ( x)dx
1
f
(
ax
b
)
dx
F (ax b) C , a 0
a

8.

9.

у
Криволинейная трапеция-это фигура:
Ограниченная графиком непрерывной
функции y=f(x) на отрезке [а;в]
у=f(x)
Двумя вертикальными прямыми х=а и х=в
у
А также осью
Ох
S
а
Теорема для вычисления площади
криволинейной трапеции.
(геометрический смысл интеграла)
в
х
Интеграл функции f(x) от a до b—
число, которое обозначается
а и b –пределы интегрирования, причем анижний,b-верхний предел.
Функция f(x) называется
подынтегральной функцией, переменная
х-переменной интегрирования
Если f(x) –неотрицательная , непрерывная
функция на отрезке [а;в], а F(x)-её
первообразная на данном отрезке,то площадь
S соответствующей криволинейной трапеции
равна приращению первообразной на отрезке
[а;в]:
S=F(b)-F(a)
b
S f ( x) dx
a
ps

10.

b
S ( f ( x) g ( x)) dx
a
Площадь фигуры, ограниченной
графиками непрерывных функций
y=f(x) и y=g(x) таких, что f(x) g(x) для
любого x [a;b], где а и в –абсциссы
точек пересечения графиков функций:

11.

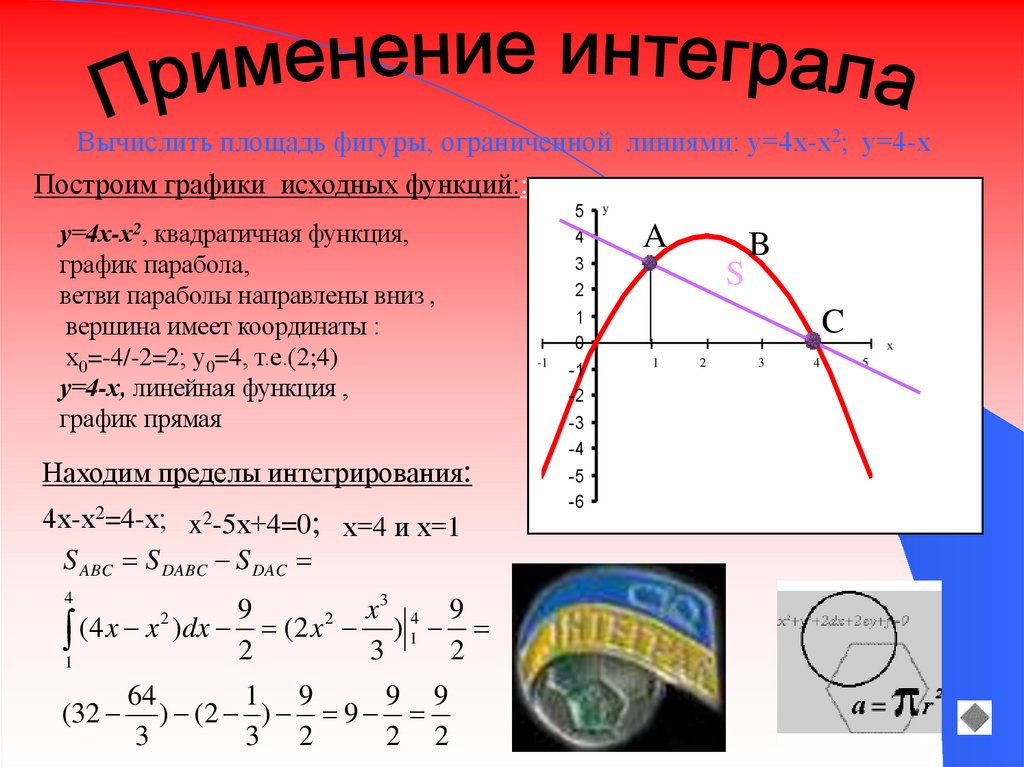
Вычислить площадь фигуры, ограниченной линиями: у=4х-х2; у=4-х
Построим графики исходных функций::
у=4х-х2, квадратичная функция,
график парабола,
ветви параболы направлены вниз ,
вершина имеет координаты :
х0=-4/-2=2; у0=4, т.е.(2;4)
у=4-х, линейная функция ,
график прямая
Находим пределы интегрирования:
4х-х2=4-х; x2-5х+4=0; х=4 и х=1
S ABC S DABC S DAC
4
9
x3 4 9
2
1 (4 x x )dx 2 (2 x 3 ) 1 2
2
(32
64
1 9
9 9
) (2 ) 9
3
3 2
2 2
-1
5
4
3
2
1
0
-1
-2
-3
-4
-5
-6
y
A
S
B
C
x
1
2
3
4
5

12.

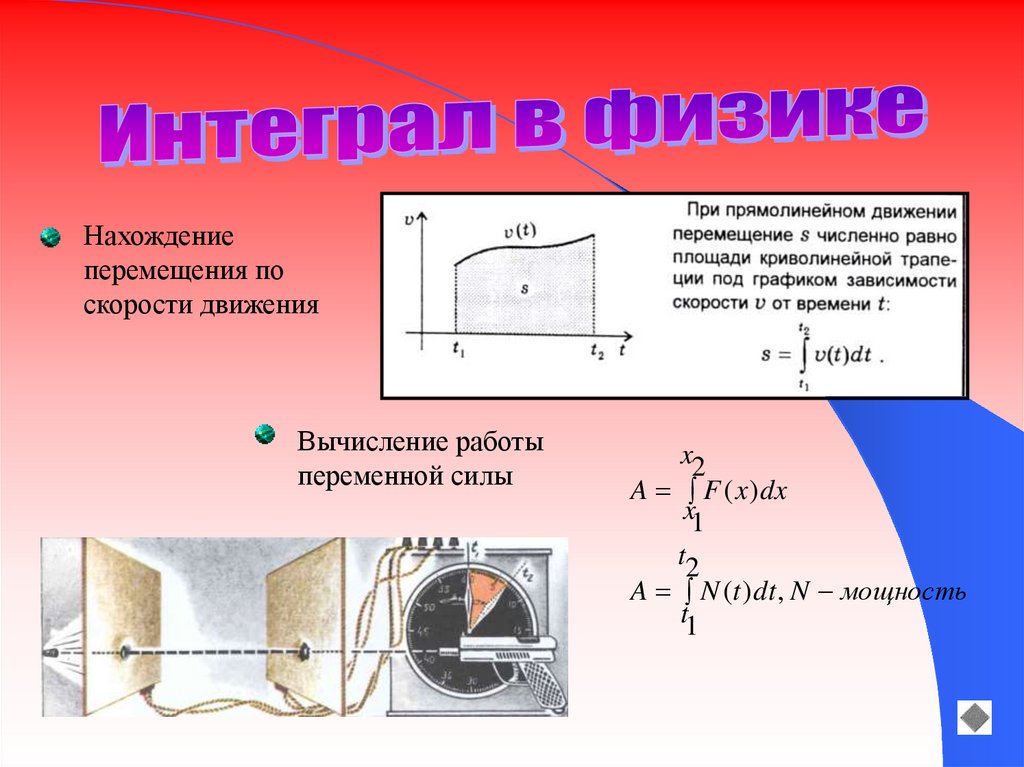
Нахождение
перемещения по
скорости движения
Вычисление работы
переменной силы
x2
A F ( x ) dx
x1
t2
A N (t ) dt , N мощность
t1

13.

Объем тела, полученного в результате
вращения вокруг оси х криволинейной
трапеции, ограниченной графиком непрерывной и
неотрицательной функции y=f(x) на отрезке [а;в]
b
V f 2 ( x)dx
a
Объем тела, заключенного между двумя
перпендикулярными к оси х плоскостями х=а
и х=в;
b
V S ( x)dx
a
Где S(x)-площадь сечения плоскостью,
проходящей через точку х [а;в] и
перпендикулярной к оси х.
Задача. Пирамида Хеопса представляет собой
Правильную четырехугольную пирамиду высотой 147 м,
в основании которой квадрат со стороной 232 м. Она
построена из камня, плотность которого 2,5 г/см2..Найти
работу против силы тяжести , затраченную при
постройке.

14.

Пусть высота пирамиды равна Н, сторона основания
в, плотность камня р. Обозначим чрез А(х) работу,
которую надо совершить для постройки пирамиды от
основания до высоты х; найдем у-сторону квадрата,
полученного в горизонтальном сечении пирамиды на
высоте х.. Из подобия треугольников получаем
H x y b
; y H ( H x)
H b
Рассмотрим тонкий слой пирамиды, расположенный на расстоянии х от
основания. Пусть толщина слоя равна dx.Cлой можно приблизительно
считать параллелепипедом. Масса его dm равна py dx p b ( H x) dx
2
2
2
H
2
При подъеме этого слоя на высоту х была проделана работа dA, равная (gdm) x,
где g-ускорение силы тяжести т.е.
H
H
b2
A A( H ) dA gp 2 x( H x) 2 dx
H 0
0
gpb 2 H 4 2 H 4 H 4
gpb 2 2
(
)
H
2
2
3
4
12
H
Подставляя числовые данные получим
А=2, 37*1012Дж

15.

Торопись,ведь дни проходят.
Ты у времени в гостях.
Не рассчитывай на помощь.
Помни: все в твоих руках!