Similar presentations:
Синус, косинус и тангенс угла. Основное тригонометрическое тождество
1.
Синус, косинус итангенс угла.
Основное
тригонометрическое
тождество
2.
ПовторениеНайти
К
sin K , cos K ,
tgK
sin В, cos В, tgВ
AB
AK
cos B sin B
sin K
KB
KB
AK
AB
sin B cos B
cos K
KB
KB
AB
tgK
KA
В
A
KA
tgB
AB
1
tgK
tgB
3.
Повторение1
sin 30 cos 600
2
A
0
300
3
0
sin
60
cos 30
2
0
2
3
1
3
tg 30
3
3
0
1
tg 60
0 3
tg30
0
В
1
C
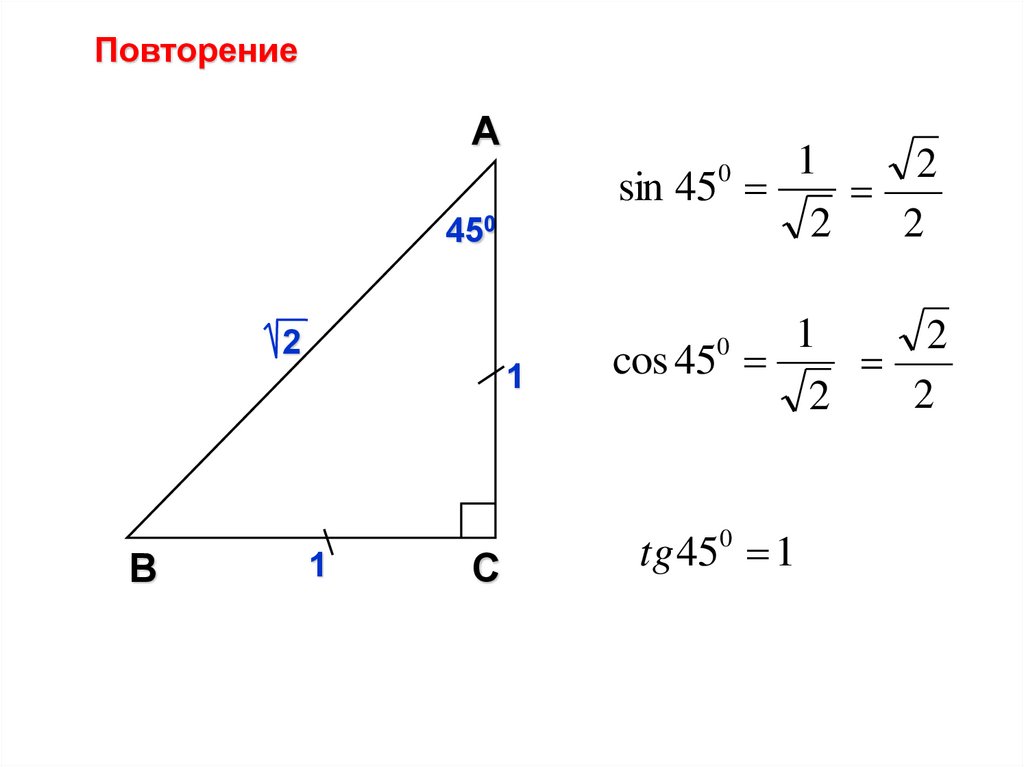
4.
ПовторениеA
1
2
sin 45
2
2
0
450
2
1
В
1
2
cos 45
2
2
0
1
C
tg 450 1
5.
300 450 600sin
cos
tg
1
2
2
2
3
2
3
2
2
2
1
2
3
3
1
3
6.
Единичная полуокружностьr=1
MD
sin
OМ
у
sin
1
y
h
sin у
M(x;y)
y
O
x
x
D
*
OD
cos
OМ
x
cos
1
cos х
*
7.
Для любого углаиз промежутка 0 180
0
0
называется ордината y точки М, а !
косинусом угла – абсцисса x точки М.
0
0
y
sin 0 0,
0
синусом угла
cos 00 1,
C(0;1)
90
sin 90 1,
0
0
cos 90 0,
0
180
B(-1;0)
O
A(1;0)
x
0
sin 1800 0,
cos1800 1.
8.
острый, то sin 0 и cos 0!
Если угол тупой, то sin 0 и cos 0
y
Если угол
1 0 sin 1
II
-1
!
I
O 0
1 cos 1
1
!
x
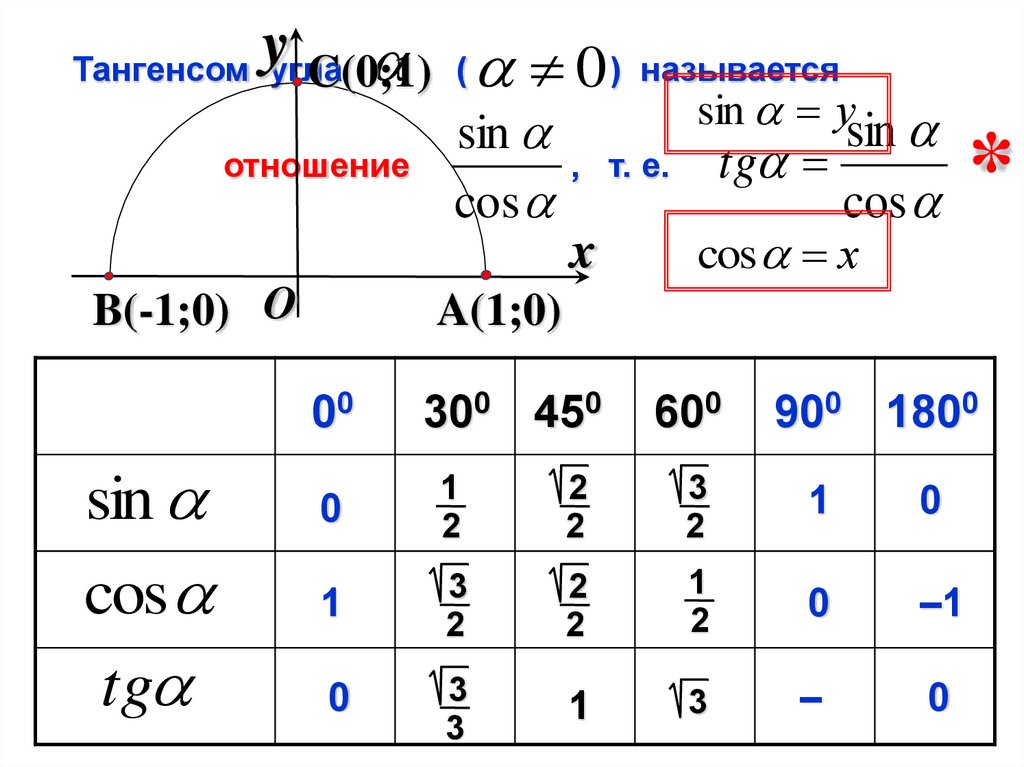
9.
yТангенсом угла
C(0;1) (
отношение
B(-1;0) O
sin
cos
tg
0 ) называется
sin у
sin
sin
, т. е. tg
cos
cos
x
cos х
*
A(1;0)
00
300 450
600
900 1800
0
1
2
2
2
3
2
1
0
1
3
2
2
2
1
2
0
–1
0
3
3
1
3
–
0
10.
Основное тригонометрическое тождествоr=1
y
x 2 + y2 = 1
M(x;y)
1
O
x
y
x
D
C(0; 0)
cos х
sin у
sin2a + cos2a = 1
*
11.
точкаsin2a + cos2a = 1 cos sin tg
M1(1; 0)
12 + 02 = 1
1
0
0
Ox
M2(0; 1)
02 + 12 = 1
0
1
–
Oy
M3(-1;0) (-1)2 + 02 = 1
-1
0
0
Ox
1 2
( 2 ) + ( 23 )2 = 1
1
2
3
2
3
I
M5(- 12 ; 23 ) (- 1 )2 + ( 3 )2 = 1
- 12
3
2
- 3
II
M6( 2 ; 2)
( 22)2 + ( 2 )2 = 1
2
2
2
2
2
1
I
M7(- 23; 12 )
(- 23 )2 + ( 12 )2 = 1
- 23
1
2
- 3
II
M4( 12 ; 23)
2
2 2
2
3
четв.
12.
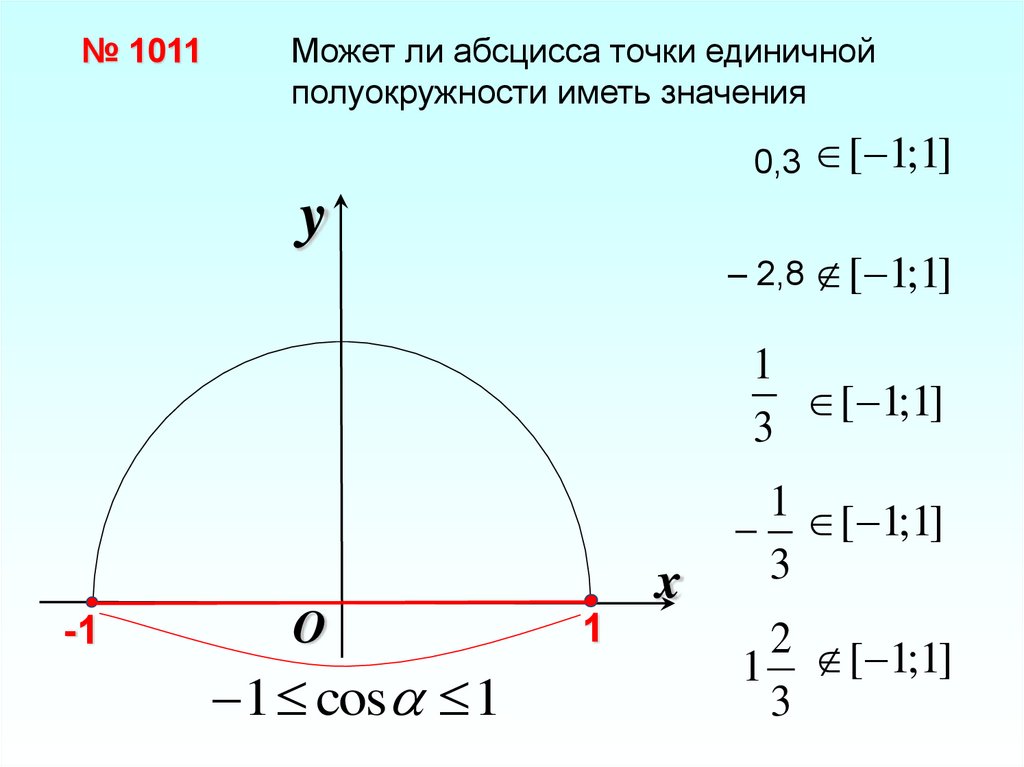
№ 1011Может ли абсцисса точки единичной
полуокружности иметь значения
0,3 [ 1;1]
y
– 2,8 [ 1;1]
1
[ 1;1]
3
x
-1
O
1 cos 1
1
1 [ 1;1]
3
2 [ 1;1]
1
3
13.
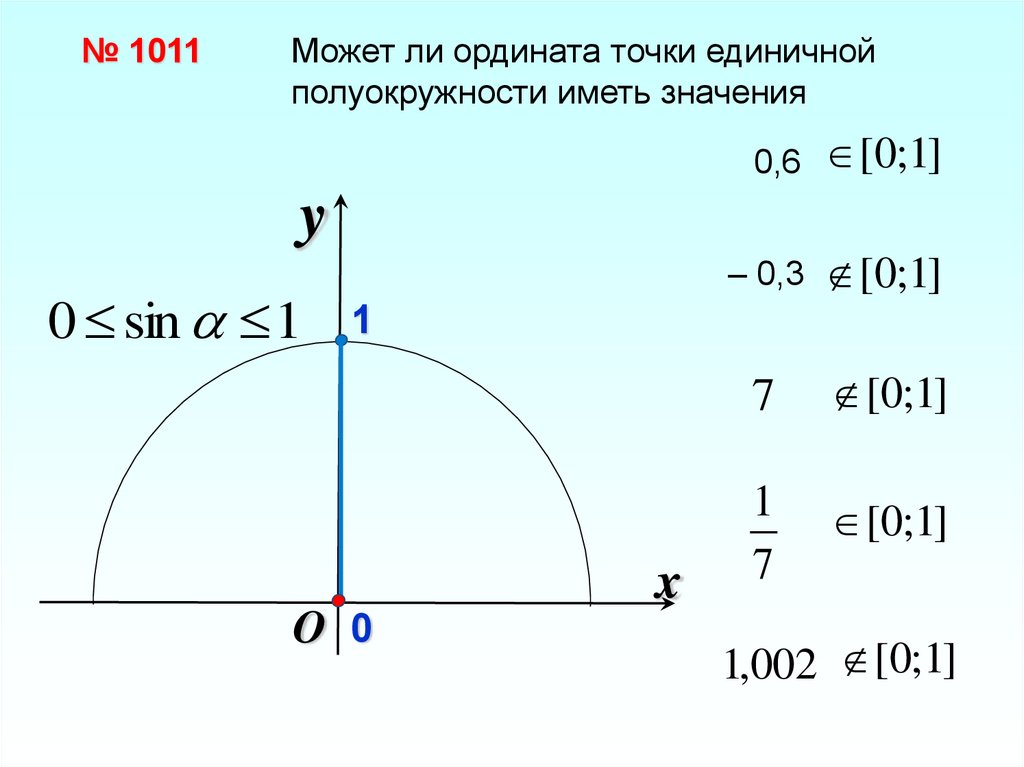
№ 1011Может ли ордината точки единичной
полуокружности иметь значения
0,6 [0;1]
y
0 sin 1
– 0,3 [0;1]
1
x
O 0
7
[0;1]
1
7
[0;1]
1,002 [0;1]








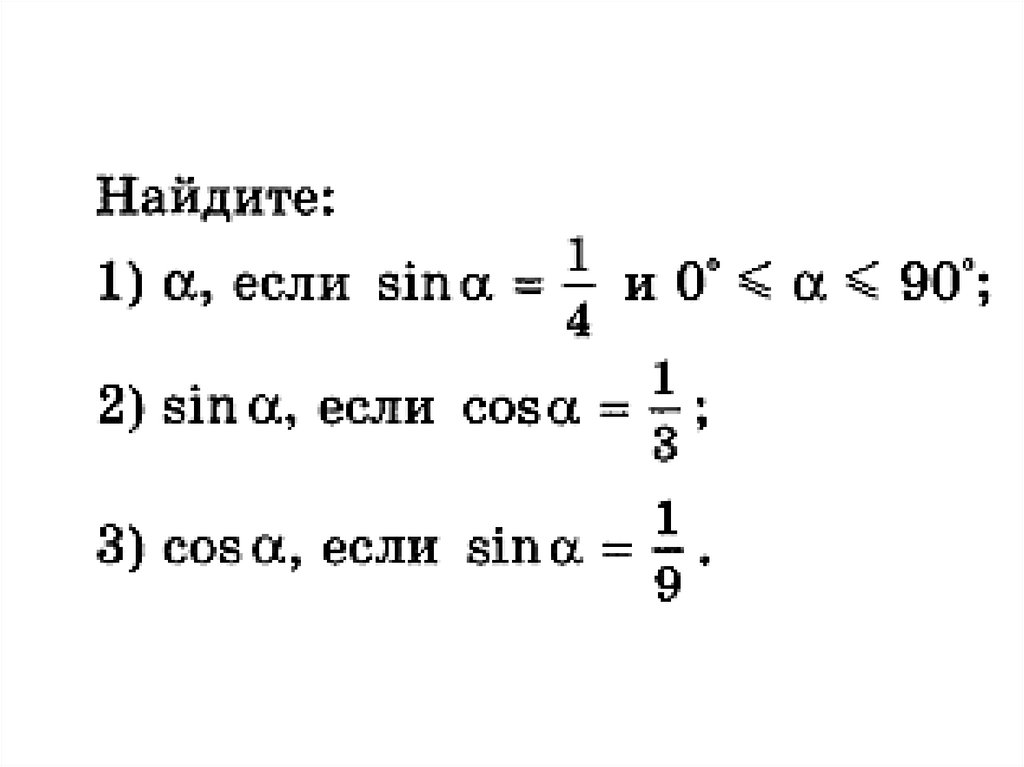
 mathematics
mathematics








