Правильные многогранники в нашей жизни

1.

Государственное бюджетное профессиональное образовательное учреждение
«Нижегородский Губернский колледж»
Учебно-исследовательский проект
по математике
на тему: «Правильные многогранники в нашей
жизни»
Выполнила студентка группы 11Л:
Преподаватель:
Нижний Новгород, 2020
А.С. Никеенкова
Н.П. Боброва

2.

Цели и задачи работы:
Цель научно-исследовательского проекта - познакомиться с правильными
многогранниками и их применением в окружающем мире.
Достижение указанной цели осуществлялось путём решения следующих
основных задач:
1. дать понятие правильных многогранников;
2. изучить виды правильных многогранников;
3. показать, что правильные многогранники встречаются в нашей жизни.

3.

Основные понятия
Многогранником называется геометрическое тело, ограниченное
со всех сторон плоскими многоугольниками - гранями.
Многогранник называется правильным, если все его грани равные друг другу правильные многоугольники, к каждой вершине
примыкает одинаковое количество граней и двугранные углы между
смежными гранями одинаковы.

4.

Виды правильных многогранников
Тетра́эдр (греч. τετραεδρον четырёхгранник) —
многогранник с четырьмя
треугольными гранями, в
каждой из вершин которого
сходятся по 3 грани.
У тетраэдра:
4 грани,
4 вершины,
6 рёбер.
Куб или правильный гексаэдр правильный многогранник,
каждая грань которого
представляет собой квадрат.
Окта́эдр -восьмигранник,
тело, ограниченное восемью
правильными
треугольниками.
Октаэдр имеет
8 треугольных граней,
12 рёбер,
6 вершин,
в каждой его вершине
сходятся 4 ребра.

5.

Виды правильных многогранников
Икоса́эдр — правильный
выпуклый
многогранник, двадцатигранник.
Каждая из 20 граней
представляет собой
равносторонний треугольник.
У икосаэдра:
30 ребер,
12 вершин,
59 звездчатых форм.
Додека́эдр - двенадцатигранник —
правильный многогранник,
составленный из 12 правильных
пятиугольников.
Каждая вершина додекаэдра
является вершиной трёх правильных
пятиугольников.
Додекаэдр имеет 12 граней
(пятиугольных), 30 рёбер
и 20 вершин (в каждой
сходятся 3 ребра).

6.

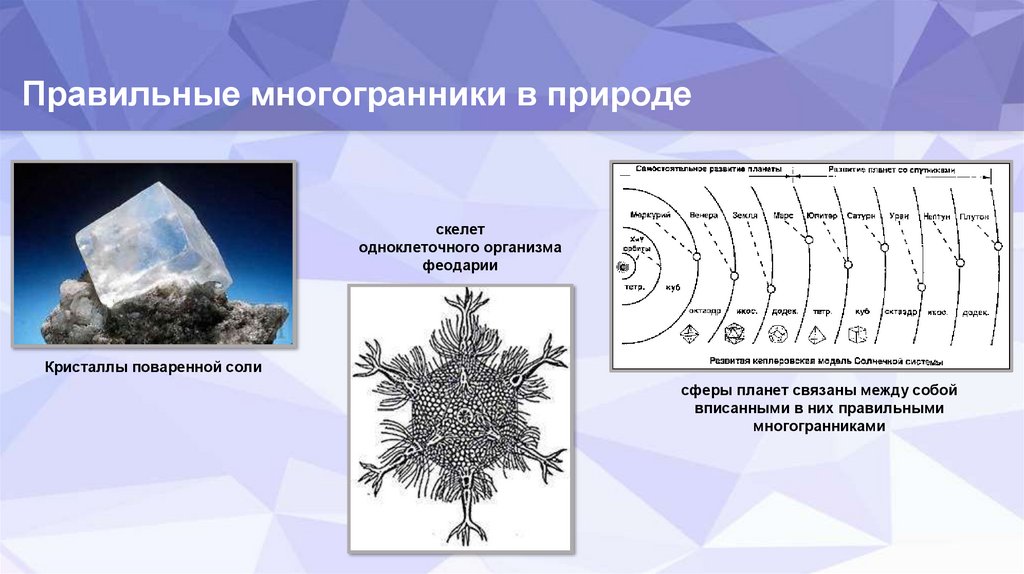
Правильные многогранники в природе
скелет
одноклеточного организма
феодарии
Кристаллы поваренной соли
сферы планет связаны между собой
вписанными в них правильными
многогранниками

7.

Правильные многогранники в архитектуре
Великая египетская пирамида
Хеопса в Гизе
Храм Артемиды Эфесской

8.

Правильные многогранники в живописи
Изображения Леонардо да Винчи
додекаэдра
Мауриц Корнелис Эшер
«Порядок и хаос»
Сальвадор Дали «Тайная
Вечеря»

9.

Изготовление правильных многогранников
Моделирование – построение моделей, процесс познания действительных объектов, метод
изучения технических сооружений, мыслительный и практический вид деятельности.
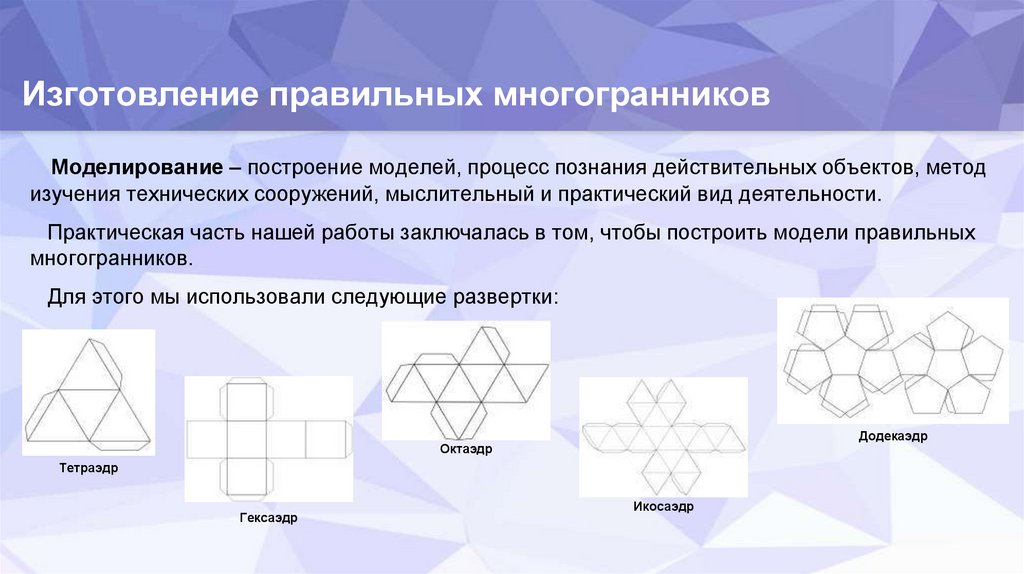
Практическая часть нашей работы заключалась в том, чтобы построить модели правильных
многогранников.
Для этого мы использовали следующие развертки:
Додекаэдр
Октаэдр
Тетраэдр
Гексаэдр
Икосаэдр

10.

Вывод по проделанной работе
В процессе работы, мы выяснили, что многогранники играют немало
важную роль в окружающем нас мире. Многогранные формы
окружают нас в повседневной жизни повсюду.
Мы рассмотрели правильные многогранники,
рассмотрели развёртки правильных
многогранников, сумели сами выполнить
модели многогранников.

11.

Список литературы:
1. Гусев, В. А. Геометрия : учебное пособие для среднего профессионального образования / В. А. Гусев,
И. Б. Кожухов, А. А. Прокофьев. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. —
280 с. — (Профессиональное образование). — ISBN 978-5-534-08897-7. — Текст : электронный // ЭБС
Юрайт [сайт]. — URL: https://urait.ru/bcode/449003 (дата обращения: 17.12.2019).
2. Богомолов, Н. В. Математика : учебник для среднего профессионального образования / Н. В.
Богомолов, П. И. Самойленко. — 5-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2020. —
401 с. — (Профессиональное образование). — ISBN 978-5-534-07878-7. — Текст : электронный // ЭБС
Юрайт [сайт]. — URL: https://urait.ru/bcode/449006 (дата обращения: 28.01.2020).
3. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: учебник М., 1992.
4. Смирнова И.М. В мире многогранников. М., 1990.
5. Ворошилов А.В. Математика и искусство. - М. просвещение, 1992. – 352