Similar presentations:
Правильные многогранники
1. Правильные многогранники.
Шаферов С.Ладейщиков П.
10”А”
2. Определение.
Выпуклый многогранник называетсяправильным, если все его грани –
равные правильные многоугольники и в
каждой его вершине сходится одно и то
же число ребер. Правильных
многогранников всего пять: тетраэдр,
гексаэдр, октаэдр, додекаэдр, икосаэдр.
3. Примеры правильных многогранников:
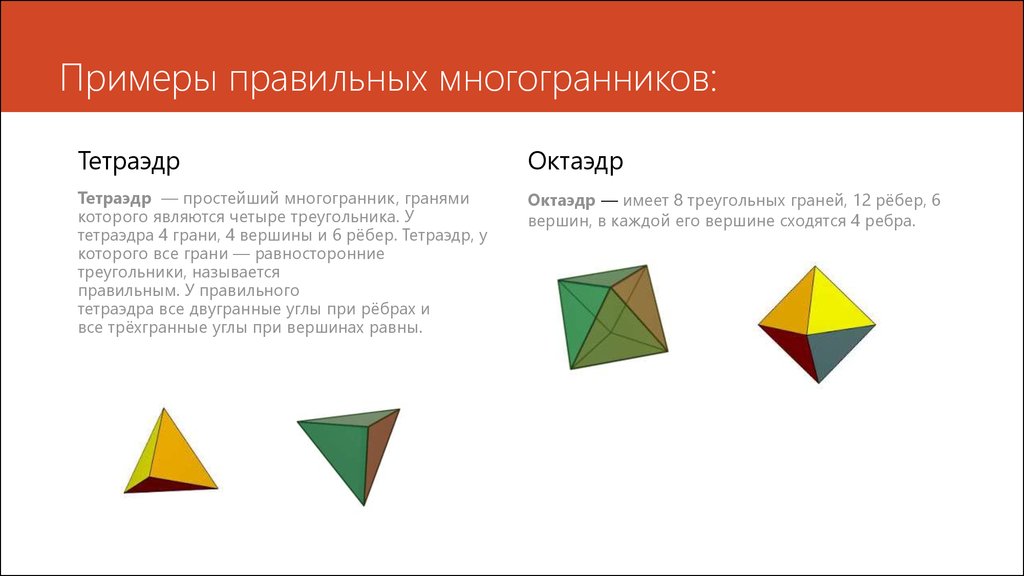
ТетраэдрОктаэдр
Тетраэдр — простейший многогранник, гранями
которого являются четыре треугольника. У
тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у
которого все грани — равносторонние
треугольники, называется
правильным. У правильного
тетраэдра все двугранные углы при рёбрах и
все трёхгранные углы при вершинах равны.
Октаэдр — имеет 8 треугольных граней, 12 рёбер, 6
вершин, в каждой его вершине сходятся 4 ребра.
4. Примеры правильных многогранников:
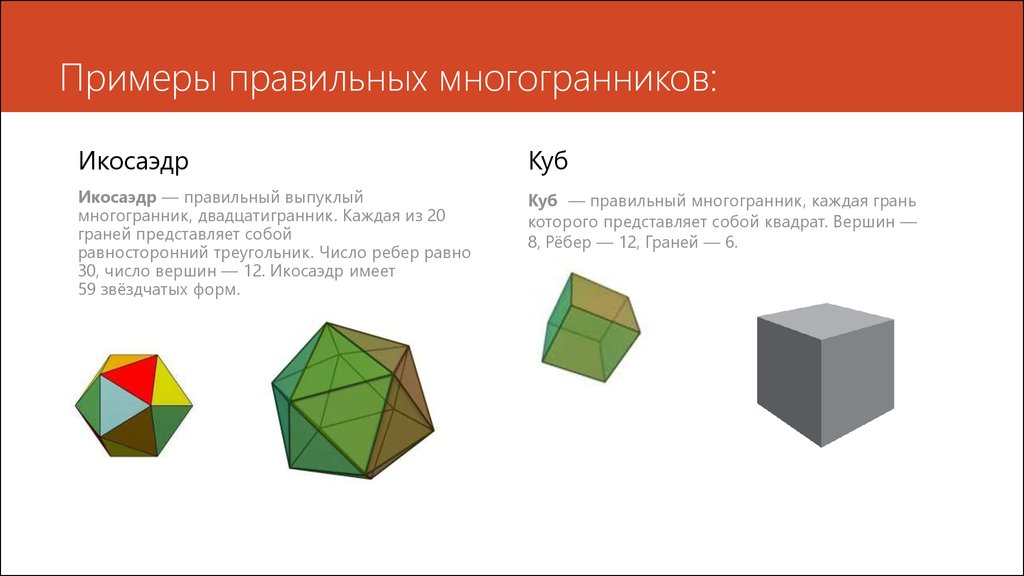
ИкосаэдрКуб
Икосаэдр — правильный выпуклый
многогранник, двадцатигранник. Каждая из 20
граней представляет собой
равносторонний треугольник. Число ребер равно
30, число вершин — 12. Икосаэдр имеет
59 звёздчатых форм.
Куб — правильный многогранник, каждая грань
которого представляет собой квадрат. Вершин —
8, Рёбер — 12, Граней — 6.
5. Примеры правильных многогранников:
ДодекаэдрДодекаэдр — составлен из
двенадцати правильных
пятиугольников, являющихся его
гранями.
Каждая вершина додекаэдра
является вершиной трёх правильных
пятиугольников. Таким образом,
додекаэдр имеет 12 граней
(пятиугольных), 30 рёбер и 20
вершин (в каждой сходятся 3 ребра).
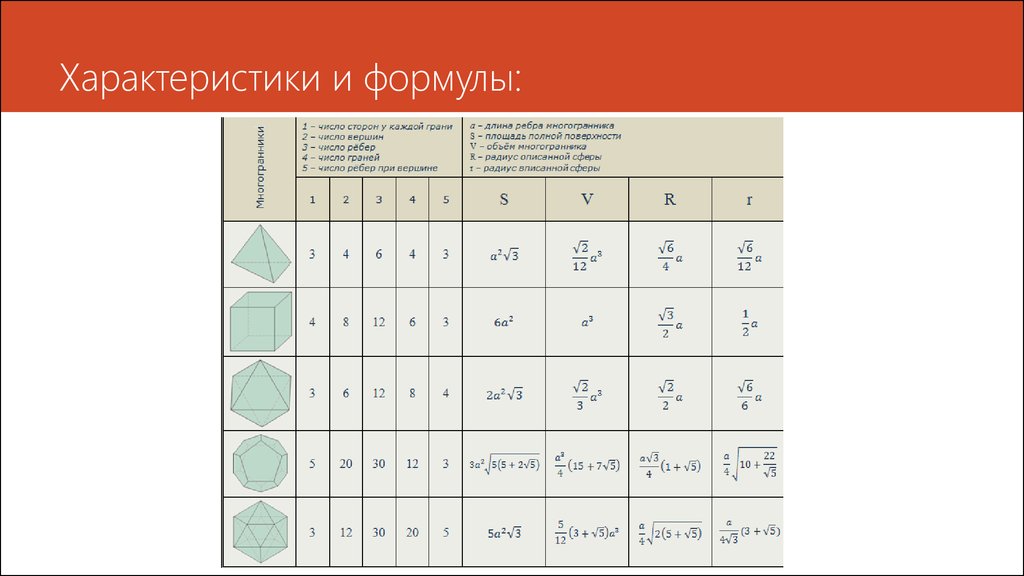
6. Характеристики и формулы:
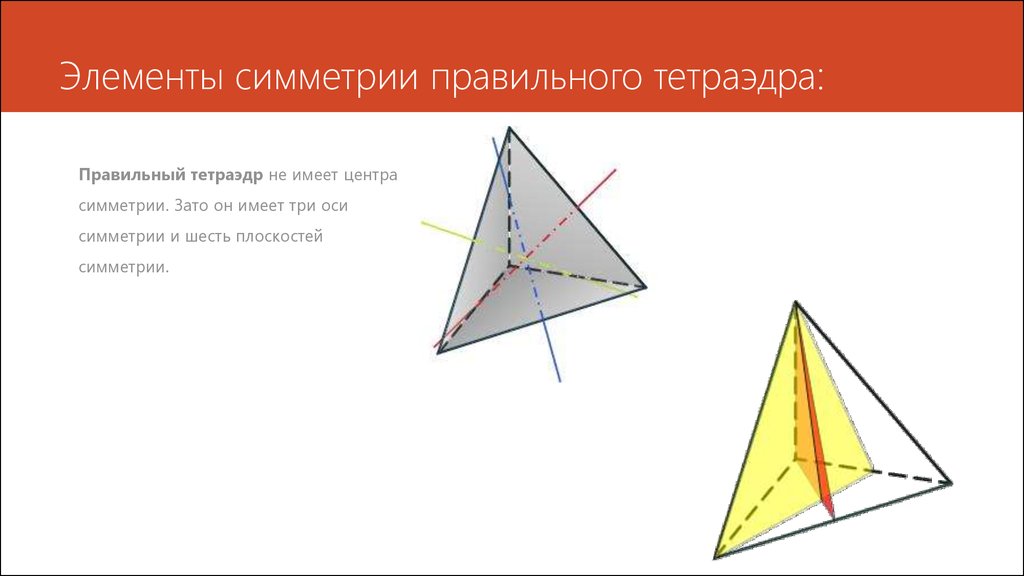
7. Элементы симметрии правильного тетраэдра:
Элементы симметрии правильного тетраэдра:Правильный тетраэдр не имеет центра
симметрии. Зато он имеет три оси
симметрии и шесть плоскостей
симметрии.
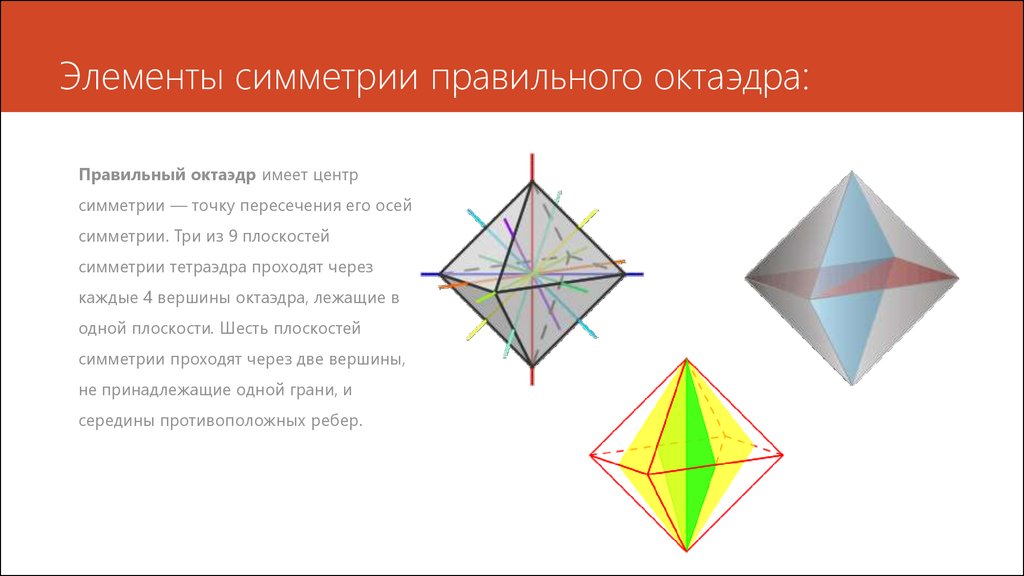
8. Элементы симметрии правильного октаэдра:
Правильный октаэдр имеет центрсимметрии — точку пересечения его осей
симметрии. Три из 9 плоскостей
симметрии тетраэдра проходят через
каждые 4 вершины октаэдра, лежащие в
одной плоскости. Шесть плоскостей
симметрии проходят через две вершины,
не принадлежащие одной грани, и
середины противоположных ребер.
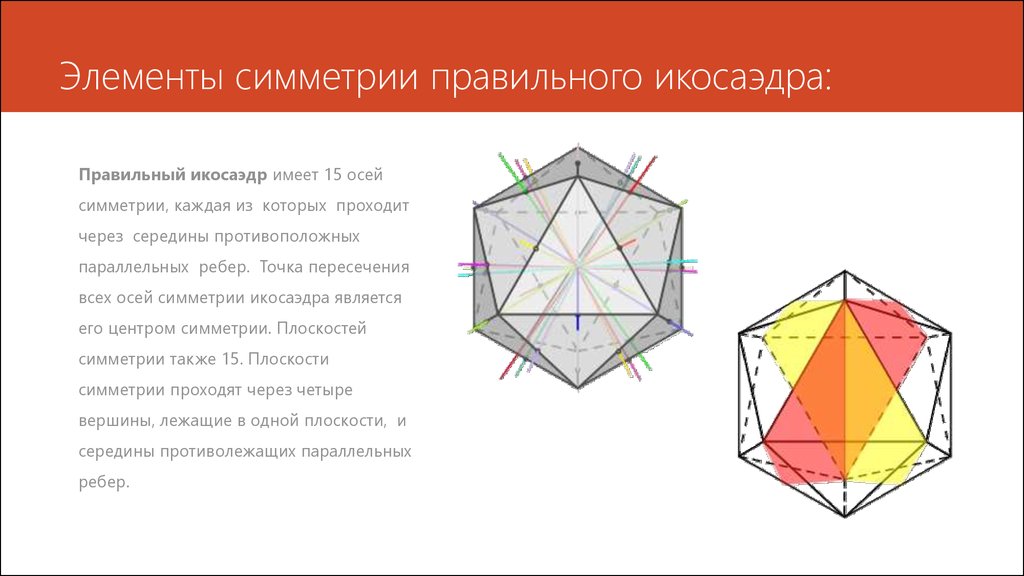
9. Элементы симметрии правильного икосаэдра:
Правильный икосаэдр имеет 15 осейсимметрии, каждая из которых проходит
через середины противоположных
параллельных ребер. Точка пересечения
всех осей симметрии икосаэдра является
его центром симметрии. Плоскостей
симметрии также 15. Плоскости
симметрии проходят через четыре
вершины, лежащие в одной плоскости, и
середины противолежащих параллельных
ребер.
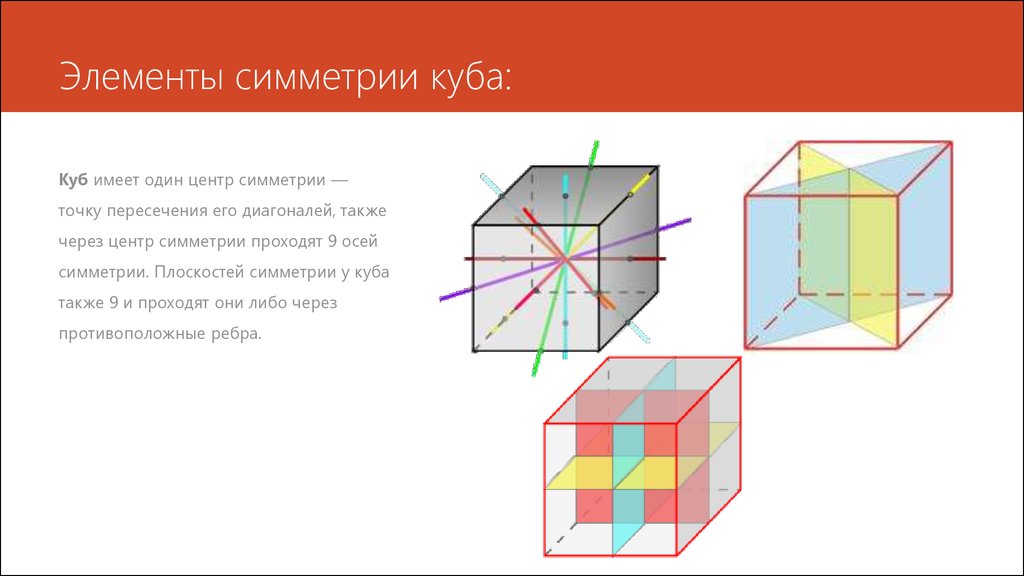
10. Элементы симметрии куба:
Куб имеет один центр симметрии —точку пересечения его диагоналей, также
через центр симметрии проходят 9 осей
симметрии. Плоскостей симметрии у куба
также 9 и проходят они либо через
противоположные ребра.
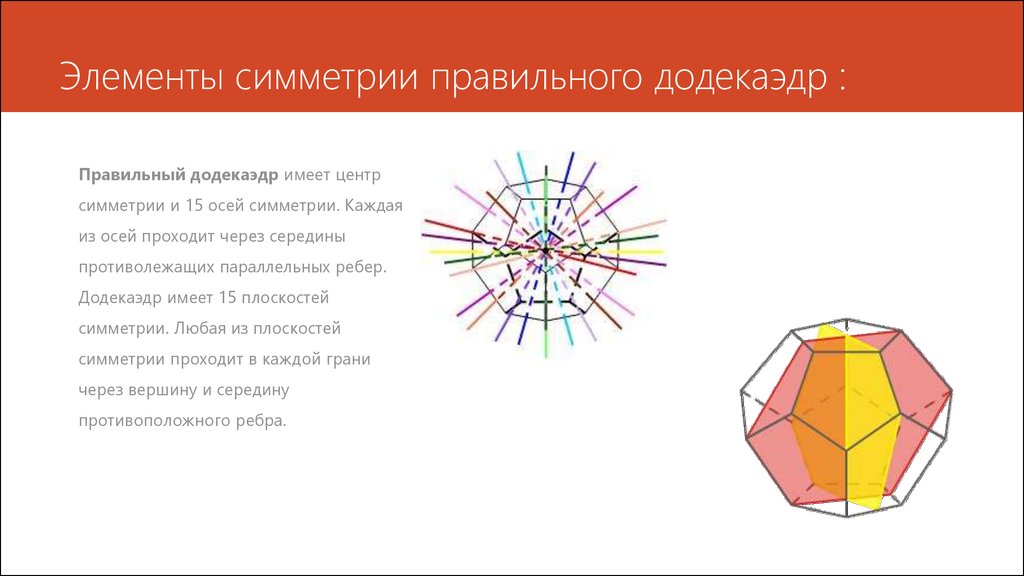
11. Элементы симметрии правильного додекаэдр :
Правильный додекаэдр имеет центрсимметрии и 15 осей симметрии. Каждая
из осей проходит через середины
противолежащих параллельных ребер.
Додекаэдр имеет 15 плоскостей
симметрии. Любая из плоскостей
симметрии проходит в каждой грани
через вершину и середину
противоположного ребра.
12. Вся информация взята из:
• http://licey102.k26.ru/• http://math4school.ru
• wikipedia.org
• Учебник за 10-11 класс по геометрии





 mathematics
mathematics








