Similar presentations:
Повторяем правила дифференцирования
1.
1.Повторяем правила дифференцирования2. В чем состоит геометрический смысл
производной?
3.В чем состоит физический смысл производной?
4.Написать формулы дифференцирования.
5.Написать уравнения касательной
6.Какие точки называются критическими?
7.В чем состоит необходимое условие экстремума?
8.В чем состоит достаточный признак
существования экстремума?
9.Алгоритм отыскания наибольшего и
наименьшего значений функции у= f(x),
непрерывной на отрезке [a; b].
2.
Алгоритм отыскания наибольшего и наименьшегозначений функции у= f(x), непрерывной на отрезке
[a; b].
1.Найти f ‘(x).
2.Найти критические точки, т.е. где f 'x)=0 и f ‘(x) не
существует, и отобрать из них те, что лежат внутри
отрезка [a; b].
3.Вычислить значения функции y=f(x) в
критических точках и на концах отрезка, и выбрать
из них наибольшее и наименьшее; они и будут
соответственно наибольшим и наименьшим
значениями функции y=f(x) на отрезке [a;b],
которые обозначают так:
max[a;b] y(x) и
m in[a;b]y(x).
3.
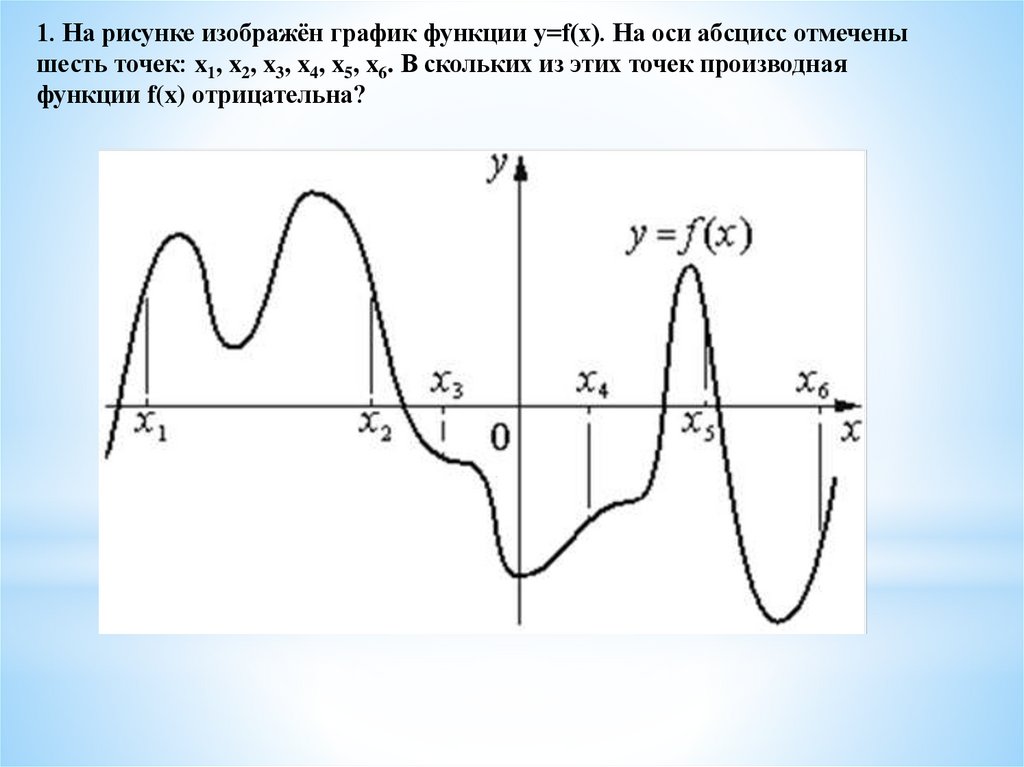
1. На рисунке изображён график функции y=f(x). На оси абсцисс отмеченышесть точек: x1, x2, x3, x4, x5, x6. В скольких из этих точек производная
функции f(x) отрицательна?
4.
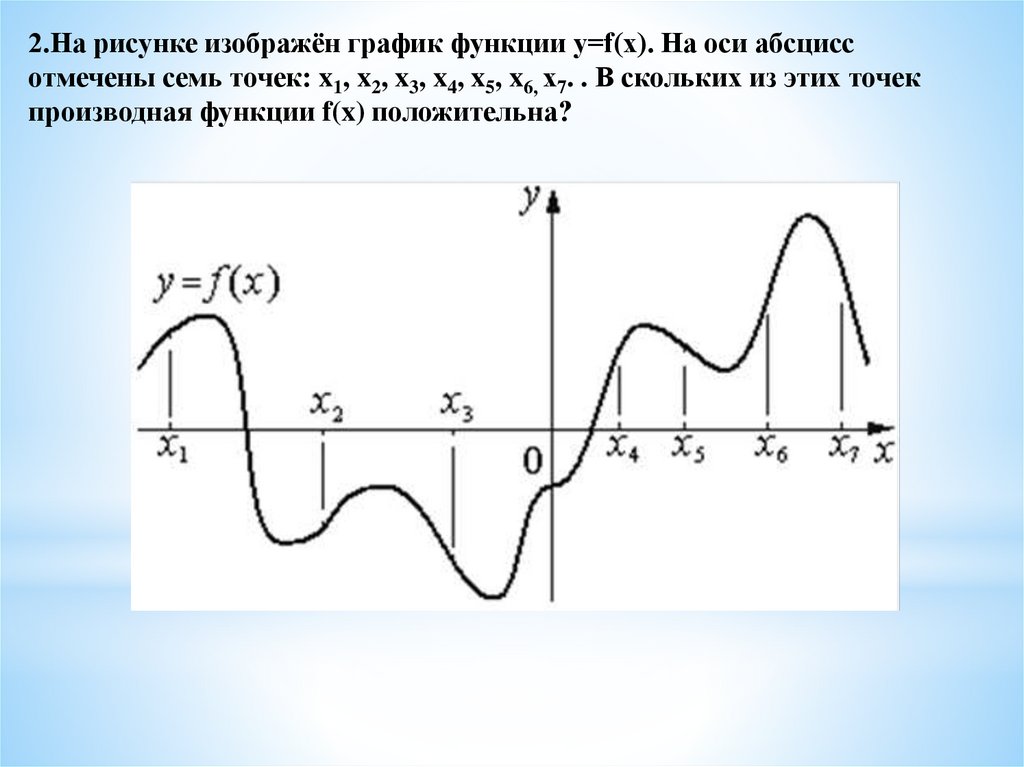
2.На рисунке изображён график функции y=f(x). На оси абсциссотмечены семь точек: x1, x2, x3, x4, x5, x6, х7. . В скольких из этих точек
производная функции f(x) положительна?
5.
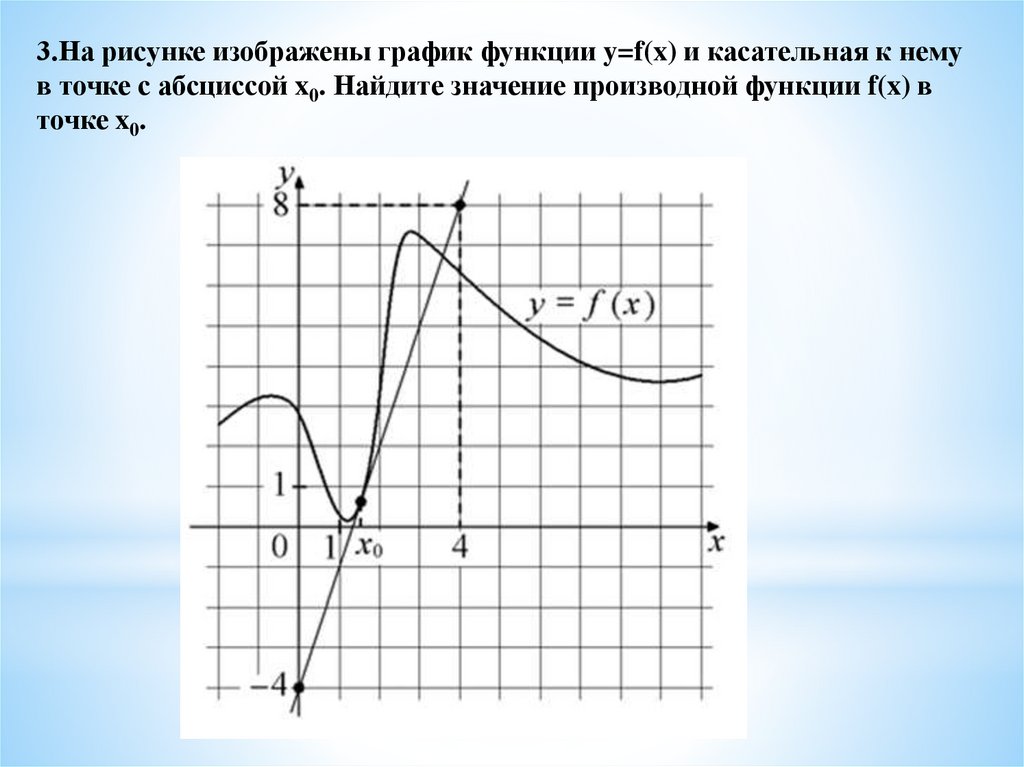
3.На рисунке изображены график функции y=f(x) и касательная к немув точке с абсциссой x0. Найдите значение производной функции f(x) в
точке x0.
6.
4.Найдите наименьшеезначение
функции y=x3−x2−8x+4 на
отрезке [1; 7]
7.
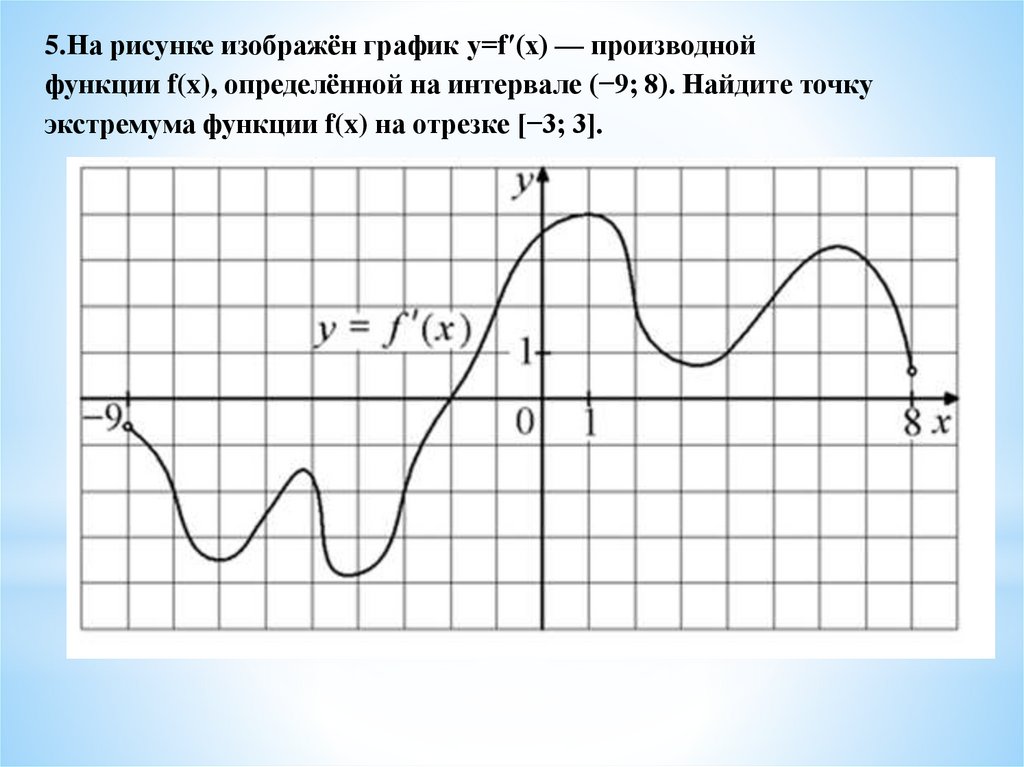
5.На рисунке изображён график y=f′(x) — производнойфункции f(x), определённой на интервале (−9; 8). Найдите точку
экстремума функции f(x) на отрезке [−3; 3].
8.
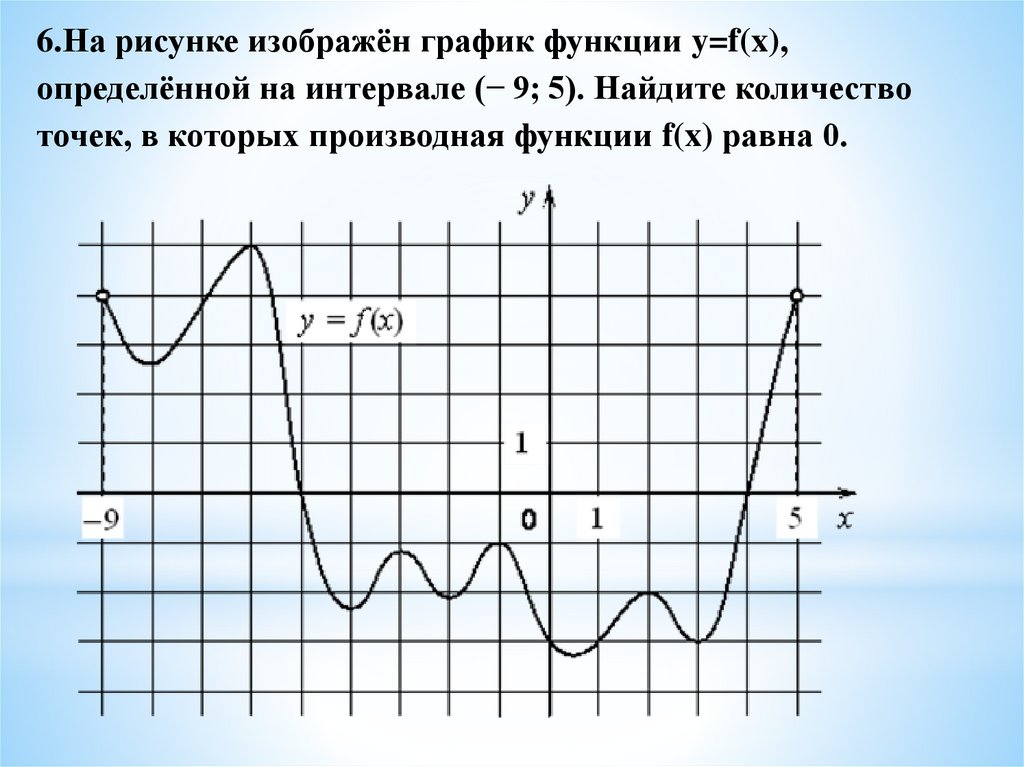
6.На рисунке изображён график функции y=f(x),определённой на интервале (− 9; 5). Найдите количество
точек, в которых производная функции f(x) равна 0.
9.
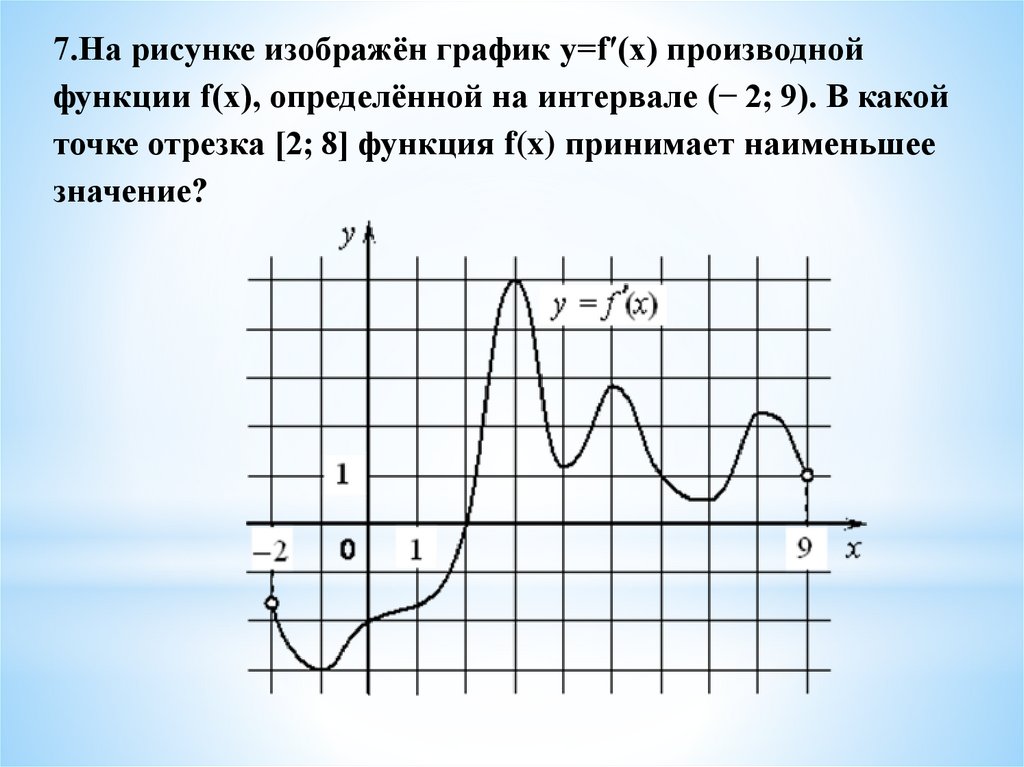
7.На рисунке изображён график y=f′(x) производнойфункции f(x), определённой на интервале (− 2; 9). В какой
точке отрезка [2; 8] функция f(x) принимает наименьшее
значение?
10.
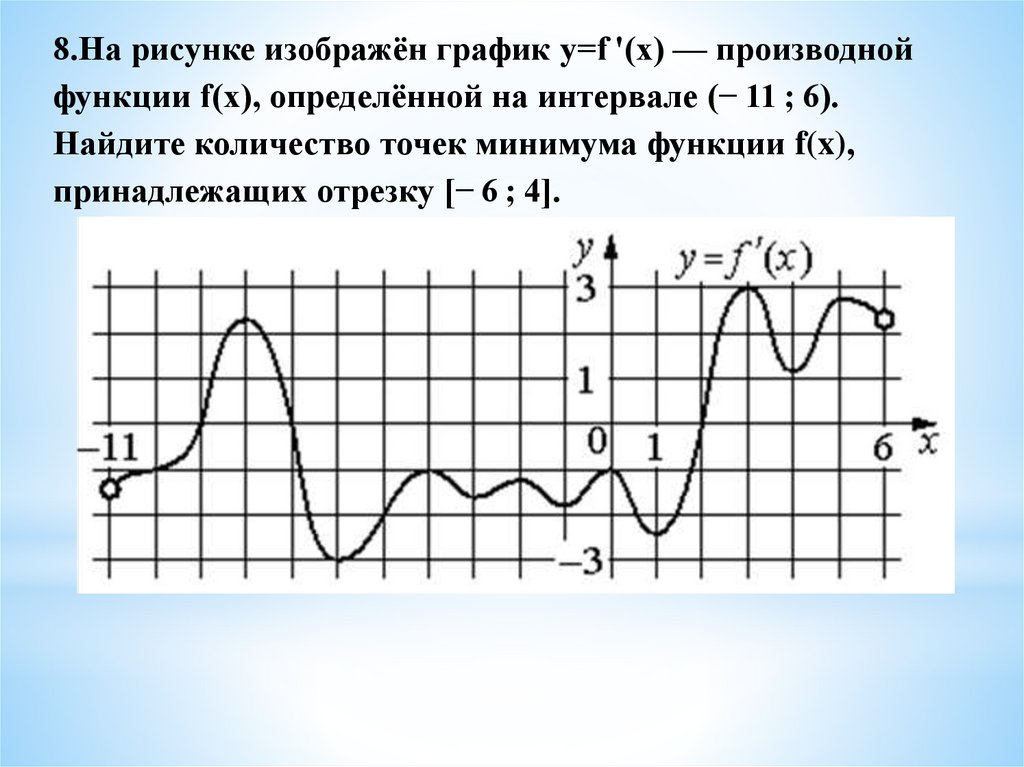
8.На рисунке изображён график y=f '(x) — производнойфункции f(x), определённой на интервале (− 11 ; 6).
Найдите количество точек минимума функции f(x),
принадлежащих отрезку [− 6 ; 4].
11.
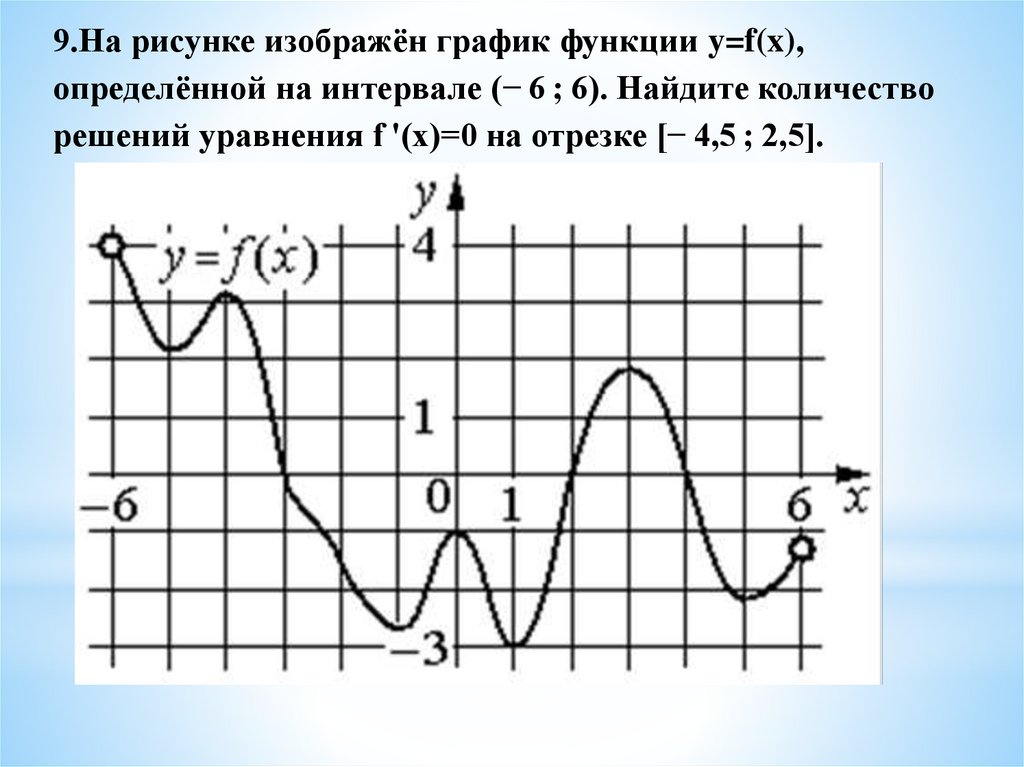
9.На рисунке изображён график функции y=f(x),определённой на интервале (− 6 ; 6). Найдите количество
решений уравнения f '(x)=0 на отрезке [− 4,5 ; 2,5].
12.
10.Материальная точка движетсяпрямолинейно по закону
x(t)=16 t3−2 t2+6 t+250,
где x — расстояние от точки отсчёта в
метрах, t — время в секундах,
измеренное с момента начала
движения. В какой момент времени
(в секундах) её скорость была равна
96 м/с?
13.
Найдите силу F , действующую на материальную точку смассой m , движущуюся прямолинейно по закону
х( t ) =5 t 3 - 4t 2 ,при t = 5.
14.
р(t) = t2- 5 t+12,где t- время в секундах. В какой момент времени (в
секундах) скорость движения «пробки» вулкана будет
равна 15 м/с?
15.
Зависимость численности популяции тигров заданаформулой N(t)= 5 t3-4 t2+1. Найдите прирост популяции
в момент времени t = 3.






 mathematics
mathematics








