Similar presentations:
Производная показательной, логарифмической и степенной функций при подготовке к ЕГЭ по математике
1. Производная показательной, логарифмической и степенной функций при подготовке к ЕГЭ по математике
ПРОИЗВОДНАЯПОКАЗАТЕЛЬНОЙ,
ЛОГАРИФМИЧЕСКОЙ И
СТЕПЕННОЙ ФУНКЦИЙ ПРИ
ПОДГОТОВКЕ К
ЕГЭ ПО
МАТЕМАТИКЕ
2. Ум заключается не только в знании, но и в умении применять знания на практике
УМ ЗАКЛЮЧАЕТСЯ НЕ ТОЛЬКО ВЗНАНИИ, НО И В УМЕНИИ
ПРИМЕНЯТЬ ЗНАНИЯ НА
ПРАКТИКЕ
Аристотель
3.
Цель урокаПовторить и закрепить производную показательной,
логарифмической и степенной функций ;
закрепить методы решения наибольшего и
наименьшего значения функции ; совершенствовать
применение полученных знаний при решении
заданий 7 и 12;
развитие познавательного интереса и внимания при
решении задач по готовым чертежам
Задача урока
отработка навыка работы с производной при
подготовке к ЕГЭ
4. Определение производной и ее геометрический смысл
ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ И ЕЕГЕОМЕТРИЧЕСКИЙ СМЫСЛ
y f (x)
y
y
tg k
x
k – угловой
коэффициент
прямой(секущей)
y
y kx b
y
Обозначение:
0
х0
х
0 х
х
f ( x )
П роизводно й функции f ( x ) в т оч ке х 0 назы вает ся
f ( x)
ч исло , к кот орому ст ремит ся от нош ение
при х 0 .
x
5. устная работа 1. Какая функция называется показательной? 2. Какая функция называется логарифмической? 3. Какая функция
УСТНАЯ РАБОТА1. КАКАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ ПОКАЗАТЕЛЬНОЙ?
2. КАКАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ
ЛОГАРИФМИЧЕСКОЙ?
3. КАКАЯ ФУНКЦИЯ НАЗЫВАЕТСЯ СТЕПЕННОЙ?
4. ЧЕМУ РАВНА ПРОИЗВОДНАЯ ПОКАЗАТЕЛЬНОЙ,
ЛОГАРИФМИЧЕСКОЙ , СТЕПЕННОЙ ФУНКЦИЙ?
5. ЧТО ТАКОЕ НАТУРАЛЬНЫЙ ЛОГАРИФМ?
6.
Математический диктант.х
1. Верно ли, что х
1
.
х
2
2 х 1 .
2. Верно ли, что
3. Верно ли, что u v u v .
4. Верно ли, что С u C u .
5. Верно ли, что С 0 .
6. Верно ли, что
7. Верно ли, что
е е .
х
а
х
х
ах
.
ln а
8. Верно ли, что u u v u v .
2
v
v
9. Верно ли, что уравнение касательной
у f ( х0 ) f ( х0 )( х х0 )
записывается так
7.
Запомниа а
х
х
ln а
а
ln( ах в) ах в , а 0
k
log а (kх в)
(kх в) ln а
1
, х 0, а 0.
log а х
х ln а
1
ln х
х
е е
х
х
8. Найти производную функции
НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИу е 2х
х
3 4
3
f ( x) x 2 x x 5
4
2
f ( x) 4 x
x
x
f ( x) 7e ln 2 x
f ( x) sin 3x
9. Вычислить производную сложной функции
ВЫЧИСЛИТЬ ПРОИЗВОДНУЮ СЛОЖНОЙФУНКЦИИ
10. Общий вид уравнения касательной
ОБЩИЙ ВИД УРАВНЕНИЯКАСАТЕЛЬНОЙ
Чему равен угловой
коэффициент касательной?
f ( х 0 ) tg k
11.
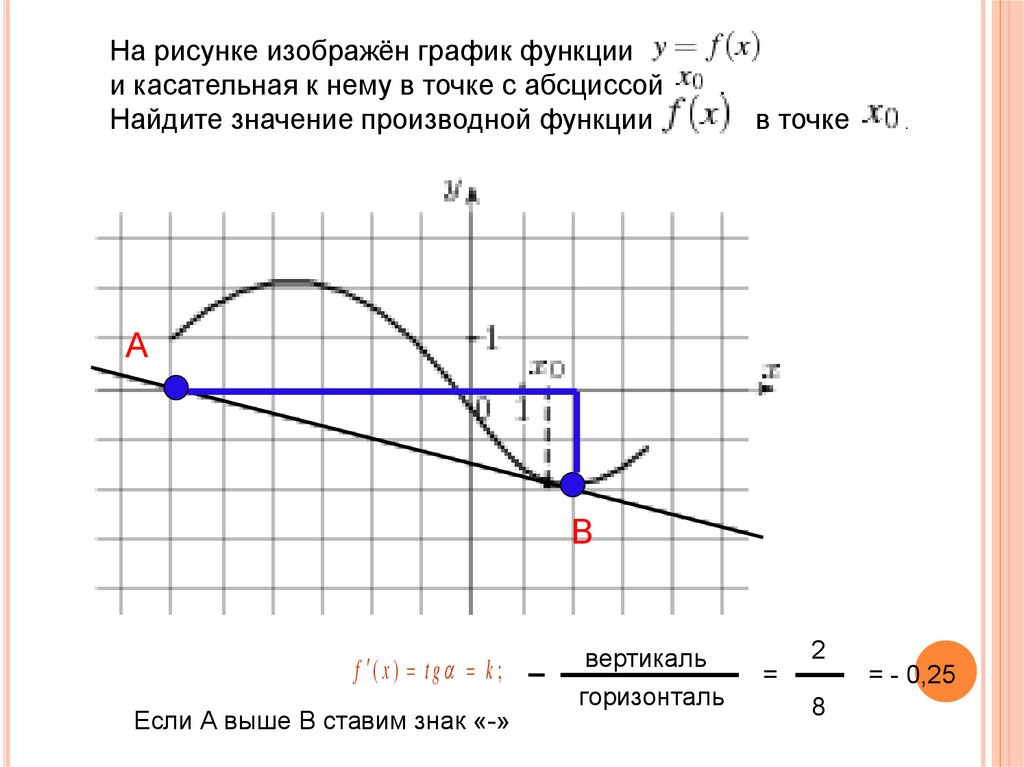
На рисунке изображён график функциии касательная к нему в точке с абсциссой
Найдите значение производной функции
.
в точке
.
А
В
f ( x ) t g k ;
Если А выше В ставим знак «-»
вертикаль
горизонталь
2
=
= - 0,25
8
12.
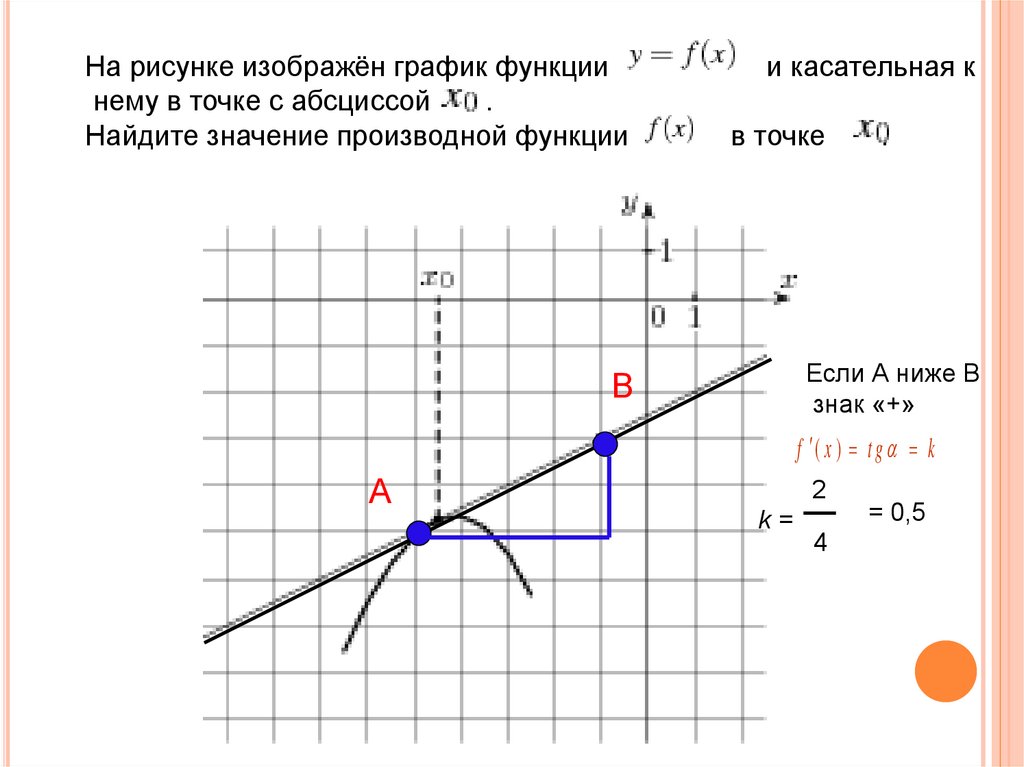
На рисунке изображён график функциинему в точке с абсциссой
.
Найдите значение производной функции
и касательная к
в точке
.
Если А ниже В
знак «+»
В
f ( x ) t g k
А
2
k=
4
= 0,5
13.
Прототип B9 № 27504На рисунке изображён график функции y=f(x) и касательная к нему
в точке с абсциссой x0. Найдите значение производной
функции f(x) в точке x0.
Ответ: 0,25.
14. Экстремумы функции
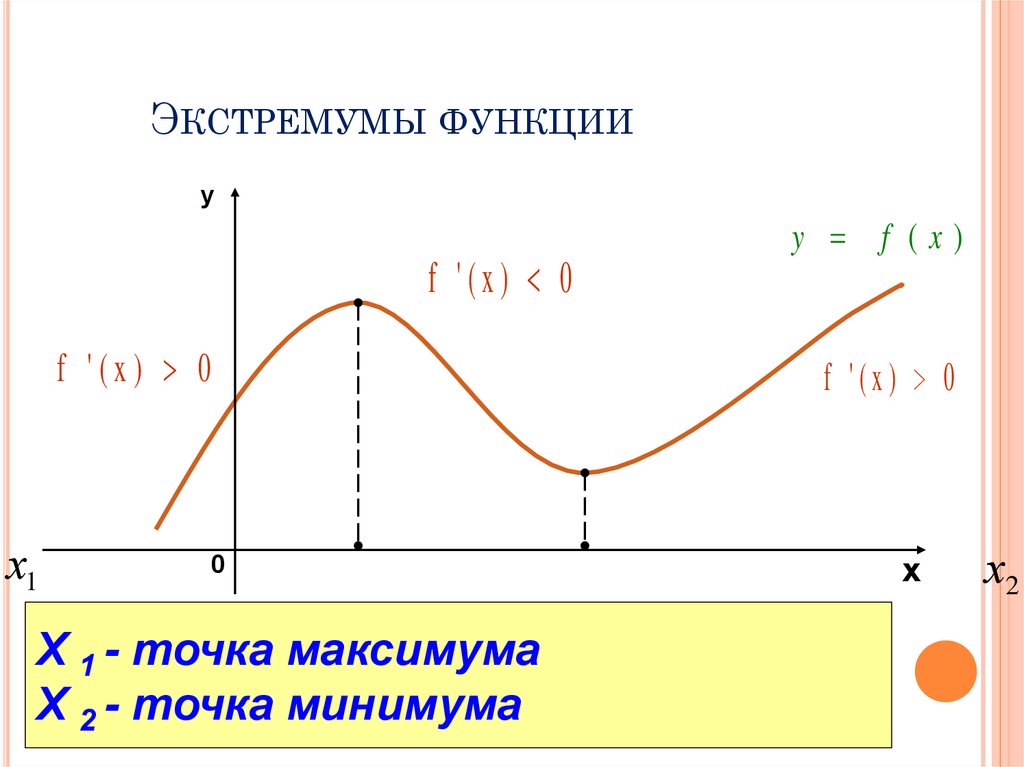
ЭКСТРЕМУМЫ ФУНКЦИИy
f '(x) 0
f '(x) 0
х1
y f (x)
f '(x) 0
0
X 1 - точка максимума
X 2 - точка минимума
х
х2
15.
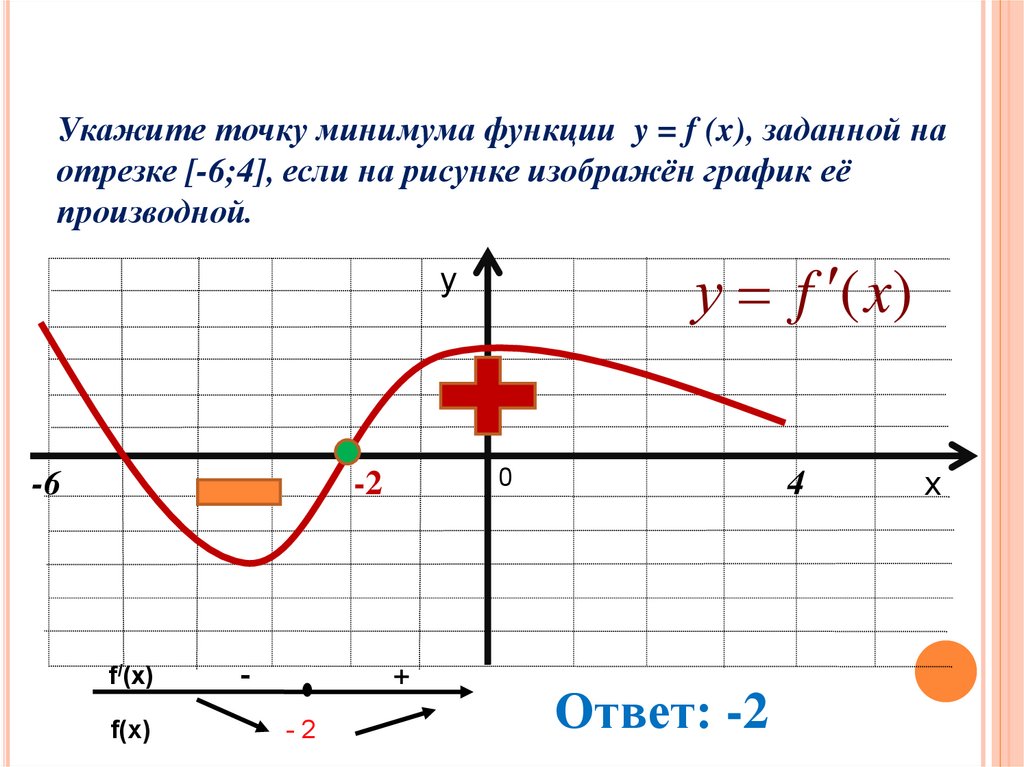
Укажите точку минимума функции y = f (x), заданной наотрезке [-6;4], если на рисунке изображён график её
производной.
у f (x)
у
-6
0
-2
f/(x)
f(x)
-
+
-2
4
Ответ: -2
х
16.
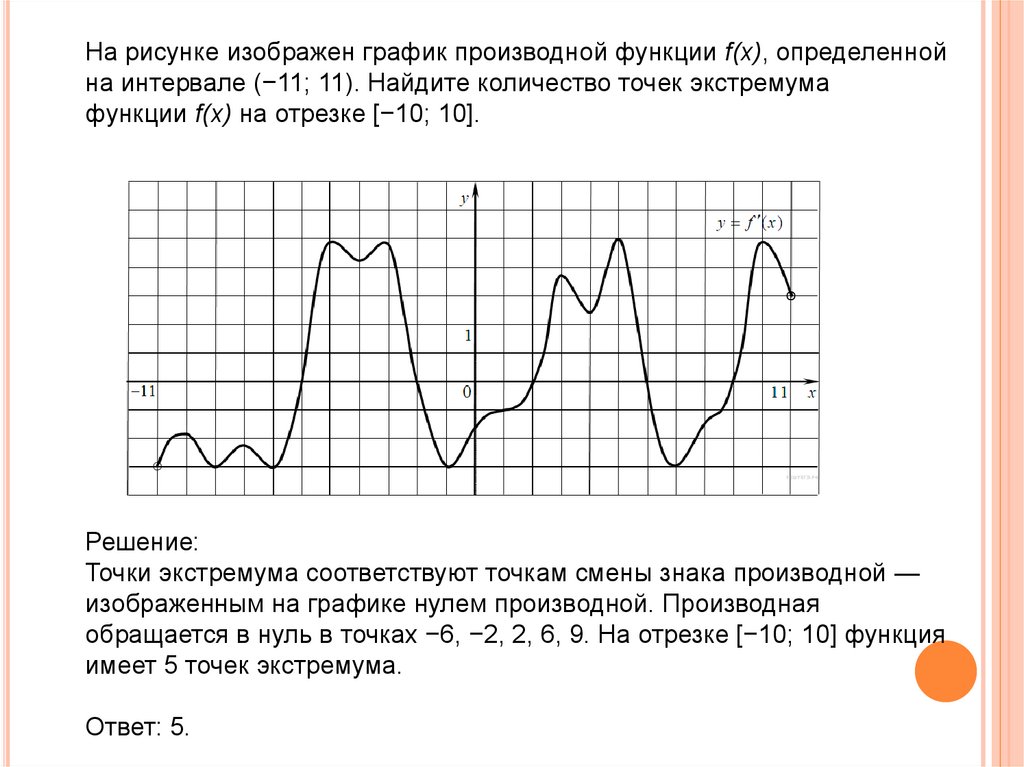
На рисунке изображен график производной функции f(x), определеннойна интервале (−11; 11). Найдите количество точек экстремума
функции f(x) на отрезке [−10; 10].
Решeние:
Точки экстремума соответствуют точкам смены знака производной —
изображенным на графике нулем производной. Производная
обращается в нуль в точках −6, −2, 2, 6, 9. На отрезке [−10; 10] функция
имеет 5 точек экстремума.
Ответ: 5.
17. Наибольшее и наименьшее значение функции на отрезке
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕФУНКЦИИ НА ОТРЕЗКЕ
y
y f (x)
0
a
х0
b
х
1. Находим критические точки
2. Вычислить значение функций во всех критических точках, f(a) и f(b)
3. Сравнивая значения f(a), f(b), f(x0), определяем наибольшее
и наименьшее значение функции на отрезке.
18. Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
АЛГОРИТМ НАХОЖДЕНИЯНАИБОЛЬШЕГО И
НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Найти производную функции
Найти критические точки функции
Если критических точек
на отрезке нет, значит
функция на этом отрезке
монотонна, и своего
наибольшего и наименьшего
значения функция достигает
на концах отрезка
Если критические точки на
отрезке есть, значит нужно
вычислить значения функции
во всех критических точках и
на концах отрезка, и выбрать
из полученных чисел
наибольшее и наименьшее
19.
Найдите наибольшее значение функцииy x 3x 4
3
Решение.
,
на отрезке
2;0
y ( 2) ( 2) 3 3( 2) 4
1) y ( x) 3 x 3
8 6 4 2
2 ) y ( x) 0
y ( 1) ( 1) 3( 1) 4
,
2
3
3x2 3 0
1 3 4 6
3( x 2 1) 0
y (0 ) 4
x 1 2;0
x 1
Ответ: 6
20.
Найдите точку максимума (минимума) функцииРешение.
y x 3x 2
3
2
1) y , ( x) 3 x 2 6 x
2) 3 x 2 6 x 0
3 x( x 2) 0
x 0 x 2
+
min
max
+
0
2
21.
Найдите наименьшее значение функцииy=x3−x2−8x+4
на отрезке
[1;7]
Найдите наибольшее значение функции
y=11·ln(x+4)−11x−5
на отрезке
[−3,5;0]
22.
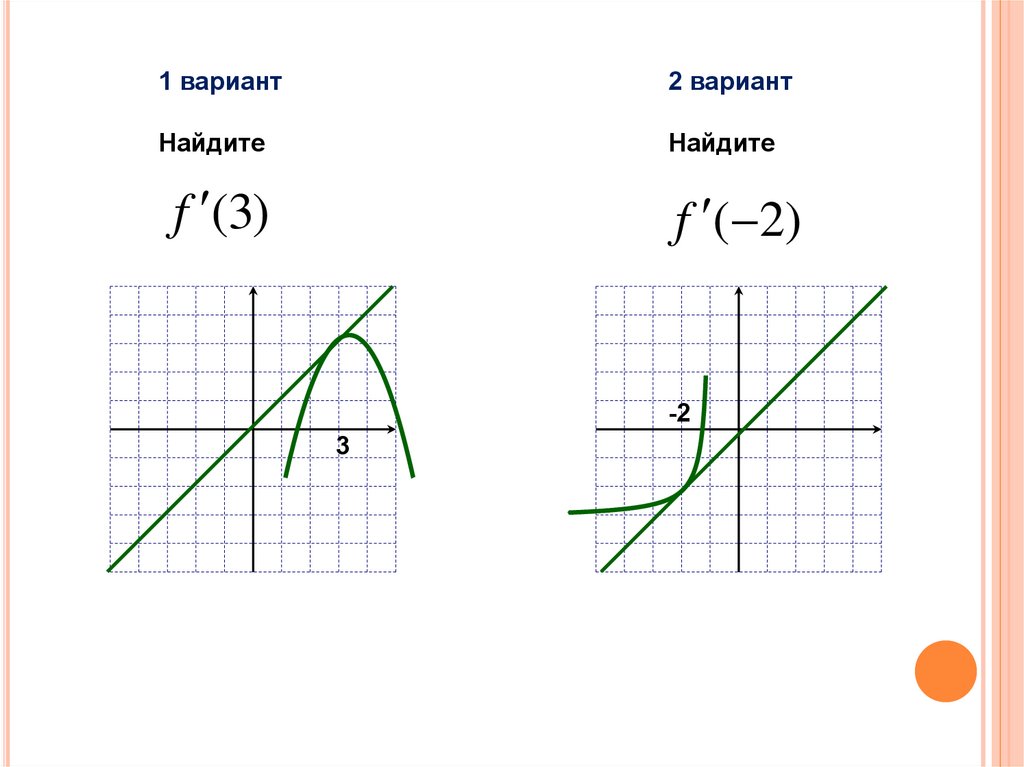
1 вариант2 вариант
Найдите
Найдите
f (3)
f ( 2)
-2
3
23.
1 вариантНайдите наименьшее
значение функции на
отрезке
[ 4;11] по
алгоритму
3
2
y =x - 10x + 25x+ 7
2 вариант
Найдите наибольшее
значение функции на
отрезке
[ -1/4;1]
по алгоритму
3
у = 3х – 4х






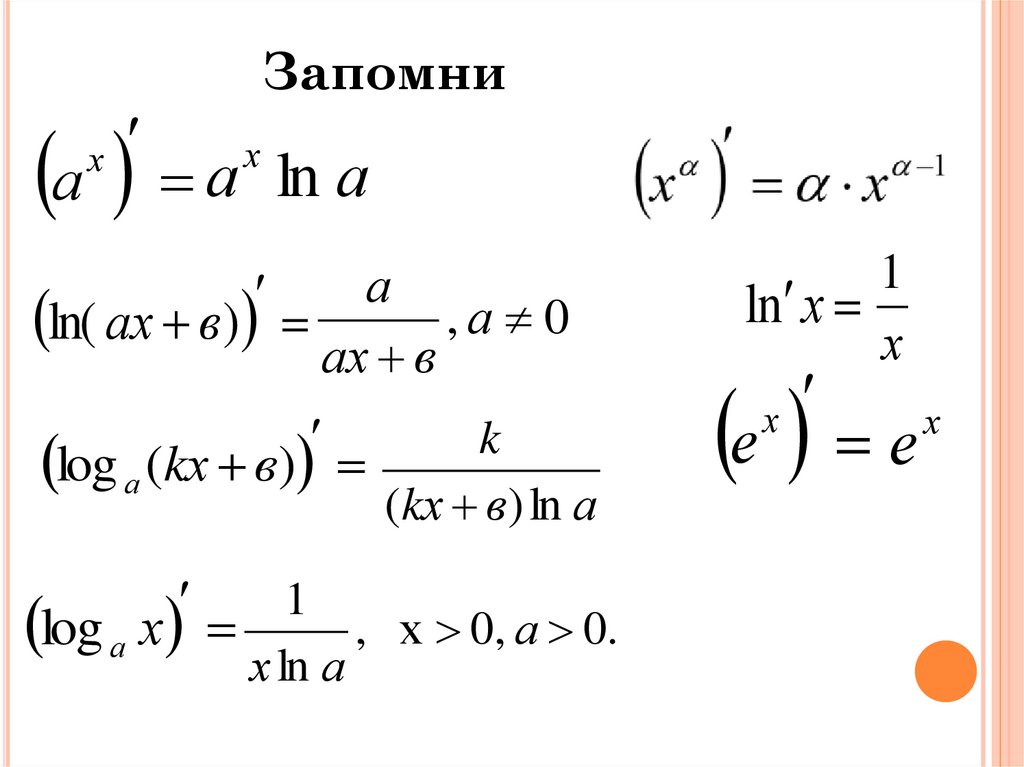


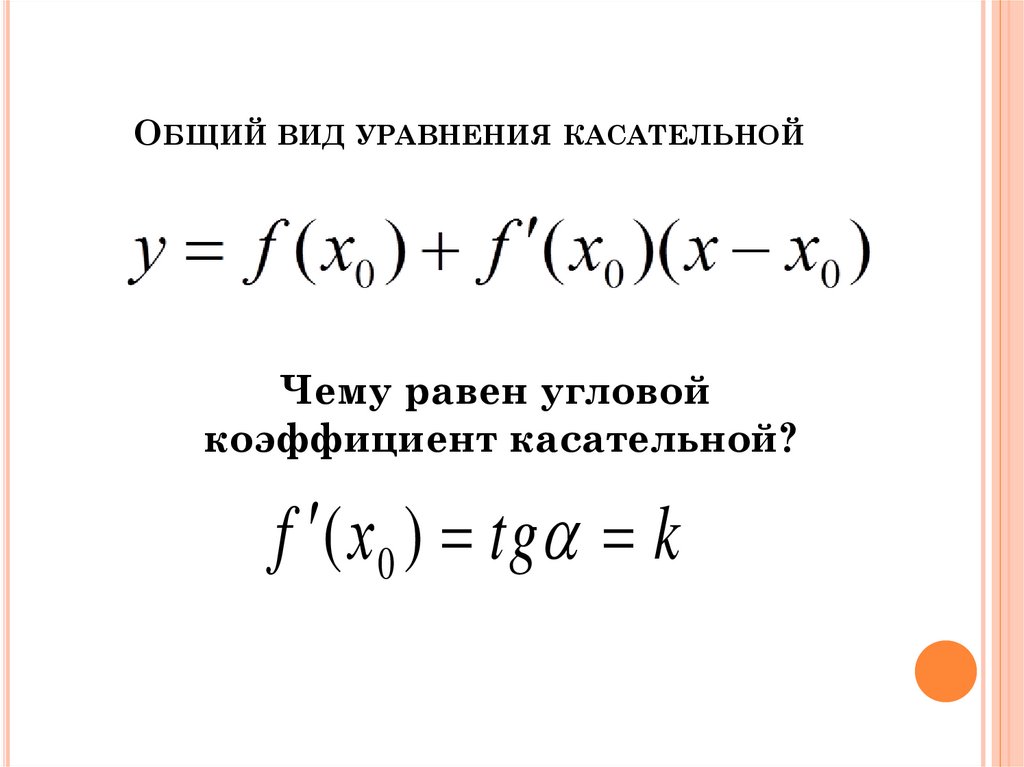







 mathematics
mathematics








