Similar presentations:
Теоретическая механика. Лекция 1С
1. Лекция 1С 1 Предмет «Теоретическая механика»
1. Теоретическая механика – естественно-научная дисциплина, изучающая общиезаконы механического движения и механического взаимодействия материальных тел.
Объектами изучения в теоретической механике являются:
материальная точка – тело, размерами которого можно пренебречь в данной задаче;
система материальных точек (механическая система) – совокупность материальных
точек, положение и движение каждой из которых зависит от положения и движения
остальных точек системы;
абсолютно твердое тело – это тело, расстояние между двумя любыми точками
которого остается неизменным в процессе его движения и взаимодействия с другими
телами.
Перечисленные объекты – это модели реальных тел.
Теоретическую механику подразделяют на три раздела.
Статика – раздел теоретической механики, изучающий методы эквивалентного
преобразования систем сил, в частности их максимального упрощения, и определение
условий равновесия систем сил, приложенных к твердому телу (системе твердых тел).
Кинематика – раздел теоретической механики, изучающий виды движений
материальных объектов с геометрической точки зрения, то есть вне связи с силами,
порождающими это движение.
Динамика – раздел теоретической механики, в котором изучается движение
материальных объектов в зависимости от действующих на них сил.
2. Лекция 1С 2 Учебники и учебные пособия
Учебники:
Лачуга Ю. Ф. Ксендзов В. А. Теоретическая механика. Москва «КолосС»
2005, 2010.
Ксендзов В. А., Паршков А. В. Теоретическая механика. Курс лекций. РГАТУ. 2012
Яблонский А. А., Никифорова В. М. Курс теоретической механики. ч. 1 и 2, 1984 и
последующие издания.
Бутенин Н. В., Лунц Я. Л., Меркин Р. М. Курс теоретической механики. т.1 и 2, 1985 и
последующие издания.
Курс теоретической механики. Под ред. К. С. Колесникова. Изд. МГТУ им. Н. Э.
Баумана, М. 2000, 2005.
Тарг С. М. Краткий курс теоретической механики. 1986 и последующие издания.
Мещерский И. В. Сборник задач по теоретической механике. 1990 и последующие
издания.
Учебные пособия:
Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и
задачах. ч.1, 2 1964 и последующие издания.
Григорьян А. Т. Механика от античности до наших дней. 1974.
3. Лекция 1С 3 Сила и системы сил в теоретической механике
nР
А
n
Рис.1
Мерой механического взаимодействия тел является сила.
Сила – величина векторная и характеризуется величиной,
направлением и точкой приложения. Прямая n-n, по которой
направлено действие силы, называется линией ее действия,
рис. 1. На схемах силу изображают в виде стрелки и
обозначают жирными латинскими буквами F, либо с чертой F
Единица силы в системе СИ – Ньютон (Н). 1Н = 1кгм/с2.
• Система сил – совокупность нескольких сил, действующих на данное тело.
• Рассмотрим свободное твердое тело, то есть тело, свобода движения которого
ничем не ограничена. Твердое тело (или точка) может находиться в состоянии покоя
или определенного вида движения. Назовем это состояние тела его кинематическим
состоянием.
• Если при замене одной системы сил другой тело сохраняет свое кинематическое
состояние, то такие системы сил являются эквивалентными (взаимозаменяемыми).
• Сила, эквивалентная некоторой системе сил, называется ее равнодействующей.
• Силу, равную по модулю равнодействующей и направленную по линии ее
действия в противоположную сторону, называют уравновешивающей.
• Система сил, приложенная к некоторому телу и не изменяющая его
кинематического состояния, называется уравновешенной (взаимно уравновешенной)
или эквивалентной нулю.
• Внешними называют силы, действующие на материальные точки (тела) данной
механической системы со стороны точек (тел), не входящих в эту систему.
• Внутренними называют силы взаимодействия между точками (телами),
принадлежащими данной системе.
4. Лекция 1С 4 Аксиомы статики
Аксиомы – это опытные законы, установленные на основе наблюдений и изученияявлений окружающего нас реального мира.
I.
Аксиома равновесия двух сил.
Две силы образуют уравновешенную систему сил только в том случае, если их
модули равны и они направлены по одной прямой в противоположные стороны.
II. Аксиома присоединения и исключения уравновешенной системы сил.
Если к некоторой системе сил, действующих на данное тело, присоединить
или из нее исключить уравновешенную систему сил, то полученная система сил
эквивалентна исходной.
С л е д с т в и е. Не изменяя кинематического состояния
n
абсолютно твердого тела, силу можно переносить
Р1
вдоль линии ее действия в любую точку, сохраняя
неизменным ее модуль и направление.
Обратимся к рис.2 Пусть к твердому телу в точке А приложена
сила Р.
Приложим в точке В две силы Р1 и Р2, равные по модулю
силе Р и направленные по линии ее действия в
противоположные стороны.
Затем отбросим силы Р и Р2, как образующие
уравновешенную систему сил. Тогда к телу в точке В будет
приложена сила Р1, эквивалентная силе Р в точке А.
n
Тем самым доказано, что сила – вектор скользящий
(в задачах статики).
В
Р2
Р
А
Рис.2
5.
Лекция 1СF1
O
Рис.3
P2
Рис.4
F2
5
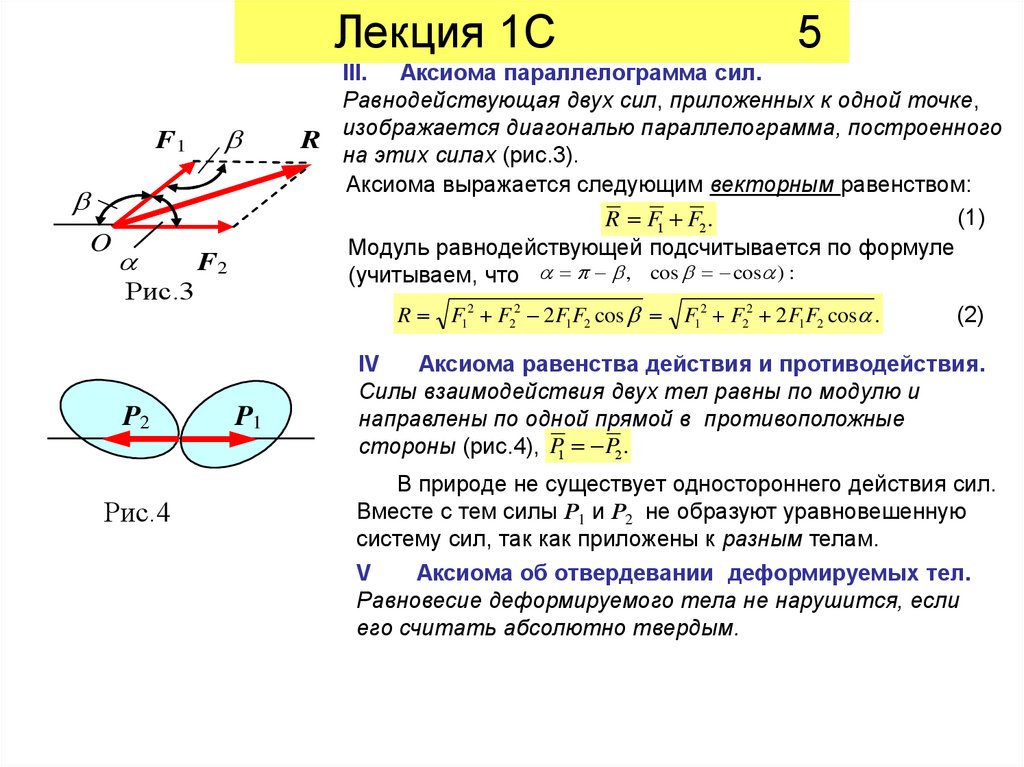
III. Аксиома параллелограмма сил.
Равнодействующая двух сил, приложенных к одной точке,
изображается диагональю параллелограмма, построенного
R
на этих силах (рис.3).
Аксиома выражается следующим векторным равенством:
(1)
R F1 F2 .
Модуль равнодействующей подсчитывается по формуле
(учитываем, что , cos cos ) :
R F12 F22 2 F1F2 cos F12 F22 2 F1F2 cos .
P1
(2)
IV
Аксиома равенства действия и противодействия.
Силы взаимодействия двух тел равны по модулю и
направлены по одной прямой в противоположные
стороны (рис.4), P1 P2 .
В природе не существует одностороннего действия сил.
Вместе с тем силы Р1 и Р2 не образуют уравновешенную
систему сил, так как приложены к разным телам.
V
Аксиома об отвердевании деформируемых тел.
Равновесие деформируемого тела не нарушится, если
его считать абсолютно твердым.
6. Лекция 1С 6 Связи и реакции связей
Твердое тело, свобода движения которого ничем не ограничена, называется свободным.Твердое тело, свобода движения которого ограничена другими телами, называется несвободным.
Тело, ограничивающее движение рассматриваемого тела, является по отношению к нему связью.
Силы, действующие на несвободное тело, разделяют на заданные (активные) и реакции связей.
Реакцией связи называется сила, с которой связь действует на рассматриваемое тело.
Одним из основных положений механики является принцип освобождения от связей, согласно
которому несвободное твердое тело можно рассматривать как свободное, на которое
помимо заданных (активных) сил действуют также реакции связей.
То есть при решении задач статики связи (тела) отбрасывают, а их действие на тело, равновесие
которого рассматривается, показывают в виде реакций связей.
Для определения каждой реакции связи необходимо знать ее модуль, направление действия и
точку ее приложения. В задачах механики, как правило, известной является точка приложения реакции
связи. Направление реакции связи бывает известным лишь для некоторых их видов и неизвестной
(подлежащей определению) – модуль реакции связей.
Рассмотрим ряд соединений тел и задание направлений реакций связей.
1. Тело находится на гладкой поверхности, рис.5. Реакция поверхности N перпендикулярна этой
поверхности.
2. Тело подвешено на гибкой и нерастяжимой нити или на стержне с шарнирами по его концам,
рис.6. Реакция направлена по нити или по линии, соединяющей шарниры.
3. Тело опирается своими острыми углами о гладкую поверхность, либо своей гладкой
поверхностью об острый угол, рис.7. Реакции направлены перпендикулярно гладким поверхностям.
4. Реакция цилиндрического подвижного шарнира на катках, рис.8, направляется перпендикулярно
плоскости качения.
N1
N
N
N1
N2
N2
N3
Рис.5
Рис.6
Рис.7
Рис.8
7. Лекция 1С 7 Связи и реакции связей
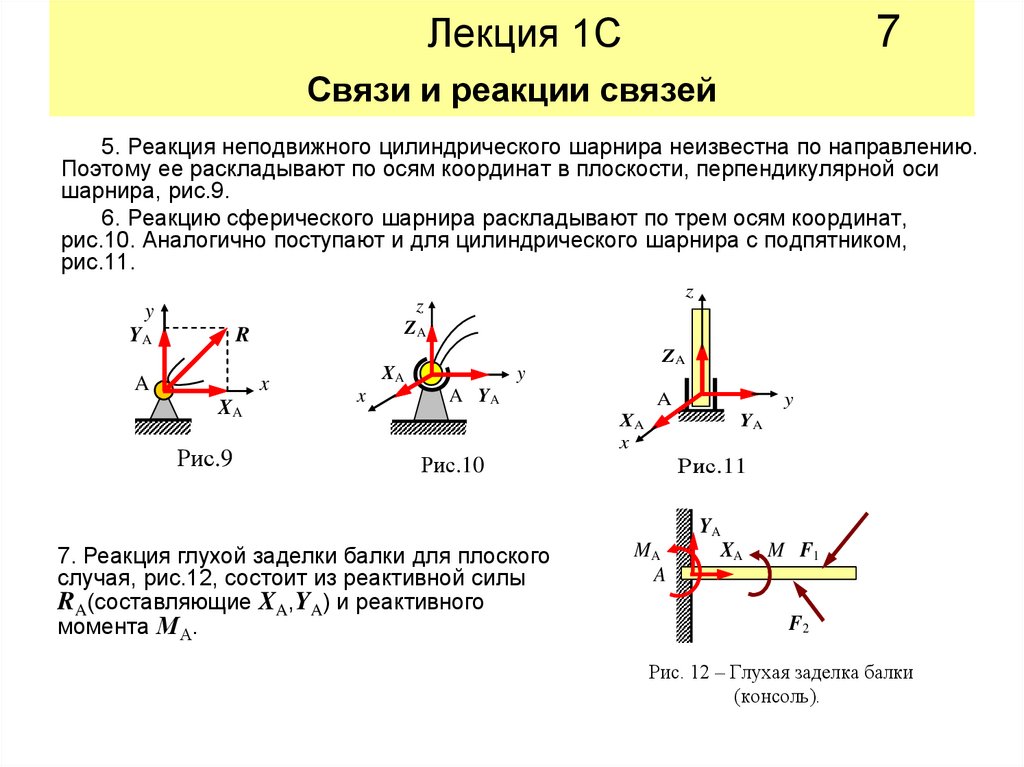
5. Реакция неподвижного цилиндрического шарнира неизвестна по направлению.Поэтому ее раскладывают по осям координат в плоскости, перпендикулярной оси
шарнира, рис.9.
6. Реакцию сферического шарнира раскладывают по трем осям координат,
рис.10. Аналогично поступают и для цилиндрического шарнира с подпятником,
рис.11.
YA
R
A
x
XA
Рис.9
z
z
ZA
y
XA
x
ZA
y
A YA
Рис.10
7. Реакция глухой заделки балки для плоского
случая, рис.12, состоит из реактивной силы
RA(составляющие XA,YA) и реактивного
момента МА.
A
XA
x
y
YA
Рис.11
MA
A
YA
XA
M F1
F2
Рис. 12 – Глухая заделка балки
(консоль).
8.
Лекция 1С8
Система сходящихся сил
плоские
СИСТЕМЫ СИЛ
пространственные
сходящихся
параллельных произвольных
1. Система сходящихся сил – линии действия сил пересекаются в одной точке, рис.1.
При исследовании системы сил необходимо ответить на вопросы: как упростить
систему сил? Каков простейший вид системы? Каковы условия равновесия системы сил?
Упрощение системы сил методом параллелограмма.
1. Перенесем все силы по линии их действия в точку пересечения О.
2. Сложим первые две силы
F1 и F2, получим силу F12:
F12 F1 F2
F1
3. Затем сложим силы F3 и F12,
F123 F1 F2 F3
получим силу F123:
F2
F12
F123
4. Затем сложим F4 и F123, получим результирующую силу
R, которую называют равнодействующей:
R
4
R F1 F2 F3 F4 Fi
O
i 1
В общем случае R
F3
n
F,
i 1
i
(1) где n – число сил.
Рис. 1
F4
9. Лекция 1С 9
9Лекция 1С
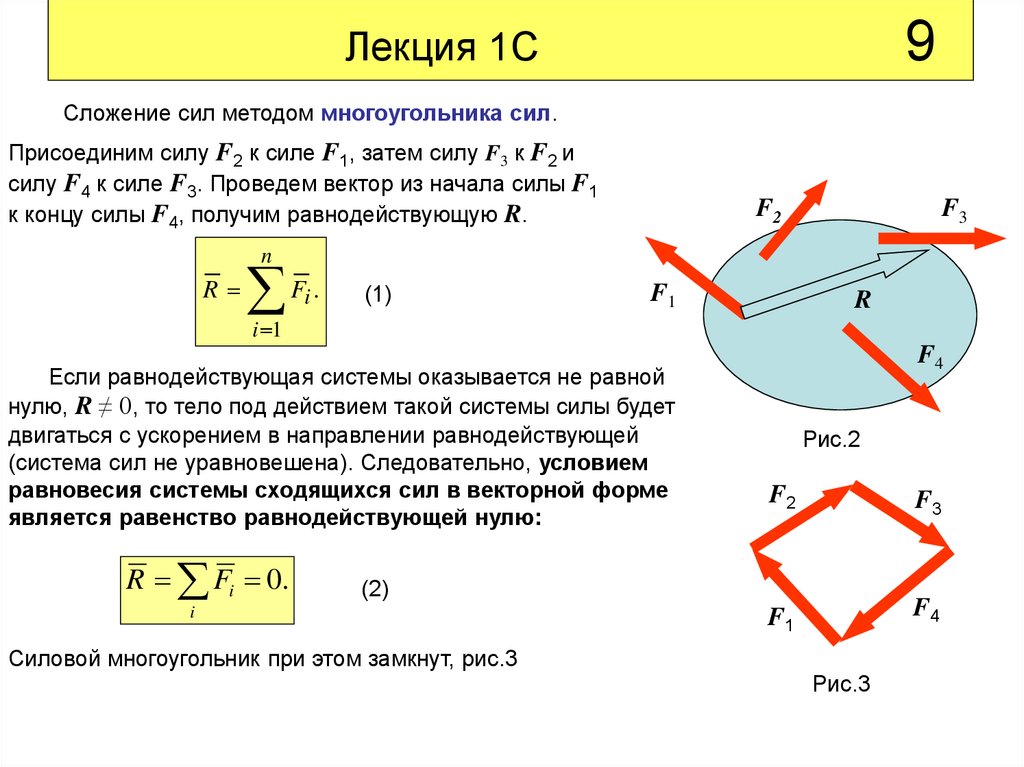
Сложение сил методом многоугольника сил.
Присоединим силу F2 к силе F1, затем силу F3 к F2 и
силу F4 к силе F3. Проведем вектор из начала силы F1
к концу силы F4, получим равнодействующую R.
F2
F3
n
R
F .
i
(1)
F1
R
i 1
Если равнодействующая системы оказывается не равной
нулю, R ≠ 0, то тело под действием такой системы силы будет
двигаться с ускорением в направлении равнодействующей
(система сил не уравновешена). Следовательно, условием
равновесия системы сходящихся сил в векторной форме
является равенство равнодействующей нулю:
R Fi 0.
F4
Рис.2
F2
F3
F1
F4
(2)
i
Силовой многоугольник при этом замкнут, рис.3
Рис.3
10. Лекция 1С 10
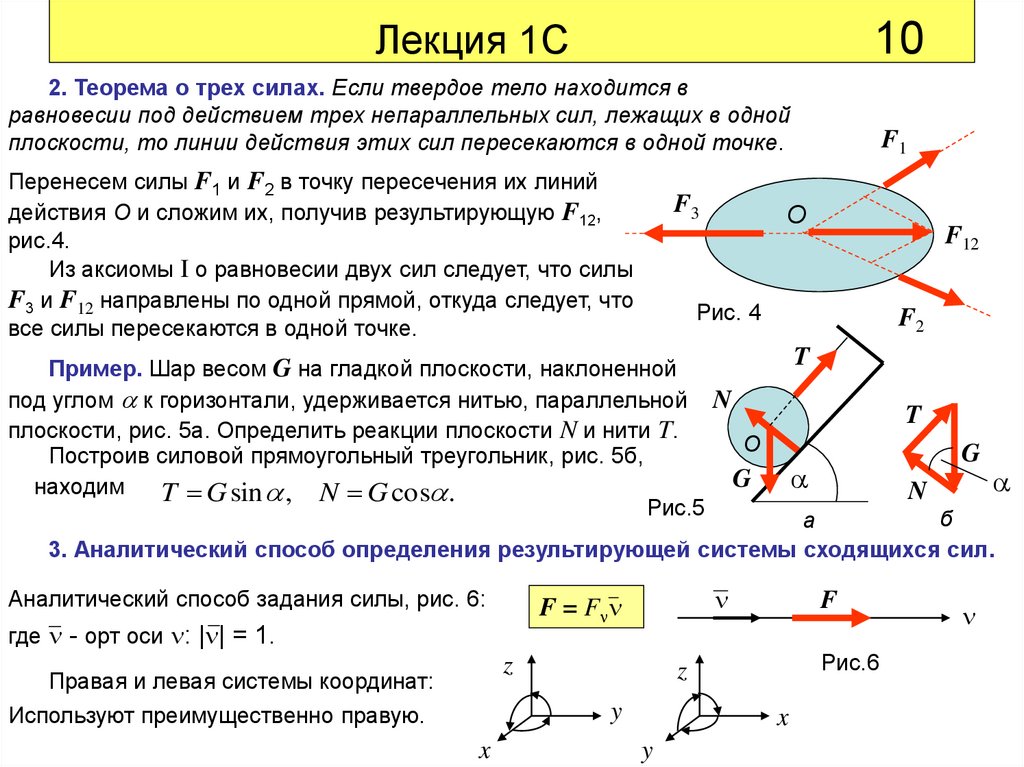
2. Теорема о трех силах. Если твердое тело находится вравновесии под действием трех непараллельных сил, лежащих в одной
плоскости, то линии действия этих сил пересекаются в одной точке.
Перенесем силы F1 и F2 в точку пересечения их линий
действия О и сложим их, получив результирующую F12,
рис.4.
Из аксиомы I о равновесии двух сил следует, что силы
F3 и F12 направлены по одной прямой, откуда следует, что
все силы пересекаются в одной точке.
F3
F1
O
F12
Рис. 4
F2
T
Пример. Шар весом G на гладкой плоскости, наклоненной
под углом к горизонтали, удерживается нитью, параллельной N
плоскости, рис. 5а. Определить реакции плоскости N и нити T.
O
Построив силовой прямоугольный треугольник, рис. 5б,
G
находим
T G sin , N G cos .
Рис.5
T
G
N
б
а
3. Аналитический способ определения результирующей системы сходящихся сил.
Аналитический способ задания силы, рис. 6:
F = F
где - орт оси : | | = 1.
z
Правая и левая системы координат:
x
Рис.6
z
y
Используют преимущественно правую.
F
x
y
11. Лекция 1С 11
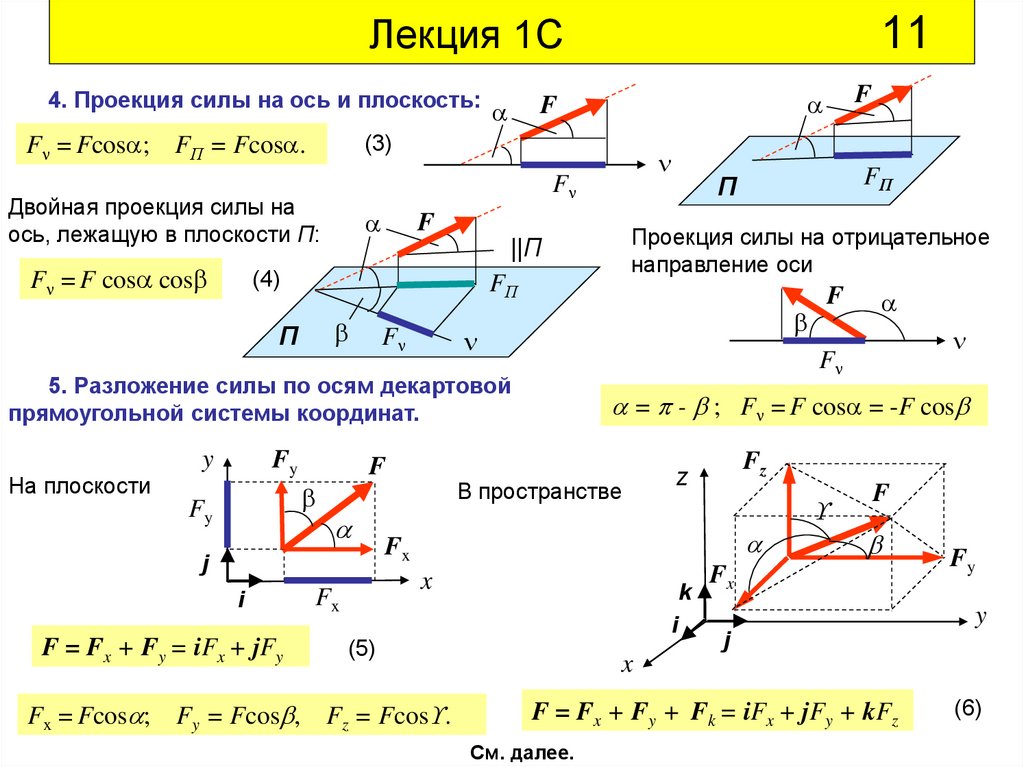
Лекция 1С4. Проекция силы на ось и плоскость:
F
FП
П
F
На плоскости
F
Fy
j
i
В пространстве
Fx = Fcos ; Fy = Fcos ,
Fz
z
Fx
k
i
F = Fx + Fy = iFx + jFy
(5)
Fz = Fcos .
= - ; F = F cos = -F cos
x
Fx
F
F
5. Разложение силы по осям декартовой
прямоугольной системы координат.
Fy
FП
П
Проекция силы на отрицательное
направление оси
||П
(4)
y
F
Двойная проекция силы на
ось, лежащую в плоскости П:
F
F
(3)
F = Fcos ; FП = Fcos .
F = F cos cos
11
F
Fx
Fy
y
j
x
F = Fx + Fy + Fk = iFx + jFy + kFz
См. далее.
(6)
12.
Лекция 1СНаправляющие косинусы: cos
Модуль результирующей:
12
Fy
Fx
F
, cos
, cos z . cos 2 cos 2 cos 2 1
F
F
F
F Fx2 Fy2 Fz2
(7)
6. Расчет равнодействующей системы сходящихся сил.
R = iRx+jRy+kRz = Fi = i Fix +j Fiy+k Fiz.
Модуль равнодействующей:
Rx = Fix ; Ry = Fiy ; Rz = Fiz .
R Rx2 Ry2 Rz2
Направляющие косинусы: cos R
F F F
2
2
ix
Ry
Rx
R
, cos R
, cos R z .
R
R
R
2
iy
iz
(8)
(9)
7. Условия равновесия системы сходящихся сил. Исходя из R = 0, имеем
Rx = Fix = 0; Ry = Fiy = 0; Rz = Fiz = 0.
Пример. Условие задачи см. выше.
Fix = T - Gsin = 0; Fiy = N - Gcos = 0.
Откуда
T G sin ,
N G cos
(10)
x
T
y
N
G
Рис. 5.







 physics
physics








