Метод естественного электрического поля

1. Метод естественного электрического поля:

современное состояние

2.

Self-potential: The ugly duckling of environmental geophysics
JONATHAN E. NYQUIST, and CHARLES E. CORRY. The Leading
Edge, 2002.

3. Содержание

1.
2.
3.
4.
5.
6.
7.
8.
9.
Происхождение естественного электрического поля
Основные понятия о двойном электрическом слое
Электрокинетические явления
Вычисление поля фильтрационной природы
Интенсивность потенциала течения
Источники поля фильтрационной природы
Диффузионный и мембранный потенциалы
Методика полевых работ и интерпретации данных
Примеры применения естественного поля

4. 1. Происхождение естественного электрического поля

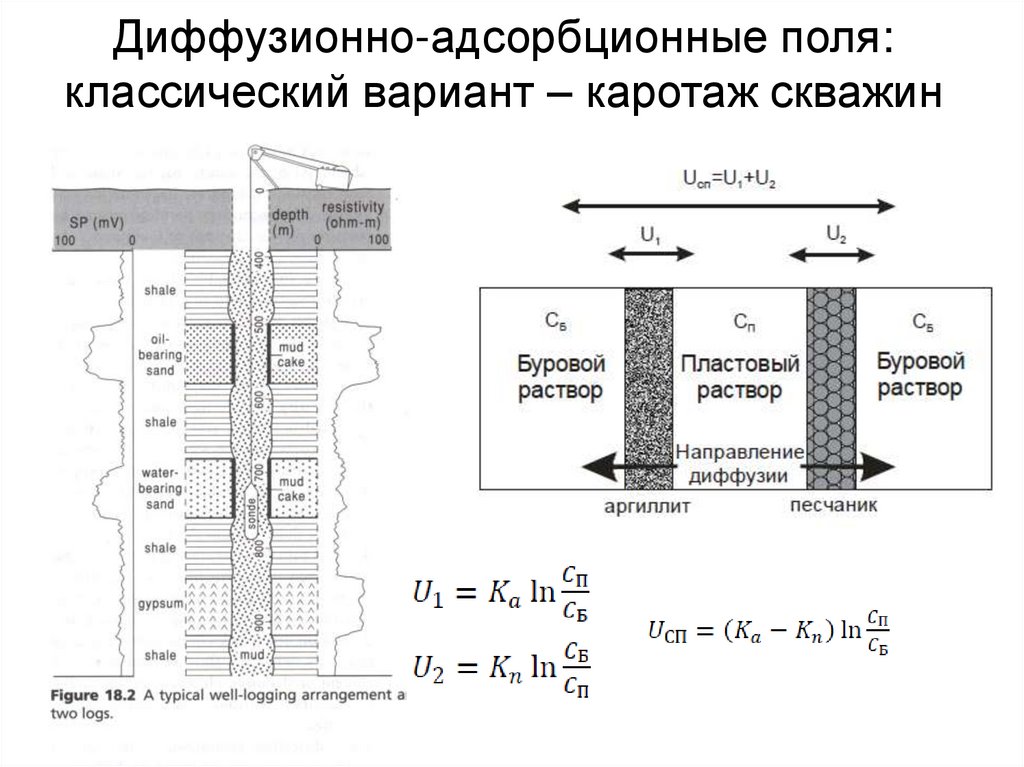
• Поля электрохимической природы
• Диффузионно-адсорбционные поля
• Фильтрационные поля

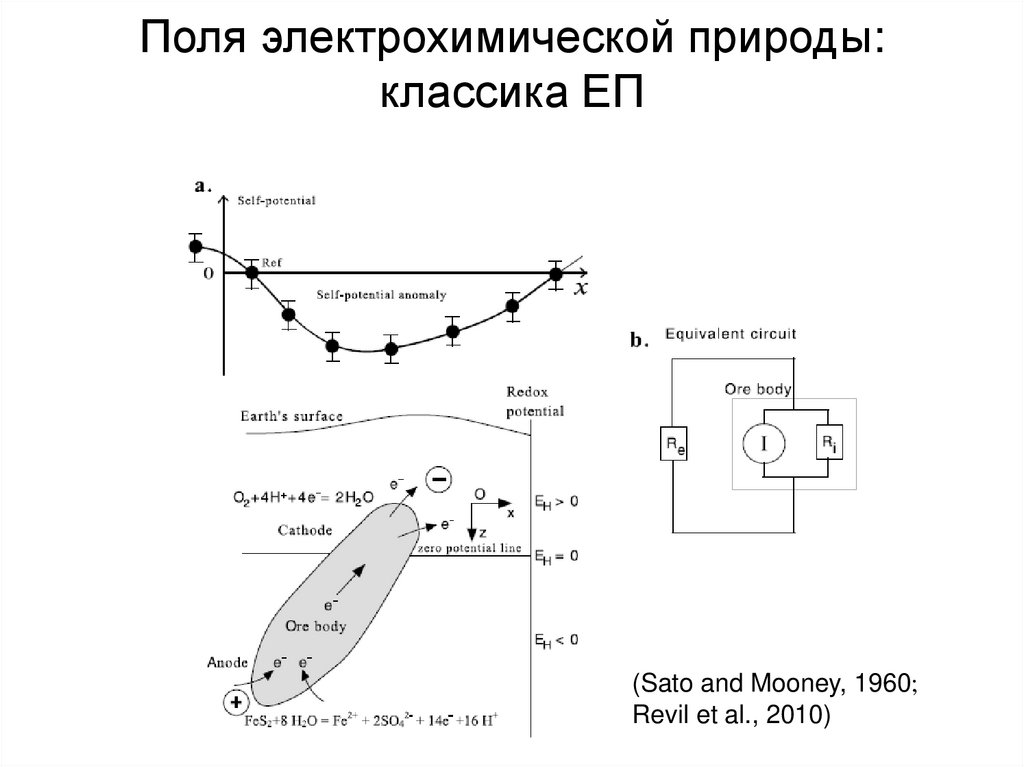
5. Поля электрохимической природы: классика ЕП

(Sato and Mooney, 1960;
Revil et al., 2010)

6.

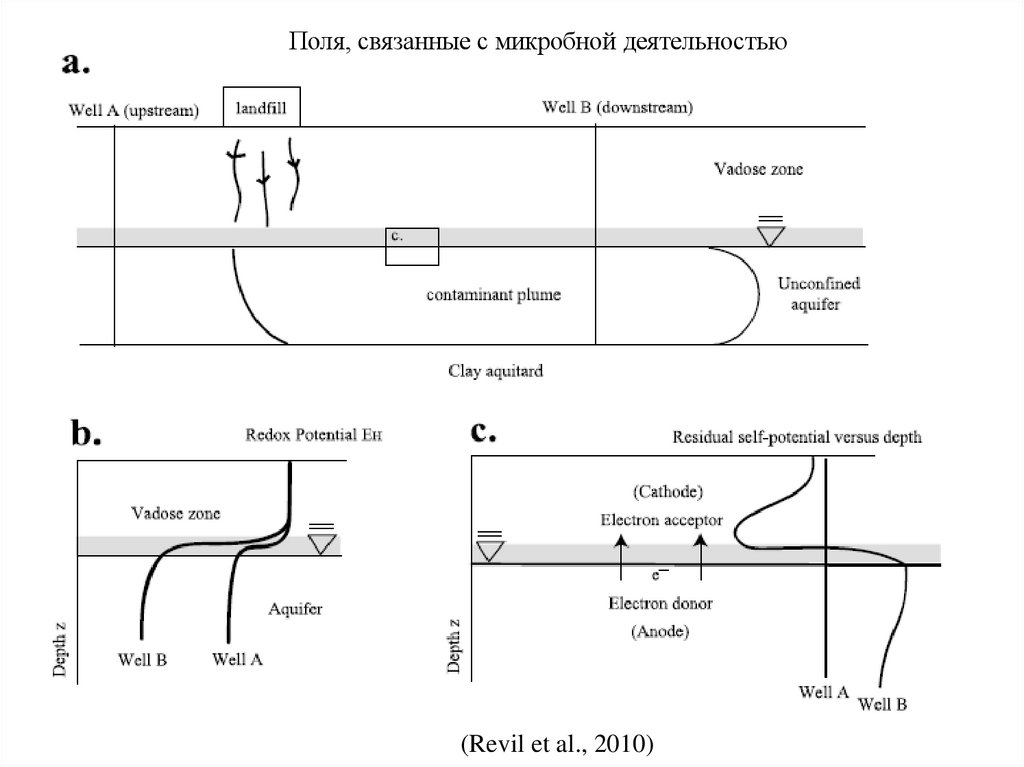
Поля, связанные с микробной деятельностью
(Revil et al., 2010)

7.

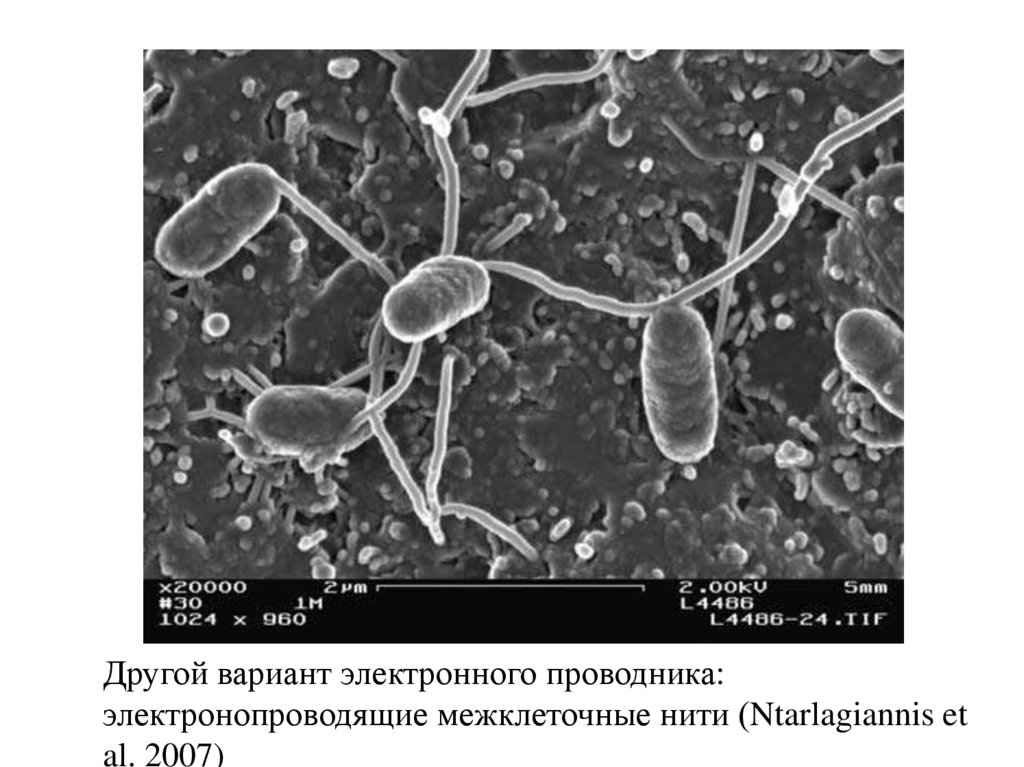
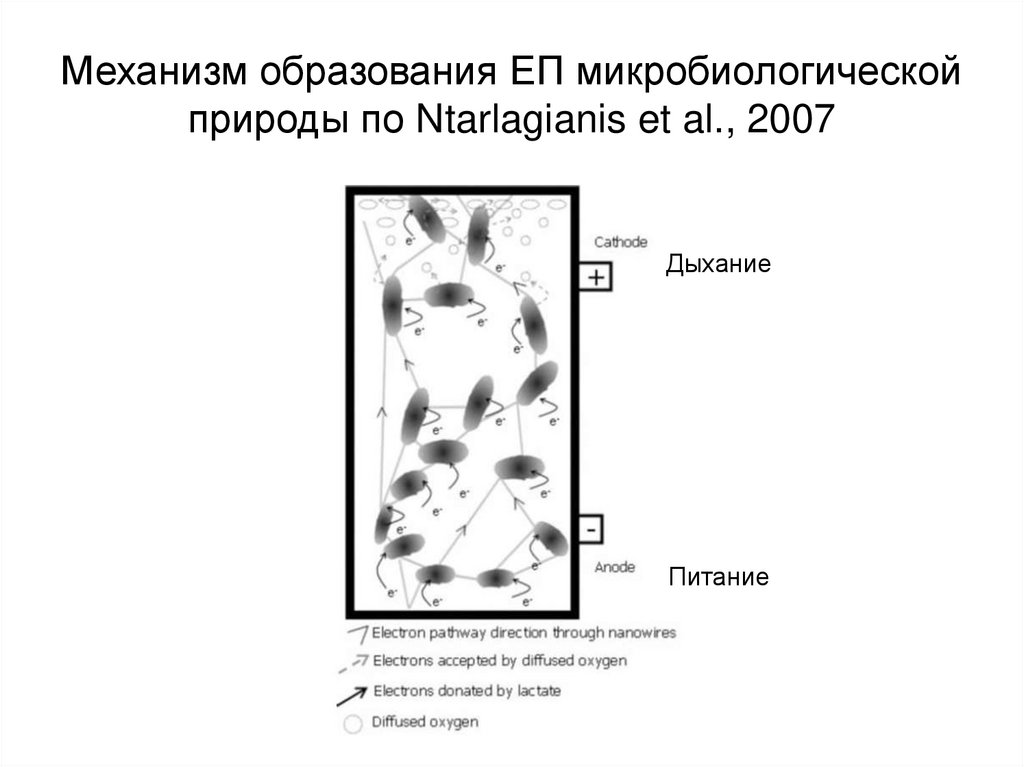
Другой вариант электронного проводника:
электронопроводящие межклеточные нити (Ntarlagiannis et
al. 2007)

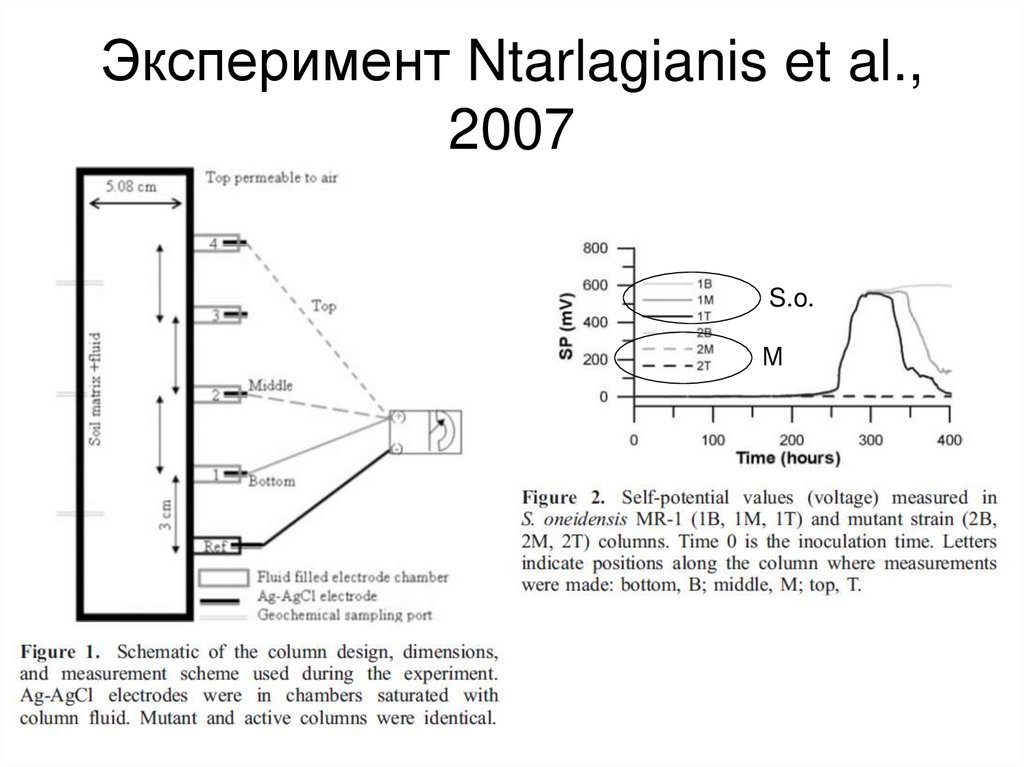
8. Эксперимент Ntarlagianis et al., 2007

S.o.
М

9. Механизм образования ЕП микробиологической природы по Ntarlagianis et al., 2007

Дыхание
Питание

10. Диффузионно-адсорбционные поля: классический вариант – каротаж скважин

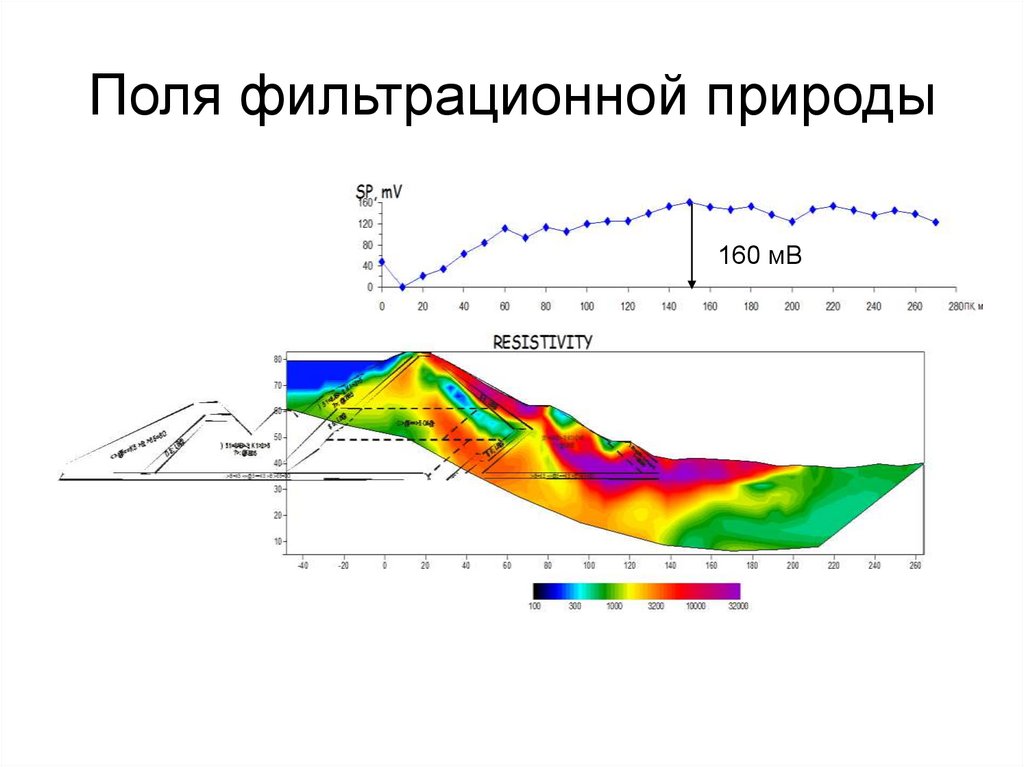
11. Поля фильтрационной природы

12. Поля фильтрационной природы

160 мВ

13. 2. Основные понятия о двойном электрическом слое

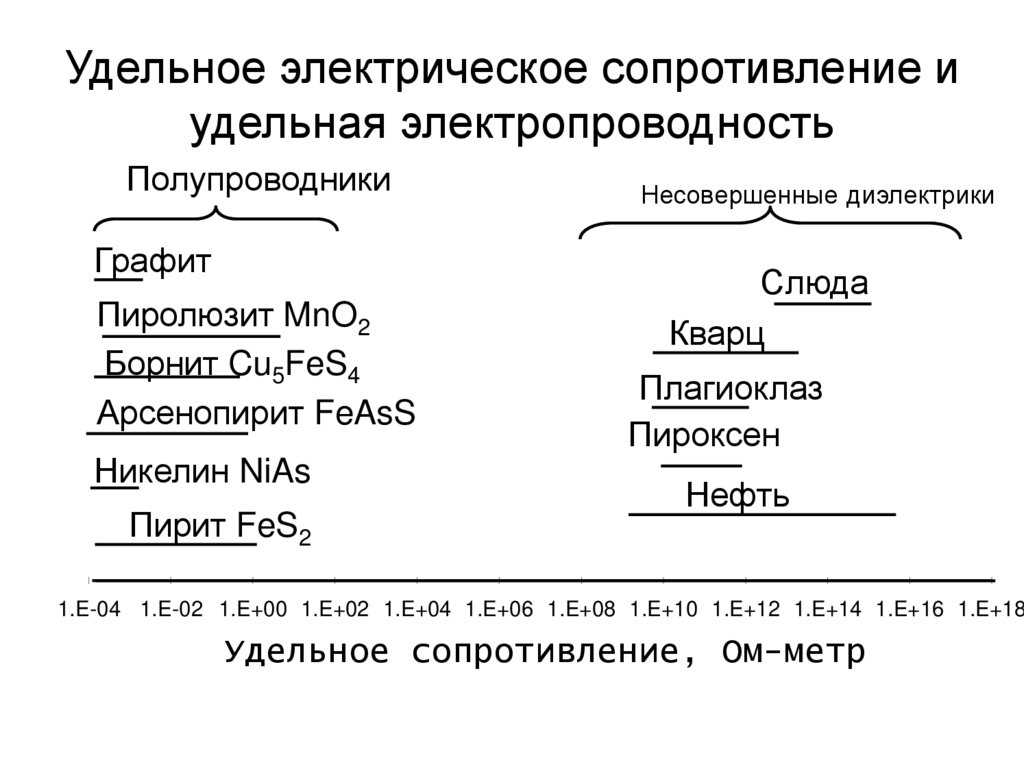
14. Удельное электрическое сопротивление и удельная электропроводность

Полупроводники
Графит
Пиролюзит MnO2
Борнит Cu5FeS4
Арсенопирит FeAsS
Никелин NiAs
Пирит FeS2
Несовершенные диэлектрики
Слюда
Кварц
Плагиоклаз
Пироксен
Нефть
1.E-04 1.E-02 1.E+00 1.E+02 1.E+04 1.E+06 1.E+08 1.E+10 1.E+12 1.E+14 1.E+16 1.E+18
Удельное сопротивление, Ом-метр

15.

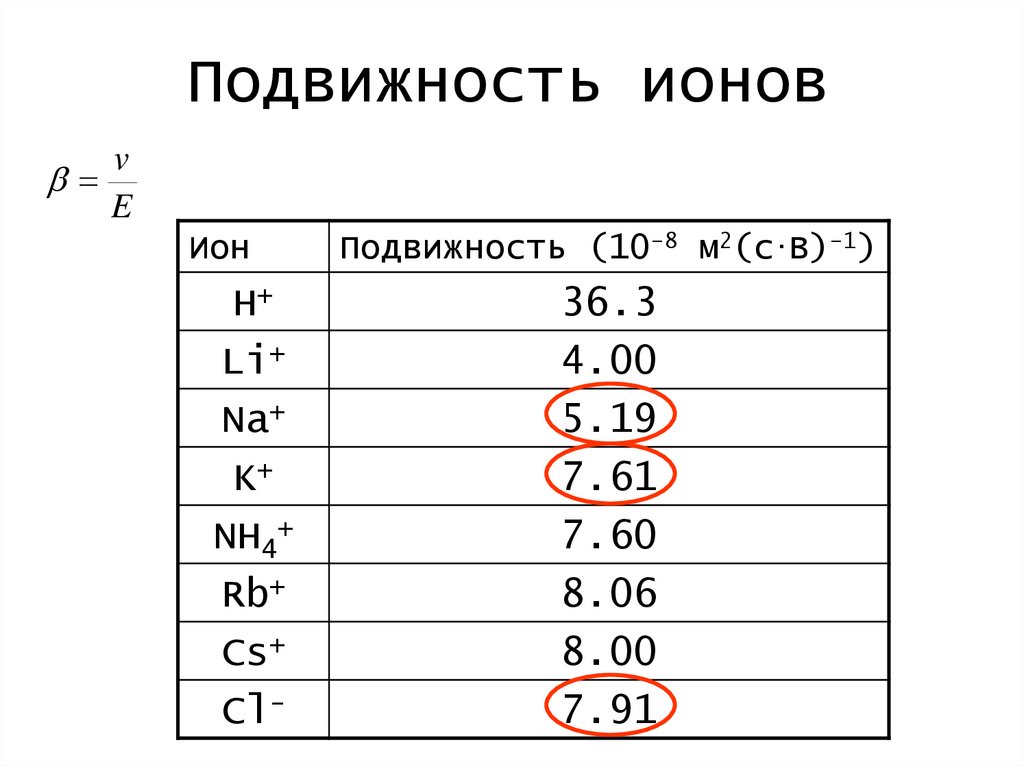
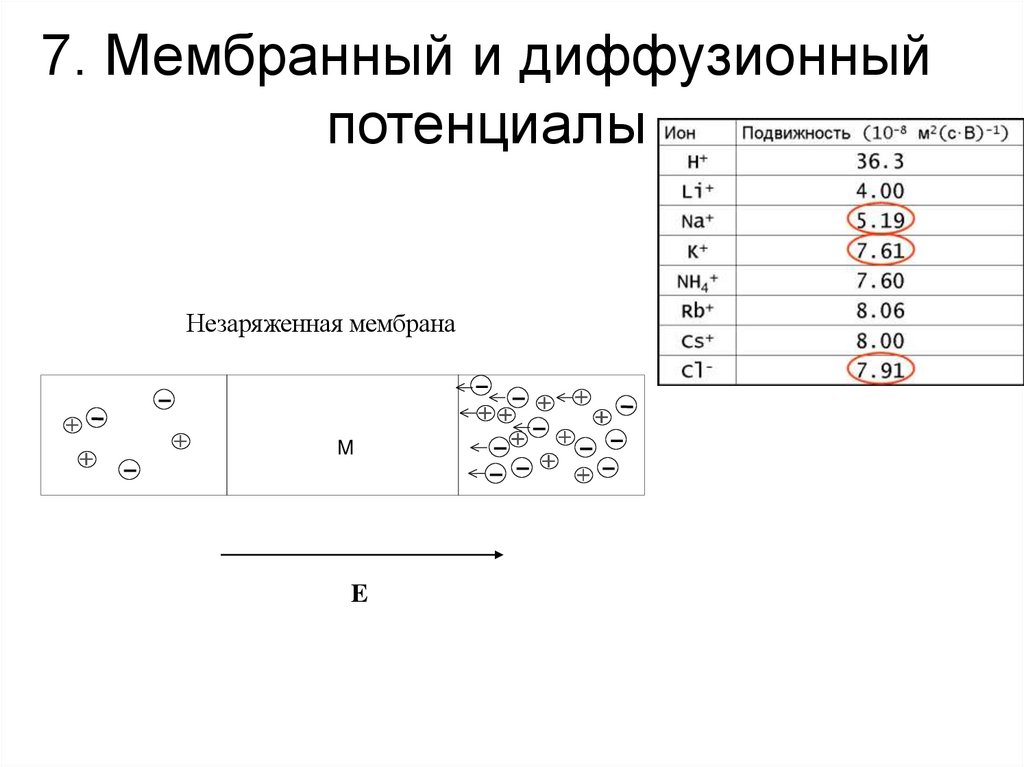
Подвижность ионов
v
E
Ион
H+
Li+
Na+
K+
NH4+
Rb+
Cs+
Cl-
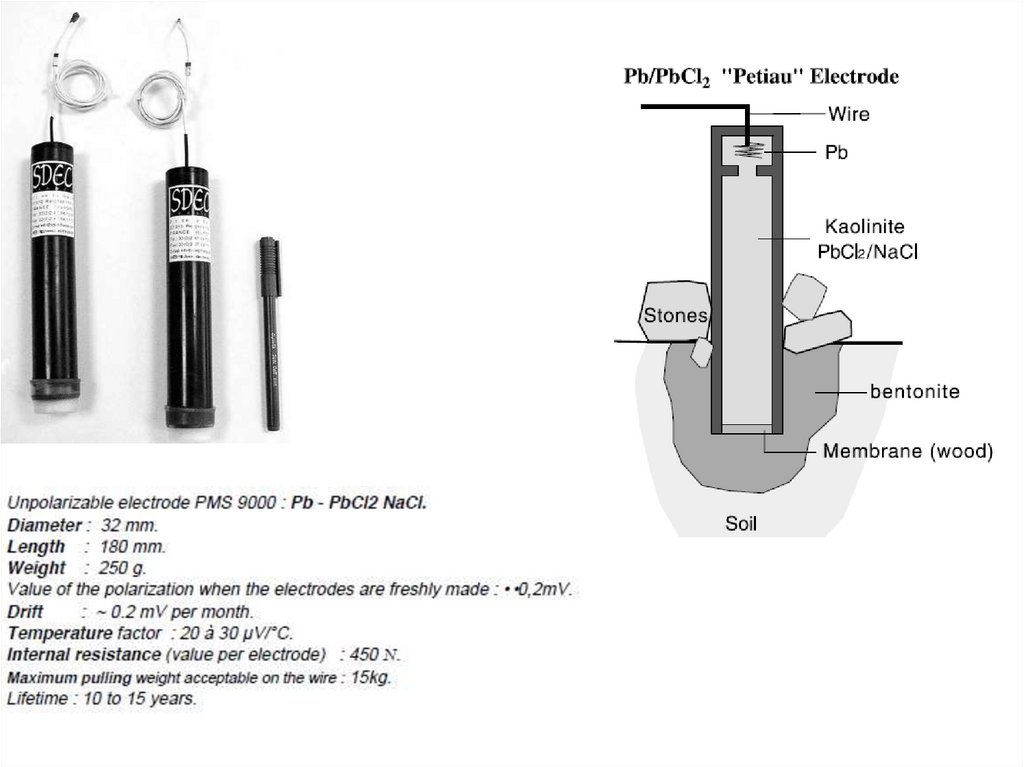
Подвижность (10-8 м2(с.В)-1)
36.3
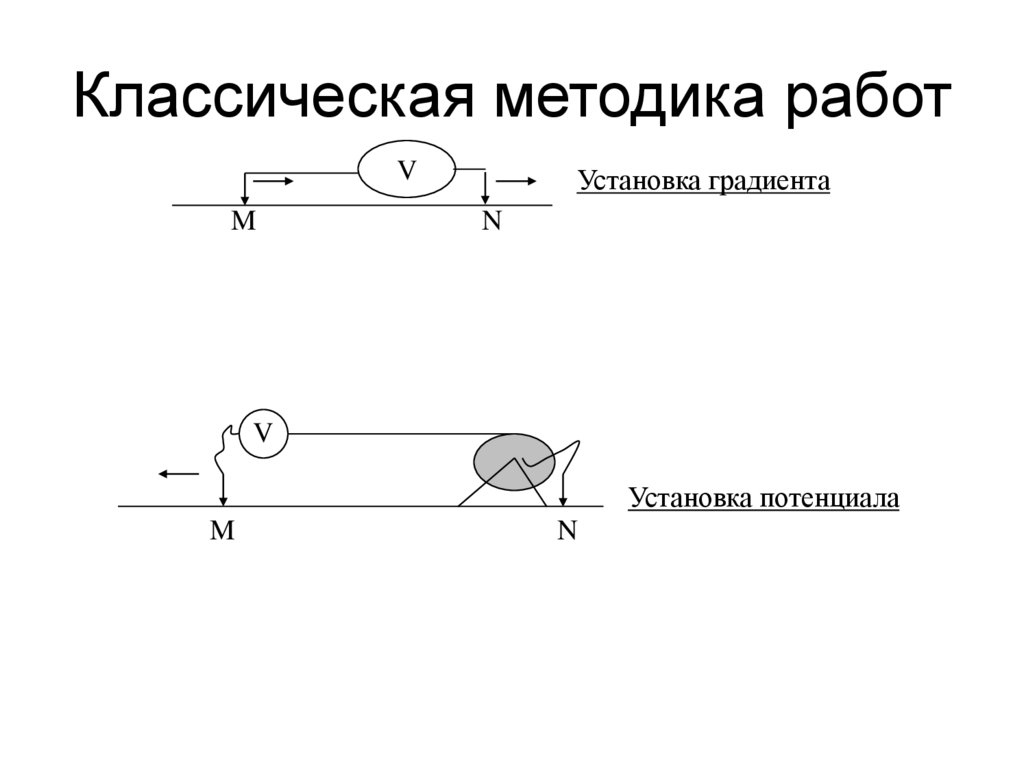
4.00
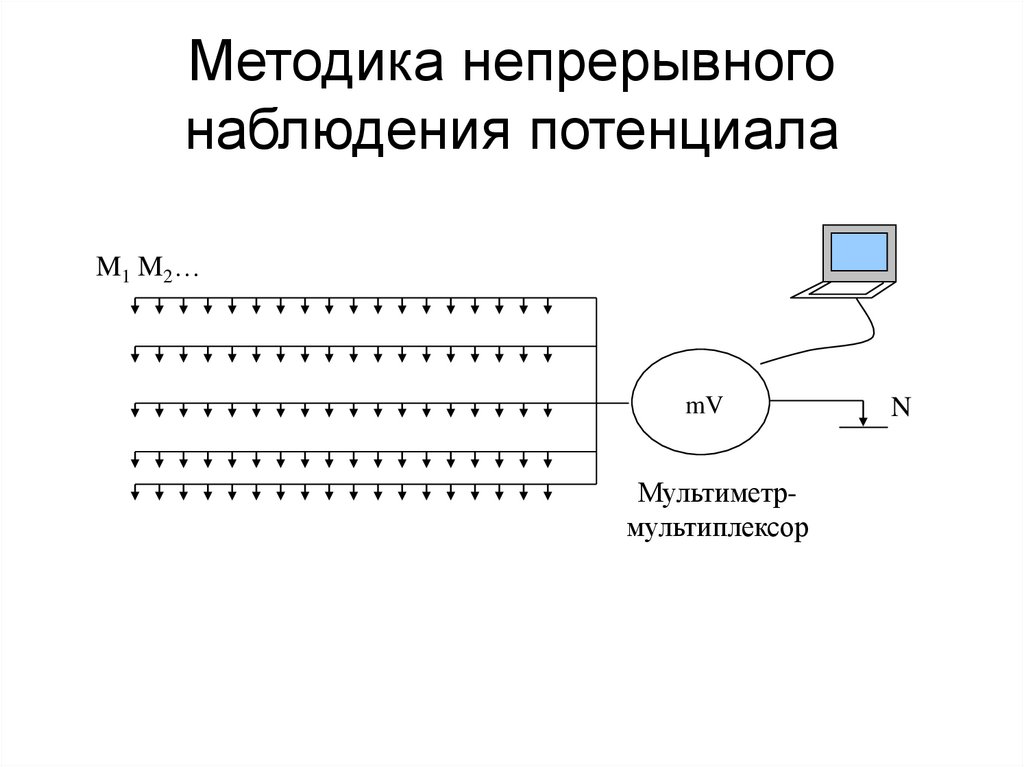
5.19
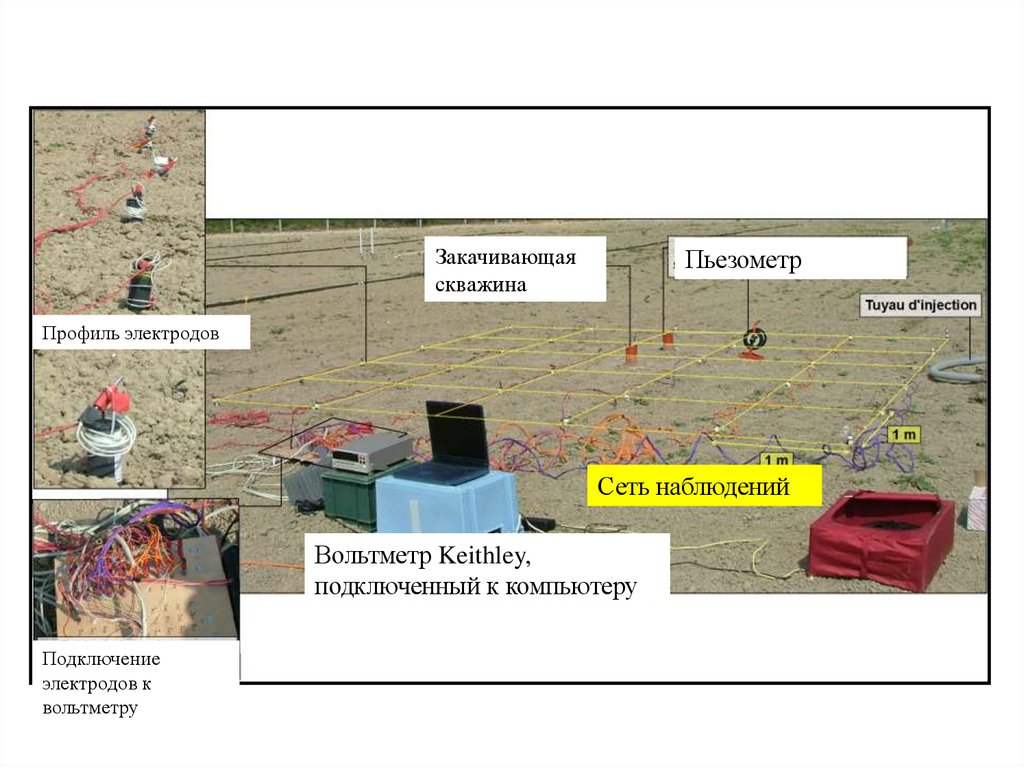
7.61
7.60
8.06
8.00
7.91

16.

Электропроводность растворов
• Постоянная Фарадея, F=96485 Кулон/Моль
(К.Моль-1);
• Валентность, z;
• Концентрация ионов C (Моль.м-3)в теории,
или минерализация (г.л-1) на практике;
• q=zFC К.м-3;
• Электропроводность:s= q=zF C См.м-1;
• sc=zF cCc – “Катионная электропроводность”;
• sa=zF aCa – “Анионная электропроводность”.
Числа переноса ионов:
sc
tc
sc sa
sa
ta
sc sa
tc t a 1

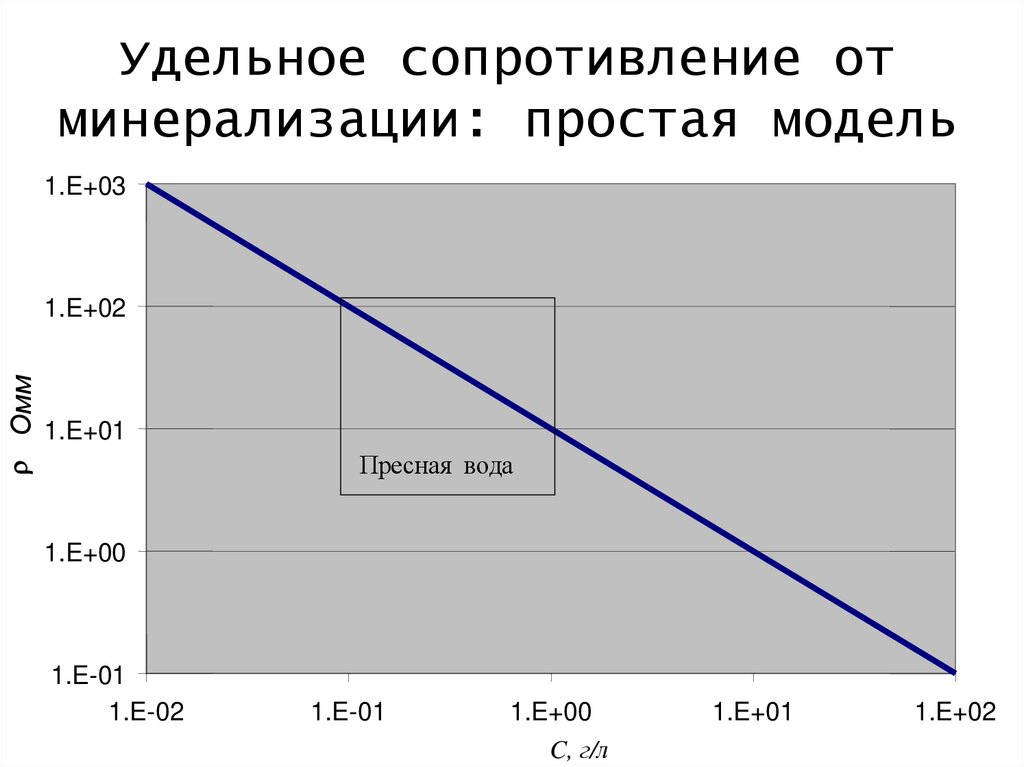
17.

Удельное сопротивление от
минерализации: простая модель
1.E+03
r Омм
1.E+02
1.E+01
Пресная вода
1.E+00
1.E-01
1.E-02
1.E-01
1.E+00
C, г/л
1.E+01
1.E+02

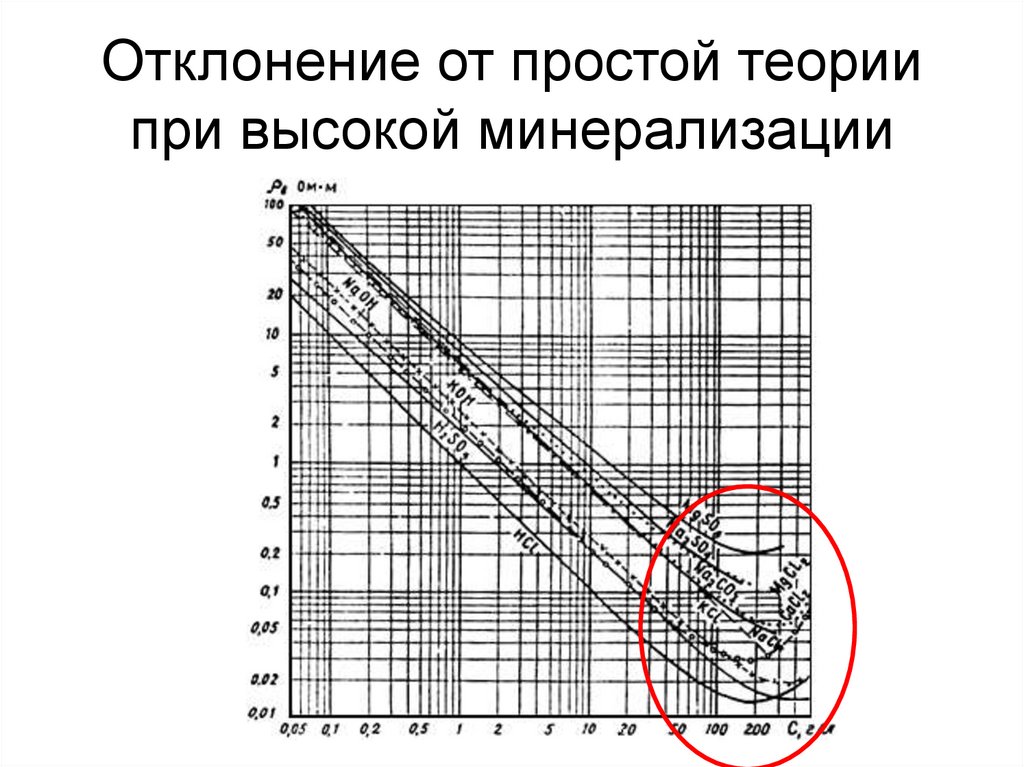
18. Отклонение от простой теории при высокой минерализации

19.

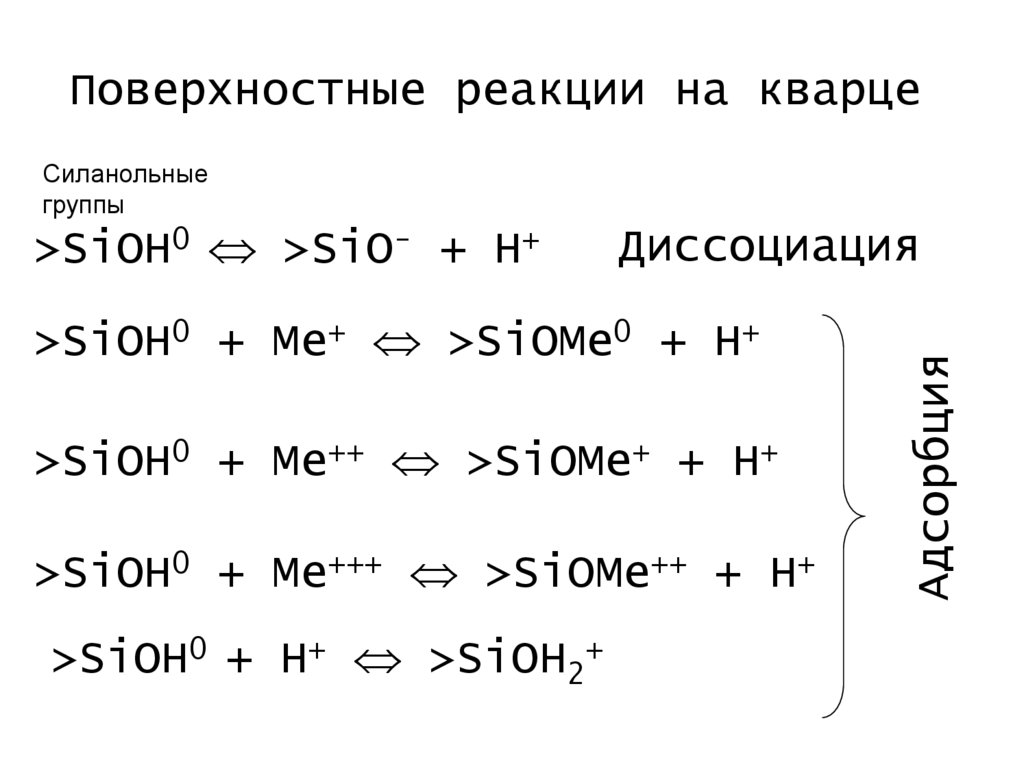
Поверхностные реакции на кварце
Силанольные
группы
Диссоциация
>SiOH0 + Me+ >SiOMe0 + H+
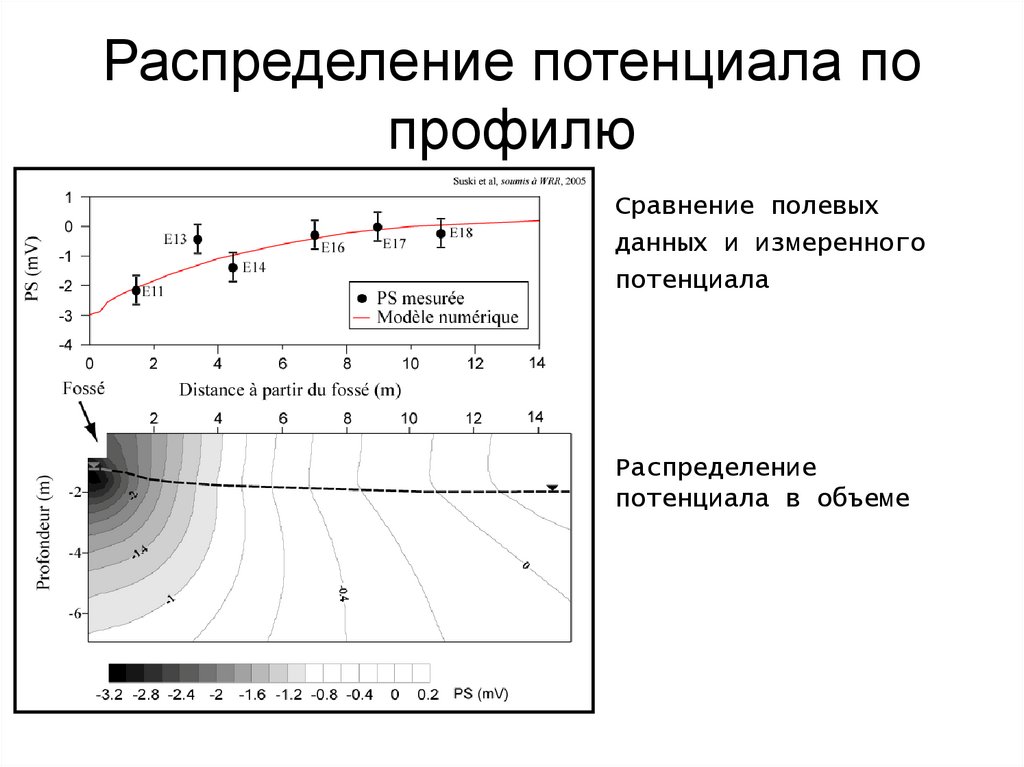
>SiOH0 + Me++ >SiOMe+ + H+
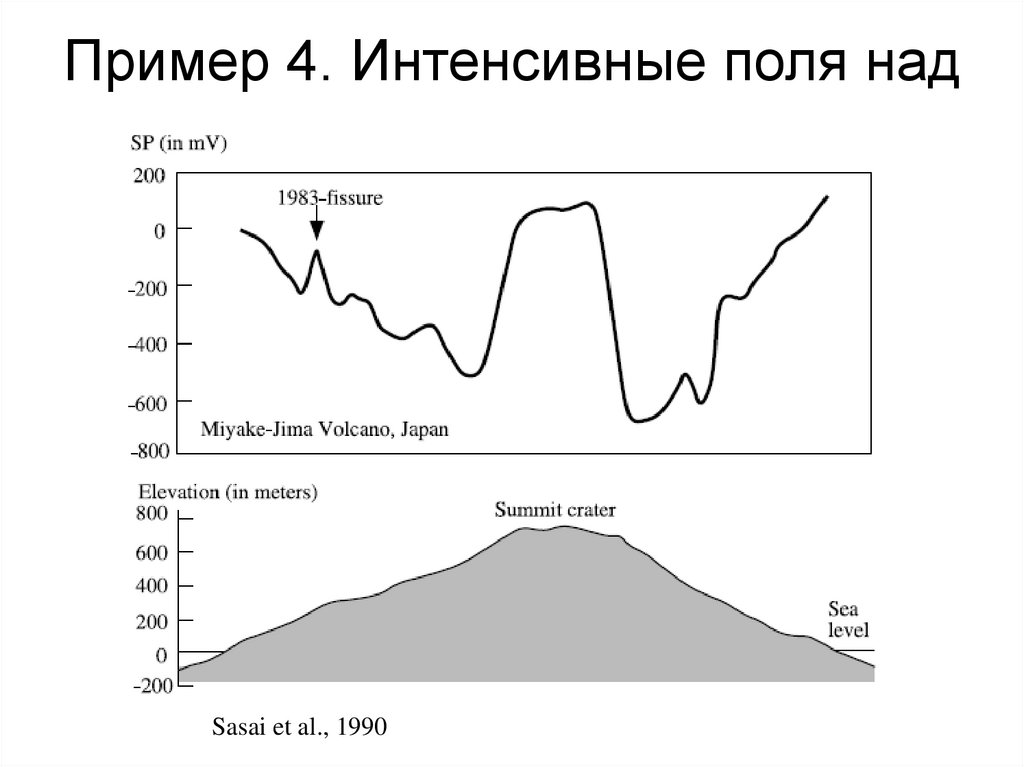
>SiOH0 + Me+++ >SiOMe++ + H+
>SiOH0 + H+ >SiOH2+
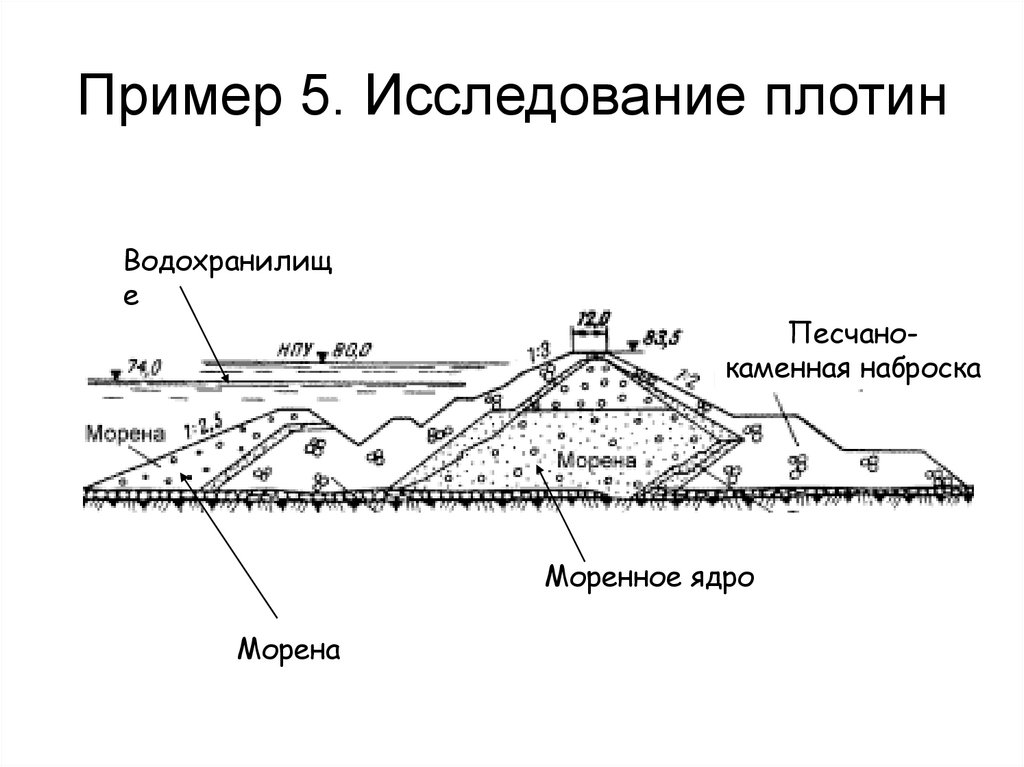
Адсорбция
>SiOH0 >SiO- + H+

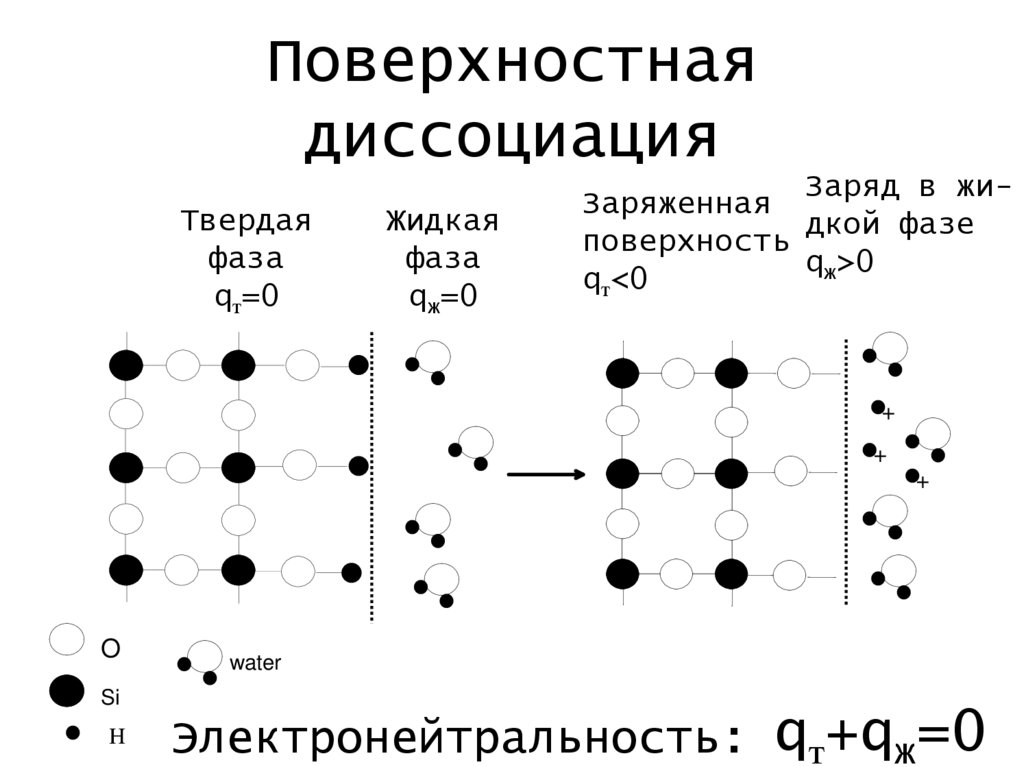
20.

Поверхностная
диссоциация
Твердая
фаза
qт=0
Жидкая
фаза
qж=0
Заряд в жиЗаряженная
дкой фазе
поверхность
qж>0
qт<0
+
+
+
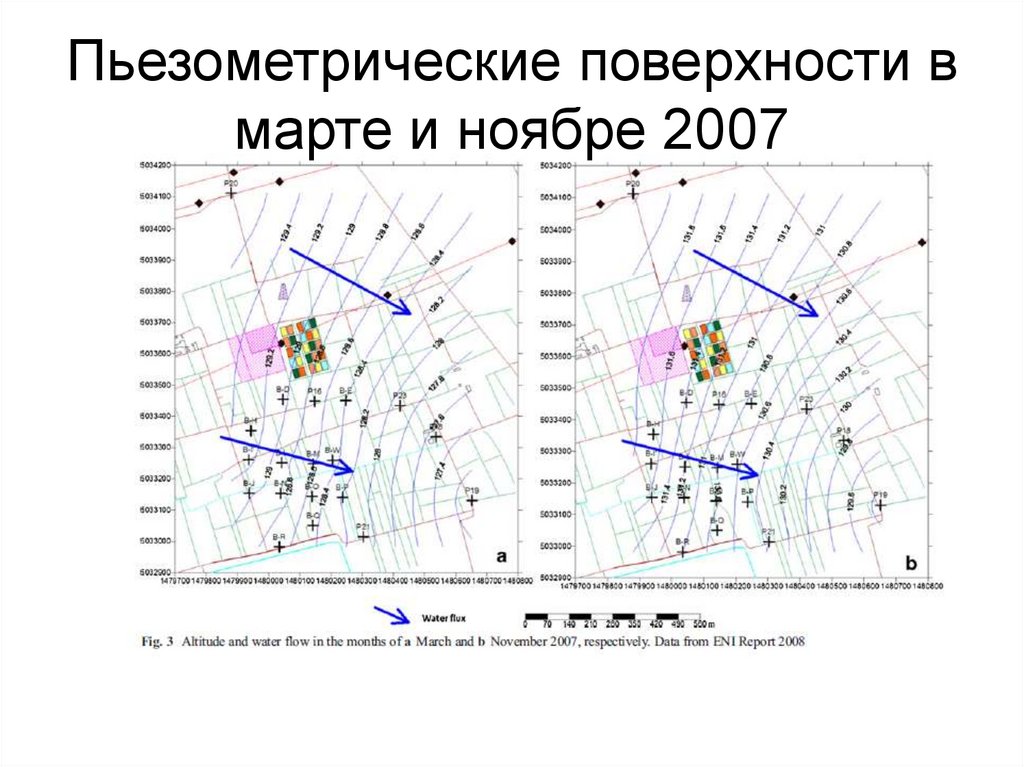
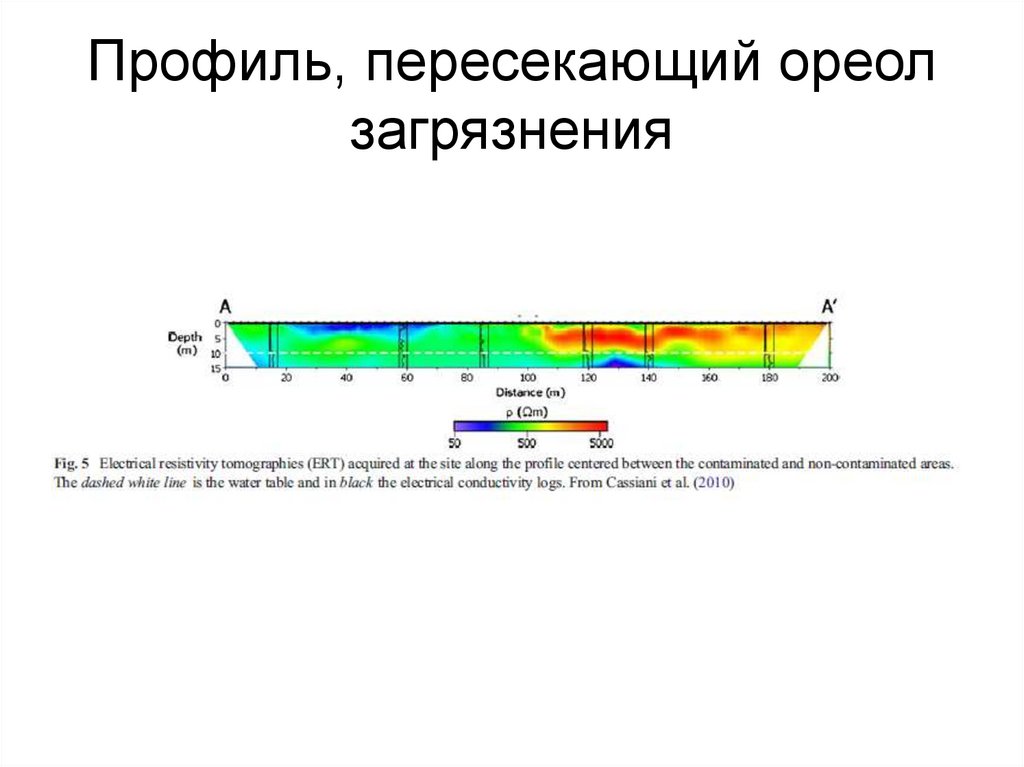
O
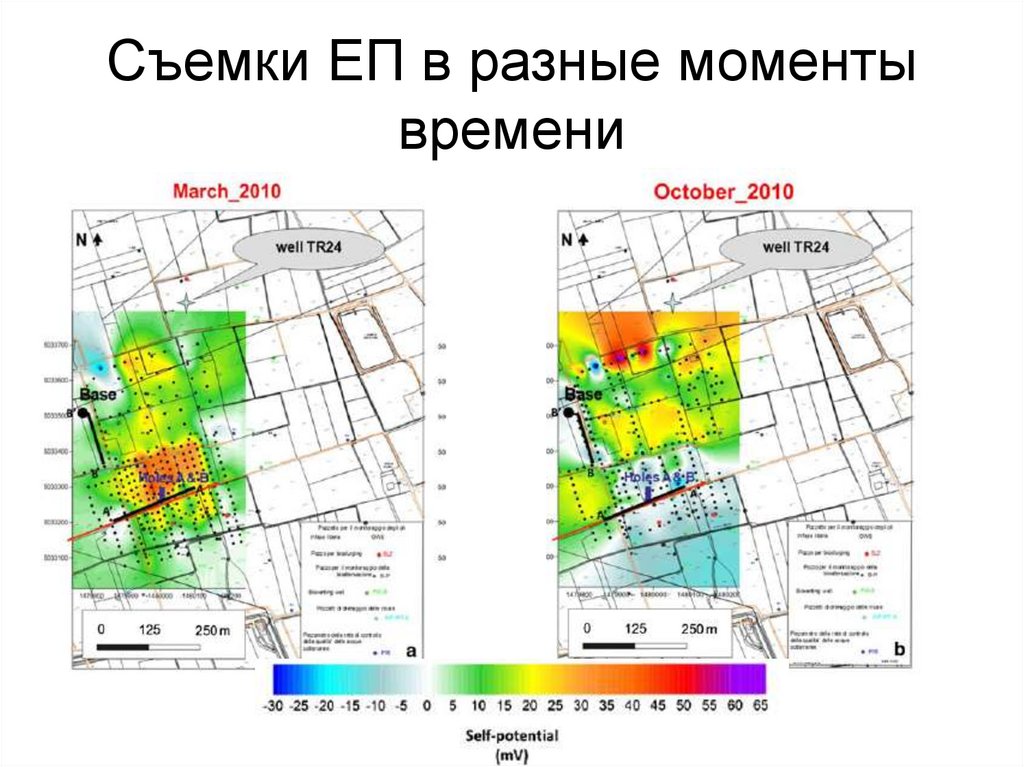
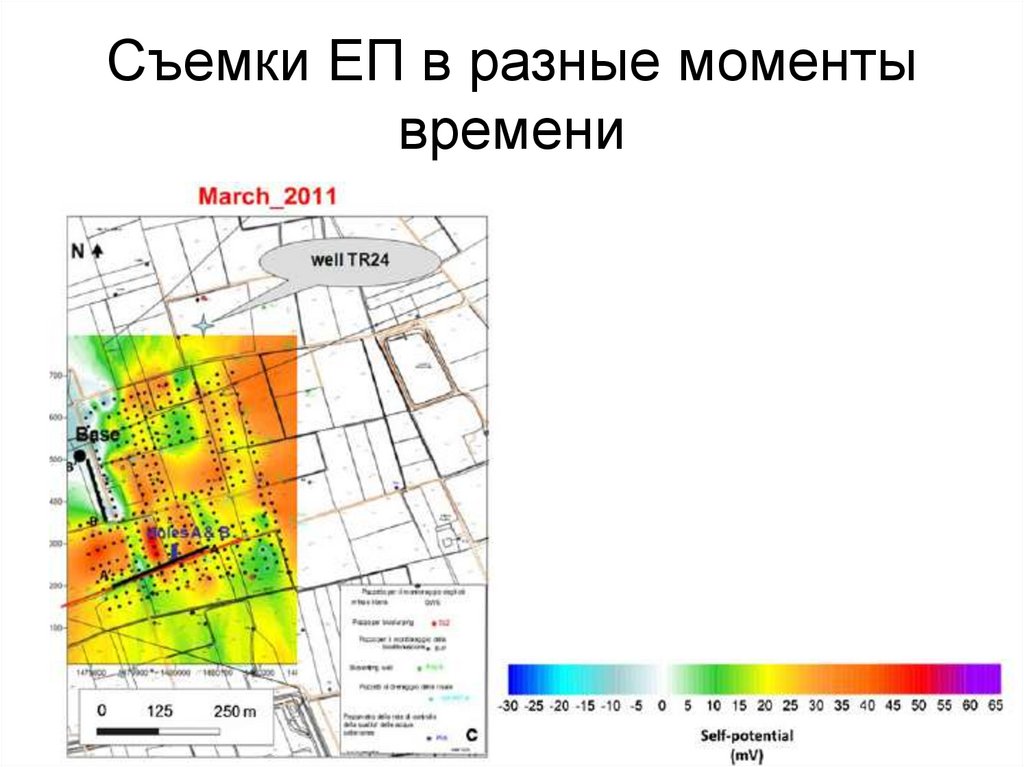
Si
H
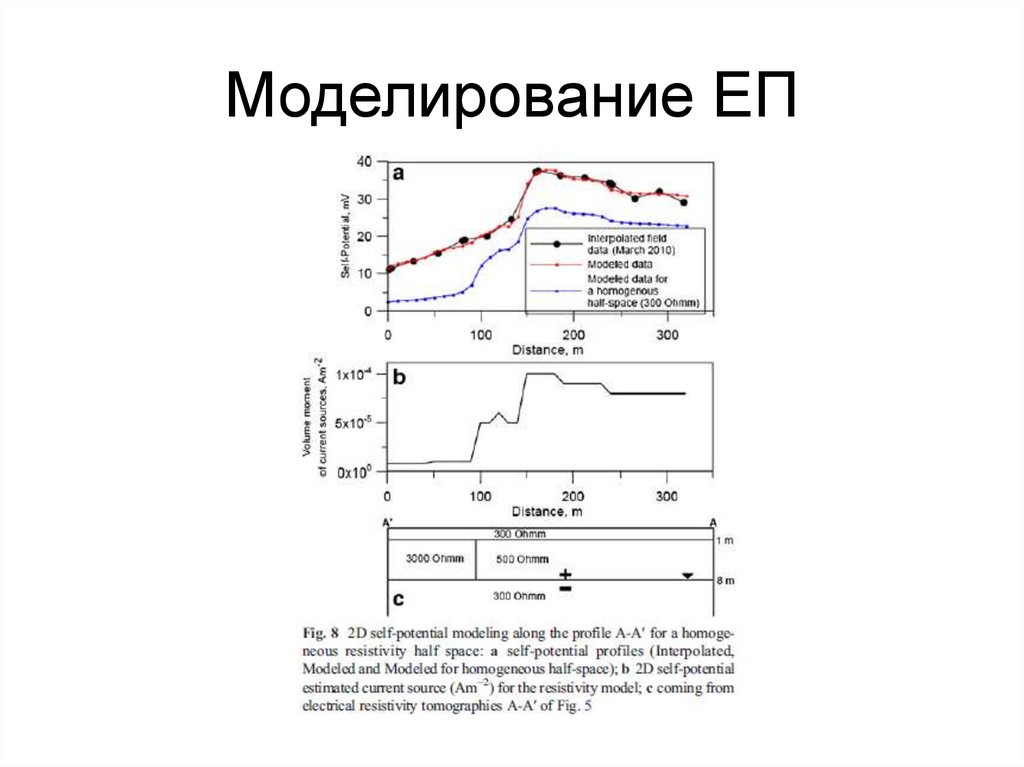
water
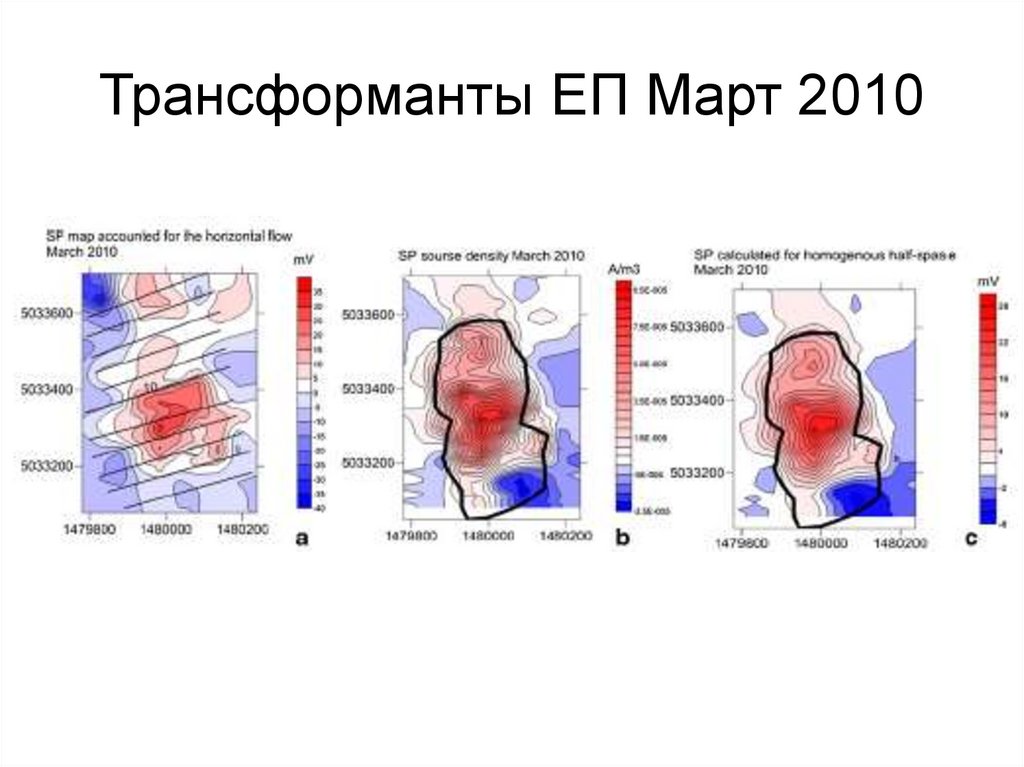
Электронейтральность: qт+qж=0

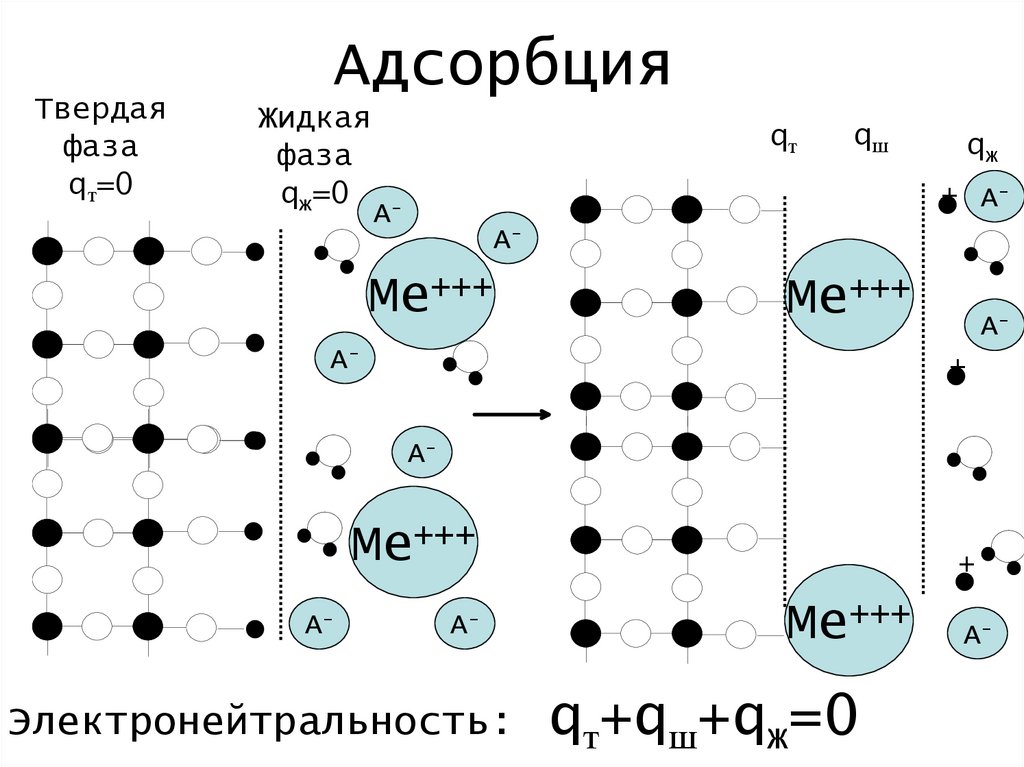
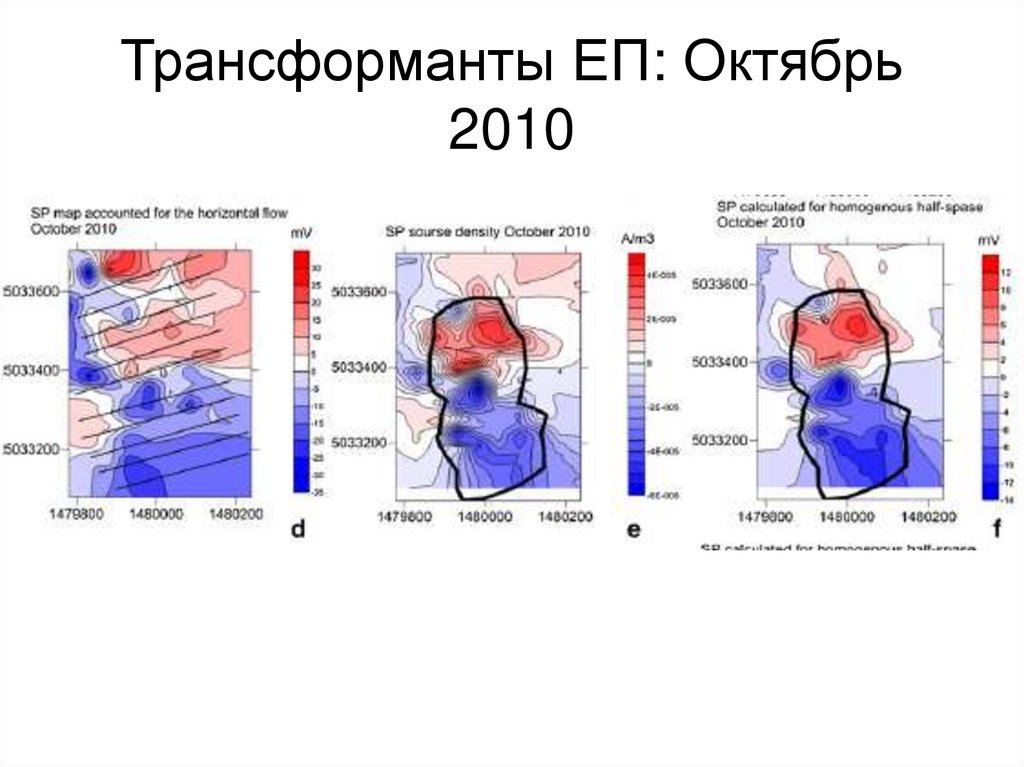
21.

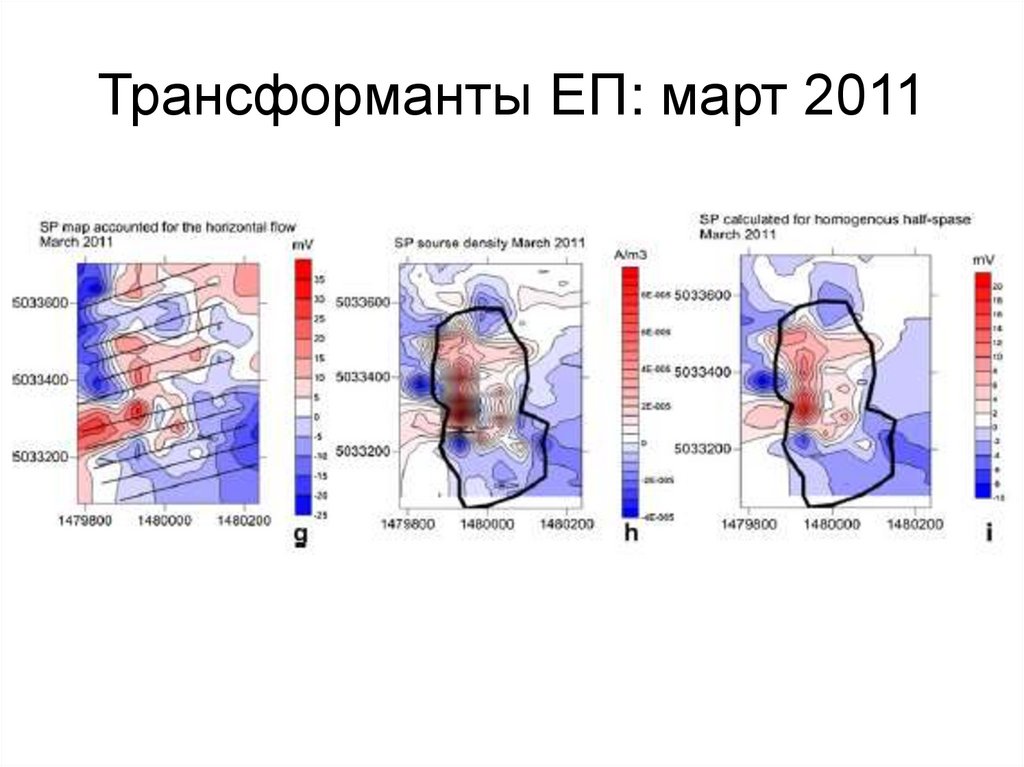
Твердая
фаза
qт=0
Адсорбция
Жидкая
фаза
qж=0 -
qт
qш
qж
+ A-
A
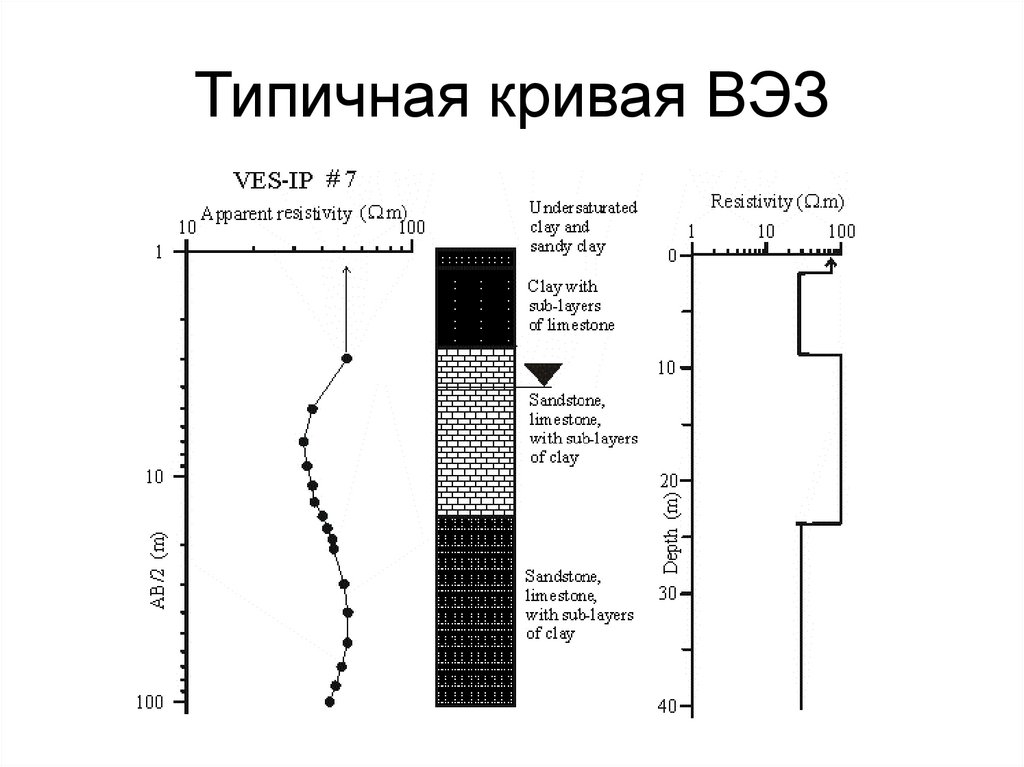
A-
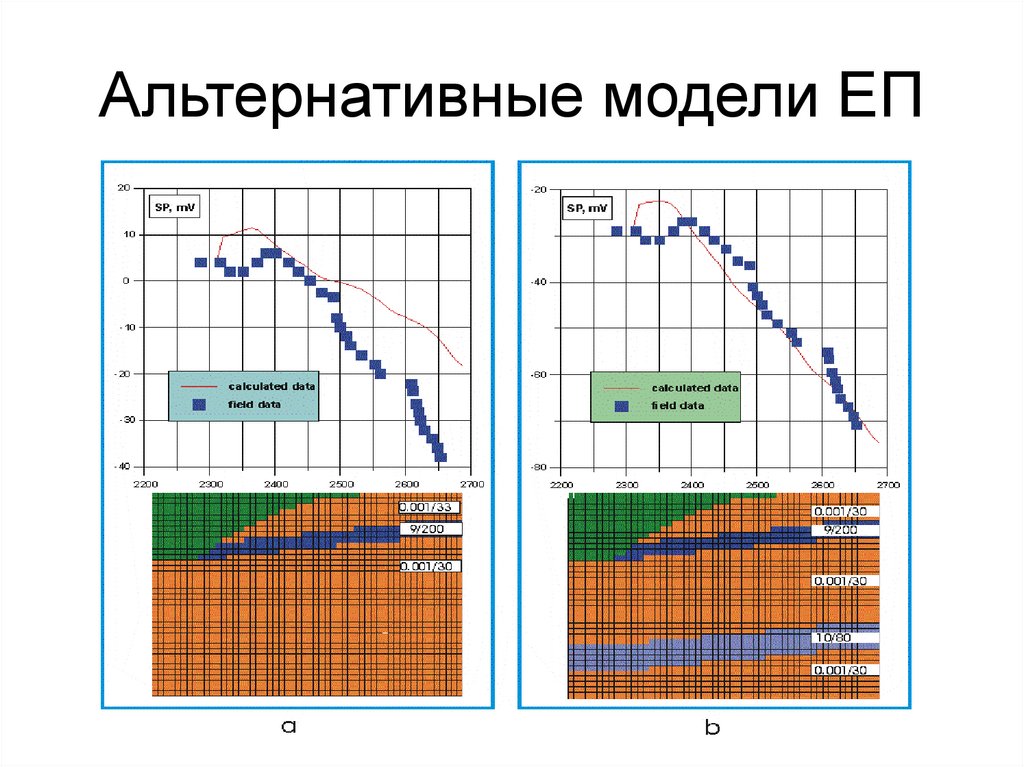
Me+++
Me+++
A-
A+
A-
Me+++
A-
A-
Электронейтральность:
+
Me+++
qт+qш+qж=0
A-

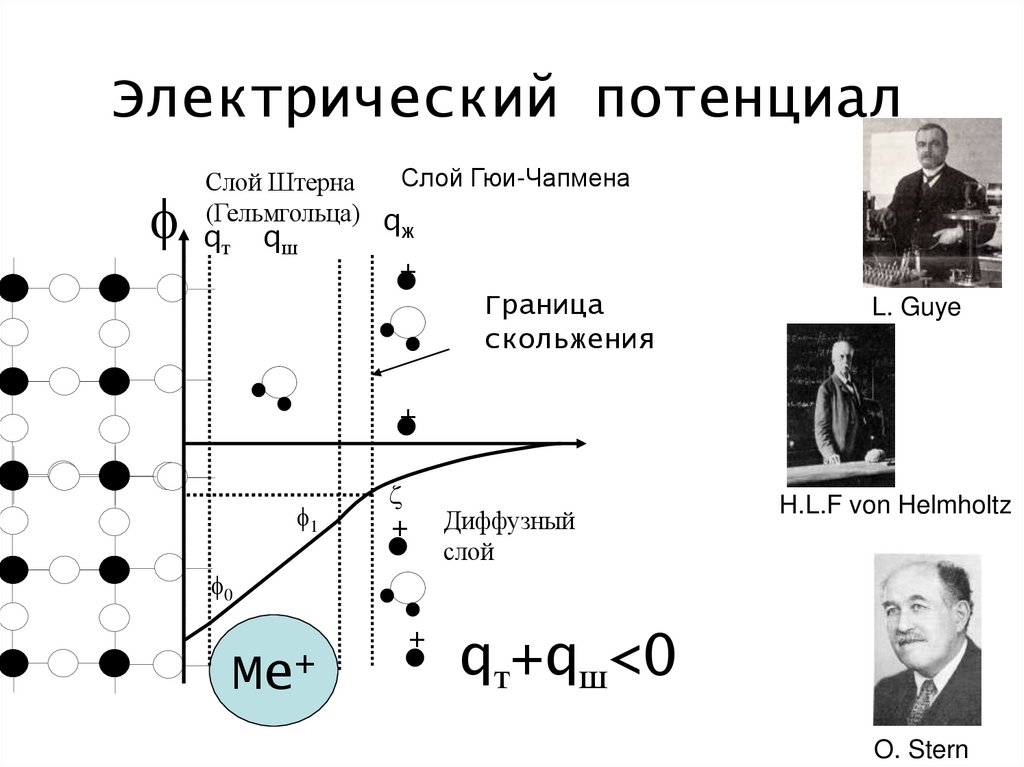
22.

Электрический потенциал
Слой Штерна
(Гельмгольца)
f q
qш
т
Слой Гюи-Чапмена
qж
+
Граница
скольжения
L. Guye
+
f1
z
+
Диффузный
слой
+
qт+qш<0
H.L.F von Helmholtz
f0
Me+
O. Stern

23.

Взаимосвязь потенциала и
концентрации в диффузном слое
Замечание: перемещение вещества
и перемещение заряда в
электрическом поле
jc s c f zF cCc f
Φc cCc f
(Aм-2 – поток заряда)
(Моль(м-2с-1) – поток вещества)
j zFΦ

24.

d D
D
dCc
dx
RT
zF
Закон Фика
Соотношение Эйнштейна
D – коэффициент диффузии, м2с-1;
R=8.31 Дж(0K моль)-1 – универсальная газовая
постоянная;
T – абсолютная температура (oK)
RT kbT
zF
ze

25.

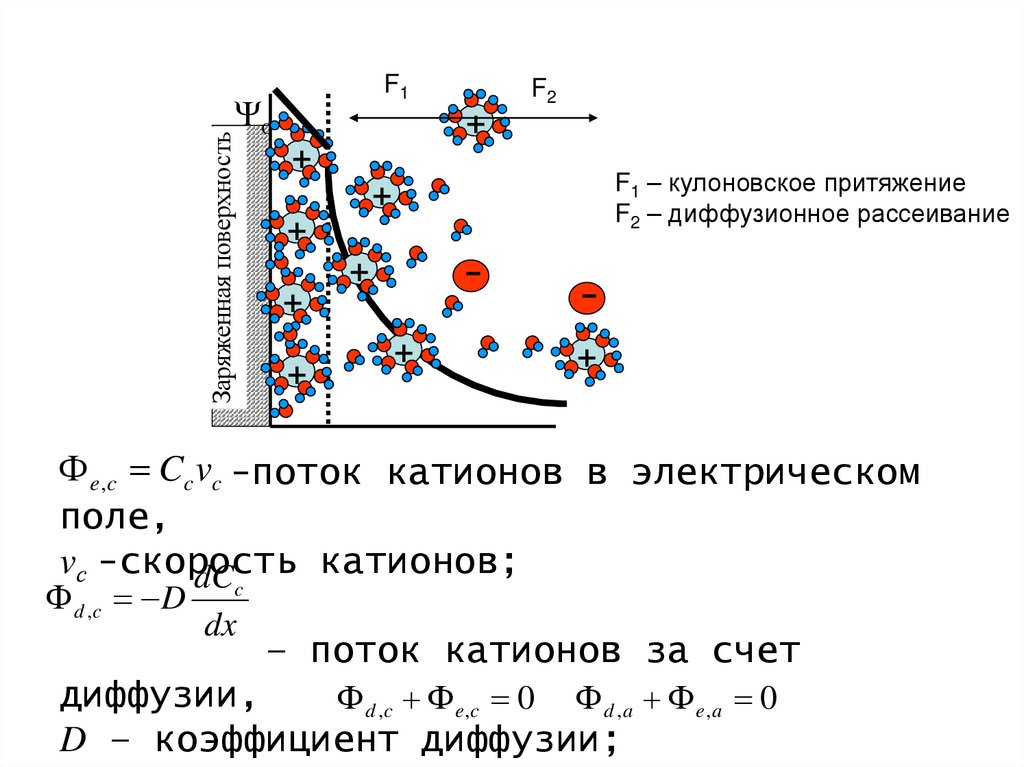
F1
Заряженная поверхность
Yo
F2
+
+
F1 – кулоновское притяжение
F2 – диффузионное рассеивание
+
+
+
+
+
+
+
e ,c Cc vc -поток катионов в электрическом
поле,
vс -скорость
катионов;
dC
d ,c D
c
dx
– поток катионов за счет
диффузии,
d ,c e ,c 0 d , a e , a 0
D – коэффициент диффузии;

26.

Плотность электрического тока
катионов за счет диффузии:
dCc
RT dCc
j zF
RT
zF
dx
dx
d
c
(*)
Плотность электрического тока
катионов в электрическом поле:
df
e
jc zF Cc
(**)
dx
Приравняем уравнения (*) и (**) :
1 dCc
zF df d ln Cc
zF df
zF
ln Cc
f const
;
;
dx
RT dx
RT
Cc dx
RT dx

27.

Граничные условия:
x , f 0, Cc C0;
C0 – концентрация в равновесном свободном растворе
(далеко от стенки поры)
Распределение Больцмана:
zFf
Cc C0 exp
RT
Аналогично:
zFf
Ca C0 exp
RT

28.

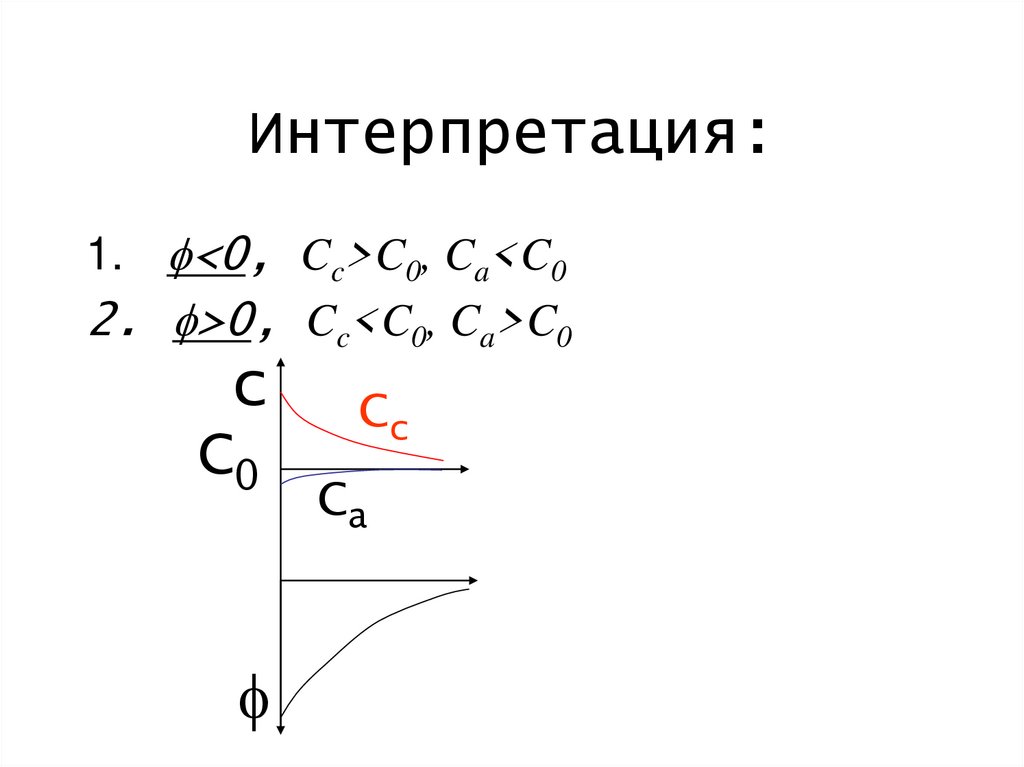
Интерпретация:
1. f<0, Cc>C0, Ca<C0
2. f>0, Cc<C0, Ca>C0
c
C0
f
Cc
Ca

29.

Интерпретация:
3.
zFf [Кл.В.Моль-1]=[Дж.Моль-1]
Электрическая энергия 1 моля
4.
.Моль-1]
[Дж
RT
Тепловая энергия 1 моля

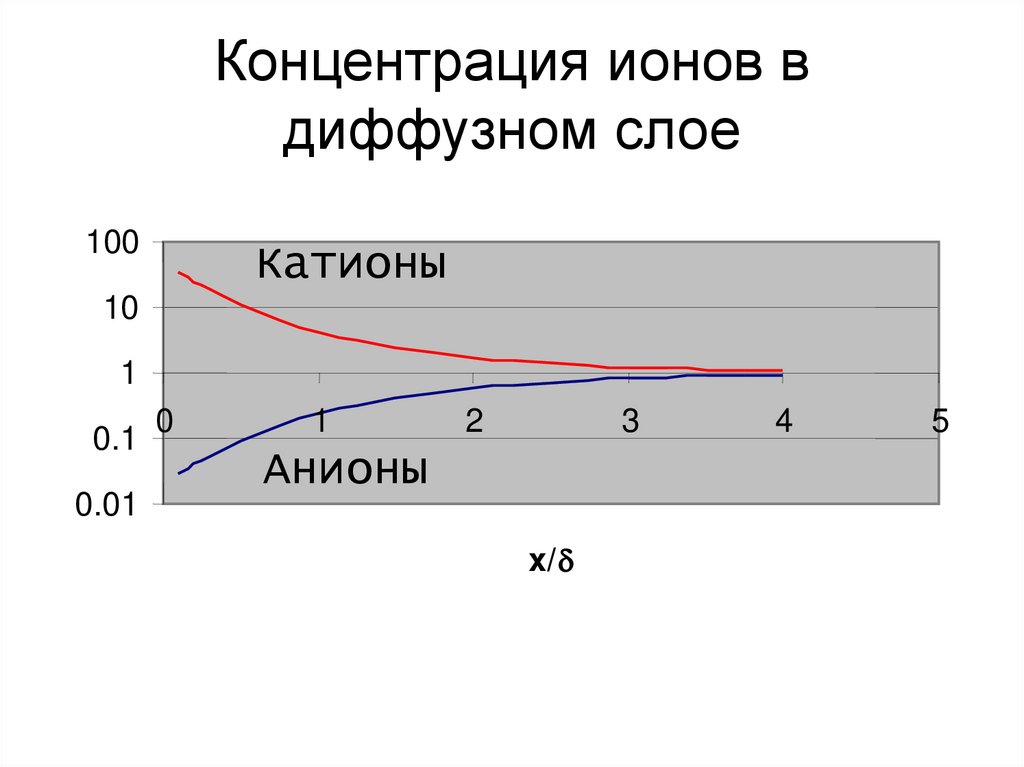
30. Концентрация ионов в диффузном слое

100
Катионы
10
1
0.1
0.01
0
1
2
3
Анионы
x/ d
4
5

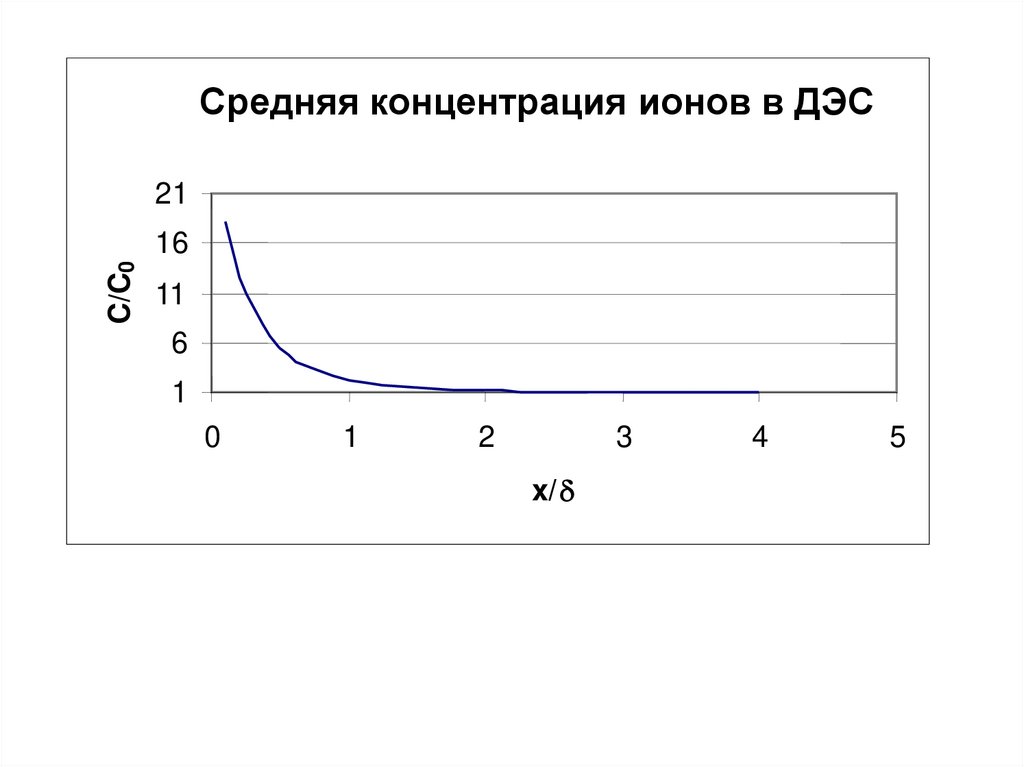
31.

Средняя концентрация ионов в ДЭС
21
C/C0
16
11
6
1
0
1
2
3
x/ d
4
5

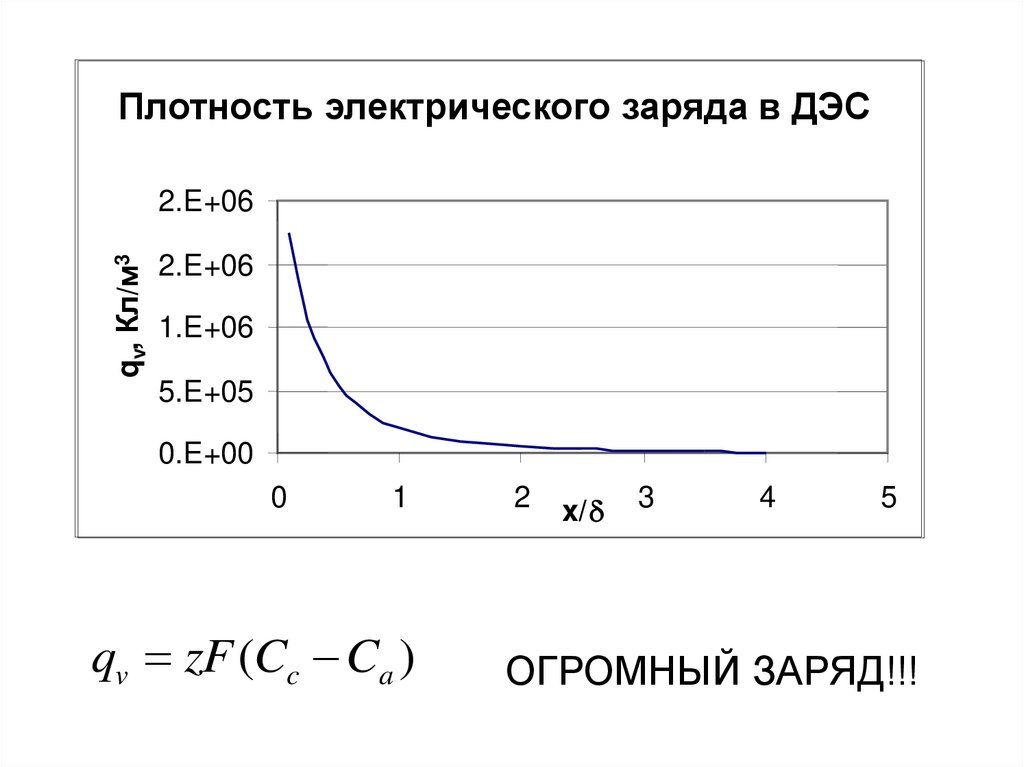
32.

Плотность электрического заряда в ДЭС
qv, Кл/м3
2.E+06
2.E+06
1.E+06
5.E+05
0.E+00
0
1
qv zF (Cc Ca )
2
x/ d
3
4
5
ОГРОМНЫЙ ЗАРЯД!!!

33.

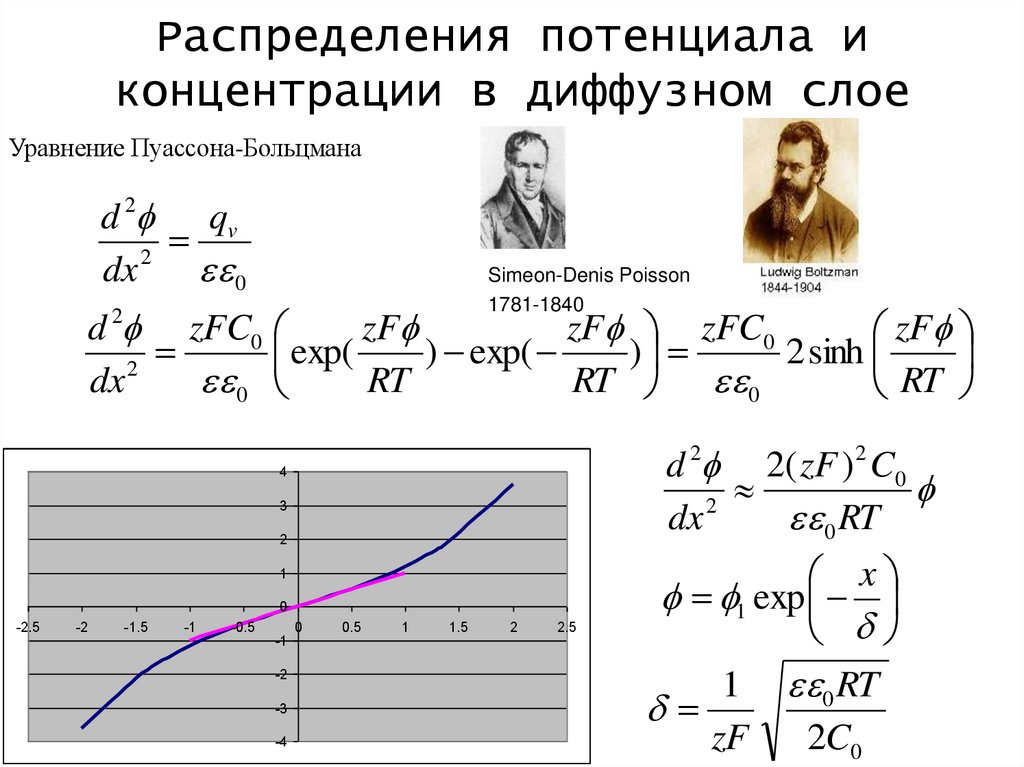
Распределения потенциала и
концентрации в диффузном слое
Уравнение Пуассона-Больцмана
d 2f qv
2
dx
0
Simeon-Denis Poisson
1781-1840
d 2f zFC0
zFf
zFf zFC0
zFf
) exp(
)
2 sinh
exp(
2
dx
0
RT
RT 0
RT
d 2f 2( zF ) 2 C0
f
2
dx
0 RT
4
3
2
1
0
-2.5
-2
-1.5
-1
-0.5
-1
-2
-3
-4
0
0.5
1
1.5
2
2.5
x
f f1 exp
d
1 0 RT
d
zF
2C0

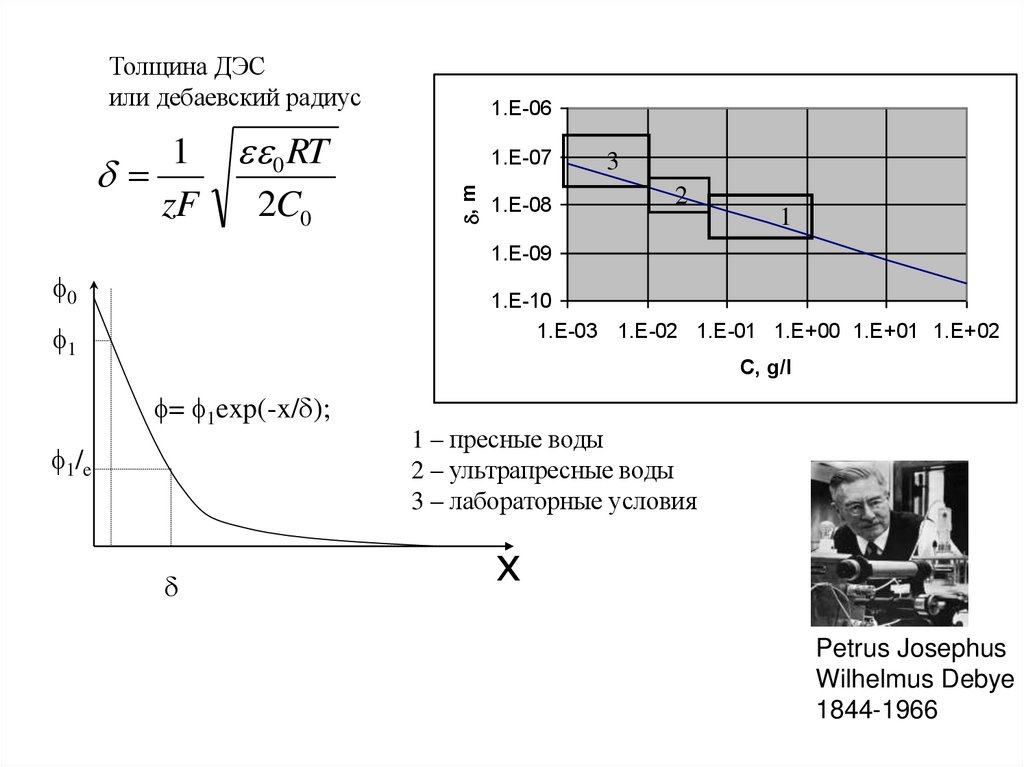
34.

Толщина ДЭС
или дебаевский радиус
0 RT
2C0
1.E-07
d, m
1
d
zF
1.E-06
1.E-08
3
2
1
1.E-09
f0
1.E-10
1.E-03 1.E-02 1.E-01 1.E+00 1.E+01 1.E+02
f1
C, g/l
f= f1exp(-x/d);
f1/e
d
1 – пресные воды
2 – ультрапресные воды
3 – лабораторные условия
x
Petrus Josephus
Wilhelmus Debye
1844-1966

35.

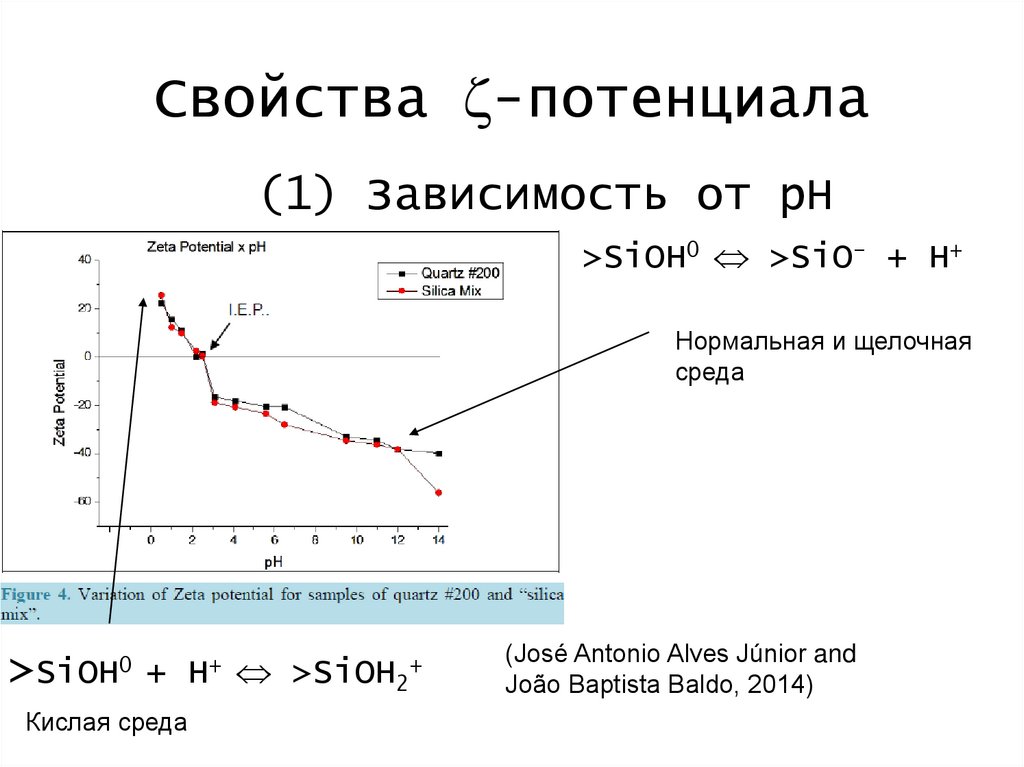
Свойства z-потенциала
(1) Зависимость от pH
>SiOH0 >SiO- + H+
Нормальная и щелочная
среда
>SiOH0 + H+ >SiOH2+
Кислая среда
(José Antonio Alves Júnior and
João Baptista Baldo, 2014)

36.

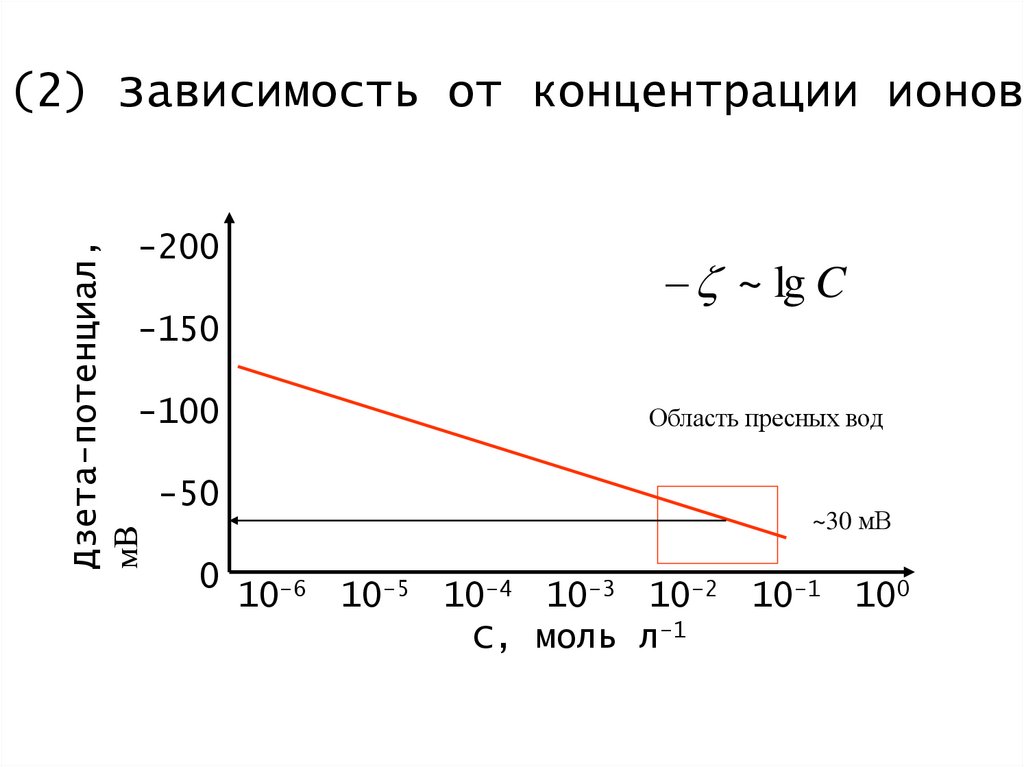
(2) Зависимость от концентрации ионов
Дзета-потенциал,
мВ
-200
z ~ lg C
-150
-100
-50
0
Область пресных вод
~30 мВ
10-6 10-5 10-4 10-3 10-2 10-1 100
С, моль л-1

37.

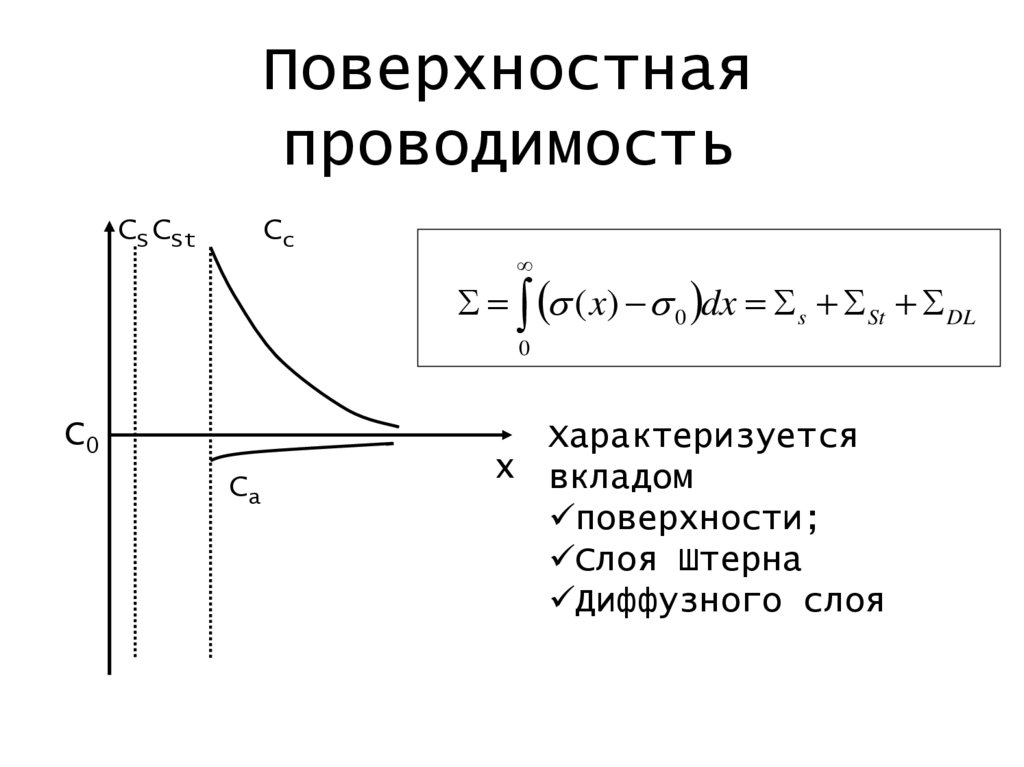
Поверхностная
проводимость
CS CSt
Cc
s ( x) s 0 dx s St DL
0
C0
Ca
Характеризуется
x вкладом
поверхности;
Слоя Штерна
Диффузного слоя

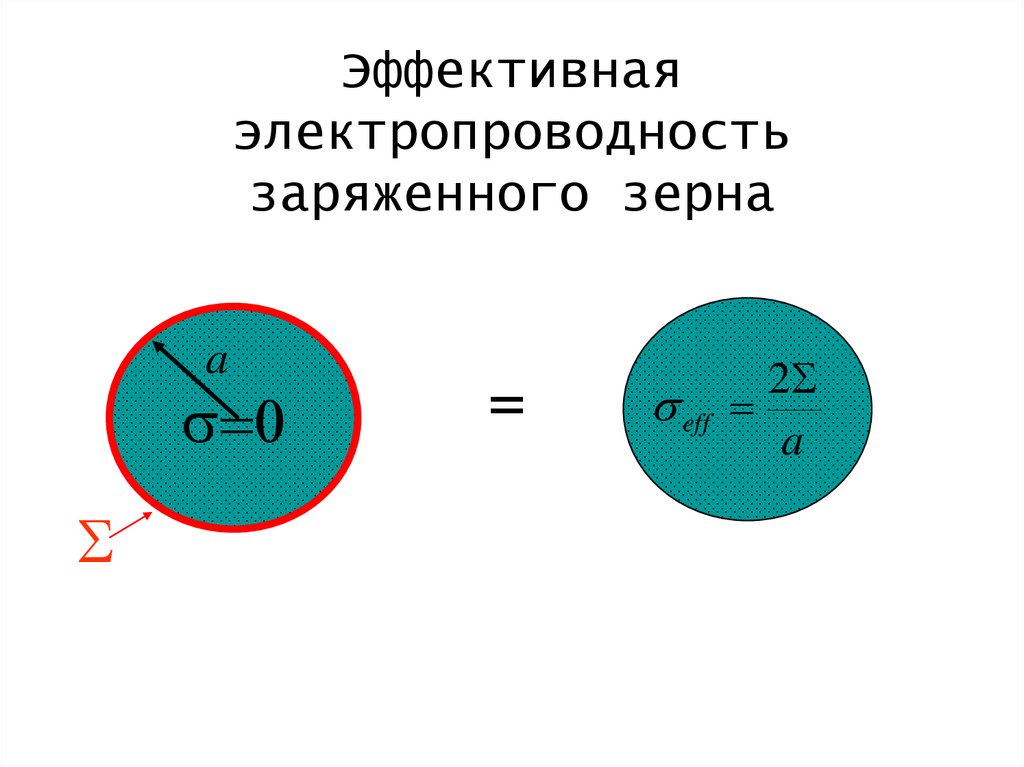
38.

Эффективная
электропроводность
заряженного зерна
a
s 0
=
2
s eff
a

39. 3. Электрокинетические явления

40.

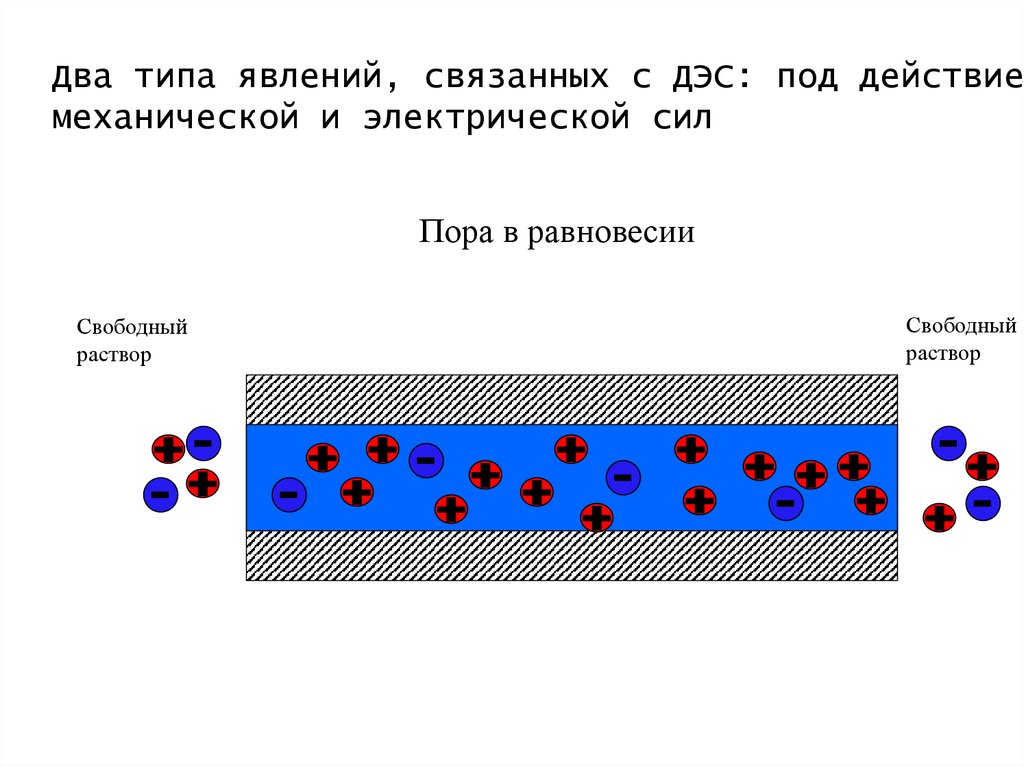
Два типа явлений, связанных с ДЭС: под действием
механической и электрической сил
Пора в равновесии
Свободный
раствор
Свободный
раствор

41.

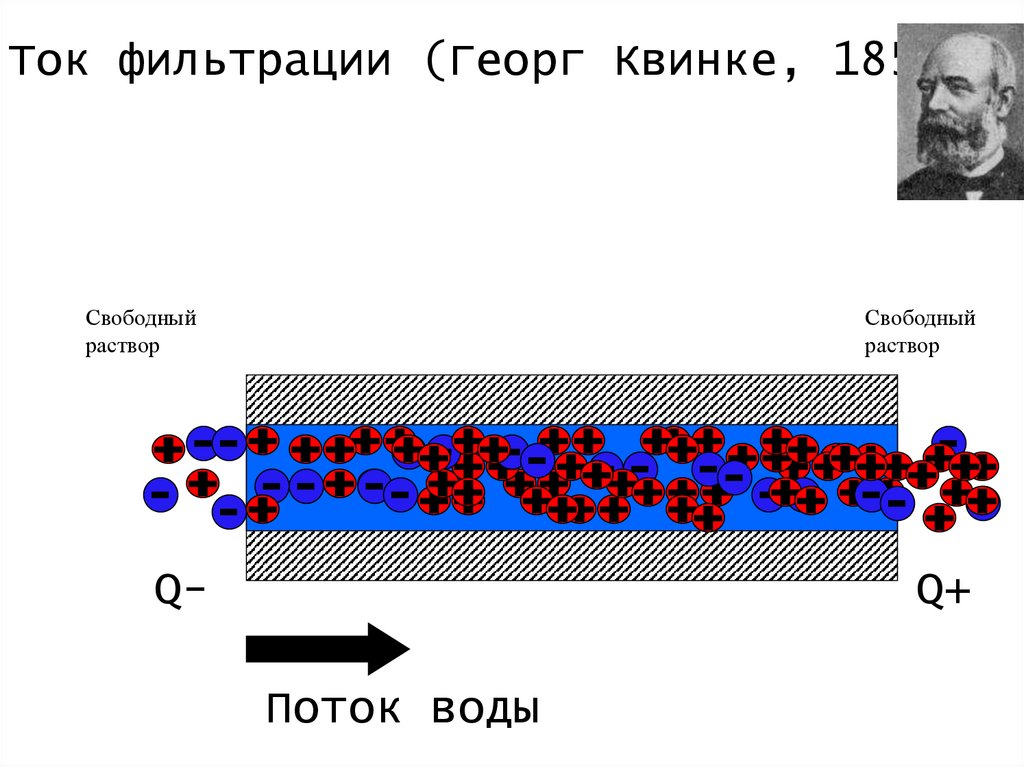
Ток фильтрации (Георг Квинке, 1859)
Свободный
раствор
Свободный
раствор
Q-
Q+
Поток воды

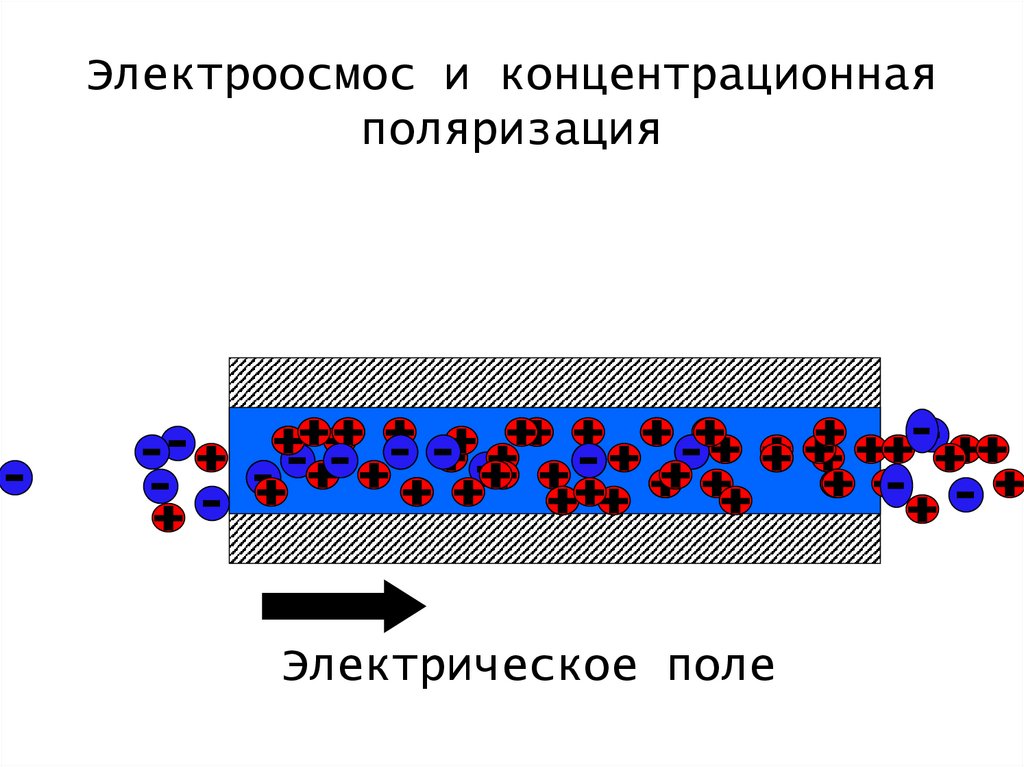
42.

Электроосмос и концентрационная
поляризация
Электрическое поле

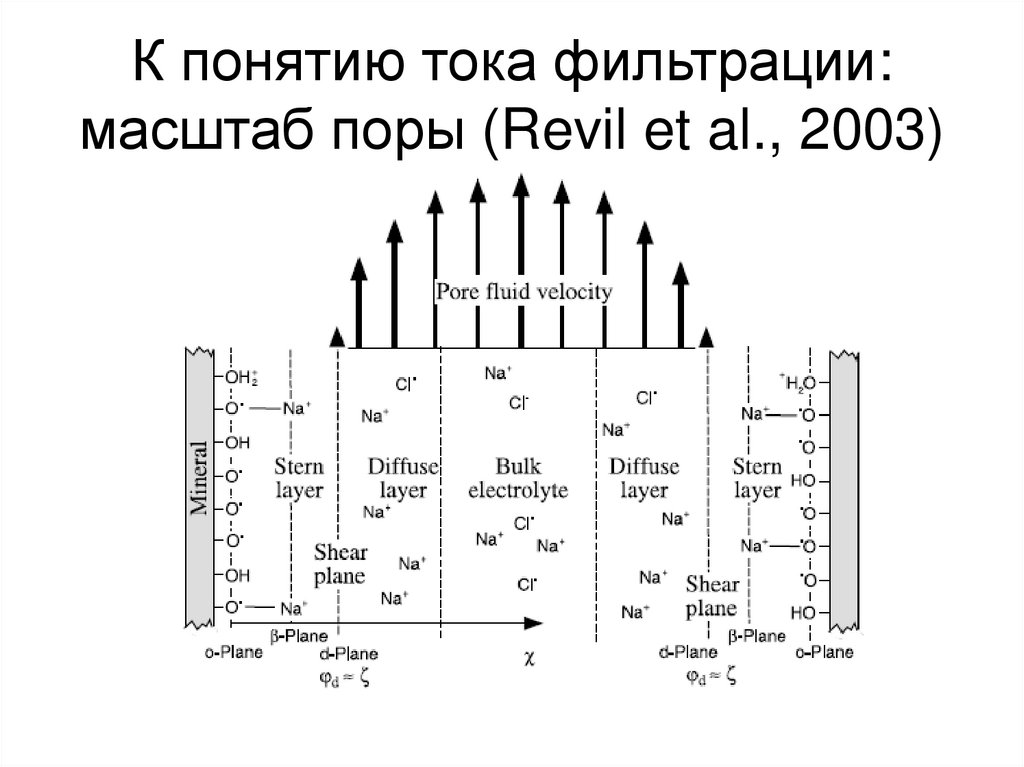
43. К понятию тока фильтрации: масштаб поры (Revil et al., 2003)

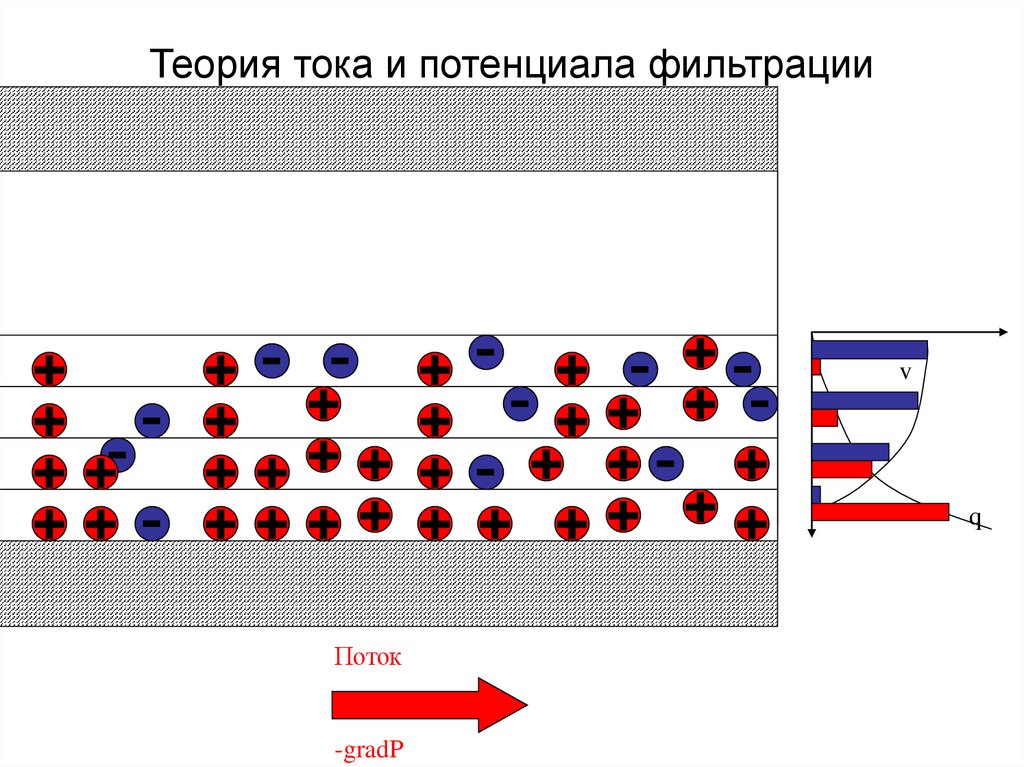
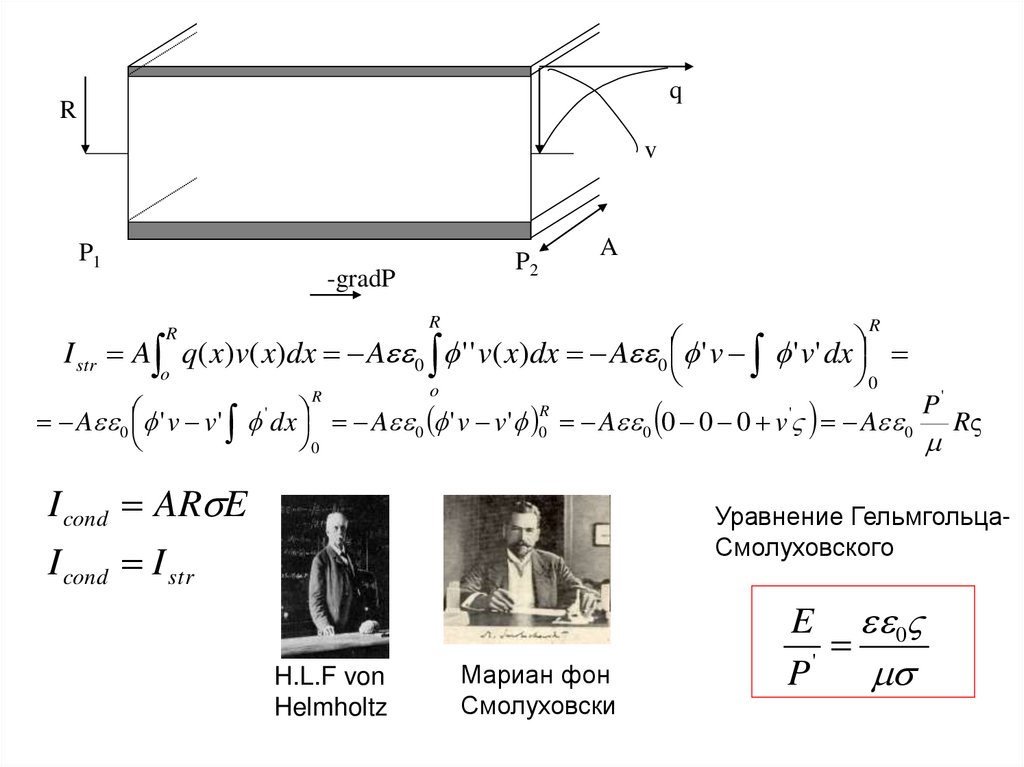
44. Теория тока и потенциала фильтрации

v
q
Поток
-gradP

45.

q
R
v
P1
P2
-gradP
A
R
R
I str A q( x)v( x)dx A 0 f ' ' v( x)dx A 0 f ' v f ' v' dx
o
0
o
R
R
P'
R
'
'
A 0 f ' v v' f dx A 0 f ' v v'f 0 A 0 0 0 0 v A 0 Rς
0
I cond ARsE
Уравнение ГельмгольцаСмолуховского
I cond I str
H.L.F von
Helmholtz
Мариан фон
Смолуховски
E 0
'
P
s

46. Первые оценки

E 0
8
2
.
12
10
r
'
P
s
0 =8.85 .10-12 Ф/м;
=80
z~0.03 В;
=10-3Па.с;
h[m] 104Па
E 0
0.21 r
'
H
s
мВ/м
В/Па

47.

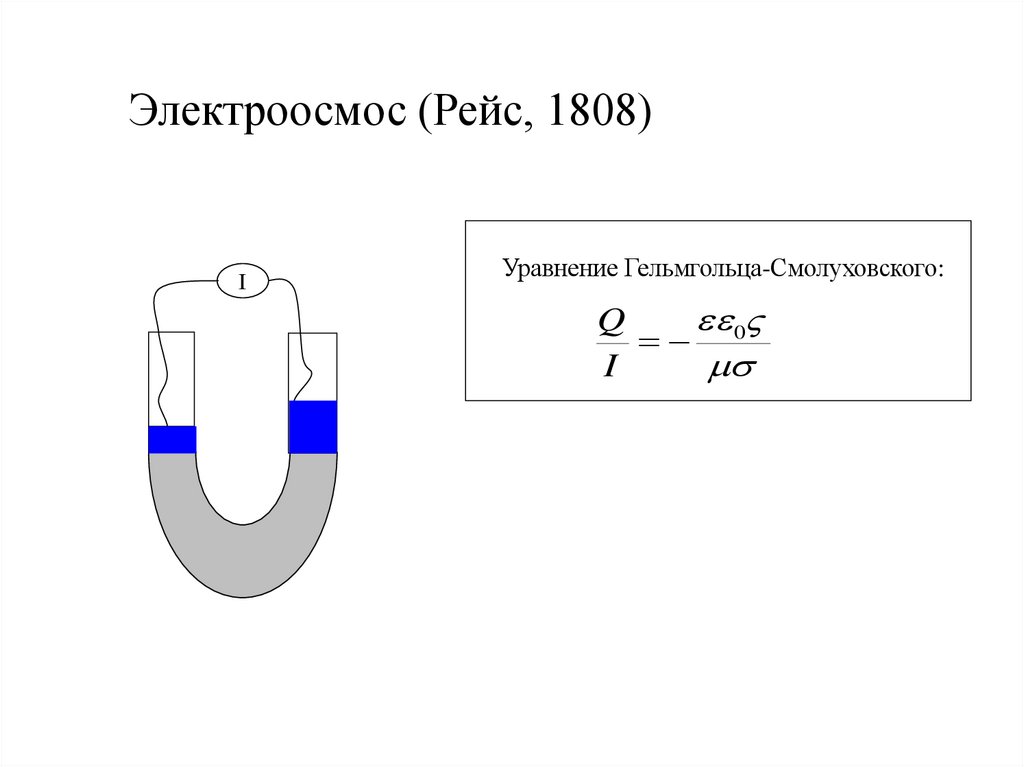
Электроосмос (Рейс, 1808)
I
Уравнение Гельмгольца-Смолуховского:
Q
0
I
s

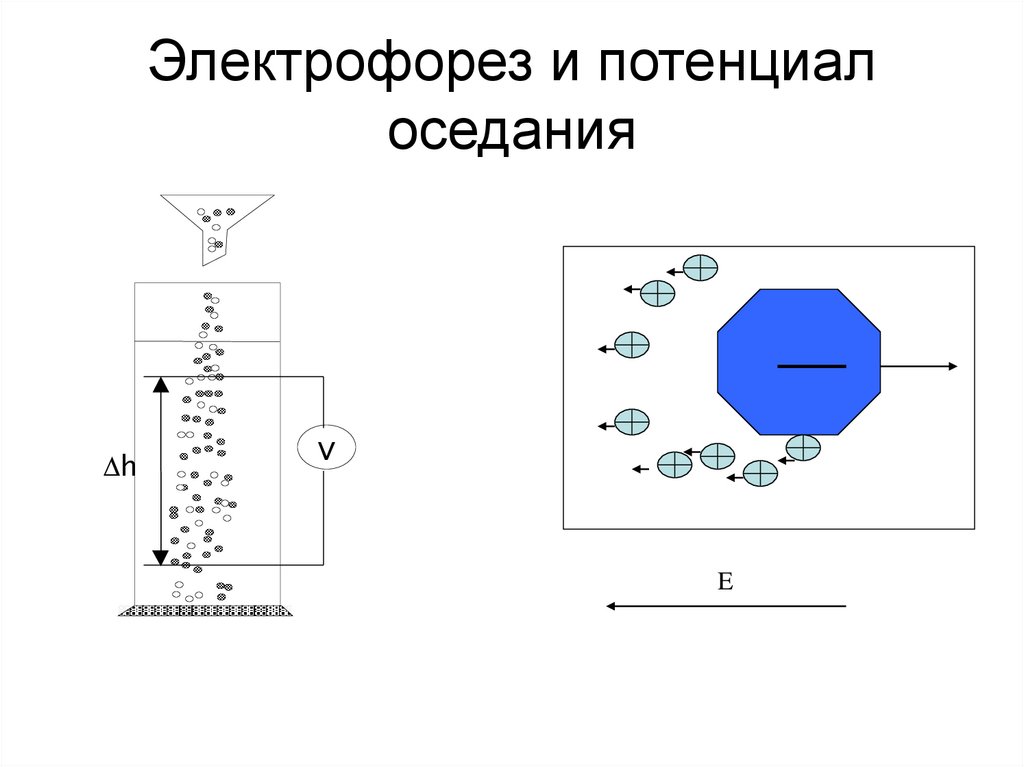
48. Электрофорез и потенциал оседания

Dh
V
E

49. Потоки и силы

j
u
s
l U
k
p
l
j sE l p
u lE
k
p
Электропроводность + ток фильтрации
Течение Дарси + электроосмос

50. 4. Вычисление поля фильтрационной природы

j sE l p sE lrg h sE L h
0z
l
0 rgz
L
Коэффициент тока фильтрации
Модифицированный коэффициент
тока
фильтрации

51.

L
j s E h
s
C
L
s
Коэффициент потенциала фильтрации
j s E C h
j 0
Уравнение неразрывности
s U L h
Уравнение Пуассона для
U

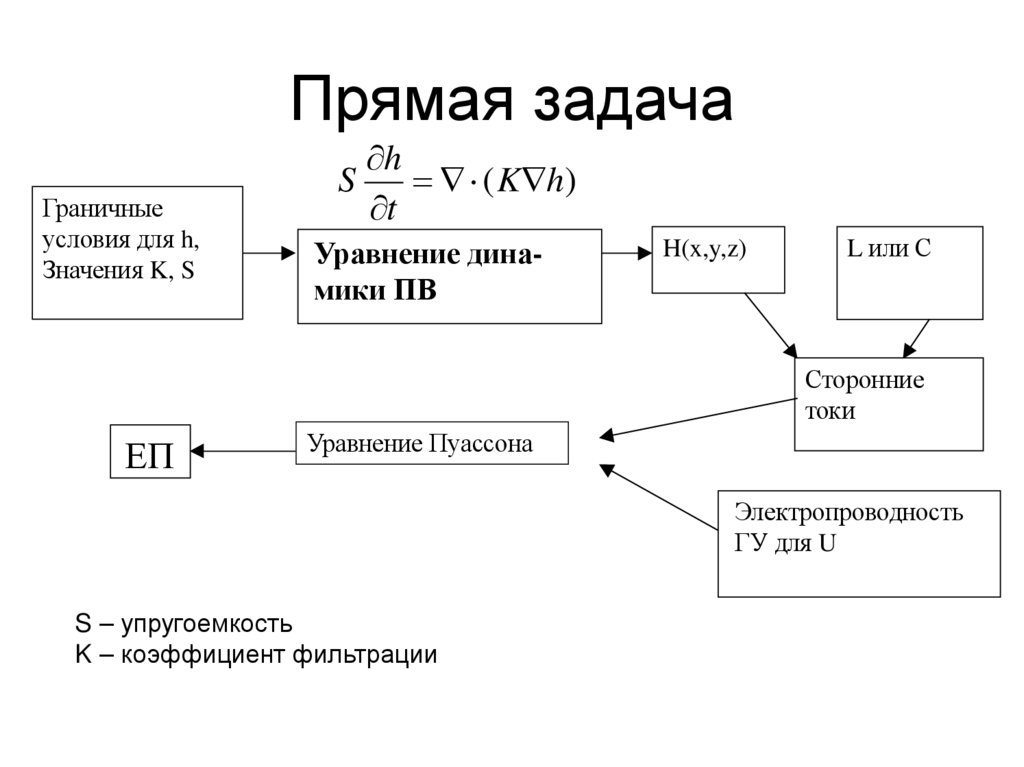
52. Прямая задача

Граничные
условия для h,
Значения K, S
h
S
( K h )
t
Уравнение динамики ПВ
H(x,y,z)
L или С
Сторонние
токи
ЕП
Уравнение Пуассона
Электропроводность
ГУ для U
S – упругоемкость
K – коэффициент фильтрации

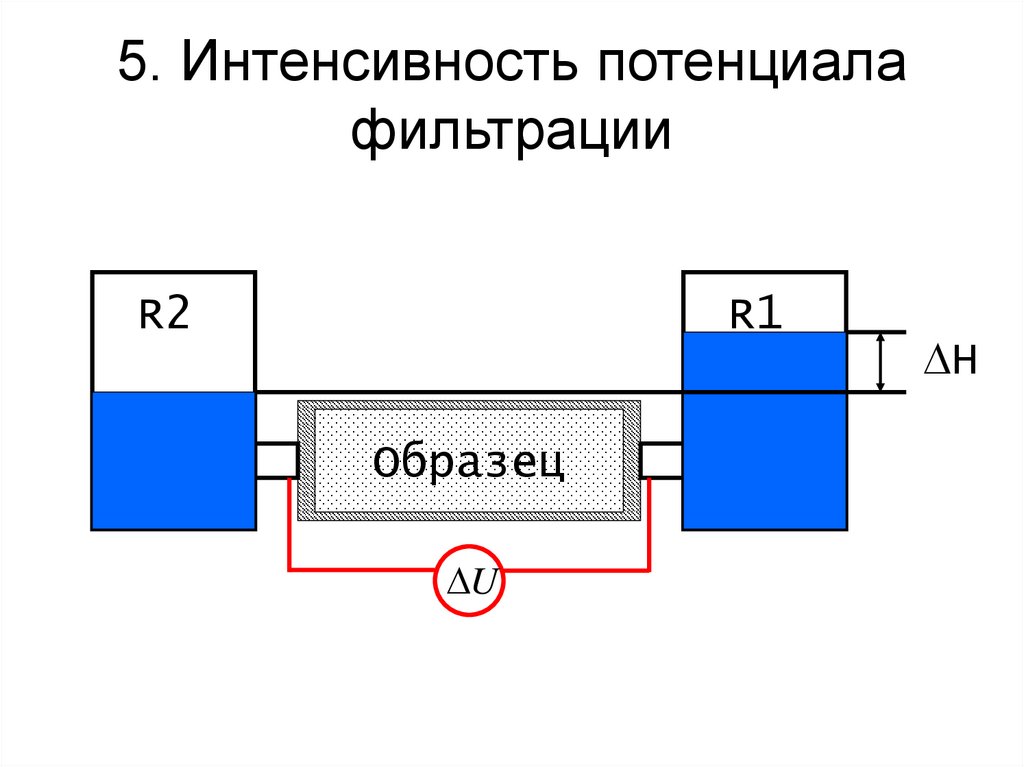
53. 5. Интенсивность потенциала фильтрации

R2
R1
Образец
DU
DH

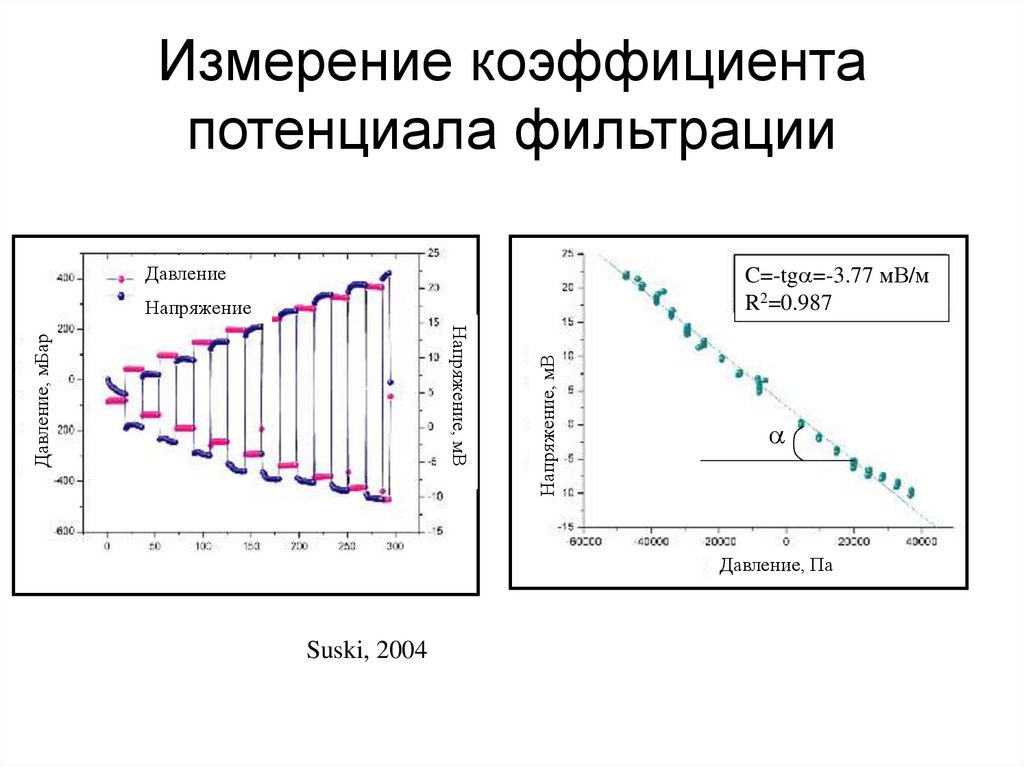
54. Измерение коэффициента потенциала фильтрации

Давление
C=-tga=-3.77 мВ/м
R2=0.987
Давление, мБар
Напряжение, мВ
Напряжение, мВ
Напряжение
a
Давление, Па
Suski, 2004

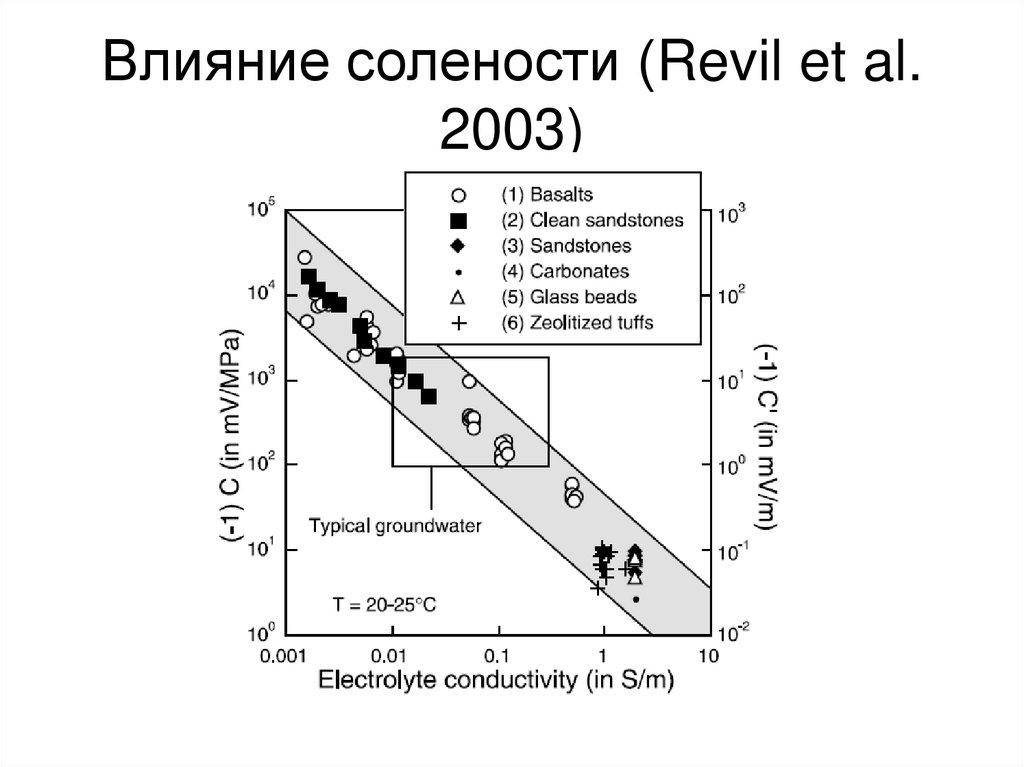
55. Влияние солености (Revil et al. 2003)

56. Влияние текстуры (глинистости)

0z
0z
C
Fs s
s В
s В s S
Породы с высоким
содержанием глины
Где
s В s S
“Чистые” породы
F – параметр пористости,
s В – электропроводность воды,
s s – поверхностная проводимость,
r В - плотность воды
(Revil et al., 2003)

57. Альтернативная формулировка (Revil and Leroy, 2004, Bolève et al., 2007)

jСТ sE - QV u
где
Q V эффективный избыточный заряд в диффузной части двойного слоя
С учетом закона Дарси:
u K h
QV K
L QV K
C
s

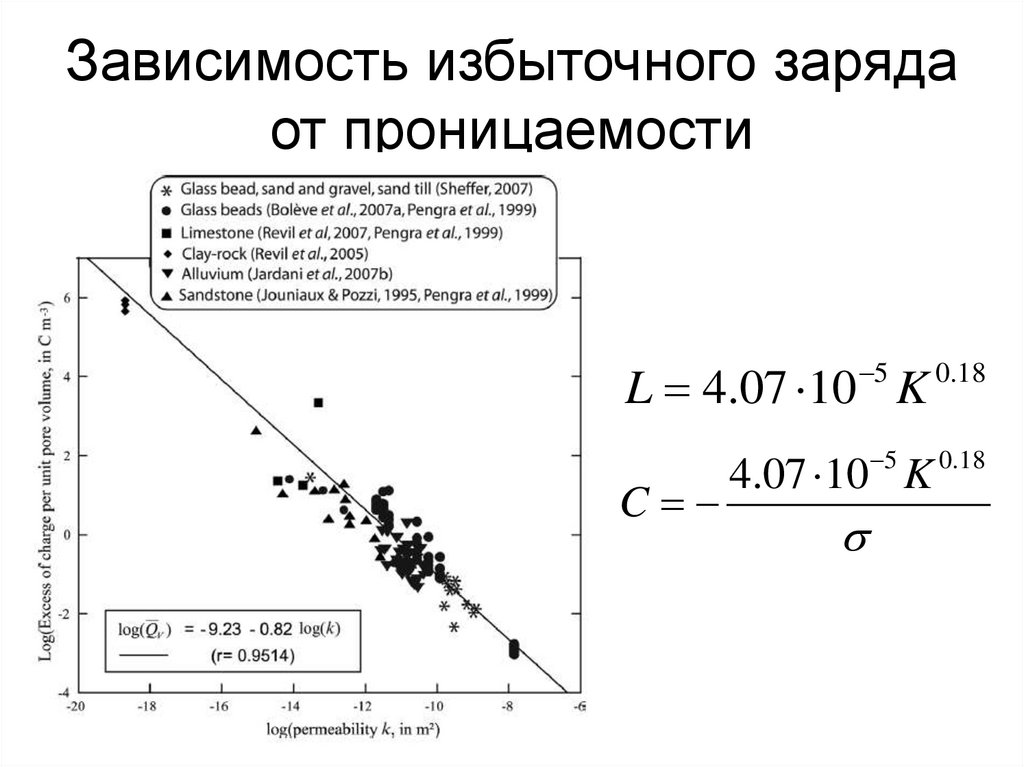
58. Зависимость избыточного заряда от проницаемости

L 4.07 10 5 K 0.18
C
4.07 10 5 K 0.18
s

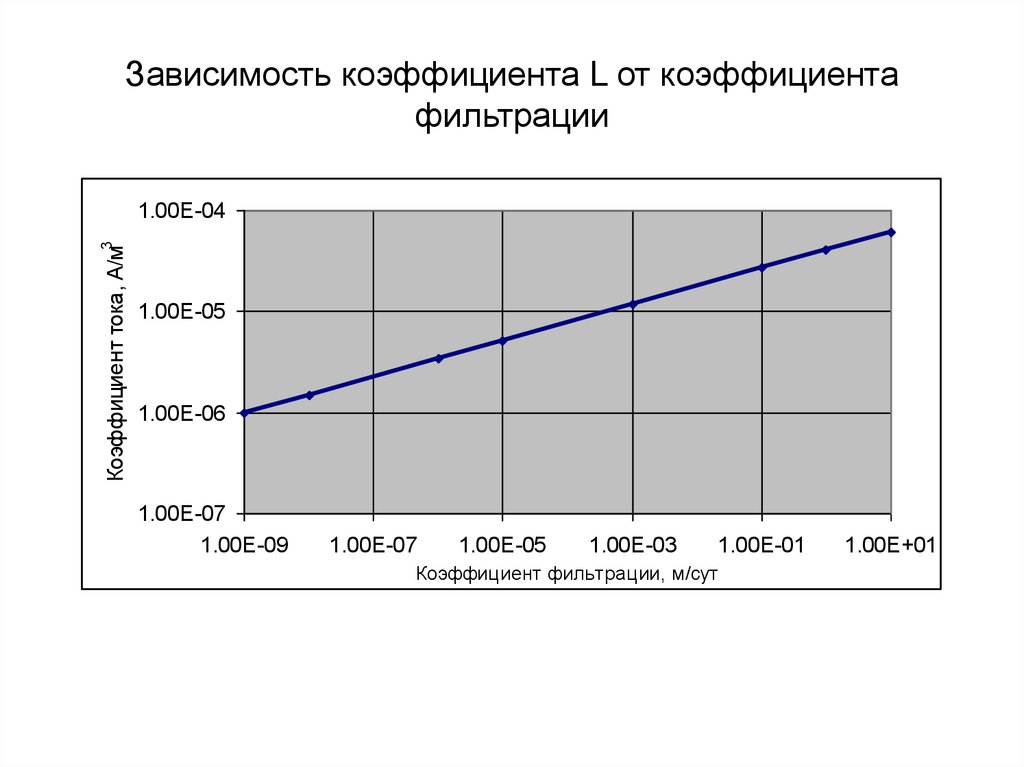
59. Зависимость коэффициента L от коэффициента фильтрации

Коэффициент тока, А/м3
1.00E-04
1.00E-05
1.00E-06
1.00E-07
1.00E-09
1.00E-07
1.00E-05
1.00E-03
1.00E-01
Коэффициент фильтрации, м/сут
1.00E+01

60. 6. Где локализованы источники электрического поля?

j s U L h s U sC h
j 0
(Cs )
U C h
h ln s U
s
h
S
q ( K h )
t
2
2
S h
q
h
ln K h
K t
K
2
Cq CS h
K
U
C h ln(
) ln s U
K
K t
Cs
2

61.

Cq CS h
K
U
C h ln(
) ln s U
K
K t
Cs
2
1
2
3
4
1 – первичные источники, где вода входит (+) или выходит (-) из пористой
среды
2 – источники, связанные с нестационарным режимом течения
3 – вторичные источники гидродинамического типа, где поток пересекает
границы неоднородности по свойствам c, s, K
4 – вторичные источники электрического типа.

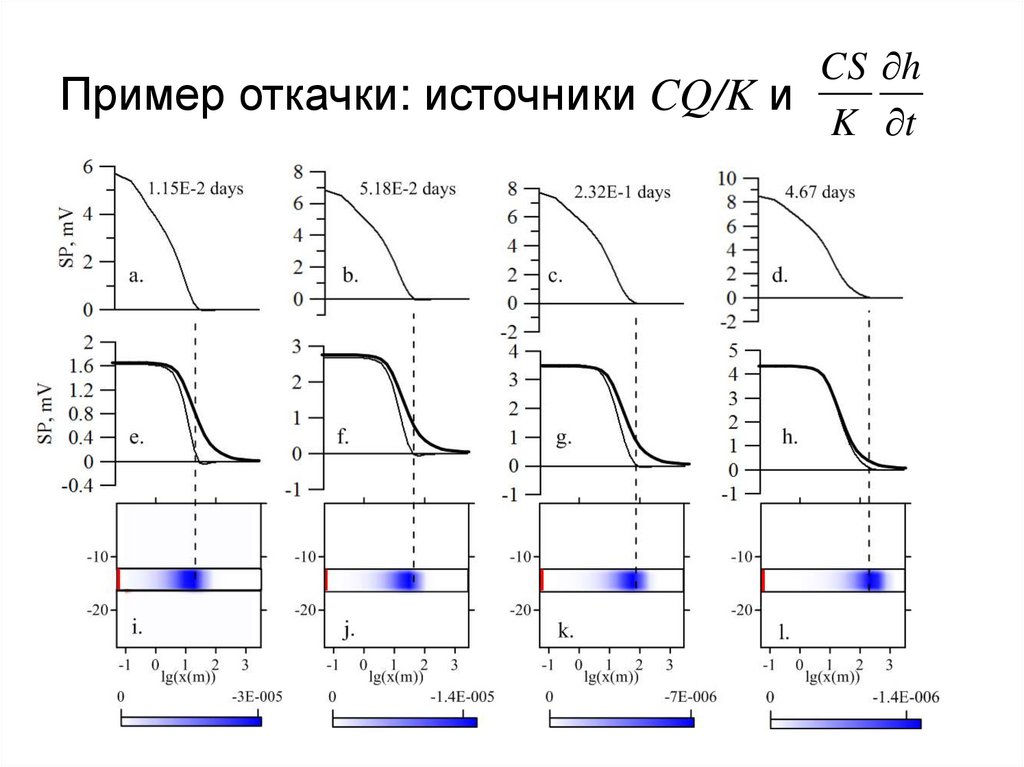
62. Пример откачки: источники CQ/K и

CS h
Пример откачки: источники CQ/K и
K t

63. 7. Мембранный и диффузионный потенциалы

Незаряженная мембрана
M
E

64. Уравнение для диффузионного потенциала

dC
dC
RT c
-плотность тока диффузии катионов
dx
dx
dC
jda RT a
-плотность тока диффузии анионов
dx
jdc zFD c
dU
dU
-плотность тока проводимости катионов
zF c C
dx
dx
dU
a
-плотность тока проводимости анионов
jпр
zF a C
dx
c
jпр
s c
с
a
jdc jda jпр
jпр
- условие равновесия
dU RT c a d ln C
dx
zF c a dx
dC
dU
c
a
RT ( )
zF ( )C
dx
dx
c
a
C c
t
C c C a
c
a
t c
a
a
Числа
переноса
RT c a C2
U 2 U1
t t ln
zF
C1

65. Диффузионный потенциал: оценки

RT
C2
c
U 2 U1
2t 1 ln
zF
C1
C2
U 2 U1 58 2t 1 lg
C1
c
Хлорид калия: tK=0.49
Хлорид натрия: tNa=0.40
r1 C2
r 2 C1
(мВ)
C2
DU 0.116 lg
C1
(мВ)
C2
DU 11.6 lg
C1
(мВ)
r1
DU 11.6 lg
r2

66. Мембранный потенциал (Revil et al., 1999)

RT
C2 2 RT c c C2
c
DU
2t 1 ln
T t ln
zF
C1
zF
C1
Для природных мембран:
t T 1
c
c
где Tc – макроскопическое число переноса в породе.
T c 1
Предельный случай идеальной мембраны:
C2
DU 58 lg
C1
мВ
t c 0.5

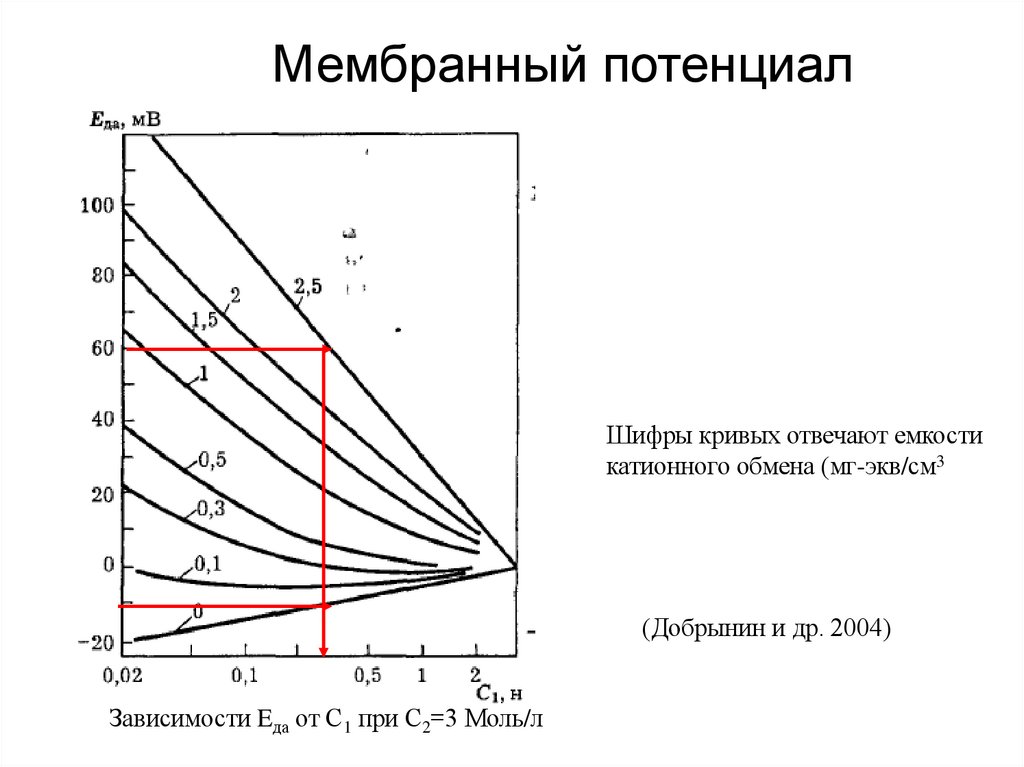
67. Мембранный потенциал

Шифры кривых отвечают емкости
катионного обмена (мг-экв/см3
(Добрынин и др. 2004)
Зависимости Eда от С1 при С2=3 Моль/л

68. 8. Методика полевых работ и интерпретации данных

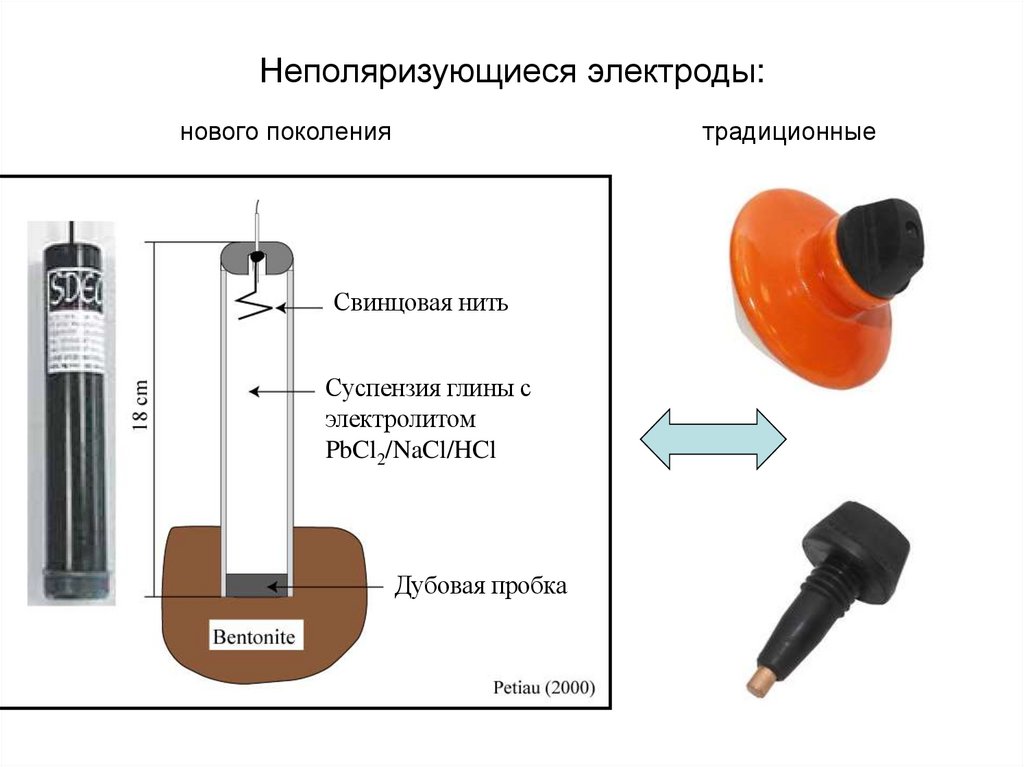
69. Неполяризующиеся электроды:

нового поколения
традиционные
Свинцовая нить
Суспензия глины с
электролитом
PbCl2/NaCl/HCl
Дубовая пробка

70.

71. Классическая методика работ

V
M
Установка градиента
N
V
Установка потенциала
M
N

72. Методика непрерывного наблюдения потенциала

M1 M2…
mV
Мультиметрмультиплексор
N

73.

Закачивающая
скважина
Пьезометр
Профиль электродов
Сеть наблюдений
Вольтметр Keithley,
подключенный к компьютеру
Подключение
электродов к
вольтметру

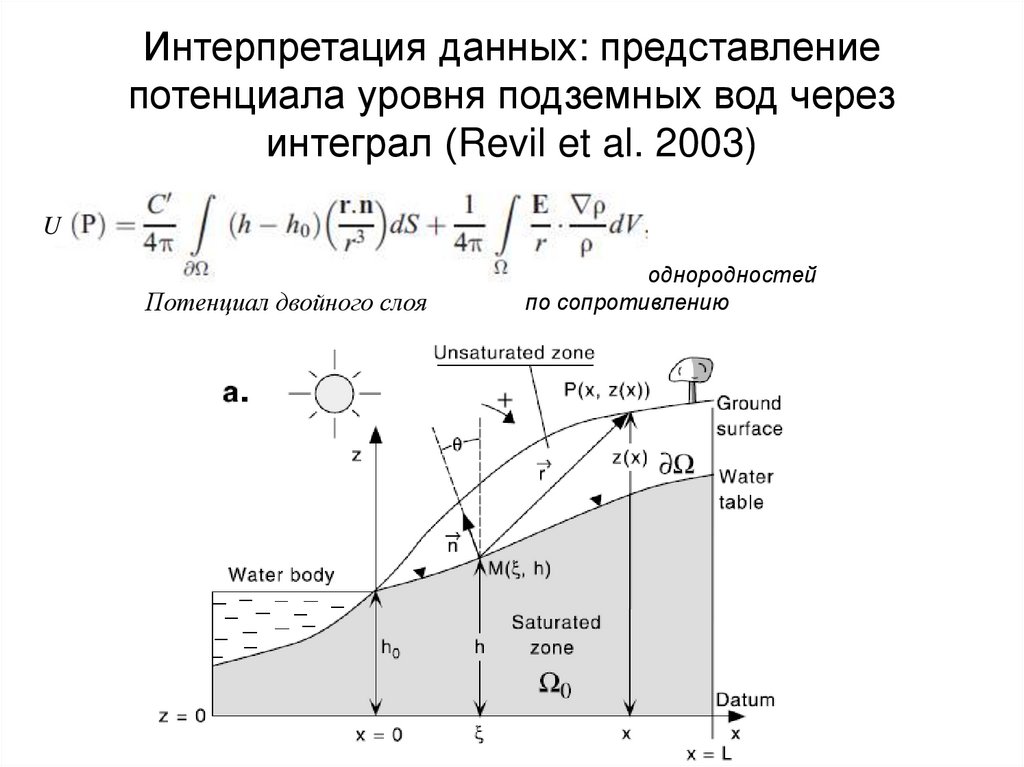
74. Интерпретация данных: представление потенциала уровня подземных вод через интеграл (Revil et al. 2003)

U
Потенциал двойного слоя
Влияние неоднородностей
по сопротивлению

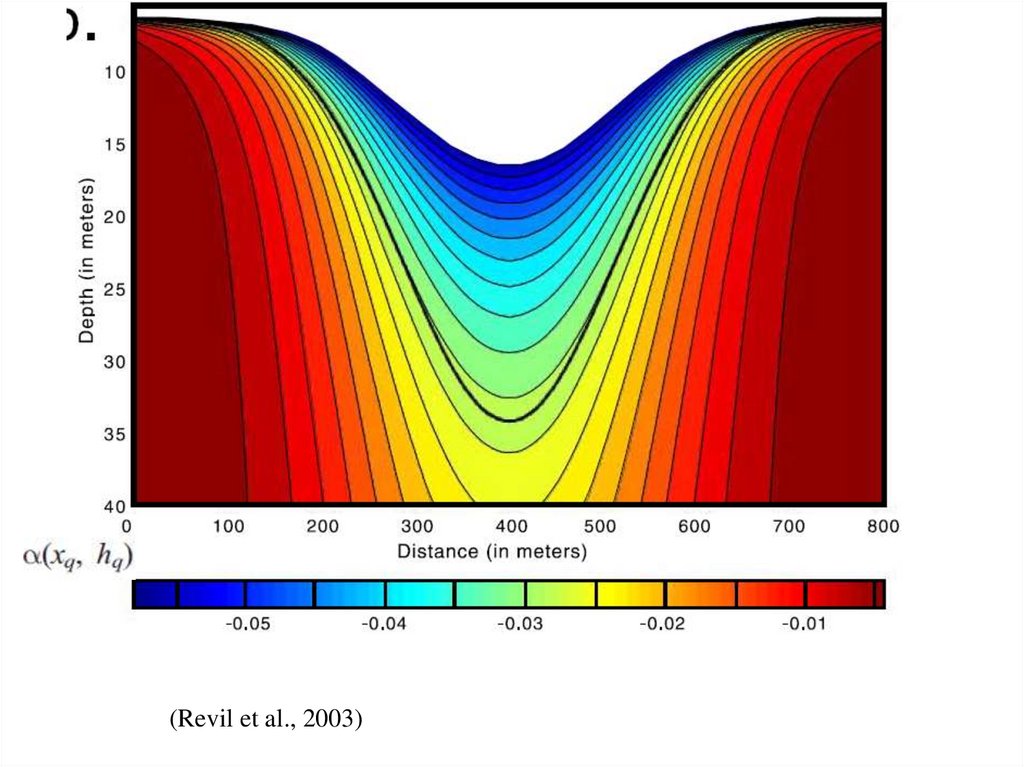
75. Решения

• Полуэмпирический подход U ( P) A(h h0 )
• Томографический подход деконволюция интеграла
C
rn
h h0 3 dS
U ( P)
4
r
с определением семейства поверхностей
h ( x, z )

76.

(Revil et al., 2003)

77. Решения

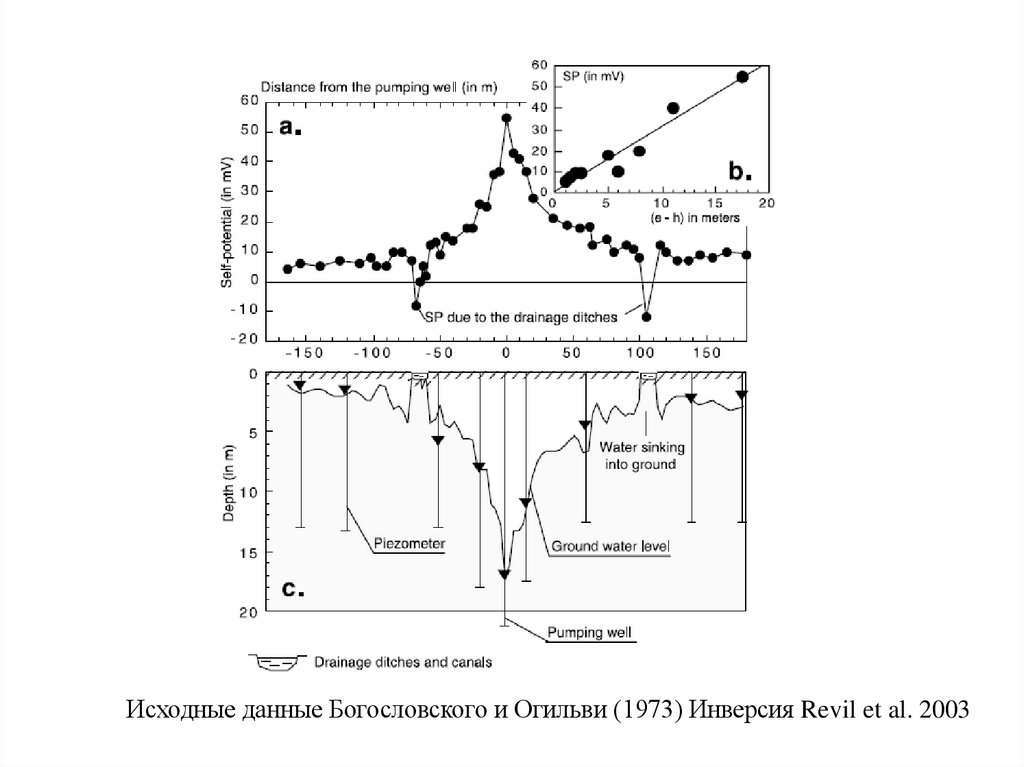
• Симплекс-алгоритм: минимизация
на основе метода наименьших квадратов

78.

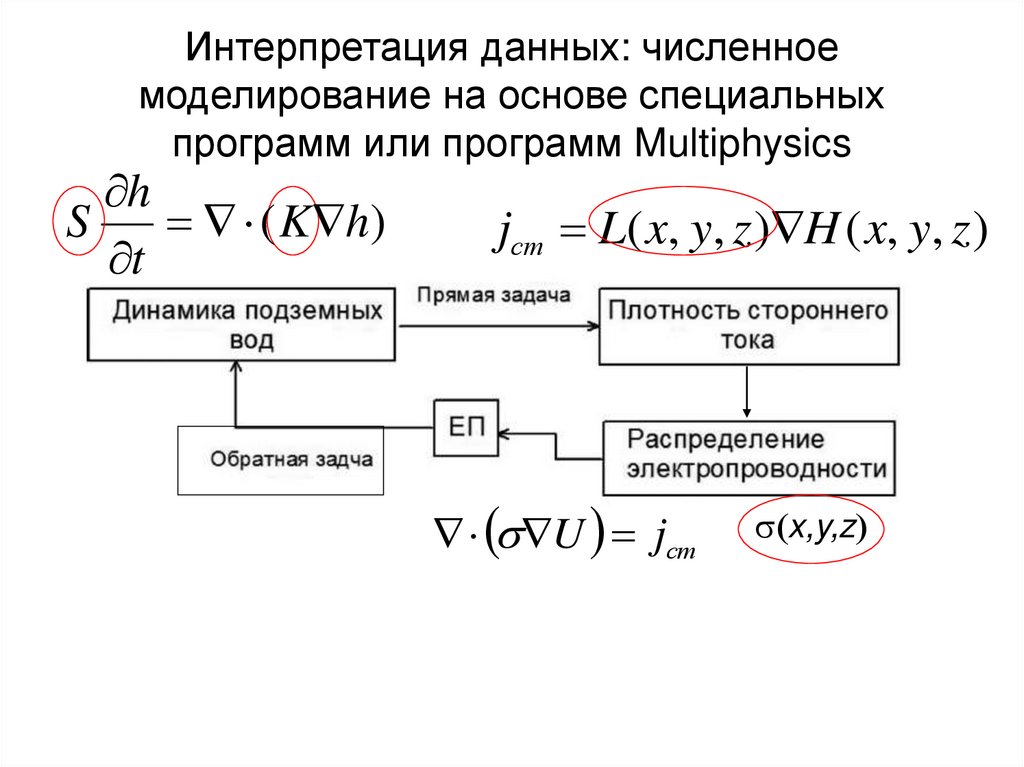
Исходные данные Богословского и Огильви (1973) Инверсия Revil et al. 2003

79. Интерпретация данных: численное моделирование на основе специальных программ или программ Multiphysics

h
S
( K h )
t
jст L( x, y, z ) H ( x, y, z )
s U jст
s x,y,z

80.

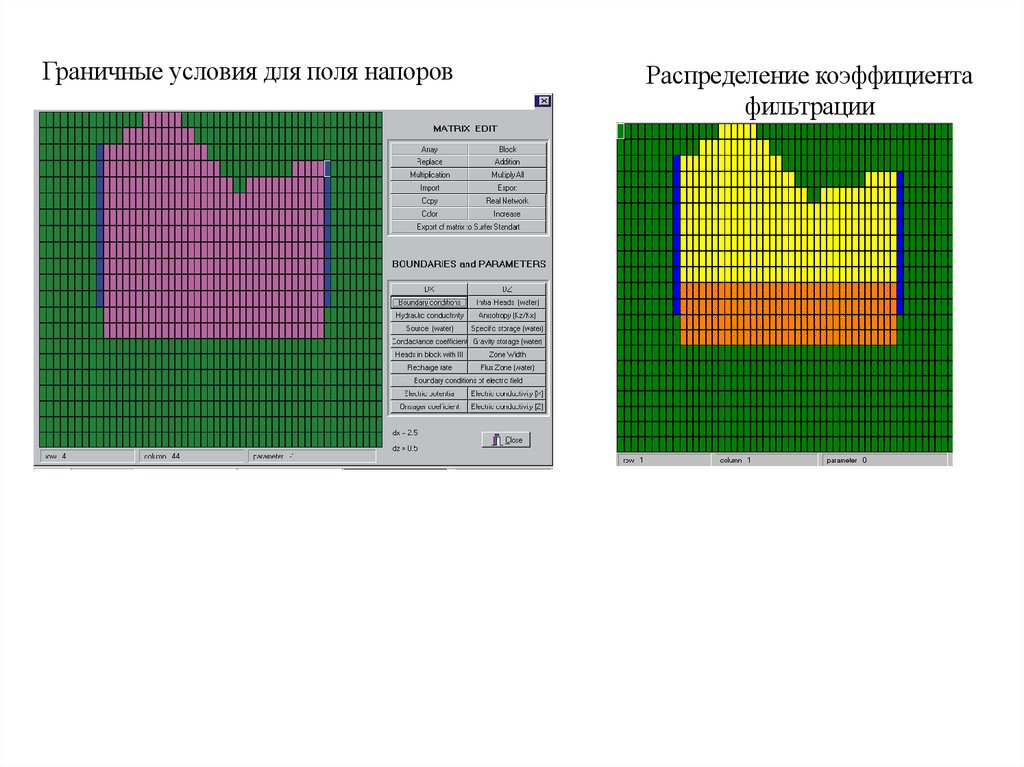
Граничные условия для поля напоров
Распределение коэффициента
фильтрации

81.

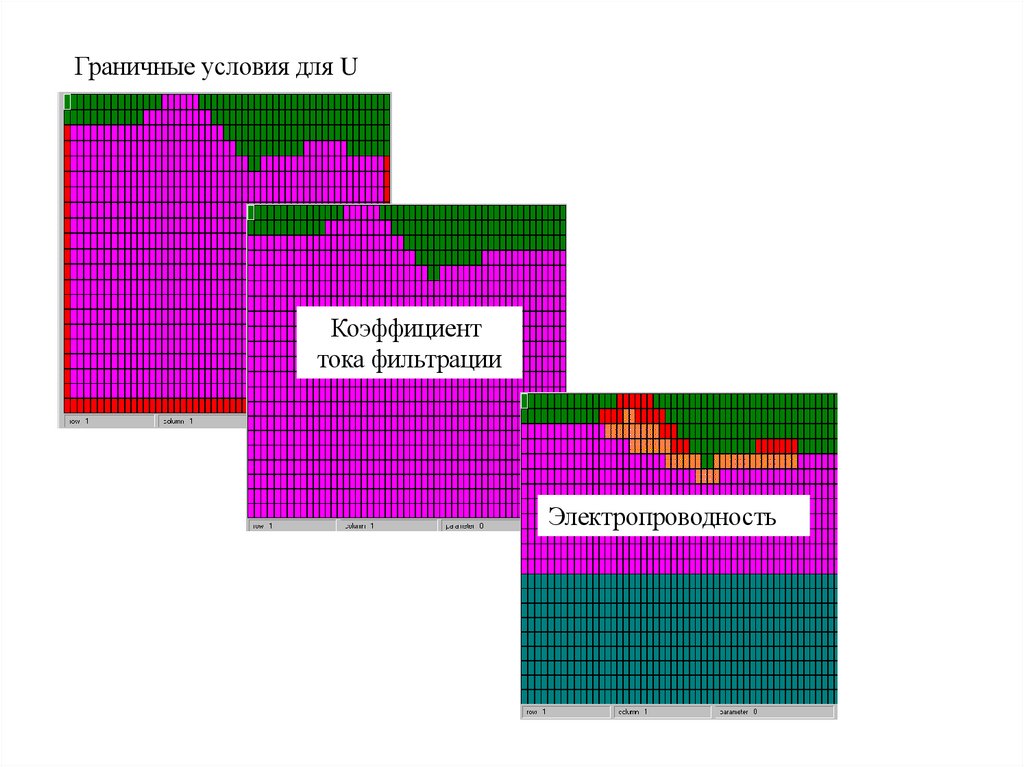
Граничные условия для U
Коэффициент
тока фильтрации
Электропроводность

82. 9. Примеры применения

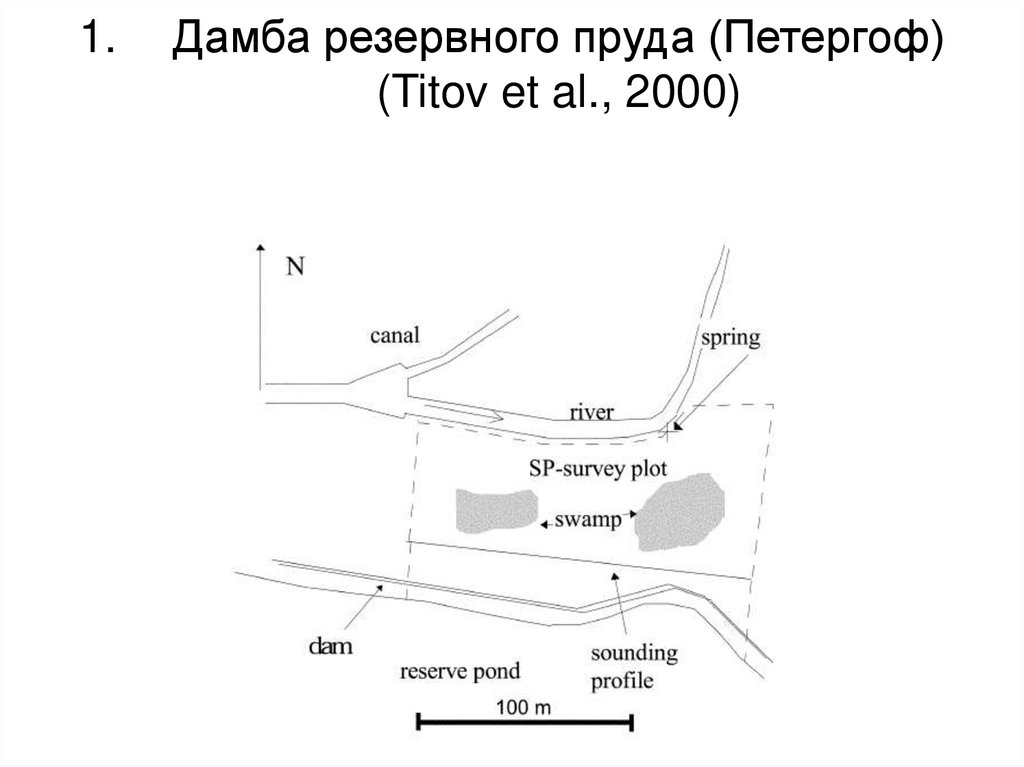
83. Дамба резервного пруда (Петергоф) (Titov et al., 2000)

1.
Дамба резервного пруда (Петергоф)
(Titov et al., 2000)

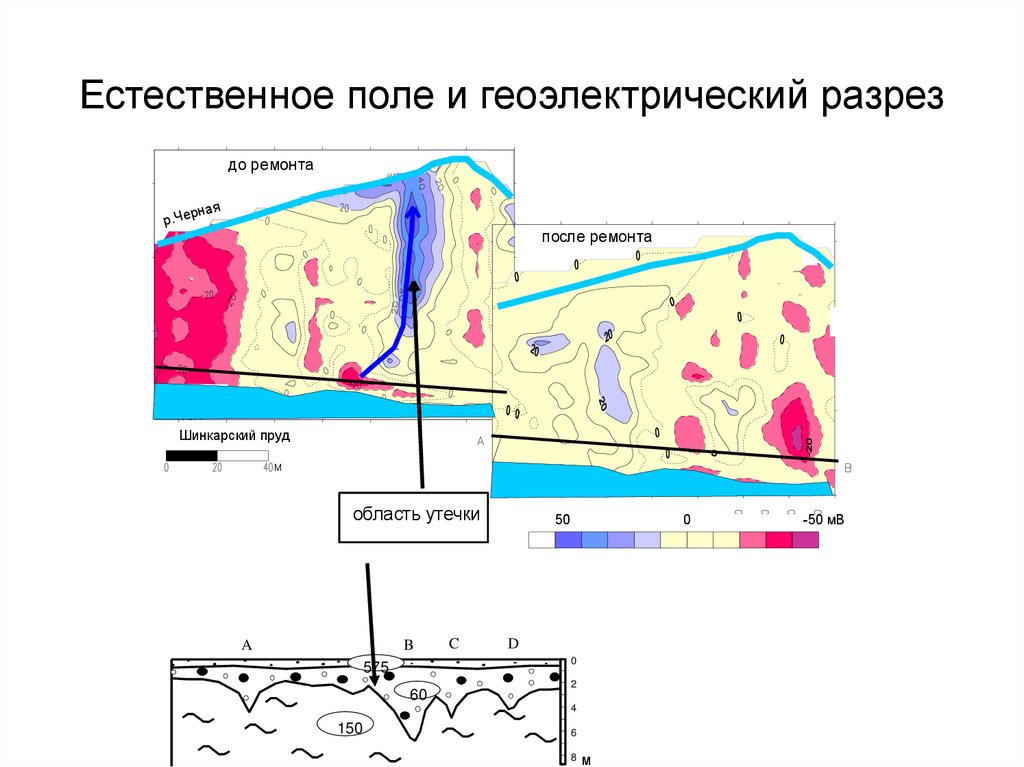
84. Естественное поле и геоэлектрический разрез

до ремонта
р. Ч е
рн а я
после ремонта
Шинкарский
пруд
Шинкарский пруд
м
Шинкарский
пруд
область утечки
A
B
C
50
U, мВ
D
0
575
60
2
4
150
6
8 м
0
-50 мВ

85.

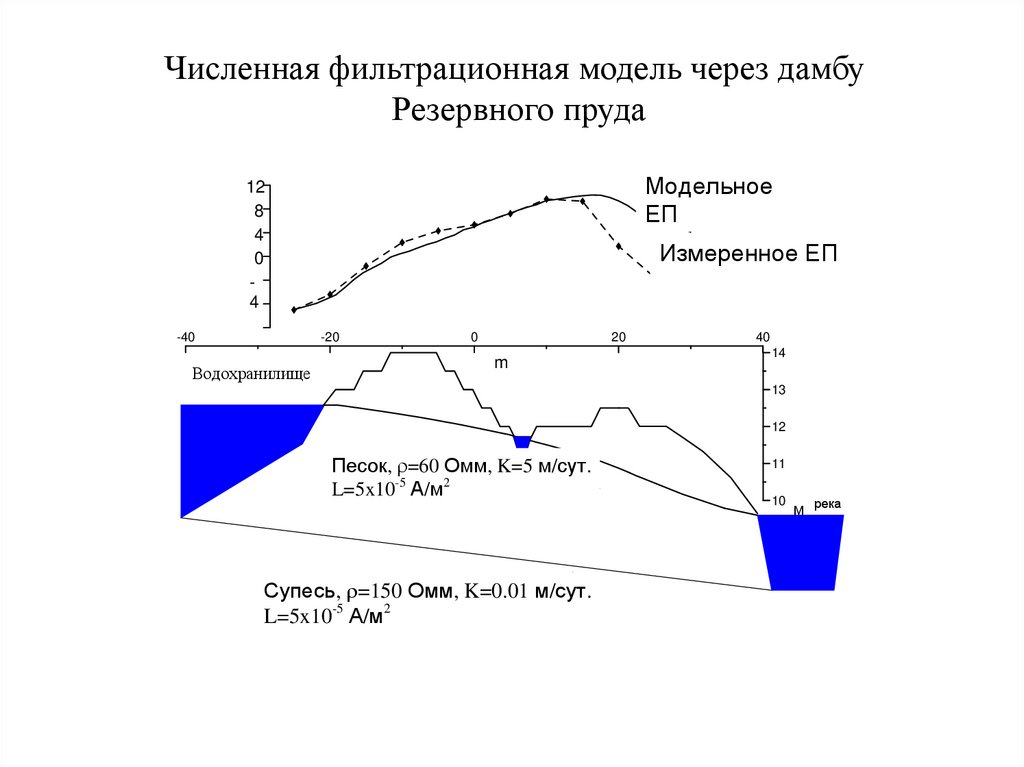
Численная фильтрационная модель через дамбу
Резервного пруда
Модельное
ЕП
12
8
4
0
4
-40
Модельное ЕП
Измеренное ЕП
Наблюденное ЕП
-20
20
0
14
m
Водохранилище
40
13
12
Песок, r=60 Омм, K=5 м/сут.
L=5x10-5 А/м2 Песок, r =60 Ом м, k =5 м/су
11
.
L = - 5.10-8 A.(Пa.м)-1
Супесь, r =150 Ohmm, k =0.01 м/сут L
Супесь, r=150
L = - 5Омм,
10 A (Пa мK=0.01
)
м/сут.
-5
2
L=5x10 А/м
.
-8
.
.
-1
10
м р е ка

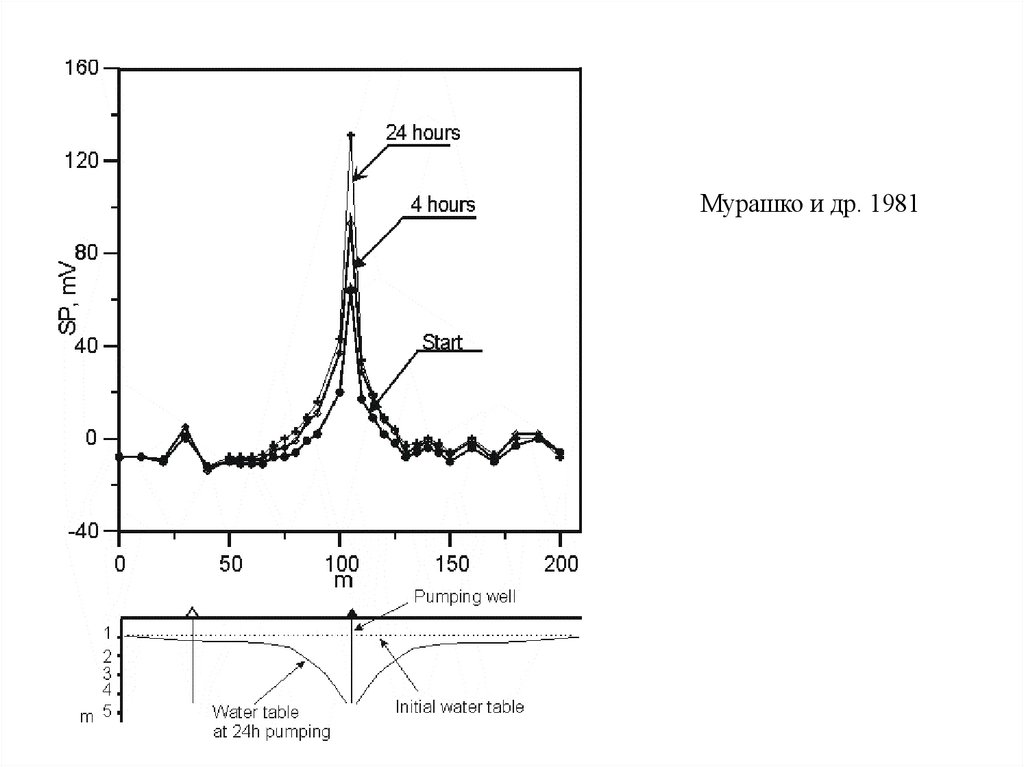
86. Примеры 2. Откачки из скважин

Ранние данные (Семенов, 1980)

87.

Мурашко и др. 1981

88. Тест водоносного горизонта Cocenza

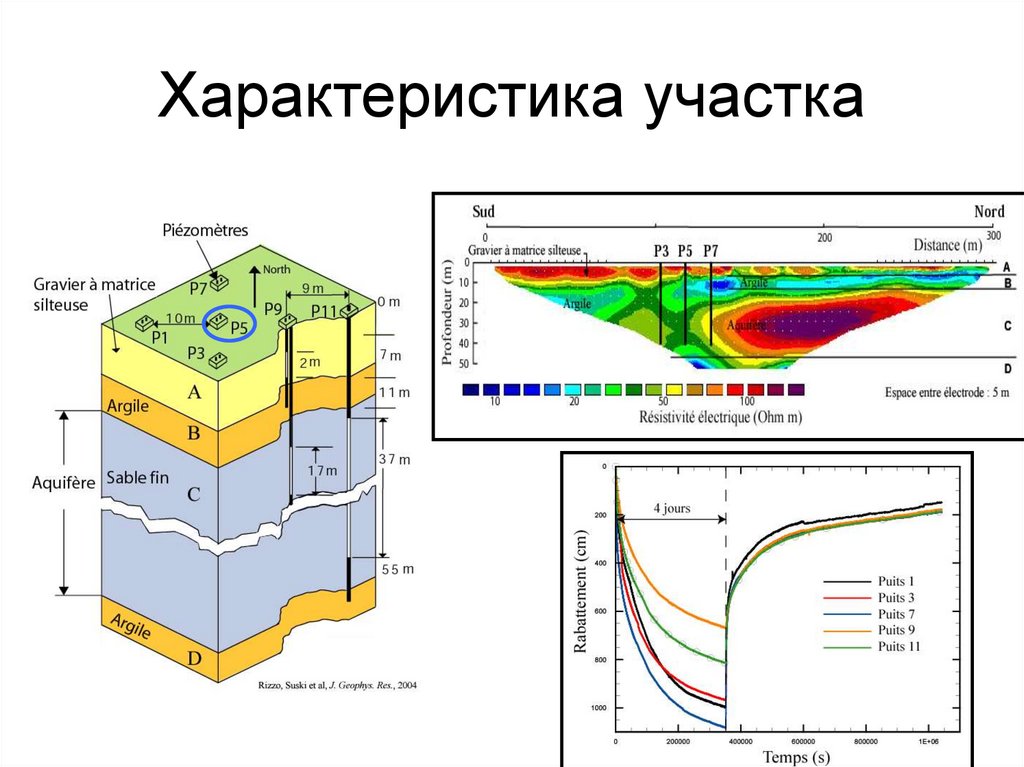
E. Rizzo, B. Suski, A. Revil, S. Straface,
JGR, 2004
K. Titov, A. Revil, P. Konosavsky, S.
Straface, S. Troisi, GJI, 2005

89. Характеристика участка

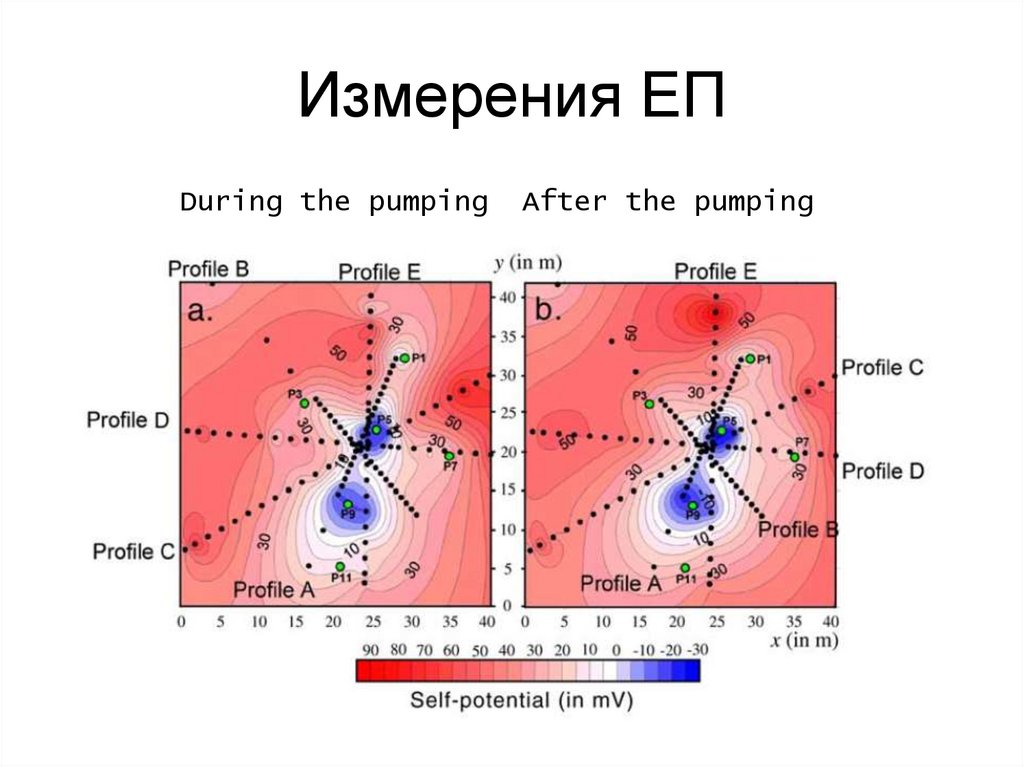
90. Измерения ЕП

During the pumping
After the pumping

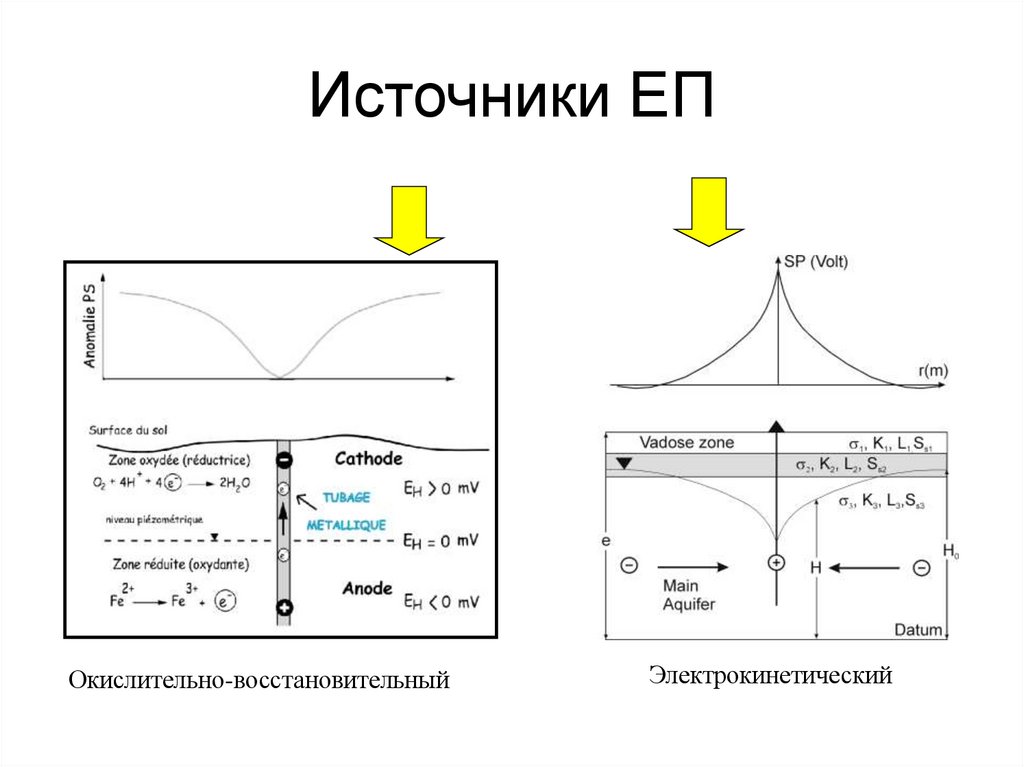
91. Источники ЕП

Окислительно-восстановительный
Электрокинетический

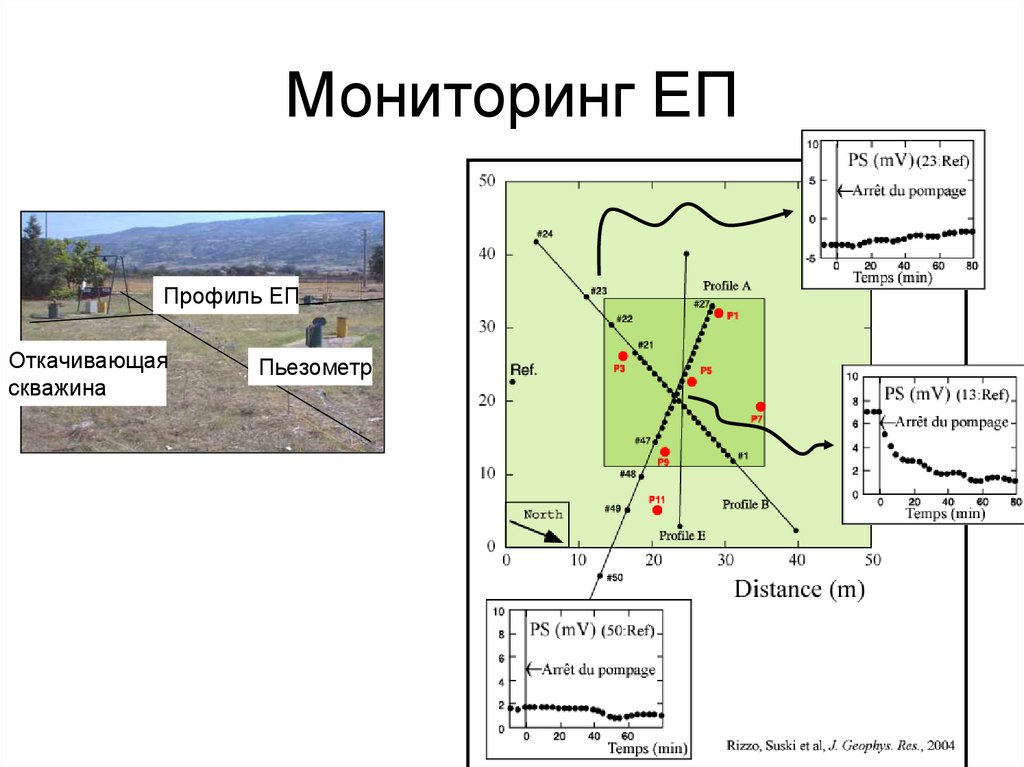
92. Мониторинг ЕП

Профиль ЕП
Откачивающая
скважина
Пьезометр

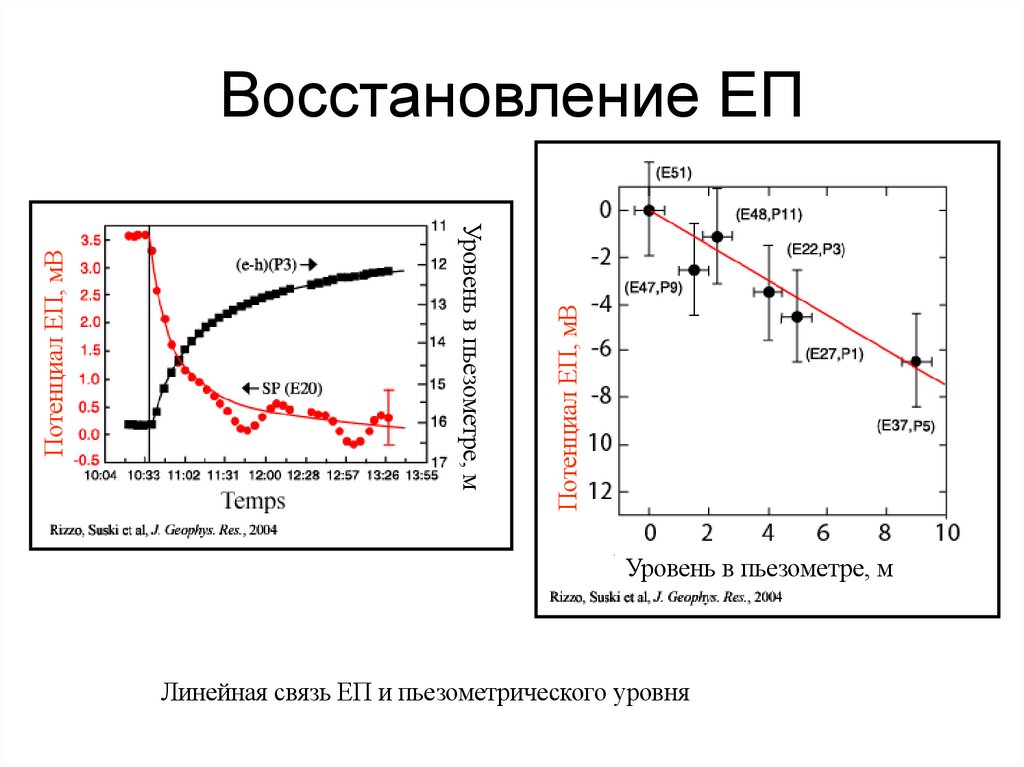
93. Восстановление ЕП

Потенциал ЕП, мВ
Уровень в пьезометре, м
Потенциал ЕП, мВ
Восстановление ЕП
Уровень в пьезометре, м
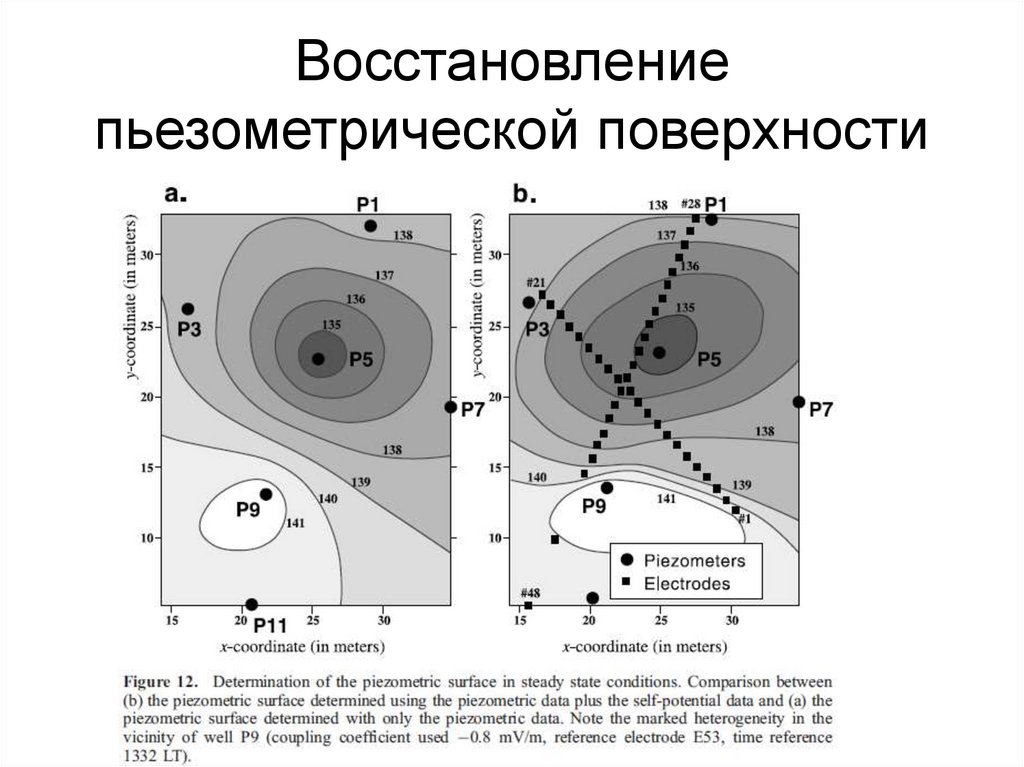
Линейная связь ЕП и пьезометрического уровня

94.

95. Восстановление пьезометрической поверхности

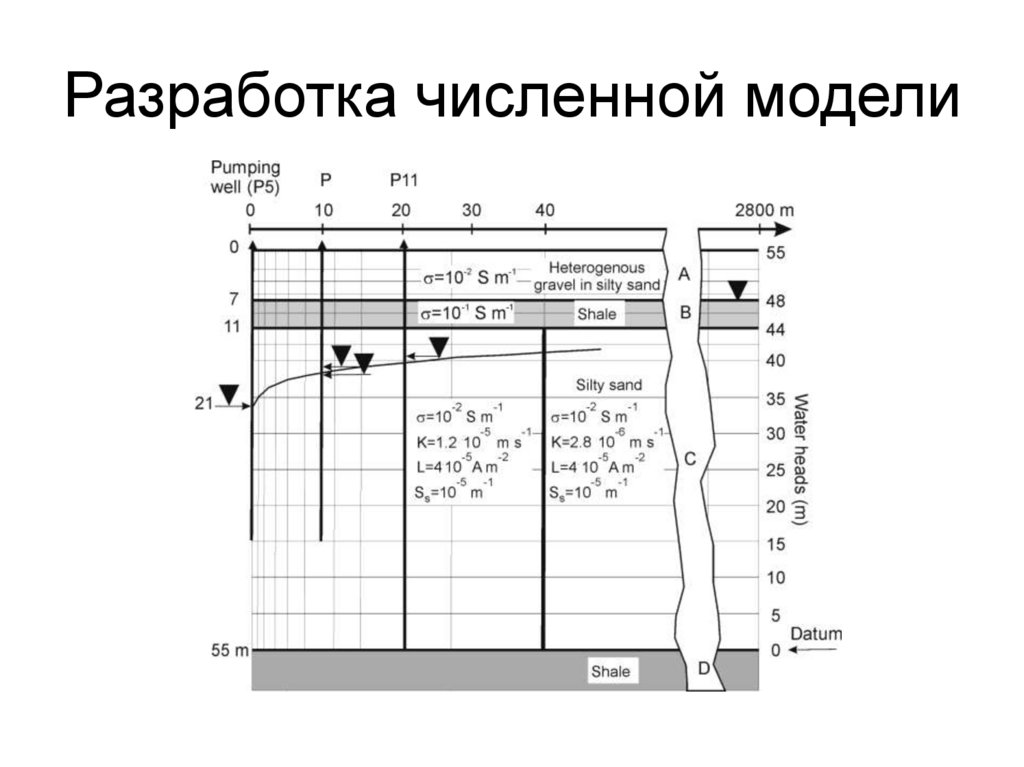
96. Разработка численной модели

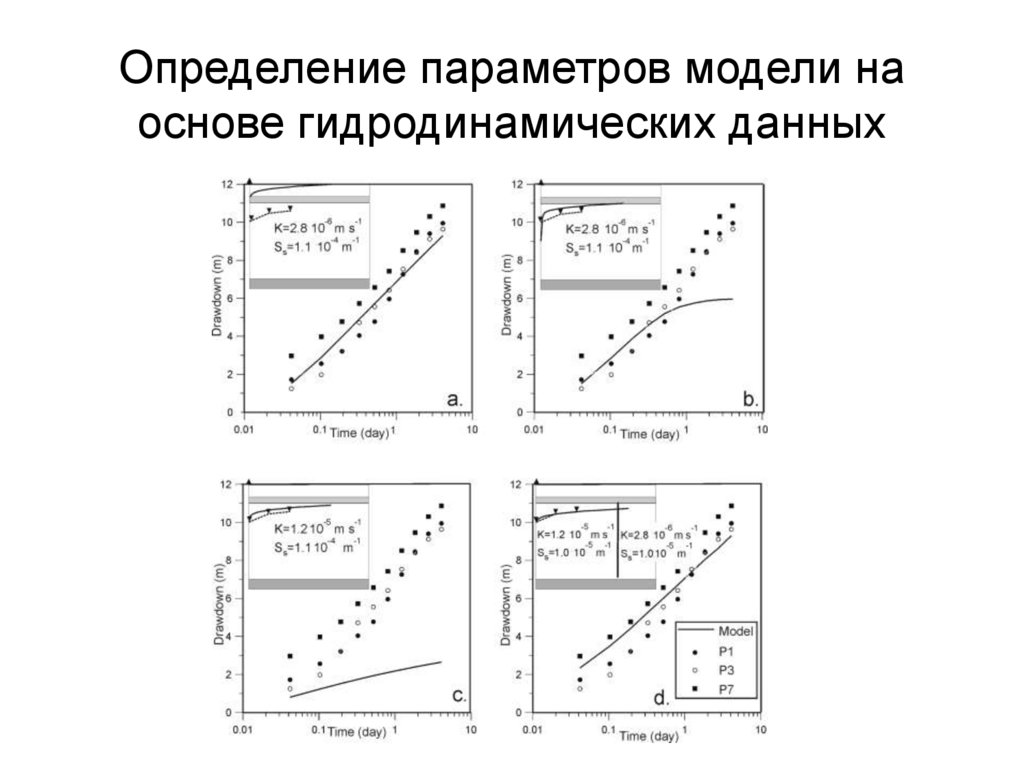
97. Определение параметров модели на основе гидродинамических данных

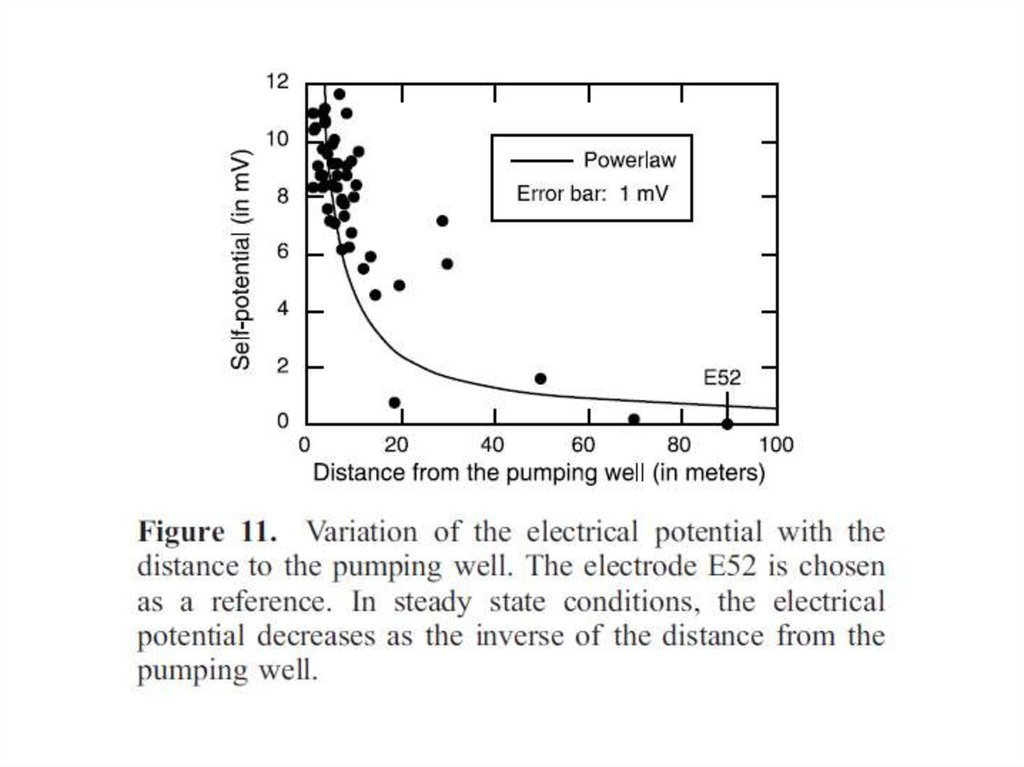
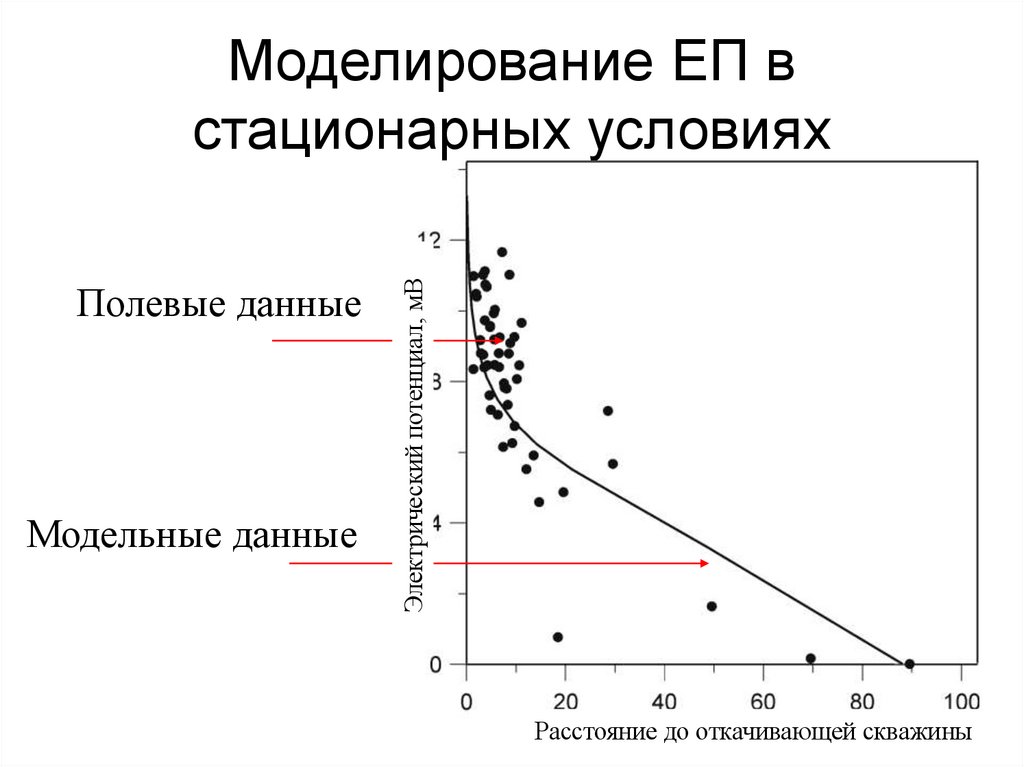
98. Моделирование ЕП в стационарных условиях

Полевые данные
Модельные данные
Электрический потенциал, мВ
Моделирование ЕП в
стационарных условиях
Расстояние до откачивающей скважины

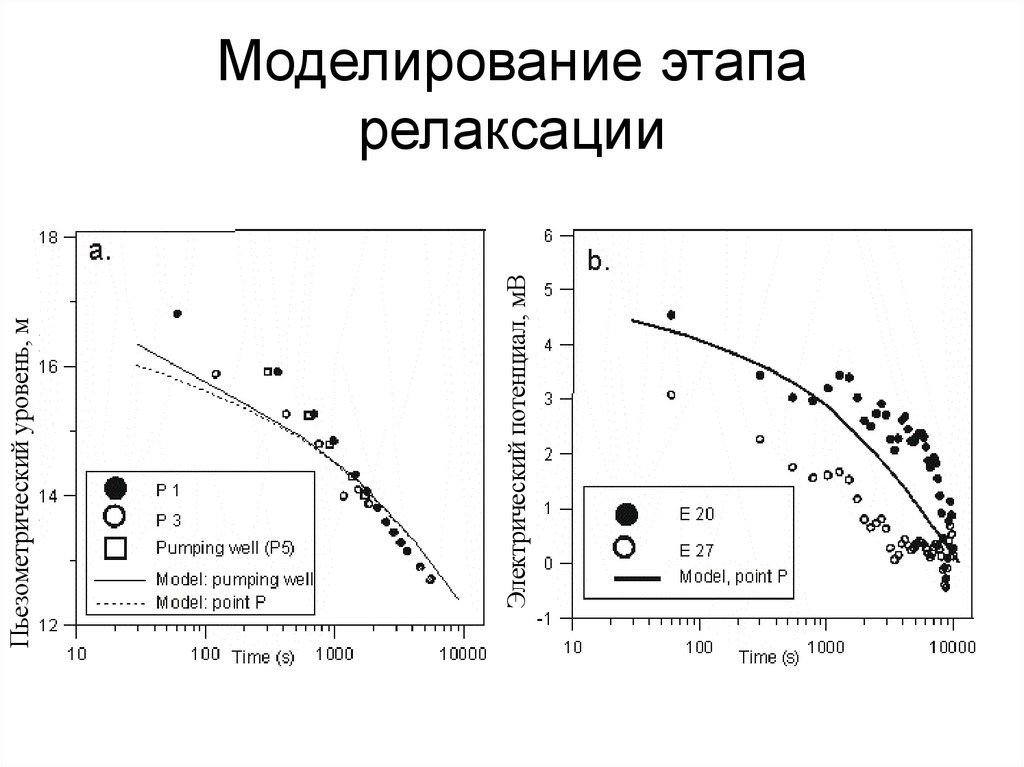
99. Моделирование этапа релаксации

Электрический потенциал, мВ
Пьезометрический уровень, м
Моделирование этапа
релаксации

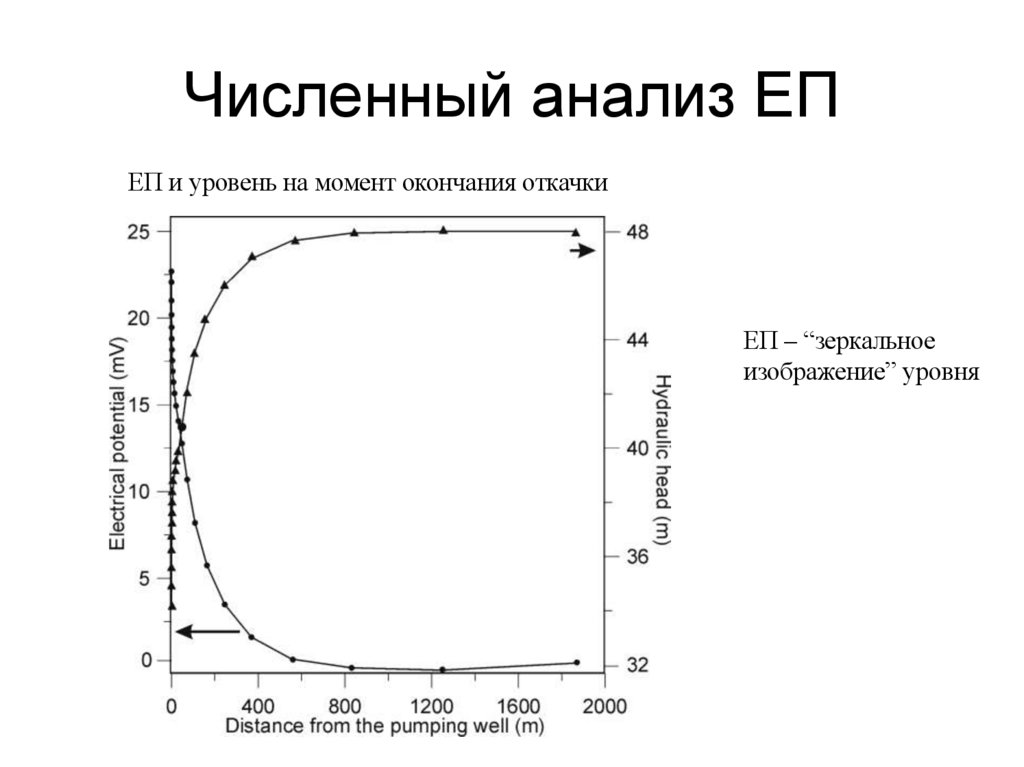
100. Численный анализ ЕП

ЕП и уровень на момент окончания откачки
ЕП – “зеркальное
изображение” уровня

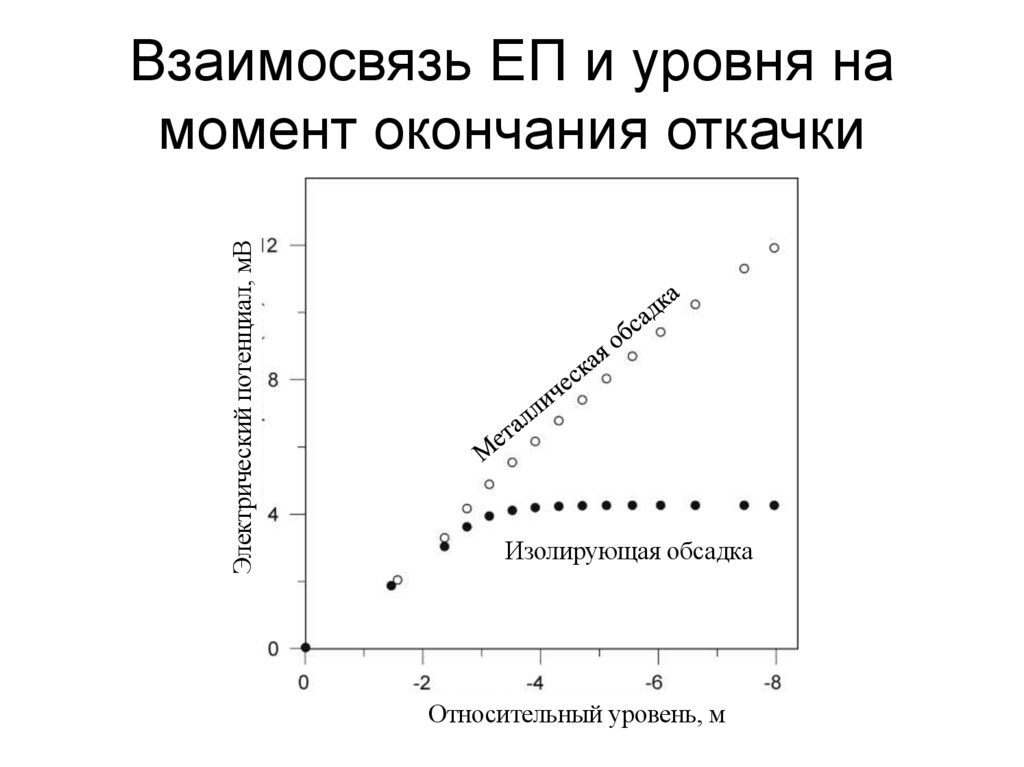
101. Взаимосвязь ЕП и уровня на момент окончания откачки

Электрический потенциал, мВ
Взаимосвязь ЕП и уровня на
момент окончания откачки
Изолирующая обсадка
Относительный уровень, м

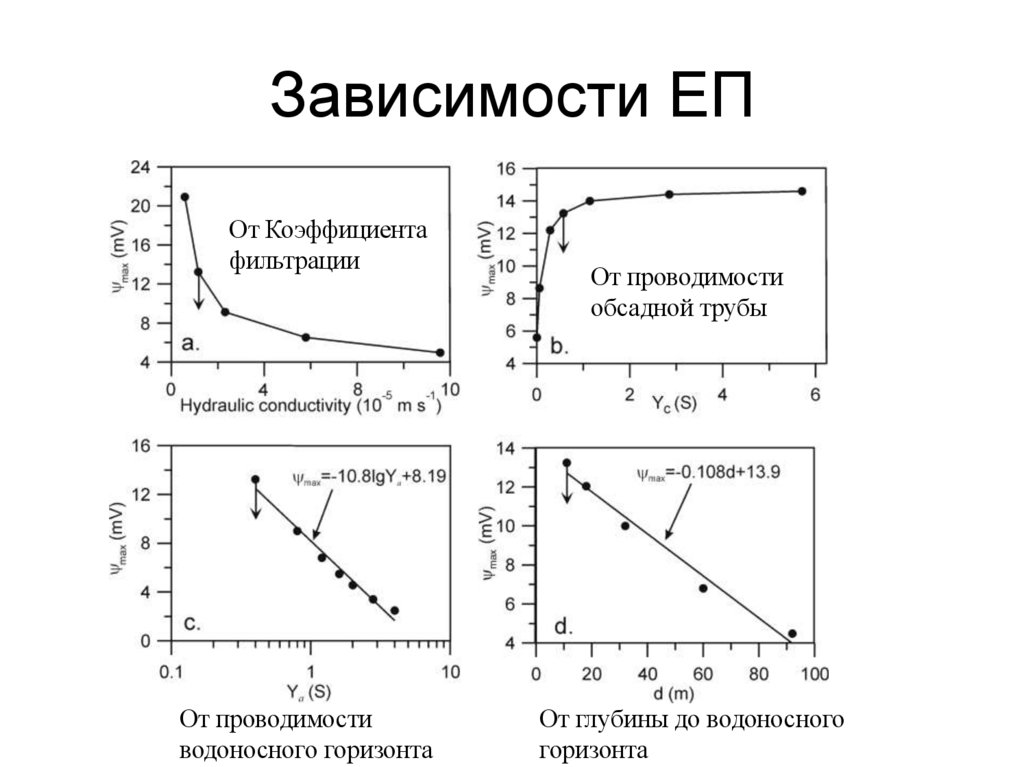
102. Зависимости ЕП

От Коэффициента
фильтрации
От проводимости
водоносного горизонта
От проводимости
обсадной трубы
От глубины до водоносного
горизонта

103. Объемное распределение ЕП

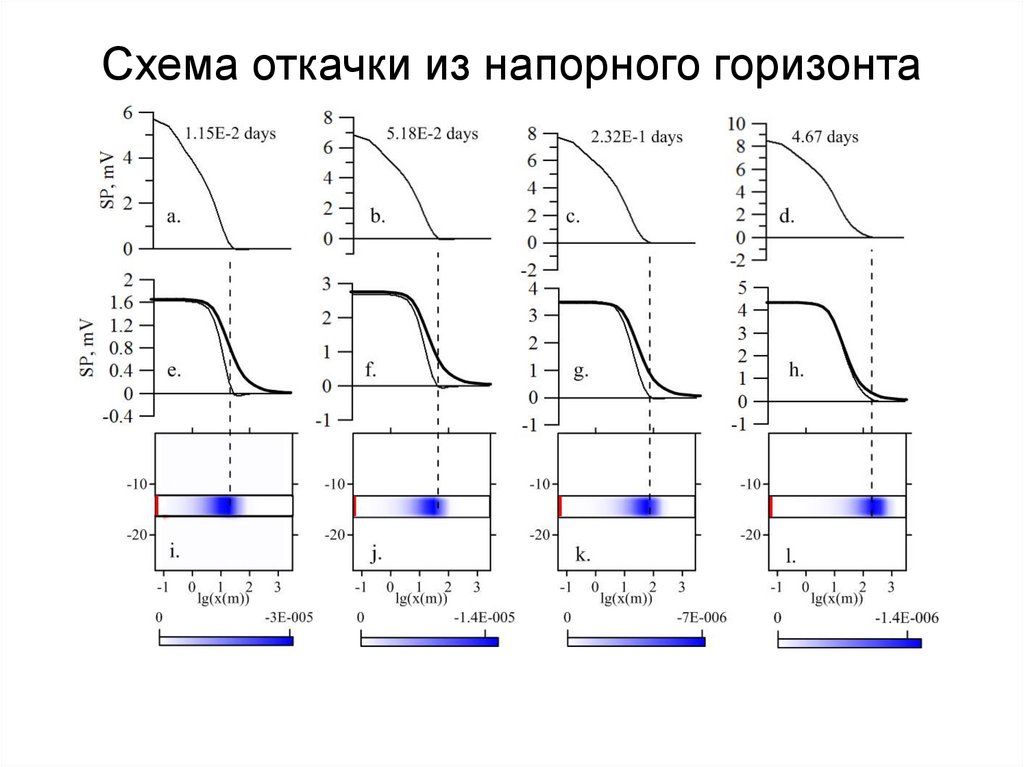
104. Схема откачки из напорного горизонта

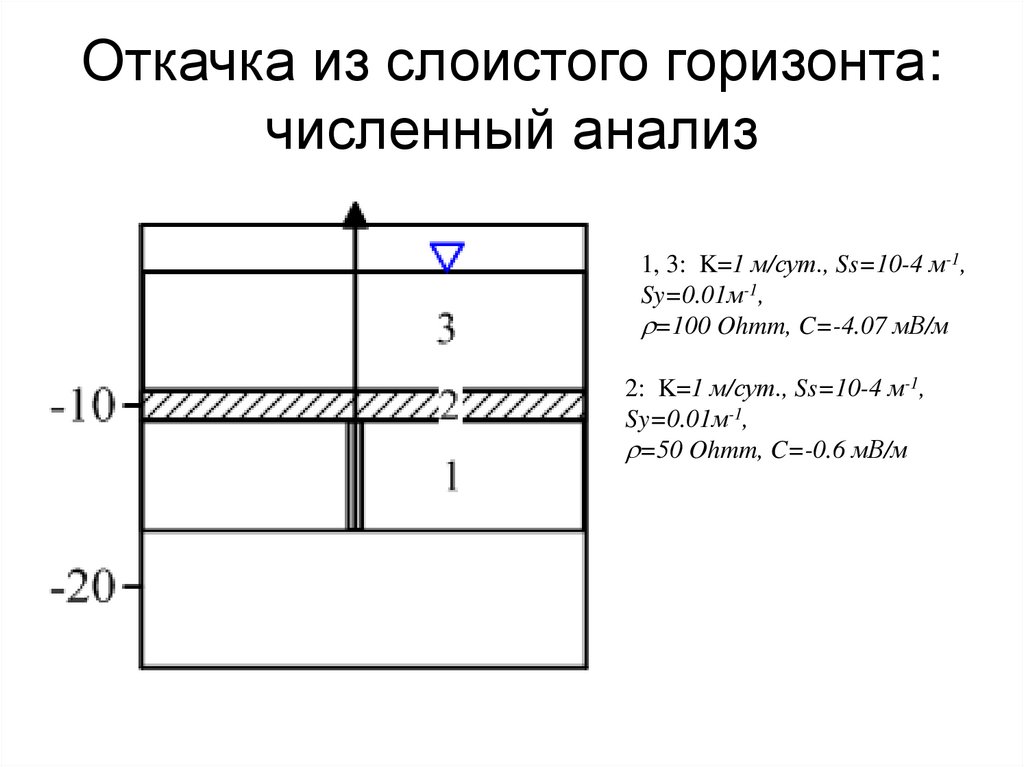
105. Откачка из слоистого горизонта: численный анализ

1, 3: K=1 м/сут., Ss=10-4 м-1,
Sy=0.01м-1,
r=100 Ohmm, C=-4.07 мВ/м
2: K=1 м/сут., Ss=10-4 м-1,
Sy=0.01м-1,
r=50 Ohmm, C=-0.6 мВ/м

106.

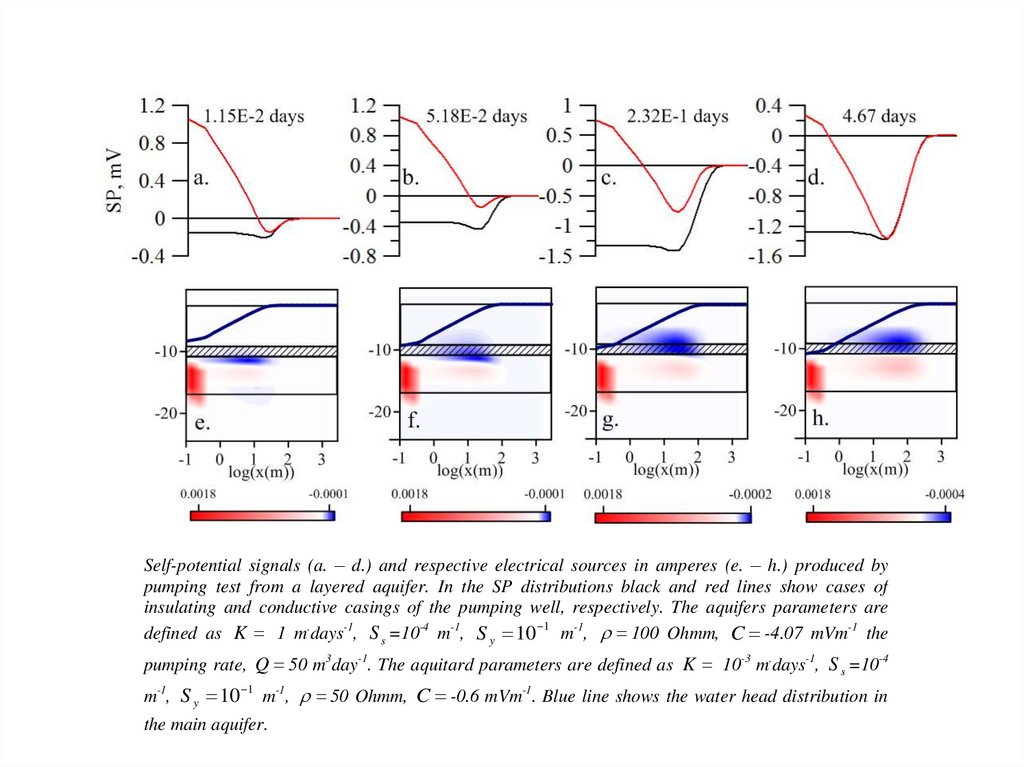
Self-potential signals (a. – d.) and respective electrical sources in amperes (e. – h.) produced by
pumping test from a layered aquifer. In the SP distributions black and red lines show cases of
insulating and conductive casings of the pumping well, respectively. The aquifers parameters are
defined as K 1 m.days-1, S s =10-4 m-1, S y 10 1 m-1, r 100 Ohmm, C -4.07 mVm-1 the
pumping rate, Q 50 m3day-1. The aquitard parameters are defined as K 10-3 m.days-1, S s =10-4
m-1, S y 10 1 m-1, r 50 Ohmm, C -0.6 mVm-1. Blue line shows the water head distribution in
the main aquifer.

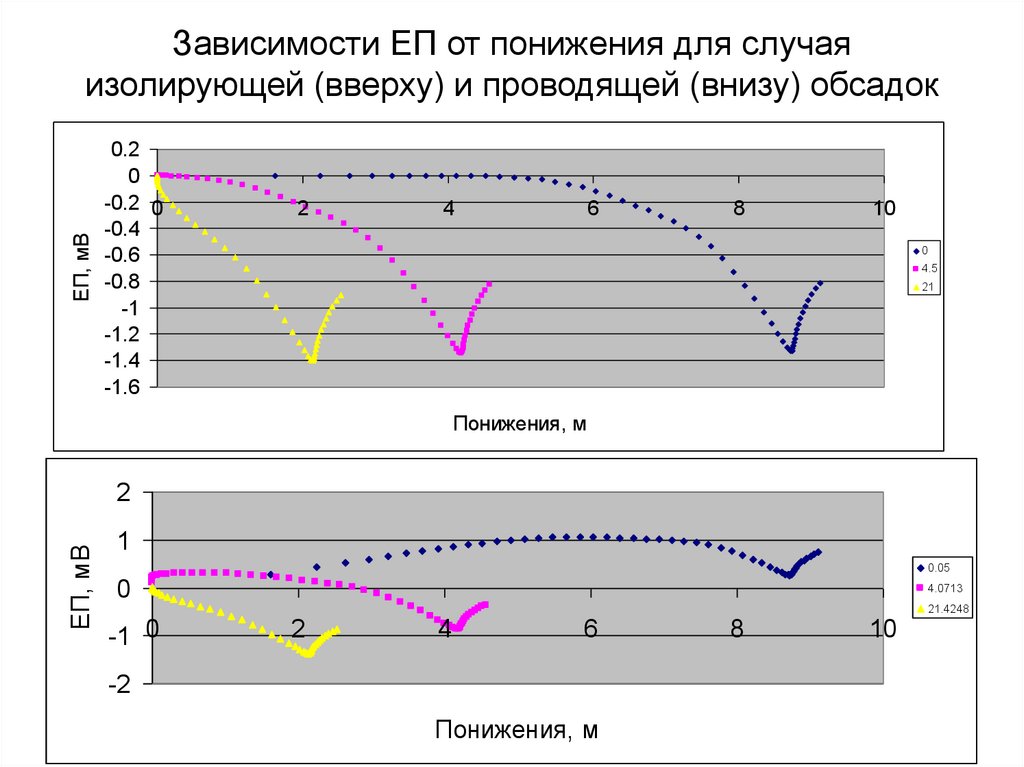
107. Зависимости ЕП от понижения для случая изолирующей (вверху) и проводящей (внизу) обсадок

ЕП, мВ
Зависимости ЕП от понижения для случая
изолирующей (вверху) и проводящей (внизу) обсадок
0.2
0
-0.2 0
-0.4
-0.6
-0.8
-1
-1.2
-1.4
-1.6
2
4
6
8
10
0
4.5
21
Понижения, м
ЕП, мВ
2
1
0.05
0
-1 0
4.0713
2
4
6
-2
Понижения, м
8
10
21.4248

108.

560
105
1.87 1.4.103
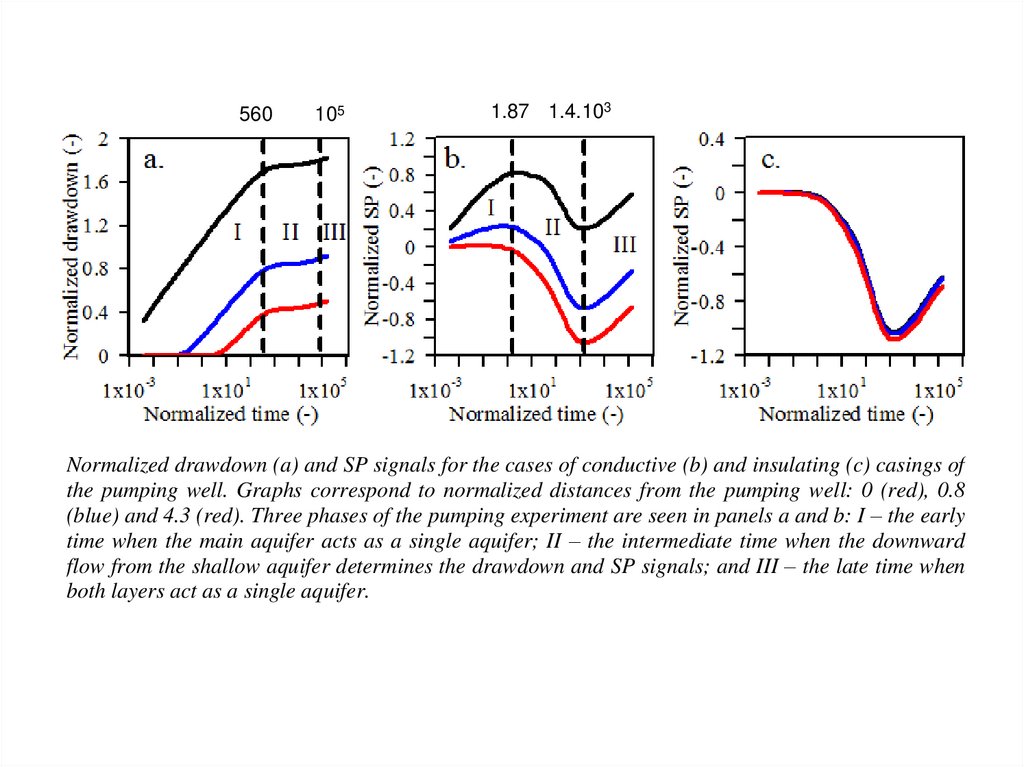
Normalized drawdown (a) and SP signals for the cases of conductive (b) and insulating (c) casings of
the pumping well. Graphs correspond to normalized distances from the pumping well: 0 (red), 0.8
(blue) and 4.3 (red). Three phases of the pumping experiment are seen in panels a and b: I – the early
time when the main aquifer acts as a single aquifer; II – the intermediate time when the downward
flow from the shallow aquifer determines the drawdown and SP signals; and III – the late time when
both layers act as a single aquifer.

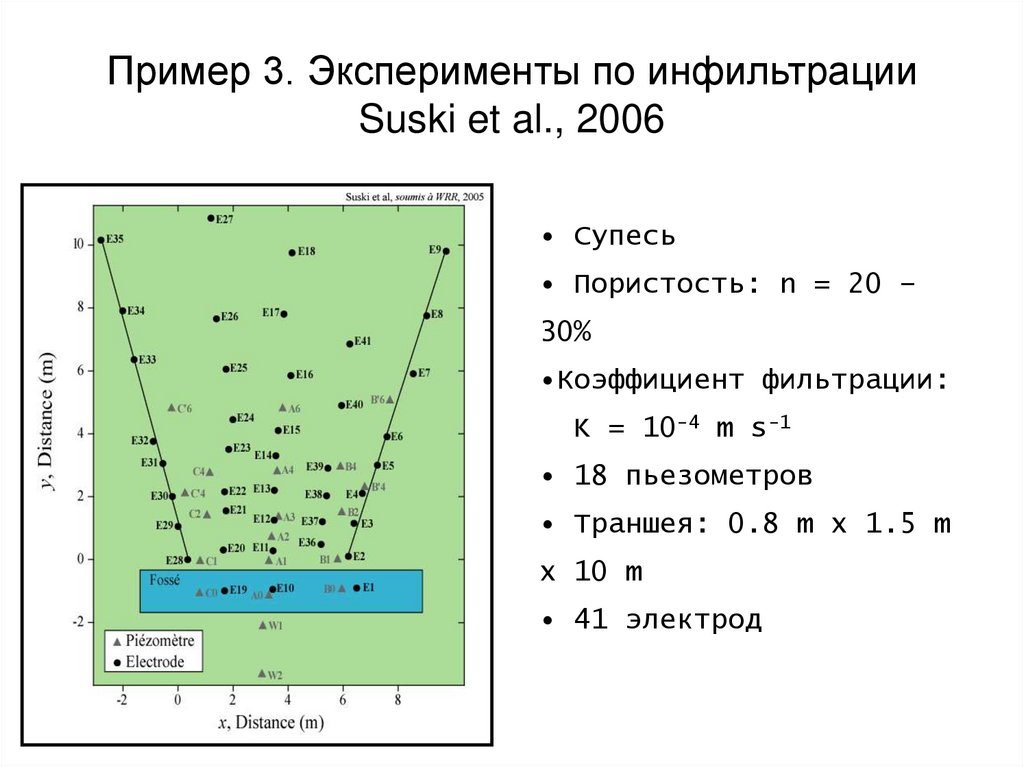
109. Пример 3. Эксперименты по инфильтрации Suski et al., 2006

• Супесь
• Пористость: n = 20 –
30%
•Коэффициент фильтрации:
K = 10-4 m s-1
• 18 пьезометров
• Траншея: 0.8 m x 1.5 m
x 10 m
• 41 электрод

110.

111.

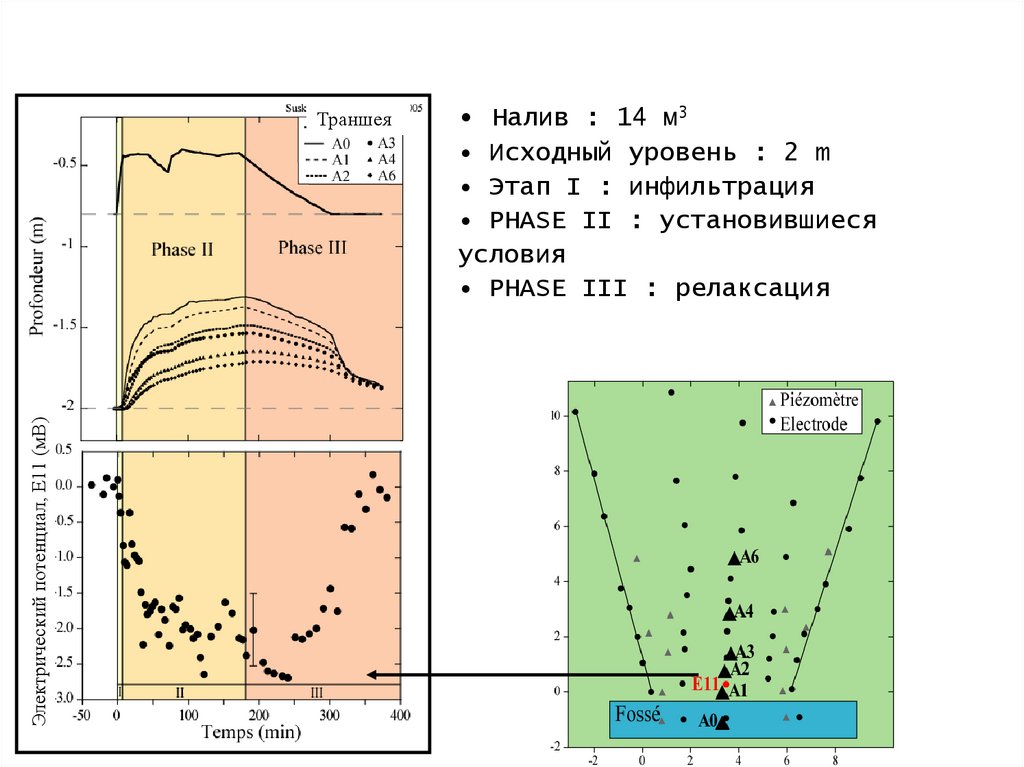
Траншея
• Налив : 14 м3
Электрический потенциал, Е11 (мВ)
• Исходный уровень : 2 m
• Этап I : инфильтрация
• PHASE II : установившиеся
условия
• PHASE III : релаксация

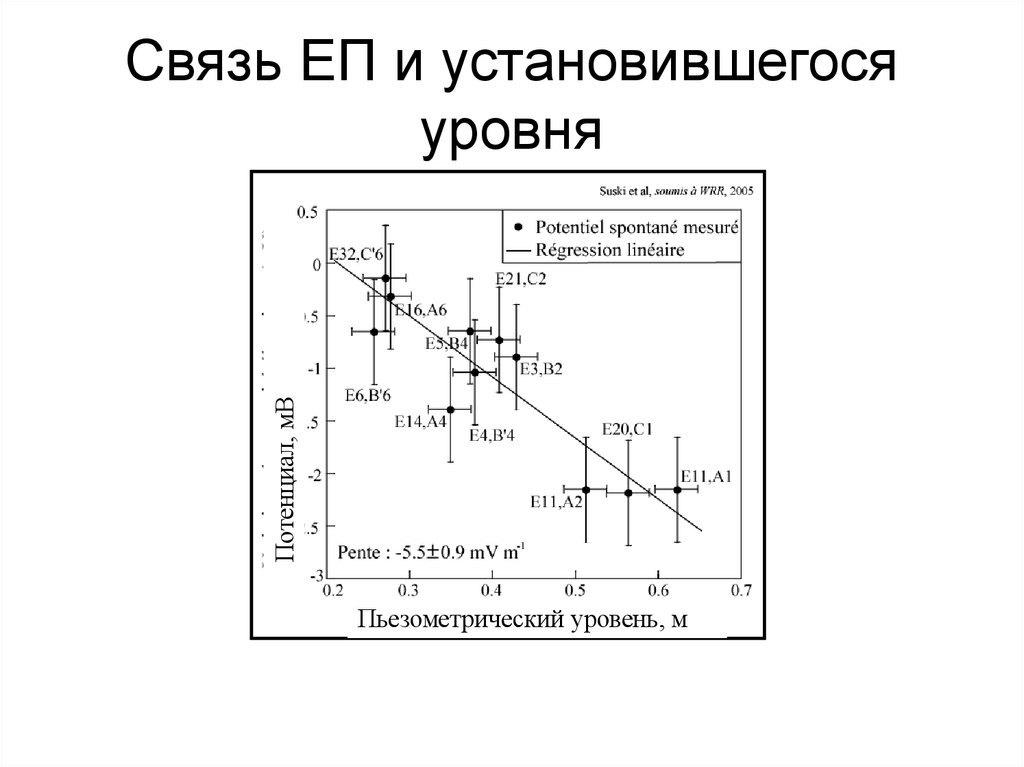
112. Связь ЕП и установившегося уровня

Потенциал, мВ
Связь ЕП и установившегося
уровня
Пьезометрический уровень, м

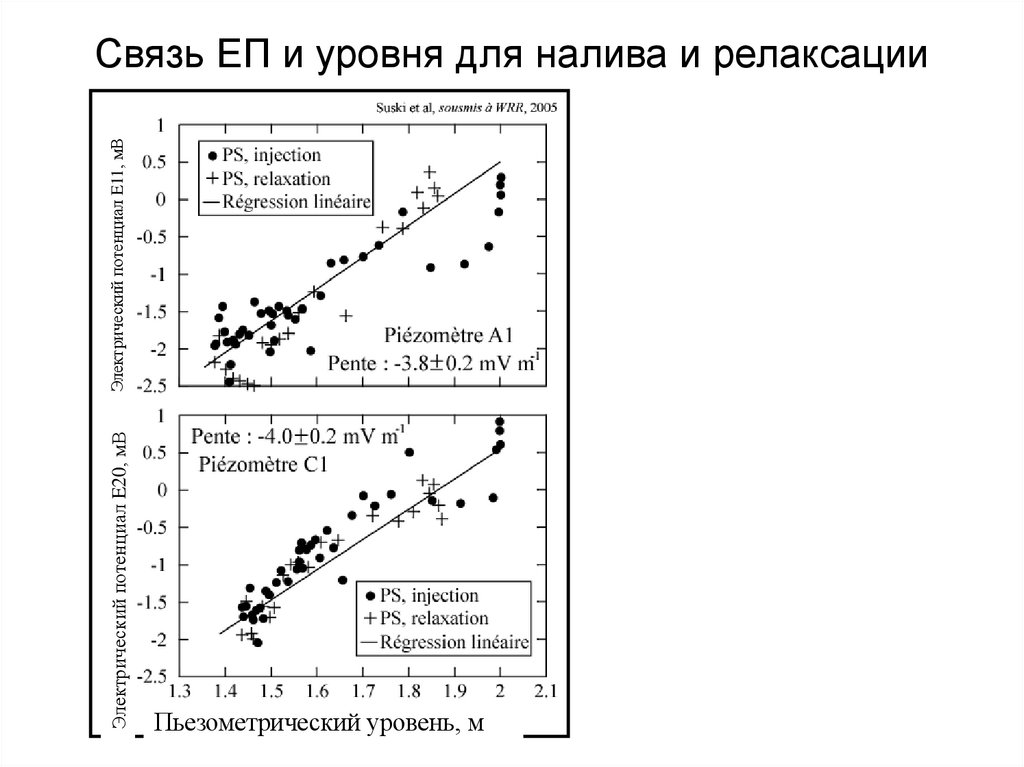
113. Связь ЕП и уровня для налива и релаксации

Электрический потенциал E20, мВ
Электрический потенциал E11, мВ
Связь ЕП и уровня для налива и релаксации
Пьезометрический уровень, м

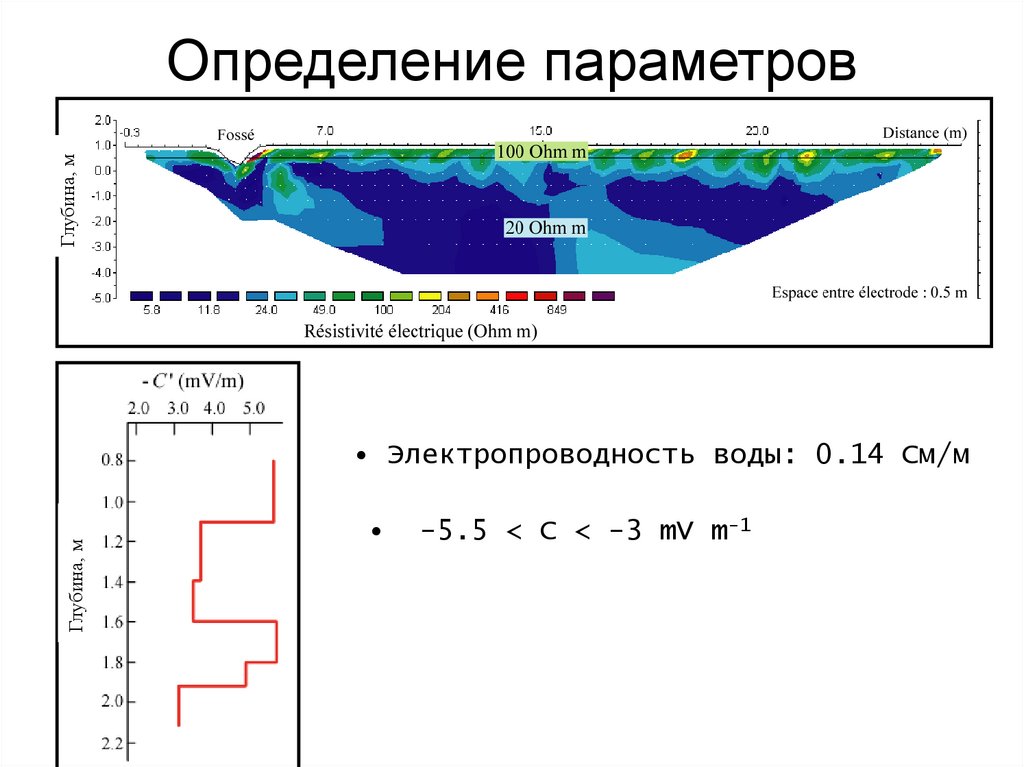
114. Определение параметров модели

Глубина, м
Определение параметров
модели
Глубина, м
• Электропроводность воды: 0.14 См/м
-5.5 < C < -3 mV m-1

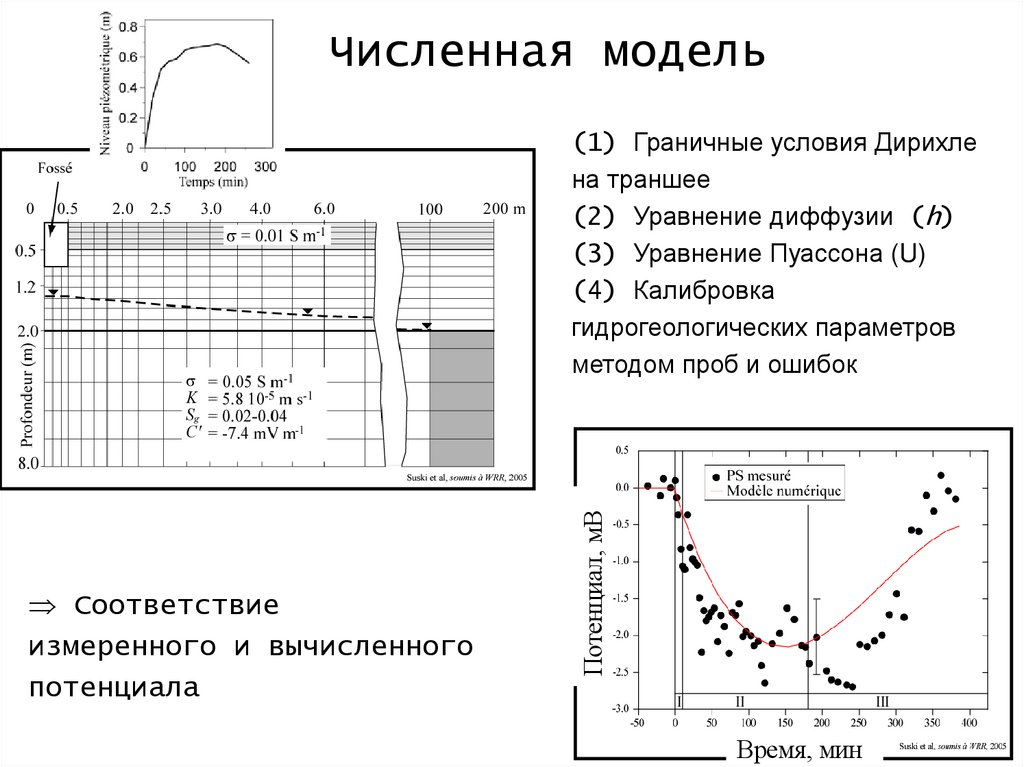
115.

Численная модель
Соответствие
измеренного и вычисленного
потенциала
Потенциал, мВ
(1) Граничные условия Дирихле
на траншее
(2) Уравнение диффузии (h)
(3) Уравнение Пуассона (U)
(4) Калибровка
гидрогеологических параметров
методом проб и ошибок
Время, мин

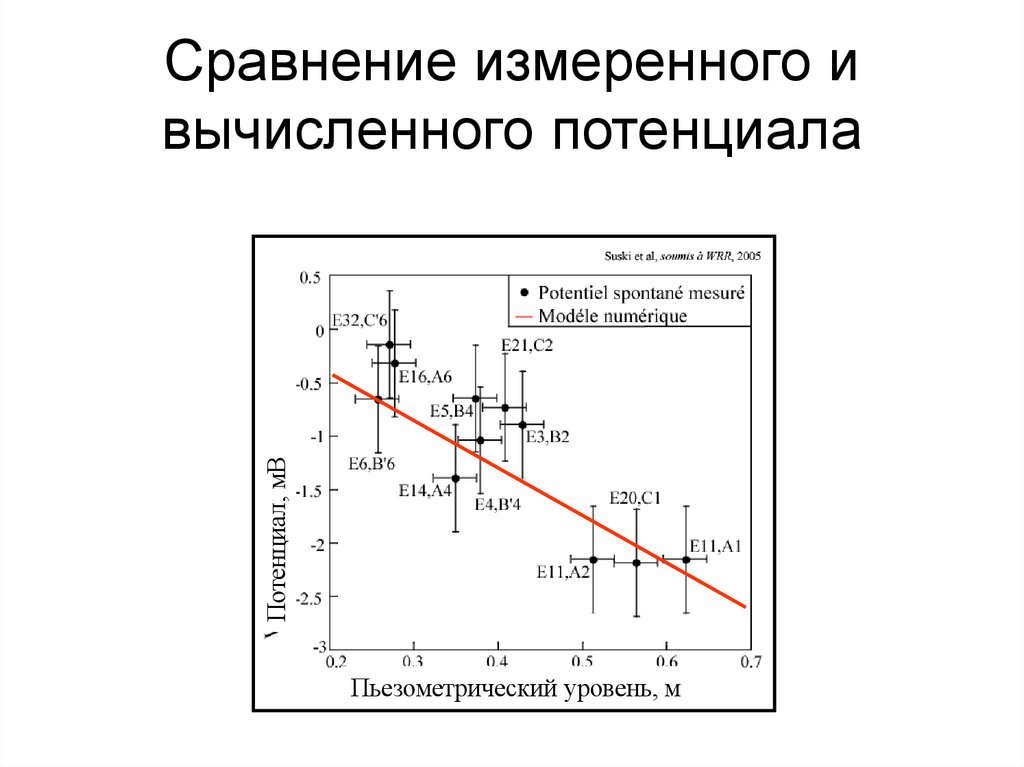
116. Сравнение измеренного и вычисленного потенциала

Потенциал, мВ
Сравнение измеренного и
вычисленного потенциала
Пьезометрический уровень, м

117. Распределение потенциала по профилю

Сравнение полевых
данных и измеренного
потенциала
Распределение
потенциала в объеме

118. Пример 4. Интенсивные поля над вулканами

Sasai et al., 1990

119.

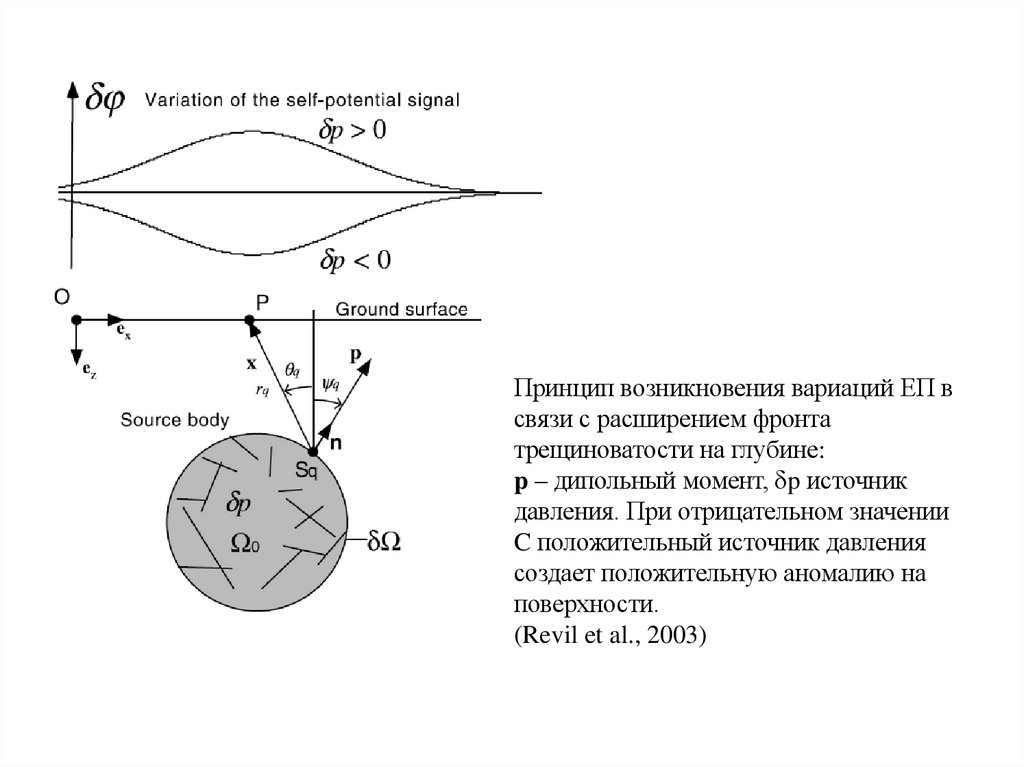
Принцип возникновения вариаций ЕП в
связи с расширением фронта
трещиноватости на глубине:
p – дипольный момент, dp источник
давления. При отрицательном значении
C положительный источник давления
создает положительную аномалию на
поверхности.
(Revil et al., 2003)

120. Пример 5. Исследование плотин

Водохранилищ
е
Песчанокаменная наброска
Моренное ядро
Морена

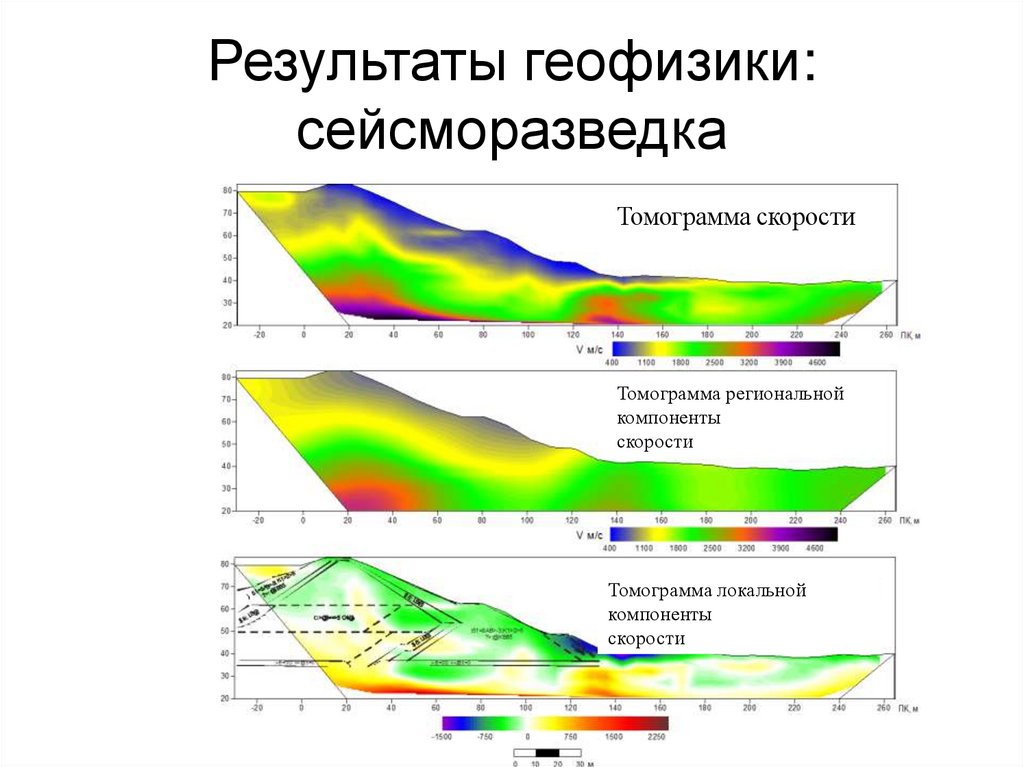
121. Результаты геофизики: сейсморазведка

Томограмма скорости
Томограмма региональной
компоненты
скорости
Томограмма локальной
компоненты
скорости

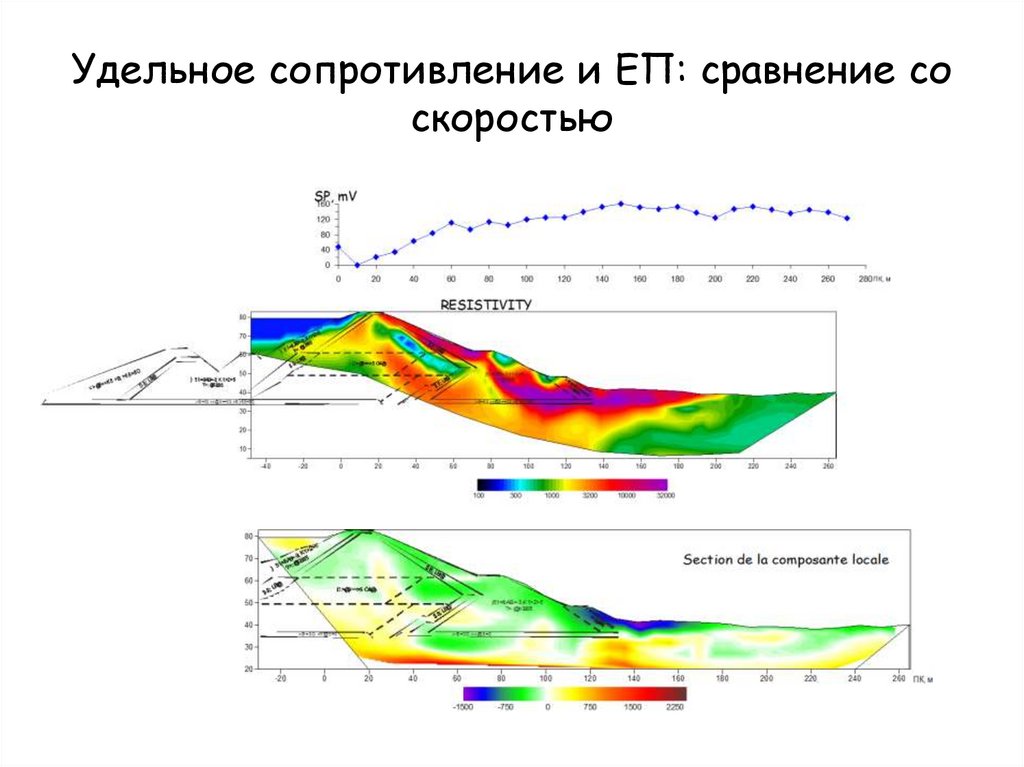
122.

Удельное сопротивление и ЕП: сравнение со
скоростью

123.

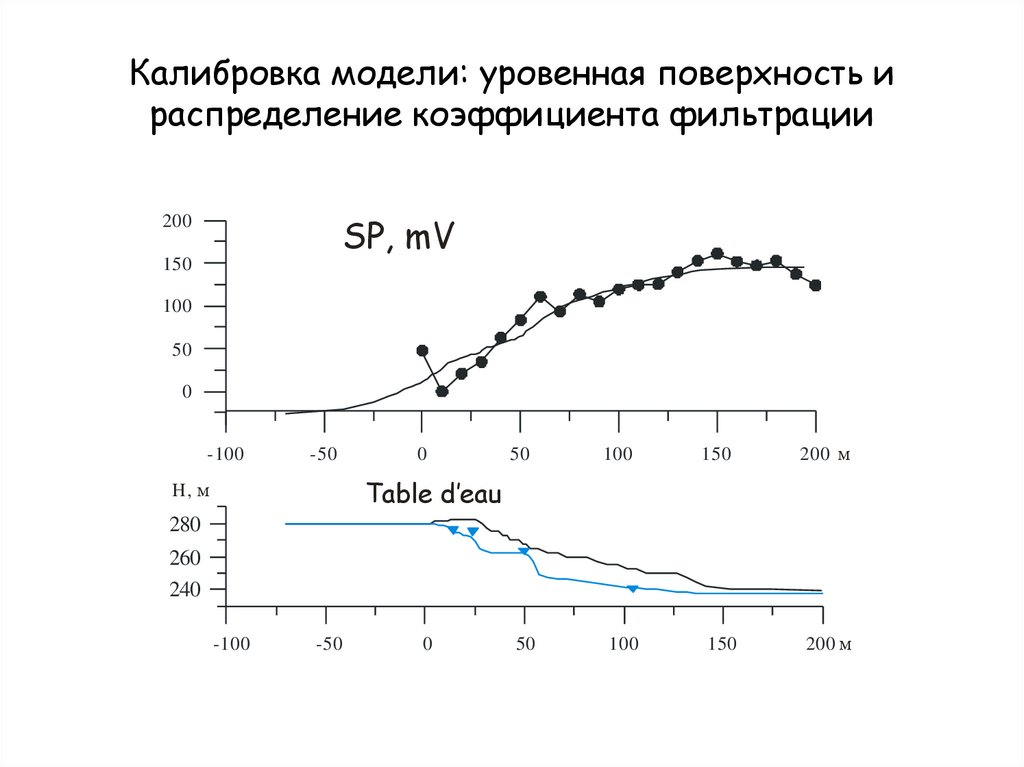
Фильтрационная модель

124.

Калибровка модели: уровенная поверхность и
распределение коэффициента фильтрации
SP, mV
200
150
100
50
0
-100
-50
0
50
100
150
200 м
50
100
150
200 м
Table d’eau
H, м
280
260
240
-100
-50
0

125. Пример 6 Антропогенные аномалии окислительно-восстановительной природы

Изучение загрязнения подземных
вод стоками поверхностной свалки
(Entressen, район Марселя)
Naudet et al., 2003

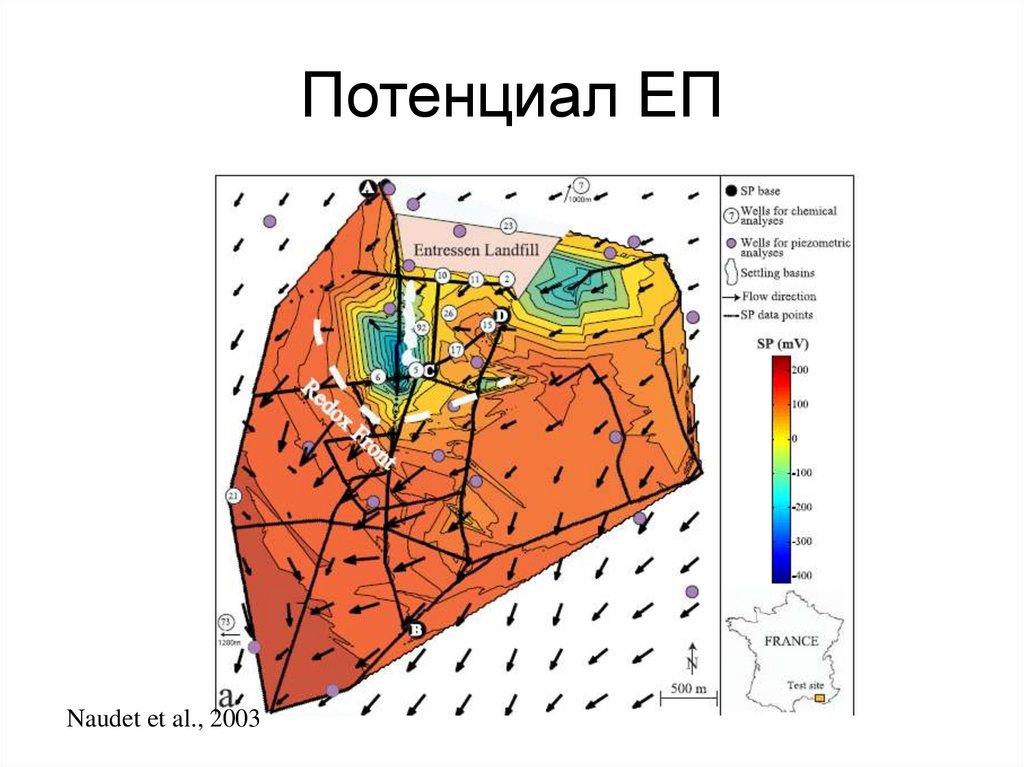
126. Потенциал ЕП

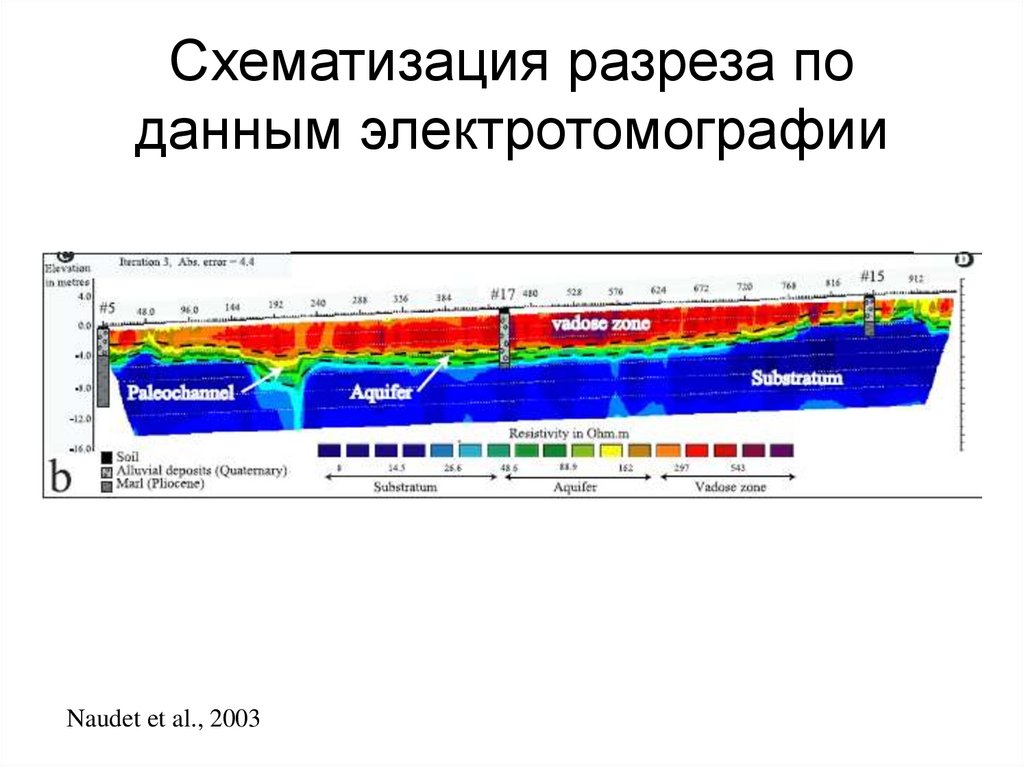
Naudet et al., 2003

127. Схематизация разреза по данным электротомографии

Naudet et al., 2003

128.

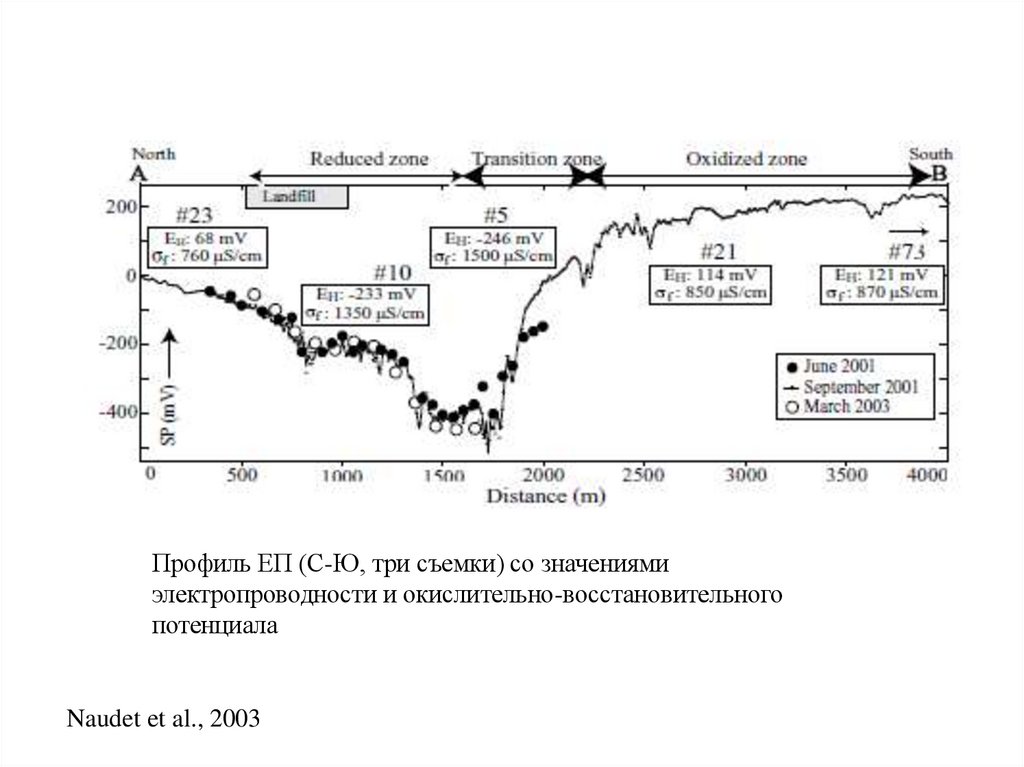
Профиль ЕП (С-Ю, три съемки) со значениями
электропроводности и окислительно-восстановительного
потенциала
Naudet et al., 2003

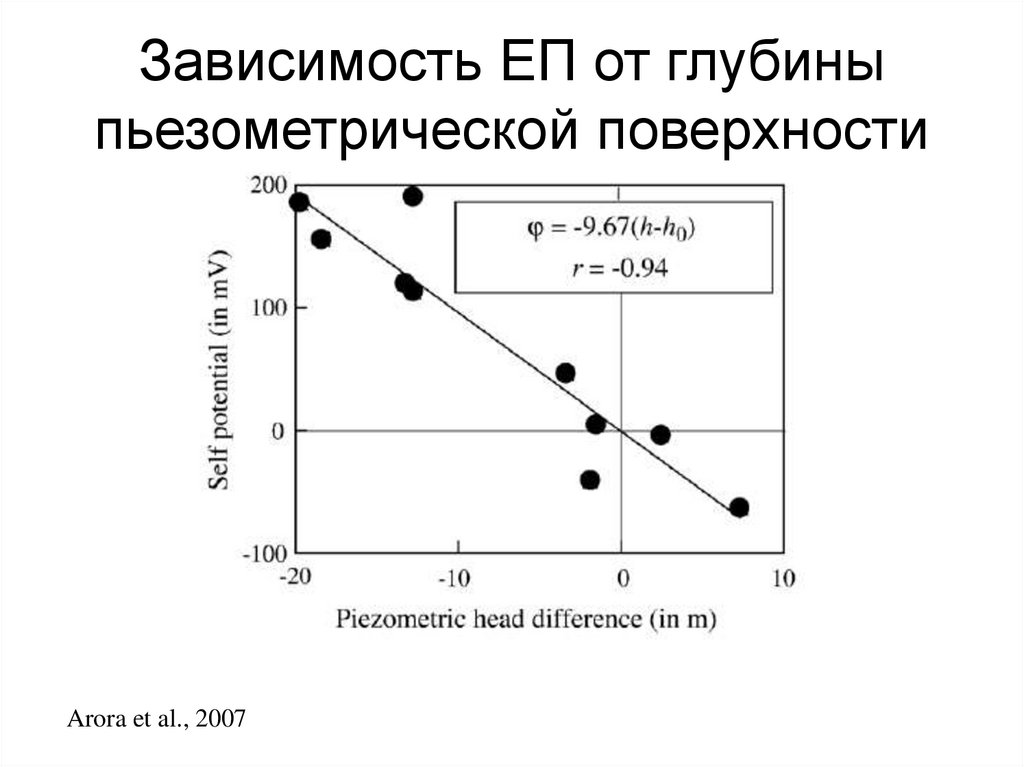
129. Зависимость ЕП от глубины пьезометрической поверхности

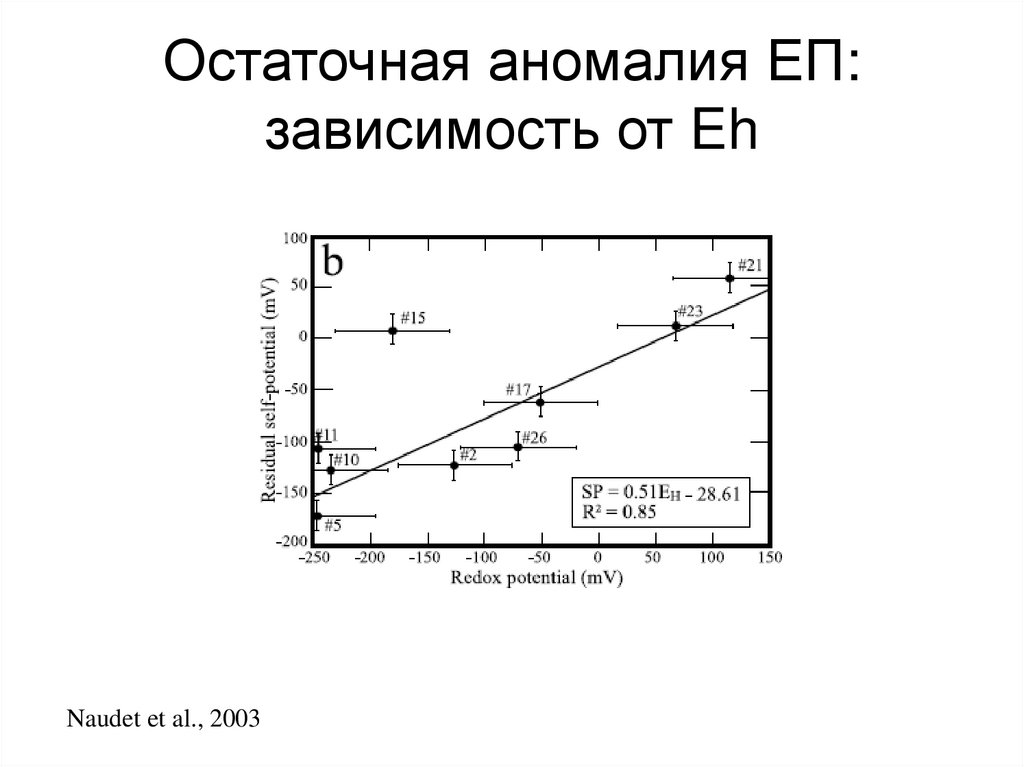
Arora et al., 2007

130. Остаточная аномалия ЕП: зависимость от Eh

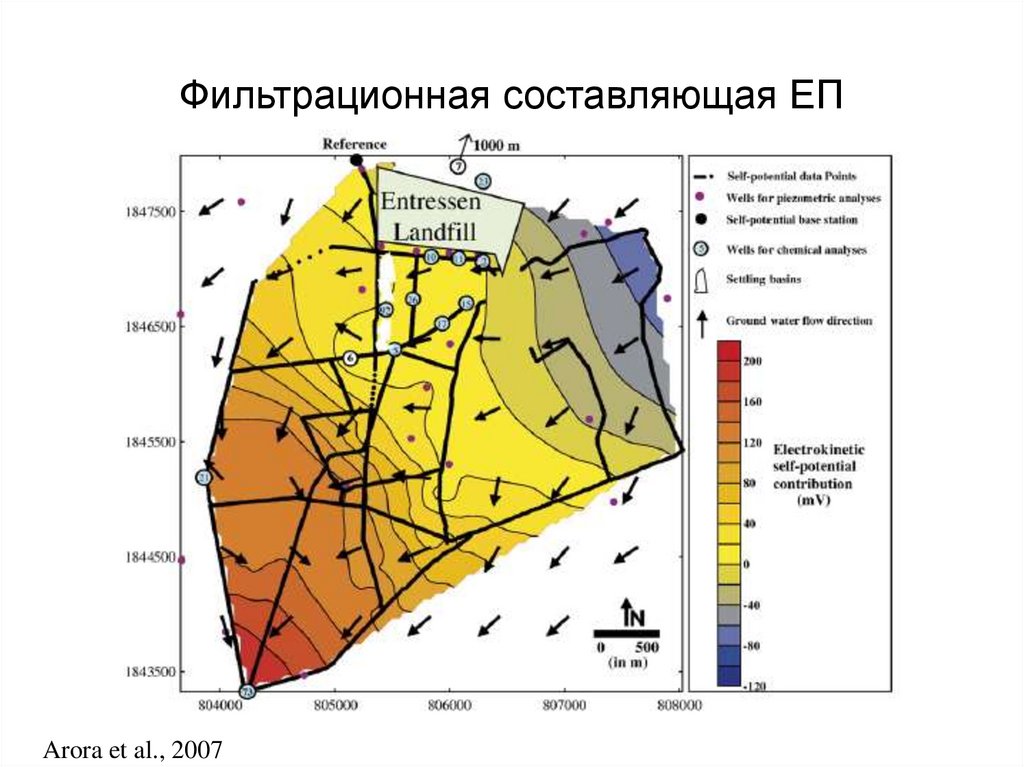
Naudet et al., 2003

131. Фильтрационная составляющая ЕП

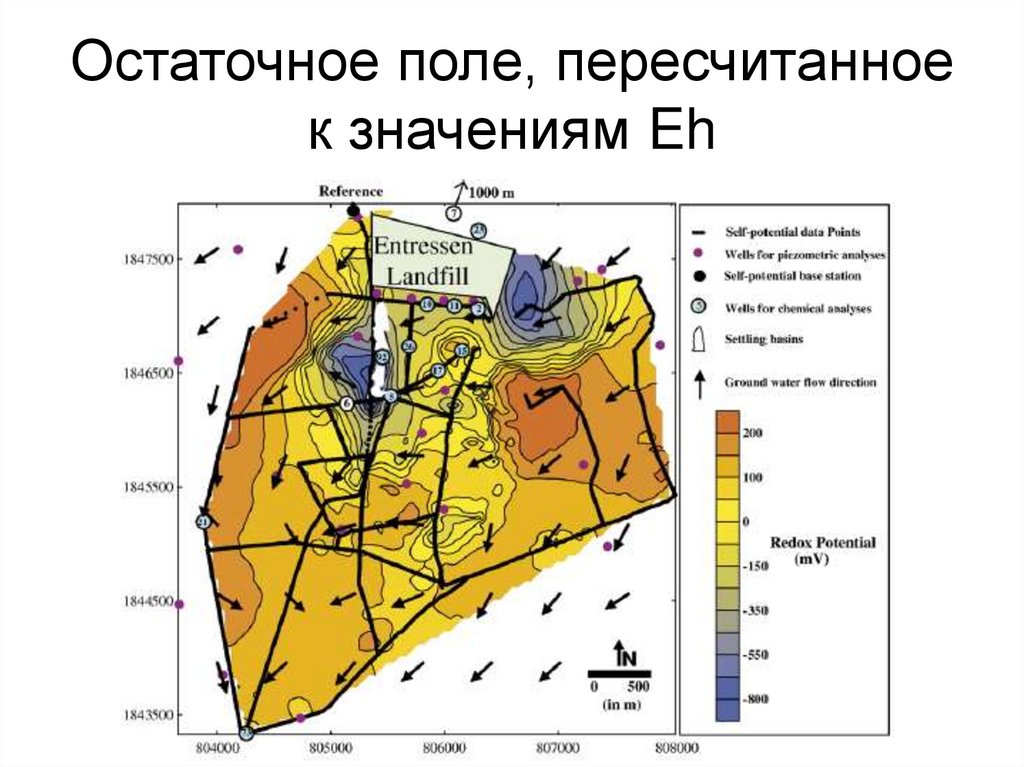
Arora et al., 2007

132. Остаточное поле, пересчитанное к значениям Eh

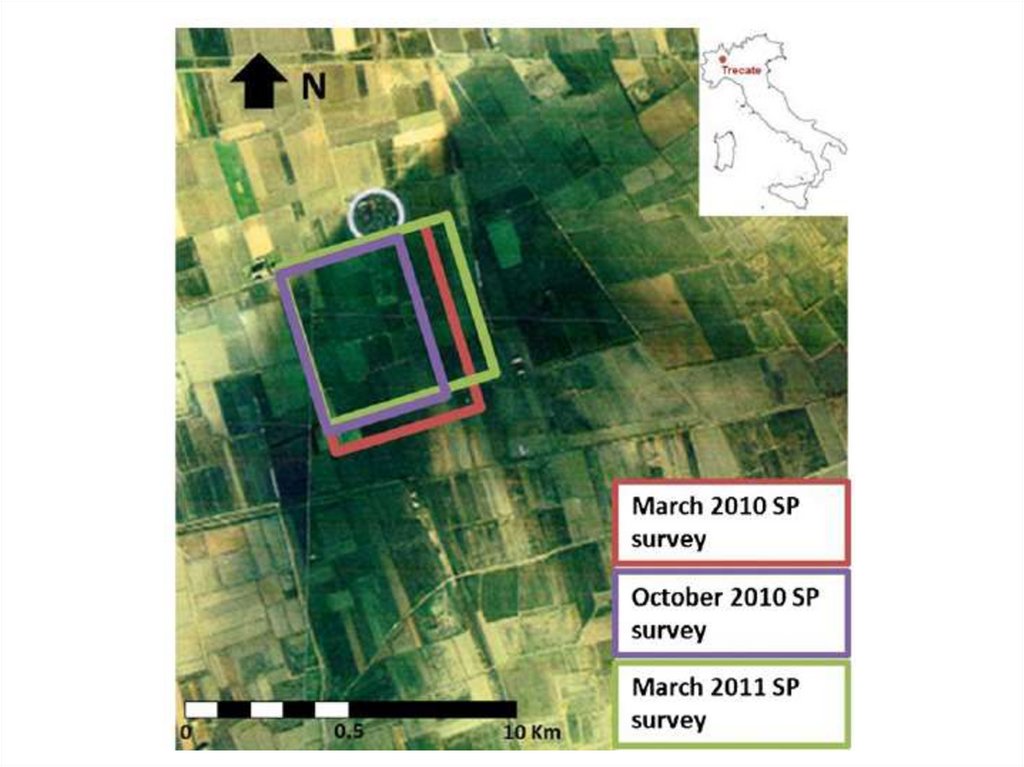
133. Пример 7: Нефтяное загрязнение (участок Трекато, сев. Италия)

Giampaolo et al. 2013

134.

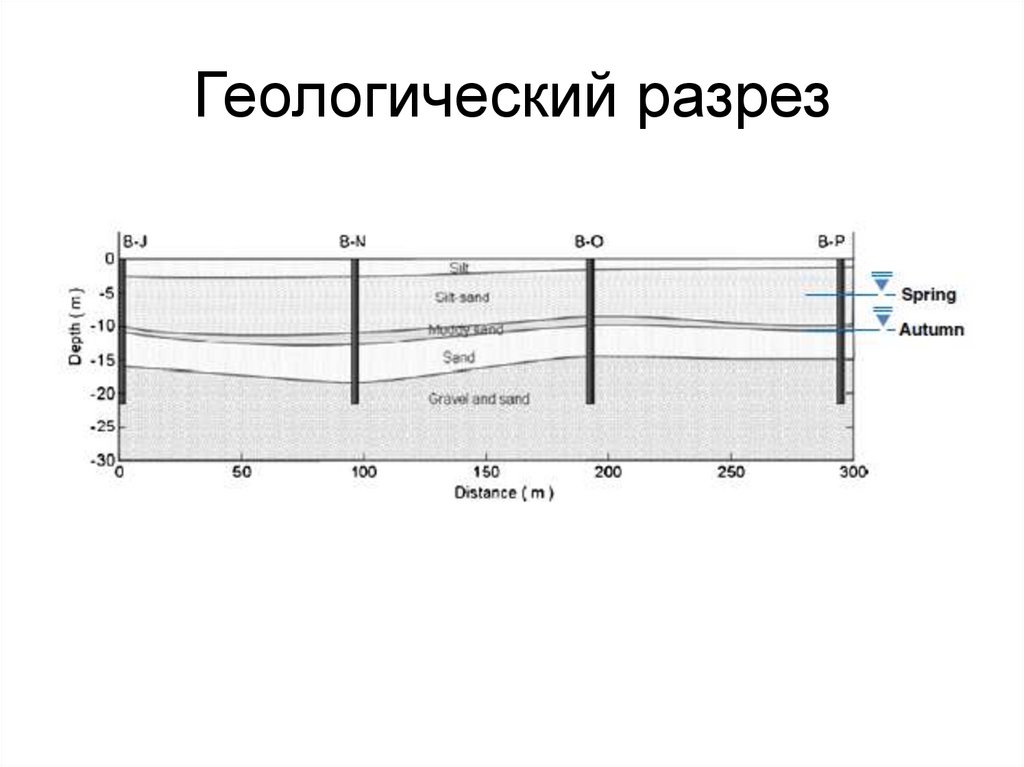
135. Геологический разрез

136. Пьезометрические поверхности в марте и ноябре 2007

137. Ореолы загрязнения на глубине 4 и 10 м

138. Профиль, пересекающий ореол загрязнения

139. Съемки ЕП в разные моменты времени

140. Съемки ЕП в разные моменты времени

141. Моделирование ЕП

142. Трансформанты ЕП Март 2010

143. Трансформанты ЕП: Октябрь 2010

144. Трансформанты ЕП: март 2011

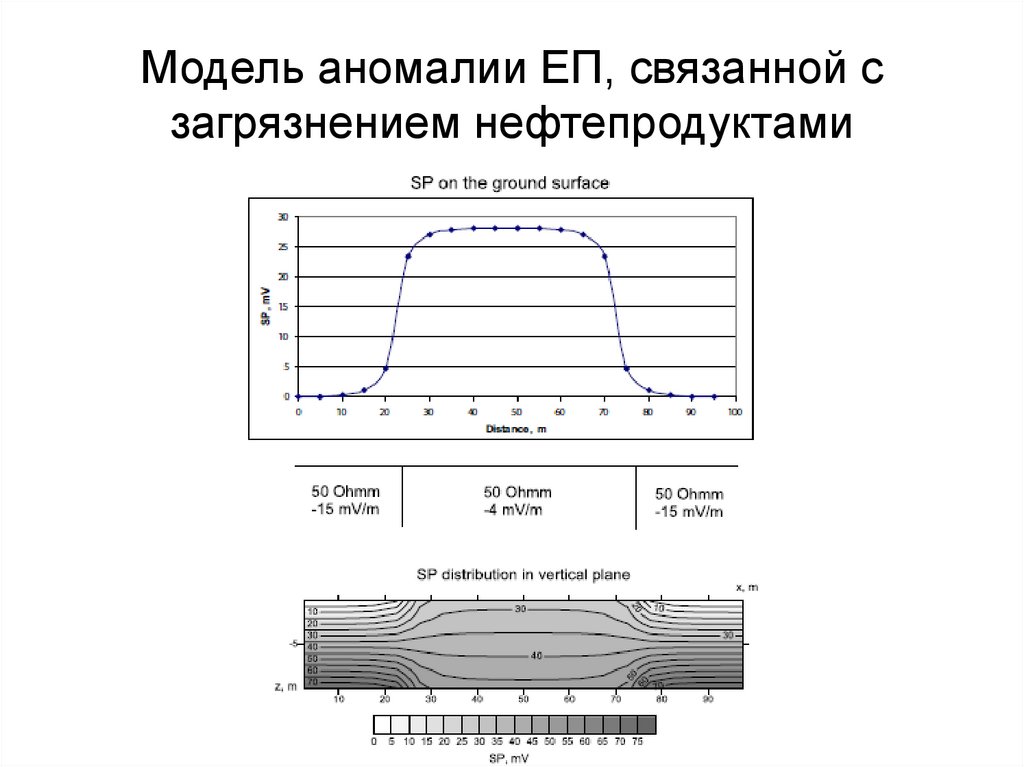
145. Модель аномалии ЕП, связанной с загрязнением нефтепродуктами

146. Пример 8. Перетекание между двумя водоносными горизонтами

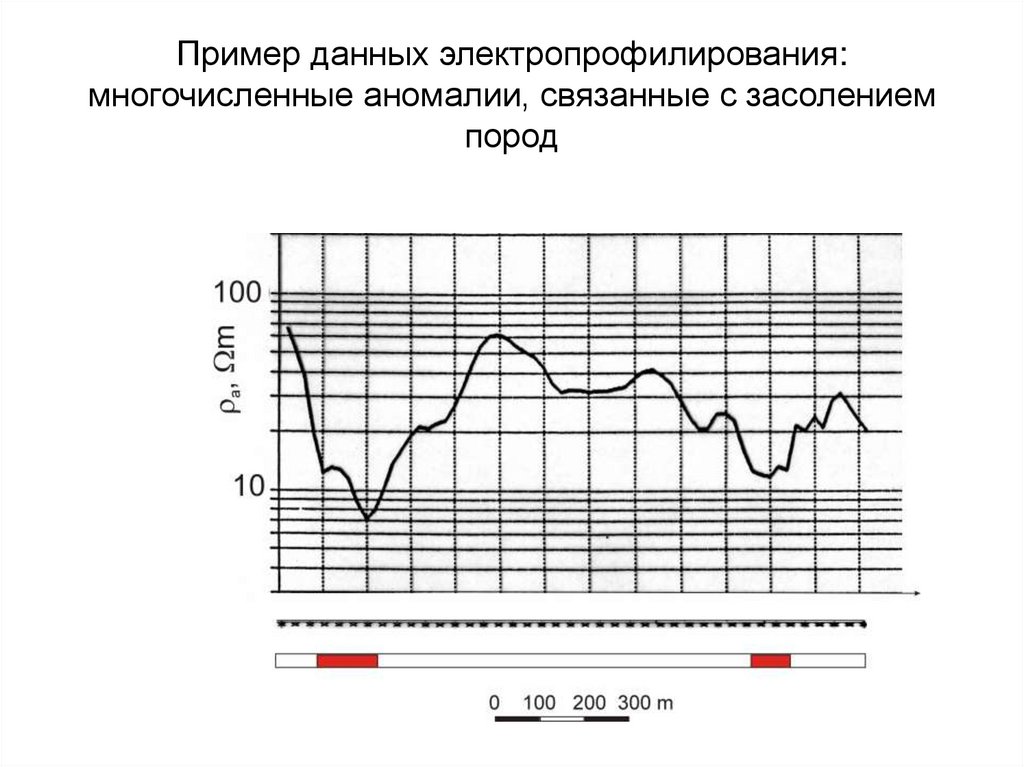
Ромашкинское месторождение

147. Пример данных электропрофилирования: многочисленные аномалии, связанные с засолением пород

148.

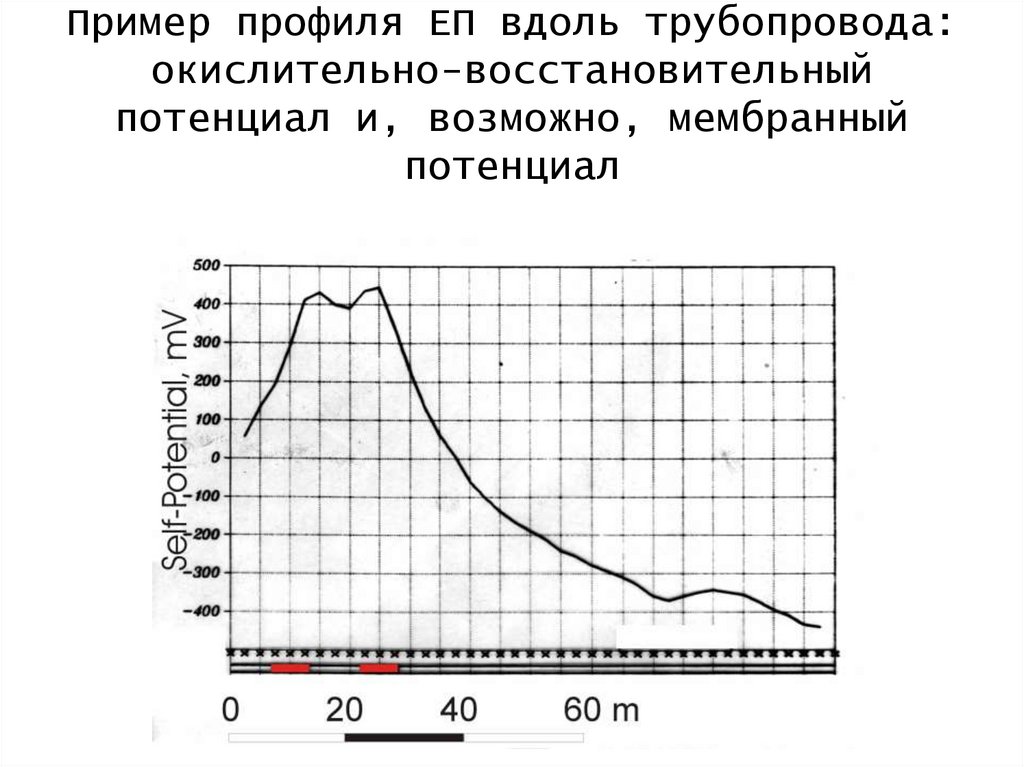
Пример профиля ЕП вдоль трубопровода:
окислительно-восстановительный
потенциал и, возможно, мембранный
потенциал

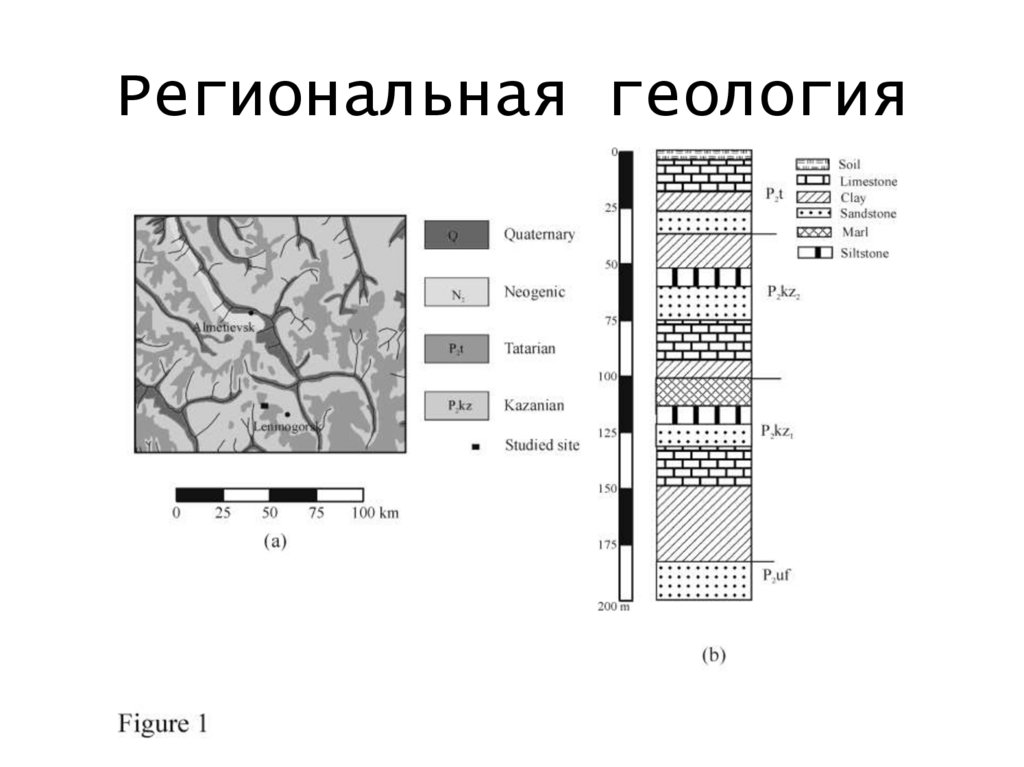
149.

Региональная геология

150.

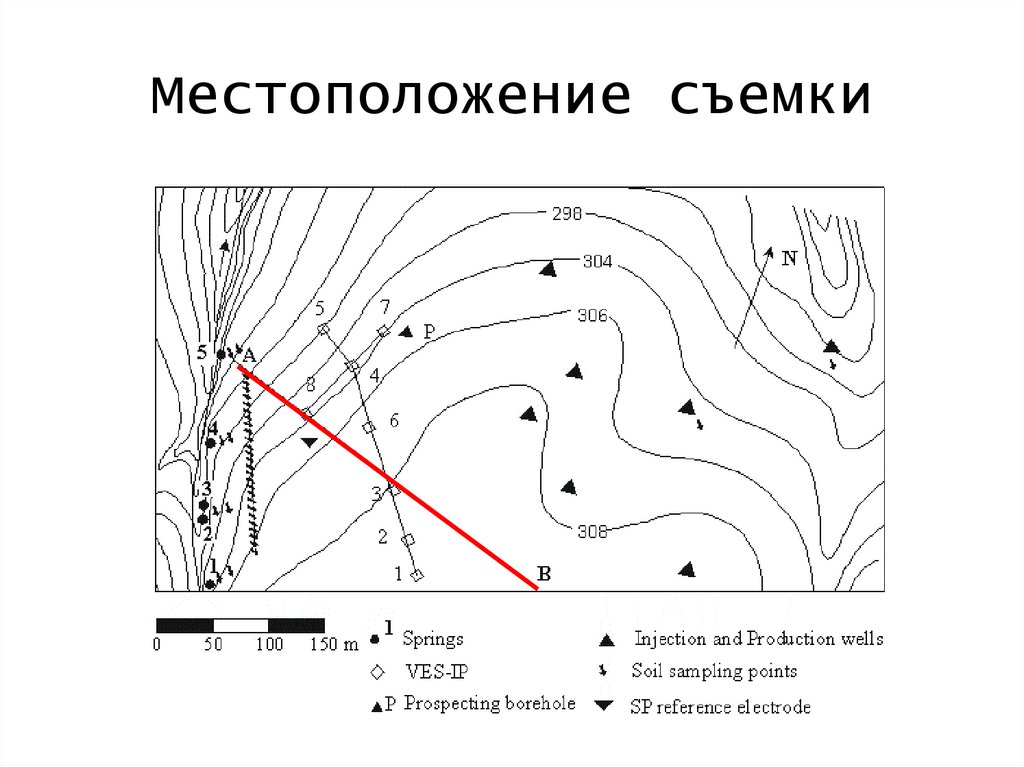
Местоположение съемки

151.

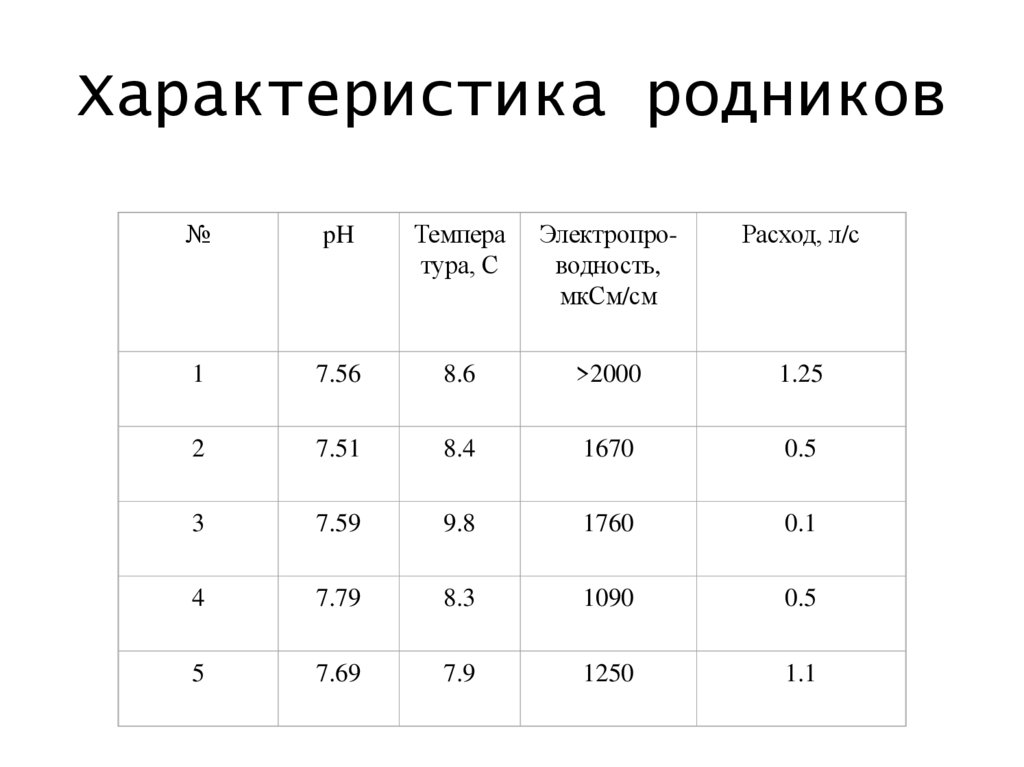
Характеристика родников
№
pH
Темпера
тура, С
Электропроводность,
мкСм/см
Расход, л/с
1
7.56
8.6
>2000
1.25
2
7.51
8.4
1670
0.5
3
7.59
9.8
1760
0.1
4
7.79
8.3
1090
0.5
5
7.69
7.9
1250
1.1

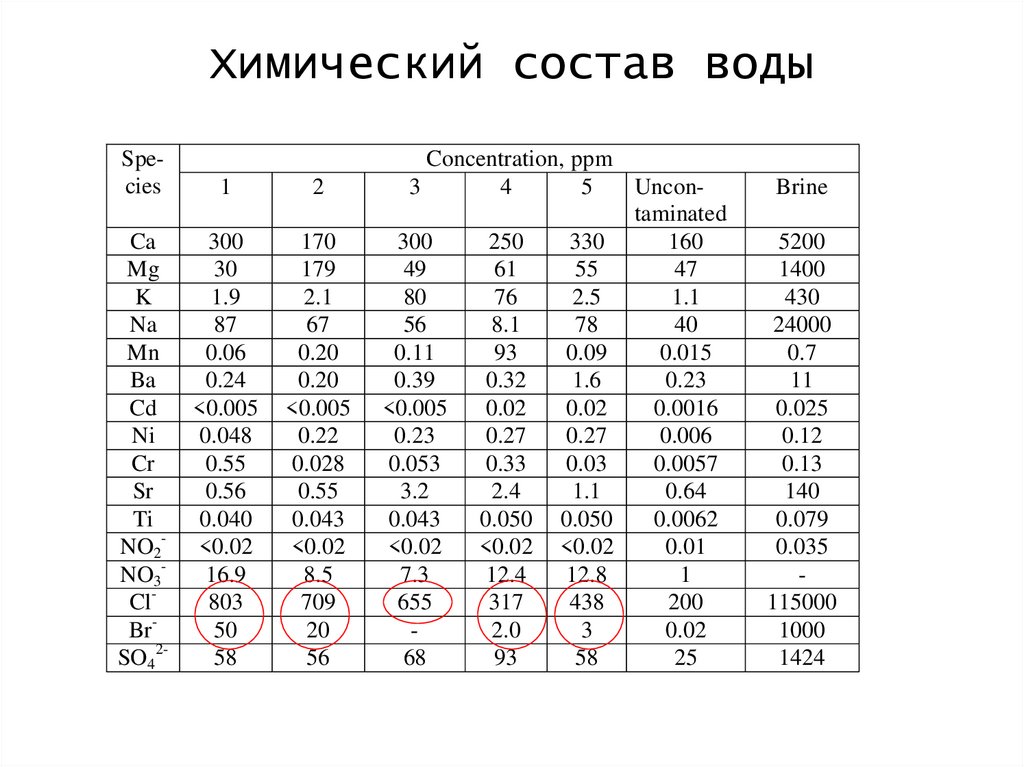
152.

Химический состав воды
Species
1
2
Ca
Mg
K
Na
Mn
Ba
Cd
Ni
Cr
Sr
Ti
NO2NO3ClBrSO42-
300
30
1.9
87
0.06
0.24
<0.005
0.048
0.55
0.56
0.040
<0.02
16.9
803
50
58
170
179
2.1
67
0.20
0.20
<0.005
0.22
0.028
0.55
0.043
<0.02
8.5
709
20
56
Concentration, ppm
3
4
5
Uncontaminated
300
250
330
160
49
61
55
47
80
76
2.5
1.1
56
8.1
78
40
0.11
93
0.09
0.015
0.39
0.32
1.6
0.23
<0.005
0.02
0.02
0.0016
0.23
0.27
0.27
0.006
0.053
0.33
0.03
0.0057
3.2
2.4
1.1
0.64
0.043
0.050 0.050
0.0062
<0.02
<0.02 <0.02
0.01
7.3
12.4
12.8
1
655
317
438
200
2.0
3
0.02
68
93
58
25
Brine
5200
1400
430
24000
0.7
11
0.025
0.12
0.13
140
0.079
0.035
115000
1000
1424

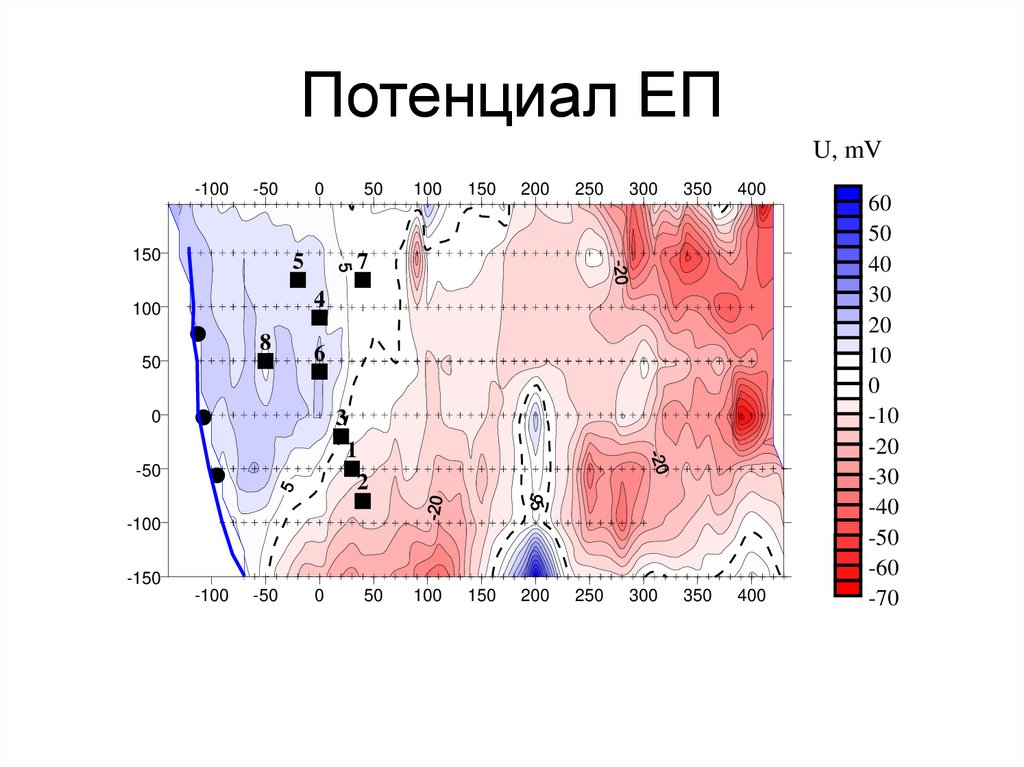
153. Потенциал ЕП

U, mV
-100
-50
150
0
5
50
100
150
200
250
300
350
400
100
150
200
250
300
350
400
7
4
100
8
50
6
3
1
2
0
-50
-100
-150
-100
-50
0
50
60
50
40
30
20
10
0
-10
-20
-30
-40
-50
-60
-70

154. Кажущееся сопротивление по данным дипольного профилирования

155. Типичная кривая ВЭЗ

156. Альтернативные модели ЕП

157. Выводы

• Усовершенствованная техника и методика позволяют
решать “динамические” задачи – мониторинг откачек и
наливов;
• Специализированные программы или программы
“Мультифизики” позволяют решать прямую задачу и
проводить количественную интерпретацию данных;
• Обязательное комплексирование с методом
сопротивления и другими методами, дающими
структурную характеристику;
• Основные помехи для изучения подземных вод –
источники поля в зоне аэрации;
• Последние представляют отдельный интерес, но
характеризуются существенной неопределенностью.

158. Литература

Bolève, A., Revil, A., Janod, F., Mattiuzzo, J.L., and Jardani, A [2007] Forward Modeling and validation of a new
formulation to compute self-potential signals associated with ground water flow. Hydrol. Earth Syst. Sci., 11, 1–11.
Darnet, M., Marquis, G. and Sailhac, P. [2003] Estimating aquifer hydraulic properties from the inversion of surface
Streaming Potential (SP) anomalies. Geophysical Research Letters 30, 1679, doi:10.1029/2003GL017631.
V. Giampaolo & E. Rizzo & K. Titov & P. Konosavsky & D. Laletina & A. Maineult & V. Lapenna [2013] Selfpotential monitoring of a crude oil-contaminated site (Trecate, Italy). Environ. Sci Pollut. Res. DOI 10.1007/s11356013-2159-y
Rizzo, E., Suski, B., Revil, A., Straface, S., and Troisi, S. [2004] Self-potential signals associated with pumping
tests experiments. Journal of Geophysical Research, 109, B10203, doi:10.1029/2004JB003049.
Titov, K., Revil, A., Konosavsky, P., Straface, S. and Troisi, S.[2005] Numerical modelling of self-potential signals
associated with a pumping test experiment. Geophysical Journal International., 162, 641–650.
Ntarlagiannis, D., Atekwana, E., Hill, E and Yuri Gorby, Y. [2007]. Microbial nanowires: Is the subsurface
‘‘hardwired’’? GEOPHYSICAL RESEARCH LETTERS, VOL. 34, L17305, doi:10.1029/2007GL030426, 2007.
Nyquist J. and Corry C. Self-Potential the ugly duckling of environmental geophysics. THE LEADING EDGE MAY
2002.
Revil, A., V. Naudet, J. Nouzaret, and M. Pessel, Principles of electrography applied to self-potential electrokinetic
sources
and hydrogeological applications, Water Resour. Res., 39(5), 1114, doi:10.1029/2001WR000916, 2003.
Revil, A., C. A. Mendonc¸a, E. A. Atekwana, B. Kulessa, S. S. Hubbard, and K. J. Bohlen (2010), Understanding
biogeobatteries: Where geophysics meets microbiology, J. Geophys. Res., 115, G00G02,
doi:10.1029/2009JG001065.
Sill W. Self-potential modeling from primary flows. GEOPHYSICS, VOL. 48, NO. 1 (JANUARY 1983); P. 76-86.
Titov K., Lukhmanov L., and Potapov A., Monitoring of water seepage from a reservoir using resistivity and selfpolarization method: case hystory of the Petergof water fountain water supply system. First break , 10.2000.
Naudet et al., Relationship between self-potential (SP) signals and redox conditions in
contaminated groundwater. GEOPHYSICAL RESEARCH LETTERS, VOL. 30, NO. 21, 2091,
doi:10.1029/2003GL018096, 2003