Использование комбинаторных объектов в теории вероятности. Комбинаторика

1. Использование комбинаторных объектов в теории вероятности

2. Комбинаторика – это раздел математики, посвящённый задачам выбора и расположения предметов из раздела множеств. Типичной

задачей комбинаторики
является задача перечисления
комбинаций, составленных из
нескольких предметов.

3. Правила суммы и произведения

• Если первое событие может произойти n1
способами, а второе - n2 способами
независимо от первого, то совместная
реализация может произойти n1 n2
способами.
• Если первое событие может произойти n1
способами, а второе - n2 способами
независимо от первого, то первое или второе
события могут произойти n1+n2 способами.

4. Пример 1

Абонент набирая номер телефона, забыл
последние 2 цифры, но помнит, что обе
цифры четные и различные. Какова
вероятность того, что набирая номер
наудачу, он попадет в нужное место?
Ответ: 1 / 20

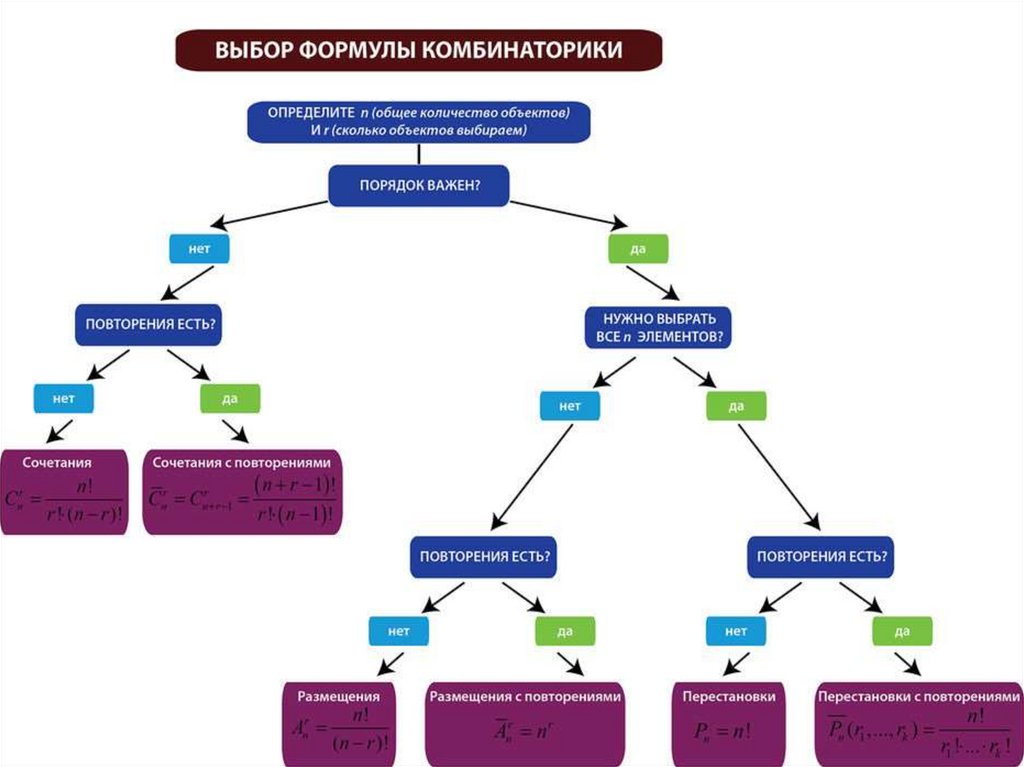
5.

6. Сочетания без повторений

Пример 1. Множество Е содержит 10 первых
букв русского алфавита. Какова вероятность
того, что случайно выбранный алфавит из
трех букв будет содержать букву «a»?
• Ответ: 36 / 120

7. Размещения

Набирая номер телефона, абонент
забыл две последние цифры и набрал
их наудачу. Найти вероятность
дозвониться в нужное место с первого
раза, если он помнил, что цифры
различны и нечетны.
Ответ: 1 / 20

8. Перестановки

Пример 3. За круглый стол на 9 стульев в
случайном порядке рассаживаются 7
мальчиков и 2 девочки. Найдите
вероятность того, что обе девочки будут
сидеть рядом.
Ответ: 0,25

9. Сочетания с повторениями

Пример 4. В библиотеке имеются книги по 16
разделам науки. Поступили очередные
четыре заказа на литературу. Считая, что
любой состав заказанной литературы
равновозможен, найти вероятности
следующих событий: А - заказаны книги из
различных разделов наук, В - заказаны книги
из одного и того же раздела науки.
Ответ: 0,47; 0,004

10. Размещения с повторениями

Пример 5. Опыт состоит в
четырехкратном выборе с
возвращением одной из букв алфавита
E = {а, б, к, о, м} и выкладывании слова
в порядке поступления букв. Какова
вероятность того, что в результате
будет выложено слово «мама»?
Ответ: 0,0016

11. Упорядоченные разбиения

Пример 6. Десять приезжих мужчин,
среди которых Петров и Иванов,
размещаются в гостинице в два
трехместных и один четырехместный
номер. Какова вероятность того, что
Петров и Иванов попадут в
четырехместный номер?
Ответ: 2 / 15