Similar presentations:
Комбинаторика и теория вероятности
1.
Автор проекта:Трищенко Виктория
Руководитель проекта:
Науменко Р.А.
2.
Умение решать комбинаторные задачи пригодиться ученикам вразных жизненных ситуациях и на многих уроках в школе.
Комбинаторные задачи встречаются в учебниках математики 5 и 6
классов. Данная тема включена на ГИА в 9 классе и ЕГЭ в 11 классе.
Накопление опыта решения комбинаторных задач и использования
теории вероятности расширяет кругозор, показывает
использование комбинаторики в смежных дисциплинах, поэтому
данная тема является актуальной.
3.
КомбинаторикаКомбинаторика — раздел математики, изучающий дискретные
объекты, множества сочетания, перестановки, размещения и перечисления
элементов, отношения на них (например, частичного порядка).
Комбинаторика – раздел математики, который изучает задачи выбора и
расположения элементов из некоторого основного множества в соответствии с
заданными правилами.
Формулы и принципы комбинаторики используются в теории вероятностей для
подсчета вероятности случайных событий и, соответственно, получения законов
распределения случайных величин.
Это, в свою очередь, позволяет исследовать закономерности массовых
случайных явлений, что является весьма важным для правильного
понимания статистических закономерностей, проявляющихся в природе и
технике.
4.
Сколько двухзначных чисел можно составитьиспользуя цифры 1,2,3 так, чтобы цифры в
числе не повторялись?
12, 13, 21, 23, 31, 32
Ответ: 6 чисел
5.
Простейшие комбинаторные задачи несколько напоминаютдетскую игру в кубики. Имеется конечное число кубиков, а нужно
посчитать количество тех или иных комбинаций, составленных из
этих кубиков. Если нужных комбинаций не слишком много, то все
их можно просто перечислить, или, как говорят, перебрать все
возможности - метод перебора вариантов. Хорошо подобранный
перебор вариантов крайне важен в более сложных ситуациях, когда
и количество возможных комбинаций достаточно велико, и подсчет
этого количества приходится вести, рассматривая различные
случаи.
6.
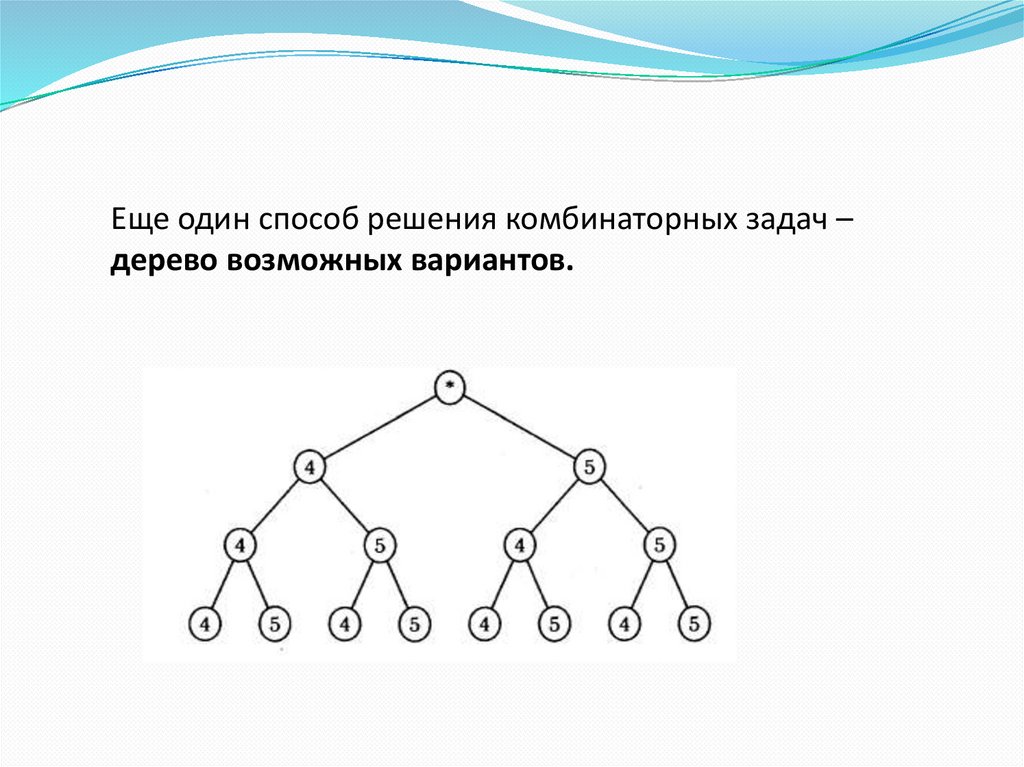
Еще один способ решения комбинаторных задач –дерево возможных вариантов.
7.
Идя на тренировку, спортсмен надевает либо майку, либо футболку.Сколько вариантов выбора (майки или футболки) у него имеется, если
его мама приготовила 3 майки и 4 футболки?
По правилу сложения 3 + 4 = 7
Ответ: 7 вариантов
8.
Для того, чтобы найти число всех возможных исходов независимoго проведениядвух испытаний А и Б, следует перемножить число всех исходов испытания А и
число всех исходов испытания Б – правило умножения
Если два действия А и В взаимно исключают друг друга, причем действие А
можно выполнить m способами, а В – n способами, то выполнить одно любое из
этих действий (либо А, либо В) можно n + m способами – правило сложения
Если в условии звучит И, то выбираем правило умножения.
Если в условии звучит ИЛИ, то пользуемся правилом сложения.
9.
Цех по изготовлению головных уборов начал выпуск трех новыхмоделей, для которых был закуплен фетр четырех цветов. Сколько
видов разных шляп может изготовить цех?
Для каждой из трех моделей можно использовать каждый из
четырех цветов
По правилу умножения 3 * 4 = 12
Ответ: 12 видов
10.
В классе учится 16 мальчиков и 10 девочек. Сколькими способамиможно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е.
дежурным может быть любой из 16 мальчиков, либо любая из 10
девочек.
По правилу суммы 16+10=26 способами.
Ответ: 26 способов
11.
Комбинаторные задачи с ограничениями.На столе лежат 6 карточек с цифрами 0, 1, 2, 3, 4, 5. С помощью этих карточек
сколько можно составить различных
а) шестизначных чисел?
б) шестизначных нечетных чисел?
Решение:
Учитывая, что на перовом месте не может стоять O.
а) на первом месте может стоять любая из 5 цифр, на втором – любая из 5, на
третьем- любая из 4 оставшихся и т.д. Всего чисел = 5*5*4*3*2*1=600
б) на последнем место может стоять 1 или 3 или 5. Действуем аналогично а,
получаем 4*4*3*2*1=96, 96*3=288
Ответ: а) 600 б) 288
12.
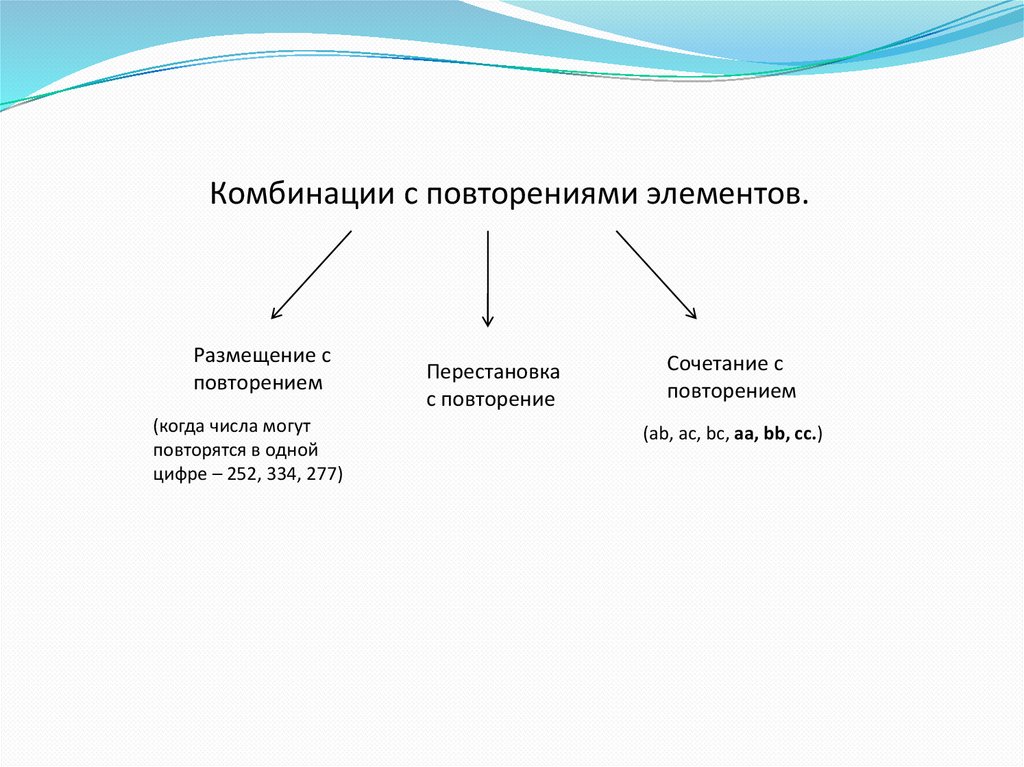
Комбинации c повторениями элементов.Размещение с
повторением
(когда числа могут
повторятся в одной
цифре – 252, 334, 277)
Перестановка
с повторение
Сочетание с
повторением
(ab, ac, bc, aa, bb, cc.)
13.
Области применения комбинаторикиХимия (анализ возможных связей между химическими
элементами)
Экономика (анализ вариантов купли-продажи акций, азартные игры
(подсчет частоты выигрышей)
Криптография (разработка методов шифрования)
Доставка почвы (рассмотрение вариантов пересылки)
Военное дело (расположение подразделений)
14.
Теория вероятностейТеория вероятностей — раздел математики, изучающий случайные
события, случайные величины, их свойства и операции над ними.
Мы постоянно наблюдаем множество событий, которые произошли, а могли и
не произойти. 1 декабря у нас шел снег, но могла быть и ясная погода .
Стрелок выстрелил в мишень и попал, но мог и промахнуться.
• Событие, которое может произойти, а может и не произойти, называется
случайным.
• Событие, которое обязательно происходит, называется достоверным.
• Событие, которое заведомо не может произойти, называется невозможным
15.
Вероятностью события А называется отношение количестваблагоприятных исходов к общему количеству исходов. (классическая)
P - вероятность события.
m - благоприятные исходы.
n - все возможные исходы.
В колоде 36 карт. Из нее наугад вынули одну карту. Событие «это карта пиковой
масти» обозначим буквой С.
P(C) = 9/36=1/4
16.
В некоторых ситуациях случайные события изучает статистика. Напримерметеорологи знают для данного места среднюю температуру воздуха в любой
день года.
Статическая вероятность: вероятность случайного события называется
число, к которому приближаются частоты наступления этого события при
возрастании числа испытаний (наблюдений).
Например, в разных странах и в разные годы частоты рождения мальчиков
приближаются к числу 0,517
17.
Операция над событиямиДля каждого события А можно рассматривать события, заключающееся в том,
что событие А не произошло . Оно называется противоположным А и
обозначается .
Если событие А – стрелок попал в мишень, то событие - стрелок
промахнулся
18.
Правило суммы: событие, состоящее в том, что происходит хотя бы одноиз событий А или Б – сумма событий А и Б.
Пример: Пусть событие А – при одном броске кубика выпала 1 , событие Б – при
одном броске выпала 2. Тогда событие А+Б – при одном броске кубика выпало
меньше 3 очков.
Правило умножения: событие, состоящее в том, что происходят оба
события (и А, и Б) – произведение событий А и Б
Пример: Событие А – из карточной колоды вынут туз, событие Б – из карточной
колоды вынута карта пиковой масти. Тогда АБ – из карточной колоды вынут
пиковый туз.
19.
Условная вероятностьВероятность произведения независимых событий равна произведению
вероятностей этих событий.
p(AB)=p(A)*p(B)
Пример: Монету подбросили два раза. Какова вероятность того, что орел выпал
дважды?
Вероятность появления орла при первом броске и при втором броске ½. Эти
события независимые. Поэтому p=1/2*1/2=1/4
20.
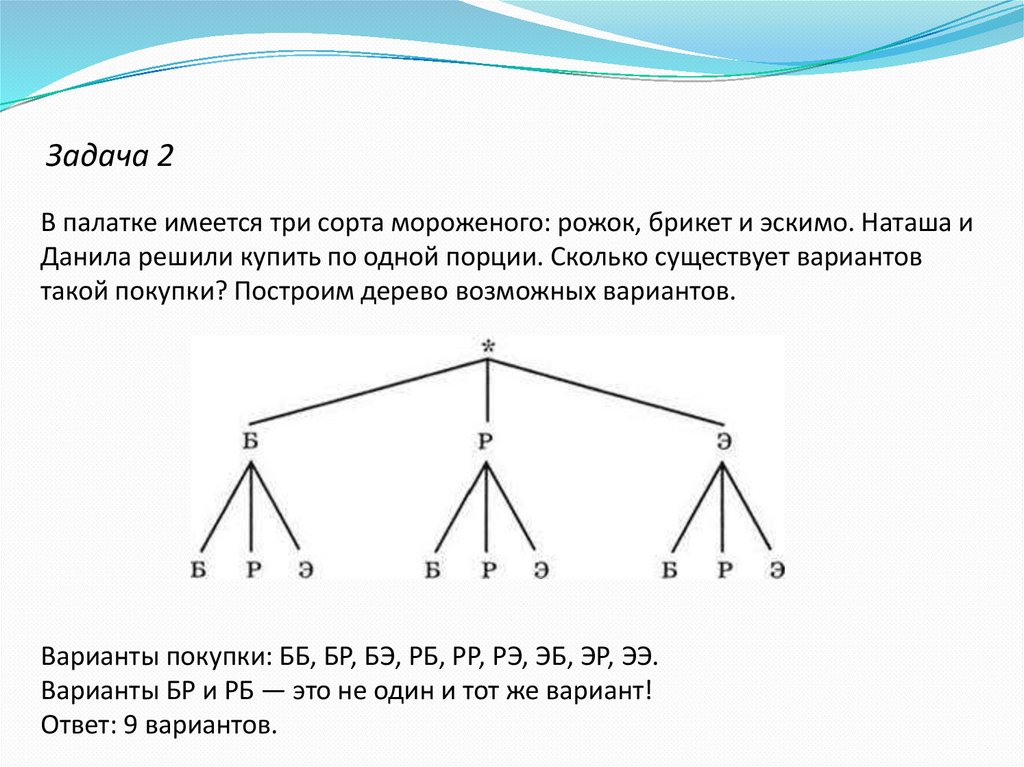
Задача 2В палатке имеется три сорта мороженого: рожок, брикет и эскимо. Наташа и
Данила решили купить по одной порции. Сколько существует вариантов
такой покупки? Построим дерево возможных вариантов.
Варианты покупки: ББ, БР, БЭ, РБ, РР, РЭ, ЭБ, ЭР, ЭЭ.
Варианты БР и РБ — это не один и тот же вариант!
Ответ: 9 вариантов.


















 mathematics
mathematics








