Элементы комбинаторики и теории вероятностей

1. Элементы комбинаторики и теории вероятностей

ЭЛЕМЕНТЫ
КОМБИНАТОРИКИ
И ТЕОРИИ
ВЕРОЯТНОСТЕЙ

2.

3.

4.

Возникновение теории вероятностей в современном смысле слова
относится к середине XVII века и связано с исследованиями Паскаля
(1623-1662), Ферма (1601-1665) и Гюйгенса (1629-1695) в области теории
азартных игр. В этих работах постепенно сформировались такие важные
понятия, как вероятность и математическое ожидание; были установлены
их основные свойства и приемы их вычисления. Наряду с задачами
азартных игр уже в самом начале возникновения теории вероятностей
появились задачи, связанные с составлением таблиц смертности
и вопросами страхования. В Лондоне уже с 1592 года велись точные записи
о смертности.
Б. Паскаль
П.Ферма
Х. Гюйгенс

5.

Крупный шаг вперед в развитии теории вероятностей связан с работами
Якова Бернулли (1654-1705). Ему принадлежит первое доказательство
одного из важнейших положений теории вероятностей – так называемый
закон больших чисел. Он гласит: явления, вероятностные при их малом
числе, при большом количестве становятся закономерными, при очень
большом – неизбежными.
Яков Бернулли

6.

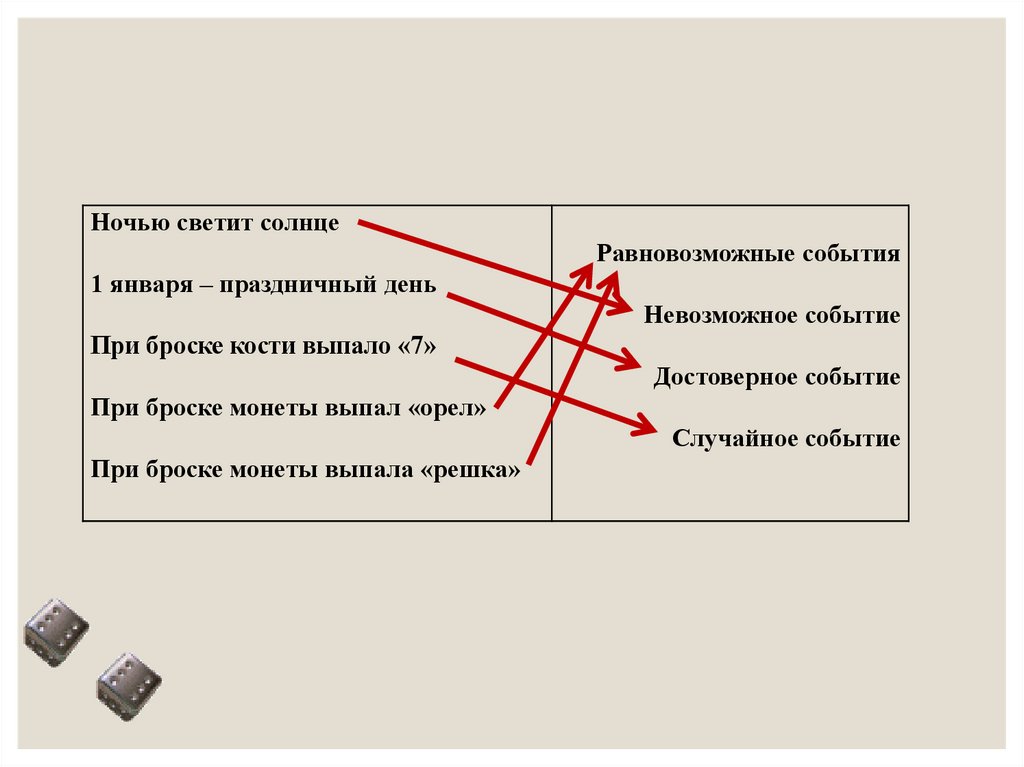
Ночью светит солнце
Равновозможные события
1 января – праздничный день
Невозможное событие
При броске кости выпало «7»
Достоверное событие
При броске монеты выпал «орел»
Случайное событие
При броске монеты выпала «решка»

7.

СЛУЧАЙНОЕ -
событие, которое может произойти, а может и не
произойти.
НЕВОЗМОЖНОЕ -
событие, которое в данных условиях (опыте) не
может произойти.
РАВНОВОЗМОЖНЫЕ - события, любое из которых не обладает никаким
преимуществом появляться чаще при
многократных испытаниях
ДОСТОВЕРНОЕ -
событие, которое при данных условиях всегда
произойдет

8.

Вероятностью события А называется
отношение числа благоприятных исходов
для события А к числу всех
равновозможных исходов.
k
- формула Лапласа
Р ( А)
n
n - число равновозможных исходов
k - число благоприятных исходов события А

9.

Алгоритм нахождения вероятности
1.Определить, что является элементарным
событием А.
2.Найти общее число элементарных событий N.
3.Определить, какие элементарные события
благоприятствуют событию А, и найти их число
N(A).
4.Найти вероятность Р(А) события А
N ( A)
P ( A)
N

10.

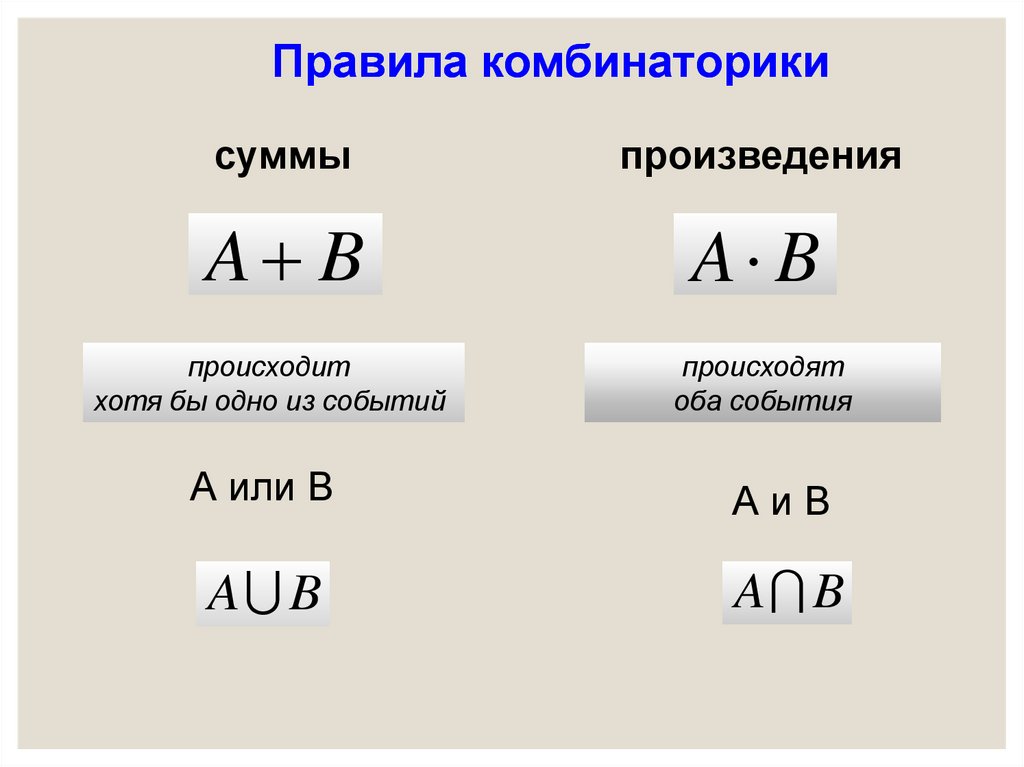
Правила комбинаторики
суммы
произведения
A B
A B
происходит
хотя бы одно из событий
происходят
оба события
А или В
АиВ
A B
A B

11. У двух школьников по четыре шариковых ручки (красная, зелёная, синяя и чёрная). Они наугад обменялись одной ручкой. Какова

вероятность того, что у одного из них
окажется две ручки чёрного цвета?
-
1
4
-вероятность того, что первый школьник
станет обменивать чёрную ручку
3
4
-вероятность того, что второй школьник станет
обменивать ручку другого цвета
Вероятность того, что обе чёрные ручки окажутся у второго школьника
1 3 3
4 4 16
Т.к. по условию школьники
не пронумерованы,
то искомая вероятность
3 3
2 0,375
16 8

12.

Выбор формулы
Учитывается ли
порядок следования элементов?
да
нет
Все ли элементы входят в
соединение?
да
нет
перестановки
размещения
Pn n!
n!
A
(n k )!
k
n
сочетания
Cnk
n!
k!(n k )!