Similar presentations:
Задачи по теории вероятностей
1. Задачи по теории вероятностей
2.
Математику, физику и психологузадают одну и ту же задачу:
"Монету бросили 100 раз, и все 100 раз выпала решка.
Что выпадет в 101-ый раз?"
Математик:"С вероятностью 1/2 выпадет орёл"
Физик: "Эксперимент показал, что должна выпасть решка"
Психолог: "Выпадет орёл".
Математик с физиком: "Но почему?"
-Ну, как же, всё решка да решка! Орлу ведь тоже хочется!
3.
«В 2012 году в ЕГЭ впервые войдут заданияпо теории вероятностей, естественно,
это будут простейшие задачи»
И.Высоцкий
Алгоритм нахождения вероятности
1.Определить, что является элементарным событием А.
2.Найти общее число элементарных событий N.
3.Определить, какие элементарные события
благоприятствуют событию А, и найти их число N(A).
4.Найти вероятность Р(А) события А
N ( A)
P ( A)
N
4.
На чемпионате по прыжкам в воду выступают 25 спортсменов,среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок
выступлений определяется жеребьёвкой. Найдите вероятность
того, что шестым будет выступать прыгун из Парагвая
N ( A) 9
P( A)
0,36
N
25
5.
Перед началом первого тура чемпионата по бадминтонуучастников разбивают на игровые пары случайным образом
с помощью жребия. Всего в чемпионате участвует 26
бадминтонистов, среди которых 10 участвуют из России, в
том числе Руслан Орлов. Найдите вероятность того, что в
первом туре Руслан Орлов будет играть с каким-либо
бадминтонистом из России.
Для Орлова возможны 25 партнеров, из них 9 русские
N ( A) 9
P( A)
0,36
N
25
6.
В группе иностранных туристов 51 человек, среди них2 француза. Для посещения маленького музея группу
случайным образом делят на 3 подгруппы,
одинаковые по численности. Найдите вероятность
того, что французы окажутся в одной подгруппе.
Будем считать, что первый француз уже занял место в какой-то
подгруппе. В каждой подгруппе 17 человек. Вероятность того, что
второй француз попадёт в ту же группу, что и первый, равна
N ( A) 16
P( A)
0,32
N
50
7.
Двое играют в кости - они по разу бросают игральный кубик.Выигрывает тот, у кого больше очков. Если выпадает поровну, то
наступает ничья. Первый бросил кубик, и у него выпало 4 очка.
Найдите вероятность того, что он выиграет.
Первый выиграет, если у второго
выпадет 1, 2 или 3.
N ( A) 3
P( A)
0,5
N
6
8.
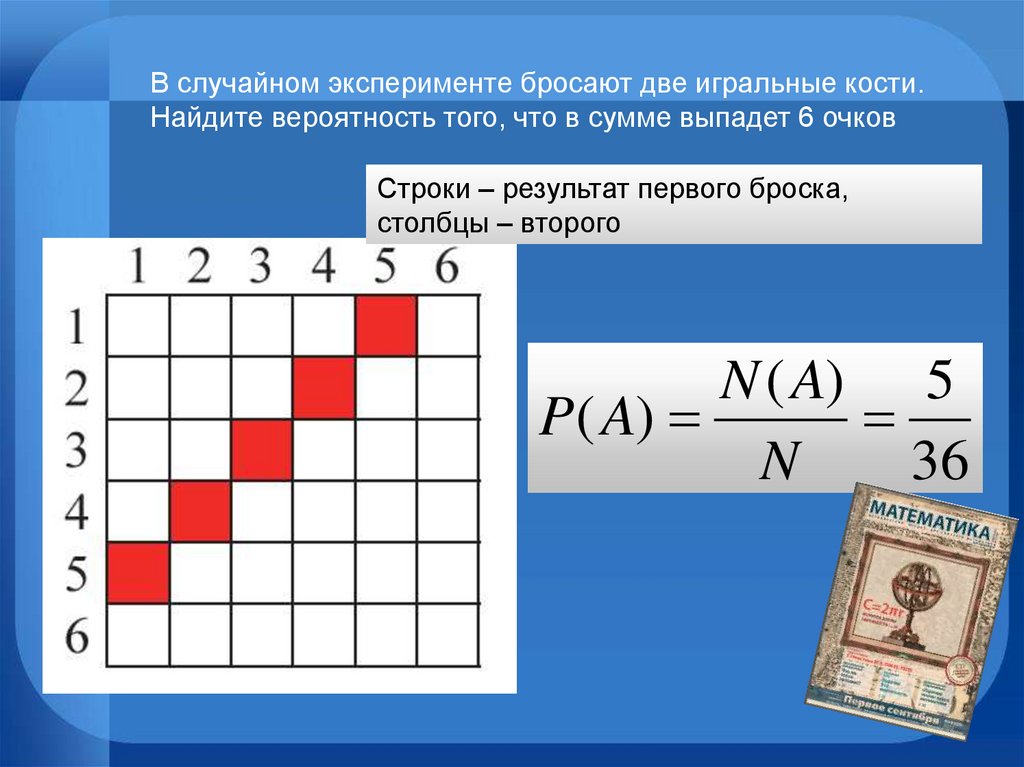
В случайном эксперименте бросают две игральные кости.Найдите вероятность того, что в сумме выпадет 6 очков
Строки – результат первого броска,
столбцы – второго
N ( A) 5
P( A)
N
36
9.
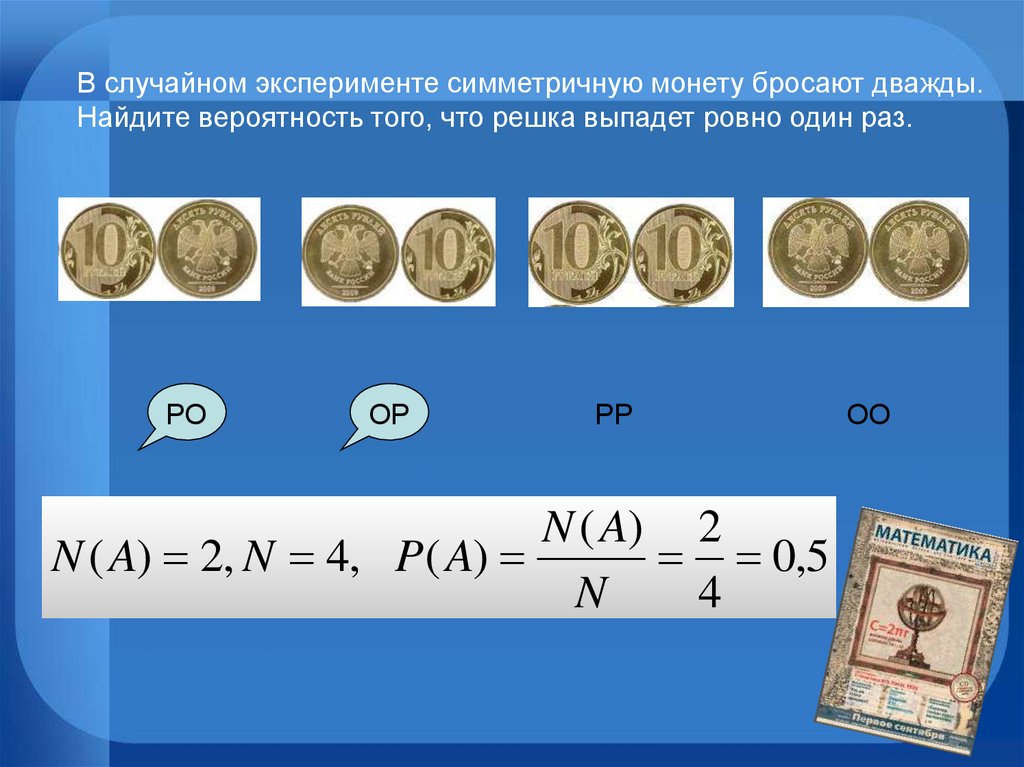
В случайном эксперименте симметричную монету бросают дважды.Найдите вероятность того, что решка выпадет ровно один раз.
РО
ОР
РР
N ( A) 2
N ( A) 2, N 4, P( A)
0,5
N
4
ОО
10.
Монету бросают трижды. Найдите вероятность того,что первые два броска оканчиваются одинаково.
ОР
ОО
РО
N ( A) 2
P( A)
0,5
N
4
РР
11.
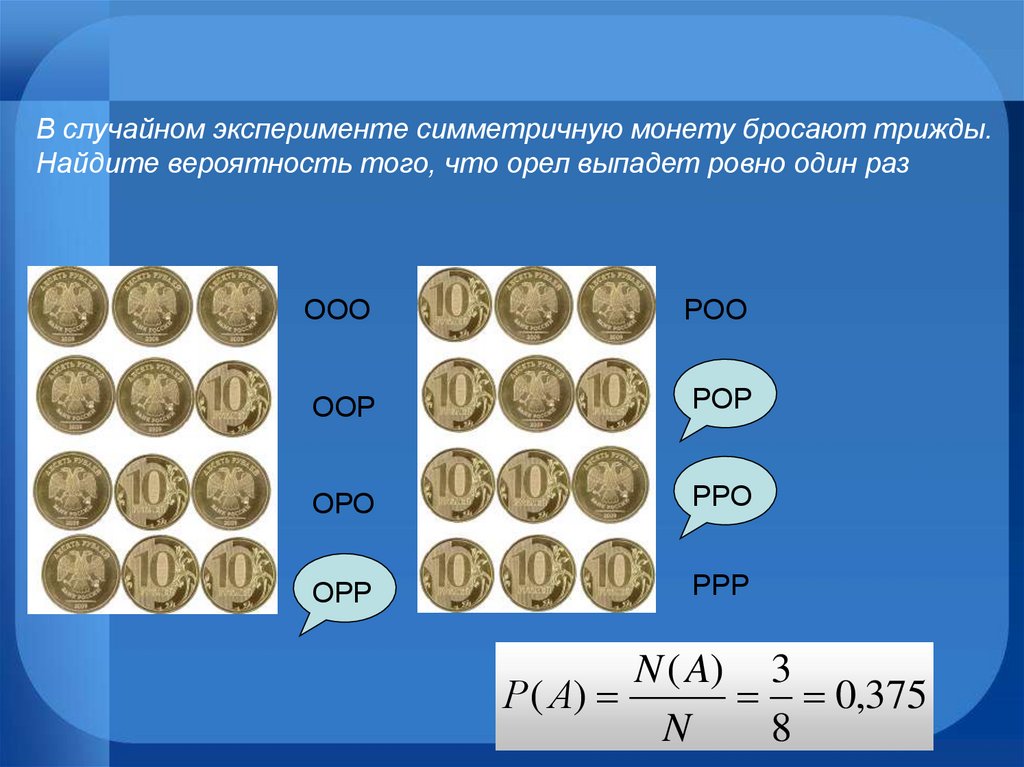
В случайном эксперименте симметричную монету бросают трижды.Найдите вероятность того, что орел выпадет ровно один раз
ООО
РОО
ООР
РОР
ОРО
РРО
ОРР
РРР
N ( A) 3
Р( А)
0,375
N
8
12.
В среднем из 1000садовых насосов,
поступивших в продажу, 5
подтекают. Найдите
вероятность того, что один
случайно выбранный для
контроля насос не
подтекает.
1000 5
0,995
1000
Фабрика выпускает сумки.
В среднем на 100
качественных сумок
приходится 3 сумки со
скрытыми дефектами.
Найдите вероятность того,
что случайно выбранная в
магазине сумка окажется
качественной.
100
100
100 3 103
В первом случае 1000 - вся выборка,
5 неисправных среди всех 1000 садовых насосов;
а во втором вся выборка 103, из нее 100 качественные
13.
Правила комбинаторикисуммы
произведения
A B
A B
происходит
хотя бы одно из событий
происходят
оба события
А или В
АиВ
A B
A B
14. У двух школьников по четыре шариковых ручки (красная, зелёная, синяя и чёрная). Они наугад обменялись одной ручкой. Какова
вероятность того, что у одного из них окажется две ручки чёрногоцвета?
1
-вероятность того, что первый школьник
4 станет обменивать чёрную ручку
3
-вероятность того, что второй школьник станет
4
обменивать ручку другого цвета
-
Вероятность того, что обе чёрные ручки окажутся у второго школьника
1 3 3
4 4 16
Т.к. по условию школьники
не пронумерованы,
то искомая вероятность
3 3
2 0,375
16 8
15.
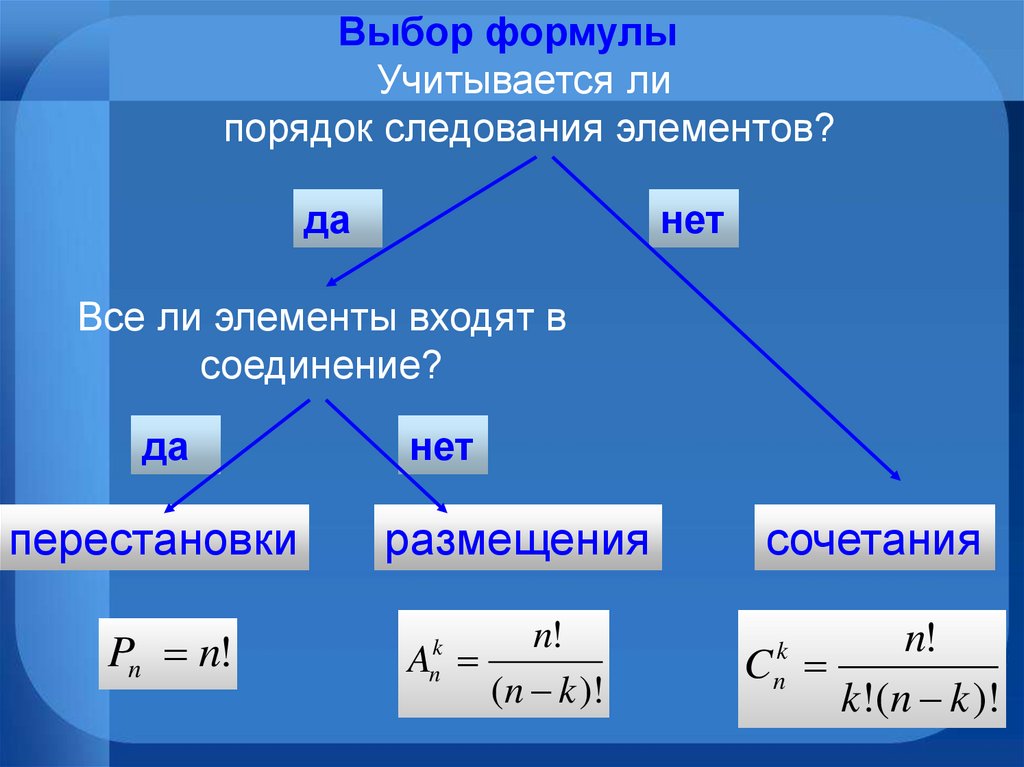
Выбор формулыУчитывается ли
порядок следования элементов?
да
нет
Все ли элементы входят в
соединение?
да
нет
перестановки
размещения
сочетания
Pn n!
n!
A
(n k )!
n!
C
k!(n k )!
k
n
k
n
16.
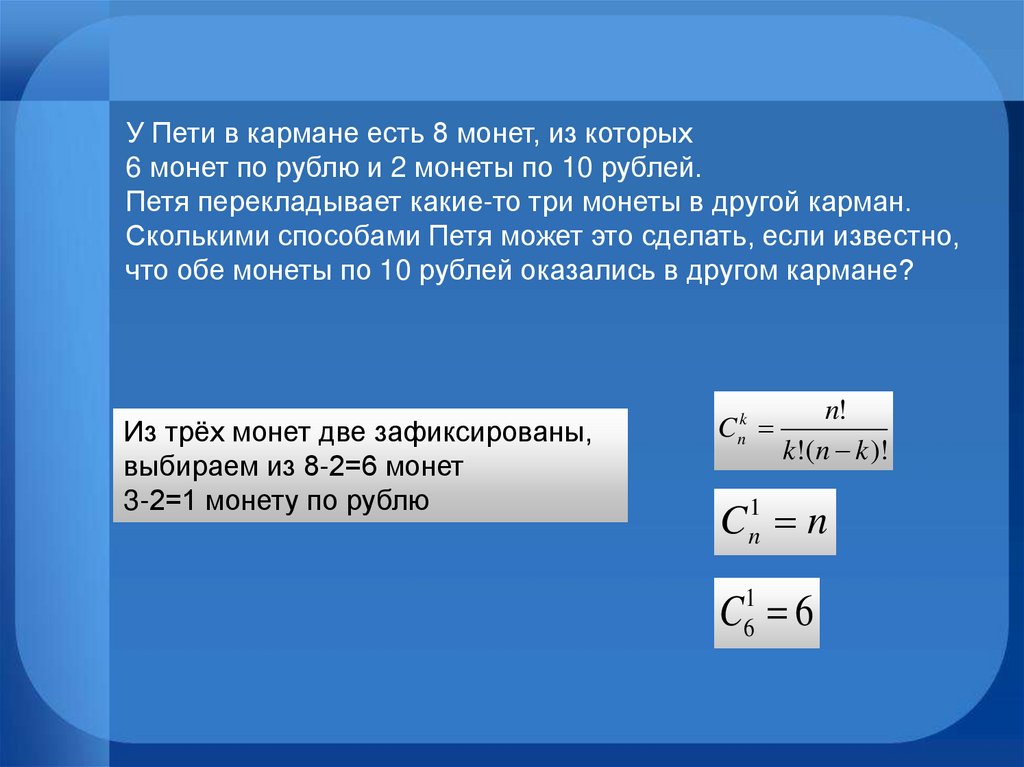
У Пети в кармане есть 8 монет, из которых6 монет по рублю и 2 монеты по 10 рублей.
Петя перекладывает какие-то три монеты в другой карман.
Сколькими способами Петя может это сделать, если известно,
что обе монеты по 10 рублей оказались в другом кармане?
Из трёх монет две зафиксированы,
выбираем из 8-2=6 монет
3-2=1 монету по рублю
Cnk
n!
k!(n k )!
C n1 n
C61 6
17. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман.
В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля.Петя, не глядя, переложил какие-то три монеты в другой карман.
Найдите вероятность того, что обе двухрублевые монеты лежат
в одном кармане.
Возможны 2 варианта: либо Петя двухрублёвые монеты вообще
не перекладывал, либо переложил сразу обе.
Если двухрублевые монеты не перекладывались, то 3 монеты
по рублю можно выбрать из 4 C43 способами.
Если обе двухрублевые монеты переложены, то еще одну рублевую
1
монету можно выбрать из 4 C4 способами.
Всего выбираем 3 монеты из 4+2=6 C63 способами.
N ( A) C43 C41
P( A)
N
C63
n!
C
k!(n k )!
k
n
4!
3! 4
С
4
3!(4 3)! 3!
3
4
C n1 n
С41 4
6!
4 5 6
С
20
3! (6 3)!
3!
4 4
P ( A)
0,4
20
3
6
18.
Чтобы пятирублевые монеты лежали в разных карманах, надопереложить только одну из них. Это можно сделать C 1
2
способами.
Всего Петя переложил 3 монеты, придется переложить
еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому
2
количество способов равно C4
Переложить 3 монеты из 6 имеющихся можно
C63
способами.
N ( A) C21 C42 2 6
P( A)
0,6
3
N
C6
20
19.
2 способ1
2
3
4
5
6
123
124
125
126
134
135
136
145
146
156
234
235
236
245
246
256
345
346
356
456
N ( A) 12
P( A)
0,6
N
20
20.
Самостоятельная работаВариант 1
Вариант 2
1. В соревнованиях по толканию ядра участвуют 4
1. В соревнованиях по толканию ядра участвуют 8
спортсмена из Эстонии, 6 спортсменов из Латвии, 3
спортсменов из Великобритании, 6 спортсменов из
спортсмена из Литвы и 7 — из Польши. Порядок, в
Франции, 5 спортсменов из Германии и 5 — из Италии.
котором выступают спортсмены, определяется жребием.
Порядок, в котором выступают спортсмены,
Найдите вероятность того, что спортсмен, который
определяется жребием. Найдите вероятность того, что
выступает последним, окажется из Литвы.
спортсмен, который выступает последним, окажется из
2. В среднем из 2000 садовых насосов, поступивших в Франции.
продажу, 14 подтекают. Найдите вероятность того, что 2. В случайном эксперименте симметричную монету
один случайно выбранный для контроля насос не
бросают трижды. Найдите вероятность того, что орел не
подтекает.
выпадет ни разу.
3. В сборнике билетов по биологии всего 25 билетов, в 9
3. В сборнике билетов по физике всего 25 билетов, в 13
из них встречается вопрос по членистоногим. Найдите
из них встречается вопрос по оптике. Найдите
вероятность того, что в случайно выбранном на экзамене вероятность того, что в случайно выбранном на экзамене
билете школьнику не достанется вопроса по
билете школьнику не достанется вопроса по оптике.
членистоногим.
21.
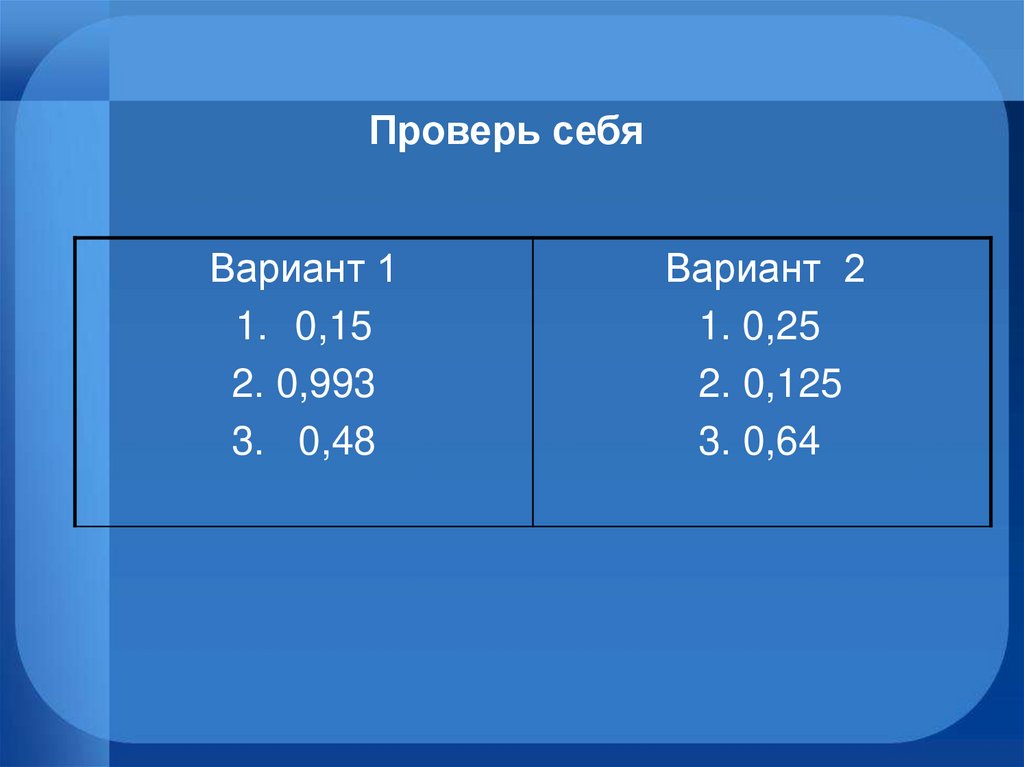
Проверь себяВариант 1
1. 0,15
2. 0,993
3. 0,48
Вариант 2
1. 0,25
2. 0,125
3. 0,64
22.
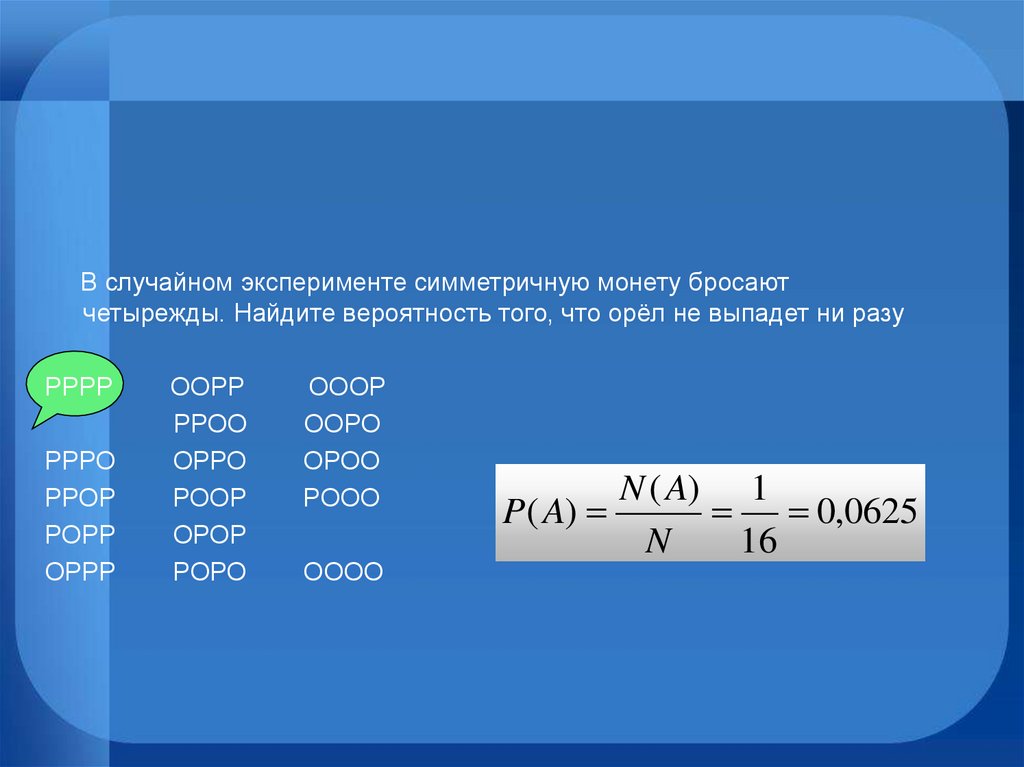
В случайном эксперименте симметричную монету бросаютчетырежды. Найдите вероятность того, что орёл не выпадет ни разу
РРРР
РРРО
РРОР
РОРР
ОРРР
ООРР
РРОО
ОРРО
РООР
ОРОР
РОРО
ОООР
ООРО
ОРОО
РООО
ОООО
N ( A) 1
P( A)
0,0625
N
16
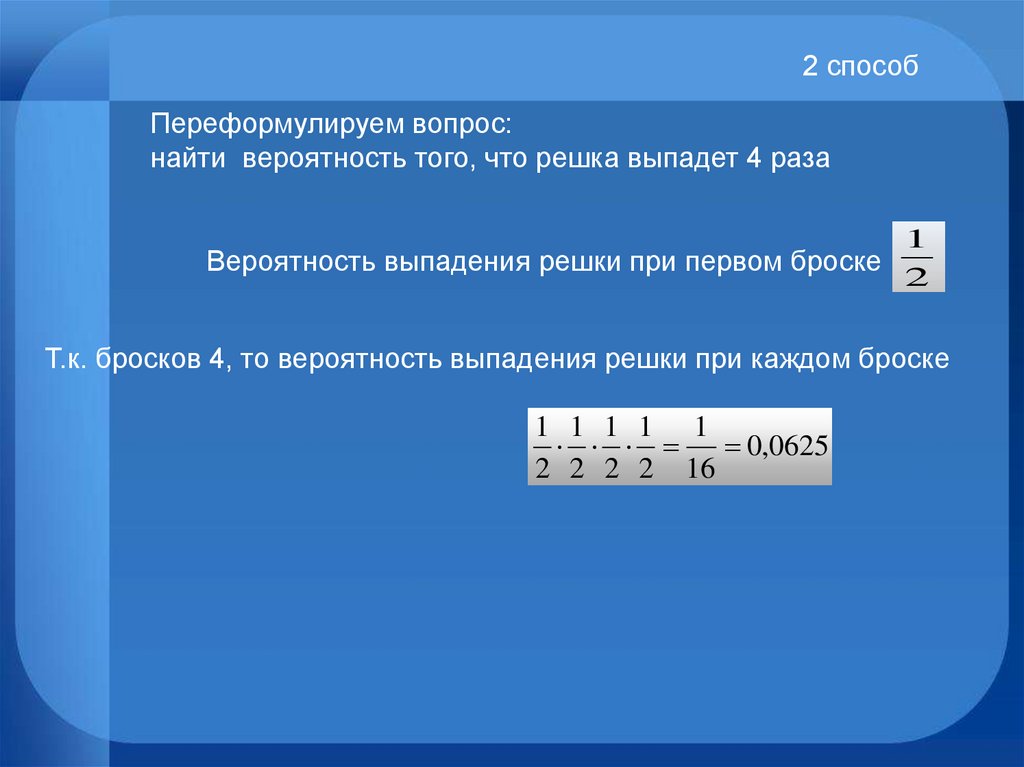
23. 2 способ
Переформулируем вопрос:найти вероятность того, что решка выпадет 4 раза
1
Вероятность выпадения решки при первом броске
2
Т.к. бросков 4, то вероятность выпадения решки при каждом броске
1 1 1 1 1
0,0625
2 2 2 2 16















 mathematics
mathematics








