Элементы комбинаторики и теории вероятностей

1. «Элементы комбинаторики и теории вероятностей»

МОУ « Сытьковская СОШ »
Учителя математики: Селиверстова Л.Н., Аничкина В.В.

2. Вероятность и статистика. Примеры заданий

ниже
Задания, включенные в представленный
список, предлагаемые для включения
в экзаменационную работу, направлены
на проверку следующих умений:
решать комбинаторные задачи, используя перебор всех
возможных вариантов или правило умножения, а в заданиях
второй части — еще и некоторые специальные приёмы;
определять такие статистические характеристики, как среднее
арифметическое, медиана, мода, выполняя при этом
необходимые подсчеты;

3. Вероятность и статистика. Примеры заданий

находить относительную частоту и вероятность
случайного события, используя готовые статистические
данные; отвечать на простейшие вопросы статистического
характера;
вычислять вероятность события в классической модели (в
заданиях первой части — в простейших ситуациях, в
заданиях второй части - с использованием комбинаторики
для определения числа исходов); вычислять
геометрическую вероятность.

4. Задания для части 2

Вероятность
Испытанием (или опытом) называется осуществление
некоторой совокупности условий.
Событием называется любой результат испытания.
Событие называется случайным (обозначается прописными
буквами А,В,…),если в данном испытании оно может или
произойти или не произойти.
Исходы при которых происходит некоторое событие,
называются благоприятными исходами.
Вероятностью случайного события А в данном
испытании называется число, обозначаемое Р(А)=m/n, где
n-число возможных элементарных событий,
рассматриваемого испытания, m- число тех элементарных
событий из всех возможных, которые благоприятствуют
появлению события А.

5.

Задание №5 (2)
1) Подбрасывают два игральных кубика. Какова
вероятность того, что в сумме выпадет 5 очков?
Решение.
При подбрасывании 1 кубика 6 исходов: 1,2,3,4,5,6 очков
При подбрасывании 2 кубика каждому исходу первого кубика
соответствует 6 вариантов другого :
1+1, 1+2, 1+3 1+4, 1+5, 1+6
2+1, 2+2, 2+3, 2+4, 2+5, 2+6
3+1, 3+2, 3+3, 3+4, 3+5, 3+6
4+1, 4+2, 4+3, 4+4, 4+5, 4+6
5+1, 5+2, 5+3, 5+4, 5+5, 5+6
6+1, 6+2, 6+3, 6+4, 6+5, 6+6
ИТОГО: 6*6=36 равновозможных исходов при подбрасывании двух кубиков.
Из предложенных вариантов благоприятными будут: 1+4,2+3, 3+2, 4+1.
Сумма очков равна 5.
Таких исходов всего 4.Вероятность равна отношению благоприятных исходов
ко всем исходам : Р(А)=4/36=1/9
Ответ: 1/9

6.

Задание №5 (2)
2) Подбрасывают два игральных кубика. Какова
вероятность того, что в сумме выпадет 6 очков?
Решение.
При подбрасывании 1 кубика 6 исходов: 1,2,3,4,5,6 очков
При подбрасывании 2 кубика каждому исходу первого кубика
соответствует 6 вариантов другого :
1+1, 1+2, 1+3 1+4, 1+5,1+6
2+1,2+2, 2+3, 2+4,2+5, 2+6
3+1,3+2, 3+3, 3+4, 3+5, 3+6
4+1,4+2, 4+3, 4+4, 4+5, 4+6
5+1,5+2.5+3, 5+4, 5+5, 5+6
6+1,6+2. 6+3. 6+4, 6+5, 6+6
ИТОГО: 6*6=36 равновозможных исходов при подбрасывании двух
кубиков.
Из предложенных вариантов благоприятными будут :
1+5, 2+4, 3+3, 5+1, 4+2.
Их всего 5. Вероятность события Р(А)=5/36
Ответ: 5/36

7.

Задание №6(2)
1) Карточки с цифрами 1,2,3,4,5 перемешивают и выкладывают в
ряд. Какова вероятность того, что получится четное число?
Решение.
Карточки с цифрами 1,2,3,4,5 перемешивают и выкладывают в ряд. Какова
вероятность того, что получится четное число?
1
2
3
4
5
При выборе случайным образом цифру 5 выбираем 5 способами,
цифру 2 выбираем 4 способами после выбора первой;
цифру 3 выбираем 3 способами после выбора первых двух;
цифру 4 выбираем 2 способами после выпада первых трех;
цифру 5 выбираем 1 способом после выпада первых четырех .
Итого: 5*4*3*2*1=120
Таких исходов ,когда на конце четная цифра 2 или 4
2*4*3*2*1 =48- количество перестановок
Отсюда вероятность равна Р(А)=48/120=0,4
Ответ: 0,4

8.

Задание №6 (2)
2) Карточки с цифрами 1,2,3.4,5,6,7 перемешивают и
выкладывают в ряд. Какова вероятность того ,что
получится четное число.
Решение.
Исходами опыта являются перестановки из 7 цифр
А(7)=7*6*5*4*3*2*1=5040
Благоприятными исходами являются варианты чисел, когда
на конце стоят цифры 2, 4 и 6
Таких исходов А(7)=3*6*5*4*3*2*1=2160
Вероятность равна Р(А)=2160/5040=3/7
Ответ: 3/7

9.

Задание №7 (2)
1)Подбрасывают два игральных кубика. Какова
вероятность того, что оба числа окажутся меньше 5?
Решение.
При подбрасывании двух игральных кубиков имеем 36
равновозможных исходов: 6*6=36
Благоприятный исход:
на первом кубике выпадает любое число от 1 до 4(это 4
варианта)
на втором кубике – любое число от 1 до 4(4 варианта) .
Всего по правилу умножения 4*4=16 благоприятных исходов.
Вероятность равна Р(А)=16/36=4/9
Ответ: 4/9

10.

Задание №7 (2)
2)Подбрасывают два игральных кубика. Какова
вероятность того , что оба числа больше 2?
Решение.
При подбрасывании двух игральных кубиков имеем 36 равновозможных
исходов:
1+1, 1+2 ,1+3, 1+4, 1+5, 1+6
2+1, 2+2, 2+3, 2+4, 2+5, 2+6
3+1, 3+2, 3+3, 3+4, 3+5, 3+6
4+1, 4+2, 4+3, 4+4, 4+5, 4+6
5+1. 5+2, 5+3, 5+4, 5+5, 5+6
6+1, 6+2, 6+3, 6+4, 6+5, 6+6
Благоприятный исход: на первом кубике выпадает любое число от 3 до 6 (это
4 варианта) и на втором кубике – любое число от 3 до 6(4 варианта)
Всего по правилу умножения 4*4=16 благоприятных исходов.
Вероятность равна Р(А)=16/36=4/9
Ответ: 4/9

11.

Задание №8 (2)
1) Буквы слова КУБИК перемешивают и случайным
образом выкладывают в ряд. С какой вероятностью
получится это же слово?
Решение.
Мы имеем перестановку из пяти букв : К,У,Б,И,К.
Их 5*4*3*2*1=5!=120
Буква К повторяется 2 раза, при любых двух перестановках
слово повторяется- КУБИК-КУБИК.
Благоприятных исходов всего 2
Вероятность равна Р(А)=2/120=1/60
Ответ: 1/60

12.

Задание №8 (2)
2) Буквы слова ХОРОШО перемешивают и случайным
образом выкладывают в ряд. С какой вероятностью
снова получится это же слово?
Решение.
Опыт имеет 6! равновозможных исходов
6*5*4*3*2*1=720 .
В слове ХОРОШО три буквы О.
Благоприятных исходов будет 3!=3*2*1=6
Вероятность равна Р(А)=3!/6!=6/720=1/120
Ответ: 1/120

13.

Задание №9 (2)
1) Игральный кубик бросили два раза . Какое из следующих
событий более вероятно:
А- «оба раза выпала пятерка»;
В- «в первый раз выпала единица . Во второй пятерка»;
С- «сумма выпавших очков равна 2»?
А. Событие А
Б.Событие В
В. Событие С
Г. Все события равновероятны
Решение:
Всего благоприятных исходов 6*6=36
Событие А –один благоприятный исход
Событие В- один благоприятный исход
Событие С – один благоприятный исход
Вероятность любого из трех событий Р(А)=1/36
Все события имеют одинаковую вероятность.
Ответ: Г

14.

Задание №9 (2)
2) Игральный кубик бросили два раза . Какое из следующих
событий более вероятно:
А- «оба раза выпала единица»;
В- «в первый раз выпала единица, во второй шестерка»;
С- «сумма выпавших очков равна 12»?
А. Событие А
Б. Событие В
В. Событие С
Г. Все события равновероятны
Решение:
Всего благоприятных исходов 6*6=36.
Событие А – один благоприятный исход;
Событие В - один благоприятный исход;
Событие С – один благоприятный исход;
Все события имеют одинаковую вероятность.
Ответ: Г

15.

Задание №10 (2)
1.На отрезке [-2;2] бросают случайную точку. Какова
вероятность того , что ее координата будет больше 1?
Решение:
-2
1
2
Длина всего отрезка равна 4=2-(-2).
Длина той его части, где координата больше 1 , равна 2-1=1.
Вероятность равна Р(А)= 1/4
Ответ: 1/4

16.

Задание №10 (2)
2) На отрезке [-3;3] бросают случайную точку. Какова
вероятность того , что ее координата будет больше 1?
Решение:
-3
1
3
Длина всего отрезка равна 3-(-3)=6.
Длина той части ,где координата меньше 1,
равна 1-(-3)=4
Вероятность равна Р(А)=4/6=2/3
Ответ:2/3

17.

Задание №11 (4)
1)В классе, где учится Наташа , по жребию выбирают
двух дежурных . Какова вероятность того, что Наташа
будет дежурить , если в классе 25 учеников ?
Решение
…
……………..
всего 25
Исходами опыта являются неупорядоченные пары :
1 и 2, 1 и 3, 1 и 4, 1 и 5,
2 и 3, 2 и 4, 2 и 5 и т.д.
Таких пар всего (25*24)/2=300.
Пары Наташа и одноклассник, одноклассник и Наташа – это
одна и та же пара. Благоприятных исходов 24- Наташа и
любой из 24 одноклассников.
Вероятность равна 24/300=2/25.
Ответ:2/25

18.

Задание №11 (4)
2)В классе, где учится Витя , по жребию выбирают
двух дежурных . Какова вероятность того, что Наташа
будет дежурить , если в классе 20 учеников ?
Решение
…
……………..
всего 20
Исходами опыта являются неупорядоченные пары :
1 и 2, 1 и 3, 1 и 4, 1 и 5,
2 и 3, 2 и 4, 2 и 5 и т .д .
Таких пар всего (20*19)/2=190
Пары Витя и одноклассник , одноклассник и Витя – это одна и
та же пара. Благоприятных исходов 19. Витя и любой из 19
одноклассников.
Вероятность равна 19/190=1/10
Ответ:1/10

19.

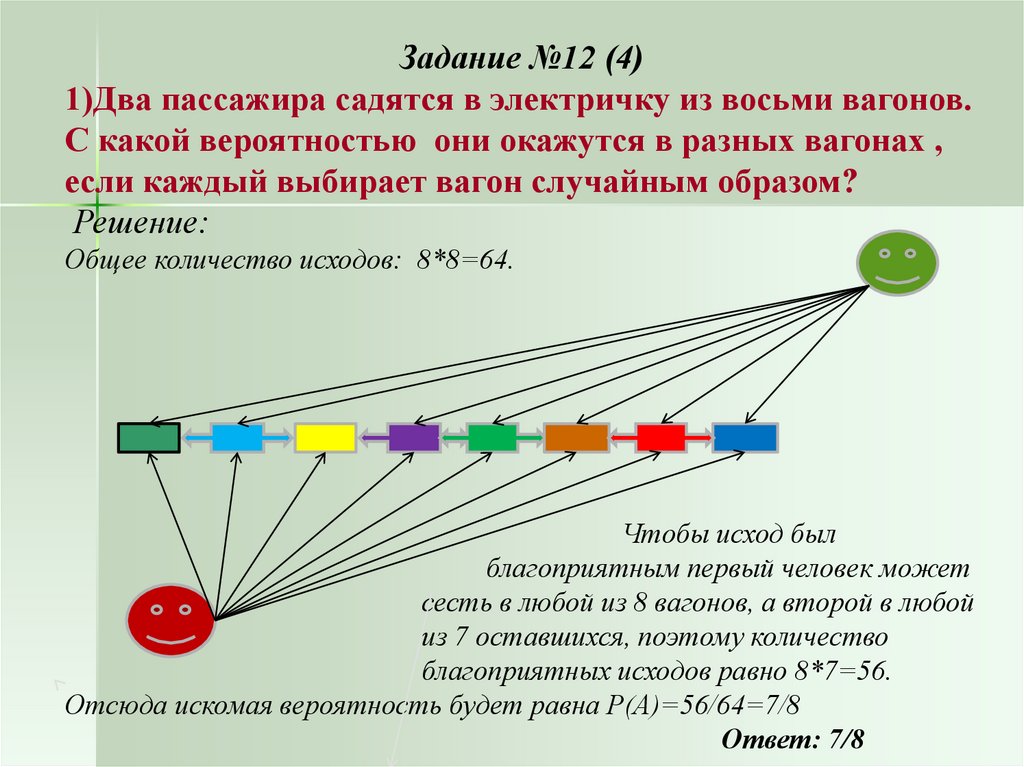
Задание №12 (4)
1)Два пассажира садятся в электричку из восьми вагонов.
С какой вероятностью они окажутся в разных вагонах ,
если каждый выбирает вагон случайным образом?
Решение:
Общее количество исходов: 8*8=64.
Чтобы исход был
благоприятным первый человек может
сесть в любой из 8 вагонов, а второй в любой
из 7 оставшихся, поэтому количество
благоприятных исходов равно 8*7=56.
Отсюда искомая вероятность будет равна Р(А)=56/64=7/8
Ответ: 7/8

20.

Задание №12 (4)
1)Два пассажира садятся в электричку из восьми вагонов. С какой
вероятностью они окажутся в одном вагоне, если каждый выбирает
вагон случайным образом?
Решение:
Общее количество исходов: 8*8=64.
Чтобы исход был
благоприятным первый человек
может сесть в любой из 8 вагонов, а второй в
любой из 7 оставшихся, поэтому количество
благоприятных исходов равно 64-8*7=8.
Отсюда искомая вероятность будет равна
Р(А)= 8/64=1/8
Ответ: 1/8

21.

Задание №13 (4)
1)Два мальчика и две девочки разыгрывают по
жребию два билета в кино. С какой вероятностью в
кино пойдут мальчик и девочка?
Решение:
Пронумеруем мысленно всех детей:1;2;3;4. Будем
считать, что номера 1 и 2 получили мальчики, а номера 3
и 4 девочки:
1
2
3
4
М
М
Д
Д
Исходами опыта являются (неупорядоченные) пары,
которые можно составить из четырех чисел.
Выпишем все эти исходы: 12; 13; 14; 23; 24; 34.
Поэтому искомая вероятность равна 4/6=2/3.
Ответ: 2/3

22.

Задание №13 (4)
2)Два мальчика и две девочки разыгрывают по
жребию два билета в кино. С какой вероятностью в
кино пойдут две девочки?
Решение:
Пронумеруем мысленно всех детей:1;2;3;4. Будем считать,
что номера 1 и 2 получили мальчики, а номера 3 и 4 девочки:
1
2
3
4
М
М
Д
Д
Исходами опыта являются (неупорядоченные) пары,
которые можно составить из четырех чисел.
Выпишем все эти исходы:12; 13; 14; 23; 24; 34.
Поэтому искомая вероятность равна 1/6.
Ответ: 1/6

23.

Задание №14 (6)
1. В урне 10 шаров белого и черного цвета. Вероятность
того , что среди двух одновременно вынутых из нее
будут оба черные , равна 1/15. Сколько в урне белых
шаров?
Решение:
Обозначим неизвестное количество черных шаров в
урне через х. Исходами опыта будут всевозможные пары,
которые можно составить из 10 шаров.
Количество таких пар равно (10*9)/2=45 (на 2 делим,
потому что порядок шаров в паре не учитывается).
Благоприятными будут всевозможные пары, которые
можно составить из х черных шаров. Количество таких пар
равно (х(х-1))/(2*45).
Получаем уравнение, которое нужно решать в
натуральных числах: х(х-1)/90=1/15, х(х-1)=6, х=3.
В урне 3 черных шара, значит белых шаров 7.
Ответ:7

24.

Задание №14 (6)
2) В урне 10 шаров белого и черного цвета. Вероятность
того , что среди двух одновременно вынутых из нее
шаров оба будут белые , равна 7/15. Сколько в урне
черных шаров?
Решение:
Обозначим неизвестное количество белых шаров в урне
через х. Исходами опыта будут всевозможные пары,
которые можно составить из 10 шаров.
Количество таких пар равно (10*9)/2=45 (на 2 делим,
потому что порядок шаров в паре не учитывается).
Благоприятными будут всевозможные пары, которые
можно составить из х белых шаров. Количество таких пар
равно (х(х-1))/(2*45).
Получаем уравнение, которое нужно решать в
натуральных числах: х(х-1)/90=7/15, х(х-1)=42, х=7.
В урне 7 белых шаров, значит черных шаров 3.
Ответ:3

25.

Задание №15 (6)
1) Номера российских автомобилей состоят из записанных
последовательно одной буквы, трех цифр и двух букв. При этом
используются только буквы АВЕКМНОРСТУХ. С какой
вероятностью все цифры в номере автомобиля будут
разными?
Решение.
1.Найдем общее количество номеров, которое можно составить
по описанным правилам. Всего в номере 6 мест.
На первом месте может стоять любая из12 букв.
На втором месте может стоять любая из 10 цифр.
На третьем месте может стоять любая из 10 цифр.
На четвертом месте может стоять любая из 10 цифр.
На пятом месте может стоять любая из12 букв.
На шестом месте может стоять любая из12 букв.
Всего по правилу умножения 12*10*10*10*12*12 номеров
2.Найдем количество номеров в которых все буквы и цифры
разные .
По правилу умножения: 12*10*9*8*11*10 номеров.
Искомая вероятность равна
12*10*9*8*11*10 /12*10*10*10*12*12 =11/20
Ответ: 11/20

26.

Задание №15 (6)
2) Номера российских автомобилей состоят из записанных
последовательно одной буквы, трех цифр и двух букв. При этом
используются только буквы АВЕКМНОРСТУХ. С какой
вероятностью все цифры в номере автомобиля будут
одинаковыми?
Решение.
1.Найдем общее количество номеров, которое можно составить по
описанным правилам. Всего в номере 6 мест.
На первом месте может стоять любая из12 букв.
На втором месте может стоять любая из 10 цифр.
На третьем месте может стоять любая из 10 цифр.
На четвертом месте может стоять любая из 10 цифр.
На пятом месте может стоять любая из12 букв.
На шестом месте может стоять любая из12 букв.
Всего по правилу умножения 12*10*10*10*12*12 номеров
2.Найдем количество номеров в которых все буквы и цифры одинаковые.
По правилу умножения: 12*10*1*1*12*12 номеров.
Искомая вероятность равна
12*10*1*1*12*12/ 12*10*10*10*12*12=1/100
Ответ: 1/100

27.

Задание №16 (6)
1)В квадрат со стороной, равной 1, бросают случайную точку.
Какова вероятность того, что расстояние от этой точки до
ближайшей стороны квадрата не превосходит 0,25?
Решение.
.
Площадь всего квадрата равна 1.
Множество точек, расстояние от которых до ближайшей
его стороны не превосходит 0,25 – это закрашенная на
рисунке часть квадрата (внутри данного квадрата
расположен квадрат со стороной, равной 0,5).
Площадь этой части равна 1-0,5² =0,75.
Отсюда вероятность равна Р(А)= 0,75/1=0,75
Ответ: 0,75

28.

Задание №16 (6)
2)В квадрат со стороной, равной 1, бросают случайную точку.
Какова вероятность того, что расстояние от этой точки до
ближайшей стороны квадрата больше 0,25?
Решение.
Площадь всего квадрата равна 1.
Множество точек, расстояние от которых до ближайшей его
стороны больше 0,25 – это закрашенная на рисунке часть
квадрата (внутри данного квадрата расположен квадрат
со стороной, равной 0,5).
Площадь этой части равна 0,5²=0,25.
Отсюда вероятность равна Р(А)=0,25/1=0,25
Ответ:0,25

29. Цели :

образовательная
обучать решению задач по комбинаторике
развивающая
развивать логическое мышление
расширять математический кругозор
развивать навыки научно-исследовательской
деятельности
воспитательная
воспитывать культуру письма, речи
развивать умения работать в группе
формировать чувство ответственности за принятое
решение

30. Спасибо за внимание!