Источники дискретных сообщений

1.

3. Источники дискретных сообщений
3.1. Энтропия эргодического источника
3.2. Свойство энтропии эргодических источников
3.3. Избыточность источника сообщений
3.4. Поток информации источника сообщений
4. Источники непрерывных сообщений
4.1. Дифференциальная энтропия
4.2. Свойства дифференциальной энтропии
4.3. Эпсилон - энтропия источника сообщений
4.4. Эпсилон-производительность источника
4.5. Избыточность источника непрерывных сигналов
4.6. Количество информации

2.

ИСТОЧНИКИ ДИСКРЕТНЫХ СООБЩЕНИЙ
Энтропия эргодического источника
Эргодический источник r-го порядка называется такой источник, у которого вероятность
появления некоторого символа xj зависит от r предыдущих. Для такого источника может быть
найдено конечное число характерных состояний S1, S2,..., таких, что условная вероятность
появления очередного символа зависит лишь от того, в каком из этих состояний находится
источник. Вырабатывая очередной символ, источник переходит из одного состояния в другое либо
возвращается в исходное состояние.
Определим энтропию эргодического источника в предположении, что он работает длительное
время и, всякий раз, когда мы ждём появления очередного символа, нам известно, какие символы
были выбраны ранее, и, следовательно, известно, в каком характерном состоянии находится
источник.
Обозначим через P(Si) вероятность того, что источник находится в состоянии Si, причём

3.

4.

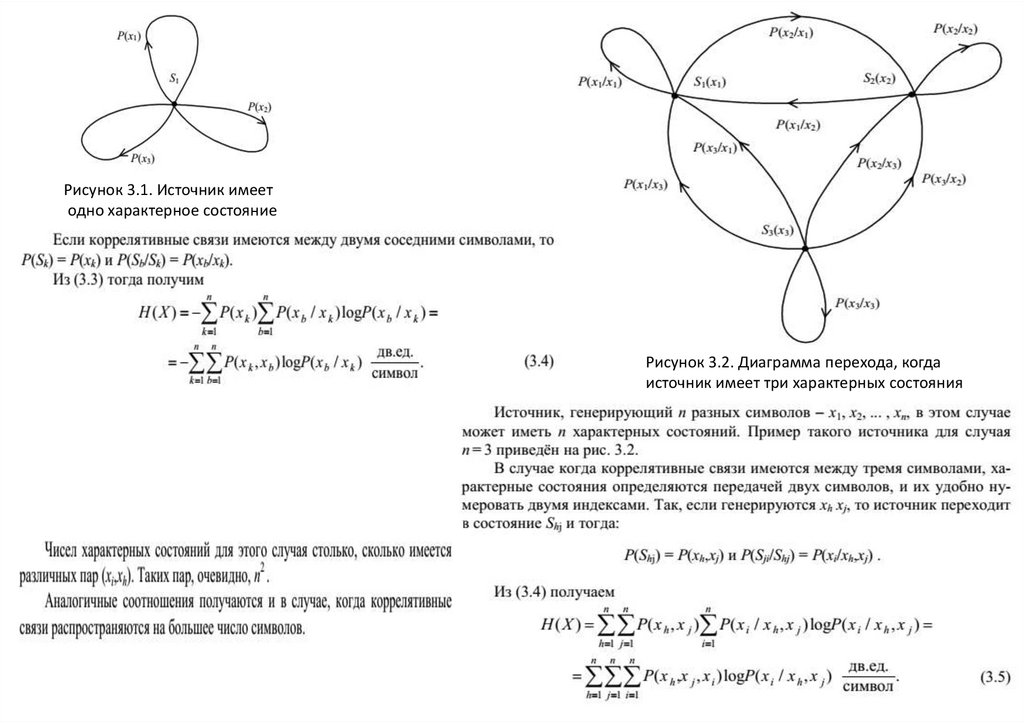
Рисунок 3.1. Источник имеет
одно характерное состояние
Рисунок 3.2. Диаграмма перехода, когда
источник имеет три характерных состояния

5.

Свойство энтропии эргодического источника

6.

7.

8.

Избыточность источника сообщений

9.

Поток информации источника сообщений

10.

11.

12.

ИСТОЧНИКИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
Дифференциальная энтропия

13.

14.

15.

16.

Чтобы избавить теорию от бесконечности, имеется единственная возможность – ввести относительную
меру неопределенности исследуемой непрерывной случайной величины Х по отношению к заданной Х0 . В
качестве заданной величины Х0 возьмем непрерывную случайную величину, равномерно распределенную на
интервале с шириной e = b - a. Тогда её плотность вероятности
W ( X0) = 1 /e , а энтропия
Положив для простоты записи e = 1, составим разность
которая показывает, насколько неопределенность непрерывной случайной величины Х с законом
распределения W(X) больше [HD (X) >0] или меньше [HD (X) <0] неопределенности случайной
величины, распределенной равномерно на интервале e = 1. Поэтому величину
называют относительной дифференциальной энтропией или просто дифференциальной
энтропией непрерывного источника информации (непрерывного распределения случайной
величины Х). В отличие от энтропии источников дискретных сообщений H D ( X ) может принимать
положительные, отрицательные и нулевые значения. Величиной H D (X ) можно характеризовать
информационные свойства источников непрерывных сообщений.

17.

Аналогично, используя операции квантования и предельного перехода, найдем выражение
для условной энтропии непрерывного источника сообщений.
Эта величина конечна и называется относительной дифференциальной условной энтропией,
или просто дифференциальной условной энтропией непрерывного источника. Она характеризует
неопределенность выбора непрерывной случайной величины Х при условии, что известны
результаты реализации значений другой статистически связанной с ней непрерывной случайной
величины Y, и по сравнению со средней неопределенностью выбора случайной величины Х0,
изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение
вероятностей.

18.

Свойства дифференциальной энтропии
1. Величина HД(X) изменяется при изменении масштаба измерения Х. Изменим масштаб случайной
величины Х в k раз, оставив неизменным масштаб равномерно распределенной в единичном
интервале случайной величины Х0, принятой за эталон.
2. Дифференциальная энтропия не зависит от конкретных значений случайной величины Х и, в
частности, от изменения всех её значений на постоянное. Действительно, масштаб Х при этом не
меняется и справедливо равенство
3. Если единственным ограничением для случайной величины Х является область её возможных
значений [a, b], то максимальной дифференциальной энтропией обладает равномерное
распределение вероятностей в этой области, т.е. при W(X) = (b - a)-1:
H Δ( X ) = log( b - a ).
(4.9)
4. Если ограничения на область значений непрерывной случайной величины Х отсутствуют, но
известно, что дисперсия её ограничена, то максимальной дифференциальной энтропией, равной
обладает нормальное (Гауссовское) распределение
величин Х:

19.

m- математическое ожидание, σ2 –дисперсия случайной величины Х – стандартное отклонение от
математического ожидания, симметричное m, σ –среднеквадратичное отклонение (стандартное),
σ2 и σ характеризуют разброс данных, т.е. ошибку измерений, чем больше σ, тем больше ошибка

20.

5. Соотношения для дифференциальной энтропии объединения
статистически
зависимых
непрерывных
источников
аналогичны соответствующим формулам для дискретных
источников:
6. Если статистические связи между X и Y отсутствуют, то
HD(X,Y) = HD(X) + HD(Y). (4.13)

21.

Эпсилон - энтропия источника сообщений
Эпсилон–энтропия – это то среднее количество информации в одном независимом отсчете
непрерывного случайного процесса Х(t), которое необходимо для воспроизведения этого сигнала с
заданной среднеквадратичной погрешностью Ɛо.
Предположим, что передавался сигнал Х(t), а был принят сигнал Y(t). Пусть в канале действует
аддитивная помеха E(t), тогда Y(t) = X(t) + E(t) . Расстояние между сигналами X(t) и Y(t) определяется
величиной
где T – длительность сигналов.
Если e 20 < e 2 , то сигналы называют e0 -близкими. 0
В соответствии с определением эпсилон-энтропии можно записать, что
H (X ) e = min I (Y , X ) = H D (X ) - max H D ( X / Y ) . (4.15)
Так как X (t ) = Y (t ) - E(t ) , то условная энтропия H D (X / Y ) при принятом Y(t) полностью
определяется “шумом” воспроизведения E(t). Поэтому max H D (X/Y) = max H D (E). (4.16)
Учитываем, что мощность помехи ограничена величиной e0 2, тогда максимальная энтропия помехи,
отнесенная к одному отсчету, определяется по формуле (4.10)
где σ Е – среднеквадратическое значение помехи.
С учетом (4.17)
Эпсилон-энтропия имеет максимальное значение, когда
процесс X(t) так же является гауссовским:

22.

Эпсилон-производительность источника
Если источник выдает независимые отсчеты сигнала Х(t) в дискретные моменты времени со
скоростью v t = 1/ D t, где интервал дискретизации D t = 1/2 D Fm (D Fm – полоса частот сигнала X(t)),
то эпсилон-производительность источника (эпсилон-энтропия, приходящаяся на единицу времени).
Если время непрерывное, то
За время Т существования сигнала максимальный объем V информации, выданной источником,
составит
Объем сигнала – это максимальное количество информации, которое сигнал может переносить.

23.

Избыточность источника непрерывных сигналов
Избыточность определяют так же, как и для источника
дискретных сигналов:
Избыточность источника равна нулю только в случае, когда
распределение сигнала является гауссовским.
При
определении
эпсилон-характеристик
источников
непрерывных
сигналов
критерием
близости
служило
среднеквадратичное отклонение одного сигнала от другого. Если
выбрать другую меру близости сигналов – другую метрику
пространства сигналов, можно получить другие эпсилонхарактеристики источников. Наибольшее распространение
получил среднеквадратический критерий близости сигналов.

24.

Количество информации
Количество информации, содержащееся в одной непрерывной
случайной величине относительно другой, определим как разность
безусловной и условной дифференциальных энтропий:

25.

КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какова особенность определения энтропии непрерывного
источника информации?
2. Дайте определение дифференциальной энтропии.
3. Перечислите свойства дифференциальной энтропии.
4. Какие распределения обладают максимальной
дифференциальной энтропией при ограничении на область
изменения случайной величины и при ограничении на
дисперсию случайной величины?
5. Что такое эпсилон-энтропия источника непрерывных
сообщений?
6. Дайте определение эпсилон-производительности
источника.
7. Запишите выражение для определения источника
непрерывных сообщений.