Similar presentations:
Гиперзвуковой пограничный слой (лекция 12)
1.
Лекция 12Гиперзвуковой пограничный слой
Пластина в гиперзвуковом потоке Постановка задачи.
Краевые условия и уравнения. Параметры пограничного
слоя, используемые в приложениях. Примеры численных
расчетов. Пограничный слой на теплоизолированной
пластине: профили скорости и температуры при разных
числах Маха, рост толщины с ростом числа Маха.
Пограничный слой на холодной пластине: особенности
профилей скорости и температуры при разных числах Маха,
рост толщины с ростом числа Маха.
1
2.
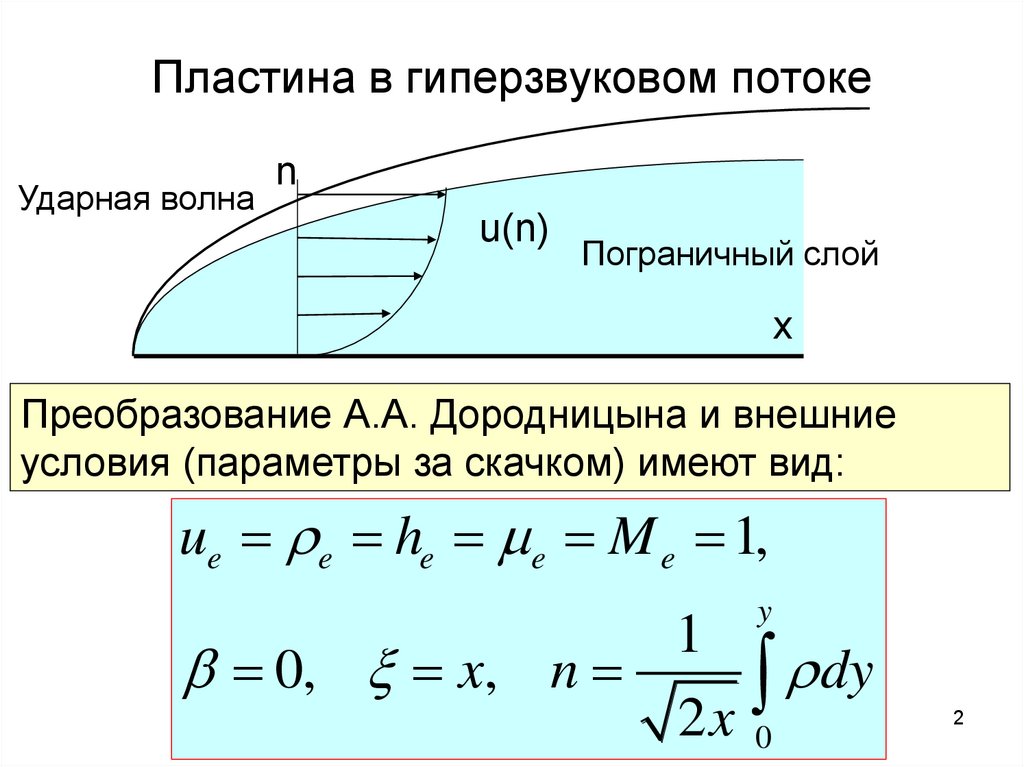
Пластина в гиперзвуковом потокеУдарная волна
n
u(n)
Пограничный слой
x
Преобразование А.А. Дородницына и внешние
условия (параметры за скачком) имеют вид:
ue e he e M e 1,
y
1
0, x, n
dy
2x 0
2
3.
Пограничный слой на пластинеЗадача описывается обычными уравнениями
пограничного слоя для пластины:
mf ff 0
m
2
2
H fH 1 M mf 0
Pr
f 0 f 0 0, H 0 H w H 0 0
f H 1
3
4.
Параметры вязкого течения на пластинеКоэффициенты трения cf, теплопередачи qw, числа
Нуссельта Nu и Стантона St имеют вид:
1u1 x
1
2
w
mw f w , c f
mw f w , Re x
1
2 Re x
2 Re x
1
qw
mw H w , Nu Pr Re x St
Pr 2 Re x
qw
1
St
mw H w ,
haw hw haw hw Pr 2 Re x
Индексом 1 помечены размерные параметры за
скачком
4
5.
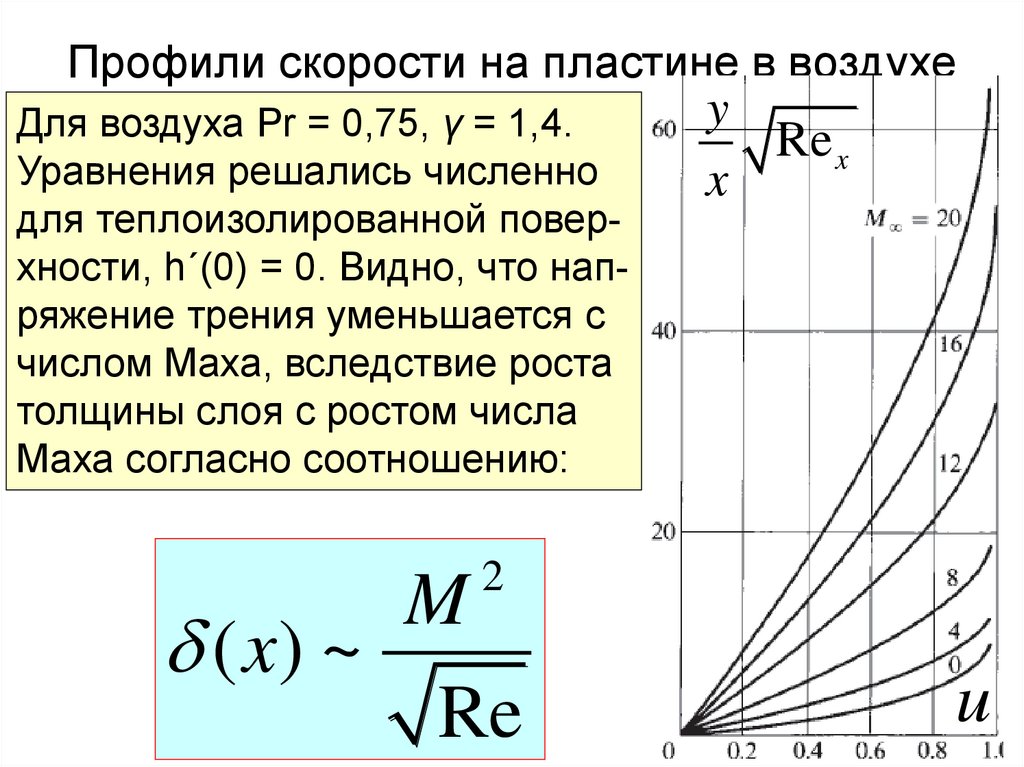
Профили скорости на пластине в воздухеДля воздуха Pr = 0,75, γ = 1,4.
Уравнения решались численно
для теплоизолированной поверхности, h΄(0) = 0. Видно, что напряжение трения уменьшается с
числом Маха, вследствие роста
толщины слоя с ростом числа
Маха согласно соотношению:
y
Re x
x
2
M
( x) ~
Re
u
6.
Профили температуры длятеплоизолированной пластины
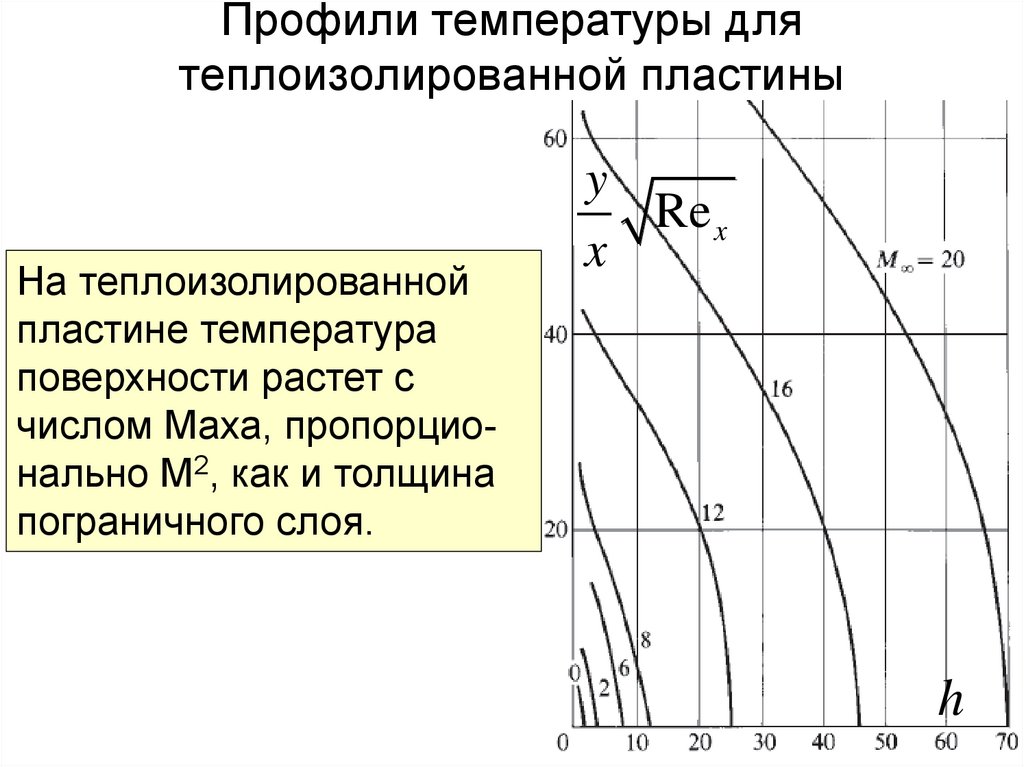
На теплоизолированной
пластине температура
поверхности растет с
числом Маха, пропорционально М2, как и толщина
пограничного слоя.
y
Re x
x
h
6
7.
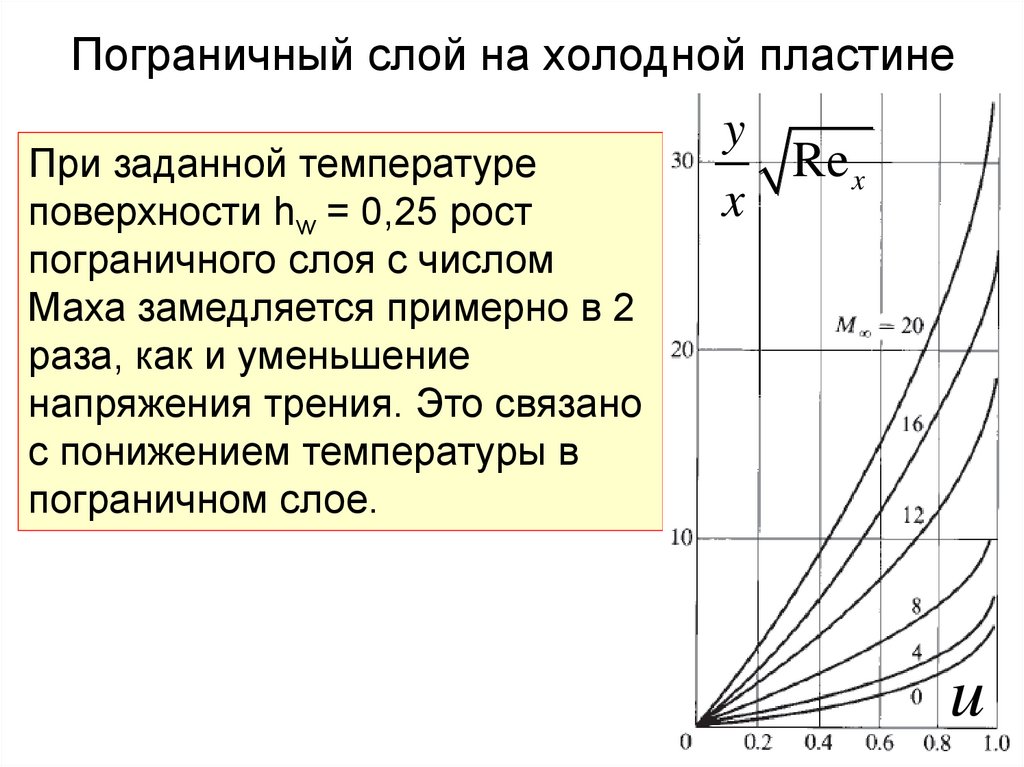
Пограничный слой на холодной пластинеПри заданной температуре
поверхности hw = 0,25 рост
пограничного слоя с числом
Маха замедляется примерно в 2
раза, как и уменьшение
напряжения трения. Это связано
с понижением температуры в
пограничном слое.
y
Re x
x
u
7
8.
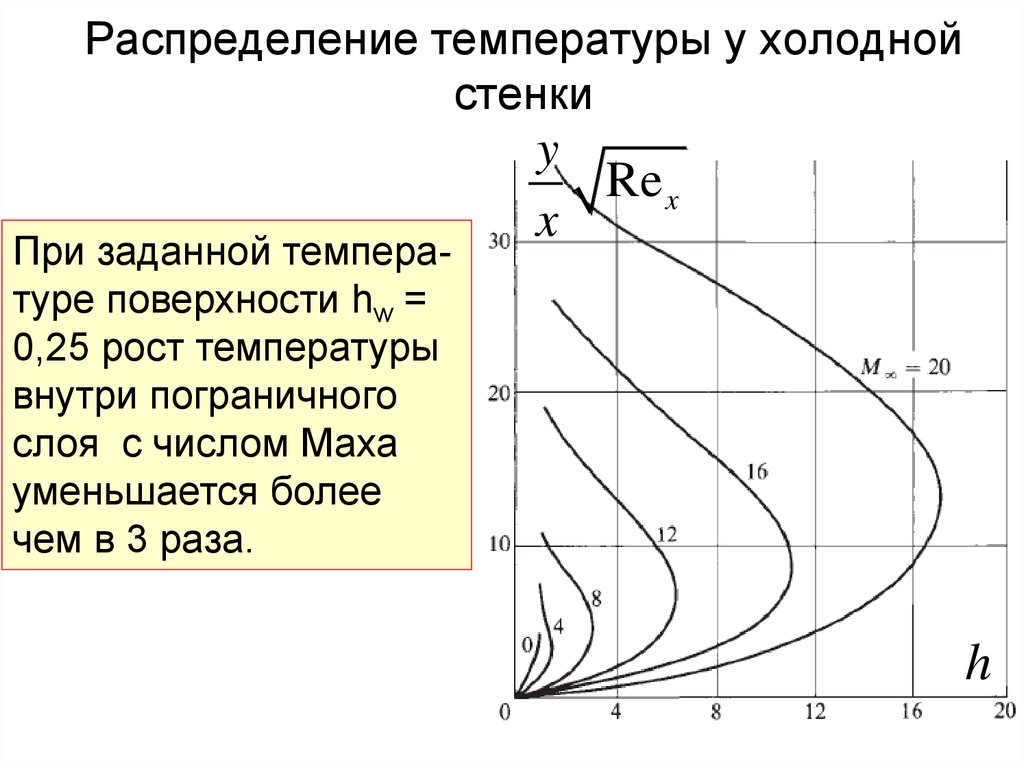
Распределение температуры у холоднойстенки
При заданной температуре поверхности hw =
0,25 рост температуры
внутри пограничного
слоя с числом Маха
уменьшается более
чем в 3 раза.
y
Re x
x
h
9.
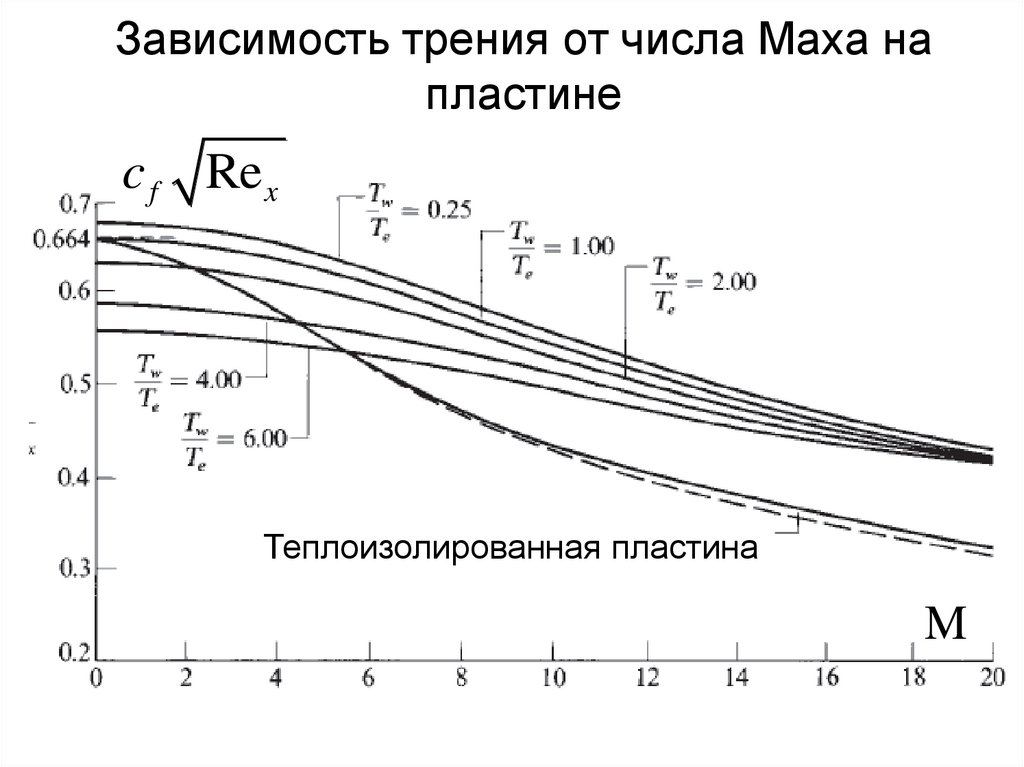
Зависимость трения от числа Маха напластине
c f Re x
Теплоизолированная пластина
M
h
10.
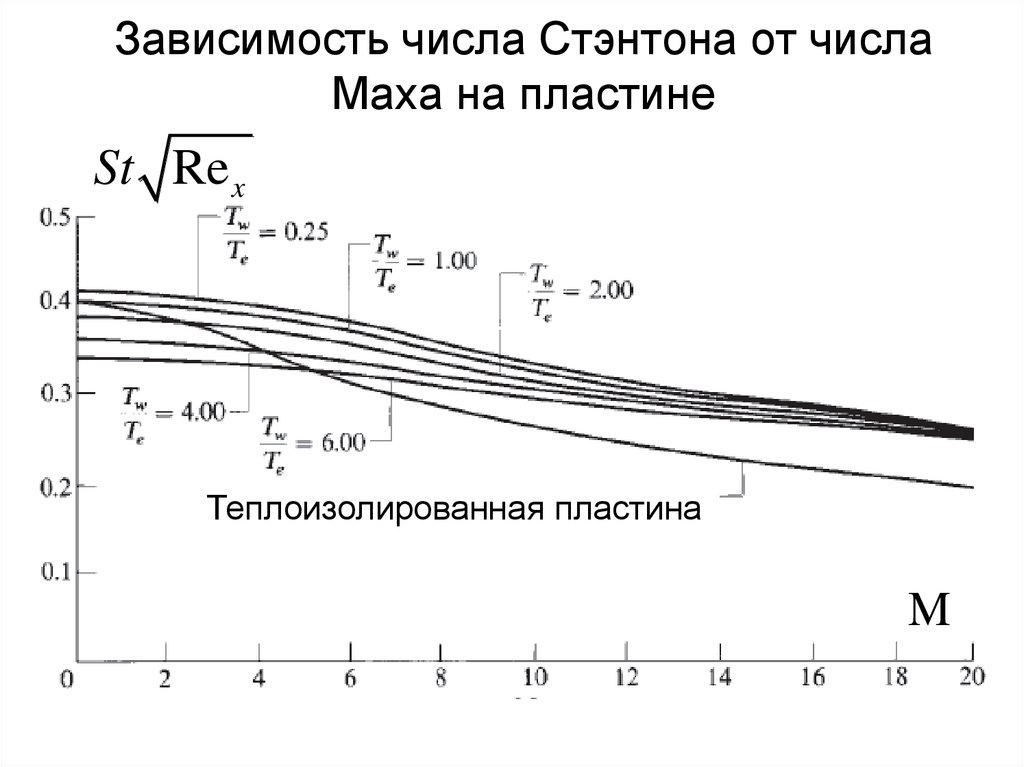
Зависимость числа Стэнтона от числаМаха на пластине
St Re x
Теплоизолированная пластина
M
11.
Формулы для теплового потока вкритической точке в ионизированном газе
Fay J., Riddel F. J. Aeronautical Scien., 1956, v. 25, N 2, pp. 73-85.
Теоретический анализ теплообмена в лобовой точке, омываемой диссоциированным воздухом. // Проблемы движения головной части ракет
дальнего действия . Ред Е.В. Самуйлов, Э.Э. Шпильрайн1959, с. 217-256.
Расчеты, представленные в этой работе дали следующую
зависимость теплового потока от параметров:
qw 0,94 w w
0,1
e e he0 hw
Pr 0, 71, hD cie hi 0
0,4
hD
0,52
a 1 Le 1
he 0
Число Льюиса Le – отношение тепловыделения в хим.
реакциях (hd – энтальпия тепловыделения). Эта формула
используется для оценок теплового потока на реальных
11
гиперзвуковых аппаратах.
12.
Лекция 9Вязко-невязкое взаимодействие в
гиперзвуковом потоке
Повышение давления в ударной волне, его связь с углом
наклона линий тока (поверхности). Параметр гиперзвукового
подобия. Толщина вытеснения и . Давление взаимодействия
в гиперзвуковом потоке; параметр взаимодействия.
Особенности пограничного слоя при больших числах Маха:
результаты расчетов. Анализ теплообмена в пограничном
слое на пластине с теплоизоляцией и заданной температурой: 1) Pr = 1, интеграл Крокко и аналогия Рейнольдса; 2) интеграл уравнения энергии при линейной зависимости вязкости от температуры и связь коэффициентов теплообмена и
12
трения.
13.
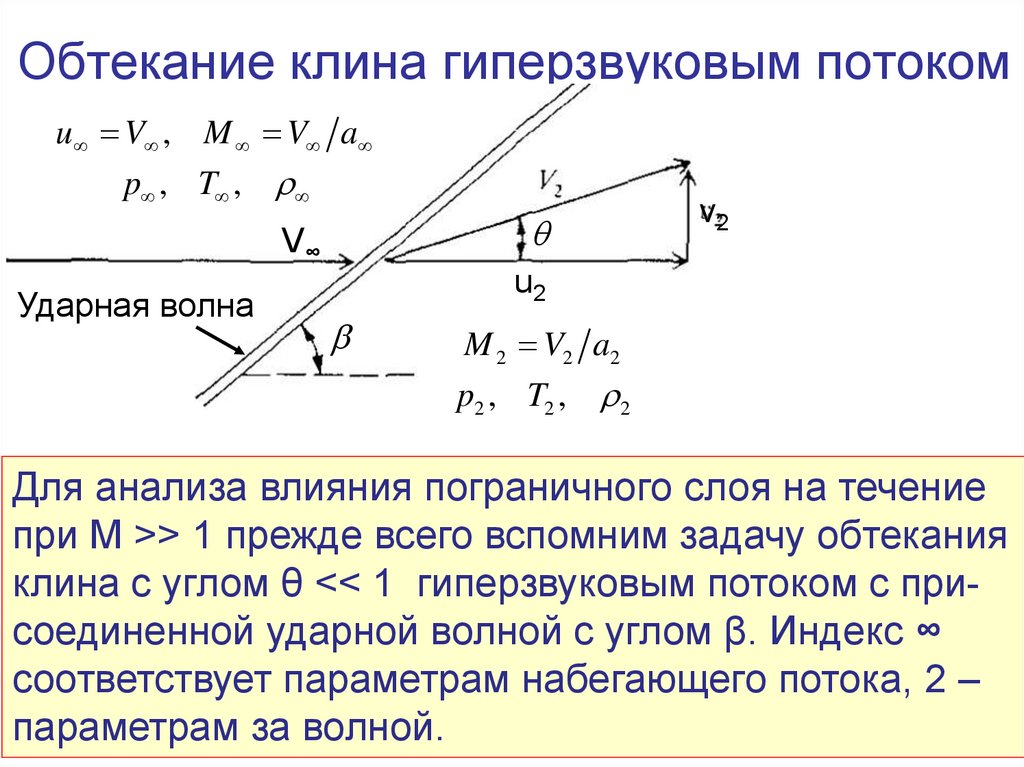
Обтекание клина гиперзвуковым потокомu V , M V a
p , T ,
u2
V∞
Ударная волна
v2
M 2 V2 a2
p2 , T2 , 2
Для анализа влияния пограничного слоя на течение
при М >> 1 прежде всего вспомним задачу обтекания
клина с углом θ << 1 гиперзвуковым потоком с присоединенной ударной волной с углом β. Индекс ∞
соответствует параметрам набегающего потока, 2 –
13
параметрам за волной.
14.
Соотношения на скачке при М∞ >> 1, β << 1p2
2
2
2
2
2 2
1
M
sin
1
M
p
1
1
M 1
1 M 2 sin 2
2
1
2
2
1 M sin 2 M 1 1
1 2 2
T2 p2
1 2
M sin
2
T 2 p
1
u2
1
V
v2
V
2 M 2 sin 2 1
1 M 2
M 1
M 1
1
2 2
M
2
2 2
1
1
2 M 2 sin 2 1 ctg
1 M 2
2 1
M 1
2
1
14
15.
Связь углов наклона скачка и клинаДля каждого угла наклона клина существует два
скачка с разными углами наклона – сильный (М2 < 1)
и слабый (М2 > 1). Сильный скачок обычно
отсоединенный. Угол наклона скорости за слабым
скачком определен формулой:
β
M 2 sin 2 1
tg 2ctg 2
M cos 2 2
М2 < 1
При 1 1:
М2 > 1
2 M 2 2 1
2
2
M 1 2 M 1 1
М1 = 2
М1 = 3
М1 = 5
М1 = ∞
1
2
θ
15
16.
Связь углов наклона скачка и клина точная зависимость для слабого скачка2 1
2 2
1 M 1
M
2
1
1
2 2 0
2 M
2
1
16
1
2
2
2
2
1 1 2 2
2
4
M 1 M
2
16
2 2
2 2
M 1 2
M 1 1 2 2
2
4
M 116
1
2
17.
Параметр гиперзвукового подобия K MИспользуя этот параметр, представим отношение
давлений и коэффициент давления Ср при М∞ >> 1
в следующей форме:
1
16
M 2 2 1 2 K 2
1 1 2
2
4
K 1
2
p2
1 2
16
1
K 1 1 2
2
p
4
K
1
1 p2
1 2
16
Cp
1
1 1 2
2
2
M p M 1
4
17
K
1
18.
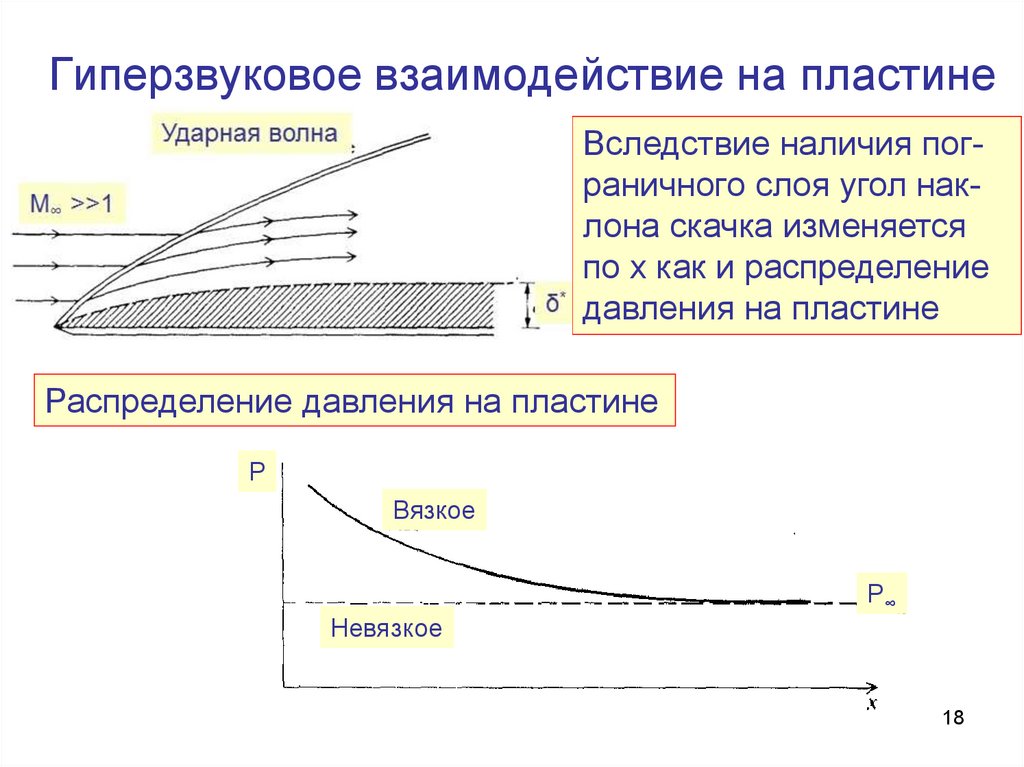
Гиперзвуковое взаимодействие на пластинеВследствие наличия пограничного слоя угол наклона скачка изменяется
по х как и распределение
давления на пластине
Распределение давления на пластине
P
Вязкое
P∞
Невязкое
18
19.
Толщина гиперзвукового пограничного слояна теплоизолированной пластине
В гиперзвуковом пограничном слое характерными параметрами являются вязкость, температура и плотность на стенке: μw,
T w и ρ w, которые соответствуют температуре торможения.
Толщина вытеснения δ* определяется соотношениями:
e ue x
bx
, Reex
,
e
Re x
w ue x w e e ue x w e
Re x
Reex
w
e w e
e w
Здесь b - постоянная, Reе – локальное число Рейнольдса по
параметрам на внешней границе пограничного слоя
19
20.
Толщина гиперзвукового пограничного слояна теплоизолированной пластине
Для упрощения рассмотрим линейную зависимость вязкости
от температуры и учтем, что давление не меняется поперек
пограничного слоя. Тогда получим
w
Tw
e peTw Tw
C ,
e
Te
w pwTe Te
В гиперзвуковом пограничном слое на теплоизолированной
стенке температура поверхности Tw порядка температуры
торможения T0, а плотность на стенке ρw, и вязкость μw,
определяются числом Маха на внешне границе Ме:
e Tw
1 2
1 r
Me
w Te
2
20
21.
Оценка влияния числа Маха на толщинугиперзвукового пограничного слоя
На этом основании получим зависимость толщины
вытеснения δ* числа Маха при гиперзвуке:
bx
Reex
Tw
Tw bx C Tw bx C
1 2
C
Me
1 r
Te
Te
2
Re x Te
Reex
Для M e 1: r
1 bxM e2 C
2
Reex
bxM e2
~
Reex
Здесь r – коэффициент восстановления, для воздуха ≈ 0,8.
Толщина гиперзвукового пограничного слоя в Ме2 раз больше
толщины при умеренных числах Маха. Это и есть причина
важности эффекта вязко-невязкого взаимодействия в
21
гиперзвуковом потоке.
22.
Сильное вязко-невязкое взаимодействие напластине в гиперзвуковом потоке
Обычно наличие пограничного слоя приводит к
изменению формы обтекаемой поверхности на
величину толщины вытеснения δ*(х) << 1, что
приводит к изменению угла наклона ударной волны
по х, т.е воздействию пограничного слоя на невязкий
поток - вязко-невязкому взаимодействию.
Рассмотрим случай сильного вязко-невязкого
взаимодействия, когда параметр гиперзвукового
подобия за ударной волной K >> 1.
K x M 1
22
23.
Приближение «локального клина»Для вычисления давления на поверхности тела, образованного толщиной вытеснения δ*(х) << 1, используем приближение «локального клина»: давление, индуцированное взаимодействием, равно давлению за скачком с углом наклона, соответствующим локальному углу наклона обтекаемой поверхности, т.е.:
pe
1 2
16
1 2
1
K 1 1 2
K
2
p
4
4
K
1
d x
K x M M
1
dx
Такой подход часто используется для расчета давления около обтекаемой поверхности на гиперзвуке и подтверждается
23
экспериментом.
24.
Сильное вязко-невязкое взаимодействие напластине в гиперзвуковом потоке
В этом случае преобразование толщины вытеснения дает
следующее соотношение (b – постоянная):
w
bx
Re x
Tw p
Tw
C
T pe
T
bx
bx
w ue x
u x w
bx C Tw
Re x T
p
pe
2
xM
Re x
w
p
u x
, Re x
pe
24
25.
Толщина пограничного слоя при сильномгиперзвуковом взаимодействии, K >> 1
Если К >> 1 из формулы «локального клина» давление
оценивается в главном приближении так:
pe
1 2
1 2 d
K
M
p
4
4
dx
2
Соответственно, для толщины вытеснения получаем оценку
2
xM
Re x
p
2 xM C
2 xM C d
C
pe K 1 Re x
dx
1 Re x
2
1
3
2 xM C
4M C
4 xM C
d
2
2
~
~ x
dx
1 Re1
1 Re1
1 Re x
26.
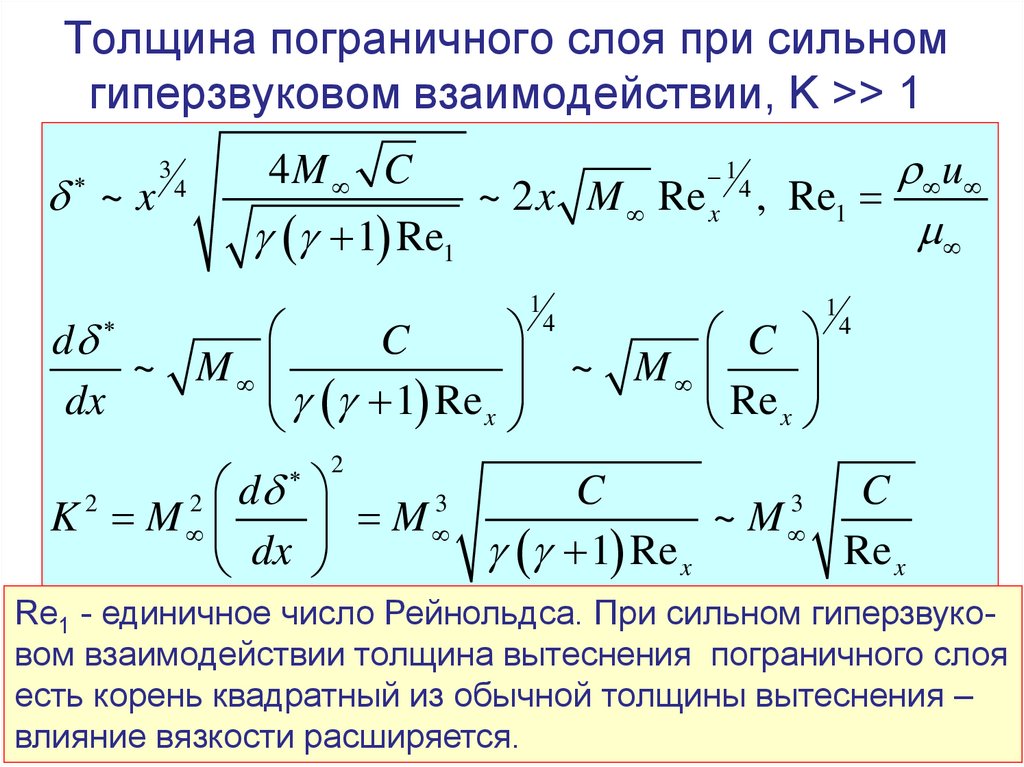
Толщина пограничного слоя при сильномгиперзвуковом взаимодействии, K >> 1
~x
3
4
4M C
1 Re1
~ 2 x M Re
C
d
~ M
dx
1 Re x
1
4
1
4
x
u
, Re1
1
C 4
~ M
Re x
2
d
C
C
3
3
~ M
K M
M
Re x
1 Re x
dx
2
2
Re1 - единичное число Рейнольдса. При сильном гиперзвуковом взаимодействии толщина вытеснения пограничного слоя
есть корень квадратный из обычной толщины вытеснения –
26
влияние вязкости расширяется.
27.
Параметр вязко-невязкого гиперзвуковоговзаимодействия, K >> 1
Таким образом, при сильном взаимодействии
pe
1
2
3
~ K ~ M C Re x 2
p
χ называется параметром вязко-невязкого взаимодействия. В общем случае распределение давления при сильном
гиперзвуковом взаимодействии можно описать формулой,
включающей часть эффектов умеренного взаимодействия
pe
a0 a1
p
Здесь а0 и а1 – постоянные, зависящая от конкретной задачи.
28.
Слабое гиперзвуковое взаимодействие, K << 1Слабое гиперзвуковое взаимодействие соответствует
пределам:
K x M
d x
dx
~
M 3
Re
M 0, M , Re
Формулы локального клина, описывающие невязкую область
течения, преобразовываются так:
1
M 1
K 2K
...
2
4
2
2
1
2
2
pe
1
1 2
2
1
K
K
1
b
b
1
2
p
4
4
2
Влияние вязкости описывается теорией пограничного слоя, в
главном приближении взаимодействие отсутствует
29.
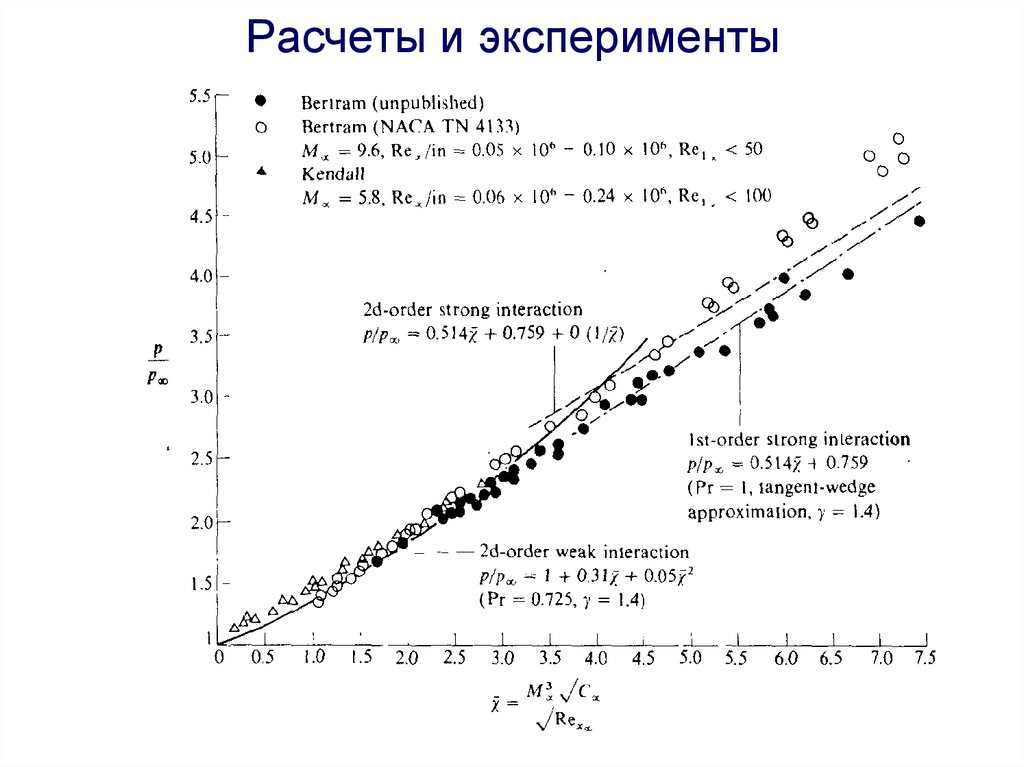
Давление на пластинеПри горячей стенке, Тw/Te ~ M∞2
pe
Сильное взаимодействие:
a0 a1 0,514 0, 759
p
pe
Слабое взаимодействие:
1 b1 b2 2 1 0,31 0, 05 2
p
При холодной стенке, Тw/Te ~ 1
pe
Сильное взаимодействие:
a0 a1 1 0,5
p
pe
Слабое взаимодействие:
1 b1 b2 2 1 0, 078
p
29



















 physics
physics








