Синусоида. Синусоидальные кривые

1.

2. Подслушанный диалог.

• Синусоида
Ах, как томительны вечные спуски,
Как утомительны вечные взлёты!..
В каждой ложбине,
На каждой вершинеТщетной надеждой - мечта о привале,
Об остановке , о передышке.
• Циклоида
Интересно, какие песни
Синусоида бы запела,
Доведись ей вот так же,
Камнем лететь с обрыва
И, едва опомнившись от удара,
Снова карабкаться по крутому склону…

3. Преобразование графиков.

Во многих случаях график функции может быть построен как результат
некоторых геометрических преобразований ( параллельный перенос,
поворот, симметричное отражение. е относительно какой – либо оси,
сжатие к оси, растяжение от оси и др.)известного графика некоторой
исходной функции у(х).
Рассмотрим, как используя график функции y= sin х построить графики
функций:
y= sin (x + b)
y= sin x + b
y= sin ax
y= a sin x
y=a sin (mx + b)
y=c sin ax +b.

4. Синусоида.

Построим график функции синус на отрезке [0;2π].Для этого
отметим на оси ординат точки(0,-1) и (0,1), а на оси абсцисс
точку с абсциссой 2п.Разделим отрезок на 16 равных частей.
Отметим на оси абсцисс, через равные промежутки, точки 0,п/2,
п,3п/2.Соединяя их плавной кривой, получаем эскиз графика
синуса на отрезке [0;2π]. Для построения графика вне этого
отрезка заметим, что sin(x+2п)=sin x (n – произвольное целое
число). Следовательно, график функции на все прямой
получается из построенного графика с помощью параллельного
переноса. вдоль оси ОХ (вправо и влево) на 2п,4п,6пи т.д.
1
0
-1
h/2
р/2
р
3 р/2
2р
x
синусоида

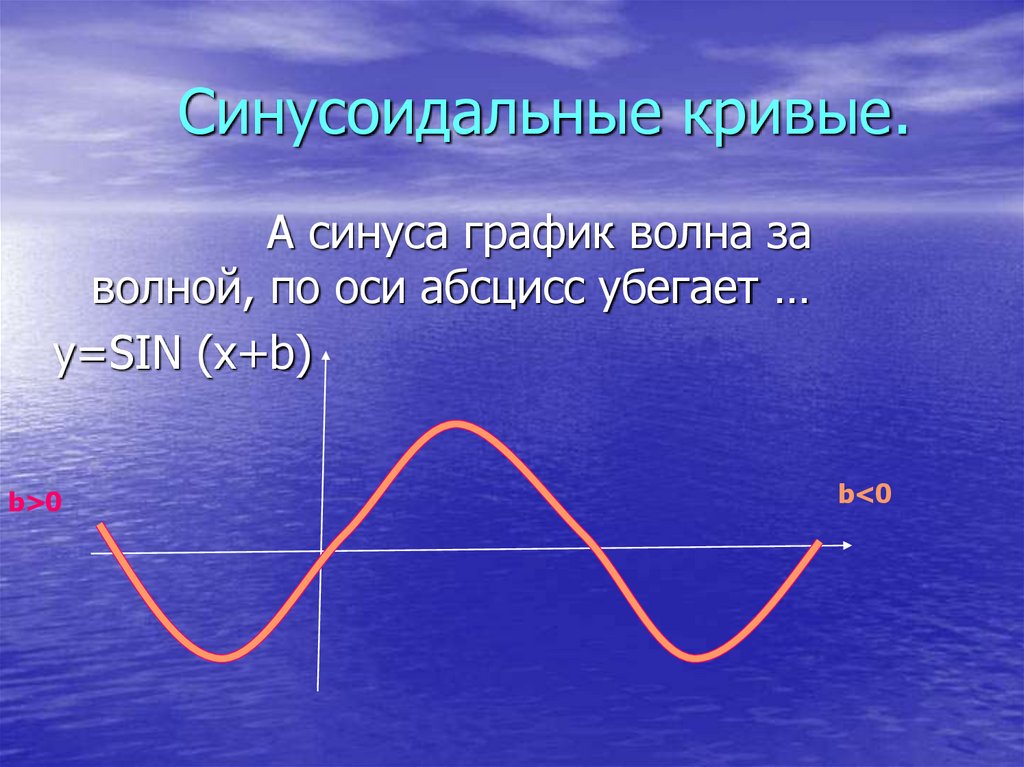
5. Синусоидальные кривые.

А синуса график волна за
волной, по оси абсцисс убегает …
y=SIN (x+b)
b>0
b<0

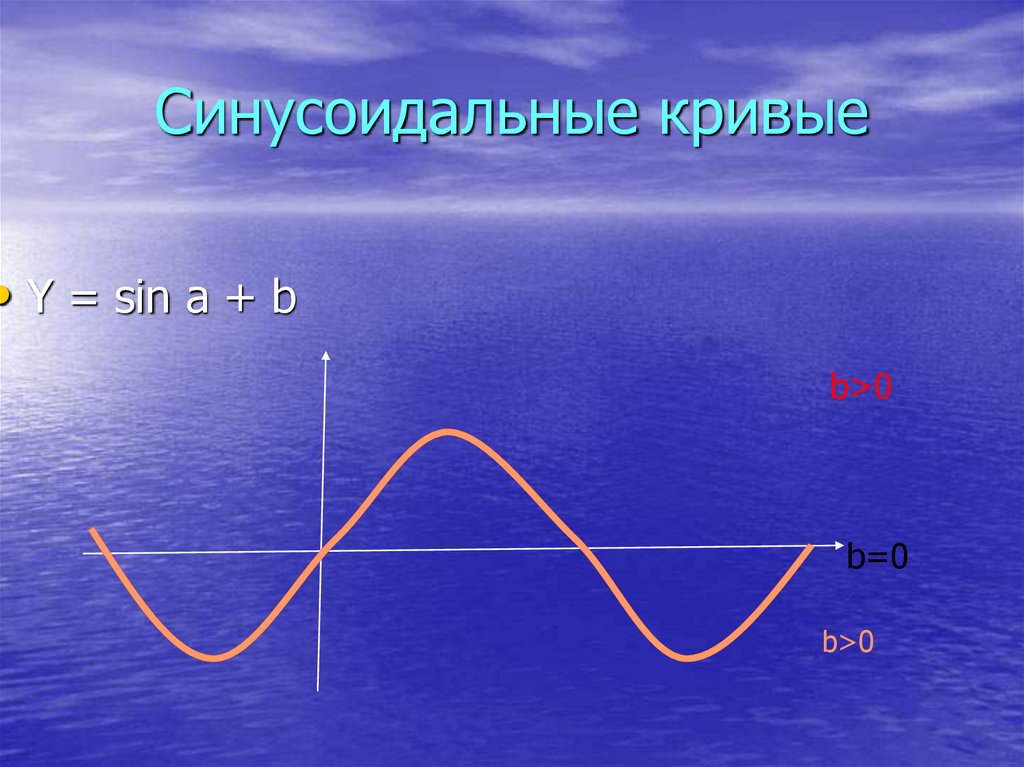
6. Синусоидальные кривые

• Y = sin a + b
b>0
b=0
b>0

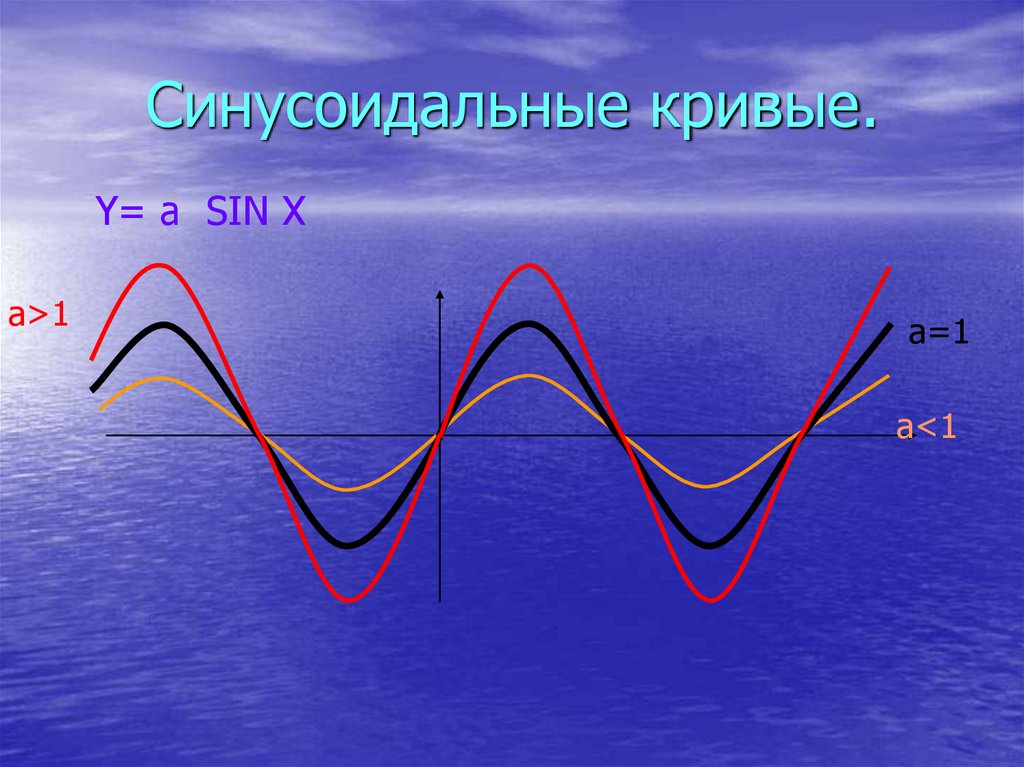
7. Синусоидальные кривые.

Y= a SIN X
a>1
a=1
a<1

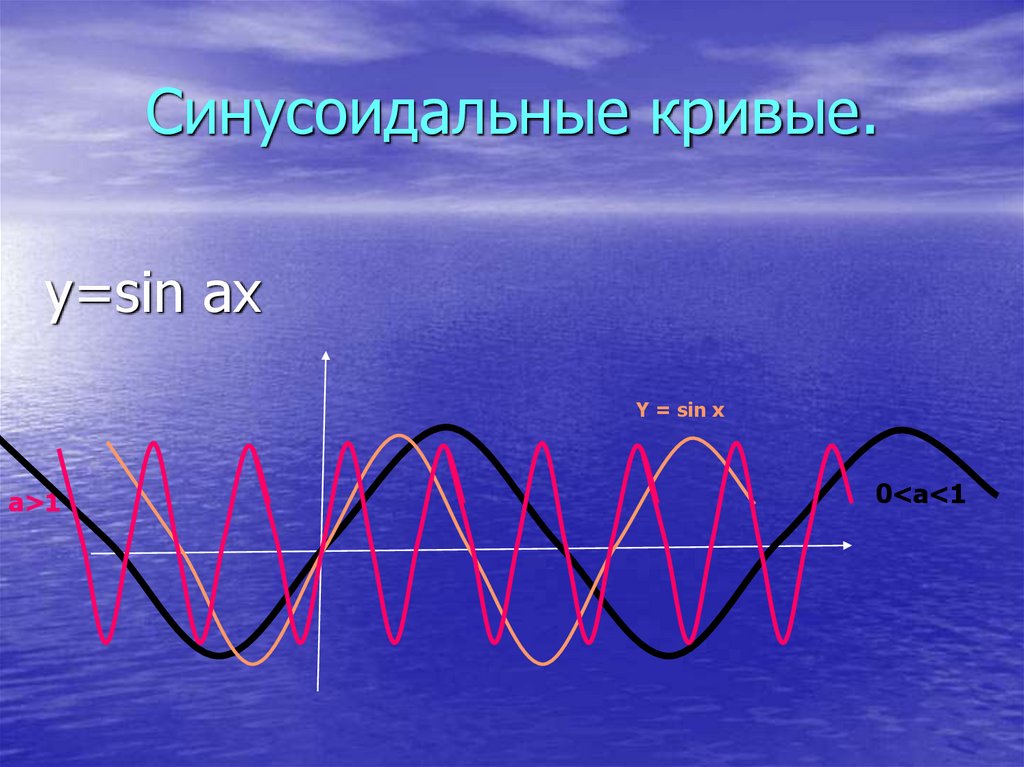
8. Синусоидальные кривые.

y=sin ах
Y = sin x
а>1
0<а<1

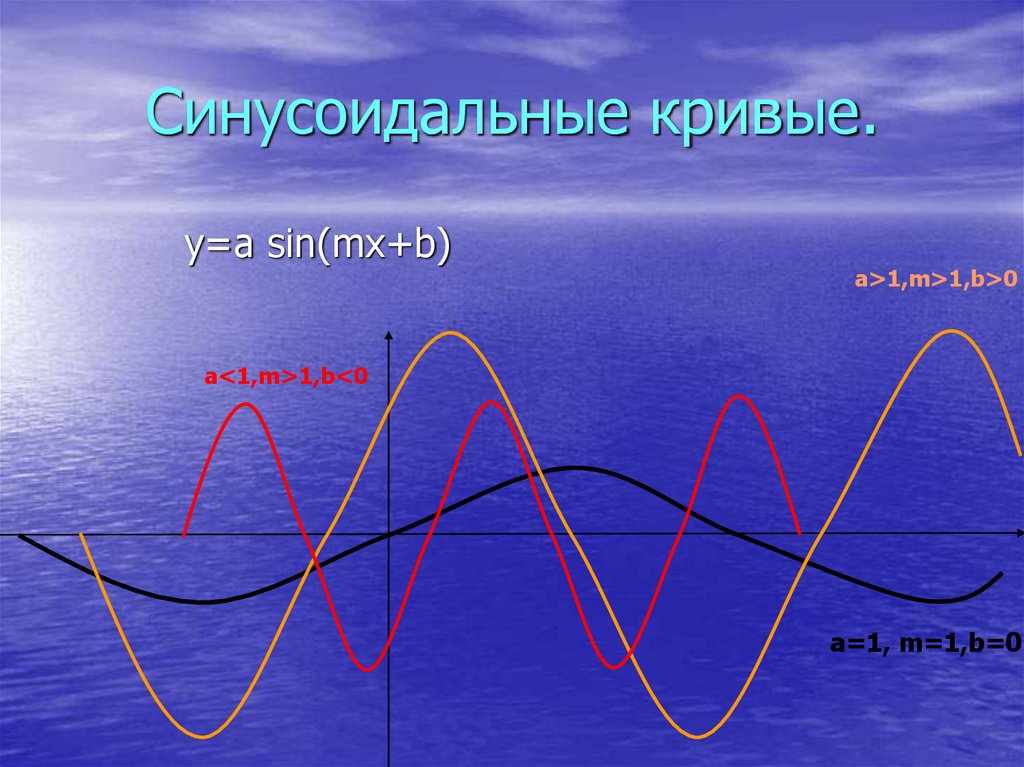
9. Синусоидальные кривые.

y=a sin(mx+b)
a>1,m>1,b>0
a<1,m>1,b<0
a=1, m=1,b=0

10. Построение графика функции у = с sin ax + b.

1.Пусть а>0.
Чтобы получить график надо произвести сжатие графика функции к оси ОУ,
т. е.абсциссы всех точек графика функции умножить в а раз. Точка
пересечения графика функции с осью ОУ останется на месте.
2. Пусть с >0.
При равных значениях аргумента х (из области определения функции)
значения функции у1(х) будут в с раз больше соответствующих значений
у2(х).Для построения графика функции у2(х) = су1(х) следует каждую
ординату графика функции у1(х) увеличить в с раз, т.е. произвести
растяжение от оси ОХ.
3.Пусть b>0.
Для построения графика функции у3(х) = у2(х) +b следует график функции
у2(х) перенести параллельно в направлении оси ординат, как единое целое
на b вверх.

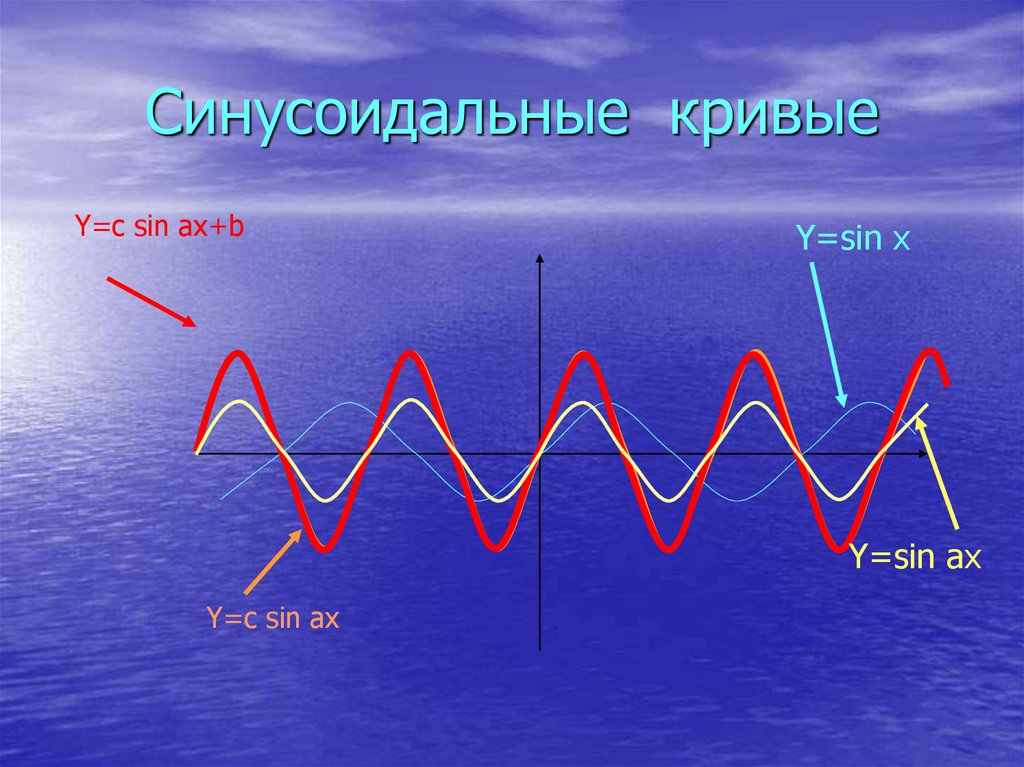
11. Синусоидальные кривые

Y=c sin ax+b
Y=sin x
Y=sin ax
Y=c sin ax

12. Примечания.

1.
2.
3.
4.
5.
Если 0<a<1, то абсциссы всех точек графика у(х) увеличить в
1/а раз (произвести растяжение графика f(х) от оси ОУ).
Если а<0, то к преобразованию сжатия (растяжения)
присоединяется симметрия относительно оси ОУ.
Если 0<с<1, то ординату уменьшить в 1/с раз (произвести
сжатие графика f(х) к оси ОХ).
Если с<0, то к преобразованию сжатия (растяжения)
присоединяется симметрия относительно оси ОХ.
Если b<0, то график функции у2(х) переносится параллельно
вниз на b единиц.

13.

.
1. Приготовить шаблоны функций
У= cos x,
y= tg x,
y = ctg x,
y=x²
2. Построить в одной системе координат графики функций
У= sin x+2
У= sin x - 3
У=2 sin x
У= -3 sin x