Алгоритмизация расчета вектора состояния навигационного спутника ГЛОНАСС на основе неоперативной информации

1.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«Санкт-Петербургский государственный университет
аэрокосмического приборостроения»
Институт аэрокосмических приборов и систем (институт №1)
Кафедра эксплуатации и управления аэрокосмическими системами (кафедра №13)
Тема дипломной работы:
«Алгоритмизация расчета вектора состояния
навигационного спутника ГЛОНАСС на основе
неоперативной информации»
Выполнил: студент группы №Z9131K
Фрунтов А. Е.
Научный руководитель: доцент кафедры №13
Слюсаренко А.С., к.т.н.
Санкт-Петербург 2024
1

2.

Актуальность темы: спутниковые радионавигационные системы
СРНС применяются для повышения эффективности решения задач
национальной безопасности страны, но если РСБН и РСДН насчитывают
множество систем, то СРНС «Глонасс» и «Навстар» лишь находятся в
стадии интенсивного развертывания и нередко возникают некоторые
характерные проблемы в обеспечении заданной точности выдаваемых
результатов измерений.
Цель
исследования: алгоритмизировать
расчет
состояния ГЛОНАСС на основе неоперативной информации.
вектора
Задачи исследования:
1) Исследовать теоретические аспекты реализации расчета вектора
состояния навигационного спутника ГЛОНАСС на основе неоперативной
информации;
2) Рассмотреть алгоритмическое обеспечение навигационного спутника
ГЛОНАСС на основе неоперативной информации;
3)
Проанализировать
стандарты
на
разработку
программного
обеспечения;
4) Провести описание программного изделия.
2

3.

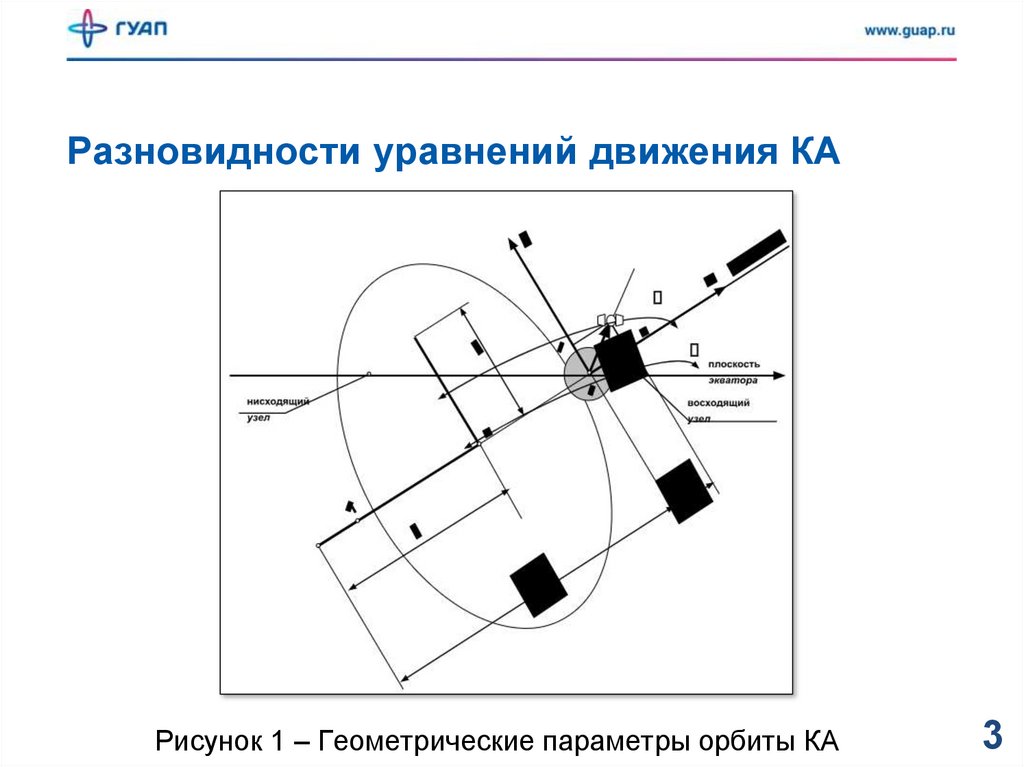
Разновидности уравнений движения КА
Рисунок 1 – Геометрические параметры орбиты КА
3

4.

Определение положения КА в пространстве
Рисунок 2 – Положение КА низкоорбитальной СРНС в
горизонтной системе координат
4

5.

Основные недостатки текущих методов
ГЛОНАСС - реализации измерений относятся к классу
процессорных измерительных информационных систем (ПрИС).
1. ПрИС требует метрологической аттестации, но требование
характеристик
погрешности
вычислений
вступает
в
противоречие со стандартами на разработку ПО.
2. Ошибки процессорных преобразований данных, искажающие
результаты измерений, известны, но инструментарий для их
оценки не имеет необходимой общности и эффективности.
3. Оценка процессорных ошибок затруднена псевдослучайным
характером их проявления, зависящим от величины
операндов и траектории вычислений.
Наиболее эффективные формальные подходы к верификации
результатов - вычислительные эксперименты.
5

6.

Постановка задач ВКР
● Провести разработку методов расчета эфемерид КА с
метрологическим автосопровождением их программных
реализаций.
● Обеспечить использование А-технологии компьютерной
обработки данных (АТ_КОД) в качестве альтернативы
традиционной технологии разработки программ обработки
данных.
● Разработать алгоритмическую основу предвычисления
эфемерид КА на основе простой Кеплеровой модели
движения КА по орбите.
● Разработать алгоритмы поверки расчета кеплеровых
параметров орбиты КА и моделей поверки схем частных
реализаций методов решения системы дифференциальных
уравнений, описывающих движение КА по орбите.
6

7.

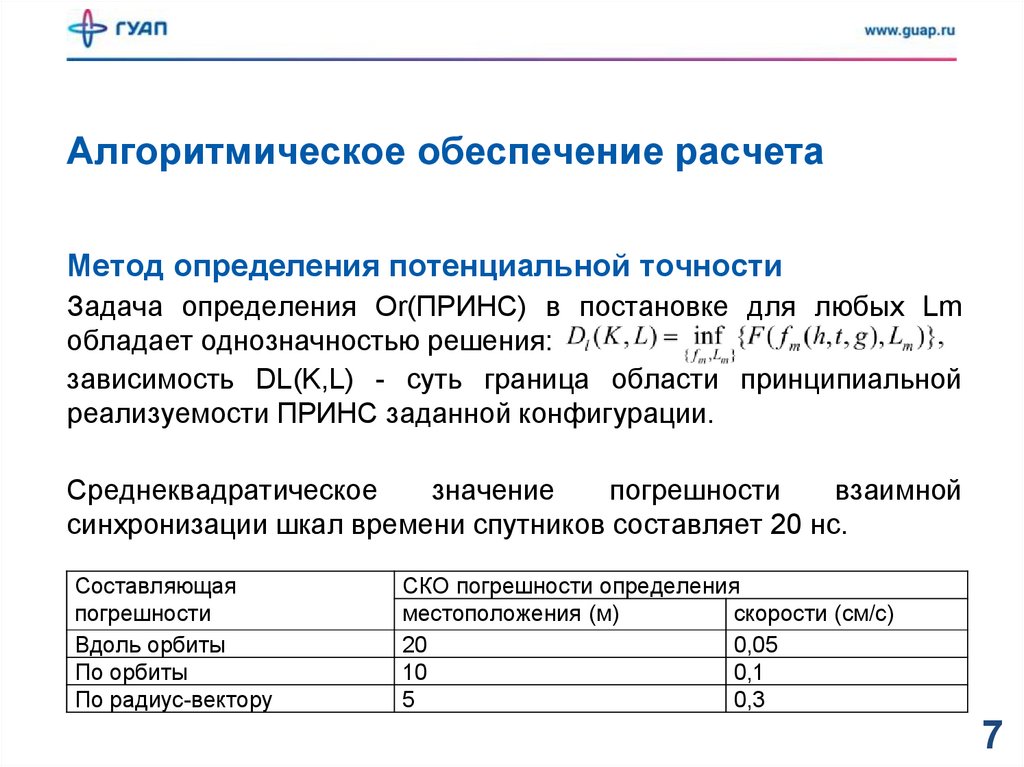
Алгоритмическое обеспечение расчета
Метод определения потенциальной точности
Задача определения Оr(ПРИНС) в постановке для любых Lm
обладает однозначностью решения:
зависимость DL(K,L) - суть граница области принципиальной
реализуемости ПРИНС заданной конфигурации.
Среднеквадратическое
значение
погрешности
взаимной
синхронизации шкал времени спутников составляет 20 нс.
Составляющая
погрешности
Вдоль орбиты
По орбиты
По радиус-вектору
СКО погрешности определения
местоположения (м)
скорости (см/с)
20
0,05
10
0,1
5
0,3
7

8.

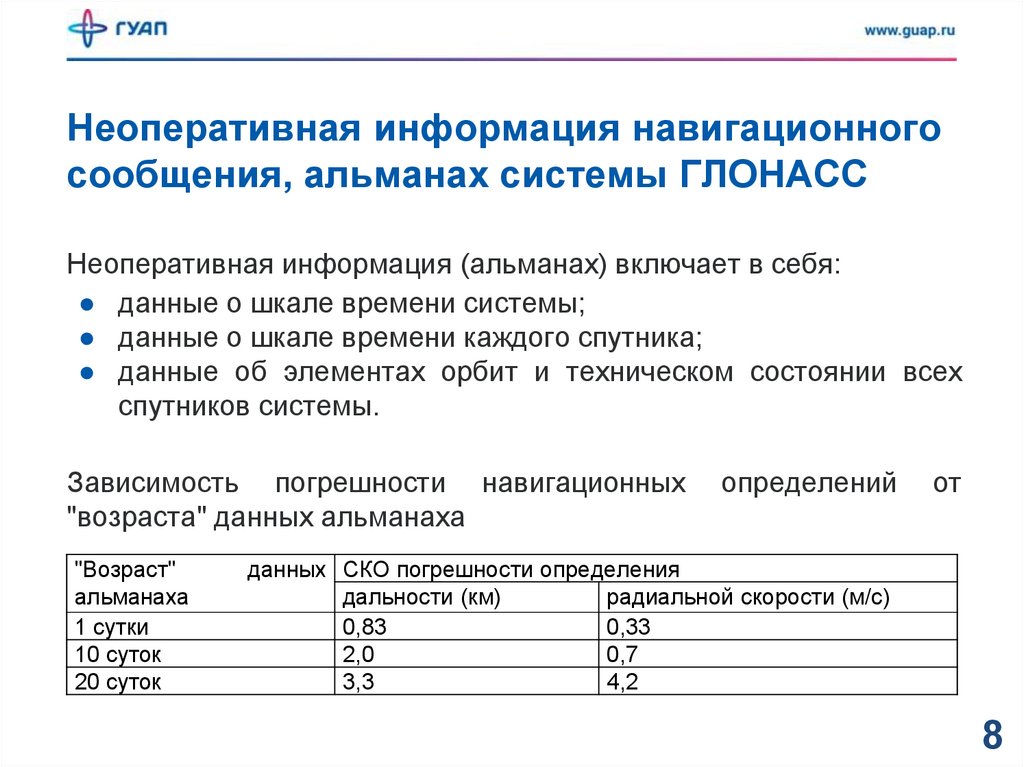
Неоперативная информация навигационного
сообщения, альманах системы ГЛОНАСС
Неоперативная информация (альманах) включает в себя:
● данные о шкале времени системы;
● данные о шкале времени каждого спутника;
● данные об элементах орбит и техническом состоянии всех
спутников системы.
Зависимость погрешности навигационных
"возраста" данных альманаха
"Возраст"
альманаха
1 сутки
10 суток
20 суток
определений
от
данных СКО погрешности определения
дальности (км)
радиальной скорости (м/с)
0,83
0,33
2,0
0,7
3,3
4,2
8

9.

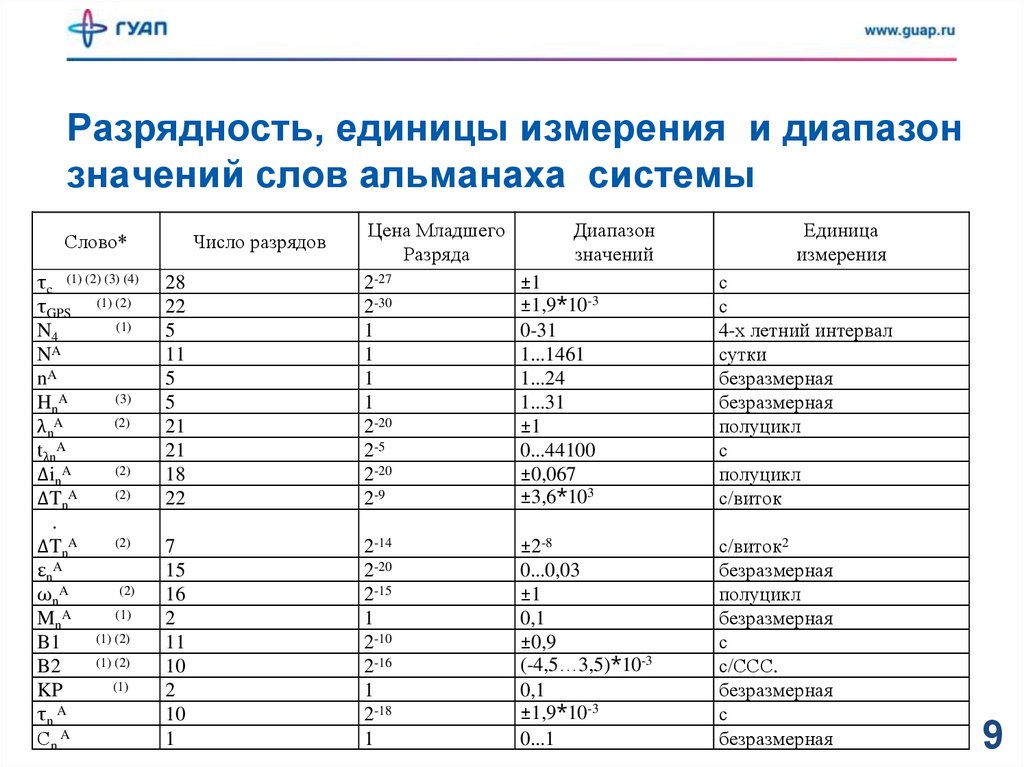
Разрядность, единицы измерения и диапазон
значений слов альманаха системы
28
22
5
11
5
5
21
21
18
22
Цена Младшего
Разряда
2-27
2-30
1
1
1
1
2-20
2-5
2-20
2-9
±1
±1,9*10-3
0-31
1...1461
1...24
1...31
±1
0...44100
±0,067
±3,6*103
с
с
4-х летний интервал
сутки
безразмерная
безразмерная
полуцикл
с
полуцикл
с/виток
7
15
16
2
11
10
2
10
1
2-14
2-20
2-15
1
2-10
2-16
1
2-18
1
±2-8
0...0,03
±1
0,1
±0,9
(-4,5…3,5)*10-3
0,1
±1,9*10-3
0...1
с/виток2
безразмерная
полуцикл
безразмерная
с
с/ССС.
безразмерная
с
безразмерная
Слово*
τc (1) (2) (3) (4)
τGPS (1) (2)
(1)
N4
NA
nA
(3)
HnA
(2)
λnA
tλnA
(2)
ΔinA
(2)
ΔTnA
.
(2)
ΔTnA
εnA
(2)
ωnA
(1)
MnA
(1) (2)
B1
(1) (2)
B2
(1)
KP
τn A
Сn A
Число разрядов
Диапазон
значений
Единица
измерения
9

10.

Определения местоположения и скорости КА
методом с регулируемой точностью
Уравнение эллиптической орбиты в полярных координатах имеет
вид:
Параметры эллиптической орбиты – величины ϕп, P и ε
определяются по начальным условиям векторам координат - R0 =
[X0, Y0]T и скоростей - V0 = [VX0, VY0]T из системы 3-х уравнений:
Итерации проводятся до появления повторяющихся вычислений,
приближающих аппроксимированный угол экстраполяции к
истинному значению:
10

11.

Вычисление координат КА
Осуществляется в три шага:
1. - вычисление (по стандартным для каждой СРНС
формулам) положения и скоростей КА и коэффициентов
для расчета ЧВП на начало и конец 20-ти секундного
интервала;
2. - векторов ускорений КА на середину 20-ти секундного
интервала для всех систем;
3. - квадратичная экстраполяция координат, линейная
скоростей и ЧВП на любой произвольный момент
времени внутри 20-ти секундного интервала.
11

12.

Сопровождение программного средства
Рисунок 3 – База данных управления конфигурацией
12

13.

Входные данные программного изделия
Рабочий массив координат спутников – Coord_N[7*3, 6*3, 5*3,
4*3], полученных потребителем с передающего центра ГЛОНАСС.
Координаты ИСЗ экстраполируются в аппаратуре ГЛОНАСС
стандартными методами. Массивы могут быть из 4, 5, 6, 7 и
более троек координат ИСЗ в различных режимах слежения.
Массив ошибок в определении координат спутников (для
моделирования). - Mist_Coord_N[7*3, 6*3, 5*3, 4*3] Структура
этого массива аналогична структуре предыдущего.
Массив координат абонента используется только для
моделирования - Coord_Abonent_For_Test [3]
Массив неизвестных сдвигов по дальности из-за смещения
шкалы времени потребителя - Dist_Shift_For_Test [4]
13

14.

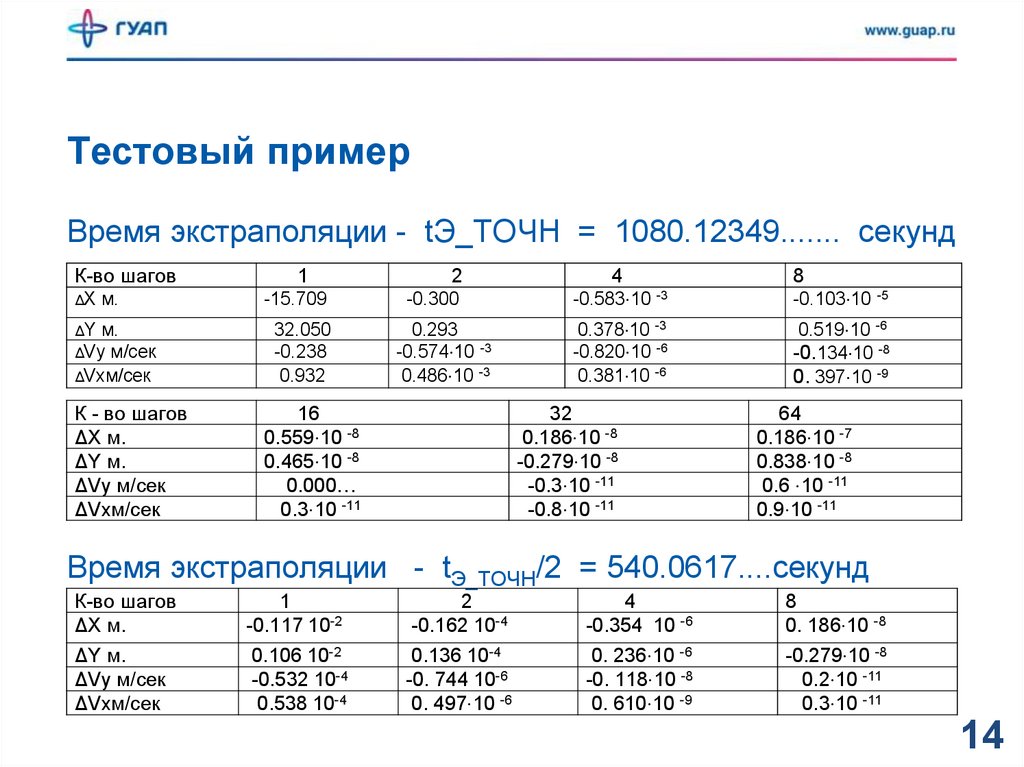
Тестовый пример
Время экстраполяции - tЭ_TОЧН = 1080.12349....... секунд
К-во шагов
1
2
4
ΔX м.
-15.709
-0.300
-0.583⋅10 -3
ΔY м.
32.050
-0.238
0.932
0.293
-0.574⋅10 -3
0.486⋅10 -3
0.378⋅10 -3
-0.820⋅10 -6
0.381⋅10 -6
ΔVу м/сек
ΔVxм/сек
К - во шагов
ΔX м.
ΔY м.
ΔVу м/сек
ΔVxм/сек
16
0.559⋅10 -8
0.465⋅10 -8
0.000…
0.3⋅10 -11
32
0.186⋅10 -8
-0.279⋅10 -8
-0.3⋅10 -11
-0.8⋅10 -11
8
-0.103⋅10 -5
0.519⋅10 -6
-0.134⋅10 -8
0. 397⋅10 -9
64
0.186⋅10 -7
0.838⋅10 -8
0.6 ⋅10 -11
0.9⋅10 -11
Время экстраполяции - tЭ_TОЧН/2 = 540.0617....секунд
К-во шагов
ΔX м.
1
-0.117 10-2
2
-0.162 10-4
4
-0.354 10 -6
8
0. 186⋅10 -8
ΔY м.
ΔVу м/сек
ΔVxм/сек
0.106 10-2
-0.532 10-4
0.538 10-4
0.136 10-4
-0. 744 10-6
0. 497⋅10 -6
0. 236⋅10 -6
-0. 118⋅10 -8
0. 610⋅10 -9
-0.279⋅10 -8
0.2⋅10 -11
0.3⋅10 -11
14

15.

Вывод
Численное
моделирование
полностью
результаты теоретических выводов.
подтвердило
● во всех вариантах принятых алгоритмов расчета вектора
состояния навигационного спутника ГЛОНАСС на основе
неоперативной информации, зафиксирована эффективность
методов
и алгоритмов
расчета
вектора
состояния
навигационного спутника ГЛОНАСС.
Принятые в качестве основы методы и алгоритмы АТ-КОД
обеспечивает эффективность решения поставленных задач
и, соответственно, достижение цели ВКР.
15