§1.5. Классификация грамматик и языков на основе иерархии Хомского

1.6.3 Условия порождения КС-грамматиками бесконечных языков

1.6.4. Преобразование УКС-грамматики в КС-грамматику

564.00K

Category:

programming

Методы компиляции

1. Методы компиляции

2. Введение

Основу курса составляют методы
компиляции, основанные на
теории формальных грамматик и
языков.

3. Литература

1.
2.
3.
4.
5.
6.
Ахо А., Ульман Дж. Теория синтаксического
анализа, перевода и компиляции. Т 1,2.
М.Мир.1972
Лебедев В.Н. Введение в системы
программирования. М.Статистика. 1975
Грис Д. Конструирование компиляторов для ЭВМ.
М. Мир. 1975.
Бек Л. Введение в системное программирование.
М. Мир, 1988
Ахо А., Сети Р., Ульман Дж. Компиляторы.
Принципы, технологии, инструменты. W. 2003
Мозговой М.В. Классика программирования:
алгоритмы, языки, автоматы, компиляторы.
Практический подход. Наука и Техника, СанктПетербург, 2006.

4. Глава 1. Формальные грамматики и языки.

§1.1. Задача и этапы трансляции, типы
трансляторов.
Задача любого транслятора –
перевести программу с некоторого
входного языка в программу на
другом языке.
программа
на входном языке
Транслятор
программа
на выходном языке

5. О языке - неформально

Основу любого языка составляет
алфавит –
набор допустимых символов – букв.
Буквы объединяются в слова – неделимые
единицы языка: идентификаторы,
константы, знаки операций и др.
Набор допустимых слов языка образует его
лексику(словарный состав языка).
В теории построения трансляторов слова
называют также лексемами.

6. О языке - неформально

Слова объединяются в предложения –
более сложные конструкции языка, такие как
условие, оператор, функция.
В теории трансляции предложения называют
также термином понятие.
Понятия строятся из лексем и других
понятий по правилам
синтаксиса.
Таким образом, можно сказать, что
синтаксис – это определение правильных
предложений языка.

7. О языке - неформально

Каждому правильному предложению
языка сопоставляется определенный
смысл (действие).
Смысл всех понятий языка образует
его
семантику.

8.

Трансляция – это изменение
алфавита,
лексики
и
синтаксиса языка
с сохранением
семантики.

9. Этапы трансляции

Очевидно, что транслятор решает при этом
не простую задачу и его работу нельзя
представить как одношаговый процесс.
Логически процесс трансляции можно
представить в виде 4 основных этапов
(просмотров), каждый из которых решает
свою задачу, получая результат работы
предыдущего этапа.

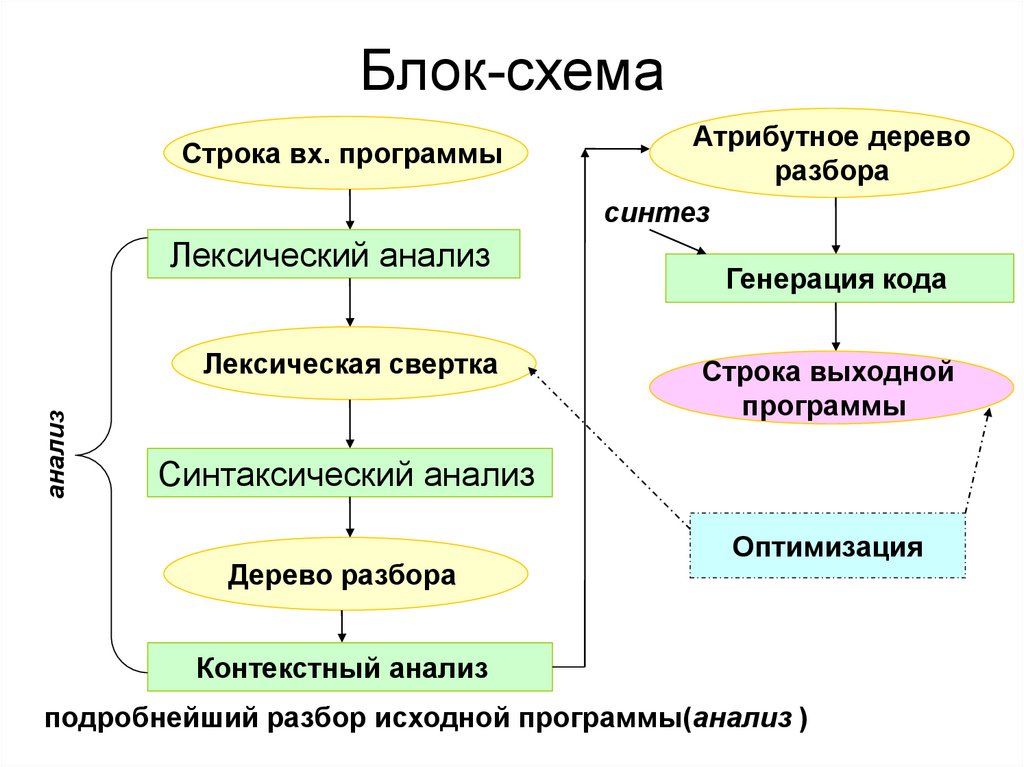
10. Блок-схема

Строка вх. программы
Лексический анализ
анализ
Лексическая свертка
Атрибутное дерево
разбора
синтез
Генерация кода
Строка выходной
программы
Синтаксический анализ
Дерево разбора
Оптимизация
Контекстный анализ
подробнейший разбор исходной программы(анализ )

11. Лексический анализ

Исходная программа – это длинная
цепочка символов.
Транслятор просматривает ее знак за
знаком и выделяет лексемы.
Лексемы заносятся в соответствующие
таблицы, например, идентификаторов,
числовых констант или распознаются
по ним – например, по таблице
служебных слов.

12. Лексическая свертка

В программе вместо лексемы формируется
дескриптор (токен), содержащий тип
лексемы и адрес ее в соответствующей
таблице
тип
адрес
Последовательность дескрипторов образует
лексическую свертку программы.
Программа приобретает стандартный и
более осмысленный вид.
Синтаксис лексем можно задать в рамках
простых грамматик.

13. Синтаксический анализ

Это этап распознавания типов предложений
и структуры программы.
Из лексем формируются понятия,
выполняется проверка соответствия понятия
синтаксису языка.
Результатом работы синтаксического
анализа является дерево разбора
программы, либо представление ее на
промежуточном языке (ПОЛИЗ).
Синтаксис понятий определяется более
сложными грамматиками – КС-грамматиками.

14. Контекстный анализ.

Цель этого этапа следующая. Дерево разбора
задает иерархическое строение понятий, входящих
в программу. На следующем этапе генерации для
построения выходной программы выполняется
регулярный обход этого дерева.
Для правильной генерации кода каждая вершина
дерева должна быть снабжена дополнительными
характеристиками или говорят
атрибутами.
Часть атрибутов определяется по контексту
программы (например, тип лексемы идентификатор
по его описанию), а часть следует из
синтаксических и семантических правил
конструирования понятия (например, правило
работы оператора while).

15. Пример

Имеется операция a+b. Её дерево,
построенное на этапе синтаксического
анализа, просто.
f
+
i->f
a
b
i
f
Но для того, чтобы грамотно сгенерировать
команду сложения, необходимо знать
значение такого атрибута переменных a и b,
как тип.
Причем, если a и b будут иметь разный тип,
то дерево будет дополнено действием
преобразования к одному типу.
Атрибут операции «+», таким образом,
будет зависеть от атрибутов вершин ее
поддерева.

16. Определение

Процесс нахождения значений
атрибутов лексем и понятий
называется
контекстным анализом.
Результатом его работы является
атрибутное дерево разбора.

17. Генерация кода

Это процесс построения выходной программы. При
этом, как уже говорилось выше, выполняется
регулярный обход дерева разбора.
Для каждой внутренней вершины выполняется
вызов
генерационной процедуры (трансдуктора).
Имя такой процедуры соответствует понятию
данной вершины, а ее аргументы – значения
атрибутов понятия.
Генерационная процедура обычно использует
шаблоны понятия. Шаблон достраивается в
зависимости от значений атрибутов понятия, и им
формируется фрагмент выходной программы.
(Например, фрагменты операторов while, for).

18. Оптимизация программы

Это этап улучшения качества программы по
времени ее работы и длине.
Пример программы, где может быть выполнена
оптимизация – чистка цикла:
for (y=1, k=0; k<n; k++) // вычисление y = ( x+1) ^ n
y = y * (x + 1);
Величина x+1 инвариантна(неизменна) в цикле
и ее вычисление может быть вынесено из него
и помещено перед ним.
r1 = x + 1;
for( y = 1, k = 0;k<n; k++)
y = y*r1;
Во многих компиляторах оптимизацию можно
отключить или подключить по желанию
пользователя.

19. Типы трансляторов

Трансляторы делятся на два основных типа:
компиляторы
и
интерпретаторы.
Компиляторы – это такие трансляторы, в
которых трансляция и выполнение
программы разделены во времени:
сначала программа транслируется,
формируется выходной код (exe – файл),
а затем программа выполняется.

20. Типы трансляторов

Интерпретаторы – это трансляторы, в
которых трансляция и выполнение
программы совмещены. Каждый оператор
транслируется и сразу же выполняется.
Существуют и другие типы трансляторов.
Например, имеется такой тип трансляторов
– эмуляторы.
Это трансляторы, которые переводят
программу с одного языка высокого уровня
на другой (например, с Фортрана на
Паскаль).

21. Методы трансляции

Различают прямые и синтаксические методы.
Прямые - это эвристические методы, которые на
основе некоторой идеи для каждой конструкции
языка подбирают свой индивидуальный алгоритм.
Ярким примером является Польская Инверсная
Запись. Основная идея – преобразовать ту или иную
конструкцию языка в эту запись, для чего
используются приоритеты операций, скобок и
служебных слов.
Недостаток – для нового языка правила
формирования ПОЛИЗ могут видоизменяться,
дополняться. А это значит, что компилятор будет
разрабатываться заново.

22. Синтаксические методы

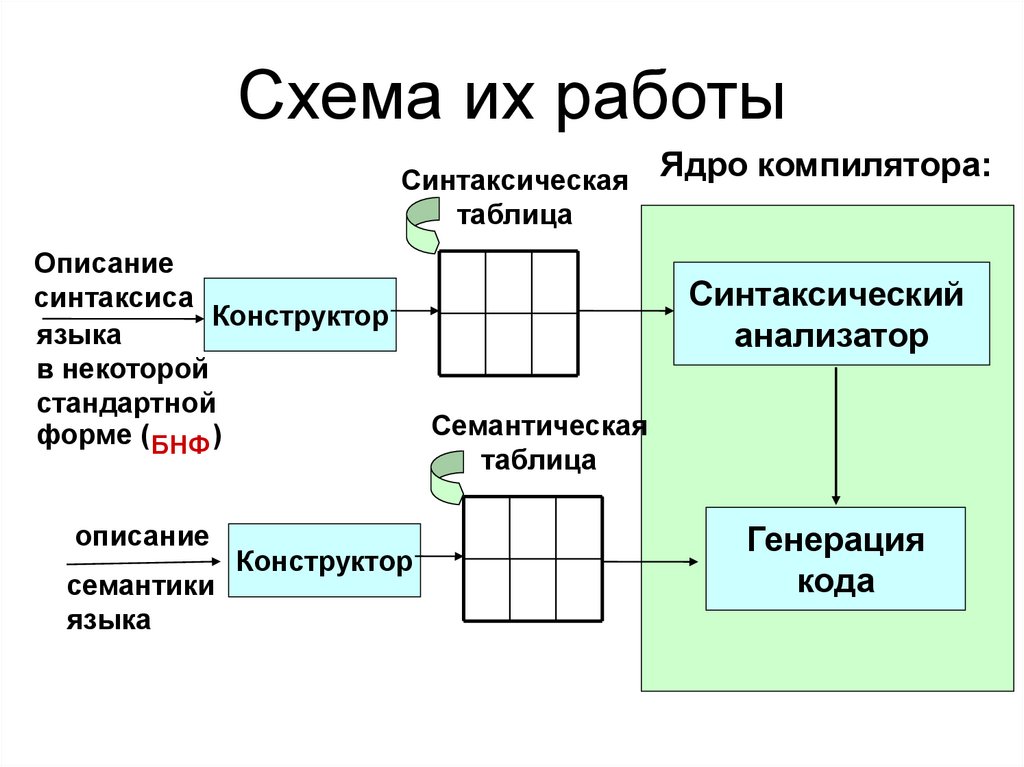
Основное достоинство синтаксических
методов – возможность использования ядра
транслятора для разных языков.
Синтаксические методы основаны на
теории формальных грамматик.
Эти методы ориентированы не на один
конкретный язык, а на класс языков,
имеющих один и тот же способ описания
синтаксиса языка.
Такие трансляторы получили название
синтаксически-ориентированных.

23. Схема их работы

Синтаксическая
таблица
Описание
синтаксиса
Конструктор
языка
в некоторой
стандартной
форме ( БНФ )
описание
семантики
языка
Конструктор
Ядро компилятора:
Синтаксический
анализатор
Семантическая
таблица
Генерация
кода

24. §1.2. Порождающие грамматики. БНФ

Набор правил синтаксиса языка образуют
грамматику языка. Определим ее
формально.
Обозначим через M* - множество конечных
последовательностей элементов (символов) из
некоторого множества M (алфавит), которые будем
называть цепочками или строками и обозначать α, β, ….
|α| - длина цепочки.
Если |α| = 0, то α – пустая цепочка e.
Если α и β две цепочки, то цепочка ω = αβ –
их конкатенация, причем α – префикс
цепочки ω, а β – её суффикс.
β – подцепочка цепочки ω, если ω = αβγ.

25. Определение

Порождающая грамматика G определяется
четверкой
G = { T, N, P, S }, где
T - множество основных или терминальных
символов (лексемы),
N – множество нетерминальных символов
(понятия, или сущности),
P – множество правил вида
α -> β, где α (T U N)*/T*, β (T U N)*,
которые называются порождающими
правилами или правилами вывода или
продукциями,
S – начальный символ (аксиома) грамматики, N.

26. Пример

Рассмотрим грамматику, определяющую
арифметическое выражение, состоящее из
идентификаторов, знаков операций +,* и круглых скобок
G 1:
Множество правил
P
1) A -> ! B !
2) B -> B + T
3) B -> T
4) T -> T * M
5) T -> M
6) M -> И
7) М -> ( B )

27. Пример

Рассмотрим грамматику, определяющую
арифметическое выражение, состоящее из
идентификаторов, знаков операций +,* и круглых скобок
G 1:
Множество терминальных символов
Множество правил
T = { !, +, *, (, ), И },
P
И – условное обозначение лексемы
1) A -> ! B !
‘Идентификатор’, ! – ограничителя
2) B -> B + T
выражения.
3) B -> T
Множество нетерминальных
4) T -> T * M
символов
5) T -> M
N = {A, B, T, M},
6) M -> И
где А – арифметическое выражение,
7) М -> ( B )
В – выражение,
Т – терм, М – множитель.
А – начальный символ грамматики.

28.

1. A -> ! B !
2. B -> B + T
3. B -> T
4. T -> T * M
5. T -> M
6. M -> И
7. М -> ( B )
Цепочка символов называется
терминальной,
если она состоит только из
терминальных символов.
Если среди правил грамматики
есть правило вида
U -> e, где U N, e – пустая цепочка,
то это e-правило.
Если имеется несколько правил с
одинаковой левой частью, но разными
правыми, то их называют альтернативами.

29. 30. БНФ

Для задания правил грамматики существуют
разные способы, в которых используются
вспомогательные символы. Такие способы
получили название метаязыков.
Международным метаязыком является БНФ –
Бэкуса-Наура Форма. (Фортран, Алгол-60)
Правила грамматики задаются в нем в виде
метаформул. Специальные знаки:
в знаках < > задаются нетерминальные
символы, терминальные пишутся явно,
::= - читается «это есть»,
знаком | разделяются альтернативы.

31. БНФ(G1):

<A> ::= ! <B> !
<B> ::= <B> + <T> | <T>
<T> ::= <T> * <M> | <M>
<M>::= И | ( <B> )
1. A -> ! B !
2. B -> B + T
3. B -> T
4. T -> T * M
5. T -> M
6. M -> И
7. М -> ( B )

32. §1.3. Вывод. Формальный язык

Определение 1. Пусть и - 2 цепочки.
Если = , = и существует правило
-> P,
то говорят, что прямо порождает , и
обозначают
=> .
(говорят также, что прямо выводима из ).

33. §1.3. Вывод. Формальный язык

Определение 1. Пусть и - 2 цепочки.
Если = , = и существует правило
-> P,
то говорят, что прямо порождает , и
обозначают
=> .
(говорят также, что прямо выводима из ).
Пример. В грамматике G1 цепочка
прямо порождает
! В + Т! => ! В + Т * М !
так как было применено правило Т -> Т * М.

34.

Определение 2. Цепочка порождает
цепочку (за ноль или более шагов)
=>* ,
если существует последовательность
цепочек
1≡ , 2, …, n ≡
(1)
такая, что
прямо порождает
i => i+1 для i = 1, 2, …, n-1.
Говорят также, что выводима из .
Последовательность (1) называется выводом
цепочки , n – длина вывода.

35. Пример

1. A -> ! B !
2. B -> B + T
3. B -> T
4. T -> T * M
5. T -> M
6. M -> И
7. М -> ( B )
В грамматике G1 цепочка
порождает
≡ А =>* ≡ ! И + И * И ! ,
т.к.
А =>! B ! => ! B + T ! =>! T + T ! => ! M + T !
1
3
2
5
6
=> ! И + T ! => ! И + T * M ! => ! И + M * M !
5
4
=> ! И + И * М ! => ! И + И * И !
6
6
(*)

36. Язык

Определение 3. Язык L(G), порождаемый
грамматикой G, есть множество
терминальных цепочек, выводимых из
начального символа грамматики S, т.е.
L(G) = { | ( T*) & (S =>* ) }.
Такие цепочки называются словами,
предложениями (сентенциями) или понятиями
языка.
Если 2 грамматики порождают один и тот же
язык, то они называются эквивалентными,
т.е.
если L(G’) L(G’’), то G’ G’’.

37.

Примечание: последовательности
терминалов и нетерминалов, выводимые
из начального символа грамматики,
называются сентециальными формами.

38. Выводы

1.
2.
3.
4.
5.
6.
существовать несколько выводов. 7.
Выводы
Для некоторой цепочки может
A -> ! B !
B -> B + T
B -> T
T -> T * M
T -> M
M -> И
М -> ( B )
Например, для цепочки = ! И + И * И !
кроме вывода (*) можно задать вывод
А => ! B ! => ! B + T ! => ! B + T * M ! =>
1
2
6
4
! B + T * И ! => ! B + М * И ! => ! В + И * И ! =>
5
6
3
! T + И * И !=>! M + И * И ! => ! И + И * И ! (**)
5
6
А =>! B ! => ! B + T ! =>! T + T ! => ! М + Т ! => ! И + T ! => ! M + T * M !
1
2
3
5
6
4
5
=>! И + M * M! => ! И + И * М ! => ! И + И * И !
6
6
(*)

39.

Различают левый и правый выводы.
Определение 4. Вывод называется
левым, если каждая цепочка i+1
получается из i заменой самого
левого нетерминального символа в i.
Правый вывод определяется аналогично
(заменой слова левый на правый).

40.

Таким образом, (*) – левый вывод,
а (**) – правый.
А =>! B ! => ! B + T ! =>! T + T ! => ! М + Т ! => ! И + T ! => ! И + T * M ! =>
1
2
3
5
6
4
5
! И + M * M! => ! И + И * М ! => ! И + И * И !
6
6
(*)
А=>! B !=>! B + T !=>! B + T * M ! => ! В + Т * И ! =>! B + M * И ! => ! В + И * И !
1
2
4
6
5
6
3
=>! T + И * И !=>! M + И * И ! => ! И + И * И !
5
6
(**)

41. Однозначные грамматики

Определение 5. Грамматика G называется
однозначной, если у каждого слова языка L(G),
порождаемого этой грамматикой, существует
единственный левый (правый) вывод.
В противном случае грамматика называется
неоднозначной.
Если некоторый язык может быть порождён
только неоднозначными грамматиками, то такой
язык называется существенно неоднозначным.

42.

Вывод некоторой цепочки может
быть задан двумя способами:
1. перечислением номеров правил,
применяемых к выводу цепочки .
В нашем примере
левый вывод - 1 2 3 5 6 4 5 6 6,
а правый – 1 2 4 6 5 6 3 5 6.
2. множество выводов некоторой цепочки можно
задать синтаксическим
деревом вывода.
А =>! B ! => ! B + T ! =>! T + T ! => ! М + Т ! => ! И + T ! => ! И + T * M ! =>
1
2
3
5
6
4
5
! И + M * M! => ! И + И * М ! => ! И + И * И !
6
6
(*)
А=>! B !=>! B + T !=>! B + T * M ! => ! В + Т * И ! =>! B + M * И ! => ! В + И * И !
1
2
4
6
5
6
3
=>! T + И * И !=>! M + И * И ! => ! И + И * И !
5
6
(**)

43. Дерево вывода

Определение 6. Помеченное упорядоченное дерево
называется деревом вывода, если выполняются
следующие условия:
• корень дерева помечен начальным символом
грамматики S;
• каждый лист помечен либо a T, либо e (пустая
цепочка);
• внутренние вершины помечены нетерминалами;
• если A – нетерминал, которым помечена внутренняя
вершина и X1, X2, …, Xn – метки её прямых потомков
в указанном порядке,
то A -> X1X2…Xn P, т.е. является правилом.

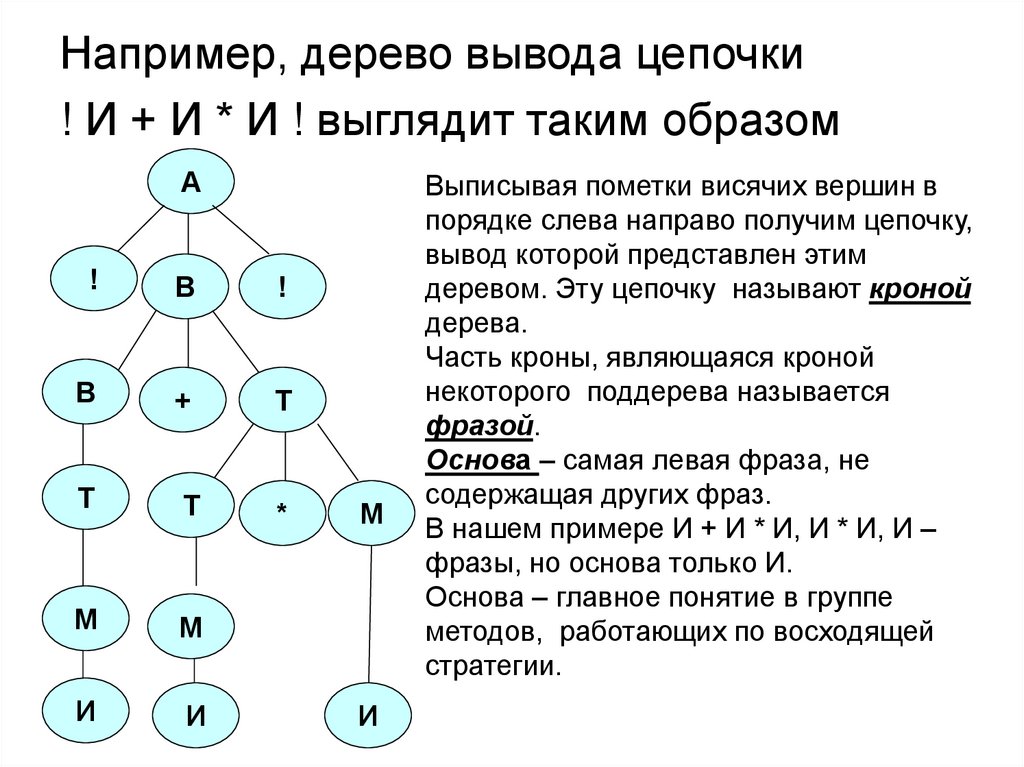
44.

Например, дерево вывода цепочки
! И + И * И ! выглядит таким образом
А
!
B
!
В
+
Т
Т
Т
*
М
М
И
И
М
И
Выписывая пометки висячих вершин в
порядке слева направо получим цепочку,
вывод которой представлен этим
деревом. Эту цепочку называют кроной
дерева.
Часть кроны, являющаяся кроной
некоторого поддерева называется
фразой.
Основа – самая левая фраза, не
содержащая других фраз.
В нашем примере И + И * И, И * И, И –
фразы, но основа только И.
Основа – главное понятие в группе
методов, работающих по восходящей
стратегии.

45. Деревья вывода и однозначные грамматики

Можно показать, что слово в языке имеет два разных
дерева вывода тогда и только тогда, когда слово имеет
два левых вывода.
Поэтому можно дать такое определение однозначной
грамматики:
Грамматика G называется однозначной, если у каждого
слова языка L(G), порождаемого этой грамматикой,
существует единственное дерево вывода.
Таким образом, в однозначной грамматике дерево
вывода каждого слова задаёт все выводы этого слова.

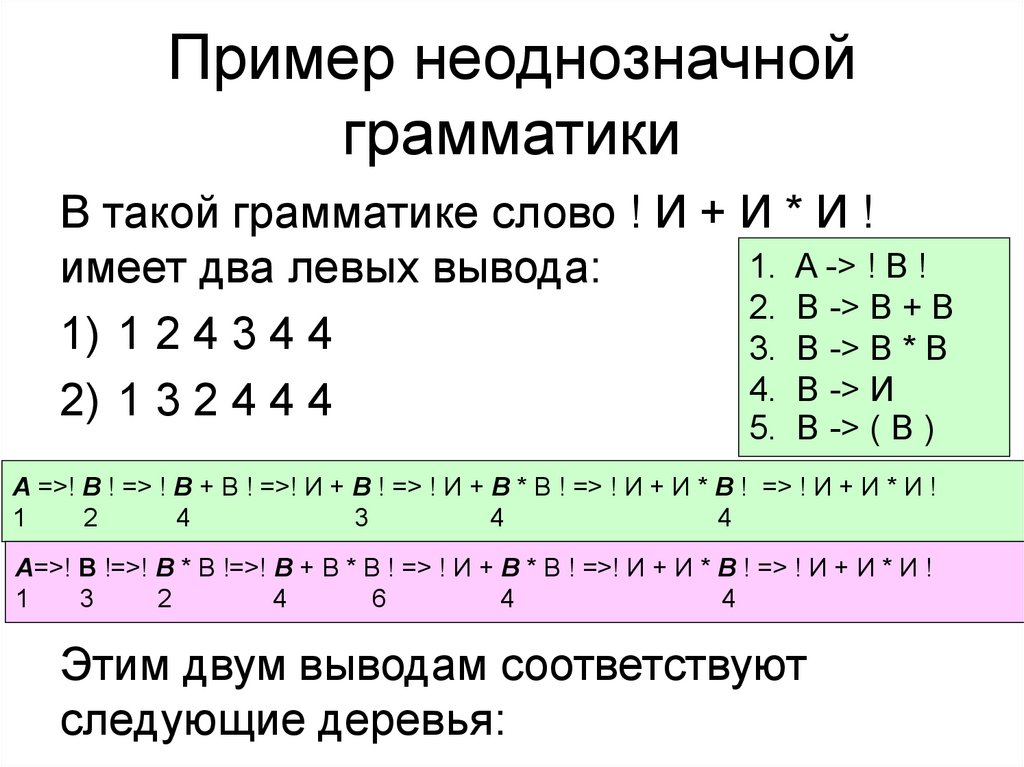
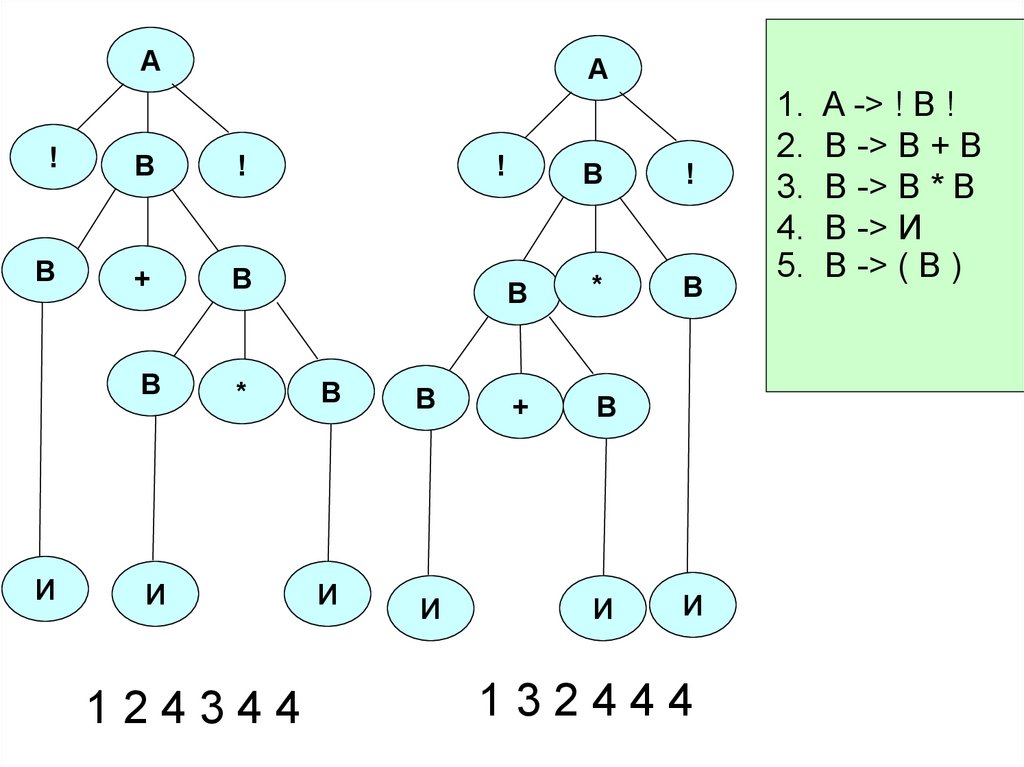
46. Пример неоднозначной грамматики

В такой грамматике слово ! И + И * И !
1. A -> ! B !
имеет два левых вывода:
2. B -> B + В
1) 1 2 4 3 4 4
3. B -> В * В
4. В -> И
2) 1 3 2 4 4 4
5. В -> ( B )
А =>! B ! => ! B + В ! =>! И + В ! => ! И + В * В ! => ! И + И * В ! => ! И + И * И !
1
2
4
3
4
4
А=>! B !=>! B * В !=>! B + В * В ! => ! И + В * В ! =>! И + И * В ! => ! И + И * И !
1
3
2
4
6
4
4
Этим двум выводам соответствуют
следующие деревья:

47.

А
А
!
B
!
В
+
В
В
*
И
И
124344
!
В
И
В
И
B
!
В
*
В
+
В
И
И
132444
1. A -> ! B !
2. B -> B + В
3. B -> В * В
4. В -> И
5. В -> ( B )

48. §1.4. Разбор. Распознаватель

Процедура, обратная порождению,
называется
приведением.
Определение 1. Цепочка прямо приводима
к цепочке , если
прямо порождает
=> .

49. §1.4. Разбор. Распознаватель

§1.4. Разбор. Распознаватель2. B -> B + T
1. A -> ! B !
3.
4.
5.
6.
7.
B -> T
T -> T * M
T -> M
M -> И
М -> ( B )
Процедура, обратная порождению,
называется
приведением.
Определение 1. Цепочка прямо приводима
к цепочке , если
прямо порождает
=> .
Например, в грамматике G1 цепочка
! И + И * И ! прямо приводима к
! И + М * И !, так как
прямо порождает
! И + М * И ! => ! И + И * И ! по правилу М -> И.

50.

Определение 2. Цепочка приводима
порождает
к , если =>* .
Например, в грамматике G1 цепочка
!И + И * И ! приводима к А, так как
Aпорождает
=>* ! И + И * И ! согласно (*) и (**).
А =>! B ! => ! B + T ! =>! T + T ! => ! М + Т ! => ! И + T ! => ! И + T * M ! =>
1
2
3
5
6
4
5
! И + M * M! => ! И + И * М ! => ! И + И * И !
6
6
(*)
А=>! B !=>! B + T !=>! B + T * M ! => ! В + Т * И ! =>! B + M * И ! => ! В + И * И !
1
2
4
6
5
6
3
=>! T + И * И !=>! M + И * И ! => ! И + И * И !
5
6
(**)

51.

52.

Определение 3. Выводу (1) из п. 1.3 соответствует
обратное преобразование - разбор с элементами
n ≡ , n-1,…, 1 ≡
(2)
Таким образом, разбор – это вывод, выполненный в
обратном порядке путем замены в цепочках правых
частей правил на левые.
Например,
! И + И * И! -> ! M + И * И ! -> ! T + И * И ! -> ! В + И * И !
3
6
5
6
-> ! B + M * И ! -> ! B + T * И ! -> ! B + T * М !
5
6
1. A -> ! B !
4
2. B -> B + T
-> ! B + T ! -> ! B ! -> A
2
1
1≡ , 2, …, n ≡
(1)
3.
4.
5.
6.
7.
B -> T
T -> T * M
T -> M
M -> И
М -> ( B )

53.

Разбор тоже можно задать и
списком номеров применяемых правил,
и
синтаксическим деревом разбора,
но в отличие от дерева вывода оно строится
от кроны к корню.
Разборов одной цепочки , как и выводов,
может быть несколько.
Различают
канонический разбор –
он приводит самую левую часть цепочки,
пока это возможно.

54.

В нашем примере канонический
разбор – (6 5 3 6 5 6 4 2 1).
Заметим, что канонический разбор
соответствует
правому выводу в обратном порядке.
Поэтому в литературе его часто называют
1. A -> ! B !
2. B -> B + T
3. B -> T
4. T -> T * M
5. T -> M
6. M -> И
7. М -> (В)
обращенный правый вывод.
Т.е. разбор 6 5 3 6 5 6 4 2 1 цепочки !И + И * И!
соответствует правому выводу (**).
! И + И * И! -> ! M + И * И ! -> ! T + И * И ! -> ! В + И * И !
-> ! B + M * И ! -> ! B + T * И ! -> ! B + T * М ! -> ! B + T ! -> ! B ! -> A
А=>! B !=>! B + T !=>! B + T * M ! => ! В + Т * И ! =>! B + M * И ! => ! В + И * И !
1
2
4
6
5
6
3
=>! T + И * И !=>! M + И * И ! => ! И + И * И !
5
6
(**)

55. Распознаватель

Основная задача синтаксического
анализа найти вывод(разбор)
заданного предложения(программы).
Если вывод (разбор) существует, то
предложение синтаксически верно, а
вывод(разбор) задает его структуру.
Алгоритм, решающий задачу вывода
(разбора), называется
распознавателем
(синтаксическим анализатором, парсером).

56. Стратегии

В соответствии с задачей построения
вывода или разбора существуют две
основные стратегии синтаксического
анализа:
• нисходящая
и
• восходящая.

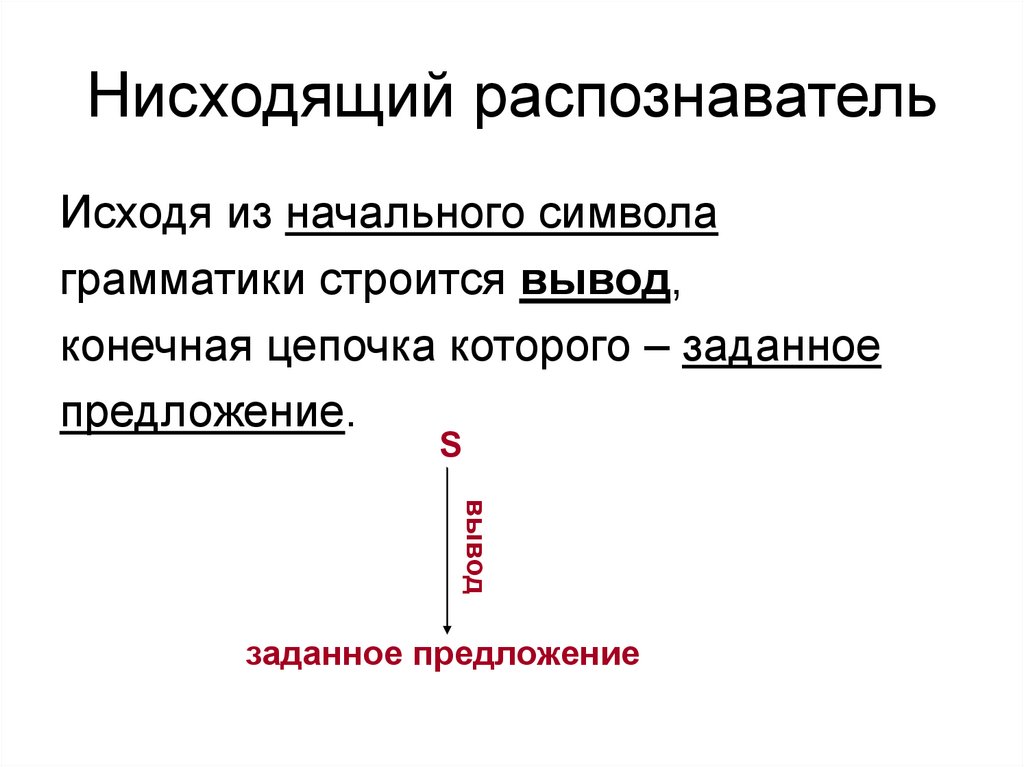
57. Нисходящий распознаватель

Исходя из начального символа
грамматики строится вывод,
конечная цепочка которого – заданное
предложение.
S
S
вывод
заданное предложение
S

58. Восходящий распознаватель

Исходя из предложения строится
разбор, конечный элемент которого начальный символ грамматики S.
разбор
S
заданное предложение

59.

Проблема распознавания разрешима,
если существует алгоритм, который за
конечное число шагов дает ответ на вопрос,
входит ли некоторая заданная цепочка в
язык L(G)?
Если такой алгоритм существует, то язык
является распознаваемым.
Если число шагов зависит от длины цепочки
и может быть оценено заранее, то язык
является легко распознаваемым.

60. §1.5. Классификация грамматик и языков на основе иерархии Хомского

Очевидно, что для теории трансляции интерес
представляют грамматики, порождающие
распознаваемые языки.
Наиболее общим классом таких грамматик являются
неукорачивающие грамматики.
Определение. Грамматика называется
неукорачивающей, если все правила подстановок
->
удовлетворяют условию
| | ≤ | |.
G1 – неукорачивающая.

61. Класс 0

Общепринятой является
классификация грамматик и языков на
основе иерархии Хомского.
Критерий классификации –
порождающие правила.
Класс 0. Правила имеют произвольный
вид
-> .
Модель естественных языков.

62. Класс 1

Класс 1. Грамматики непосредственносоставляющих (НС) – это не укорачивающие
грамматики с правилами вида
1U 2 -> 1 2,
где U N, 1, 2 – любые цепочки, возможно
пустые, но не одновременно, - не пустая
цепочка.
НС-грамматики порождают контекстнозависимые языки (КЗ-языки).
(Говорят, что подстановка вместо U возможна в
контексте 1 2 )

63. Класс 2

Класс 2. Контекстно-свободные грамматики (КС) или
безконтекстные. Это не укорачивающие грамматики
с правилами вида
1. A -> ! B !
2. B -> B + T
U -> , где e, U N.
3. B -> T
4. T -> T * M
КС-грамматики порождают КС-языки.
5. T -> M
КС-грамматики интересны тем, что ими можно 6. M -> И
описать класс языков программирования (за 7. М -> (В)
исключением некоторых конструкций), и создать
относительно несложные распознаватели на основе
автомата со стековой памятью.
G1 – КС-грамматика.

64. Класс 2а

Класс 2а. Укорачивающие КС-грамматики (УКС). Они
имеют такие же правила, как и КС-грамматики, но
могут содержать e-правила
U -> e.
e-правила доставляют проблемы при распознавании
по восходящей стратегии. Можно показать, что по
любой УКС-грамматике можно построить почти
эквивалентную ей КС-грамматику.
Почти эквивалентность может быть выражена так
L(КС) = L(УКС) – {e}.

65.

Реальные языки программирования,
как правило, порождаются УКСграмматиками.
Например, в языке С++ есть правила
<список_формальных_аргументов> -> пусто
<пустой оператор> -> пусто

66. Класс 3

Класс 3. Автоматные или регулярные грамматики.
Это не укорачивающие грамматики с правилами
вида
U -> a
U -> Va или
U ->aV, где a T; U, V N.
Автоматные грамматики порождают автоматные
языки (А-языки) или языки с конечным числом
состояний.
Автоматными грамматиками можно задать
синтаксис простых конструкций языка, таких как
лексемы, и создать эффективный распознаватель на
основе конечного автомата (КА).

67. §1.6. Свойства и типы КС-грамматик

§1.6. Свойства и типы КСграмматик
1.6.1. Допустимые преобразования
Для того, чтобы применить тот или иной метод
распознавания на правила грамматики
накладываются определенные условия.
Если грамматика им не удовлетворяет, то
можно попытаться преобразовать ее в
эквивалентную, удовлетворяющую требуемым
условиям.
Преобразования, используемые при этом,
называются допустимыми.
Рассмотрим основные.

68. 1)Удаление несущественных символов

Определение 1. Нетерминальный символ U
называется выводимым, если он начальный
или существует вывод из начального символа
цепочки, содержащей вхождение нетерминала
U, т.е.
S =>* 1U 2 или U S.
Определение 2. Нетерминальный символ U
называется производящим, если существует
вывод из него терминальной цепочки
U =>* , где T*.

69.

Определение 3. Нетерминальный символ U
называется существенным, если он –
выводимый
и
производящий,
т.е. существует вывод
S =>* U =>* T*.
В противном случае символ называется
несущественным (бесполезным).
Определение 4. КС-грамматика, все
нетерминальные символы которой
существенны, называется приведенной.

70.

Не приведенную КС-грамматику можно
преобразовать в приведенную: выбрать
подмножество существенных символов, а
затем - правила подстановок, содержащих
только существенные и терминальные
символы.
Пример,
G = {S ->a, S -> bSa, B –> d}.

71.

72.

73.

2)Подстановка правил.
Замена правила A -> B , где B N на
правило A -> , если в грамматике есть
правило B -> .
Нетерминал B может стать
несущественным.
3)Добавление нетерминала.
Замена правила A -> на два правила
A -> B и
B -> , где B N.

74.

4)Изменение направления рекурсии.
Направление рекурсии иногда требуется
изменить. Рассмотрим, как это можно сделать
на примере замены левой рекурсии на правую.
Пусть заданы правила
U -> U 1 | U 2 |…| U k | 1 | 2 |...| n ,
где 1, 2, ... n не начинаются с нетерминала
U N.
Введем новый нетерминал B N и заменим
заданные выше правила на множество правил
U -> 1 | 2 |...| n| 1B | 2B |...| nB ,
B -> 1 | 2 |…| k | 1B | 2B |…| kB
Новые правила – праворекурсивны.

75. Пример.

Синтаксис идентификатора можно
задать такими леворекурсивными
правилами
И -> a|b|c|..|z|Иa|Иb|…|Иz|И0|…|И9
Заменим их на праворекурсивные
И -> a|b|c|..|z|aB|bB|…|zB
B ->a|b|c|..|z|0|1|…|9|aB|bB|…|zB|0B|…|9B

76. 1.6.2 Типы КС-грамматик

1. Грамматика без цепных правил, т.е.
нет правил вида U -> V, где U, V N.
G1 имеет 2 цепных правила
B -> T и T -> M.
2. Грамматика без циклов, т.е. нет
выводов U =>*U.
3. Грамматика без левой рекурсии. В
грамматике нет выводов U =>* U .

77.

4. Грамматика в нормальной форме
Хомского. Грамматика не содержит eправил, кроме, возможно, правила S -> e,
причем S(начальный символ грамматики)
в этом случае не встречается в правых
частях правил, и каждое правило,
отличное от S -> e, имеет вид
A -> BC или
A -> a, где A, B, C N, a T.

78.

5. Грамматика в нормальной форме
Грейбах. Грамматика не содержит eправил кроме, возможно, правила S -> e,
причем S в этом случае не встречается в
правых частях правил.
Каждое правило имеет вид
U -> a , где a T, N* и | |>=0.

79. 1.6.3 Условия порождения КС-грамматиками бесконечных языков

1.6.3 Условия порождения КСграмматиками бесконечных языков
Для языков программирования важно,
чтобы они были бесконечны.
Рассмотрим, каким условиям должна
удовлетворять КС-грамматика для
порождения бесконечных языков.
Эти условия связаны с рекурсивным
символом.

80.

Определение 1. Вывод в КС-грамматике
В
называется рекурсивным, если в
Т
цепочках вывода найдутся 2 вхождения
некоторого нетерминала, являющиеся
М
потомком и предком друг друга.
В
(
)
Например, в грамматике G1
Т => Т * М или B =>T=>M=>(B)
Используя определение и понятие деревьев
вывода, можно доказать, что
Т
Лемма 1. Не рекурсивная грамматика Т
*
М
порождает конечный язык.

81.

Однако, условие рекурсивности грамматики условие
необходимое, но недостаточное.
Т.е. в грамматике может быть рекурсивный символ, но
она будет порождать конечный язык.
Причины:
• этот символ может быть несущественным – тогда все
выводы терминальных цепочек будут не рекурсивными.
• рекурсивная грамматика может порождать конечный
язык, если длина правых частей некоторых правил
в ней равна 1.
Например,
G = {S -> XY, X -> C, X -> a, Y -> b, C -> X }
G имеет рекурсивные выводы C=>X=>C, но грамматика
порождает только цепочку ab.

82.

Поэтому принято различать два вида
рекурсивных символов.
Определение 2. Рекурсивный символ U
называется эффективным, если
существует вывод из него цепочки
длины >1, содержащей символ U.
В противном случае U называется фиктивным.
В том случае, если все рекурсивные символы
фиктивны, грамматика тоже порождает
конечный язык.

83. Условие порождения бесконечного языка

Лемма 2. Язык, порождаемый рекурсивной
приведенной КС-грамматикой, содержащей
хотя бы один эффективный рекурсивный
символ, бесконечен.
Таким образом доказана теорема.
Теорема 1. Для того, чтобы приведенная КСграмматика порождала бесконечный язык,
необходимо и достаточно, чтобы она была
рекурсивной и содержала хотя бы один
рекурсивный эффективный нетерминал.

84. Пример

1) A -> ! B !
2) В -> В + Т
3) В -> T
4) T -> Т *М
5) T -> M
6) M ->a
7) M ->b
8) M -> (B)
Грамматика G1 порождает бесконечный
язык, т.к. содержит 2 эффективных
рекурсивных символа B и T.
A=>! B !=>!B + T !=>!B + T + T! =>
! B + T + T + T !=>! B + T*M+T + T!=>
! B + T*M*M + T + T! =>…=>
! a +b*a*(a + b) + b + a!

85. 1.6.4. Преобразование УКС-грамматики в КС-грамматику

1.6.4. Преобразование УКСграмматики в КС-грамматику
Напомним, что УКС-грамматика содержит
правила вида
U ->e.
В дальнейшем такой символ U будем
называть укорачивающим.
Укорачивающим будем также называть
символ U, если есть 2 правила вида
U -> V, V -> e (U, V – укорачивающие).

86.

Теорема 2. По любой УКС-грамматике
можно построить почти эквивалентную ей
КС-грамматику такую, что
L(КС) = L(УКС) – {e}.
Рассмотрим вопрос о построении КСграмматики.
Пусть исходная УКС-грамматика G ={ T, N, P,S}.
Надо построить КС-грамматику
G’ = {T’, N’, P’,S’}.
Рассмотрим правила подстановок исходной
УКС-грамматики. Выберем множество не
укорачивающих правил
Pn = {Ri} , i = 1, 2,…, n, Pn P.

87. Построение не укорачивающей КС

По каждому правилу Ri построим множество
правил P(Ri) таким образом. Если Ri в правой
части не содержит укорачивающих символов,
то P(Ri) = {Ri}.
В противном случае включим в P(Ri) само
правило Ri и все правила, полученные из него
последовательным вычеркиванием
укорачивающих символов.
Ri назовем главным правилом. Определим
n
G’(КС) = {N’ N, T’ T, P’ = U P(Ri), S’ S}.
i=1
По построению G’ – не укорачивающая.

88. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С.
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
СФА -> пусто
ПА -> А | ПА,А
ОФ – Определение Функции
ТВЗ – Тип Возвращаемого Значения
ИФ – Имя Функции
СФА – Список Формальных Аргументов
ПА – Перечень Аргументов
А - Аргумент
ТФ - Тело Функции

89. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С. укорачивающий символ
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
СФА -> пусто
ПА -> А | ПА,А
ОФ – Определение Функции
ТВЗ – Тип Возвращаемого Значения
ИФ – Имя Функции
СФА – Список Формальных Аргументов
ПА – Перечень Аргументов
А - Аргумент
ТФ - Тело Функции

90. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С. укорачивающий символ
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
СФА -> пусто
ПА -> А | ПА,А
Pn = { R1, R2, R3 }
R1 = ОФ -> ТВЗ ИФ(СФА){ТФ}
R2 = СФА -> ПА
R3 = ПА -> А | ПА,А

91. Пример

92. Пример

93. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С. укорачивающий символ
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
СФА -> пусто
ПА -> А | ПА,А
Pn = { R1, R2, R3 }
P(R1) = { ОФ -> ТВЗ ИФ(СФА){ТФ}, ОФ -> ТВЗ ИФ(){ТФ} }
P(R2) = { R2 } = { СФА -> ПА }
P(R3) = { R3 } = { ПА -> А | ПА,А }

94. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С. укорачивающий символ
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
e-правило - это правило удалим
СФА -> пусто
ПА -> А | ПА,А
ОФ – Определение Функции
ТВЗ – Тип Возвращаемого Значения
ИФ – Имя Функции
СФА – Список Формальных Аргументов
ПА – Перечень Аргументов
А - Аргумент
ТФ - Тело Функции

95. Пример

Проиллюстрируем процесс построения новых
правил на примере определения функции в
языке С. укорачивающий символ
ОФ -> ТВЗ ИФ(СФА){ТФ}
СФА -> ПА
e-правило - это правило удалим
СФА -> пусто
ПА -> А | ПА,А
Первое правило заменим на два
– Определение Функции
ОФ -> ТВЗ ИФ(СФА){ТФ}, ОФ
ТВЗ – Тип Возвращаемого Значения
ИФ – Имя Функции
ОФ -> ТВЗ ИФ(){ТФ}.
СФА – Список Формальных Аргументов
ПА – Перечень Аргументов
А - Аргумент
ТФ - Тело Функции

96. 1.6.5. Распознаватель для КС-языков

1.6.5.1 Общая модель
распознавателя

97.

Для каждого класса языков определяется свой
распознаватель.
Работу распознавателя обычно задают как
модель некоторого автомата,
представляющего в свою очередь некоторую
модификацию машины Тьюринга.
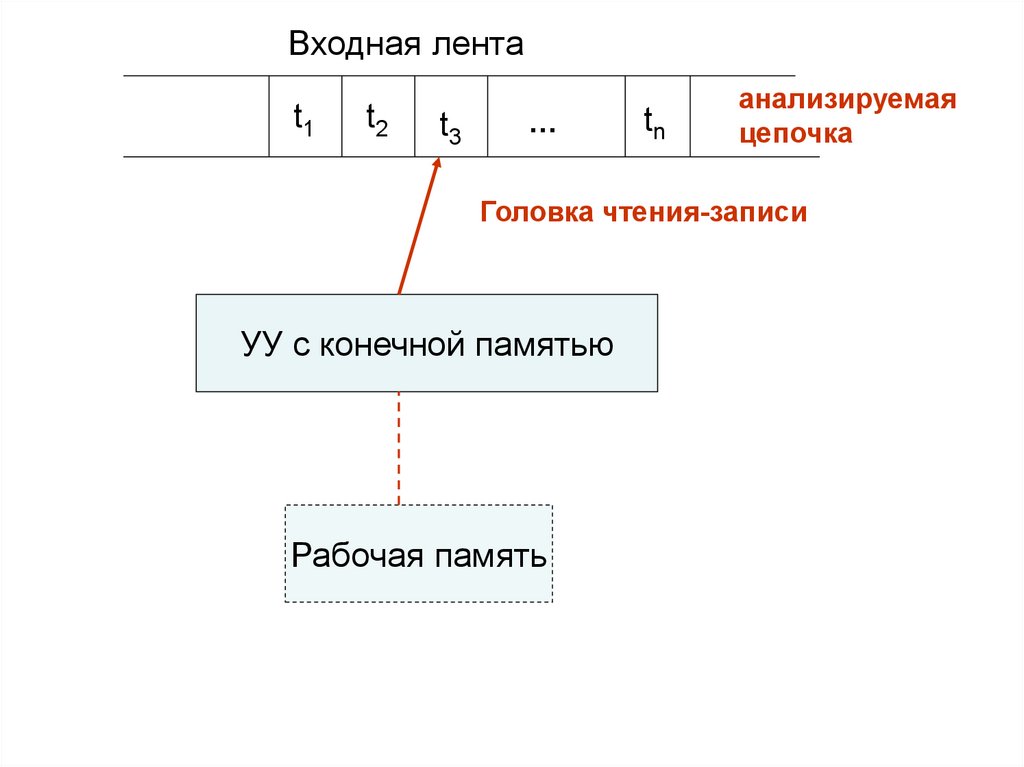
В общем случае распознаватель состоит из
трех основных частей
– входной ленты,
- управляющего устройства с конечной
памятью и, возможно, вспомогательной
(рабочей) памятью,
- головки чтения-записи.

98.

Входная лента
t1
t2
t3
…
tn
анализируемая
цепочка
Головка чтения-записи
УУ с конечной памятью
Рабочая память

99. УУ

УУ – ядро распознавателя. УУ задается
множеством состояний и функцией
отображения, которая определяет, как
меняется
• состояние УУ,
• входная лента и
• вспомогательная память
при чтении текущего символа на ленте и
текущего содержимого вспомогательной
памяти.

100. Конфигурация

Текущее состояние распознавателя
описывается конфигурацией.
Конфигурация (можно сказать, мгновенный
снимок) содержит
• состояние УУ;
• содержимое входной ленты вместе с
положением головки чтения-записи;
• содержимое рабочей памяти.
Работа распознавателя – это переход от
конфигурации к конфигурации.

101.

Конфигурация – начальная, если УУ
находится в начальном состоянии, читается
самый левый символ входной цепочки и
рабочая память содержит начальное значение.
Конфигурация – заключительная, если УУ
находится в одном из заданных
заключительных состояний, и головка
прочитала все символы на ленте (зашла за
последний символ).

102.

Распознаватель допускает цепочку ,
если исходя из начальной конфигурации,
распознаватель попадает в
заключительную конфигурацию,
проделав конечную последовательность
шагов (тактов).
Язык, определяемый распознавателем,
это множество входных цепочек,
которые он допускает.

103. Детерминированность

Распознаватель может быть
детерминированным
и
недетерминированным.
Распознаватель детерминированный,
если из текущей конфигурации возможен
переход в единственную следующую,
иначе – недетерминированный.

104. Утверждение.

Язык L автоматный тогда и только
тогда, когда он определяется конечным
автоматом (КА).
Язык L контекстно-свободный (КС)
тогда и только тогда, когда он
определяется автоматом с
магазинной памятью (МП-втоматом).
стеком!

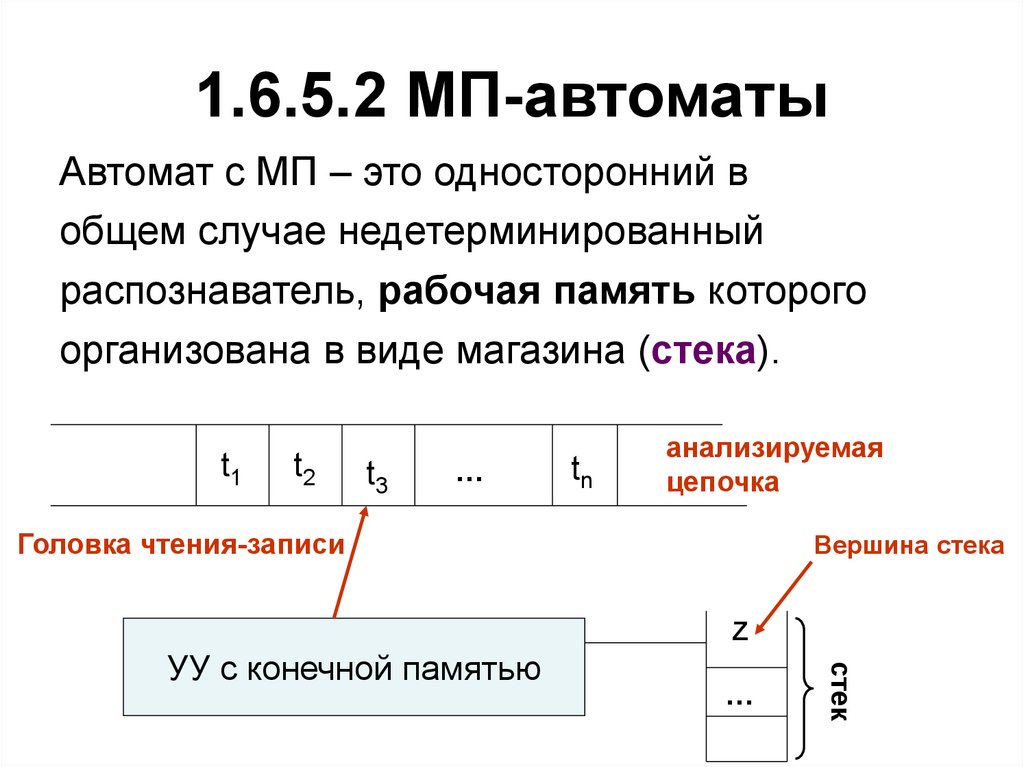
105. 1.6.5.2 МП-автоматы

Автомат с МП – это односторонний в
общем случае недетерминированный
распознаватель, рабочая память которого
организована в виде магазина (стека).
t1
t2
t3
…
tn
анализируемая
цепочка
Головка чтения-записи
Вершина стека
Z
…
стек
УУ с конечной памятью

106. Определение 1.

Автомат с магазинной памятью (МП-автомат) – это 7
объектов
P = {Q,T, , , q0, Z0, F},
где
Q – конечное множество состояний УУ;
T – конечный входной алфавит;
- конечный алфавит магазинных символов;
- отображение множества Q ( T U {e} )
во множество конечных подмножеств множества Q *;
q0 Q – начальное состояние УУ;
Z0 символ, находящийся в магазине в начальный
момент (начальный магазинный символ);
F Q – множество заключительных состояний.

107. Определение 2.

Конфигурацией МП-автомата называется
тройка
(q, , ) Q T * *,
где
q – текущее состояние УУ;
T* - непрочитанная часть входной цепочки,
первый символ её обозревается головкой чтениязаписи. Если = e, то считается, что вся входная
цепочка прочитана;
* - содержимое магазина, при этом самый
левый символ находится в вершине стека.
Если = e, то магазин пуст.

108.

Такт работы МП-автомата определяется в
виде бинарного отношения |- (переходит),
заданного на конфигурациях.
Будем говорить, что происходит переход от
конфигурации Кi к конфигурации Кi+1 и
записывать это так
(q, a , Z ) |- (q’, , ),
(1)
если множество (q, a, Z) содержит (q’, ),
где q, q’ Q, a T U {e}, T*, Z и
, *.

109. Другими словами

(q, a , Z ) |- (q’, , ),
Другими словами
автомат переходит в новую конфигурацию
Ki+1, выполнив отображение (q, a, Z),
при этом
- головка сдвигается на следующий за a
символ,
- магазинный символ Z в вершине стека
заменяется на цепочку и
- УУ переходит в новое состояние q’.
Если = e, то верхний символ Z удаляется из
стека.
Если a = e, то это e-такт: входной символ не
читается, но состояние УУ и магазина могут
измениться.

110.

Начальная конфигурация
(q0, , Z0),
заключительная
(q, e, ),
где q F, *.
МП-автомат детерминированный, если
множество
(q, a, Z)
содержит единственную пару (q’, ).

111. Определение 3.

Цепочка допускается МП-автоматом,
если
(q0, , Z0) |-k (q, e, )
для некоторых q F и * (переход из
начальной конфигурации в заключительную
происходит за k шагов - конечное число).
Языком, определяемым (допускаемым) МПавтоматом, называется множество цепочек ,
им допускаемых
L( МП) = { | (q0, , Z0) |-k (q, e, )}.

112. Пример.

(q, a , Z ) |- (q’, , ),
(1)
если множество (q, a, Z)
содержит (q’, ),
где q, q’ Q, a T U {e}, T*,
Z и
, *.
Рассмотрим язык
L = {0n1n , n 0 }
МП ={{q0, q1, q2}, {0, 1}, {Z, 0}, , q0, Z, {q0}},
где
Работа МП-автомата
(q0, 0, Z) = {(q1, 0Z) }
состоит в том,
что видя 0 в цепочке,
(q1, 0, 0) = { (q1, 00) }
он их записывает в стек,
а встретив 1,
(q1, 1, 0) = { (q2, e) }
удаляет 0 с вершины стека.
(q2, 1, 0) = {(q2, e)}
Допустимы только цепочки
вида 00001111
(q2, e, Z) = {(q0, e)}

113.

Доказательство лемм 1, 2, теорем 1, 2
приведены далее.
На экзамене – без доказательств.

114. Вопросы для повторения

1. Этапы трансляции.
2. Определение грамматики.
3. Что такое БНФ?
4. Что такое прямое порождение?
5. Что такое вывод?
6. Что такое язык, порождаемый грамматикой?
7. 2 способа задания вывода цепочки.
8. Что такое основа?
9. Что такое разбор?
10. Как разбор связан с выводом?
11. Что такое распознаватель?
12. 2 стратегии синтаксического анализа.
13. Определение не укорачивающей грамматики.
14. Определение грамматик по Хомскому.

115. Вопросы для повторения

15. Перечислите допустимые преобразования КС-грамматики.
16. Какая грамматика называется приведенной?
17. Покажите преобразование леворекурсивной грамматики в
праворекурсивную на примере грамматики идентификатора.
18. Определите грамматику в нормальной форме Хомского.
19. Определите грамматику в нормальной форме Грейбах.
20. Какой нетерминал называется эффективным?
21. Сформулируйте лемму 1.
22. Сформулируйте лемму 2.
23. Какая из этих лемм следует теорема? Что Вы можете сказать
о грамматике G1?
24. Что такое УКС-грамматика?
25. Расскажите о процедуре преобразования УКС-грамматики в КСграмматику.
26. Приведите пример этого преобразования в языке С.
27. Определите рекурсивное правило для составного оператора языка
C. (СО->{ПО} ПО->
СО Составной Оператор, ПО – Перечень Операторов )

116.

Лемма 1. Не рекурсивная КС-грамматика порождает конечный
язык.
Док-во. Пусть n – количество нетерминальных символов, m –
максимальная длина правых частей
правил. Покажем, что число различных деревьев вывода конечно.
Очевидно, что высота любого
дерева вывода не больше n. Действительно, если бы она была >n
для некоторого дерева вывода,
то существовал бы путь длины >n. Но так как нетерминалов n, гдето на этом пути повторно
встретилась бы вершина с таким же нетерминалом. Но такое
дерево соответствовало бы
рекурсивному выводу по определению 1, что противоречит
условию.
Оценим теперь количество вершин любого дерева вывода. На i-ом
уровне их не более m^i.
Следовательно, общее количество N имеет оценку
N<= 1 + m + m^2 + … + m^n < m^(n+1).

117.

Лемма 2. Язык, порождаемый рекурсивной приведенной КС-грамматикой,
содержащей хотя бы один эффективный, рекурсивный символ,
бесконечен.
Доказательство. Пусть U – эффективный рекурсивный. Так как КС –
приведенная, то все ее нетерминалы существенны, и существует
вывод
S =>* 1U 2, где 1, 2 - возможно пустые.
Так как U – эффективный, то существует вывод
U =>* 3U 4, причем max( | 3|, | 4| ) 1.
(1)
Следовательно, справедлив вывод
S =>* 1 3U 4 2.
Применим к нетерминалу U вывод (1) n-1 раз. Получим
S =>* 1 3^nU 4^n 2
\-----v---------/
Здесь …^n - конкатенация n-го порядка цепочки .
Так как грамматика приведенная, то все нетерминалы, входящие в ,
производящие. Заменим их терминальными порождениями. Получим
S =>* T( 1 3^nU 4^n 2) T( ), где
T( ) - терминальное порождение цепочки .
Так как n произвольно, устремив его к , получим бесконечную
терминальную цепочку, что доказывает бесконечность языка.

118.

Теорема 2. По любой УКС-грамматике
можно построить почти эквивалентную ей
КС-грамматику L(КС) = L(УКС) – {e}.
Рассмотрим сначала вопрос о
построении КС-грамматики.

119.

• Докажем почти эквивалентность этих грамматик.
• Сначала покажем, что L(G) – {e} L(G’). Для этого мы покажем,
что выводу любой непустой терминальной цепочки в G можно
сопоставить вывод этой же цепочки в G’. Итак, пусть n –
терминальная цепочка, а её вывод, т.е. = 0, 1, 2, …, n.
Тогда, если в не применялись укорачивающие правила, то это
вывод и в G’. Пусть в применялись укорачивающие правила,
которых нет в G’. Построим дерево вывода . Оно будет
содержать вершины-листья, соответствующие укорачивающим
символам. Пусть такая вершина x. На пути от x к корню найдем
вершину y, из которой исходит >1 дуги (такая вершина должна
быть, так как кроме нетерминалов есть еще и терминальные
символы). Если длина пути из y в x больше 1, то и
последующие вершины за y будут иметь ровно одну выходящую
дугу. Исключим из дерева вершины, идущие от y. В полученном
дереве процесс повторим, если подобные вершины еще будут.
В конце концов, получим дерево вывода той же цепочки n
(терминалы не удалялись), но без укорачивающих правил. Сам
процесс перестройки дерева аналогичен процедуре получения
неглавных правил в G’. Таким образом, полученное дерево
будет деревом вывода n в G’. Таким образом, показано, что
L(G) – {e} L(G’).

120.

Рассмотрим пример, иллюстрирующий этот процесс.
G = { S -> aBCDq, C -> M, M -> e, B -> e, D -> f, B ->r, M->b}, a,q,r,b
T ; C,M,B – укорачивающие символы.
G’ = {{S -> aBCDq, S -> aCDq, S ->aBDq, S -> aDq},D -> f, B -> r, M>b}
Пусть : S => aBCDq => aCDq => aMDq => aDq => afq,
соответствующее дереву
S (y)
S
/ / | \ \
/ | \
a B C D q
a D q
(x) | |
|
M f
f
(x)

121.

Покажем теперь, что L(G’) L(G) – {e}.
Пусть - вывод в G’ некоторой непустой терминальной цепочки
n. Если все применяемые правила были главными, то будет
выводом и в G. В противном случае пусть i – первая цепочка, к
которой применялось не главное правило R’ = A -> P(Rj) и R’
Rj, т.е. не главное. Тогда, если i = 1A 2, то (i+1) = 1 2.
Рассмотрим главное правило Rj, которое имело, например, вид
A -> . По процедуре построения неглавных правил следует, что
цепочка получена из вычеркиванием укорачивающих
символов, что равносильно применению укорачивающих
правил. Из этого следует, что => * . Применим к i правило Rj.
Получим
’(i + 1) = 1 2, но так как => * , то ’(i + 1) => * (i + 1). Заменим
часть вывода
… i => (i + 1)… на … i => ’(i + 1) =>* (i + 1)…Это уже будет
вывод в G. Рассмотрим цепочки вывода справа от данных. Если
в них также применялись неглавные правила, выполним
аналогичную замену. Таким образом, вывод любой цепочки n в
G’ может быть преобразован в вывод этой же цепочки с
применением правил из G. Чтд.

English Русский Rules