Метод операторного предшествования МОП

1. §3.3. Метод операторного предшествования МОП

Метод предложен Флойдом и
применим к грамматикам с
операторным предшествованием.

2.

Метод простого предшествования неприменим, если
отношения предшествования не единственны.
Процедура стратификации ведет к увеличению
количества нетерминальных символов и к появлению
цепных правил. В грамматике G1’ это правила
B ->B’ B’ ->T T-> T’ T’ ->M
Это, как говорят Ахо и Ульман, делают
грамматику громоздкой и «неуклюжей».
Кроме того, такие преобразования ведут к увеличению
промежуточных шагов приведения при работе
распознавателя
(например, M->T’->T->B’->B),
что в конечном итоге снижает эффективность
транслятора.
Рассмотрим модифицированный метод, также
использующий отношения предшествования.

3. 3.3.1 Грамматика с операторным предшествованием

Пусть a и b – терминальные символы,
U, C, D – нетерминалы, x, y, z – любые
цепочки, возможно пустые.

4. Определение 1.

Грамматикой с операторным
предшествованием называют приведенную
КС-грамматику без e-правил, в которой:
1. Правые части порождающих правил не
содержат рядом стоящих нетерминальных
символов, т.е. в грамматике нет правил вида
U -> xCDy
Такую грамматику называют операторной;
( грамматика G1 – операторная)

5. Определение 1. (продолжение)

2. Для каждой упорядоченной пары
терминальных символов a и b выполняется не
более, чем одно из трех отношений
предшествования:
а) a = b, если и только если существует
правило
U -> xaby
или
U -> xaCby
(говорят, что a и b стоят рядом с точностью
до нетерминала);

6.

б) a < b, если и только если существует
правило
U -> xaCy & вывод C =>* bz
или
C =>* Dbz;
( говорят, что b появляется справа от
a с точностью до нетерминала);

7.

в) a >b, если и только если существует
правило
U -> xCby & вывод C =>* za
или
C =>* zaD.
(a появляется слева от b с точностью
до нетерминала);
3. Разные порождающие правила имеют
различные правые части
(обратимая грамматика).

8.

Первое условие позволяет ограничиться
установлением отношений предшествования
только для терминальных символов.
Это значительно сокращает размер матрицы
предшествования и уменьшает разбор.
Класс реальных языков программирования,
для которых существует операторное
предшествование или которые можно свести к
ним, достаточно широк.
Второе и третье условия обеспечивают
безтупиковость алгоритма разбора.

9. 3.3.2 Распознаватель

Алгоритм также работает по методу
перенос-свертка, т.е. использует стек,
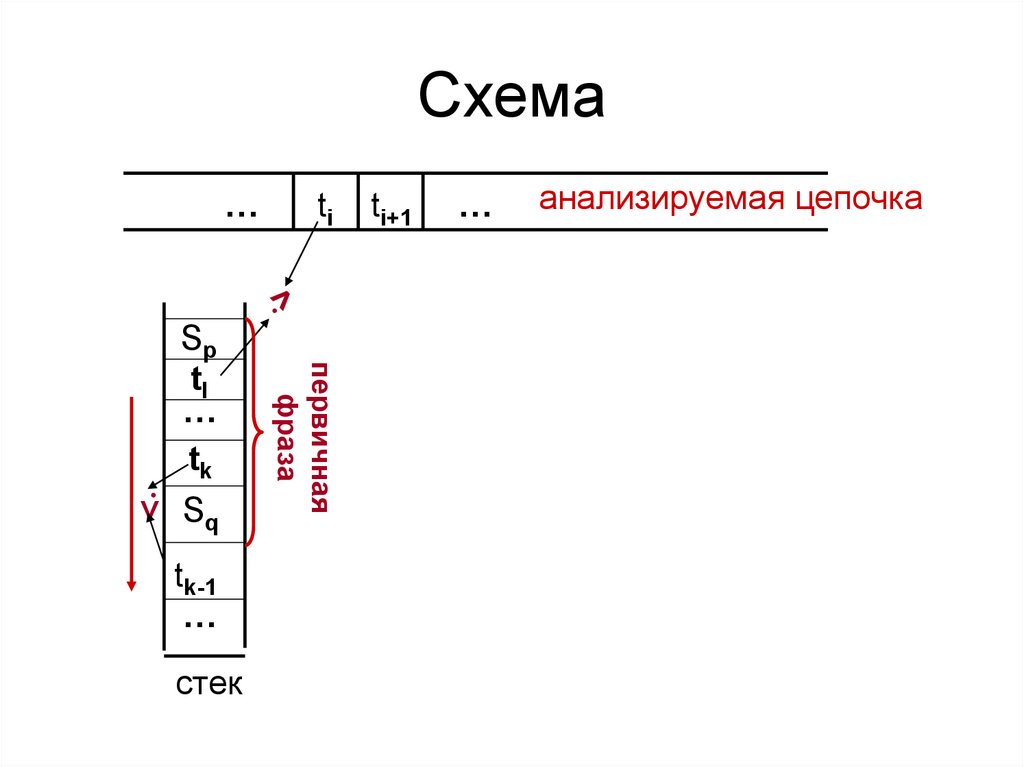
но вместо основы – первичную фразу.
Определение 2. Первичная фраза – это
фраза, не содержащая никакой другой
фразы, кроме самой себя, и содержащая,
по крайней мере, один терминальный
символ.

10. Пример.

В грамматике G1 цепочка
! T + T * M !
основа первичная фраза
содержит такие основу и первичную
фразу

11.

Из свойств грамматики с операторным
предшествованием (она КС-грамматика
и её правила имеют вид U -> ) следует,
что если x – первичная фраза то,
либо существует правило
U -> x ,
Терминал появившись –
исчезнуть не может!
либо правило
U -> x’ и вывод x’ =>* x,
в котором применялись только правила
вида Ui -> Uj , где Ui, Uj N.

12. Пример.

Проиллюстрируем это на примере грамматики
G1 .
x – первичная фраза в цепочке
!T+T!
x
Правила U -> T + T нет, но есть правило
B -> B + T
x’
и x’ => x , если применить правило B -> T.
(Ui -> Uj)

13.

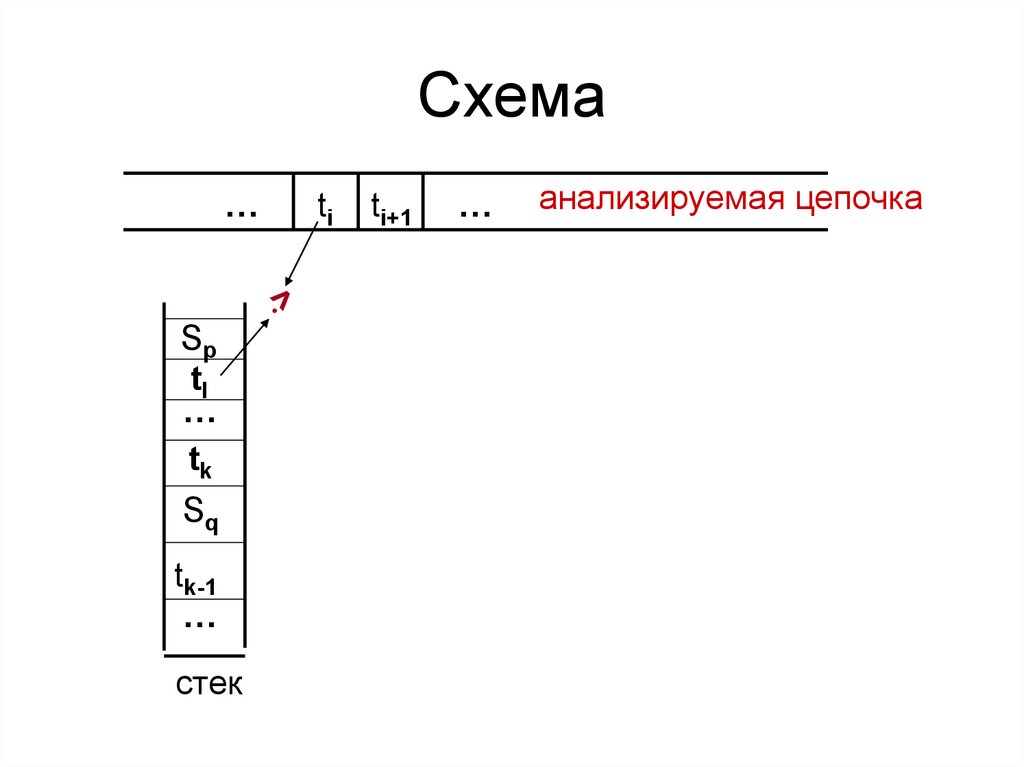
Алгоритм распознавателя разыскивает
самую левую первичную фразу.
Для этого символы входной цепочки
последовательно заносятся в стек
(переносы), пока не встретится
отношение > между терминальным
символом tl, ближайшим к вершине стека,
и текущим символом входной цепочки ti .

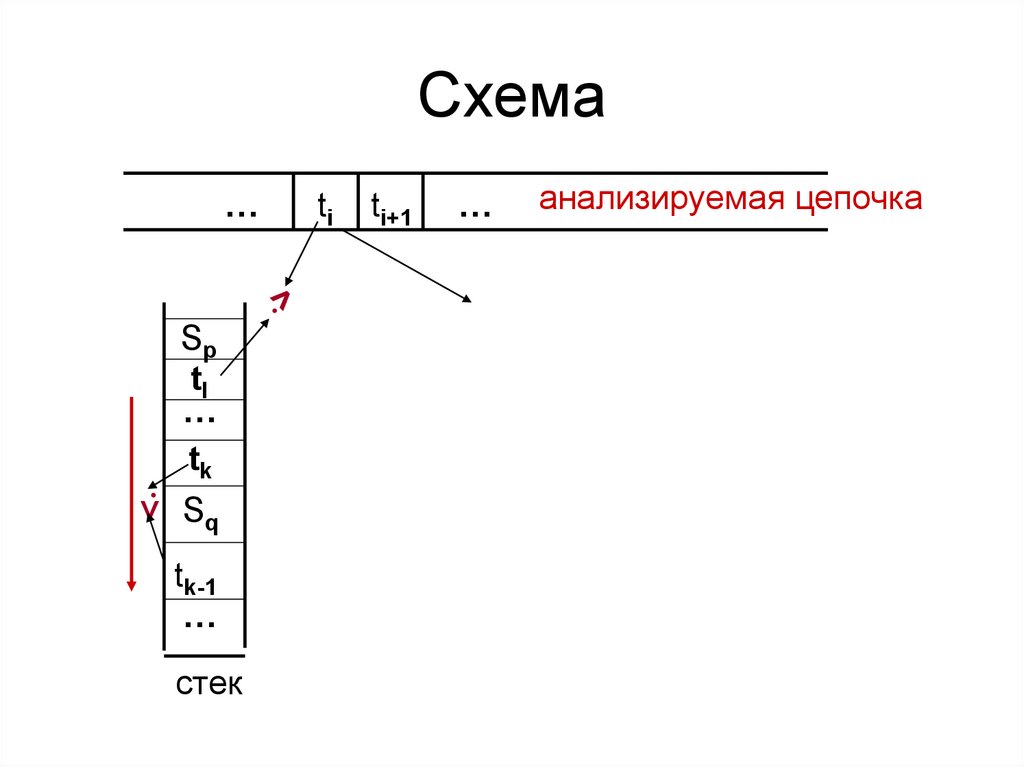
14.

Тогда стек просматривается в
направлении от вершины к началу и
отыскивается ближайшая пара (с
точностью до нетерминала)
терминальных символов такая, что
tk-1 < tk.
В этом случае часть стека выше tk-1 до
вершины – первичная фраза.

15. Свертка

Среди порождающих правил
разыскивается правило, содержащее
первичную фразу в правой части с
точностью до нетерминала.
После этого первичная фраза в стеке
заменяется на левую часть правила
(свертка).
Процесс продолжается аналогично.

16. Завершение

Если входная цепочка L(G), то она
будет вся прочитана, а в стеке останется
начальный символ грамматики.
Иначе, входная цепочка L(G).

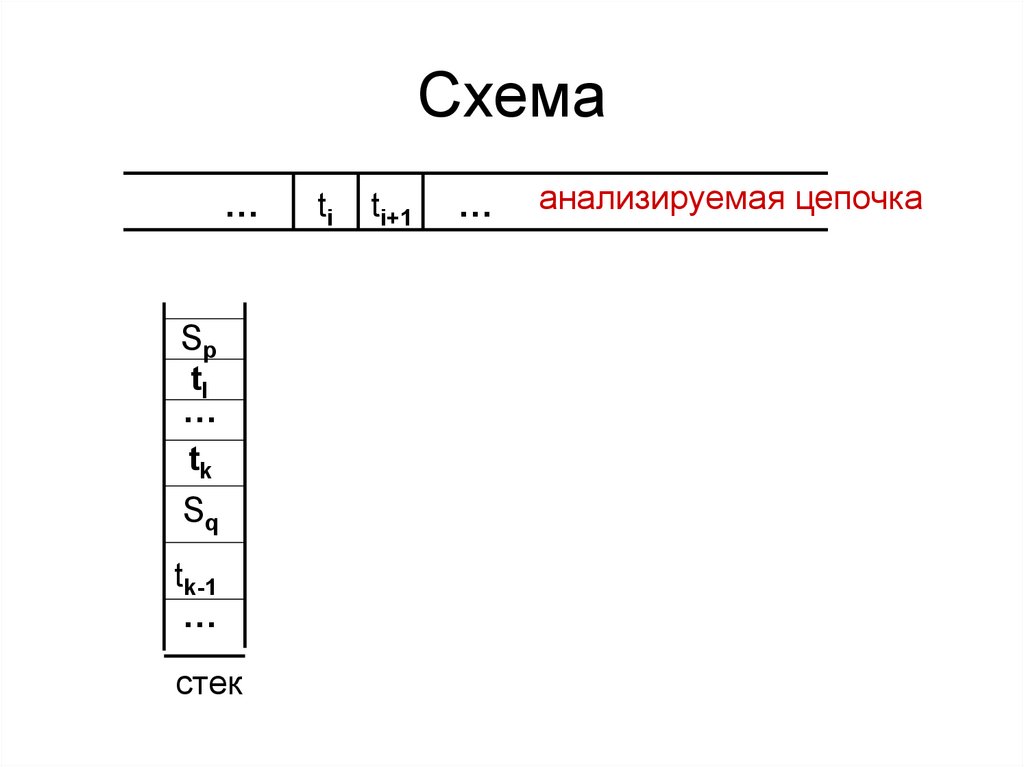
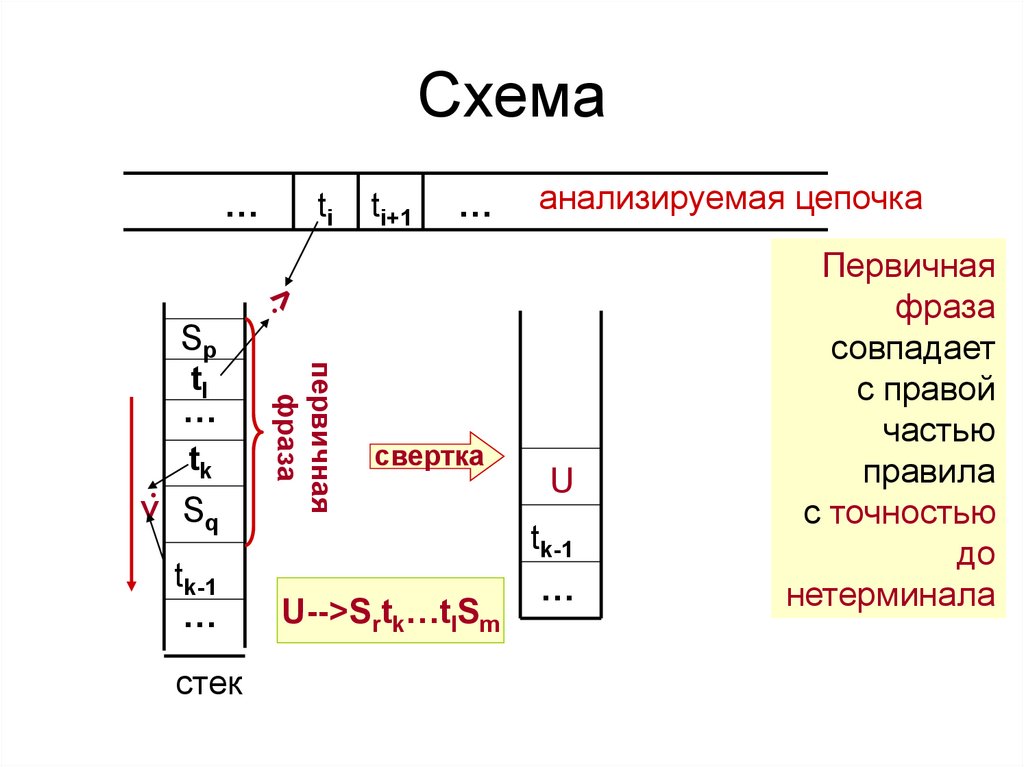
17. Схема

…
ti
ti+1
…
анализируемая цепочка

18. Схема

…
Sp
tl
…
tk
Sq
tk-1
…
стек
ti
ti+1
…
анализируемая цепочка

19. Схема

…
Sp
tl
…
tk
Sq
tk-1
…
стек
ti
ti+1
…
анализируемая цепочка

20. Схема

…
<
Sp
tl
…
tk
Sq
tk-1
…
стек
ti
ti+1
…
анализируемая цепочка

21. Схема

…
<
Sq
tk-1
…
стек
первичная
фраза
Sp
tl
…
tk
ti
ti+1
…
анализируемая цепочка

22. Схема

…
<
Sq
tk-1
…
стек
первичная
фраза
Sp
tl
…
tk
ti
ti+1
…
свертка
U-->Srtk…tlSm
анализируемая цепочка
U
tk-1
…
Первичная
фраза
совпадает
с правой
частью
правила
с точностью
до
нетерминала

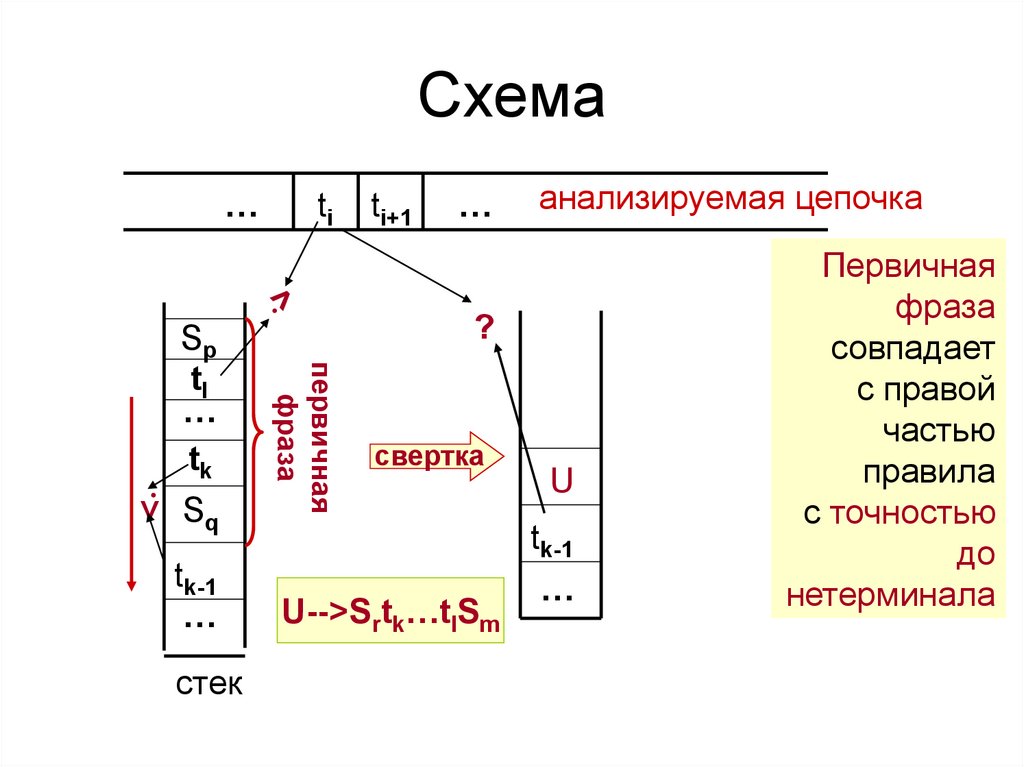
23. Схема

…
<
Sq
tk-1
…
стек
ti+1
…
анализируемая цепочка
?
первичная
фраза
Sp
tl
…
tk
ti
свертка
U-->Srtk…tlSm
U
tk-1
…
Первичная
фраза
совпадает
с правой
частью
правила
с точностью
до
нетерминала

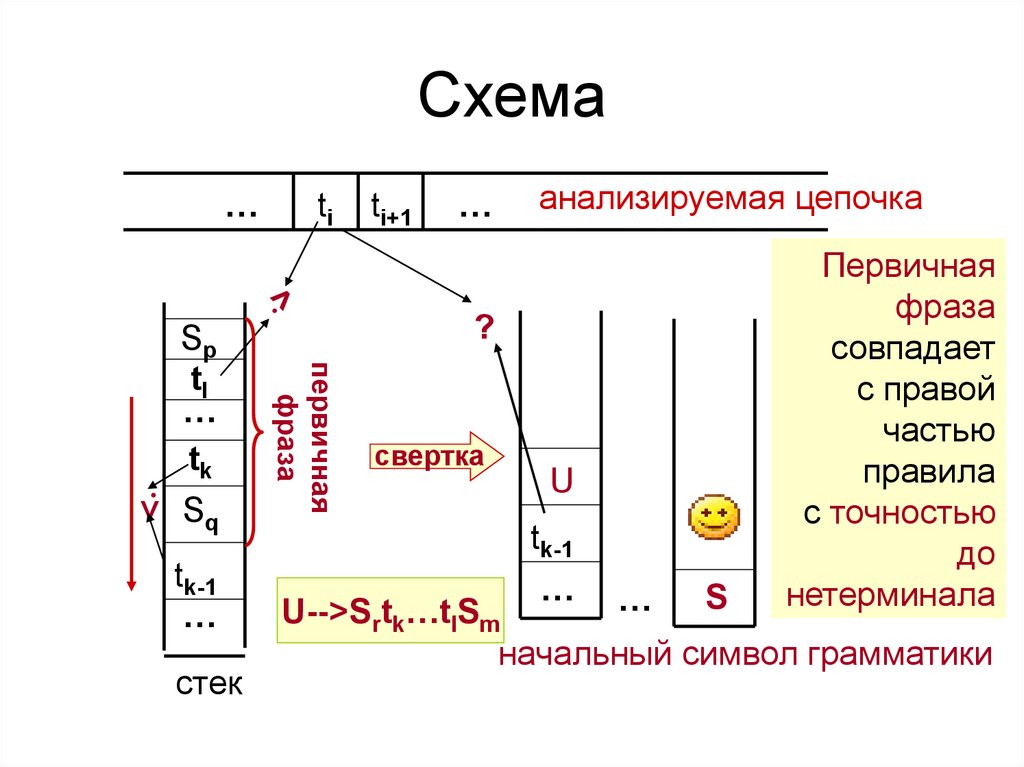
24. Схема

…
<
Sq
tk-1
…
стек
ti+1
…
анализируемая цепочка
?
первичная
фраза
Sp
tl
…
tk
ti
свертка
U
tk-1
…
Первичная
фраза
совпадает
с правой
частью
правила
с точностью
до
нетерминала
S
…
U-->Srtk…tlSm
начальный символ грамматики

25. 3.3.3 Матрица операторного предшествования (МОП)

МОП формируется только для терминальных
символов на основе множеств самых левых
(правых) терминальных символов
Lt (U) ( Rt (U) ).
Для построения этих множеств используются
порождающие правила и множества L(U) и
R(U).
(см. п. 3.1.4).

26. Lt(U)

Множества Lt (U) и Rt (U) строятся по
формулам:
Lt(U) = { t | (U=>*tz ) (U=>*Ctz)}
или, используя множества L(U),
Lt(U) = { t | (U->tz ) (U->Ctz)
(1)
(U’ L(U)& t Lt(U’))} ,

27. Lt(U)

Левые с точностью
до нетерминала C
Множества Lt (U) и Rt (U) строятся по
формулам:
Lt(U) = { t | (U=>*tz ) (U=>*Ctz)}
или, используя множества L(U),
Lt(U) = { t | (U->tz ) (U->Ctz)
(1)
(U’ L(U)& t Lt(U’))} ,

28. Rt(U)

Правые с точностью
до нетерминала C
Rt(U) = { t | (U=>*zt ) (U=>*ztC)}
или, используя множества R(U),
Rt(U) = { t| (U ->zt ) (U ->ztC)
(2)
(U’ R(U)& t Rt(U’))} .
Здесь U, U’, C – нетерминалы,
t - терминал, z – любая цепочка,
возможно пустая.

29. Rt(U)

Rt(U) = { t | (U=>*zt ) (U=>*ztC)}
или, используя множества R(U),
Rt(U) = { t| (U ->zt ) (U ->ztC)
(2)
(U’ R(U)& t Rt(U’))} .
Здесь U, U’, C – нетерминалы,
t - терминал, z – любая цепочка,
возможно пустая.

30.

Используя (1), (2), отношения
операторного предшествования
могут быть вычислены таким образом
ti = tj <--> (U -> x ti tj y) (U -> x ti C tj y) (3)
(стоят рядом с точностью до нетерминала)
ti < tj <--> (U -> x ti C y) & tj Lt( C)
(4)
ti > tj <--> (U -> x Ctj y) & ti Rt( C)
(5)

31. 3.3.4 Функции операторного предшествования

Вместо матрицы операторного
предшествования можно использовать
функции операторного предшествования,
удовлетворяющие аналогичным условиям, что
и функции простого предшествования.
Их можно вычислить по тем же алгоритмам:
• итерационному Флойда и
• графу линеаризации.

32. 3.3.5 Транслятор

Транслятор использует
• таблицу порождающих правил, в которой
нет правил, не содержащих терминальные
символы,
• матрицу (или функции) операторного
предшествования.
Алгоритм эффективнее простого
предшествования, т.к. выполняет сокращенный
разбор, не обращая внимания на
нетерминальные символы.

33. Пример

Рассмотрим работу распознавателя по
методу операторного предшествования
для грамматики G1

34. 1 этап.Построение Lt(U) и Rt(U)

Строим множества Lt(U) и Rt(U) по (1) и
(2).
Для этого нам понадобятся множества
L(U) и R(U),
построенные в п. 3.1.4.
Построение будет состоять только из
двух шагов:

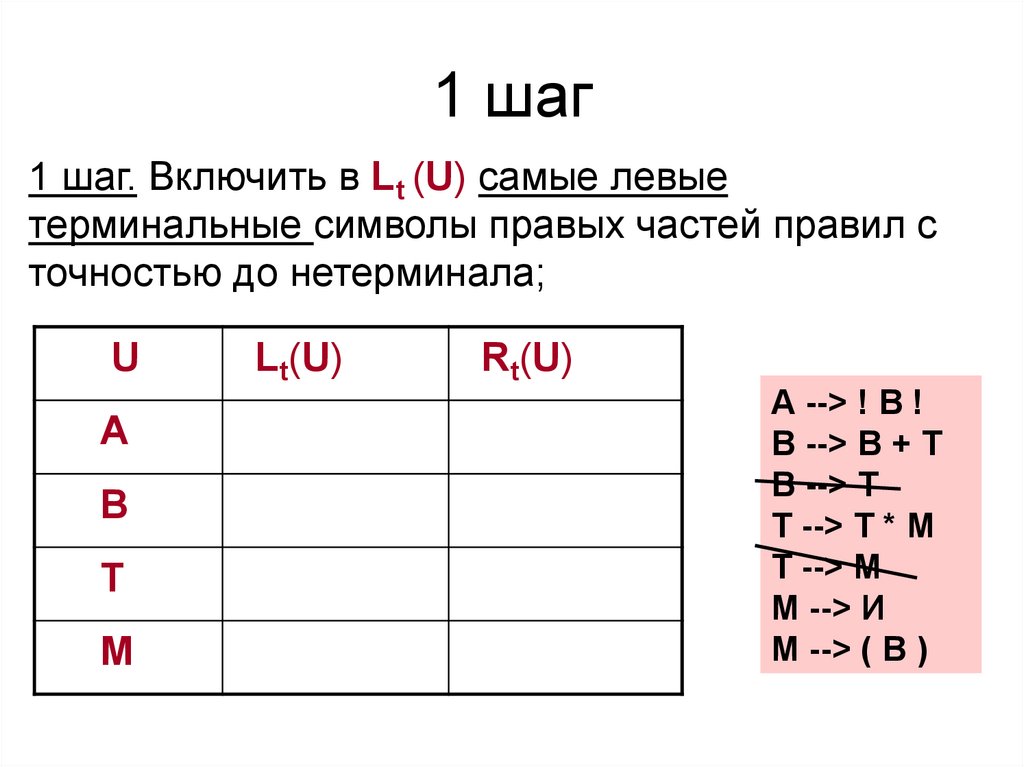
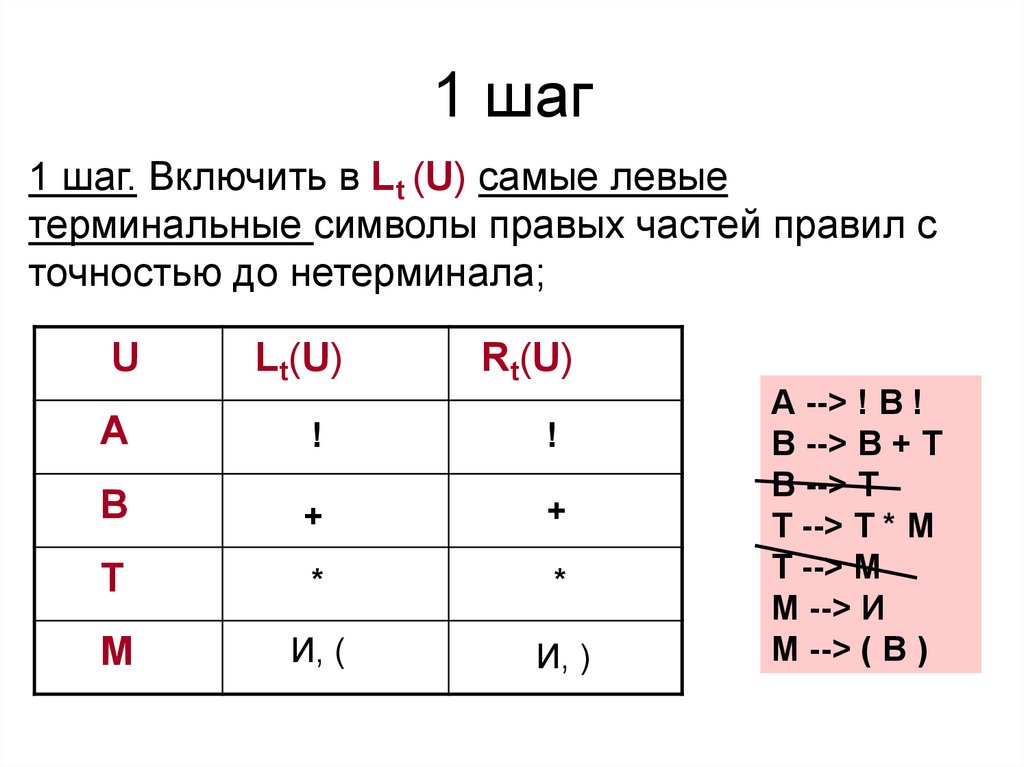
35. 1 шаг

1 шаг. Включить в Lt (U) самые левые
терминальные символы правых частей правил с
точностью до нетерминала;
U
А
В
Т
М
Lt(U)
Rt(U)
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )

36. 1 шаг

1 шаг. Включить в Lt (U) самые левые
терминальные символы правых частей правил с
точностью до нетерминала;
U
Lt(U)
Rt(U)
А
!
!
В
+
+
Т
*
*
М
И, (
И, )
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )

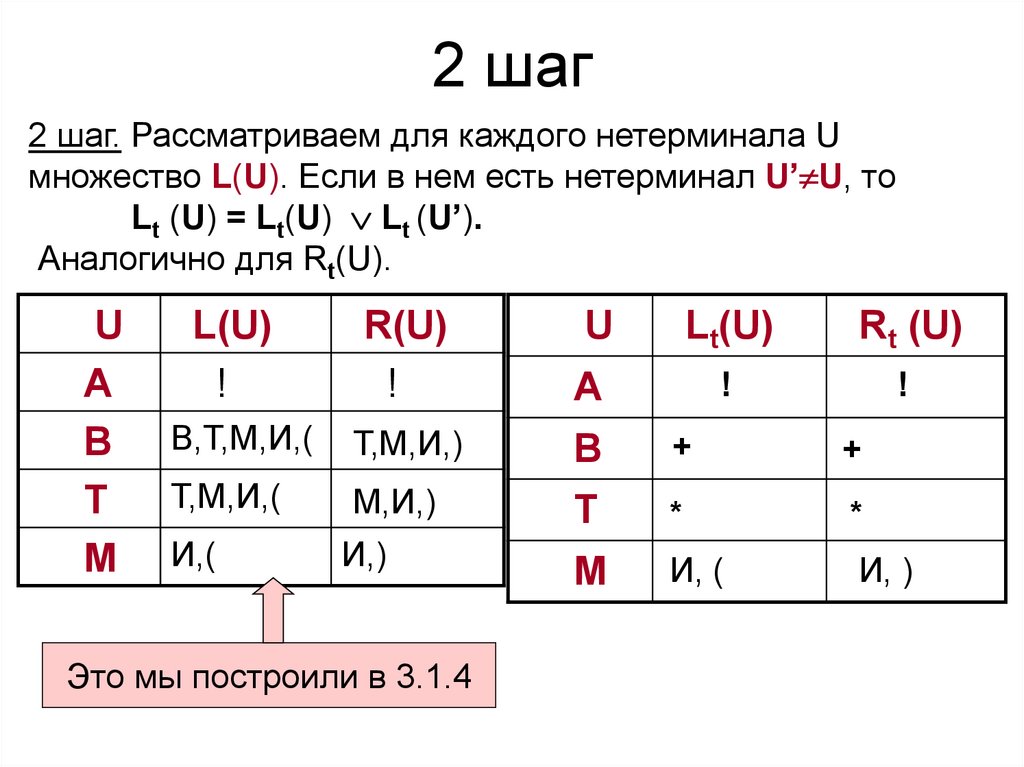
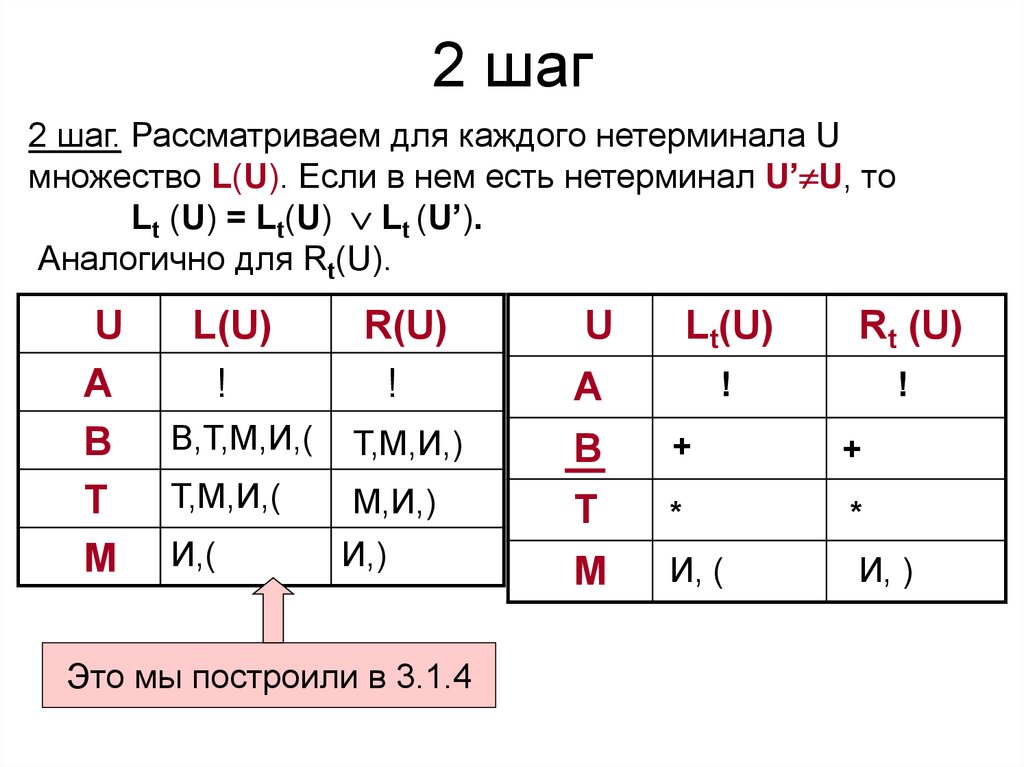
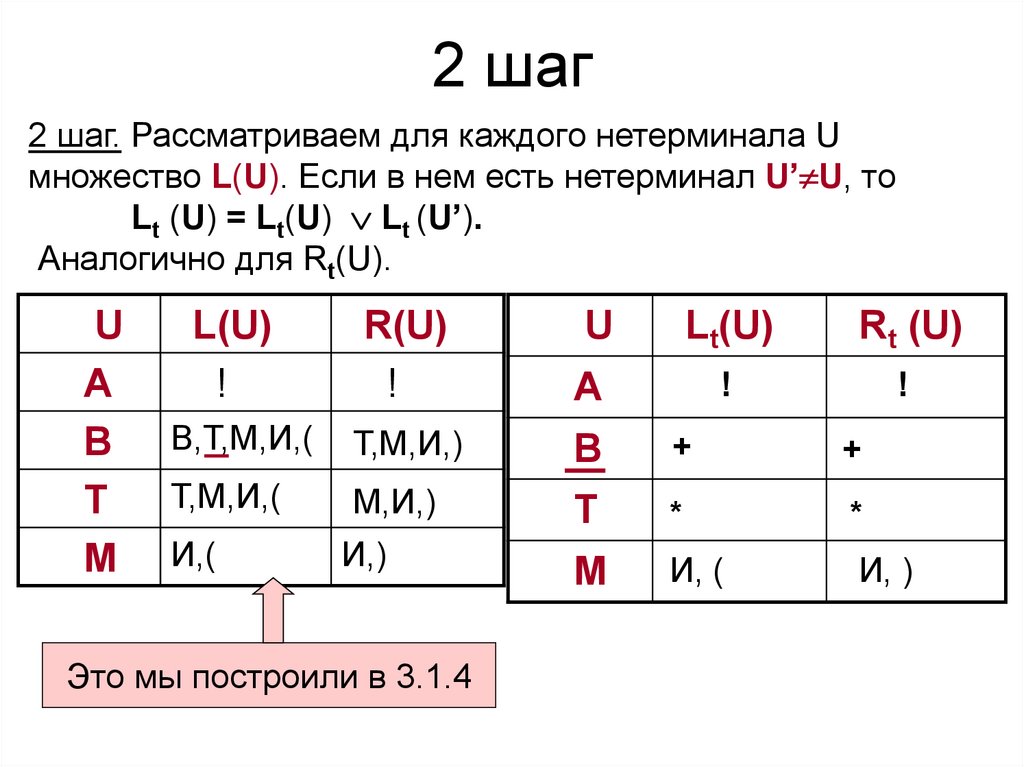
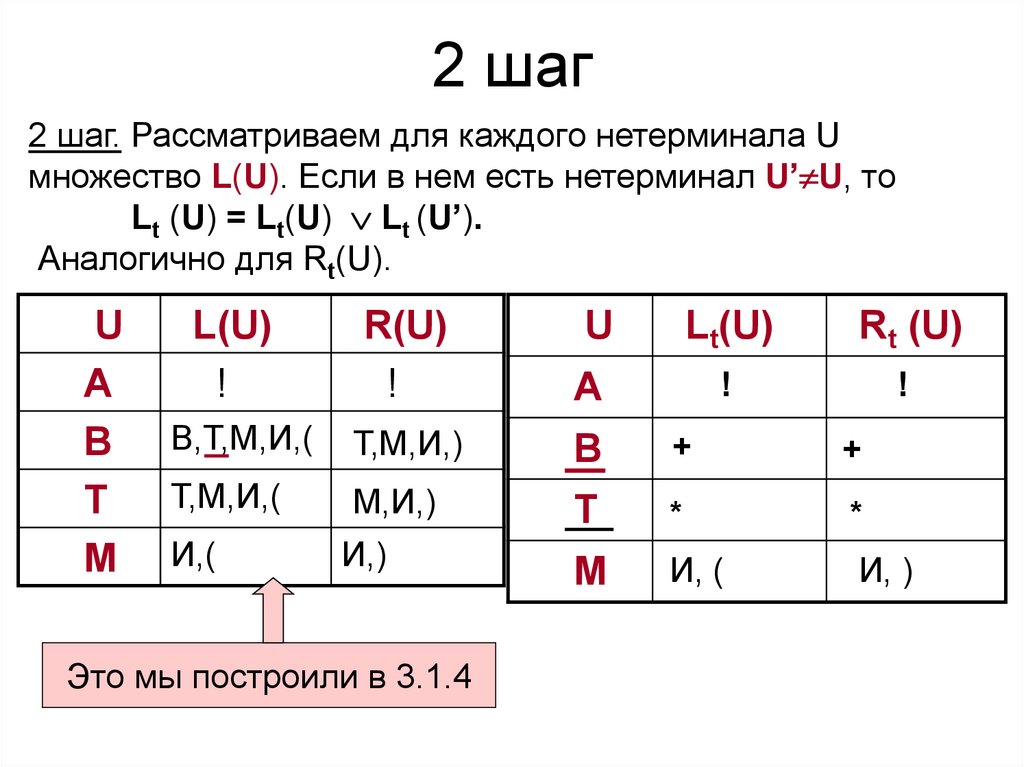
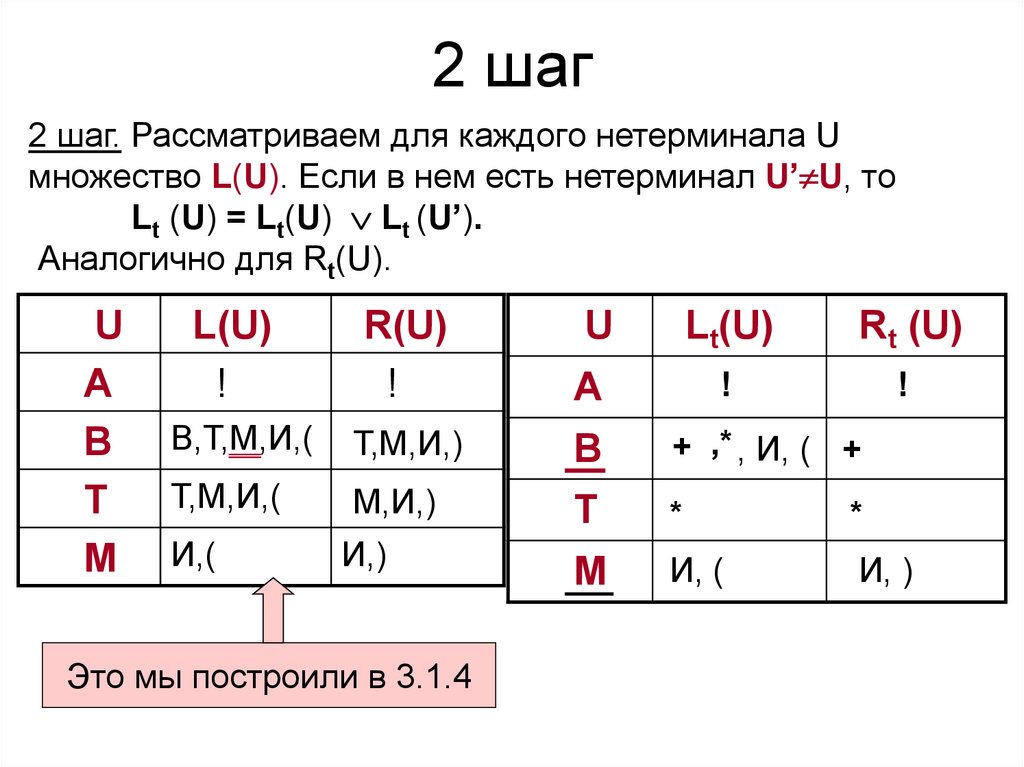
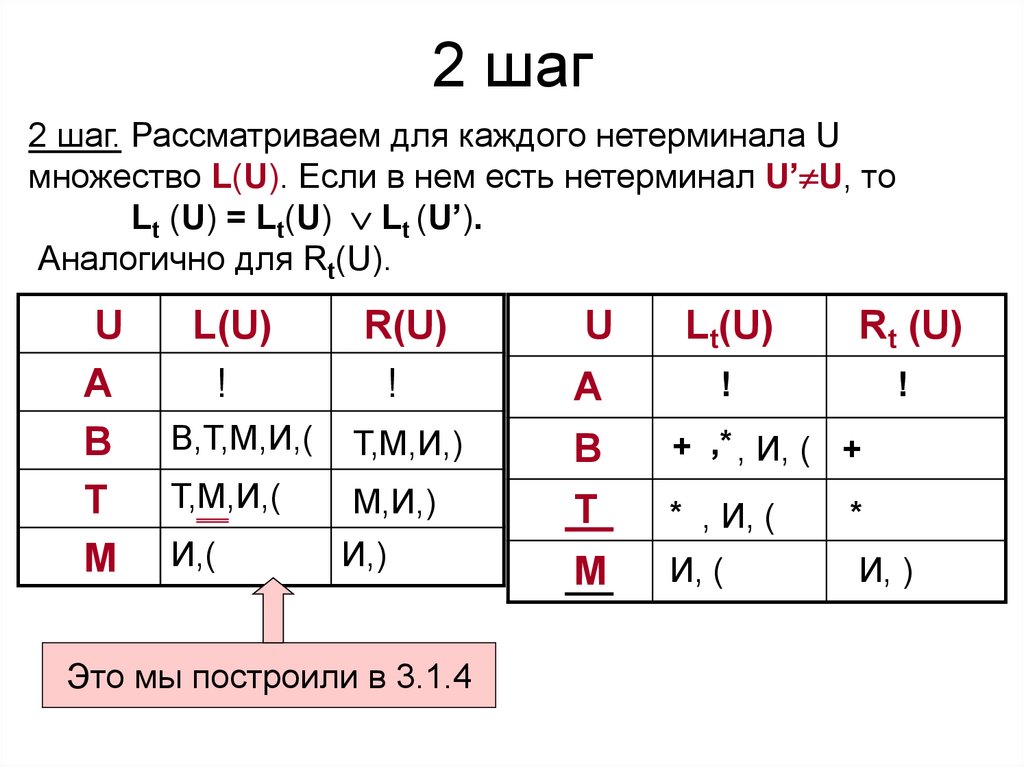
37. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

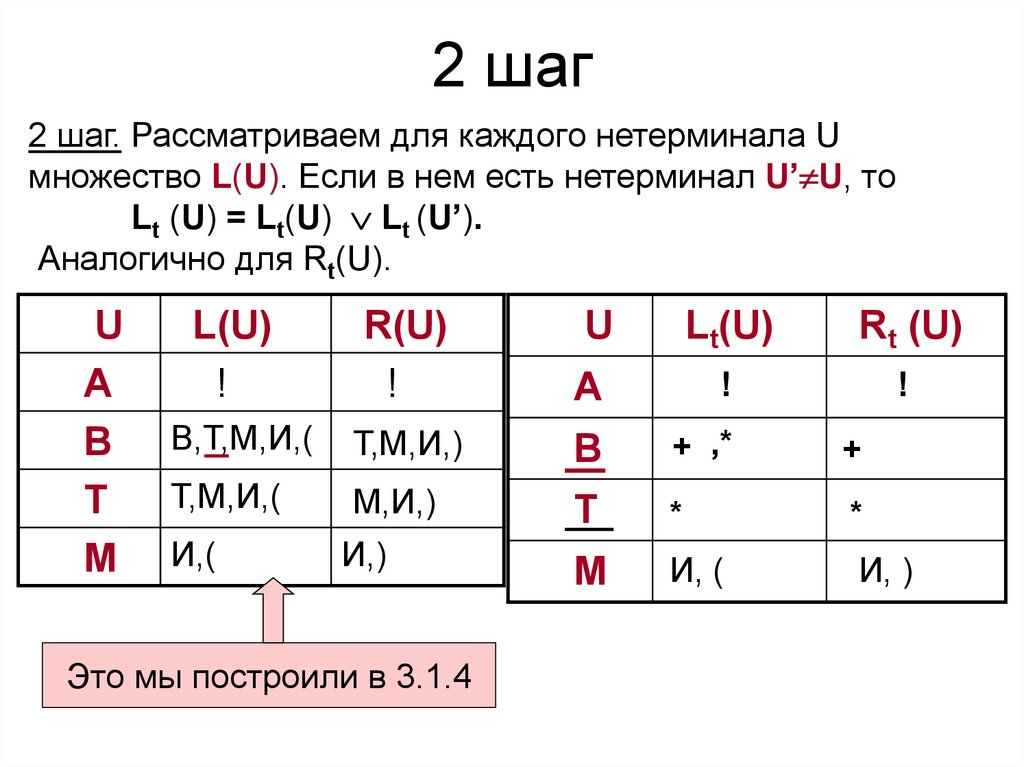
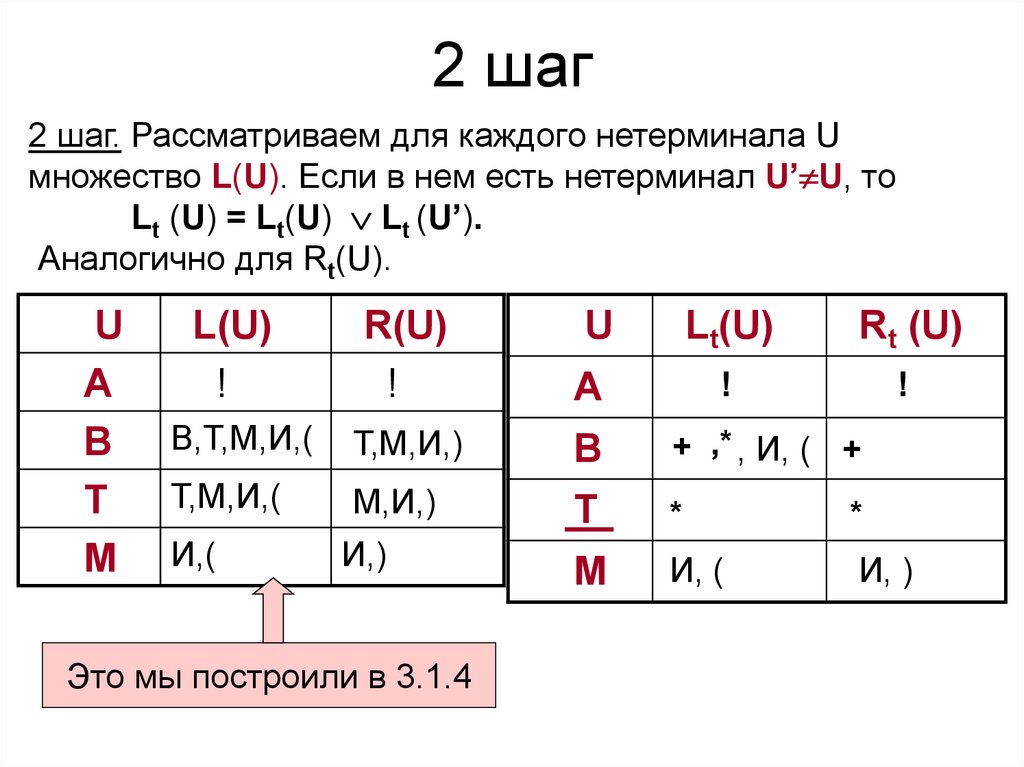
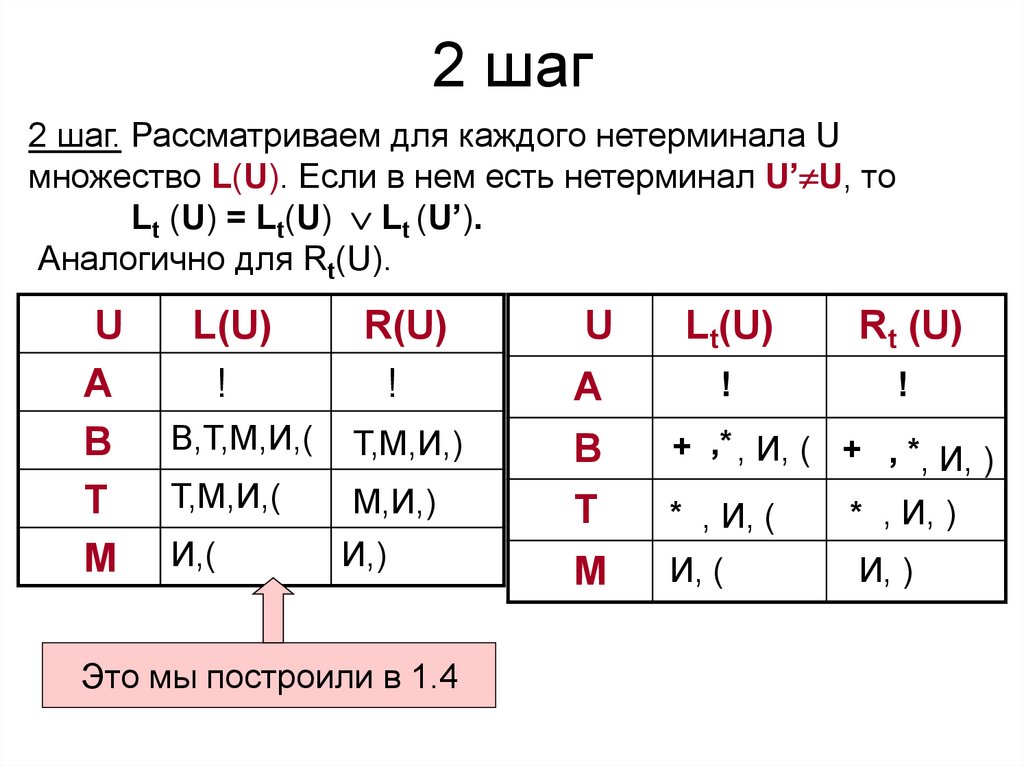
38. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

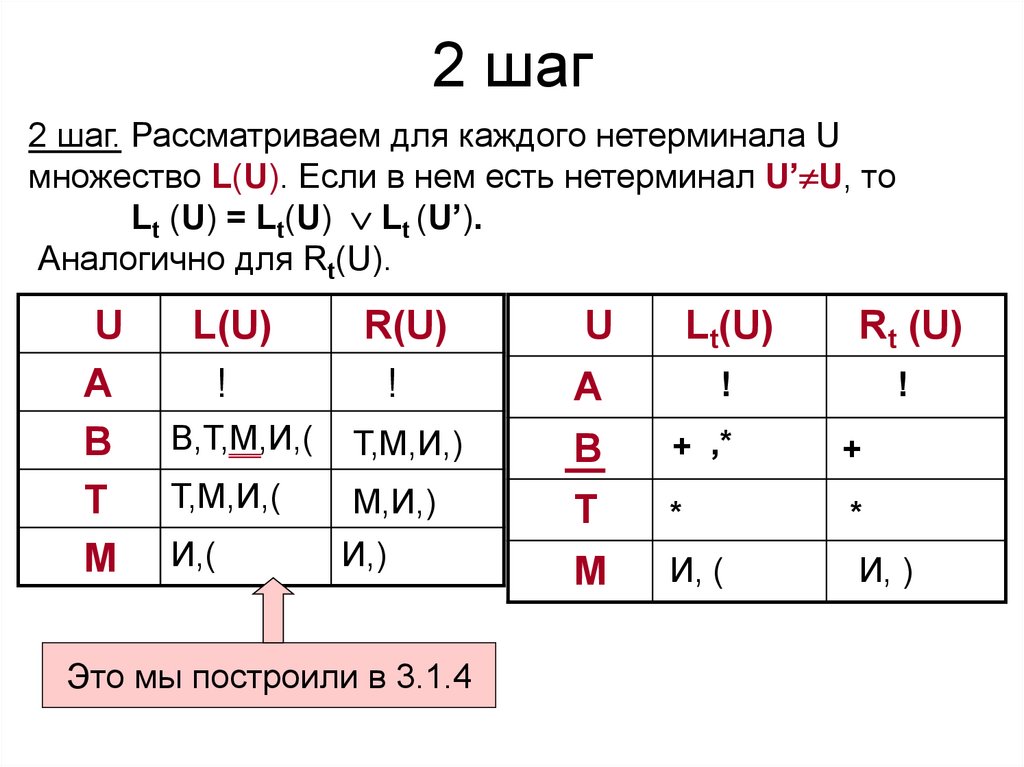
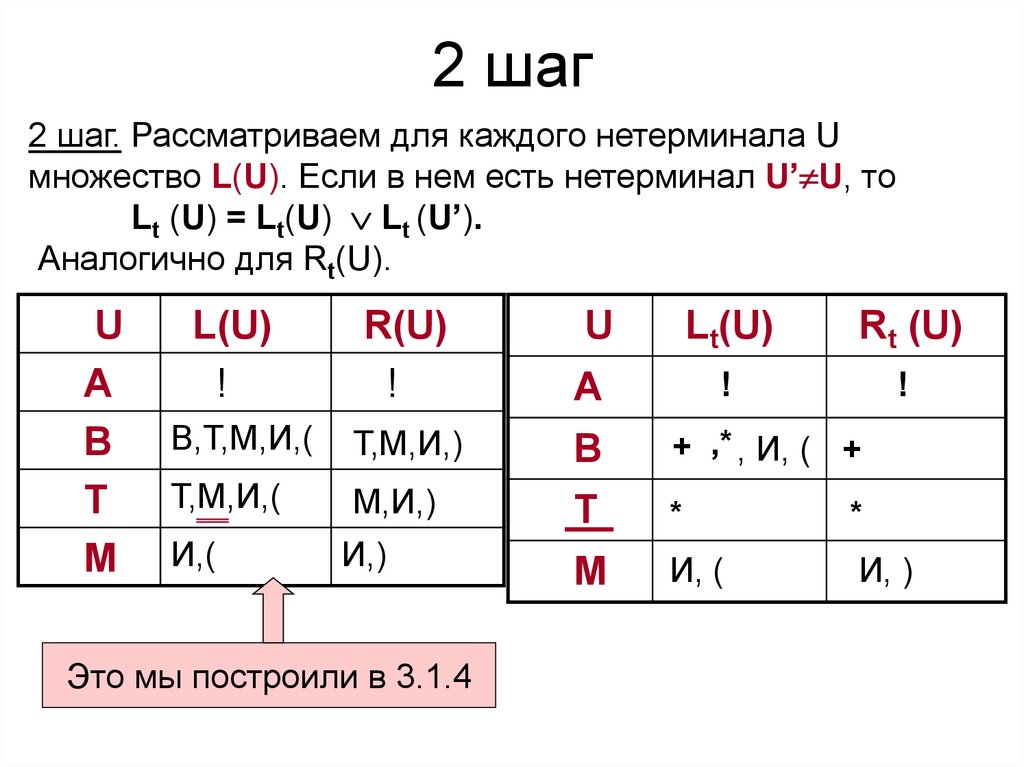
39. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

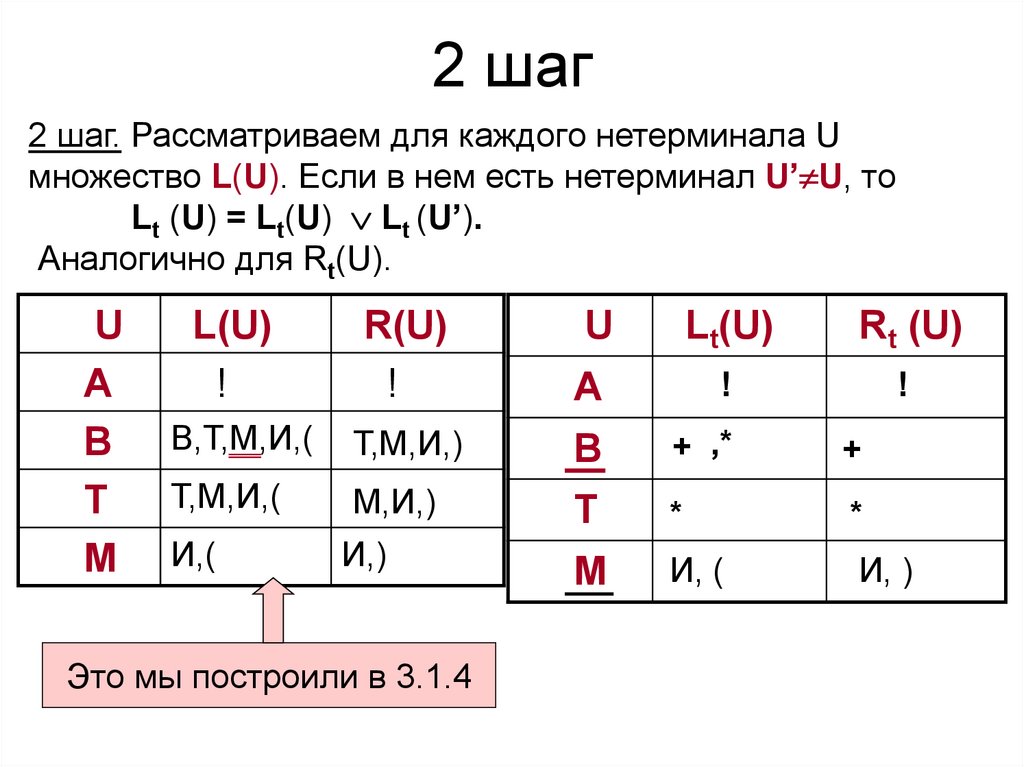
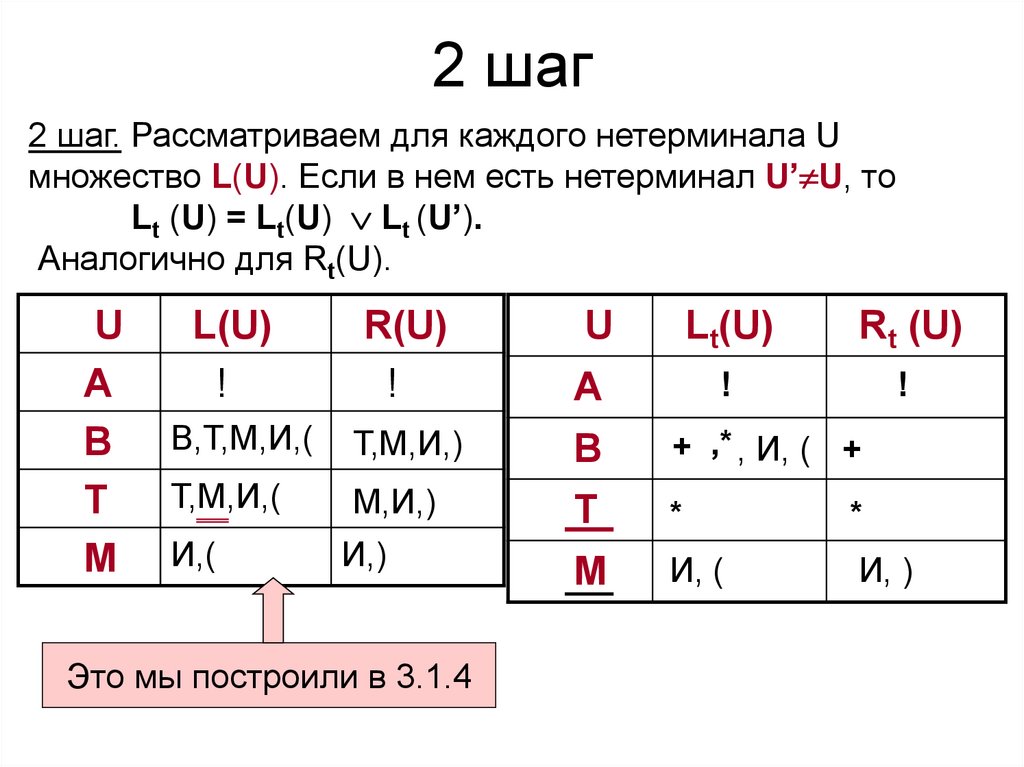
40. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

41. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,*
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

42. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,*
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

43. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,*
+
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

44. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,* , И, ( +
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

45. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,* , И, ( +
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

46. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,* , И, ( +
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

47. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,* , И, ( +
Т,М,И,(
М,И,)
Т
*
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

48. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
+ ,* , И, ( +
Т,М,И,(
М,И,)
Т
* , И, (
*
И,(
И,)
М
И, (
И, )
Это мы построили в 3.1.4

49. 2 шаг

2 шаг. Рассматриваем для каждого нетерминала U
множество L(U). Если в нем есть нетерминал U’ U, то
Lt (U) = Lt(U) Lt (U’).
Аналогично для Rt(U).
U
А
В
Т
М
L(U)
!
R(U)
!
U
Lt(U)
Rt (U)
А
!
!
В,Т,М,И,(
Т,М,И,)
В
Т,М,И,(
+ ,* , И, ( + , *, И, )
М,И,)
Т
* , И, (
* , И, )
И,(
И,)
М
И, (
И, )
Это мы построили в 1.4

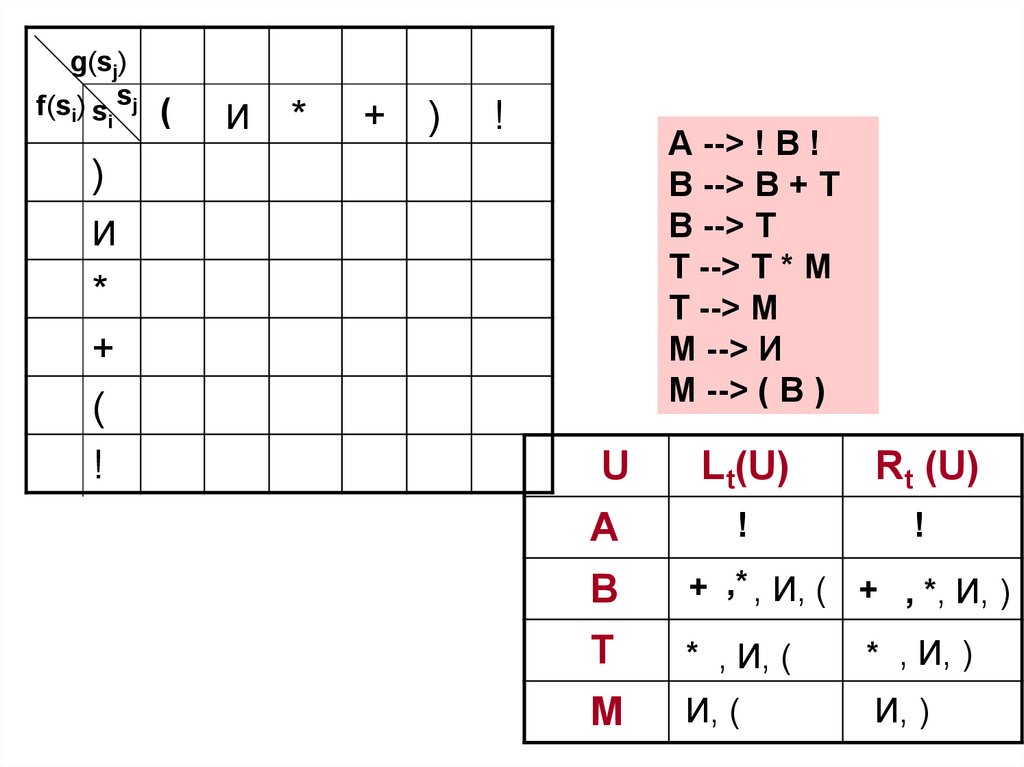
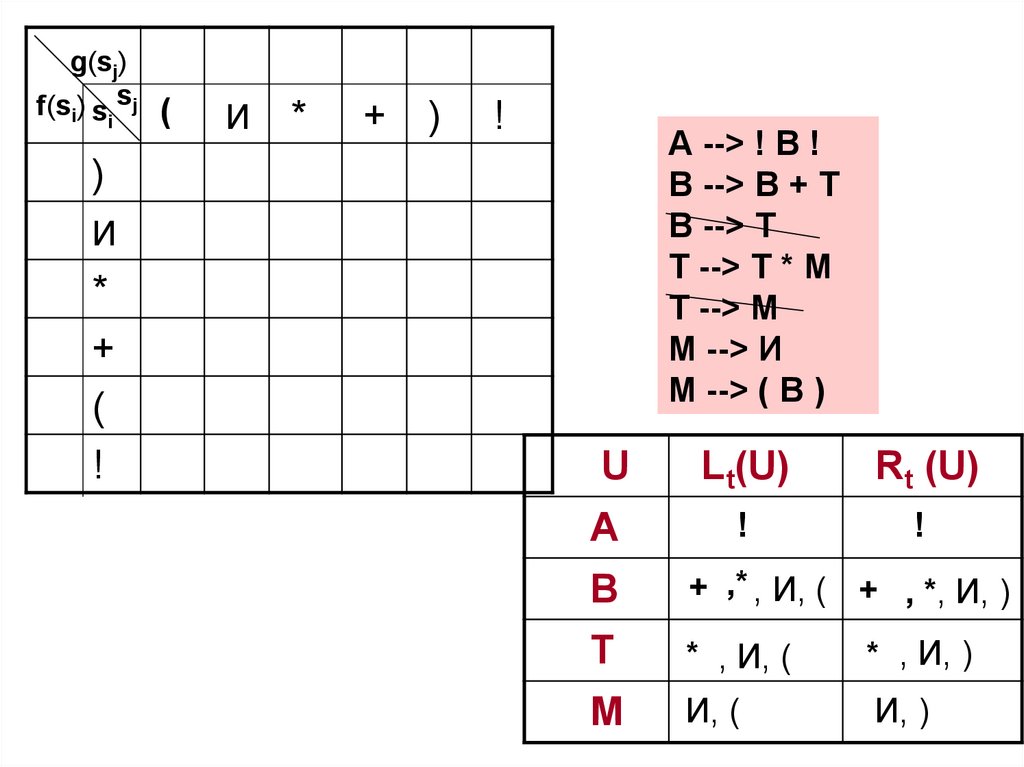
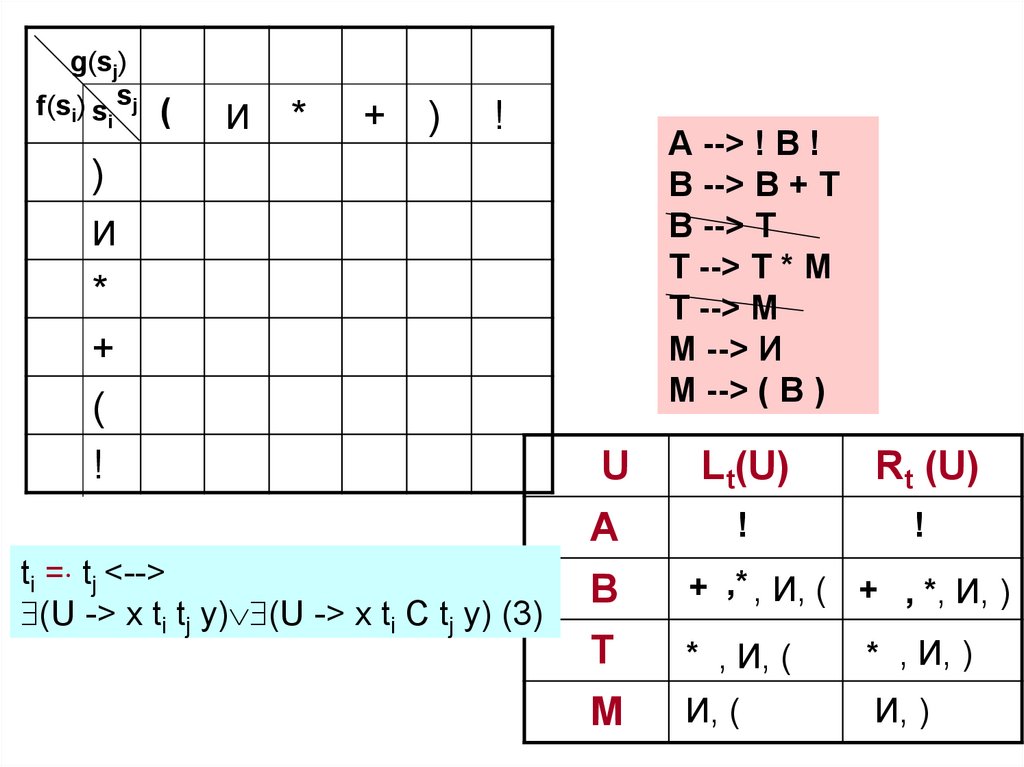
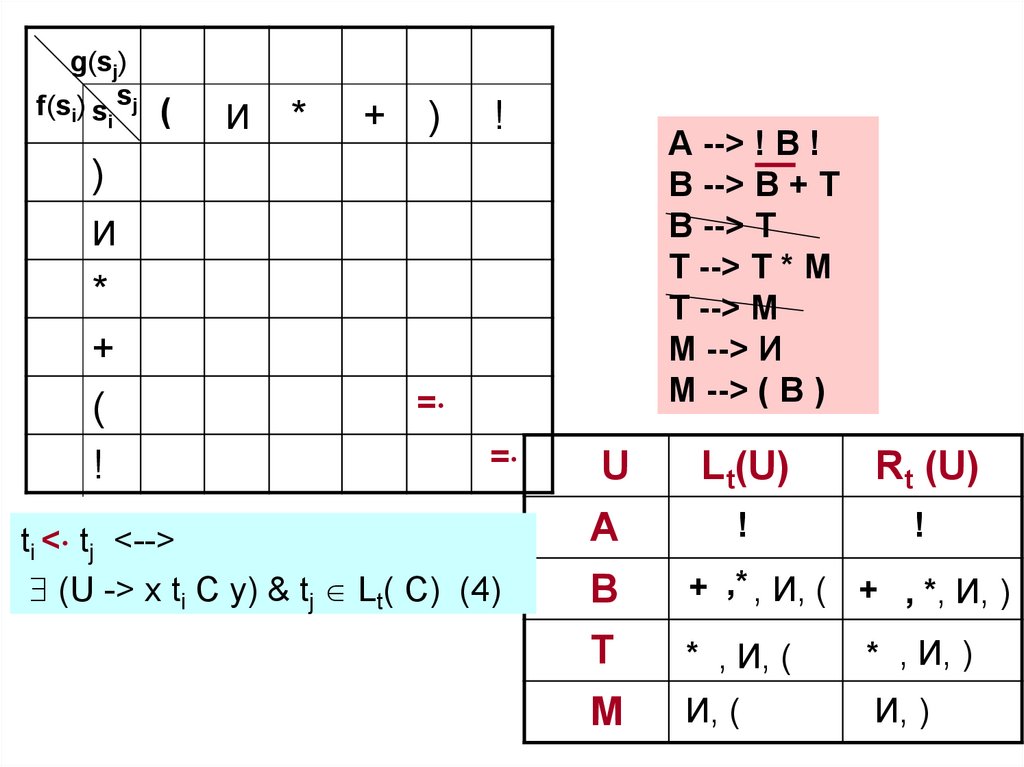
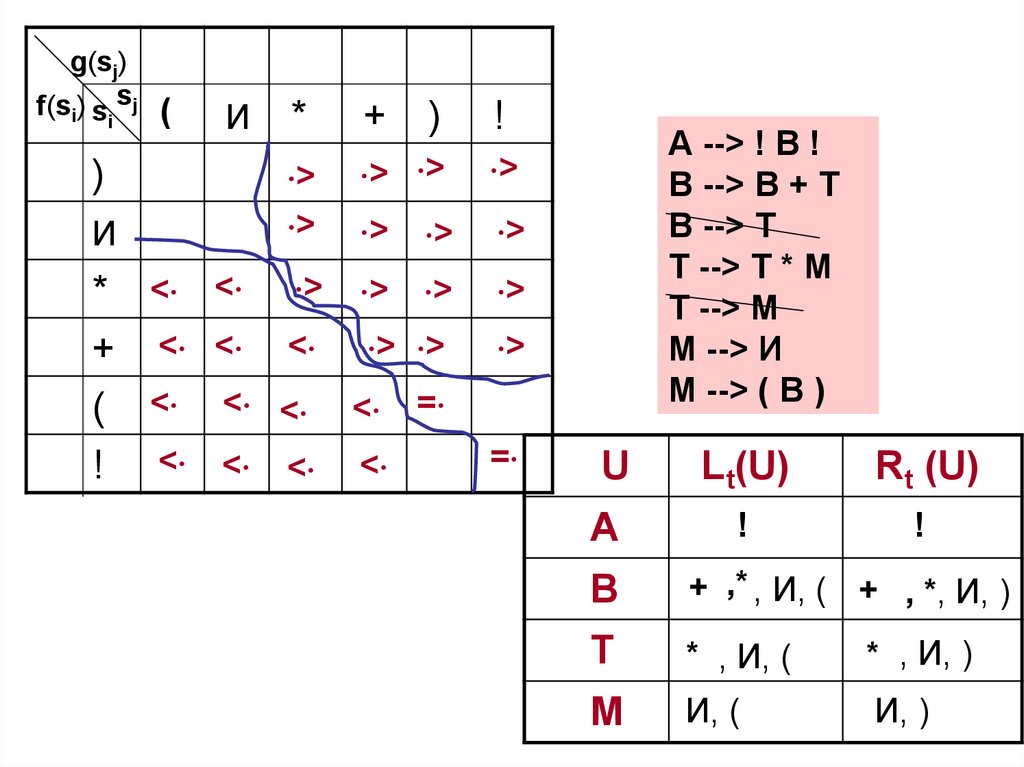
50. 2 этап. Заполнение МОП

Используя порождающие правила, множества
Lt(U) и Rt(U) и правила (3) (5) построения
отношений, заполняем МОП.

51.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

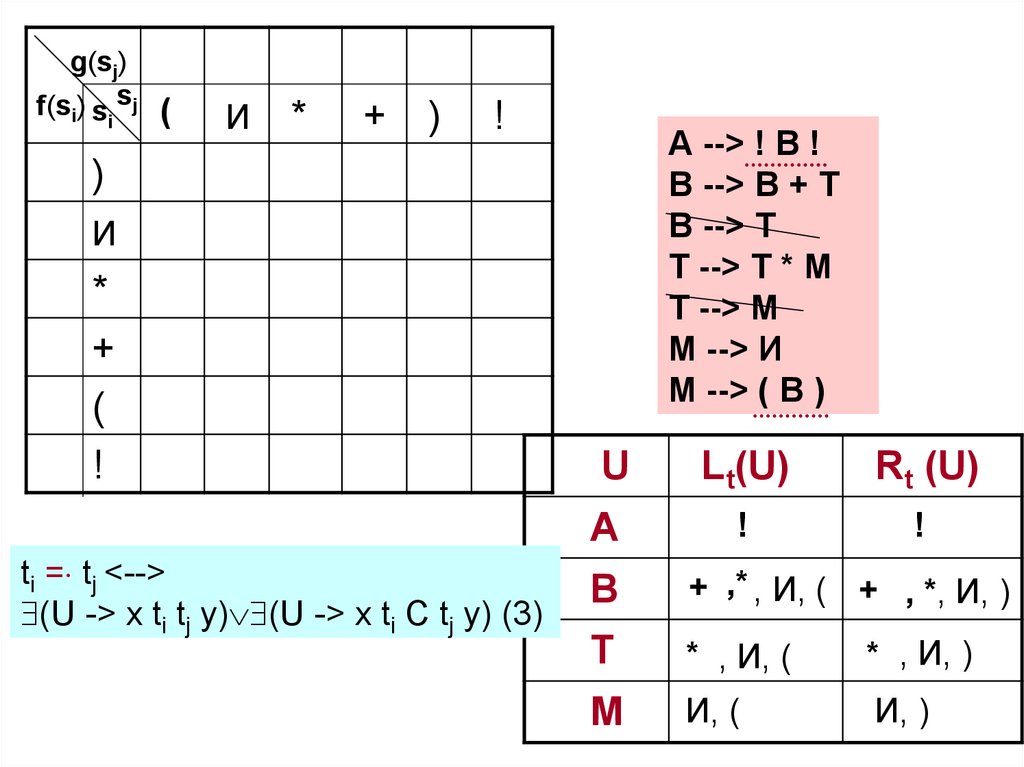
52.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

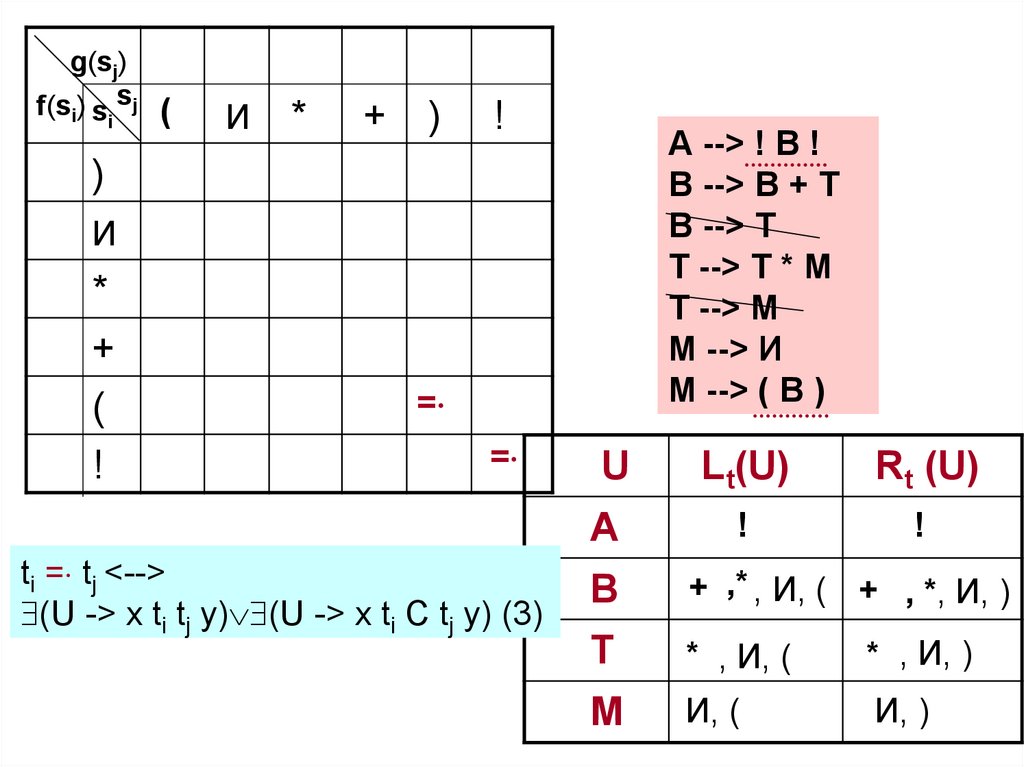
53.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
ti = tj <-->
(U -> x ti tj y) (U -> x ti C tj y) (3)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

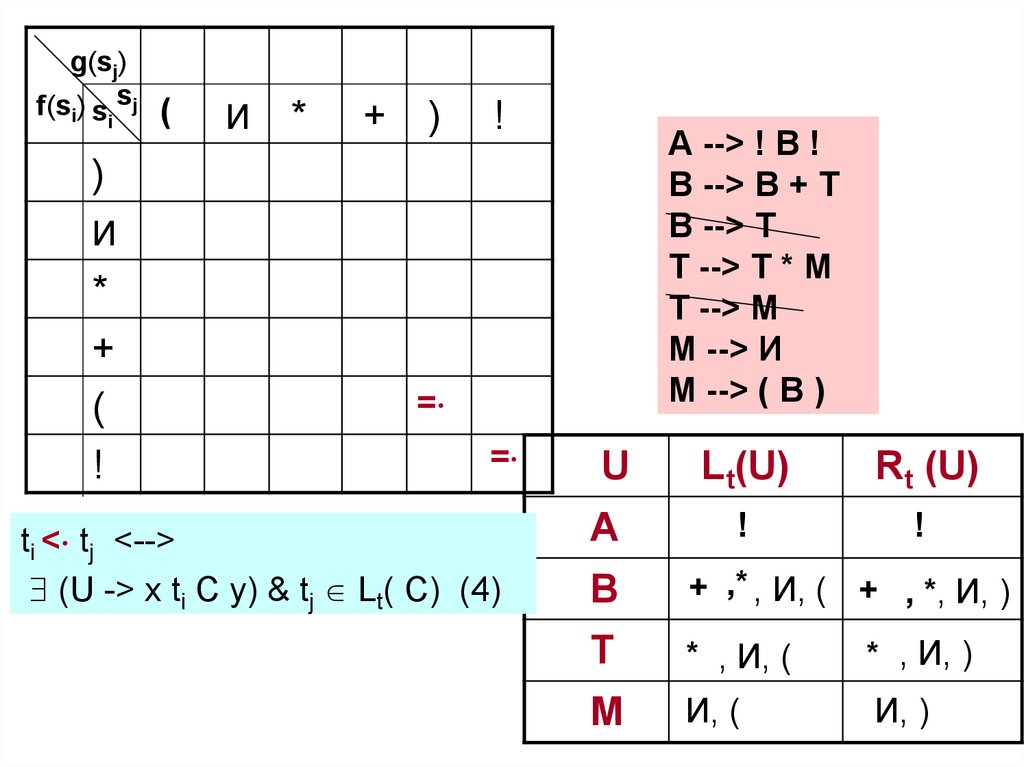
54.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
ti = tj <-->
(U -> x ti tj y) (U -> x ti C tj y) (3)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

55.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
ti = tj <-->
(U -> x ti tj y) (U -> x ti C tj y) (3)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

56.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
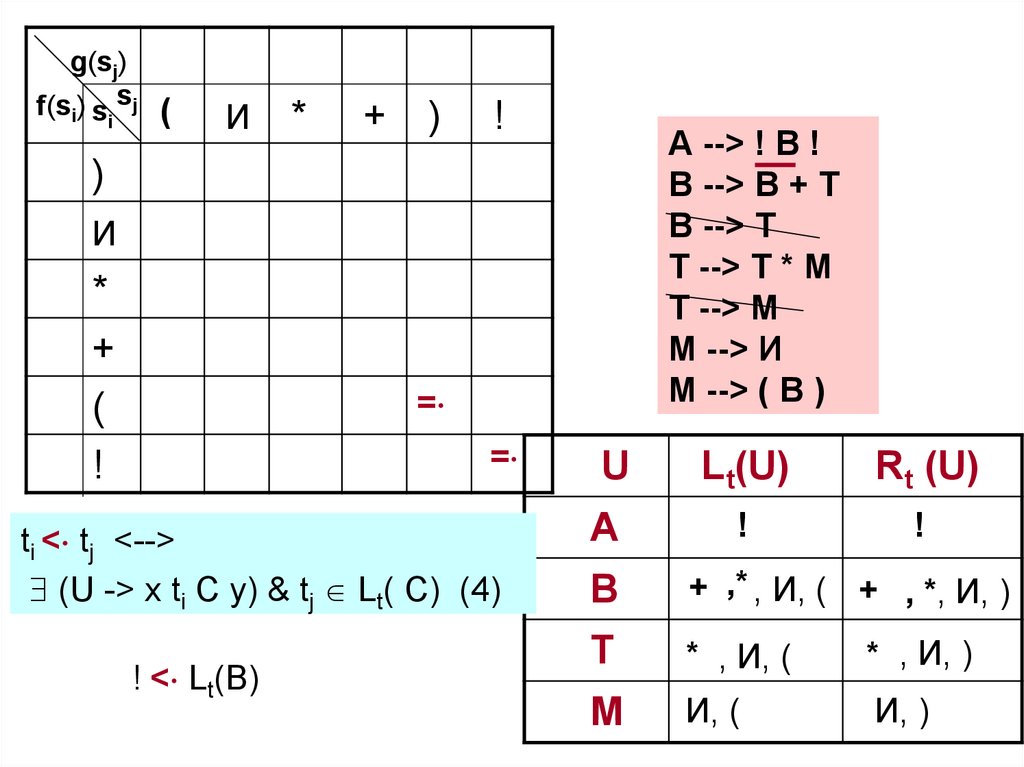
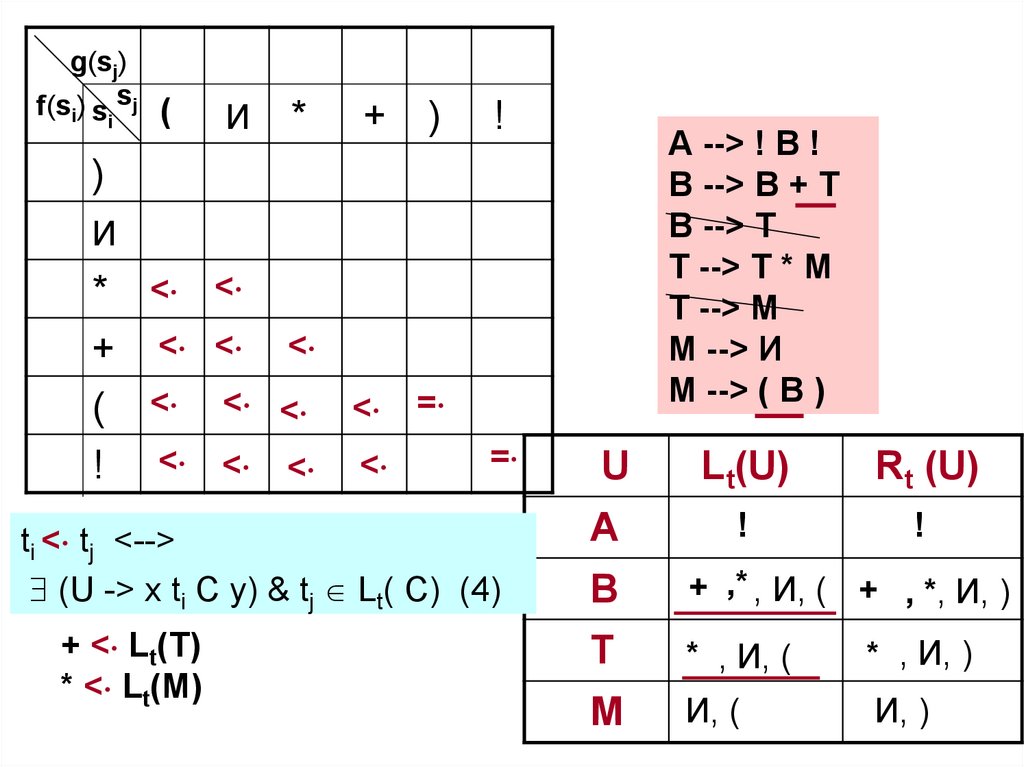
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

57.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

58.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
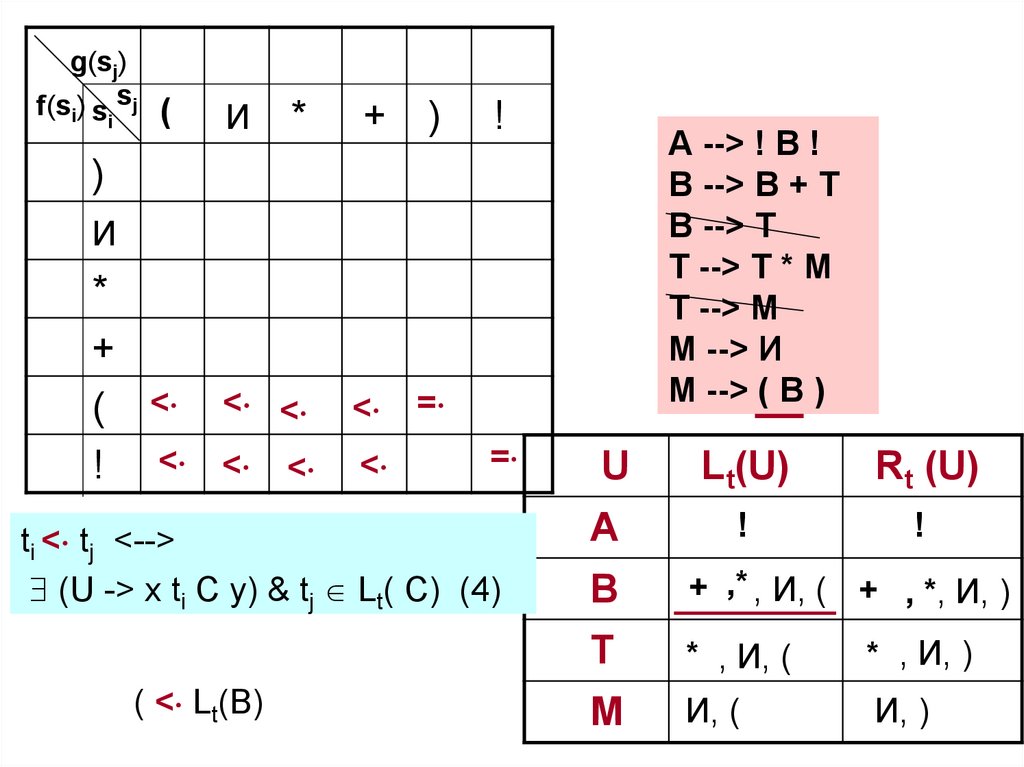
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
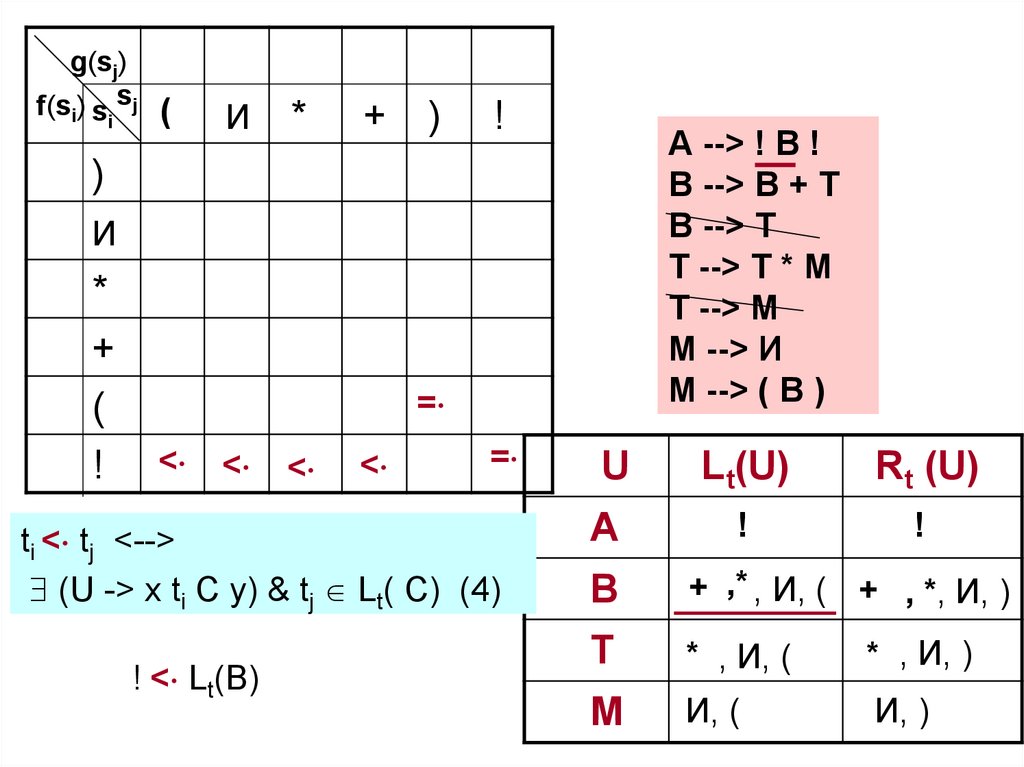
! < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

59.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
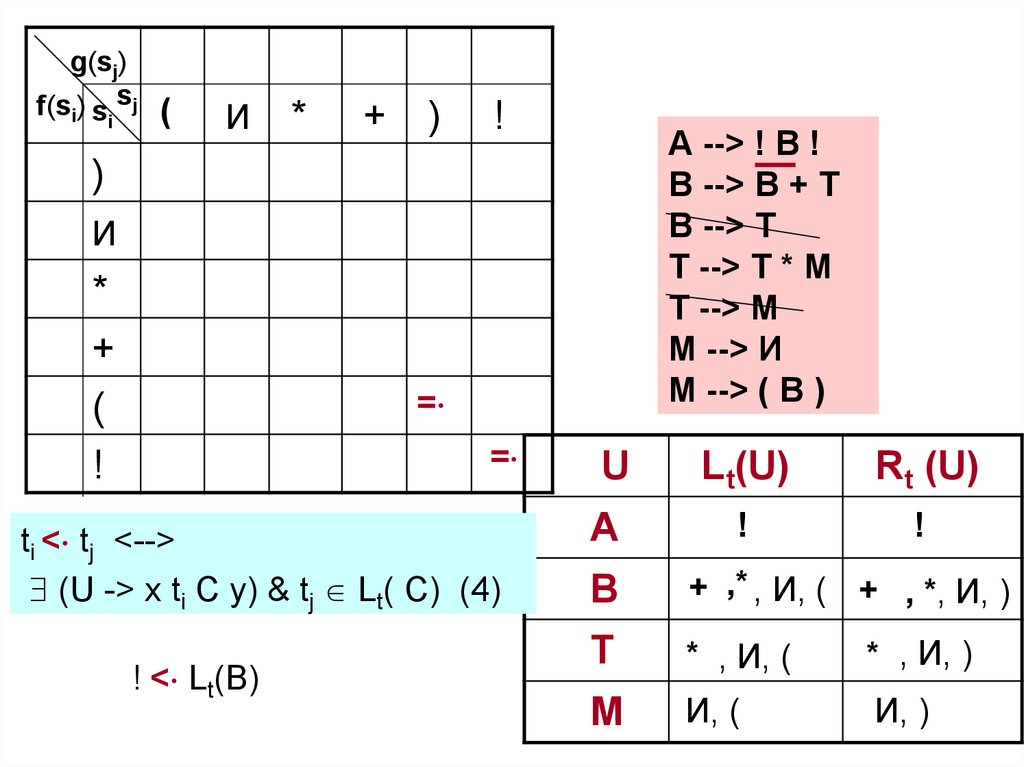
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
! < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

60.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
=
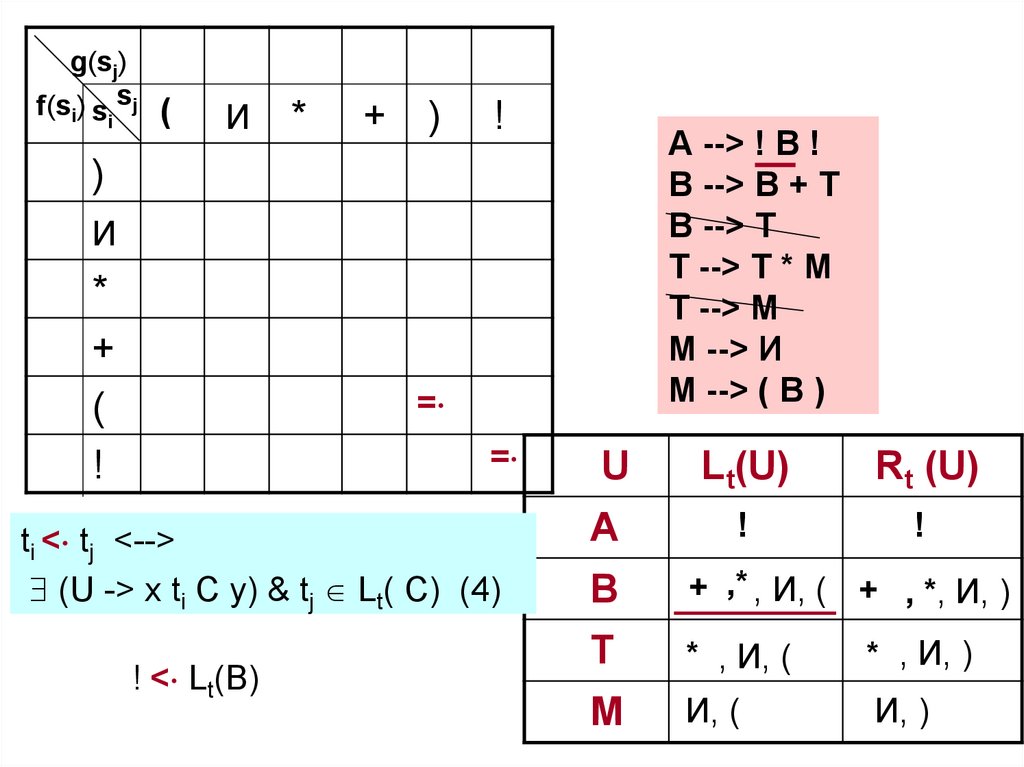
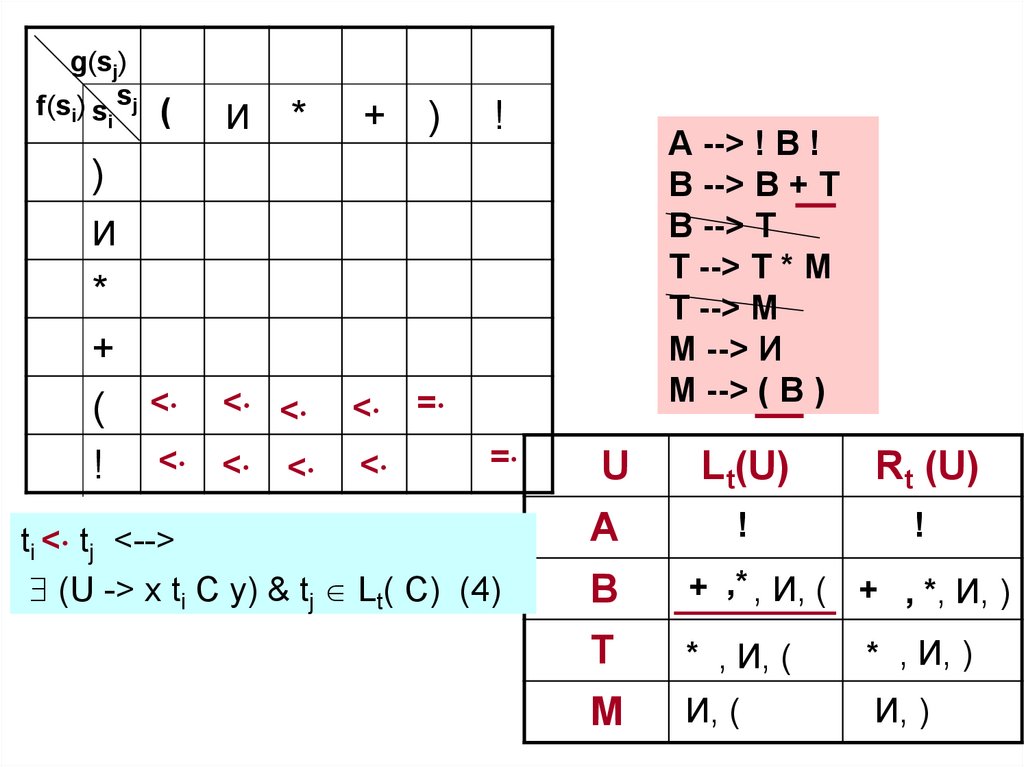
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
! < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

61.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
<
<
<
<
=
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
! < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

62.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
<
<
<
<
=
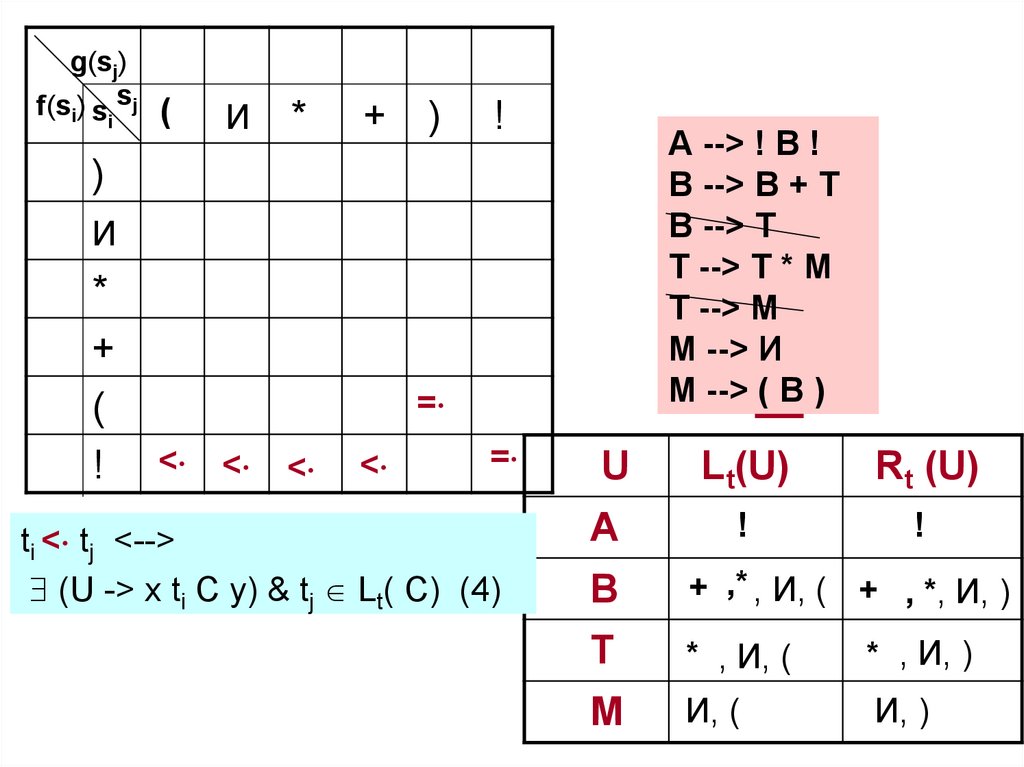
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

63.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
<
<
<
<
=
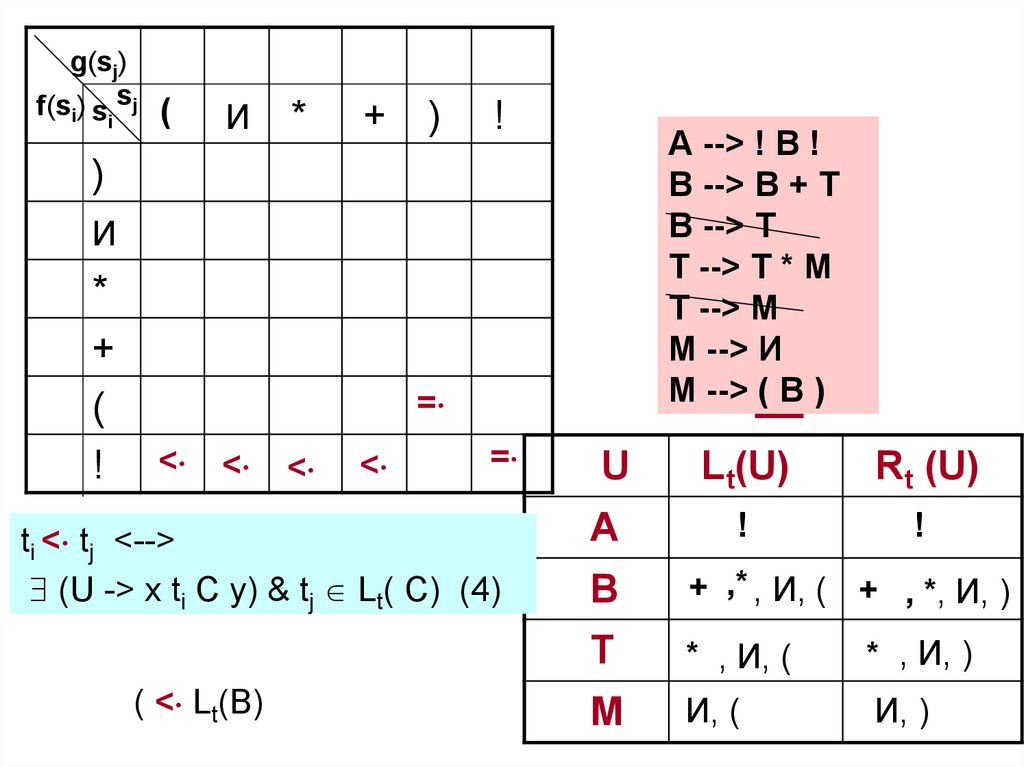
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
( < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

64.

g(sj)
f(si) si sj (
И
*
+
)
!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
*
+
(
!
=
<
<
<
<
=
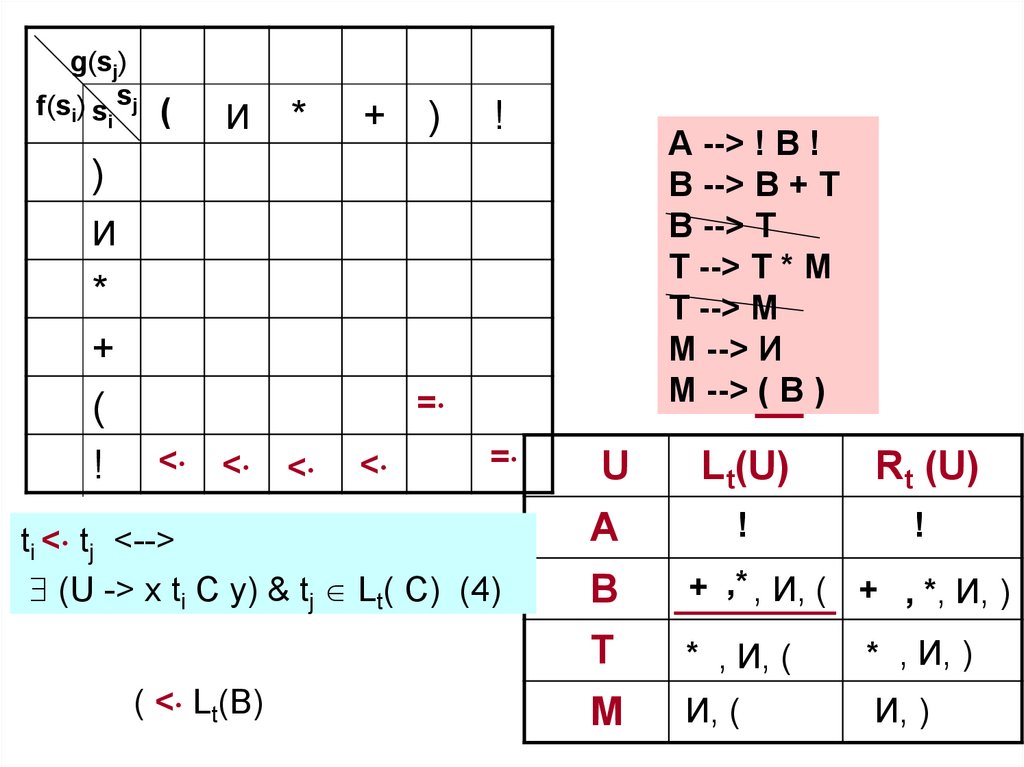
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
( < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

65.

g(sj)
f(si) si sj (
И
*
+
)
!
*
+
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
( < Lt(В)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

66.

g(sj)
f(si) si sj (
И
*
+
)
!
*
+
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

67.

g(sj)
f(si) si sj (
И
*
+
)
!
*
+
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
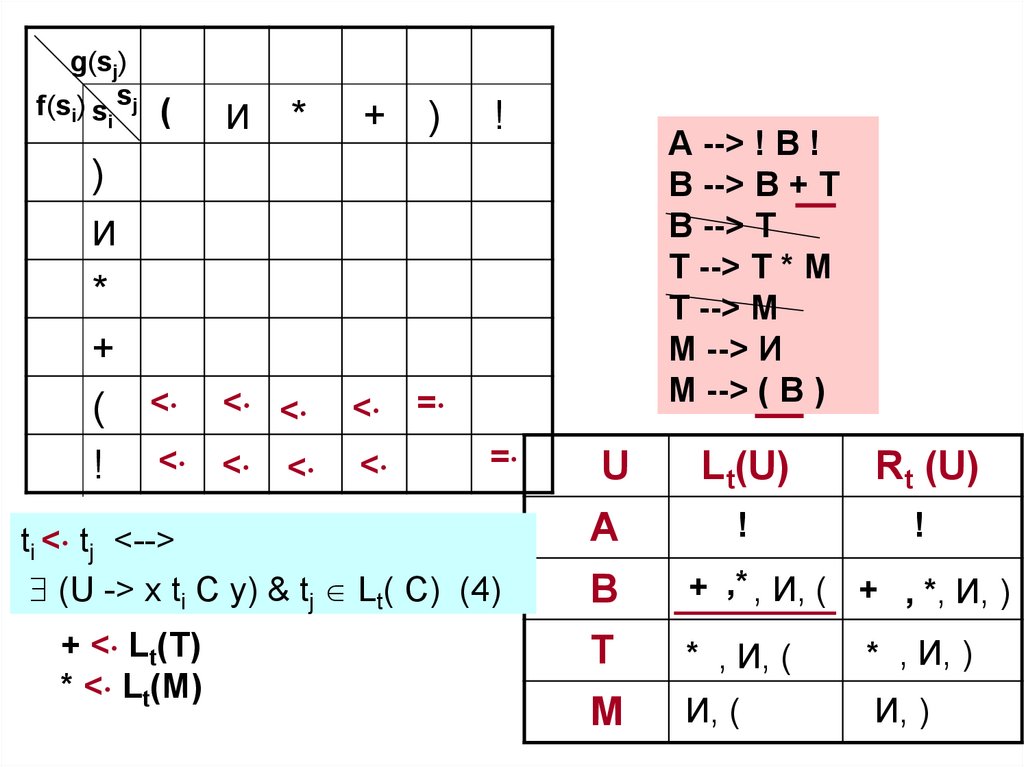
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
+ < Lt(Т)
* < Lt(М)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

68.

g(sj)
f(si) si sj (
И
*
+
)
!
*
+
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
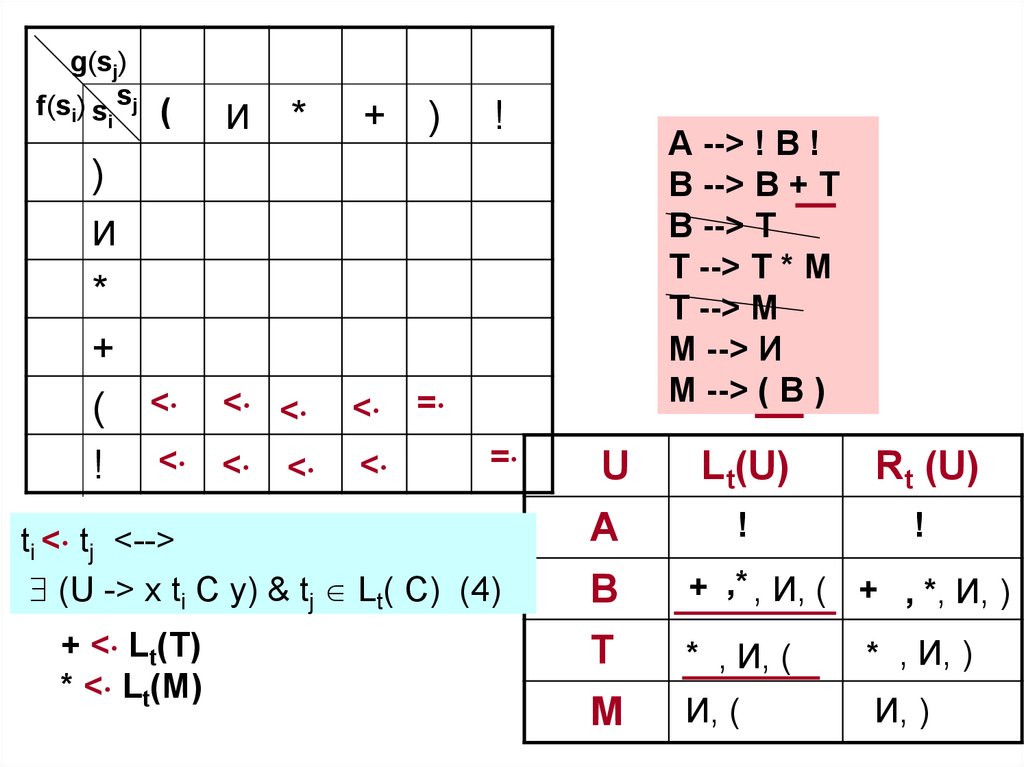
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
+ < Lt(Т)
* < Lt(М)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

69.

g(sj)
f(si) si sj (
И
*
+
)
!
* < <
+ < < <
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
ti < tj <-->
(U -> x ti C y) & tj Lt( C) (4)
+ < Lt(Т)
* < Lt(М)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

70.

g(sj)
f(si) si sj (
И
*
+
)
!
* < <
+ < < <
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
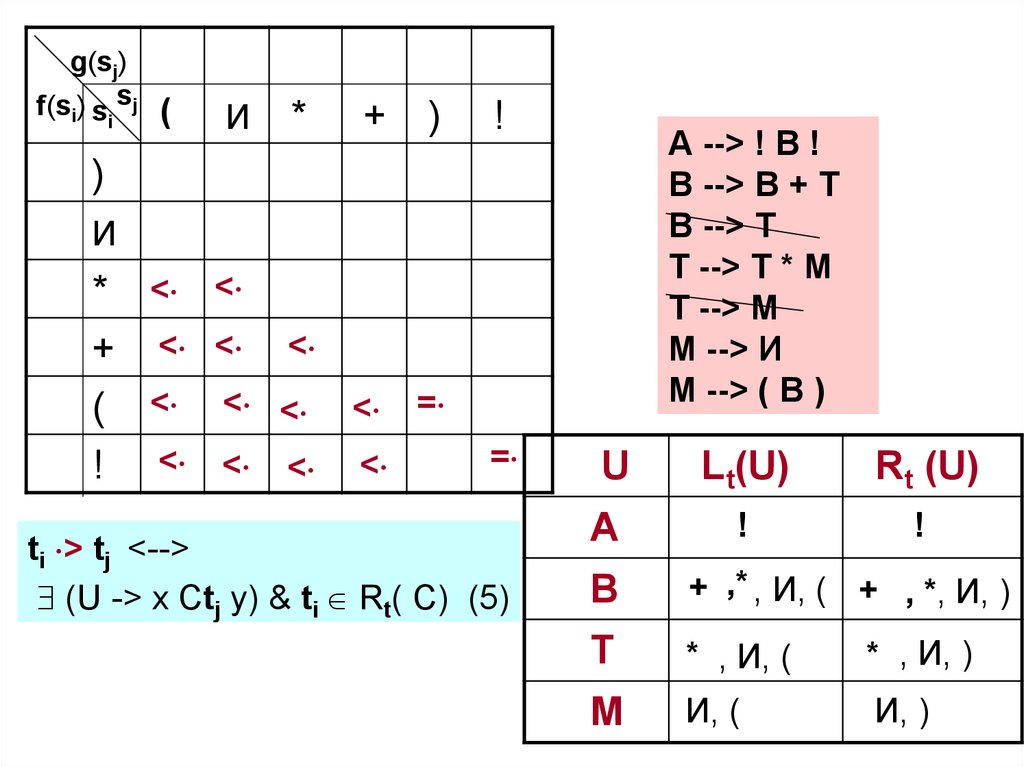
ti > tj <-->
(U -> x Ctj y) & ti Rt( C) (5)
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

71.

g(sj)
f(si) si sj (
И
*
+
)
!
* < <
+ < < <
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
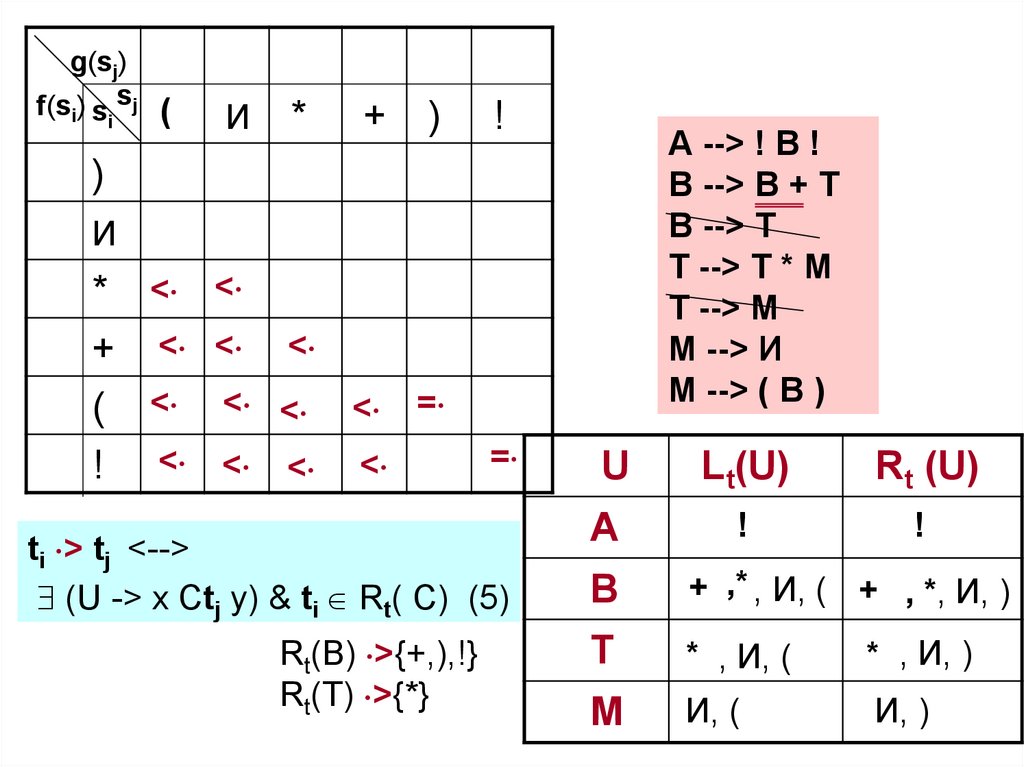
ti > tj <-->
(U -> x Ctj y) & ti Rt( C) (5)
Rt(В) >{+,),!}
Rt(Т) >{*}
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

72.

g(sj)
f(si) si sj (
И
*
+
)
!
* < <
+ < < <
( < < < < =
! < < < <
=
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
)
И
ti > tj <-->
(U -> x Ctj y) & ti Rt( C) (5)
Rt(В) >{+,),!}
Rt(Т) >{*}
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

73.

g(sj)
f(si) si sj (
)
И
И
*
+
)
!
>
>
> >
>
>
>
>
* < < > > > >
+ < < < > > >
( < < < < =
=
! < < < <
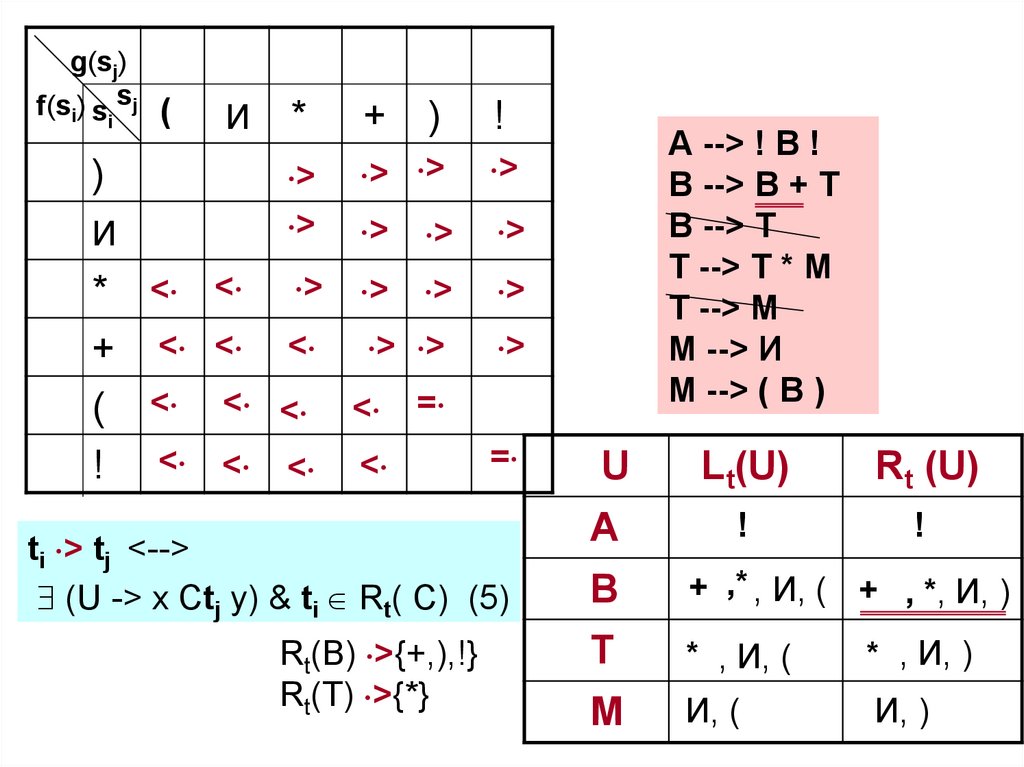
ti > tj <-->
(U -> x Ctj y) & ti Rt( C) (5)
Rt(В) >{+,),!}
Rt(Т) >{*}
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

74.

g(sj)
f(si) si sj (
)
И
И
*
+
)
!
>
>
> >
>
>
>
>
* < < > > > >
+ < < < > > >
( < < < < =
=
! < < < <
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

75.

g(sj)
f(si) si sj (
)
И
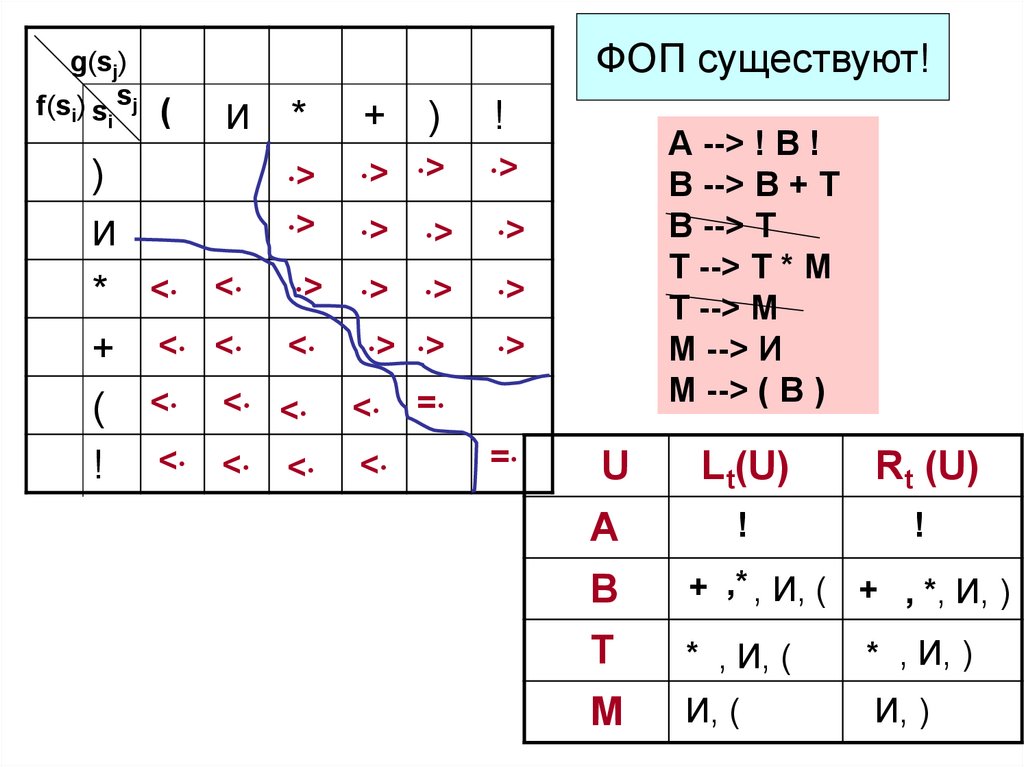
ФОП существуют!
И
*
+
)
!
>
>
> >
>
>
>
>
* < < > > > >
+ < < < > > >
( < < < < =
=
! < < < <
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

76.

g(sj) 6
f(si) si sj (
6
И
4
*
5 )
>
>
5 И
5 * < < >
3 + < < <
1 ( < < <
1 ! < < <
2
+
1
)
1
!
> >
>
>
>
>
>
>
>
> >
>
<
<
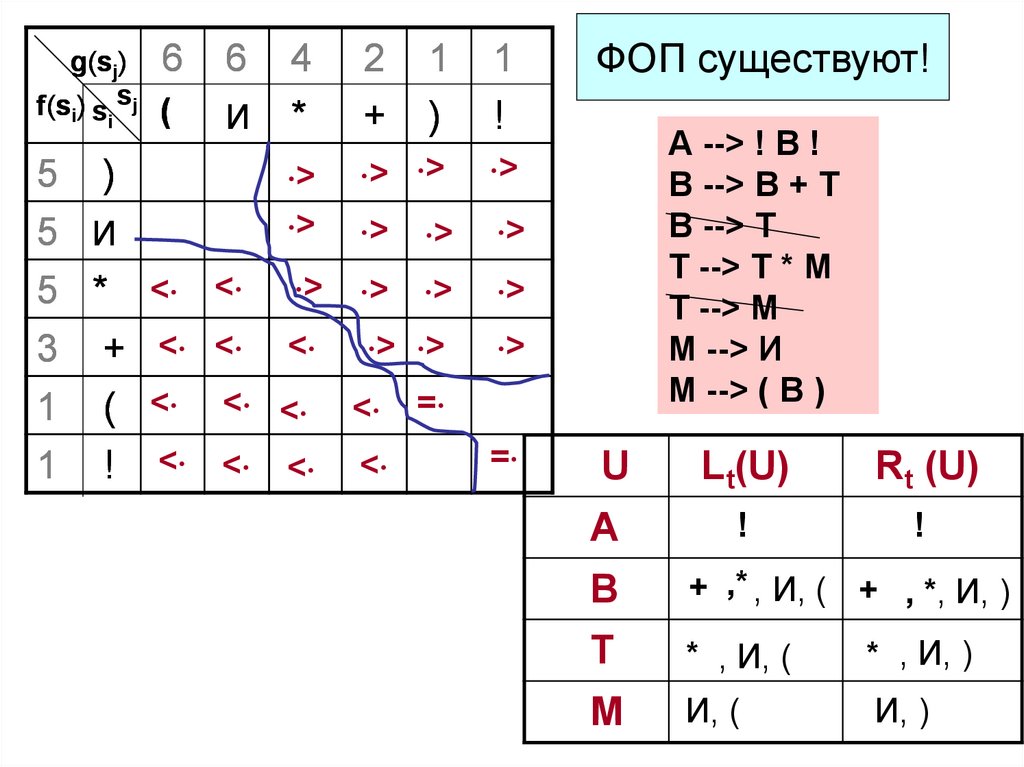
ФОП существуют!
А --> ! В !
В --> В + Т
В --> Т
Т --> Т * М
Т --> М
М --> И
М --> ( В )
=
=
U
Lt(U)
Rt (U)
А
!
!
В
+ ,* , И, ( + , *, И, )
Т
* , И, (
* , И, )
М
И, (
И, )

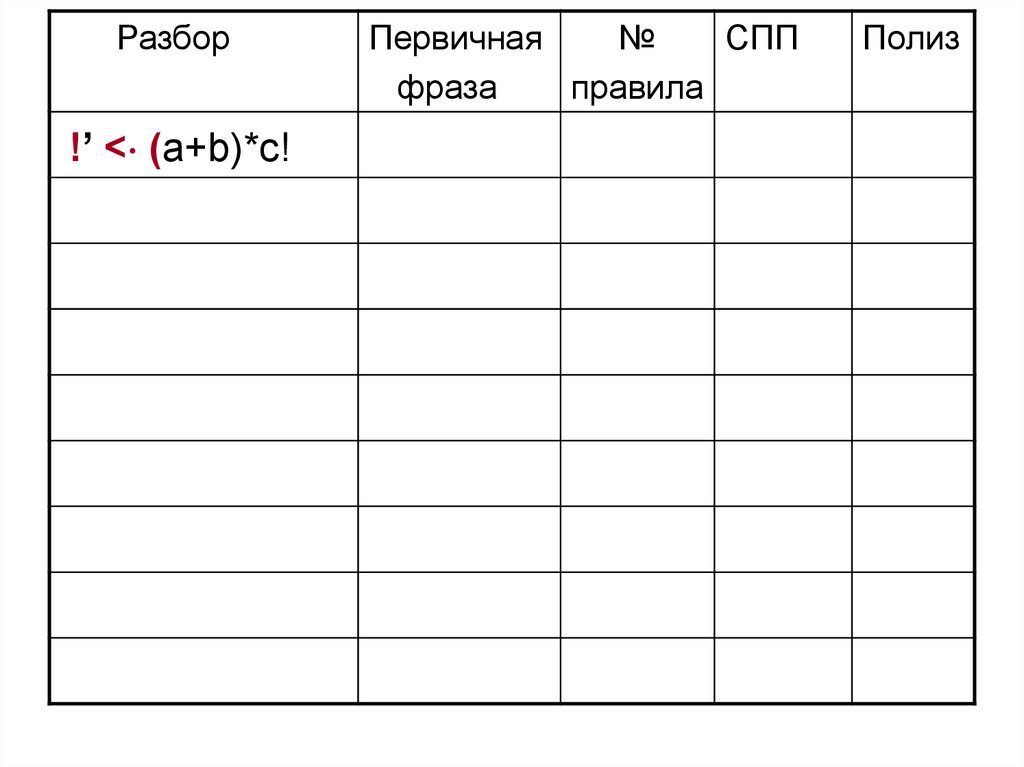
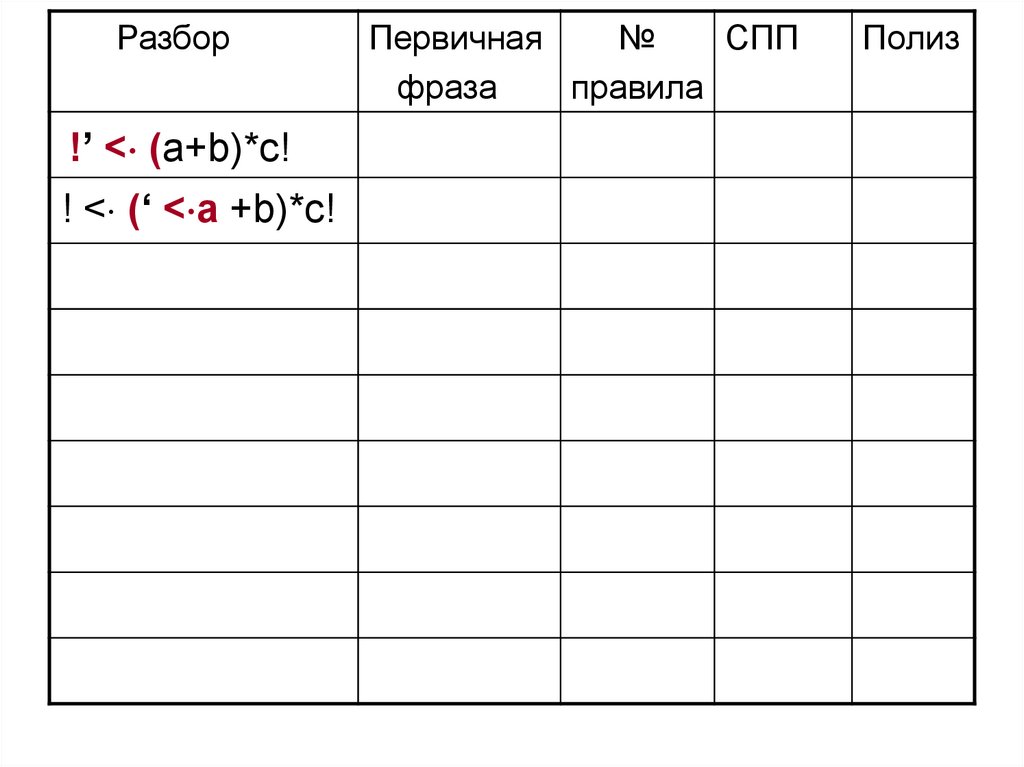
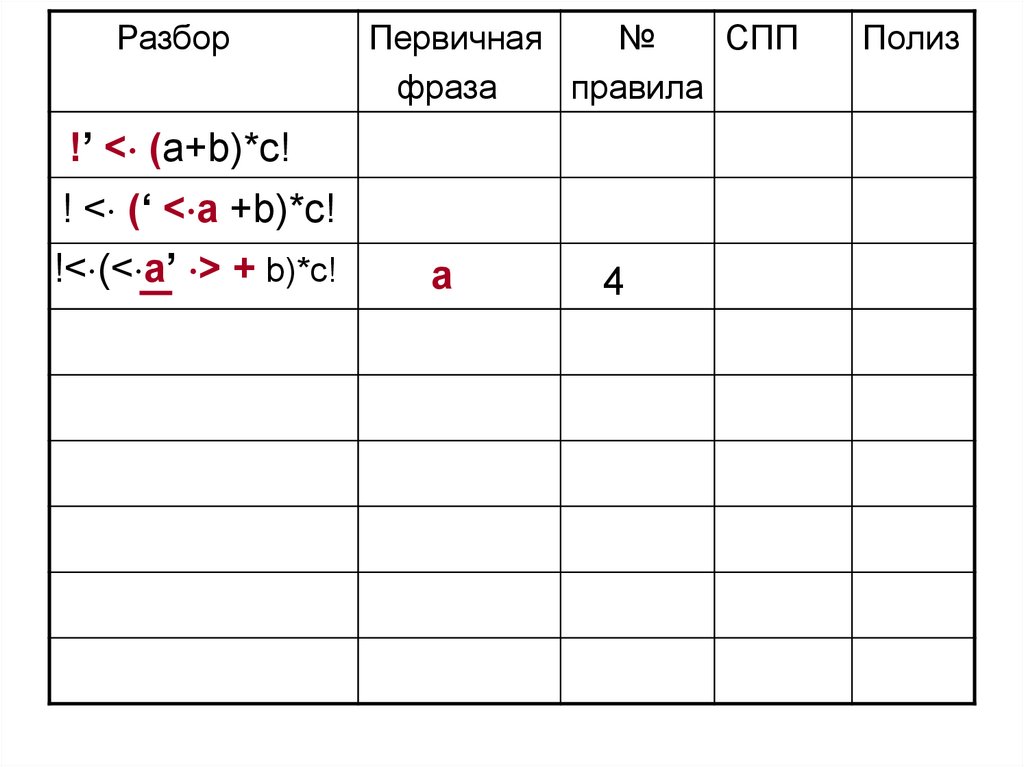
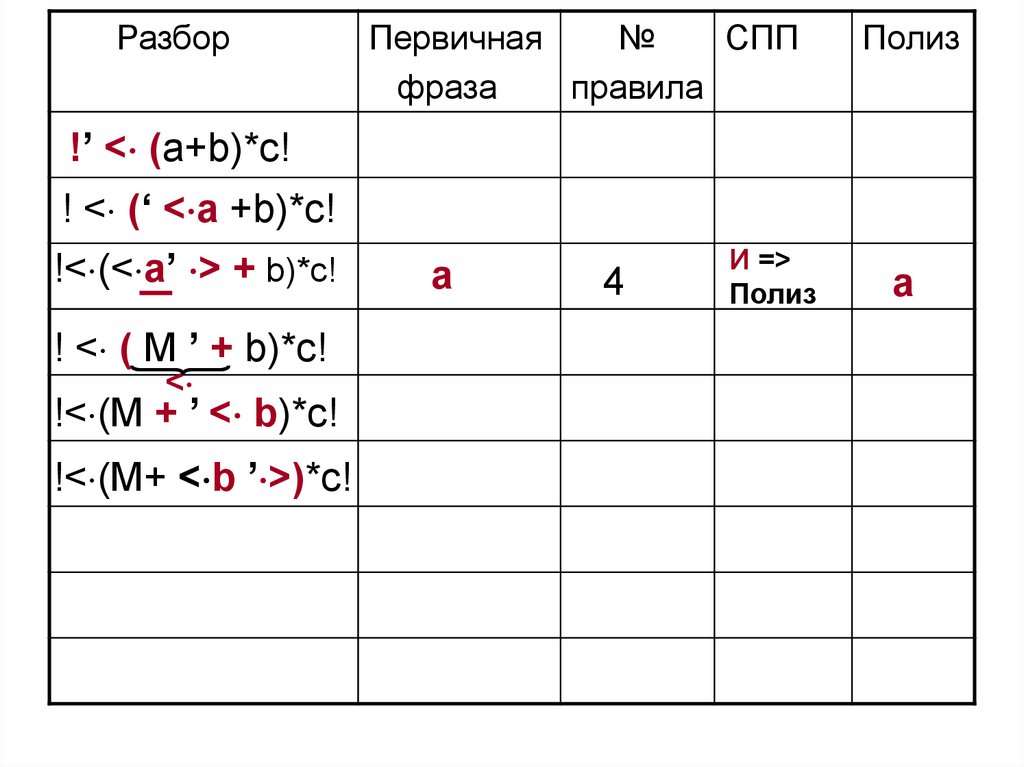
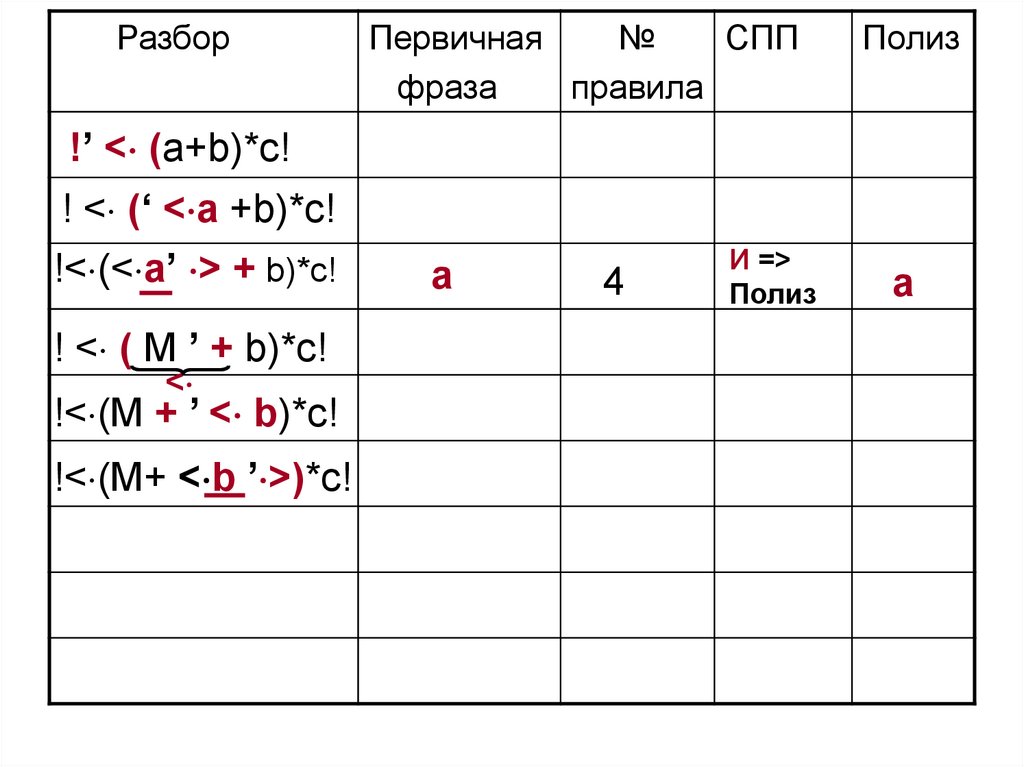
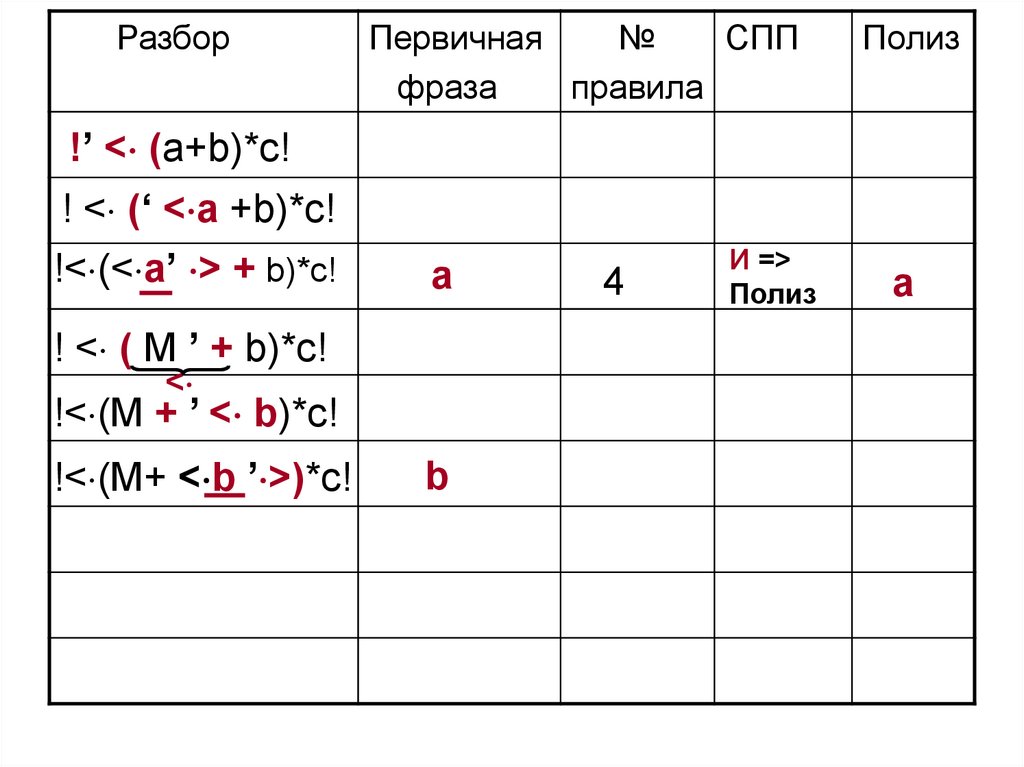
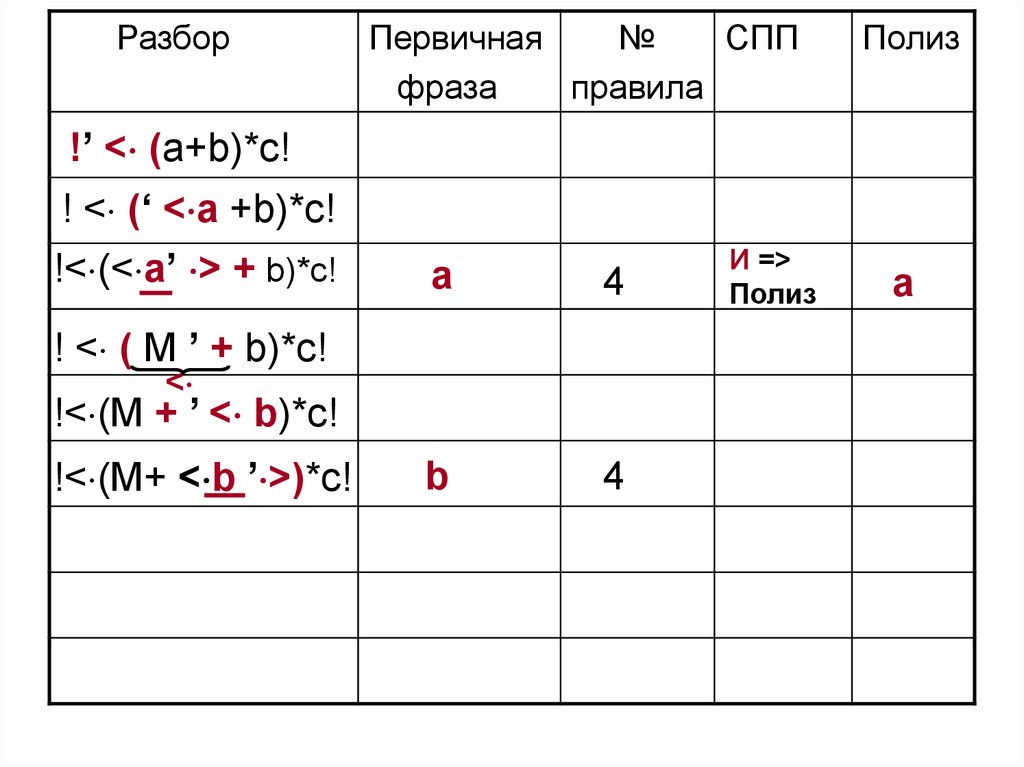
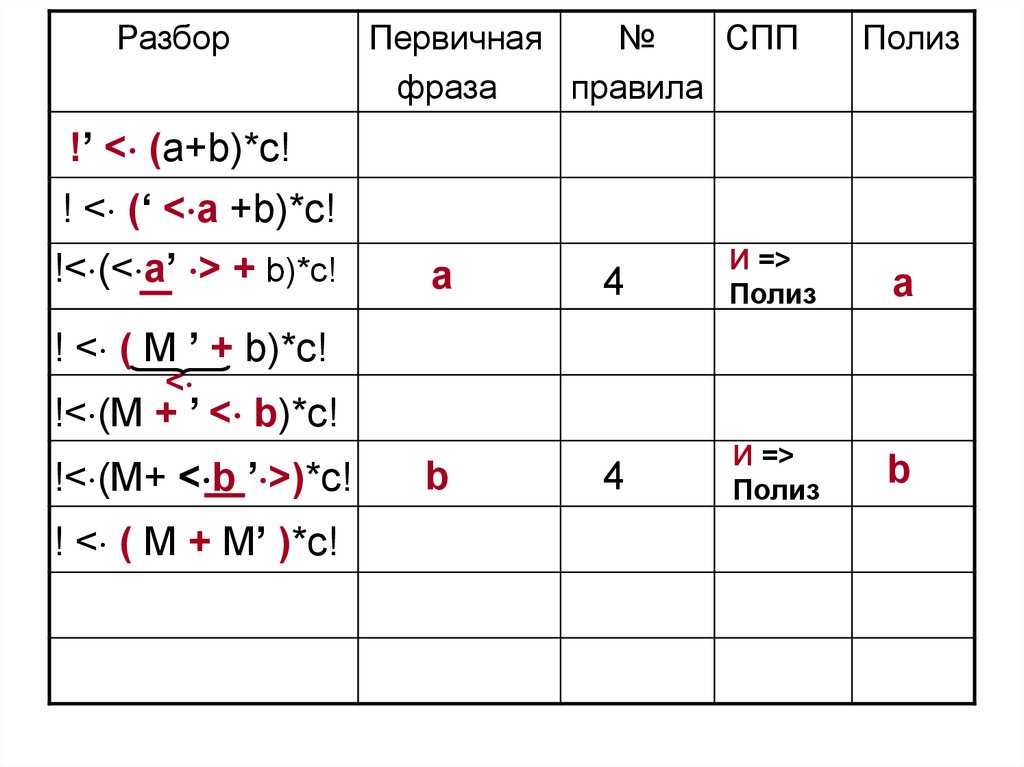
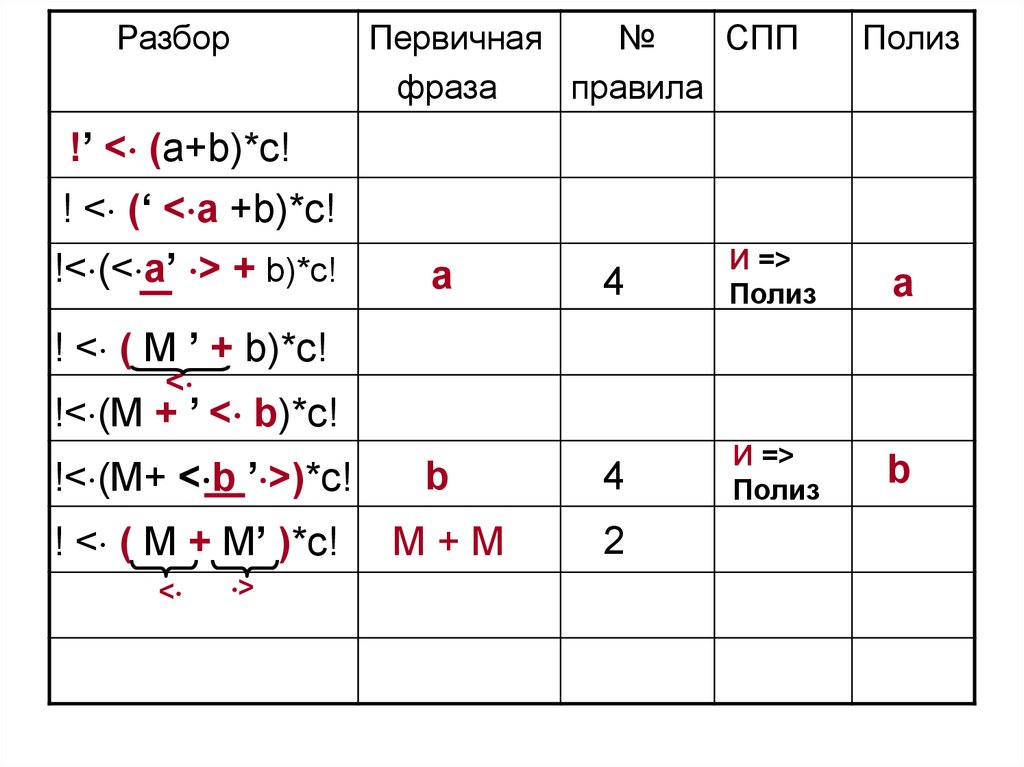
77. 3 этап. Выполним разбор цепочки !(a + b)*c!

Правила поступают на вход распознавателя в
виде
№ правило СПП
1
2
3
4
5
А->!N!
В->N+N +=>Полиз
Т->N*N
*=>Полиз
М->И
И=>Полиз
М->(N)
В первой графе знаком ‘ будем отделять стек от входной
цепочки

78.

Разбор
!’ < (a+b)*c!
Первичная
№
СПП
фраза
правила
Полиз

79.

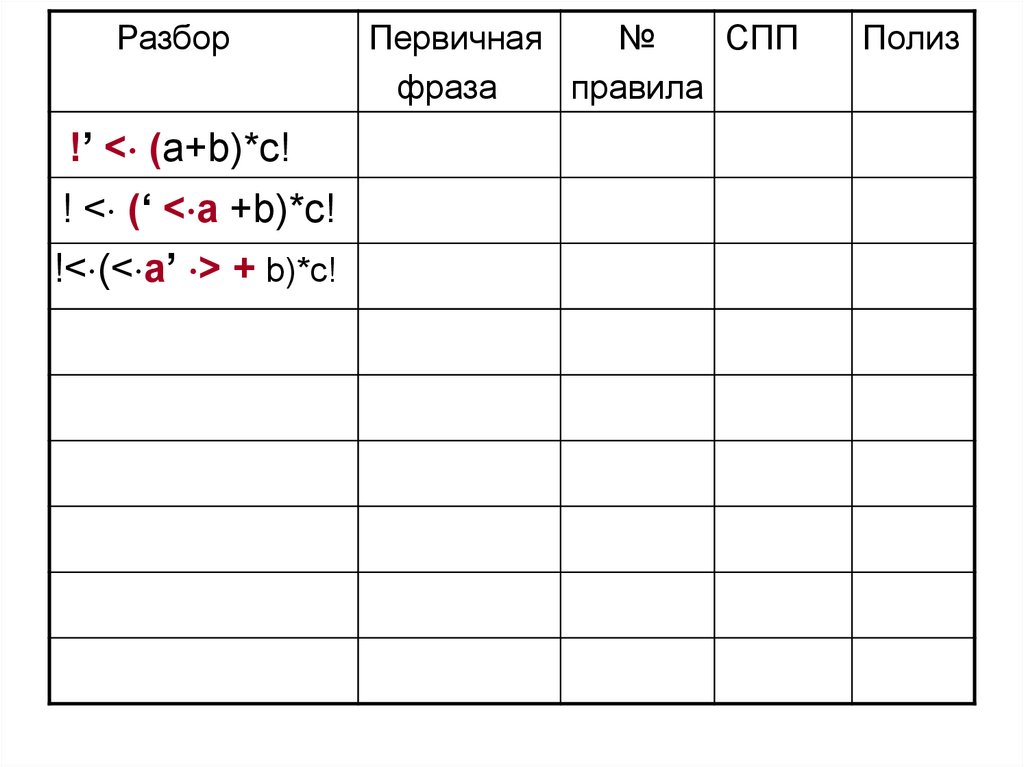
Разбор
!’ < (a+b)*c!
! < (‘ < a +b)*c!
Первичная
№
СПП
фраза
правила
Полиз

80.

Разбор
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
Первичная
№
СПП
фраза
правила
Полиз

81.

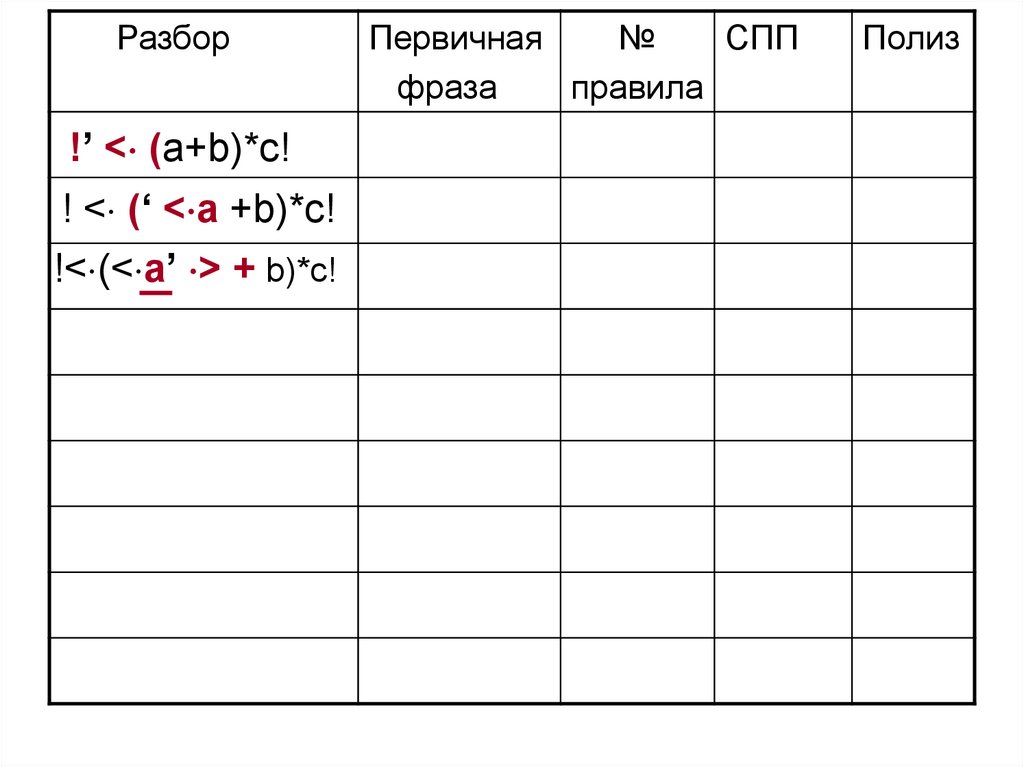
Разбор
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
Первичная
№
СПП
фраза
правила
Полиз

82.

Разбор
Первичная
№
СПП
фраза
правила
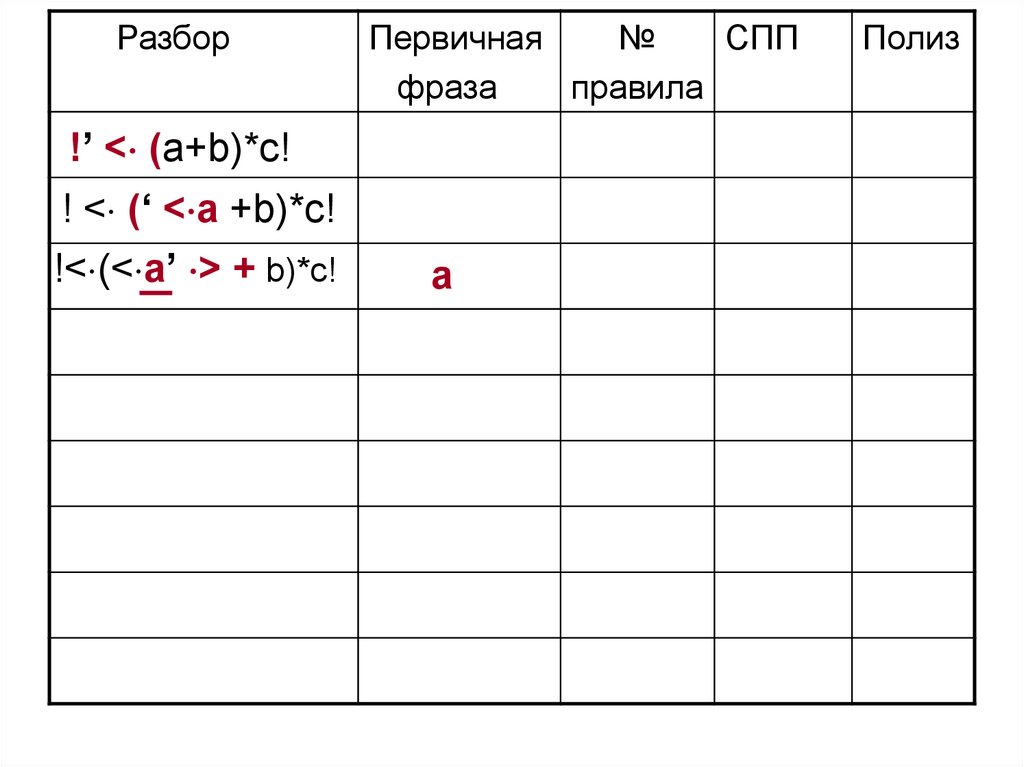
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
Полиз

83.

Разбор
Первичная
№
СПП
фраза
правила
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
Полиз

84.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a

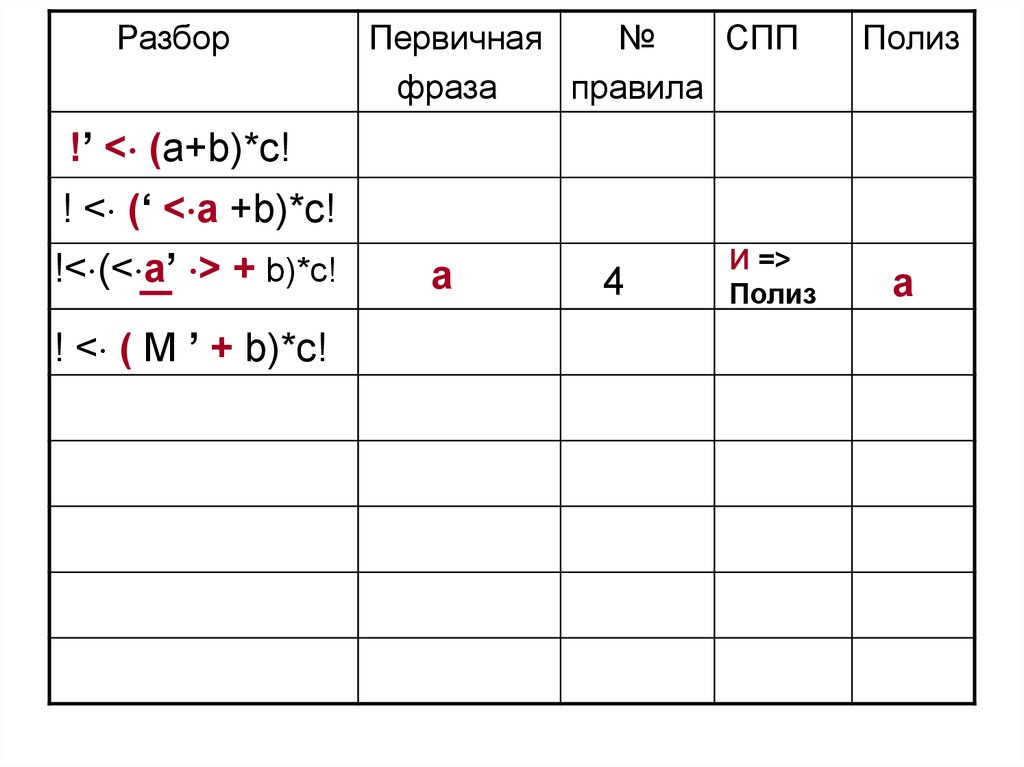
85.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
! < ( M ’ + b)*c!
a
4
И =>
Полиз
a

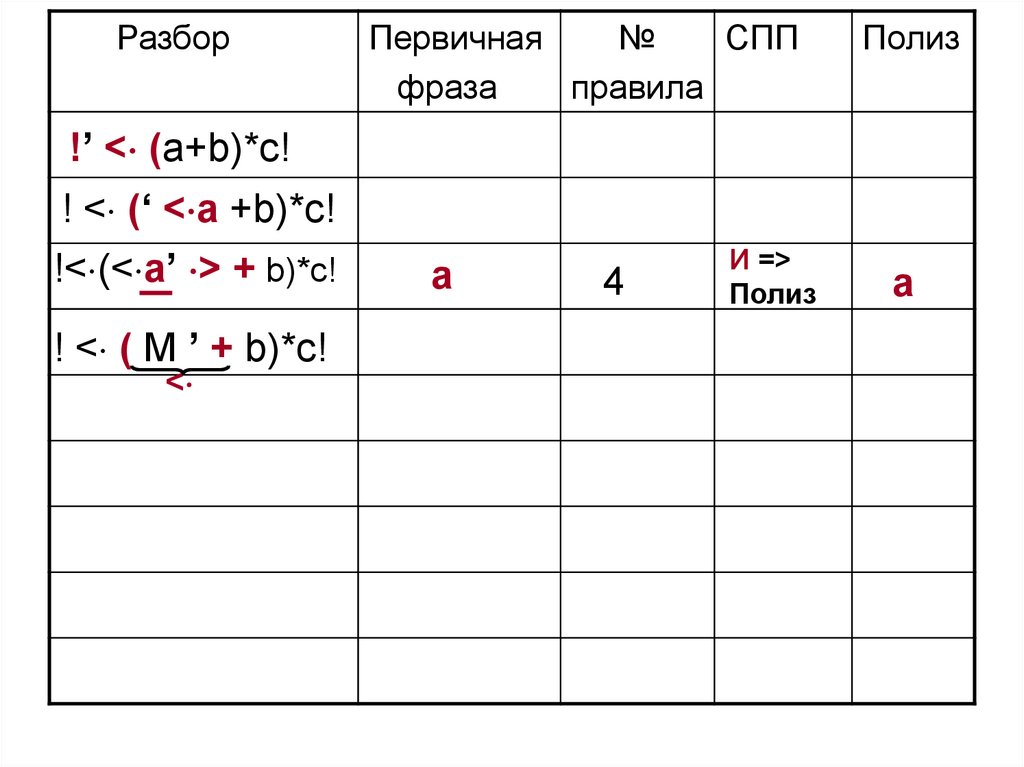
86.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
! < ( M ’ + b)*c!
<
a
4
И =>
Полиз
a

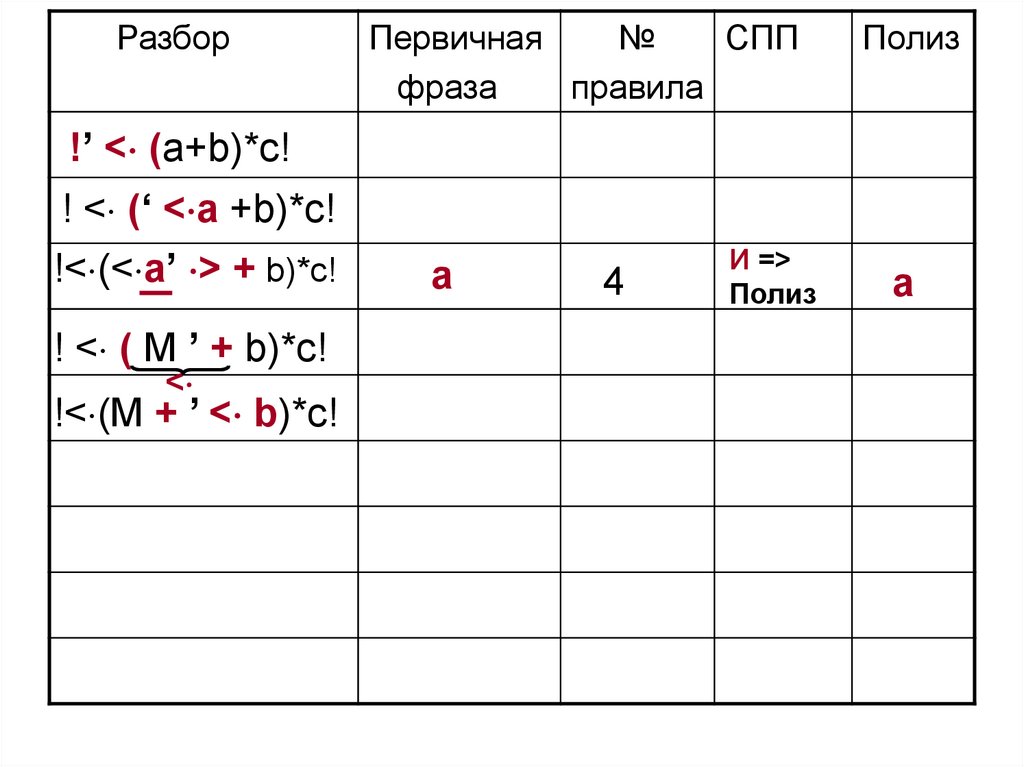
87.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
a
4
И =>
Полиз
a

88.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
a
4
И =>
Полиз
a

89.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
a
4
И =>
Полиз
a

90.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
4
И =>
Полиз
a

91.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
b
4
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
И =>
Полиз
a

92.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
4
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b

93.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
4
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
! < ( M + M’ )*c!
b

94.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
4
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
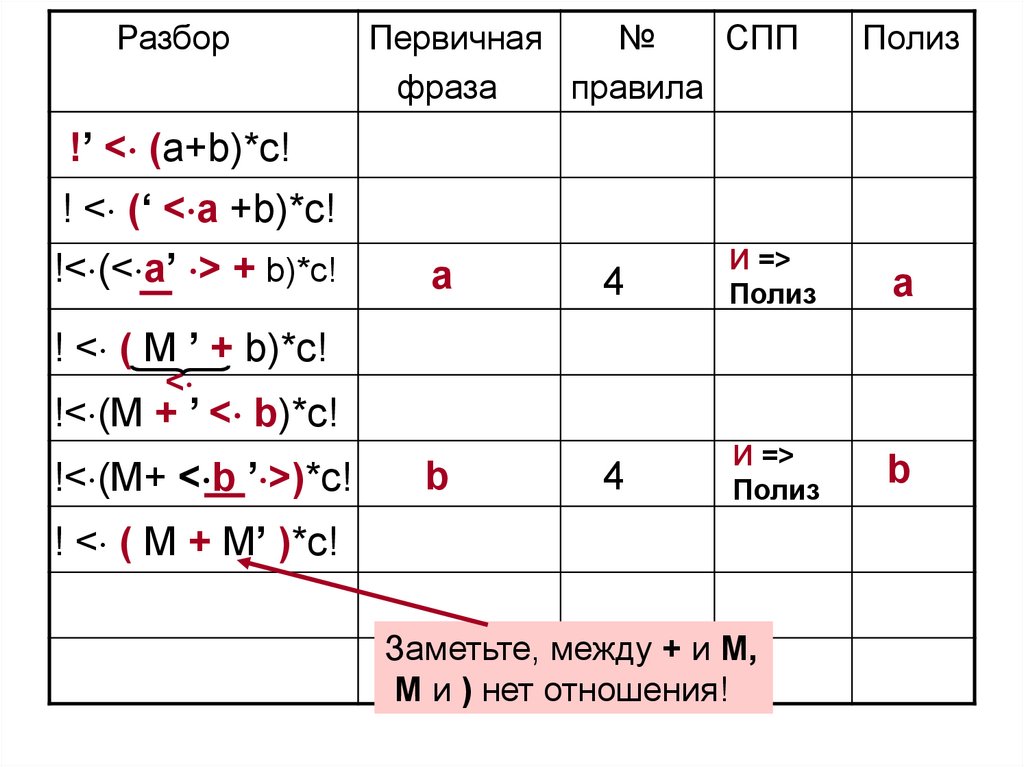
! < ( M + M’ )*c!
Заметьте, между + и М,
М и ) нет отношения!

95.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
4
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
! < ( M + M’ )*c!
<
>
b

96.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
4
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
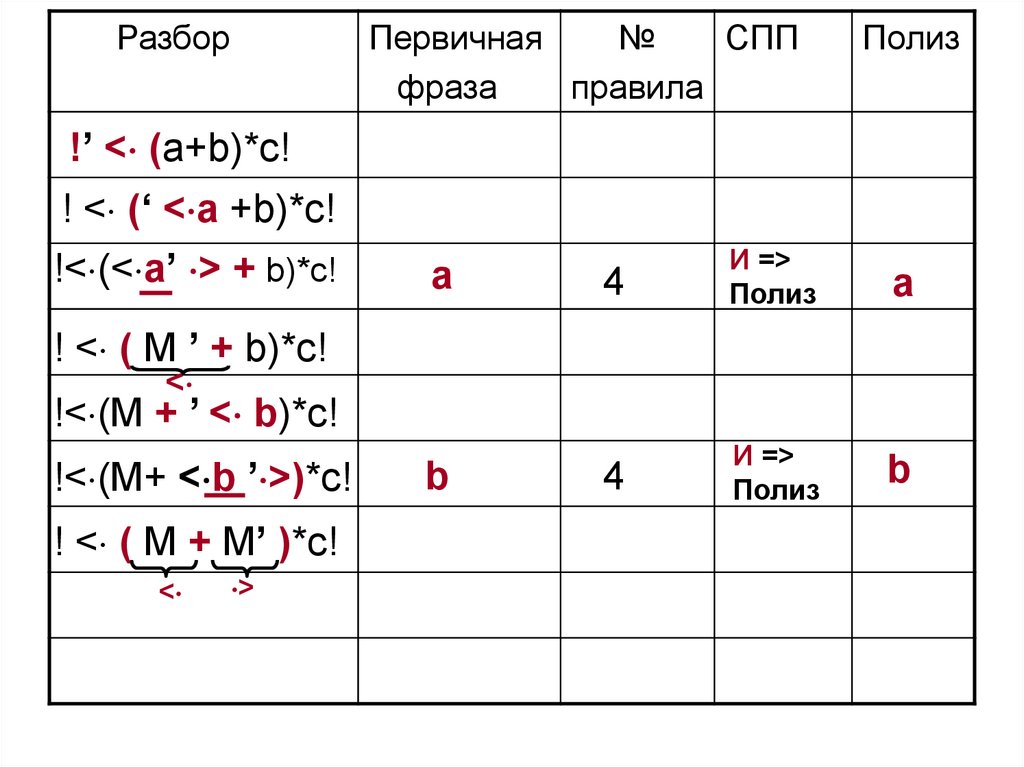
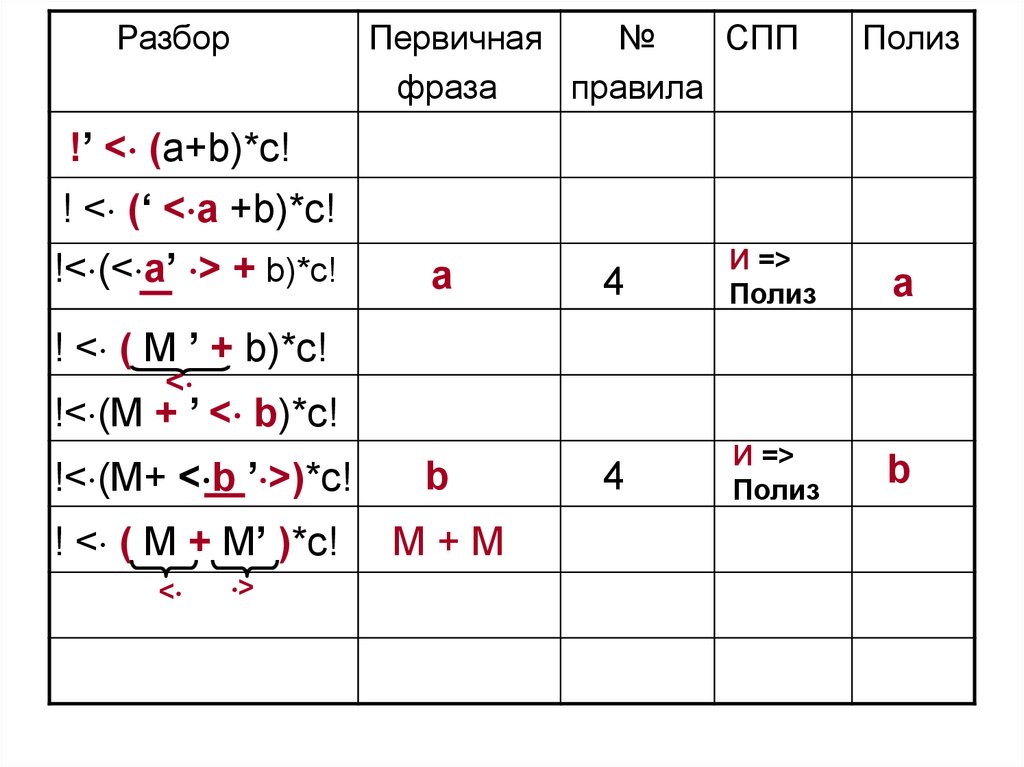
! < ( M + M’ )*c!
М+М
<
>

97.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
И =>
Полиз
b
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
4
! < ( M + M’ )*c!
М+М
2
<
>

98.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
4
! < ( M + M’ )*c!
М+М
2
<
>
И =>
Полиз
+=>
Полиз
b
+

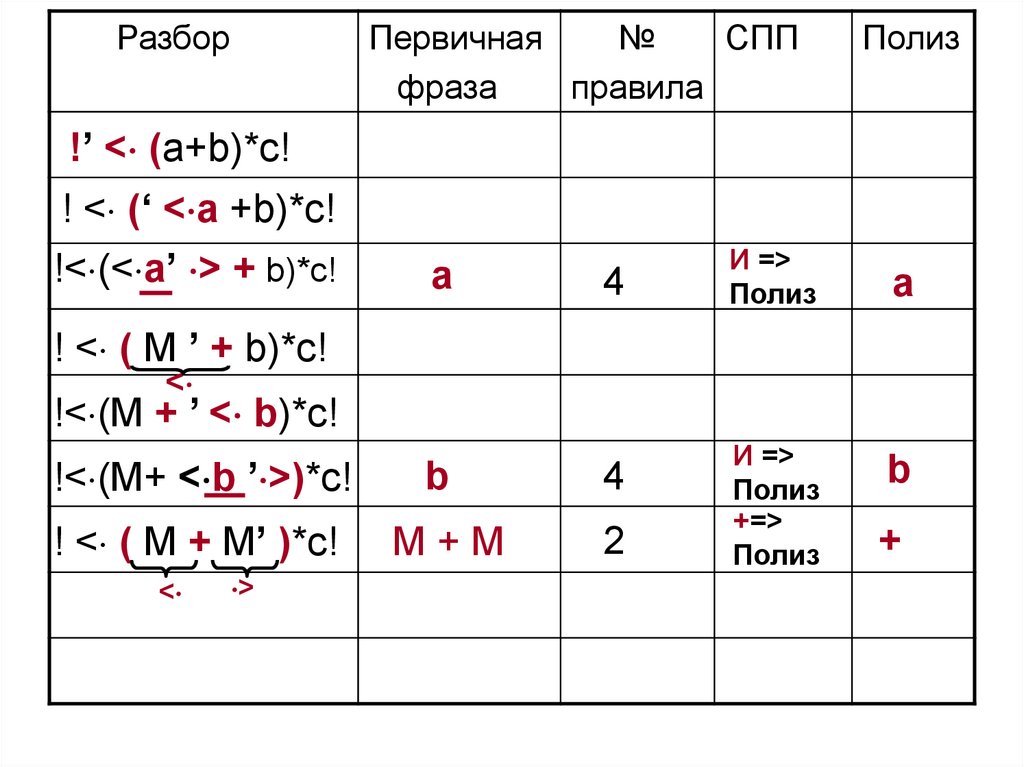
99.

Разбор
Первичная
№
СПП
фраза
правила
Полиз
!’ < (a+b)*c!
! < (‘ < a +b)*c!
!< (< a’ > + b)*c!
a
4
И =>
Полиз
a
! < ( M ’ + b)*c!
<
!< (M + ’ < b)*c!
!< (M+ < b ’ >)*c!
b
4
! < ( M + M’ )*c!
М+М
2
<
>
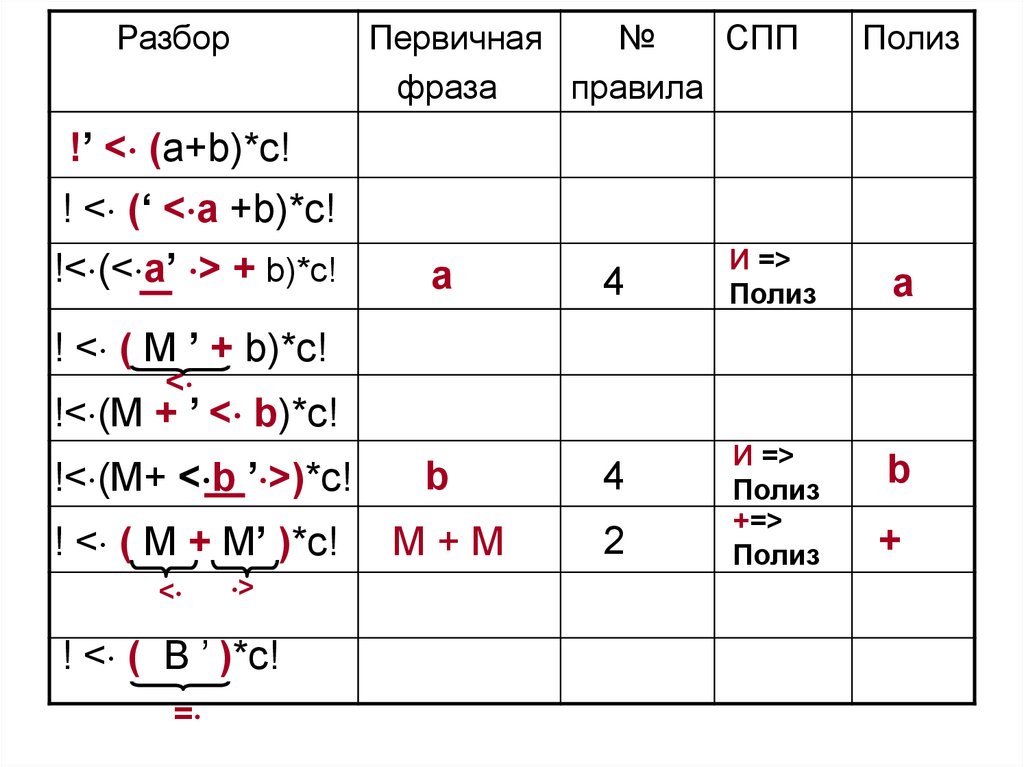
! < ( B ’ )*c!
=
И =>
Полиз
+=>
Полиз
b
+

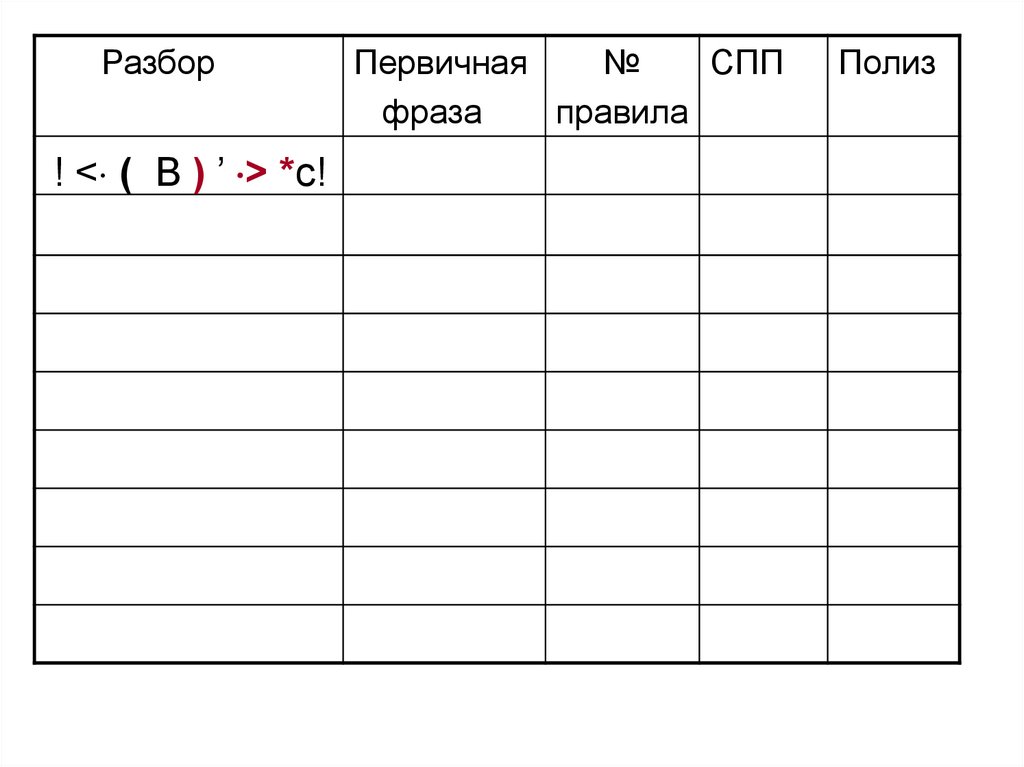
100.

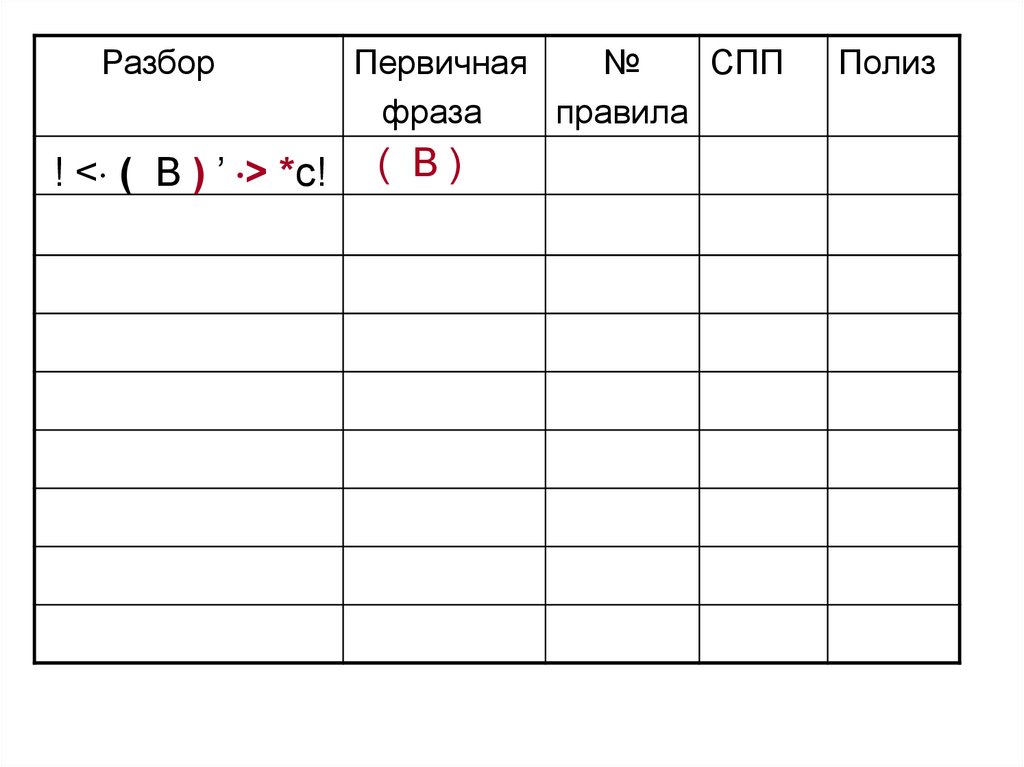
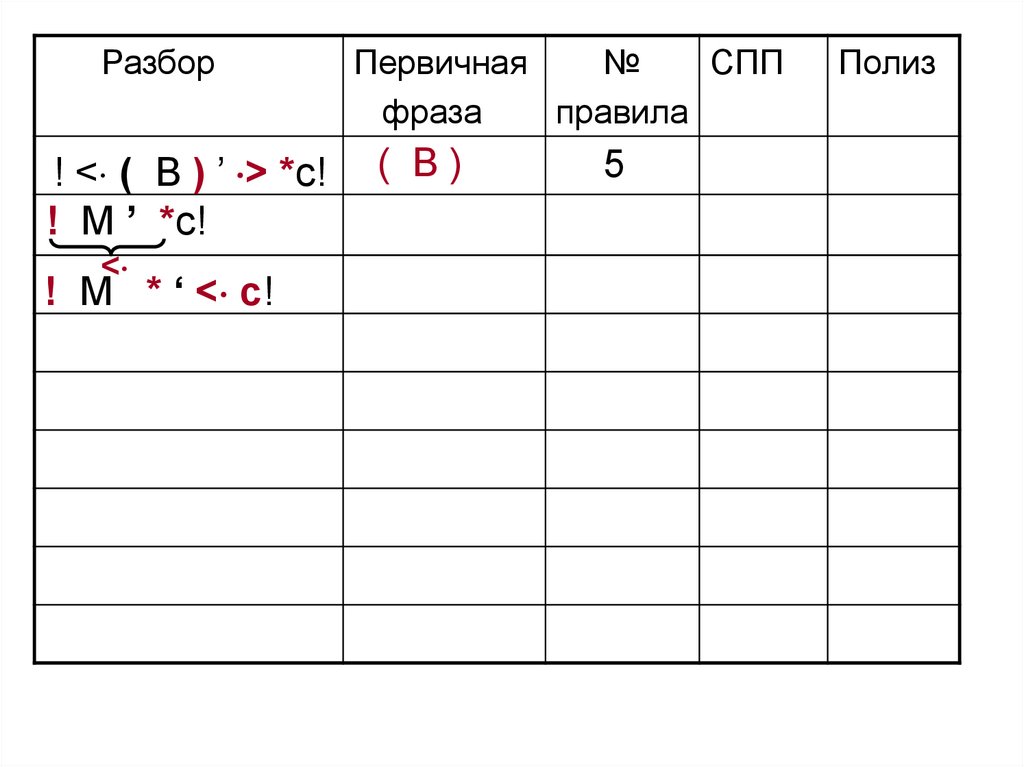
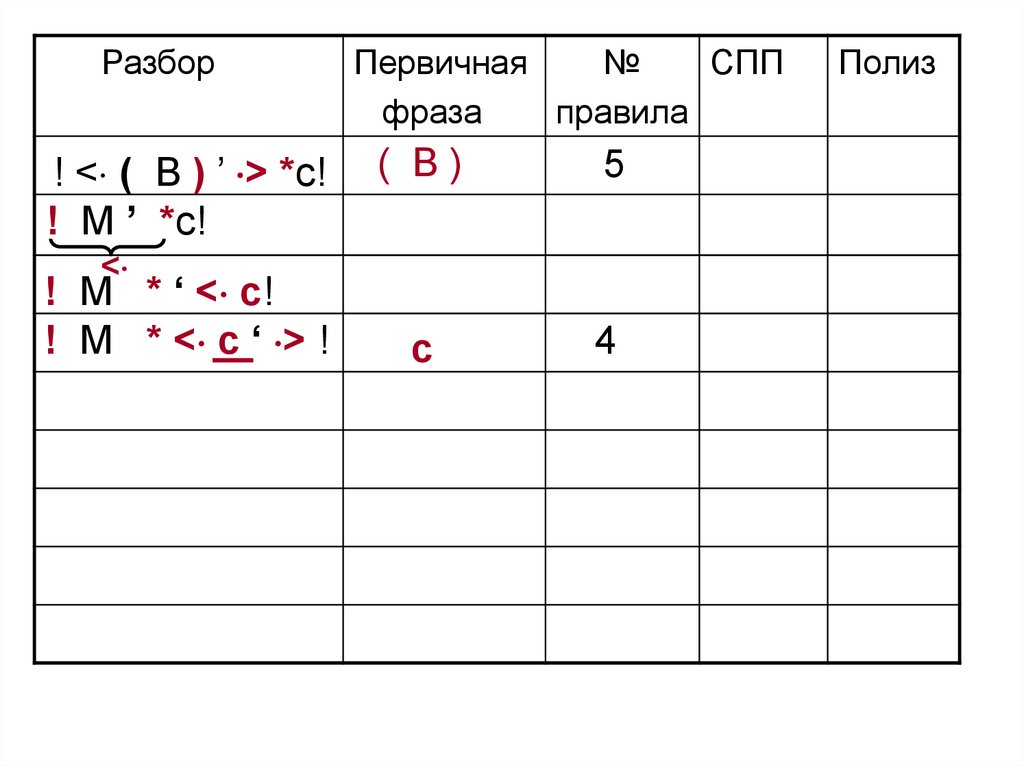
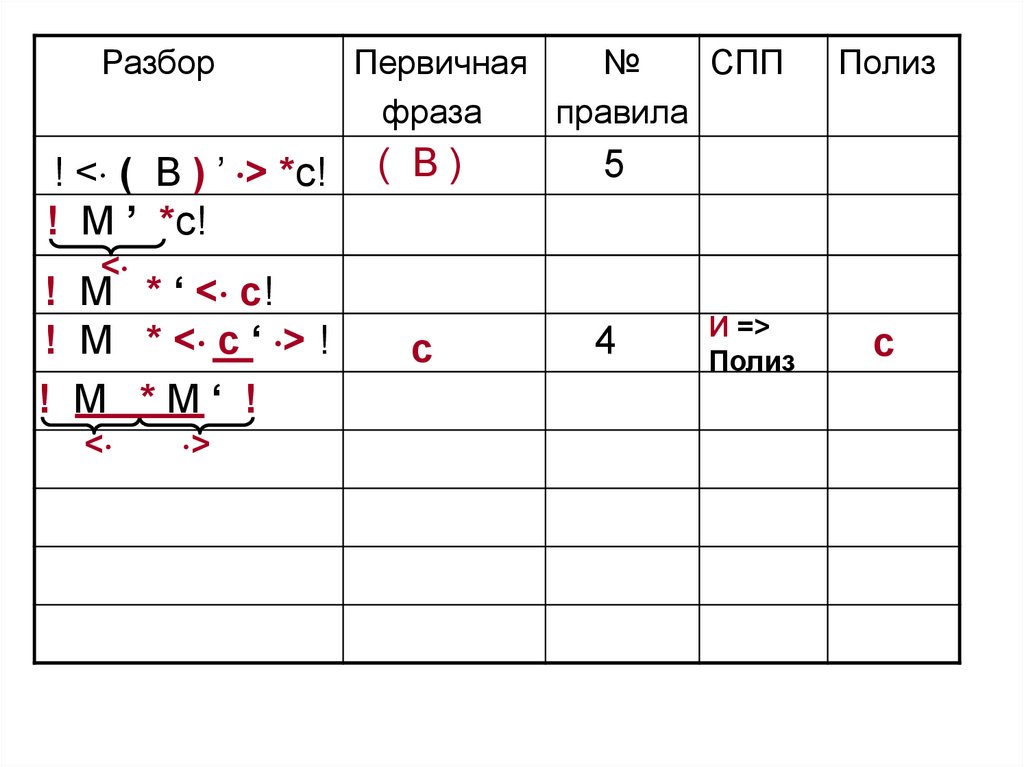
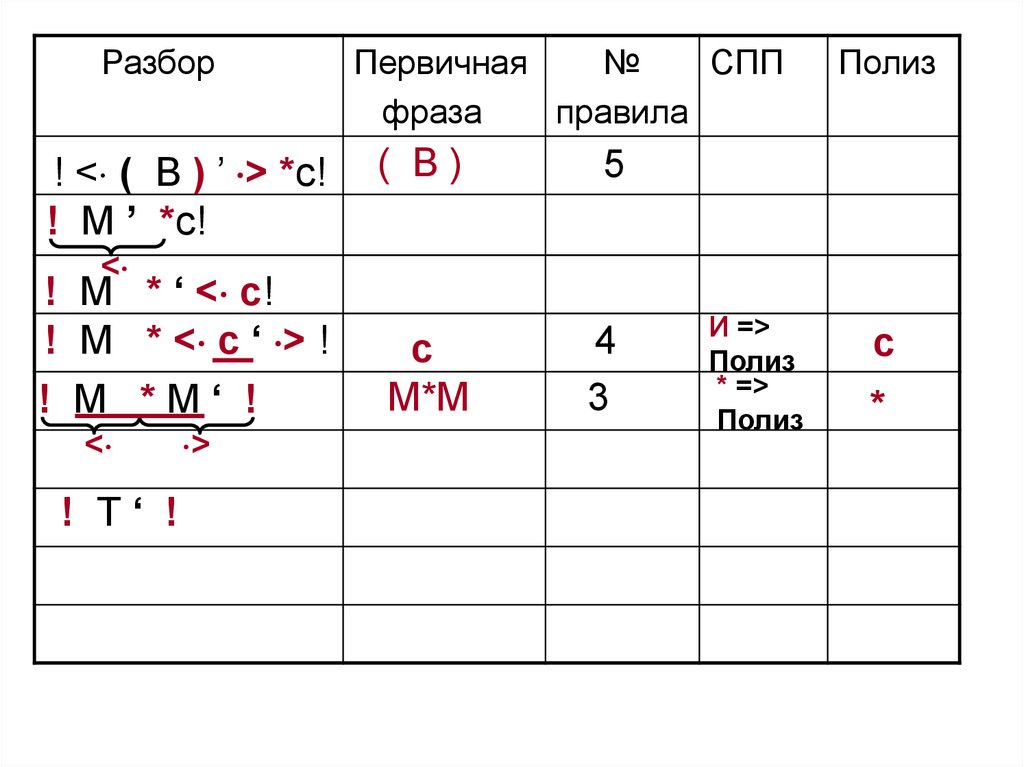
Разбор
! < ( B ) ’ > *c!
Первичная
№
СПП
фраза
правила
Полиз

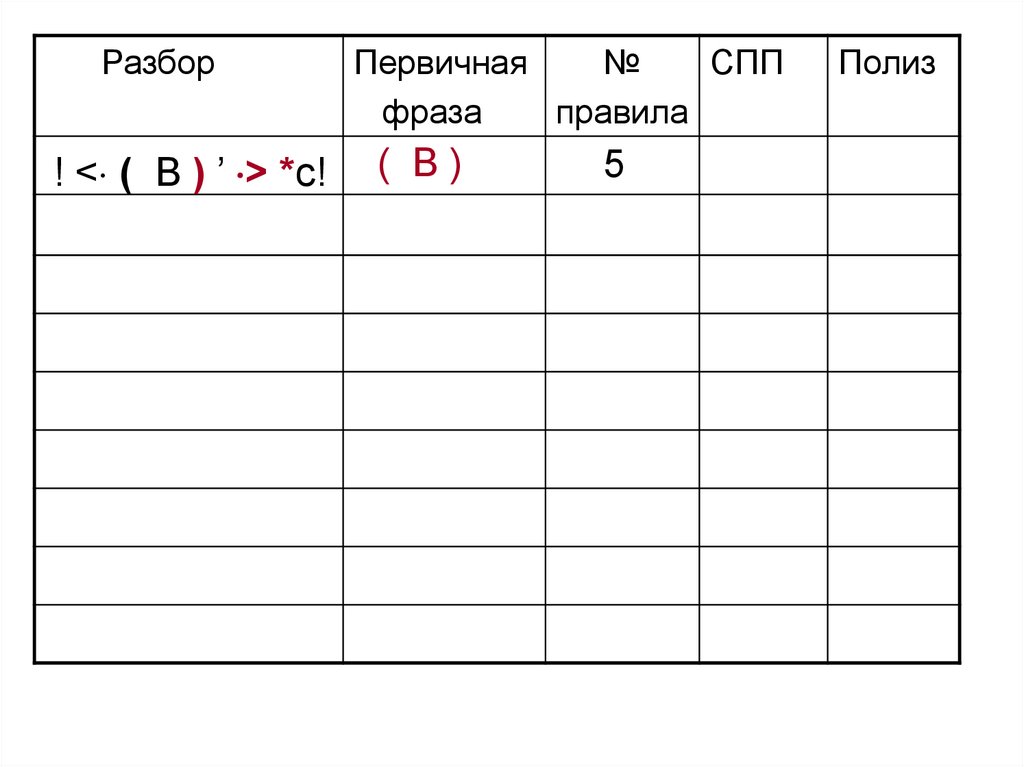
101.

Разбор
! < ( B ) ’ > *c!
Первичная
№
СПП
фраза
правила
( B)
Полиз

102.

Разбор
! < ( B ) ’ > *c!
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

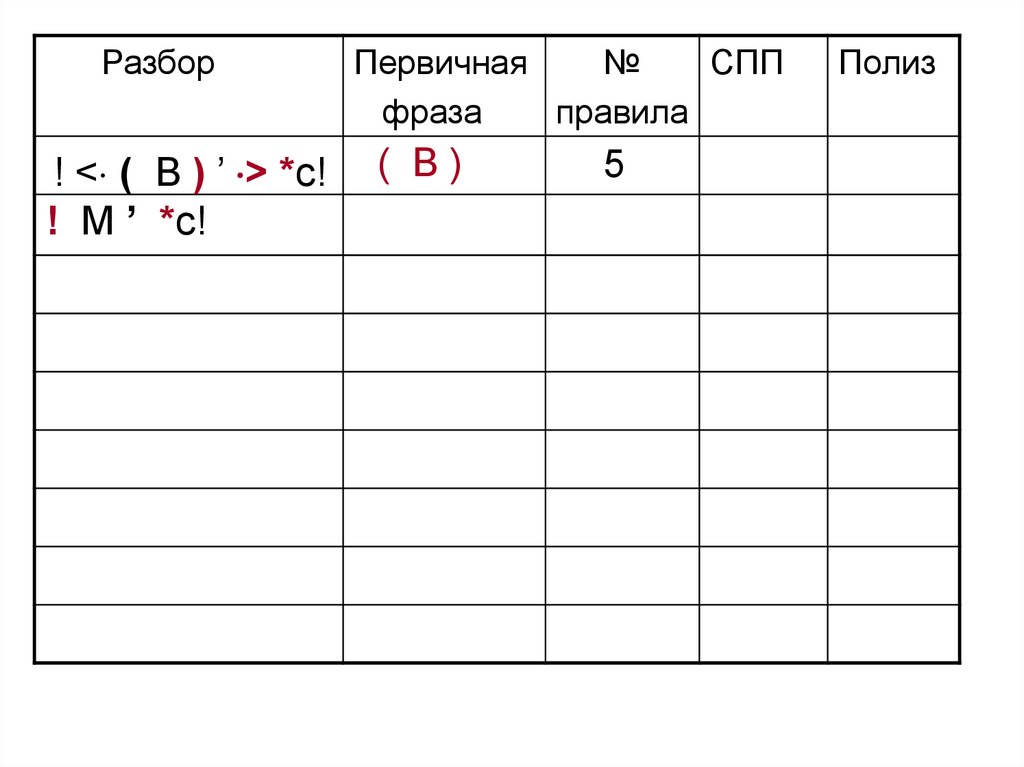
103.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

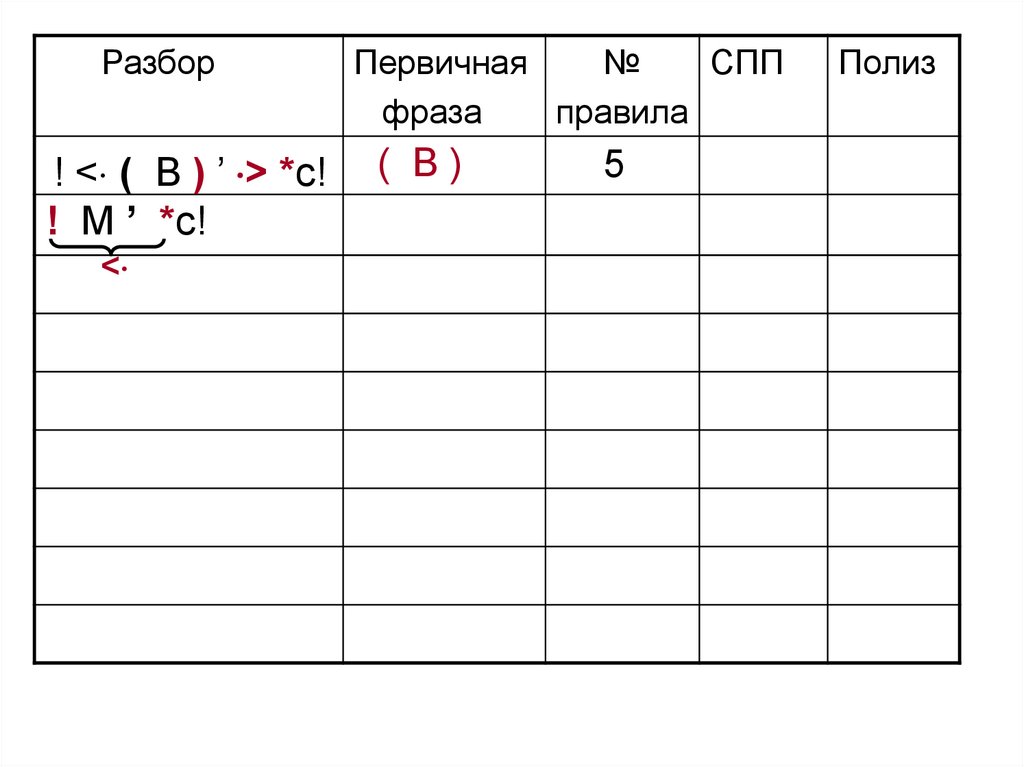
104.

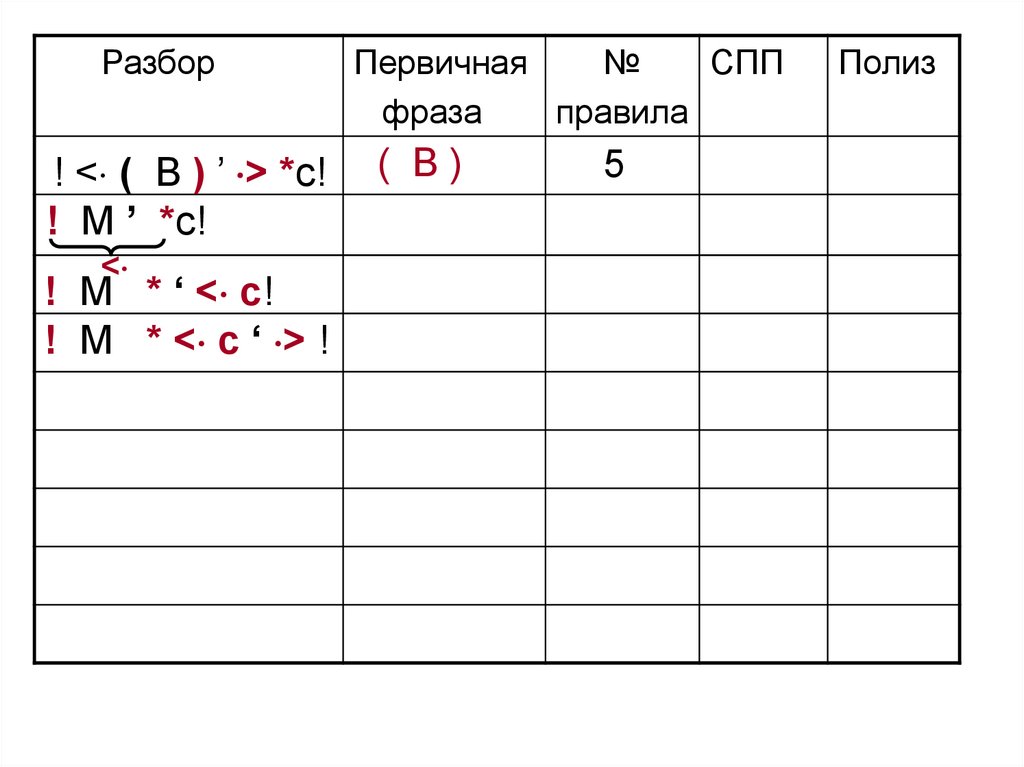
Разбор
! < ( B ) ’ > *c!
! M ’ *c!
<
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

105.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
<
! M * ‘ < c!
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

106.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
<
! M * ‘ < c!
! M * < c ‘ > !
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

107.

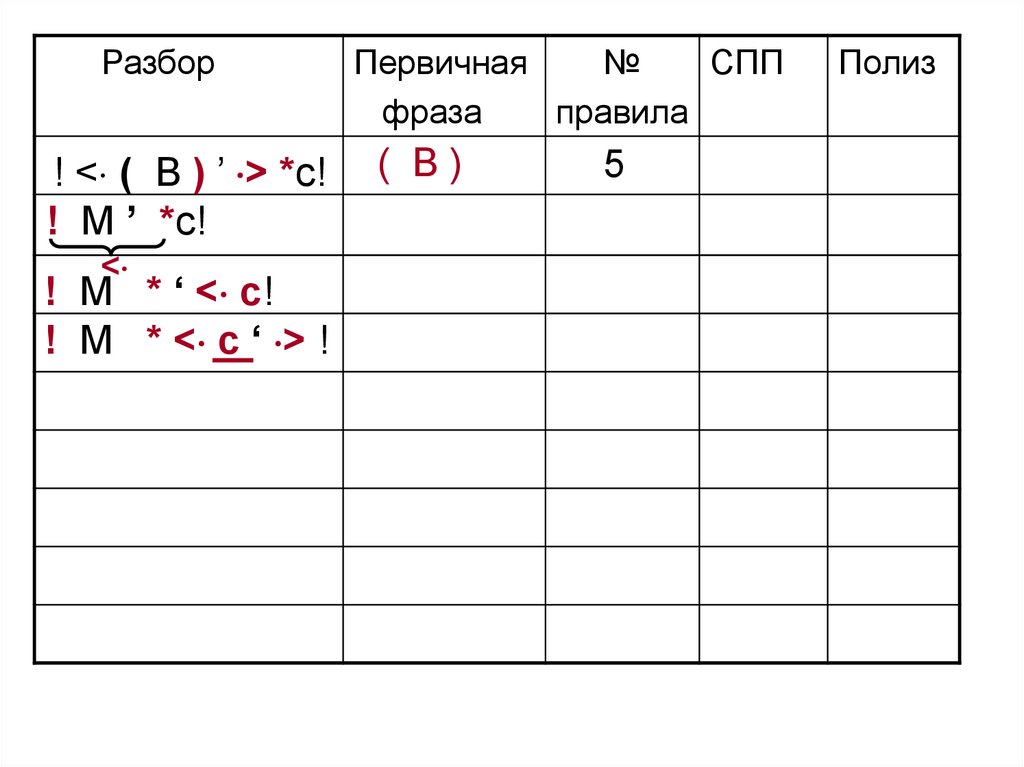
Разбор
! < ( B ) ’ > *c!
! M ’ *c!
<
! M * ‘ < c!
! M * < c ‘ > !
Первичная
№
СПП
фраза
правила
( B)
5
Полиз

108.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
<
! M * ‘ < c!
! M * < c ‘ > !
c
5
Полиз

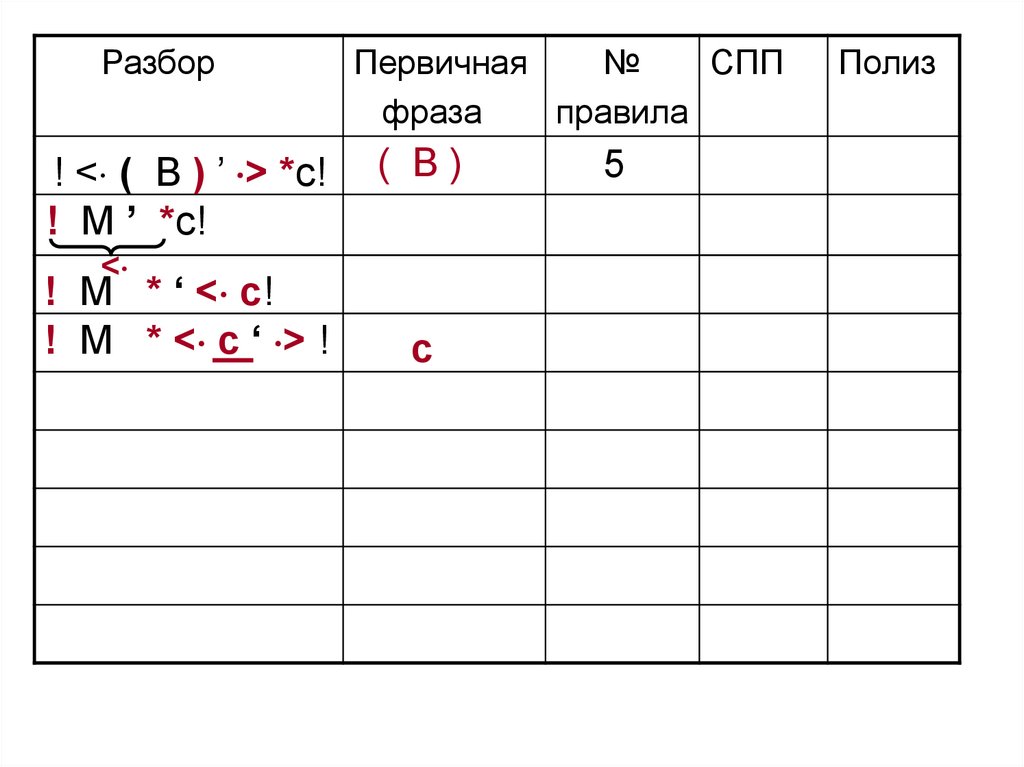
109.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
4
<
! M * ‘ < c!
! M * < c ‘ > !
Полиз

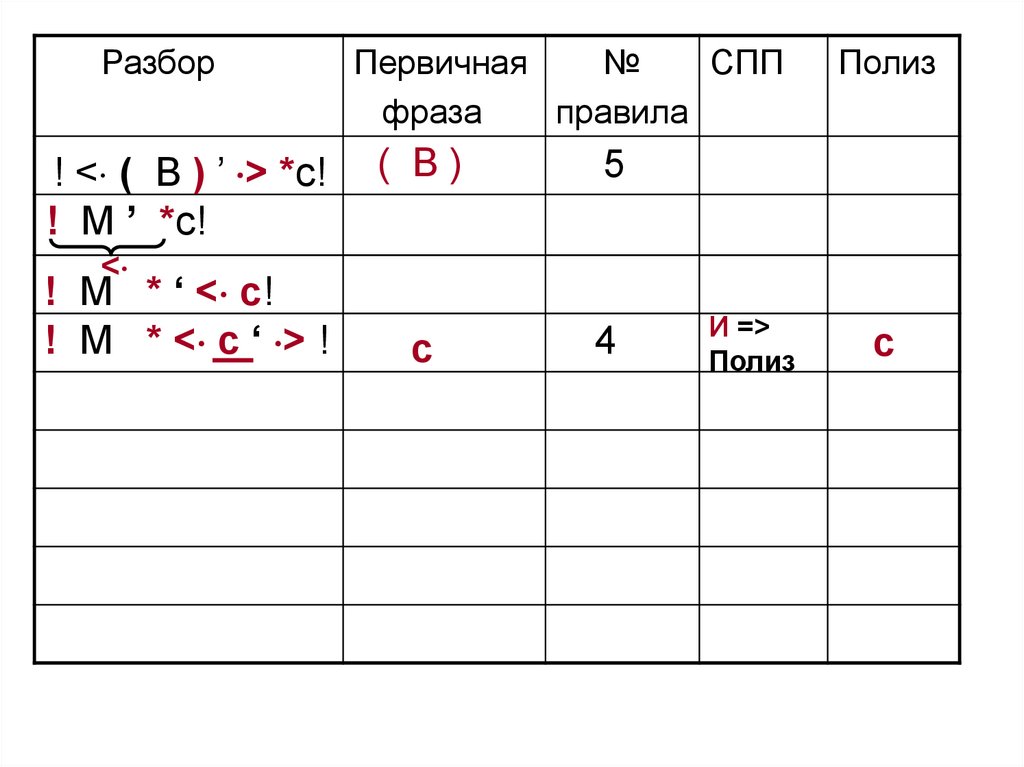
110.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
4
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
И =>
Полиз
c

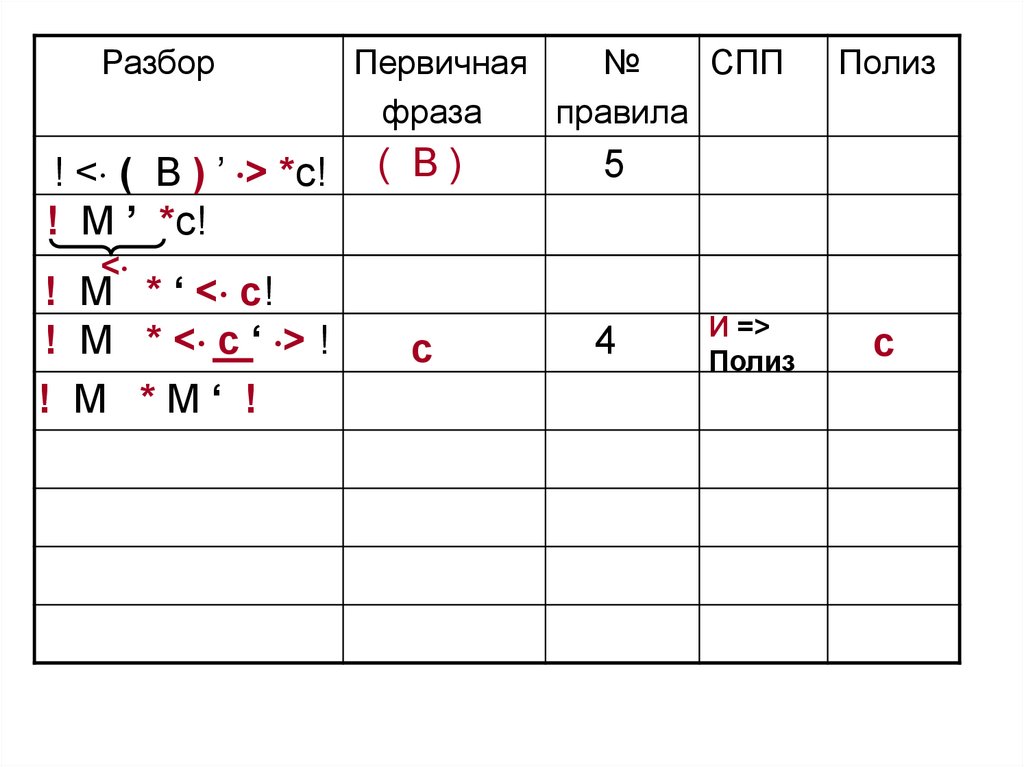
111.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
4
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
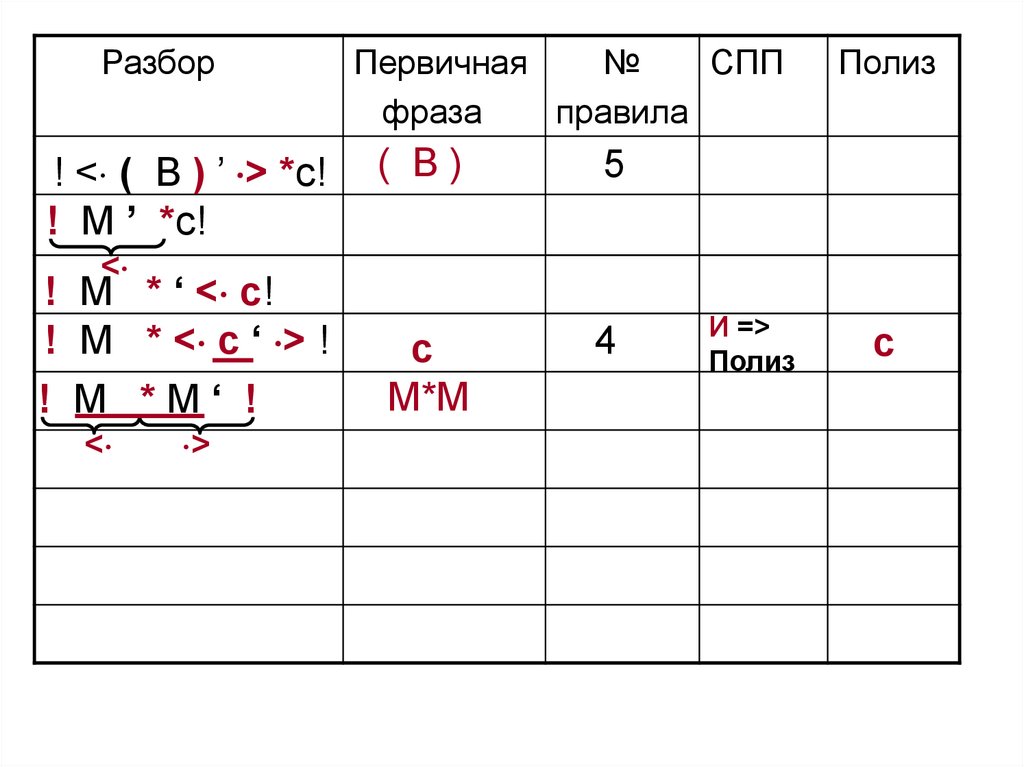
! M *М‘ !
И =>
Полиз
c

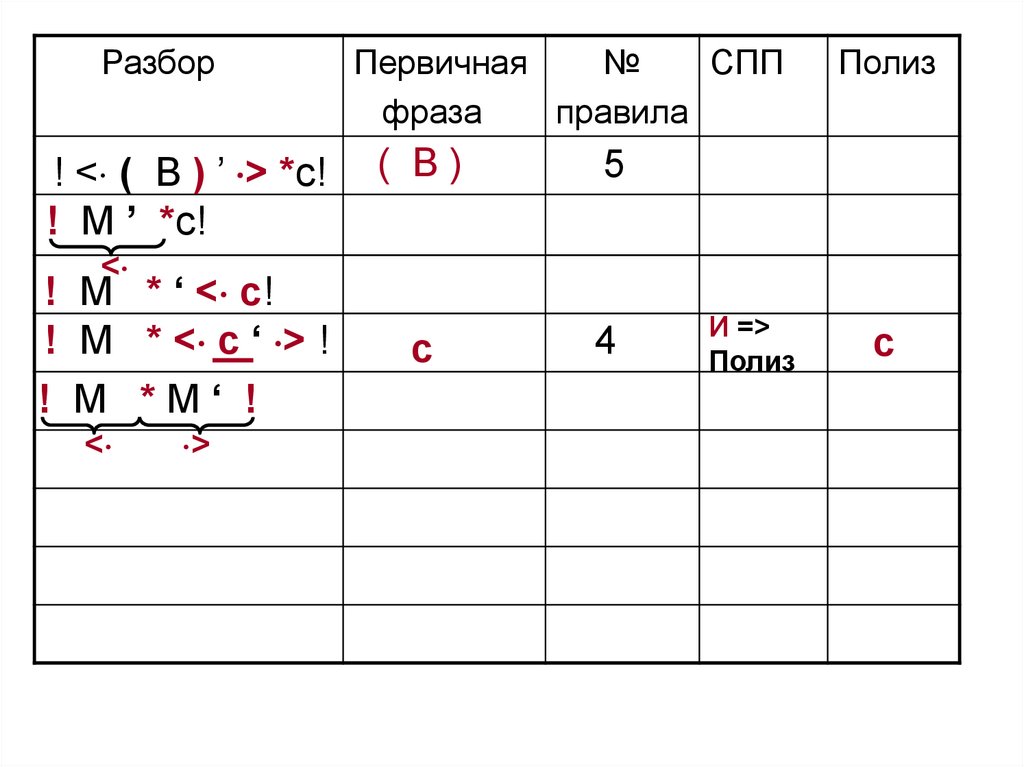
112.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
4
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
c

113.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
4
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
c

114.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
c

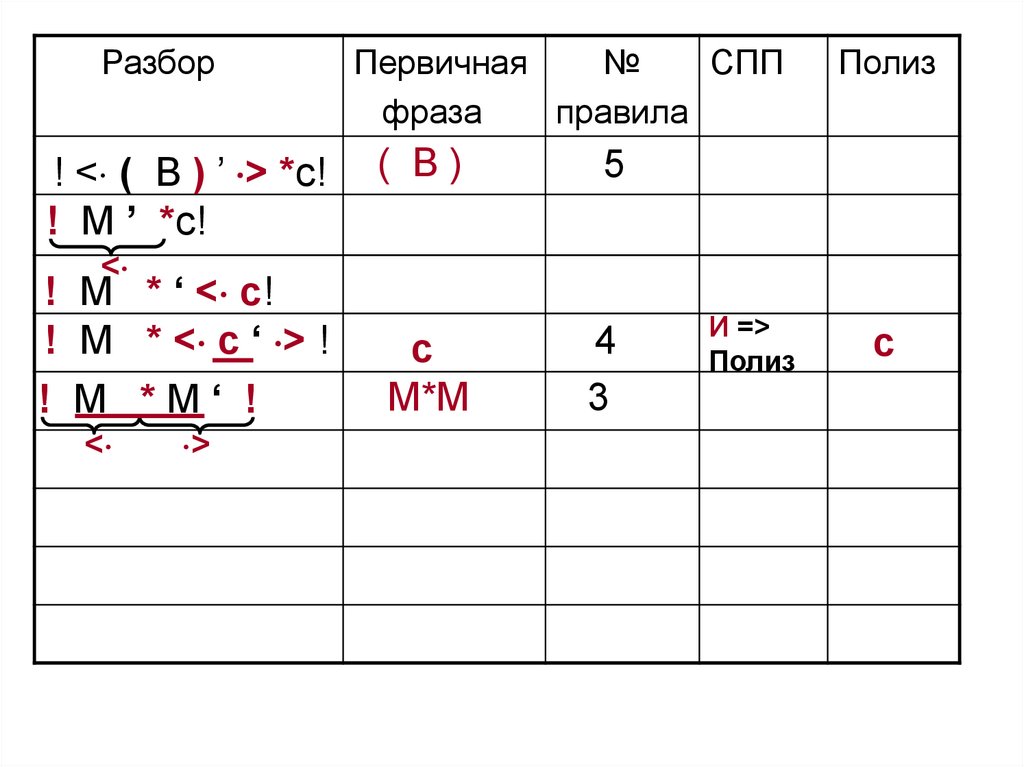
115.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
c

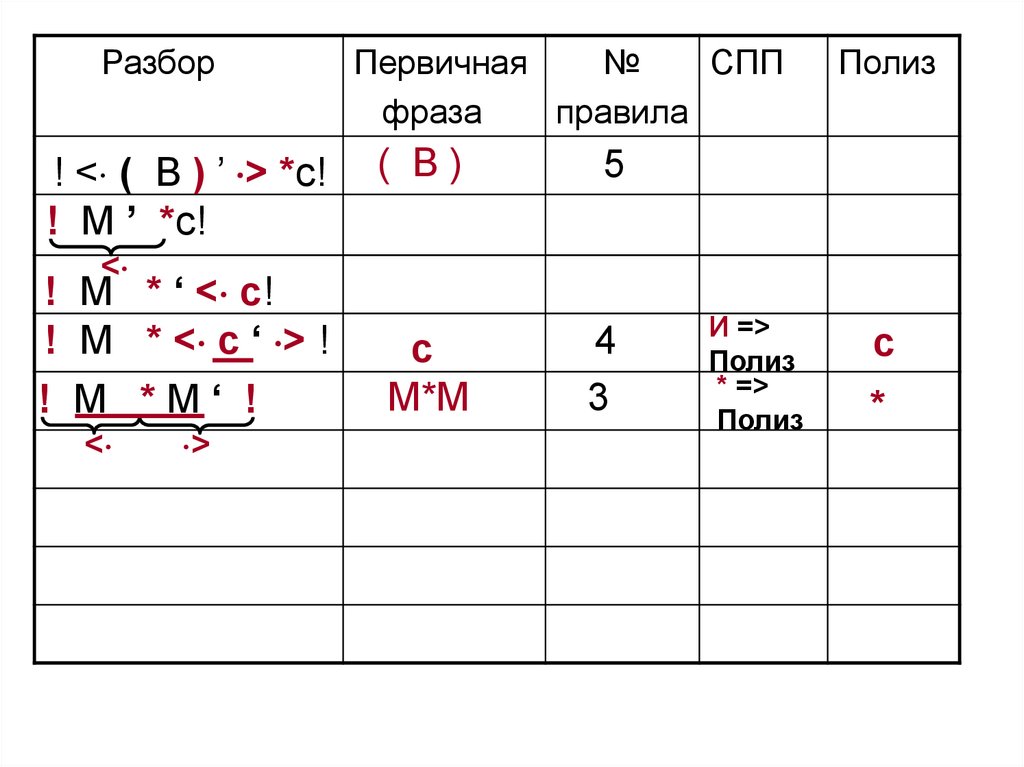
116.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
* =>
Полиз
c
*

117.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
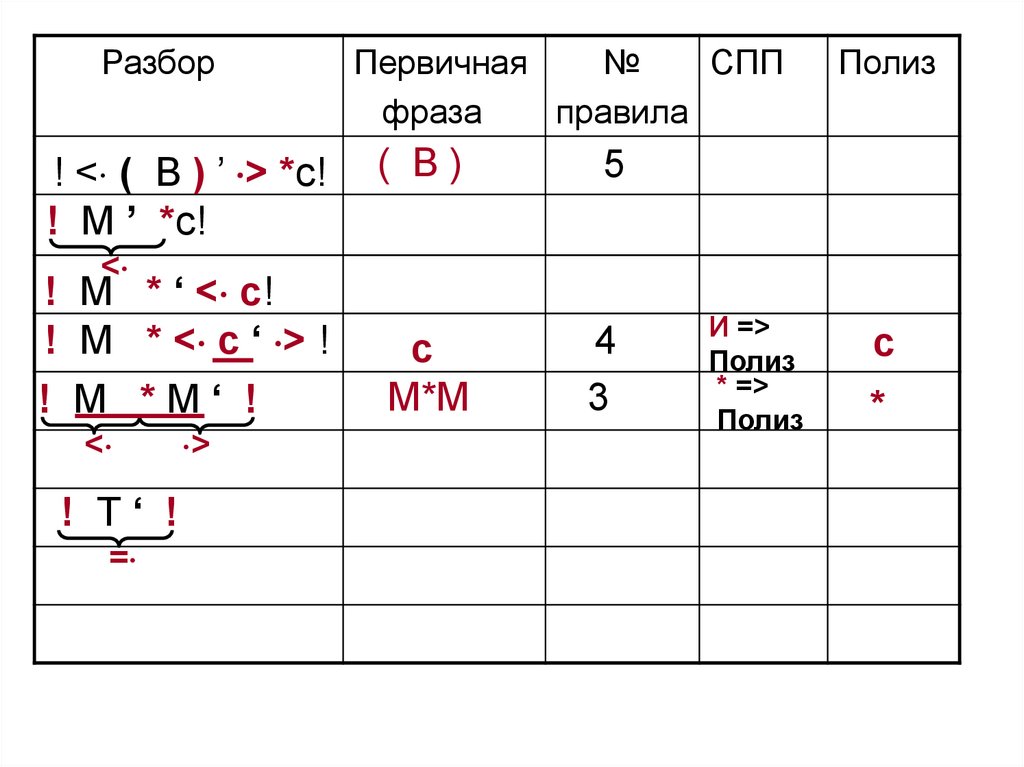
! Т‘ !
>
И =>
Полиз
* =>
Полиз
c
*

118.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
! Т‘ !
=
>
И =>
Полиз
* =>
Полиз
c
*

119.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
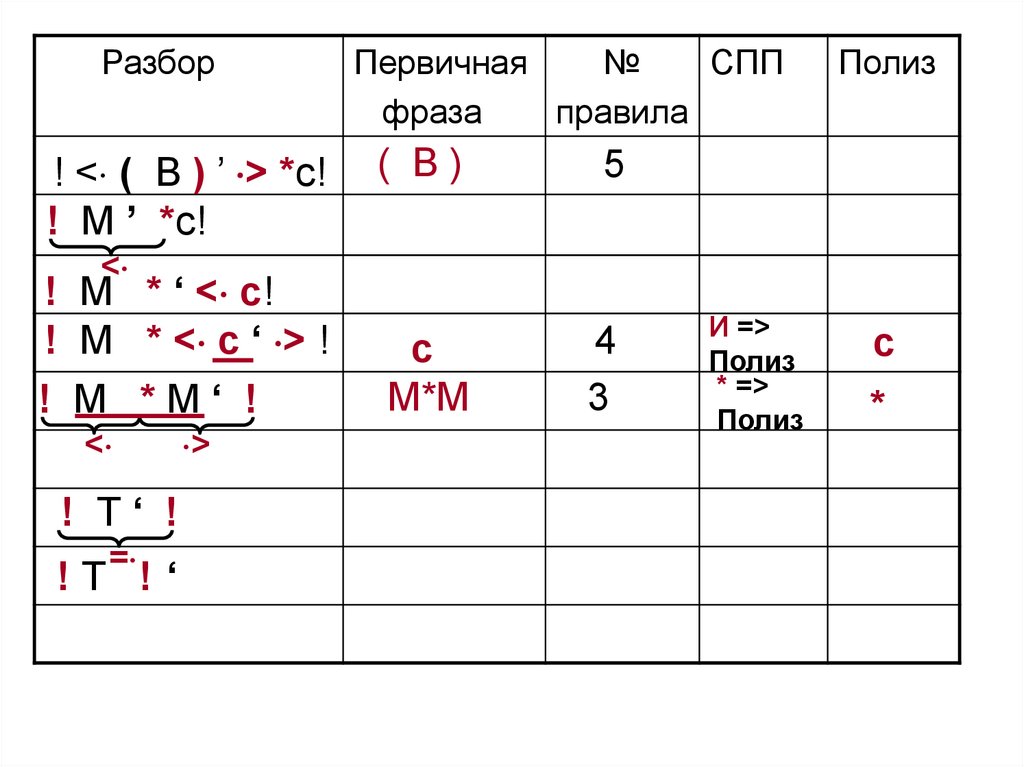
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
! Т‘ !
=
!Т !‘
>
И =>
Полиз
* =>
Полиз
c
*

120.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
! Т‘ !
=
!Т !‘
>
И =>
Полиз
* =>
Полиз
c
*

121.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
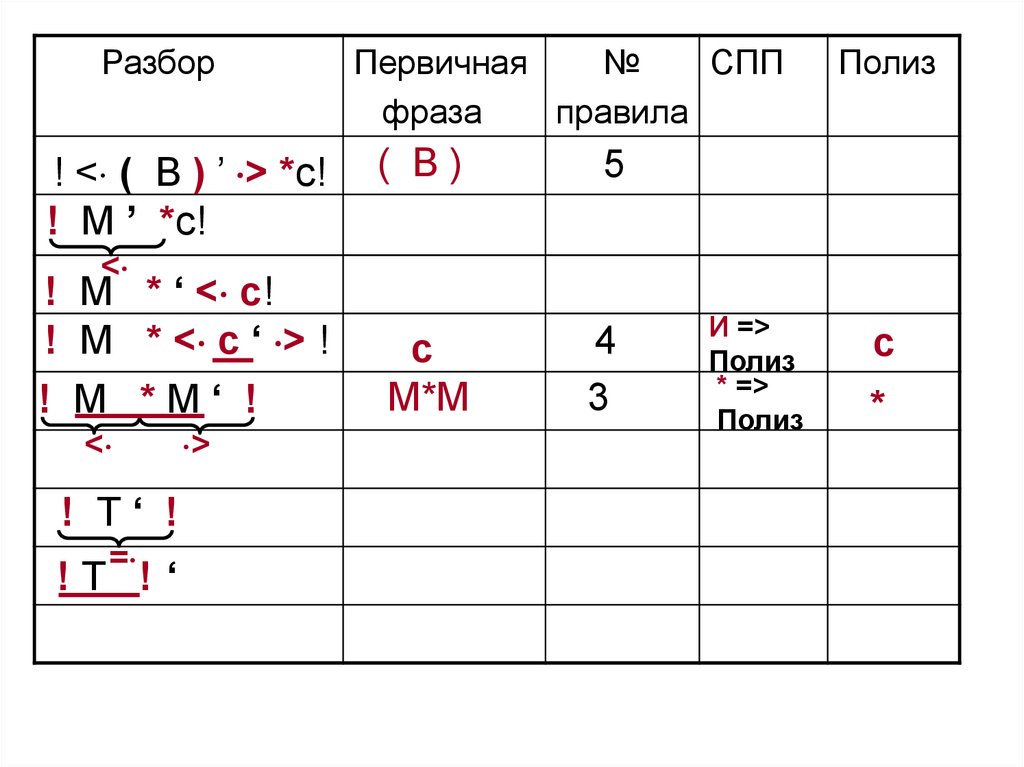
! Т‘ !
=
!Т !‘
!Т!
И =>
Полиз
* =>
Полиз
c
*

122.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
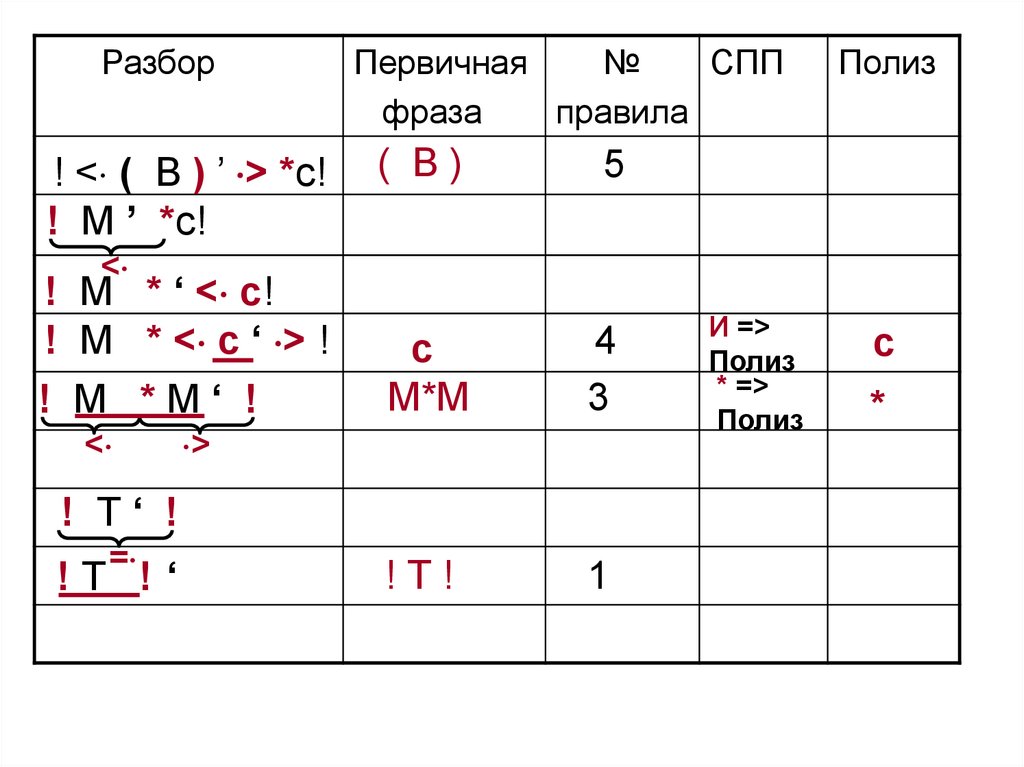
!Т!
1
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
! Т‘ !
=
!Т !‘
И =>
Полиз
* =>
Полиз
c
*

123.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
!Т!
1
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
! Т‘ !
=
!Т !‘
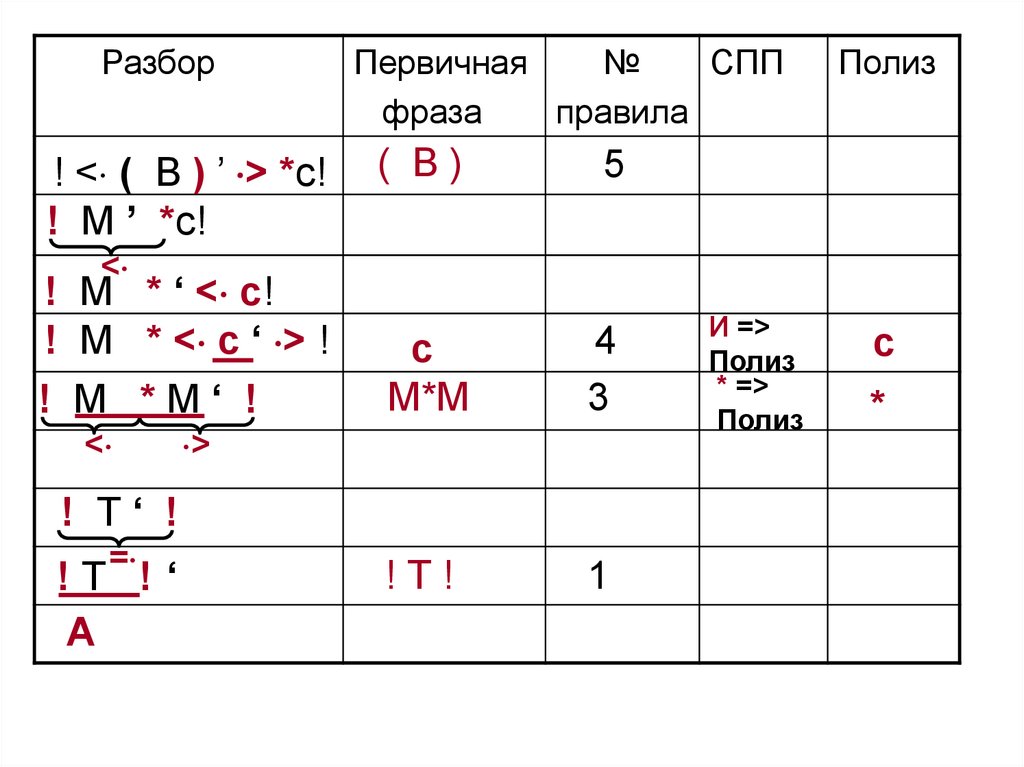
А
И =>
Полиз
* =>
Полиз
c
*

124.

Разбор
! < ( B ) ’ > *c!
! M ’ *c!
Первичная
№
СПП
фраза
правила
( B)
5
c
М*М
4
3
!Т!
!Т !‘
А
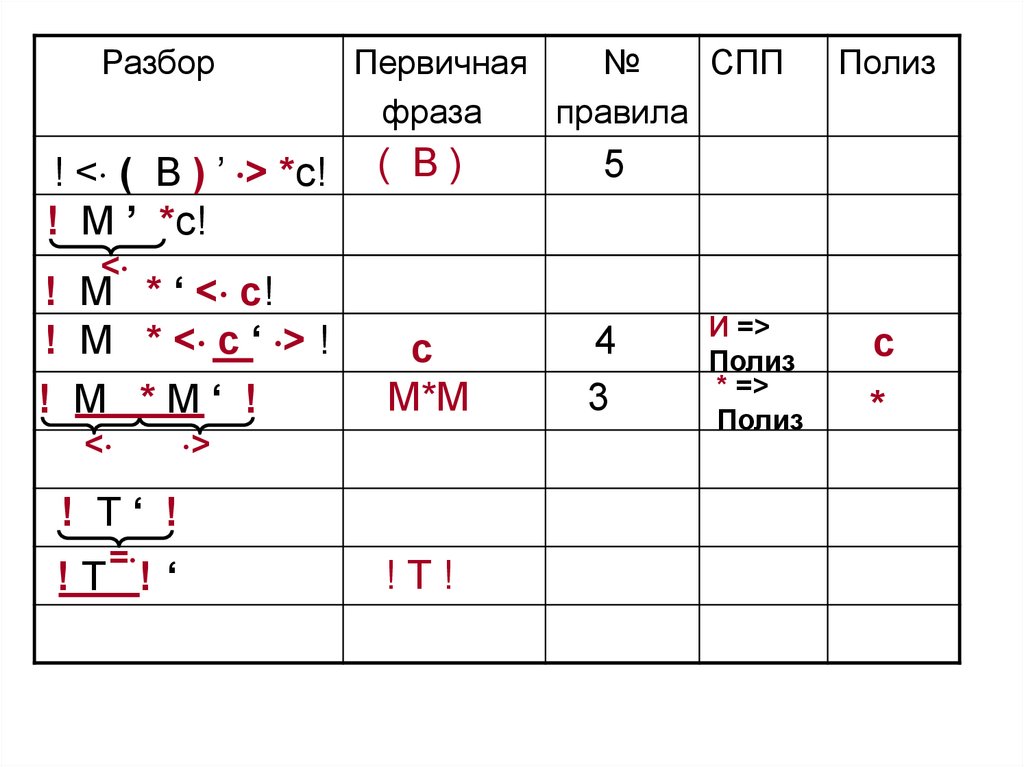
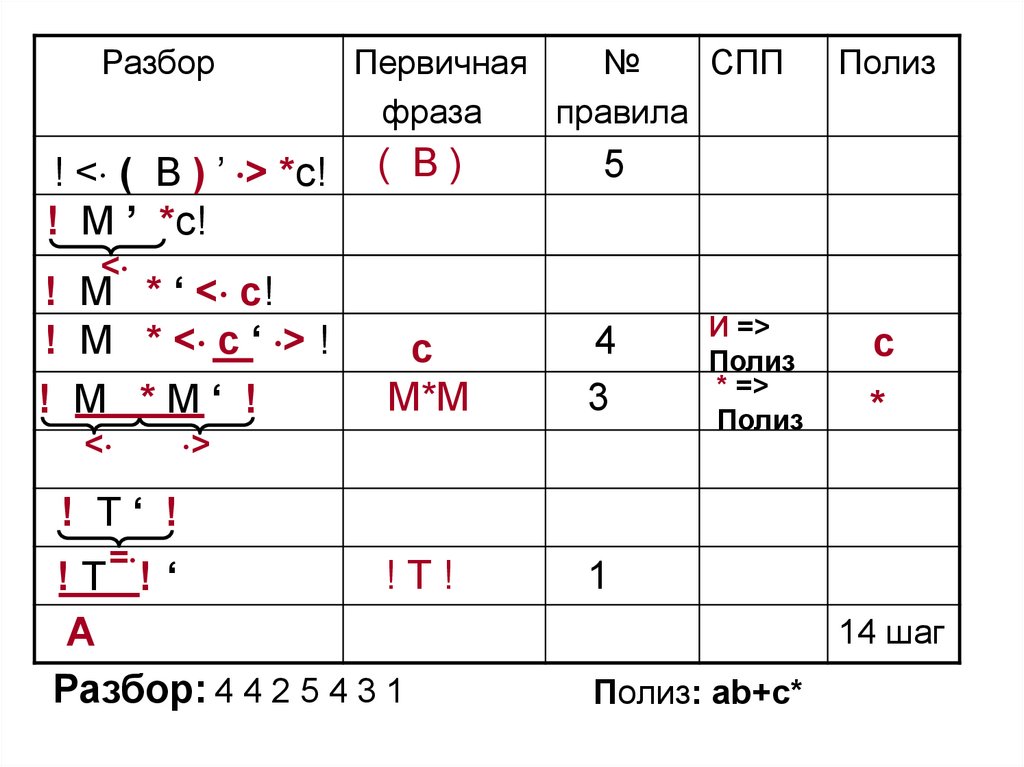
Разбор: 4 4 2 5 4 3 1
1
Полиз
<
! M * ‘ < c!
! M * < c ‘ > !
! M *М‘ !
<
>
И =>
Полиз
* =>
Полиз
c
*
! Т‘ !
=
14 шаг
Полиз: ab+c*

125.

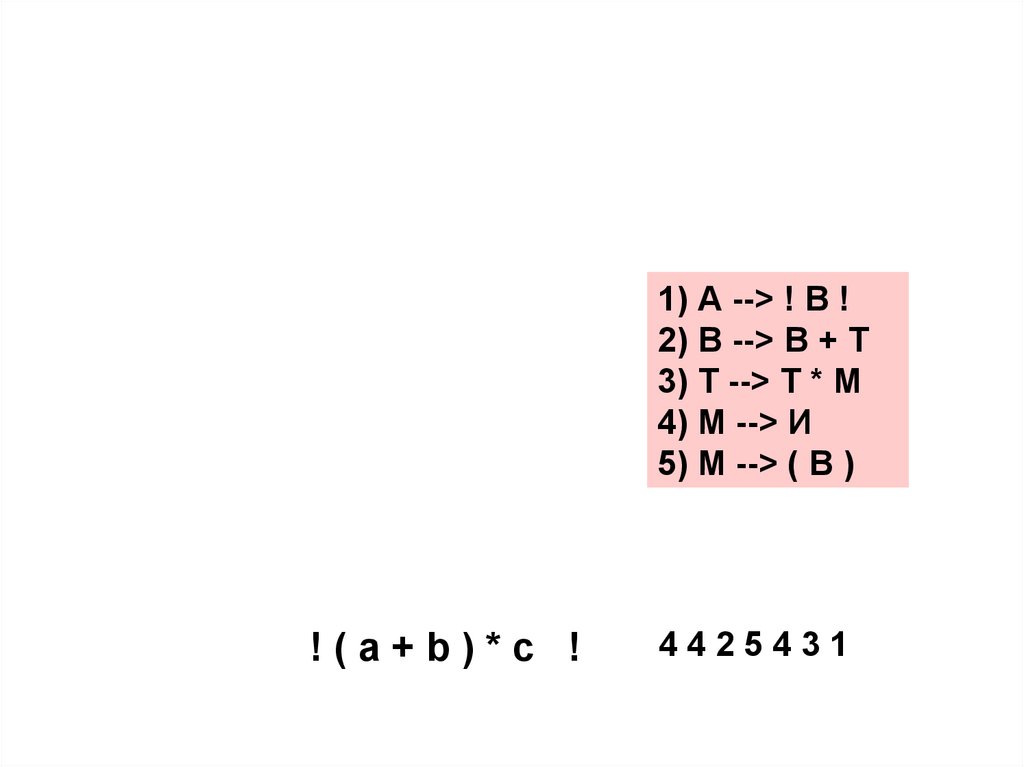
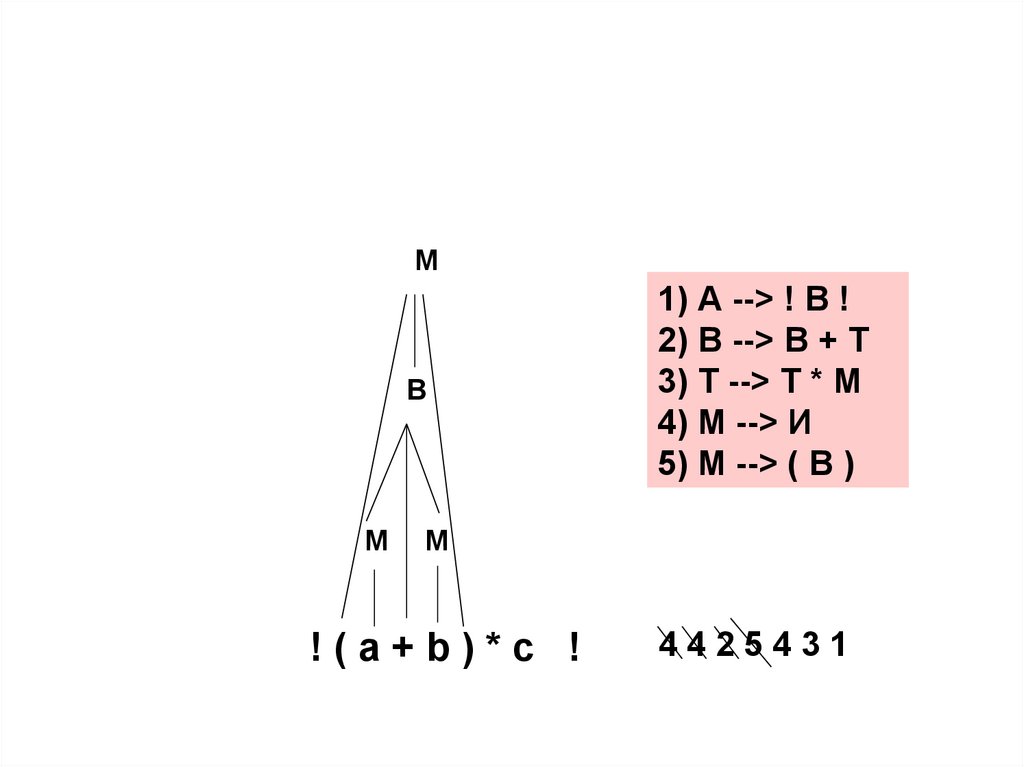
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
!(a+b)*c !
4425431

126.

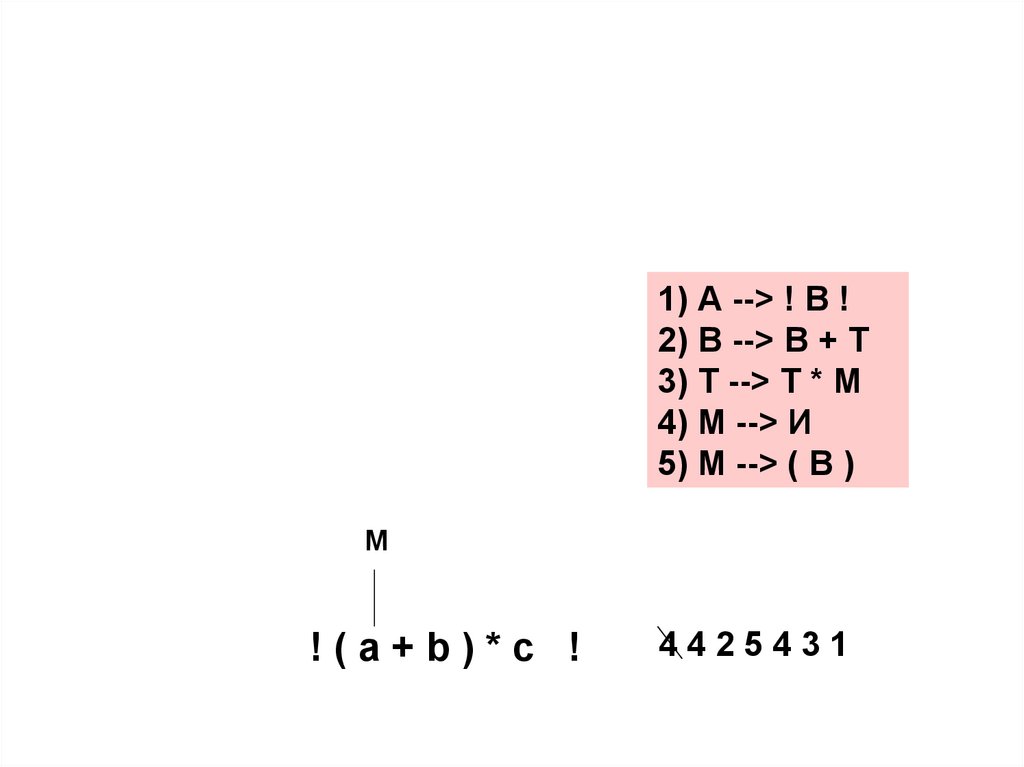
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
М
!(a+b)*c !
4425431

127.

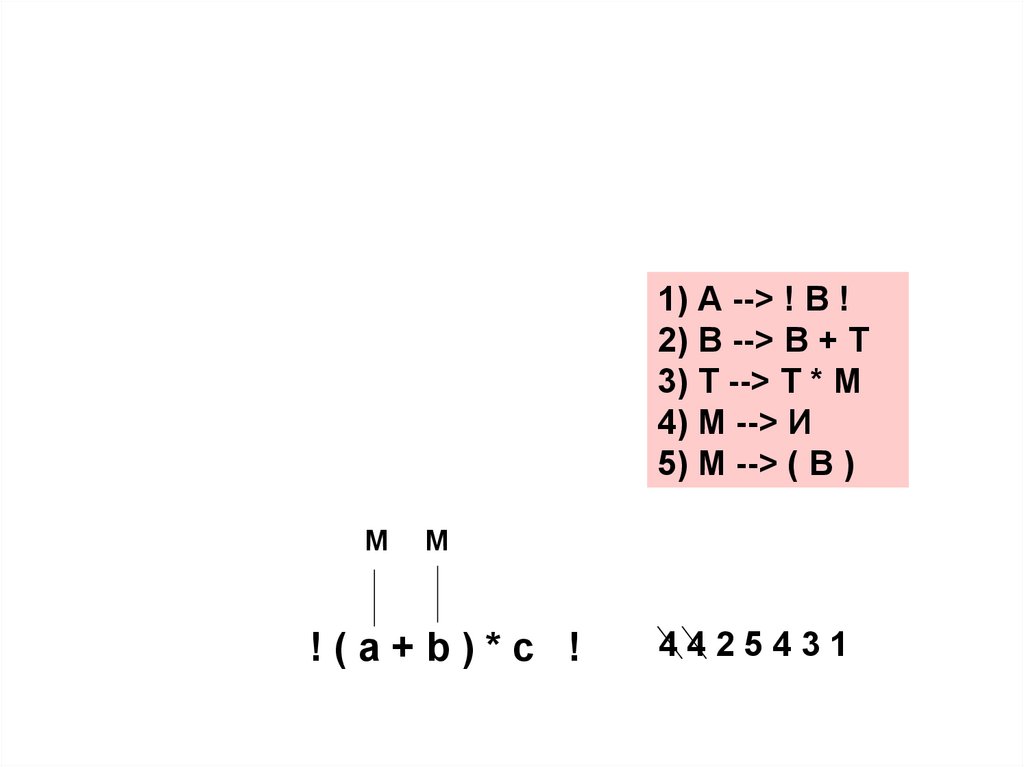
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
М
М
!(a+b)*c !
4425431

128.

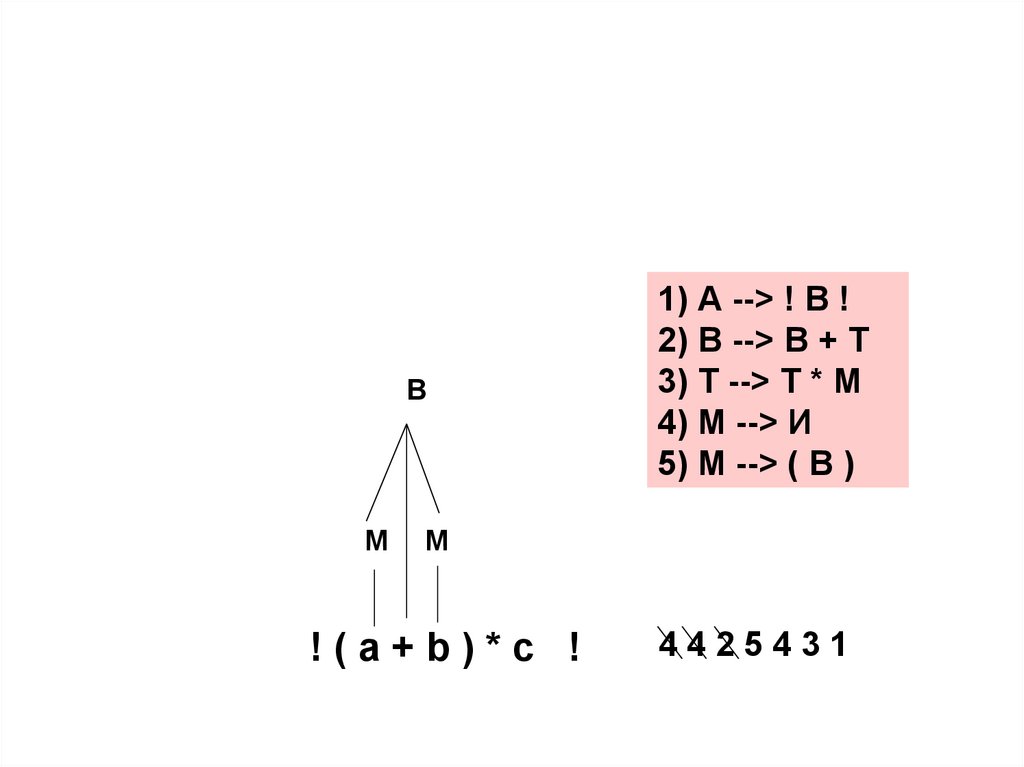
В
М
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
М
!(a+b)*c !
4425431

129.

М
В
М
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
М
!(a+b)*c !
4425431

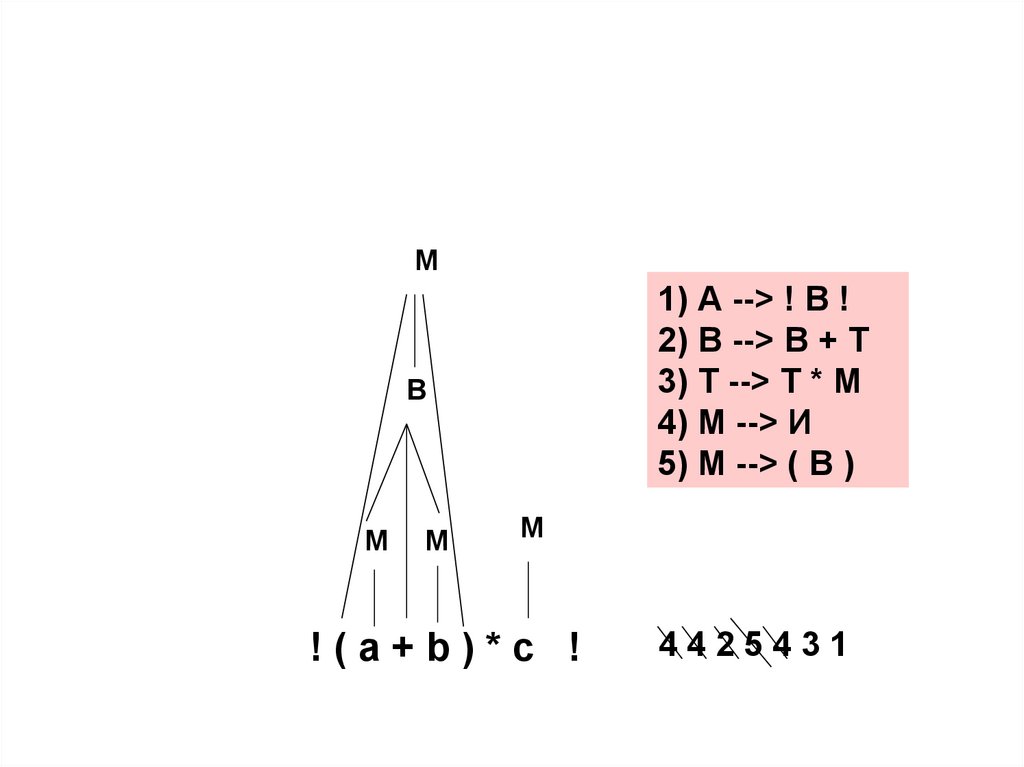
130.

М
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
В
М
М
М
!(a+b)*c !
4425431

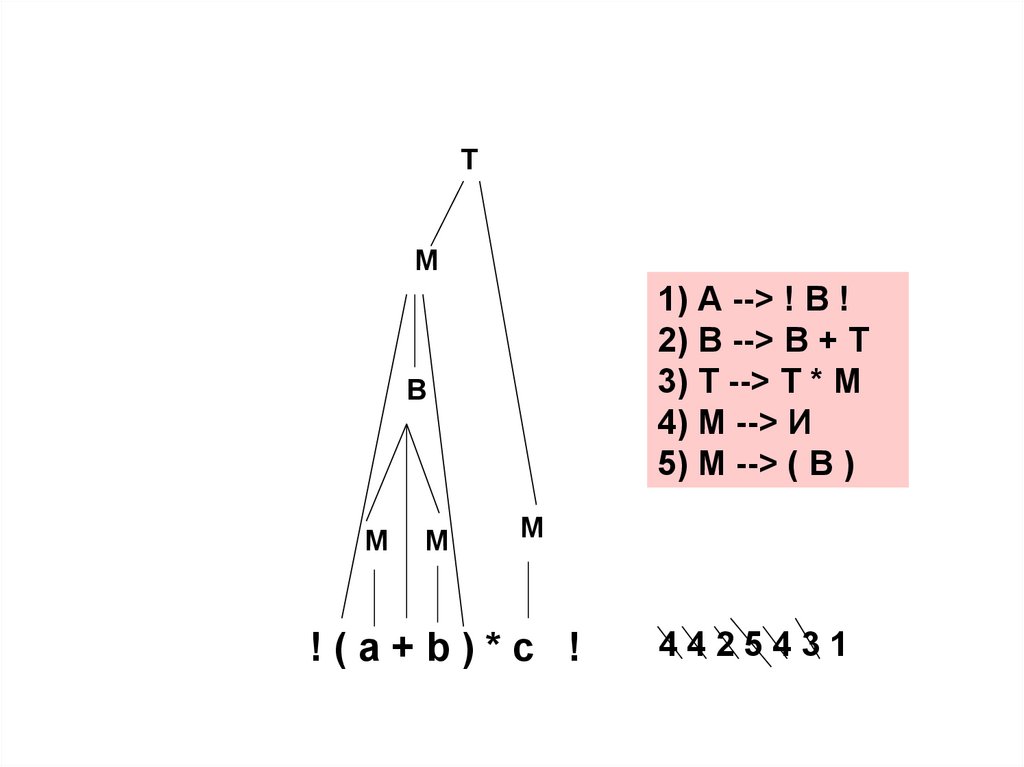
131.

Т
М
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
В
М
М
М
!(a+b)*c !
4425431

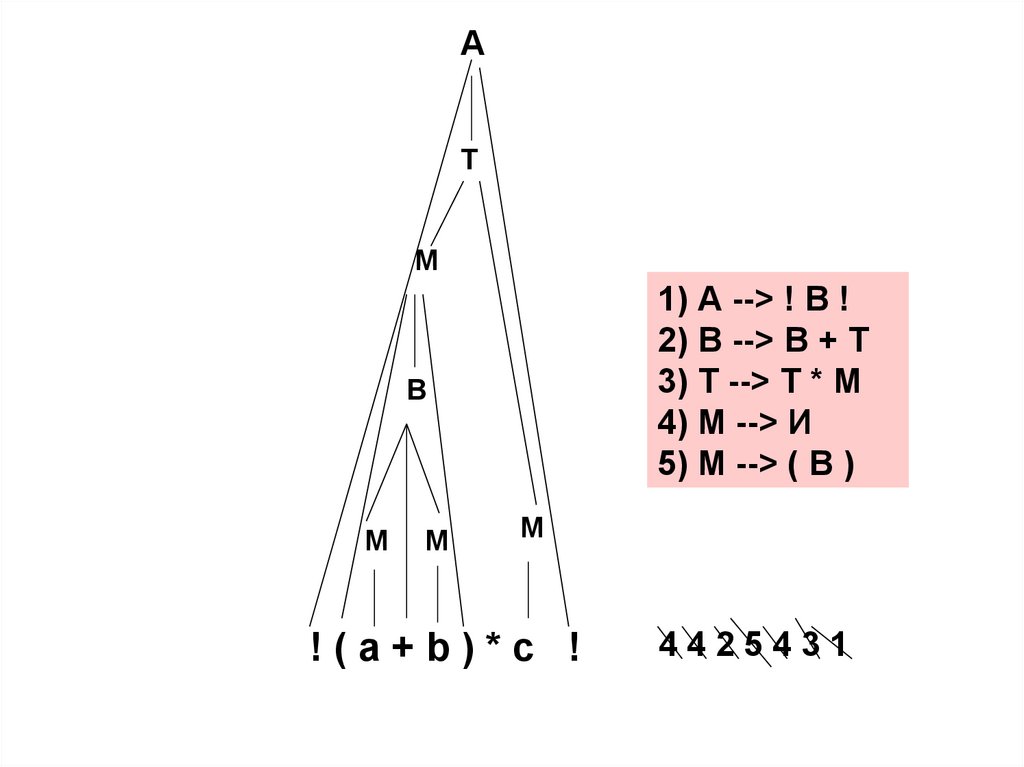
132.

А
Т
М
1) А --> ! В !
2) В --> В + Т
3) Т --> Т * М
4) М --> И
5) М --> ( В )
В
М
М
М
!(a+b)*c !
4425431

133.

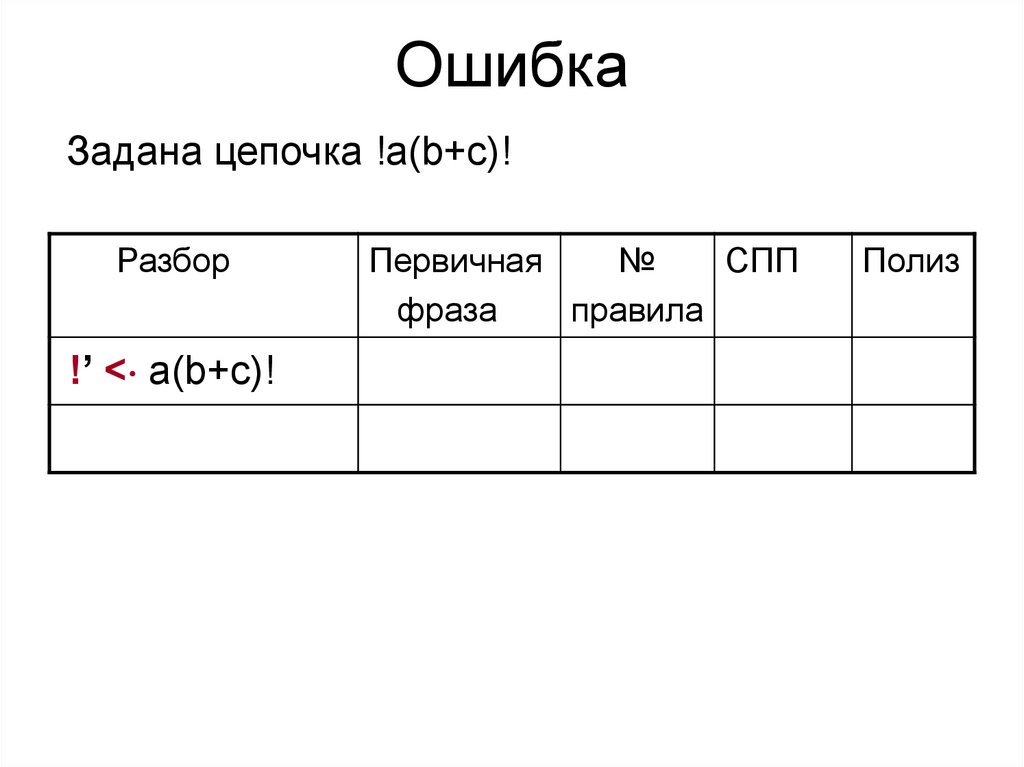
Ошибка
Задана цепочка !a(b+c)!
Разбор
!’ < a(b+c)!
Первичная
№
СПП
фраза
правила
Полиз

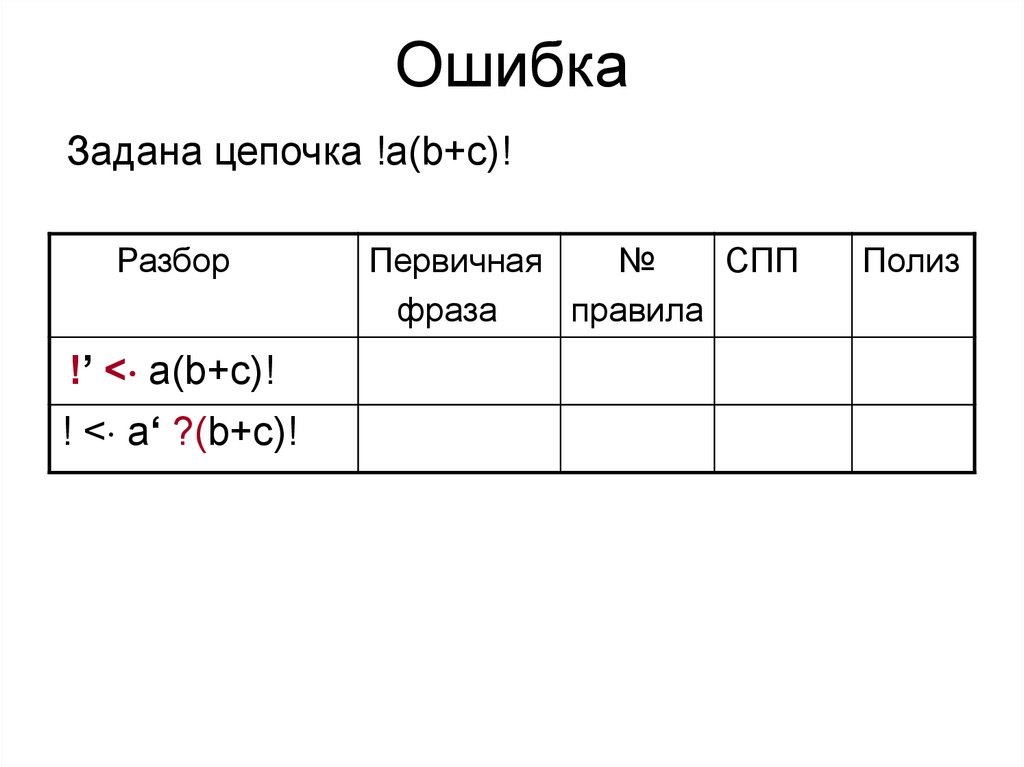
134.

Ошибка
Задана цепочка !a(b+c)!
Разбор
!’ < a(b+c)!
! < a‘ ?(b+c)!
Первичная
№
СПП
фраза
правила
Полиз

135.

Ошибка
Задана цепочка !a(b+c)!
Разбор
Первичная
№
СПП
фраза
правила
!’ < a(b+c)!
! < a‘ ?(b+c)!
Error!
Полиз

136. Вопросы для повторения

В чем отличие МПП от МОП?
Что такое операторная грамматика?
Что такое обратимая грамматика?
Что такое первичная фраза?
Как строится МОП?
Работа расознавателя.
ФОП? В каком случае? Как их можно
построить?
8. Особенность транслятора, работающего по
МОП?
1.
2.
3.
4.
5.
6.
7.