Similar presentations:
Методы трансляции. Формальные языки, грамматики и их представление
1. Учебный курс
Методы трансляцииФормальные языки, грамматики и их
представление
Шиманский Валерий Владимирович
2.
Определение 1.Алфавит или словарь V есть конечное не пустое множество символов.
Что такое символ - не определяется, как не определяется, например, точка
в геометрии.
Некоторые примеры алфавитов:
латинский{a, b, …, z, A, B, ..., Z}
греческий{α, β, ..., ω, Α, Β, …, Ω}
бинарный{0, 1}.
Определение 2.
Цепочка символов (синонимы – предложение, строка, слово) это любая
конечная последовательность символов алфавита. Цепочка, не содержащая
ни одного символа, называется пустой цепочкой (предложением). Она
обозначается греческой буквой ε.
Предполагается, что сам символ ɛ в алфавит V не входит; она лишь
помогает обозначить пустую последовательность символов.
3.
Операции над цепочкамиα · β = α β конкатенация (или сцепление) цепочек α и β. Если α = ab
и β = yx, то α · β = abyx.
Для любой цепочки α справедливы равенства: α · ɛ = ɛ · α = α
Для любых цепочек α, β, γ справедливо (α · β) · γ = α · (β · γ) =
α β γ (свойство ассоциативности операции конкатенации).
α R - обращение (или реверс) цепочки α, символы которой
записаны в обратном порядке. Для α = abcdef α R = fedcba.
n-ой степенью цепочки α (будем обозначать αn): называется
конкатенация n цепочек α: α n = α α … α α α .
Свойства степени: α 0 = ɛ; α n = α α n − 1 = α n − 1 α
| α | - Длина цепочки, это число составляющих ее символов.
При α = abbcaad, |α| = 7. |ɛ | = 0
| α |s - Число вхождений символа s в цепочку α. , | babb |a = 1,
4.
Определение 3.Если V — некоторый алфавит, то
V* обозначает множество всех предложений, составленных из символов
алфавита V, включая и пустое предложение ε.
V+ будем обозначать множество V \ {ε}. Следовательно, V * = V+∪{ɛ}.
Например,
если V= {0, 1}, то V* = {ε, 0, 1, 00, 01, 10, 11, 000, ...}, а
V+ = {0, 1, 00, 01, 10, 11, 000, ...}.
Если x ∈ V*, то | x | обозначает длину цепочки x, т. е. число
символов, её составляющих.
Определение 4.
Язык в алфавите V - это подмножество множества всех цепочек
(предложений) в этом алфавите. Если V - алфавит, L - язык, то L ⊆ V*.
5.
Определение 4 ставит три вопроса:Как представить язык, т. е. как определить цепочки (предложения),
составляющие язык?
2. Для каждого ли языка существует конечное представление?
3. Какова структура тех классов языков, для которых существуют
конечные представления?
На первый вопрос ответить легко, если язык конечен. Надо просто
перечислить все цепочки, т. е. составить список. Если язык бесконечен, то
возникает проблема нахождения способа конечного представления
бесконечного языка. Это конечное представление само будет строкой
символов над некоторым алфавитом с подразумеваемой интерпретацией,
которая связывает это конкретное представление с данным языком.
На второй вопрос ответ отрицателен. Легко можно показать, что
множество всех предложений над данным словарём счётно-бесконечно.
То, что множество всех подмножеств счётно-бесконечного множества не
является счётно-бесконечным, есть хорошо известный факт теории
множеств.
6.
Два основных подхода для представления языков:механизм распознавания и механизм порождения (генерации).
Распознавание. Задается алгоритм, который определяет, есть ли данная
цепочка в данном языке или нет.
Более общий способ - дать процедуру, которая по заданной цепочке
определяет, принадлежит ли она языку. Если принадлежит, то процедура
останавливается с ответом «да», т. е. допускает цепочку; иначе —
останавливается с ответом «нет» или зацикливается. Говорят, что такие
алгоритм и процедура распознают язык.
Порождение. Определяется процедура, которая систематически
порождает цепочки языка последовательно в некотором порядке.
Если имеется алгоритм или процедура, которые распознают предложения
языка над алфавитом V, то на их основе можно построить порождающий
механизм - алгоритм или процедуру, порождающий этот язык.
Именно, можно систематически генерировать все предложения из
множества V*, проверять каждое предложение на принадлежность его
языку с помощью распознающего механизма и выводить в список только
предложения языка.
7.
Примеры распознавателей:Машина Тьюринга (МТ). Язык, который можно задать с
помощью МТ, называется рекурсивно перечислимым. Вместо
МТ можно использовать эквивалентные алгоритмические схемы:
нормальный алгоритм Маркова (НАМ), машину Поста и др.
Линейно ограниченный автомат (ЛОА). Представляет собой
МТ, в которой лента не бесконечна, а ограничена длиной
входного слова. Определяет контекстно-зависимые языки.
Автомат с магазинной (внешней) памятью (МП-автомат). В
отличие от ЛОА, головка не может изменять входное слово и не
может сдвигаться влево; имеется дополнительная бесконечная
память (магазин, или стек), работающая по дисциплине LIFO.
Определяет контекстно-свободные языки.
Конечный автомат (КА). Отличается от МП-автомата
отсутствием магазина. Определяет регулярные языки.
8.
Распознающая процедура должна организовать проверку такимобразом, чтобы проверка одного предложения не зациклилась.
Пусть в алфавите V имеется p символов. Предложения из множества V*
можно рассматривать как числа p-ичной системы счисления, включая и
пустое предложение ε. Пронумеруем предложения из V* в порядке
увеличения длины, причём все предложения одинаковой длины будем
нумеровать в “числовом” порядке.
Например, если V= {a, b, c}, то предложения из V* будут
занумерованы следующим образом:
1. ε 5. aa 9. bb
2. a 6. ab 10. bc
3. b 7. ac 11. ca
4. c 8. ba 12. …
Тем самым показано, что множество предложений над алфавитом V
счётно.
Пусть P - распознающая процедура для языка L. Предполагается,
что она разбита на шаги так, что имеет смысл говорить об i-м шаге
этой процедуры для любого заданного предложения.
Прежде чем дать процедуру перечисления предложений языка L,
определим способ нумерации пар положительных целых.
9.
Можно отобразить всё множество пар положительныхцелых (i, j) на множество положительных целых, как показано ниже в
таблице, при помощи следующей формулы:
Пусть имеется некоторое k, k ≥1, занимающее в сетке позицию (i, j).Ясно, что k= N+ j
Здесь
Это число элементов внутри треугольной сетки с основанием, концы которого имеют
координаты (i + j − 1, 1) и (1, i + j − 1). Очевидно, что здесь n - число рядов клеток
треугольной сетки, параллельных её основанию, считая и само это основание. Очевидно
также, что i + j = n + 2. Следовательно, n = i + j – 2. Подставив это n в формулу
для N, получим приведенное ранее выражение для k.
10.
Т.о. мы можем перенумеровать упорядоченные пары целых чисел согласноприсвоенному номеру k
Несколько первых пар есть:
(1, 1), (2, 1), (1, 2), (3, 1), (2, 2), ... .
Теперь мы можем описать процедуру перечисления, т. е.
порождающую процедуру, предложений языка L.
Процедура перенумеровывает пары целых в соответствии с таблицей
предыдущего слайда. Когда пара (i, j) занумеровывается, процедура
порождает i-е предложение из множества V* и выполняет первые j шагов
распознающей процедуры P над этим предложением.
Когда процедура P определяет, что порождённое предложение
принадлежит языку L, порождающая процедура добавляет это
предложение к списку предложений языка L.
Теперь, если слово номер i принадлежит языку L, то этот факт
устанавливается при помощи процедуры P за j шагов для некоторого
конечного j. Очевидно, что таким образом организованная процедура
будет перечислять все предложения языка L.
С другой стороны, если имеется порождающая процедура для языка L,
то на её основе можно построить распознающую процедуру для этого
языка.
11.
Определение 5. Язык, предложения которого могут порождатьсяпроцедурой, называется рекурсивно перечислимым. Также
принято говорить, что язык рекурсивно перечислим, если
существует процедура распознавания предложений этого языка.
Определение 6. Язык рекурсивен, если существует алгоритм его
распознавания.
Известно, что класс рекурсивных языков является собственным
подмножеством класса рекурсивно перечислимых языков. Более
того, существуют языки, которые даже не рекурсивно
перечислимы, т. е. невозможно эффективно перечислять
предложения такого языка.
Теорема 1
Пусть L ⊆ V* — некоторый язык, а = V* \ L — его
дополнение.
Если языки L и рекурсивно перечислимы, то язык
L рекурсивен.
12.
Доказательство теоремы 1. Пусть язык L распознаётся процедурой P, а егодополнение распознаётся процедурой .
Построим алгоритм распознавания языка L, т. е. отвечающий на вопрос: “x∈ L?”,
следующим образом:
Шаг 1. i := 1.
Шаг 2. Применим i шагов процедуры P к цепочке x. Если процедура
P не завершается, то перейти к шагу 3, иначе— к шагу 4.
Шаг 3. Применим i шагов процедуры к цепочке x. Если процедура
не завершается, то i:=i+ 1 и перейти к шагу 2.
Шаг 4. При некотором i одна из этих двух процедур завершится,
распознав цепочку x, так как либо x ∈ L - и это распознаёт
процедура P, либо x ∉ L – и это распознаёт процедура P.
Соответственно распознающий алгоритм выдаёт либо
положительный, либо отрицательный ответ.
Поскольку язык L распознаётся описанным алгоритмом, то он
рекурсивен.
Что и требовалось доказать.
13.
“The little boy ran quickly”14.
В структуре предложения имеются1) грамматические термины (предложение, группа подлежащего, группа
сказуемого и т. д.), которые в теории формальных грамматик принято
называть нетерминалами;
2) слова, составляющие предложения языка, они называются
терминалами;
3) правила, левые и правые части которых состоят из нетерминалов и
терминалов;
4) главный грамматический термин, называемый начальным символом
или начальным нетерминалом грамматики, из него выводятся те
цепочки терминалов, которые считаются предложениями языка (в
рассмотренном ранее примере начальным нетерминалом является
грамматический термин 〈предложение 〈).
Определение 7. Декартовым произведением A ✕ B множеств
A и B называется множество { (a, b) | a ∈ A, b ∈ B }.
15.
Определение A.Грамматикой называется четверка G = 〈T, N, P, S〈,
где
T, N - алфавиты (словари) терминалов и
нетерминалов соответственно, причём T ∩ N = 〈,
P - конечное множество правил, каждое из которых
имеет вид
α → β,
где α ∈ V*NV*,
β ∈ V*,
V = N∪T - объединённый алфавит (словарь)
грамматики,
S - начальный нетерминал. S ∈ N и является
начальным символом (целью) грамматики.
16.
Отметим, что P - конечное подмножество множества(T ∪ N)+ ✕ (T ∪ N)*.
Элемент (α, β) множества P называется правилом вывода и записывается в
виде
α→β
- α называется левой частью правила,
- β - правой частью;
- левая часть любого правила из P обязана содержать хотя бы один
нетерминал.
Для записи правил вывода с одинаковыми левыми частями
α → β1 α → β2 ... α → βn
будем пользоваться сокращенной записью α → β1 | β2 |...| βn.
Каждое βi (i = 1, 2, ..., n) будем называть альтернативой правила
вывода из цепочки α.
Пример грамматики G1:
G1 = ✕{0, 1}, {A, S}, P, S)✕,
где P состоит из правил:
1. S→ 0A1;
2. 0A→ 00A1;
3. A→ ε.
17.
Определение 8. Выводимая цепочка грамматики G,не содержащая нетерминалов, называется
терминальной цепочкой, порождаемой
грамматикой G.
Язык L(G), порождаемый грамматикой G,- это
множество терминальных цепочек, порождаемых
грамматикой G.
В дальнейшем нетерминалы мы будем обозначать
прописными латинскими буквами, например, S, A,
B, C; терминалы - строчными буквами из начала
латинского алфавита, например, a, b, c; цепочки
терминалов - строчными буквами из конца
латинского алфавита, например x, y, z; цепочки
символов из объединённого алфавита - строчными
греческими буквами, например α, β, γ.
18.
Язык L(G), порождаемый грамматикой G,- это множествотерминальных цепочек, порождаемых грамматикой G.
Для определения языка нам потребуется ввести отношение
непосредственной выводимости ➾ G , его транзитивное ➾ G+ и
рефлексивно-транзитивное ➾ G* замыкание.
Определение 9.
Пусть α → β ∈ P — правило, γ, δ — любые цепочки из множества V*.
Тогда γαδ ➾ G γβδ читается следующим образом: “из γαδ непосредственно
выводится γβδ в грамматике G при помощи данного правила”.
Другими словами, символ связывает две цепочки тогда и только тогда,
когда вторая цепочка получается из первой применением единственного
правила.
Цепочка β ∈ ( T ∪ N )* непосредственно выводима из цепочки
α ∈(T ∪ N )+ в грамматике G = 〈 T, N, P, S 〈 (обозначается α ➾ G+ β), если
α = ξ1 γ ξ2, β = ξ1 δ ξ2, где ξ1, ξ2, δ ∈( T ∪ N )*, γ ∈( T ∪ N )+ и правило
вывода γ → δ содержится в P.
19.
Определение 10.Цепочка β ∈ (T ∪ N )* выводима из цепочки α ∈
(T ∪ N )+ в грамматике G = 〈 T, N, P, S 〈
(обозначается α ➾ G β), если существуют цепочки γ0,
γ1, ..., γn (n ≥ 0), такие, что
α = γ0 → γ1 → ... → γn = β.
Другими словами, α 〈G β, если β может быть
получена из α путем применения некоторого числа
правил из множества правил P. Последовательность
γ0, γ1, ..., γn называется выводом длины n.
Индекс G в обозначении 〈G опускают, если понятно,
какая грамматика подразумевается.
20.
Определение B.Языком, порождаемым грамматикой G = ⧼ T, N, P, S ⧽,
называется множество L(G) = {α ∈ T* | S ➾ α }. Другими
словами, L(G) — это все цепочки в алфавите T, которые
выводимы из S с помощью правил P.
Определение 11. Цепочка α ⊆ (T ∪ N )* , для которой S ➾ α,
называется сентенциальной формой в грамматике G = ✕T, N, P,
S✕.
Таким образом, язык, порождаемый грамматикой, можно
определить как множество терминальных сентенциальных форм.
Определение 12. Грамматики G1 и G2 называются эквивалентными,
если L(G1) = L(G2).
Грамматики G1 = ⧼{0,1}, {A,S}, P1, S ⧽ и G2 = ⧼{0,1}, {S}, P2, S ⧽ с правилами
P1:
P2:
S → 0A1
S → 0S1 | 01
0A
→ 00A1
A
→ɛ
эквивалентны, т. к. обе порождают язык L(G1) = L(G2) = {0 1 | n > 0}.
21.
Рассмотрим грамматику G= 〈T, N, P, S〈, гдеT = {0, 1},
N = {S},
P = {S → 0S1, S → 01}.
Здесь S - единственный нетерминал, он же - начальный; 0 и 1 - терминалы;
правил два: S → 0S1 и S → 01.
Применив первое правило n – 1 раз, а затем второе правило, получим:
S ➾G 0S1➾G 00S11➾G 03S13➾G ... ➾G 0n-1S1n-1➾G 0n 1n.
Здесь мы воспользовались обозначением
причём w0= ε.
Таким образом, эта грамматика порождает язык L(G) = {0n1n | n ≥ 1}.
Действительно, при использовании первого правила число символов
S остаётся неизменным и равно 1. После применения второго
правила число символов S в сентенциальной форме уменьшается на
единицу. Поэтому после использования правила S → 01 в
результирующей цепочке не останется ни одного символа S.
Так как оба правила имеют в левой части по одному символу S, то
единственно возможный порядок их применения - сколько-то раз
использовать первое правило, а затем один раз использовать
второе.
22.
Определение 13. Грамматики G1 и G2 почти эквивалентны, еслиL(G1) ∪ { ɛ } = L(G2) ∪ { ɛ }.
23.
С помощью ограничений на вид правил вывода определяетсячетыре типа грамматик: тип 0, тип 1, тип 2, тип 3.
Определение А дает грамматику типа 0. Класс языков типа 0
совпадает с классом рекурсивно перечислимых языков.
Каждому типу грамматик соответствует свой класс языков. Если
язык порождается грамматикой типа i (для i = 0, 1, 2, 3), то он
является языком типа i.
Грамматикой типа 1 называется контекстно-зависимая или
неукорачивающаяся грамматика.
Определение C. Грамматика G = 〈T, N, P, S〈 является
грамматикой типа 1 или контекстно-зависимой грамматикой,
если для каждого её правила α → β ∈ P выполняется условие | β |
≥ | α |.
24.
Определение Ci. Грамматика G = 〈T, N, P, S〈 называетсянеукорачивающей, если правая часть каждого правила из P не
короче левой части (т. е. для любого правила α → β ∈ P
выполняется неравенство | α | ≤ | β` |). В виде исключения в
неукорачивающей грамматике допускается наличие правила S → ɛ,
при условии, что S (начальный символ) не встречается в правых
частях правил.
Замечание.
Часто вместо термина “контекстно-зависимая грамматика”
используют КЗ-грамматика или аббревиатуру csg (context-sensitive
grammar).
Неукорачивающая грамматика называется также НС-грамматикой
или грамматикой непосредственных составляющих.
Для НС-грамматик правила имеют вид: α1Aα2 → α1βα2, где α1, α2, β
∈V*, причём β ≠ ε , а A∈N. Это мотивирует НС-грамматика тем,
что правило α1Aα2 → α1βα2 позволяет заменять A на β только, если A
25.
Можно показать, что это требование относительно контекстнойзамены не изменяет класса порождаемых языков. Действительно, любая НСграмматика
является
неукорачивающей.
Однако
любое
правило
неукорачивающей грамматики может быть преобразовано так, чтобы все
символы, его составляющие, были нетерминалами. Для этого достаточно
каждое вхождение терминала a ∈ T заменить на новый нетерминал Z,
пополнить словарь нетерминалов этим символом и включить правило Z → a в
множество правил грамматики.
Правила вида Z → a допустимы для НС-грамматик.
Правило же вида X1X2 … Xm → Y1Y2 …Ym + q , где m >0, q ≥0, Xi,Yj ∈ N, 1 ≤ i
≤ m, 1 ≤ j ≤ m + q эквивалентно группе правил:
X1X2… Xm → A1X2… Xm,
A1X2… Xm → A1A2… Xm,
…
A1A2… Xm → A1A2… Am,
A1A2… Am → Y1A2… Am,
Y1A2 …Am → Y1Y2… Am,
…
Y1Y2… Am – 1 Am → Y1Y2…Ym – 1 Am,
Am – 1 Am → Y1Y2…Y
где A1, A2, …, YA1mY2-…дополнительные
нетерминалы.
Каждое
из этих правил
m – 1 YmYm + 1 …Y
m + q,
26.
27.
28.
29.
Каждому классу грамматик соответствует класс языков.Языку приписывается тип грамматики, которой он порождается.
Например, контекстно-свободные грамматики (cfg) порождают
контекстно-свободные языки (cfl — context-free language),
контекстно-зависимые грамматики (csg) порождают контекстнозависимые языки (csl - context-sensitive language).
В соответствии с текущей практикой язык типа3 или регулярный язык
часто называют регулярным множеством (rs - regular set). Язык типа 0
называют рекурсивно перечислимым множеством (res - recursively
enumer-able set).
Иерархия классов языков
30.
31.
Определение 14. Цепочка в алфавите T принадлежит языку, порождаемомуграмматикой G = ⧼ T, N, P, S ⧽, только в том случае, если существует ее вывод из начального
символа S этой грамматики. Процесс построения такого вывода (а, следовательно, и
определения принадлежности цепочки языку) называется разбором.
из S ∈ N в КС-грамматике G =
✕ T, N, P, S ✕, называется левым (левосторонним), если в этом
выводе каждая очередная сентенциальная форма получается из
предыдущей заменой самого левого нетерминала.
Вывод цепочки β ∈ T * из S ∈ N в КС-грамматике G = ✕ T, N, P, S ✕,
Определение 15. Вывод цепочки β ∈ T *
называется правым (правосторонним), если в этом выводе каждая
очередная сентенциальная форма получается из предыдущей заменой
самого правого нетерминала.
Для цепочки a + b + a в грамматике:
Gexpr =✕ {a, b, +}, {S, T}, {S → T | T + S ; T → a | b}, S ✕
можно построить выводы:
(1) S → T + S → T + T + S → T + T + T → a + T + T → a + b + T → a + b + a
(2) S → T + S → a + S → a + T + S → a + b + S → a + b + T → a + b + a
(3) S → T + S → T + T + S → T + T + T → T + T + a → T + b + a → a + b + a
Здесь (2) — левосторонний вывод, (3) — правосторонний, а (1) не является
32.
Определение 16.В грамматике для одной и той же цепочки может
быть несколько выводов, эквивалентных в том смысле,
что в них в одних и тех же местах применяются одни и
те же правила вывода, но в различном порядке.
Например, для цепочки a + b + a в грамматике:
Gexpr =⧼ {a, b, +}, {S, T}, {S → T | T + S ; T → a | b}, S ⧽
Для КС-грамматик можно ввести удобное
графическое представление вывода, называемое
деревом вывода, причем для всех эквивалентных
выводов деревья вывода совпадают.
33.
Определение 17. Ориентированное упорядоченное дерево называетсядеревом вывода (или деревом разбора) в КС-грамматике G = ✕ T, N, P, S ✕, если
выполнены следующие условия:
(1) каждая вершина дерева помечена символом из множества N ∪ T ∪ { ɛ }, при
этом корень дерева помечен символом S; листья — символами из T ∪ { ɛ };
(2) если вершина дерева помечена символом A, а ее непосредственные потомки
— символами a1, a2, ..., an, где каждое ai ∈ T ∪ N, то A → a1, a2,...an — правило
вывода в этой грамматике;
(3) если вершина дерева помечена символом A, а ее непосредственный потомок
помечен символом ɛ, то этот потомок единственный и A → ɛ — правило вывода
в этой грамматике.
Пример дерева вывода для
цепочки a + b + a в грамматике:
Gexpr =✕ {a, b, +}, {S, T},
{S → T | T + S ; T → a | b}, S ✕
34.
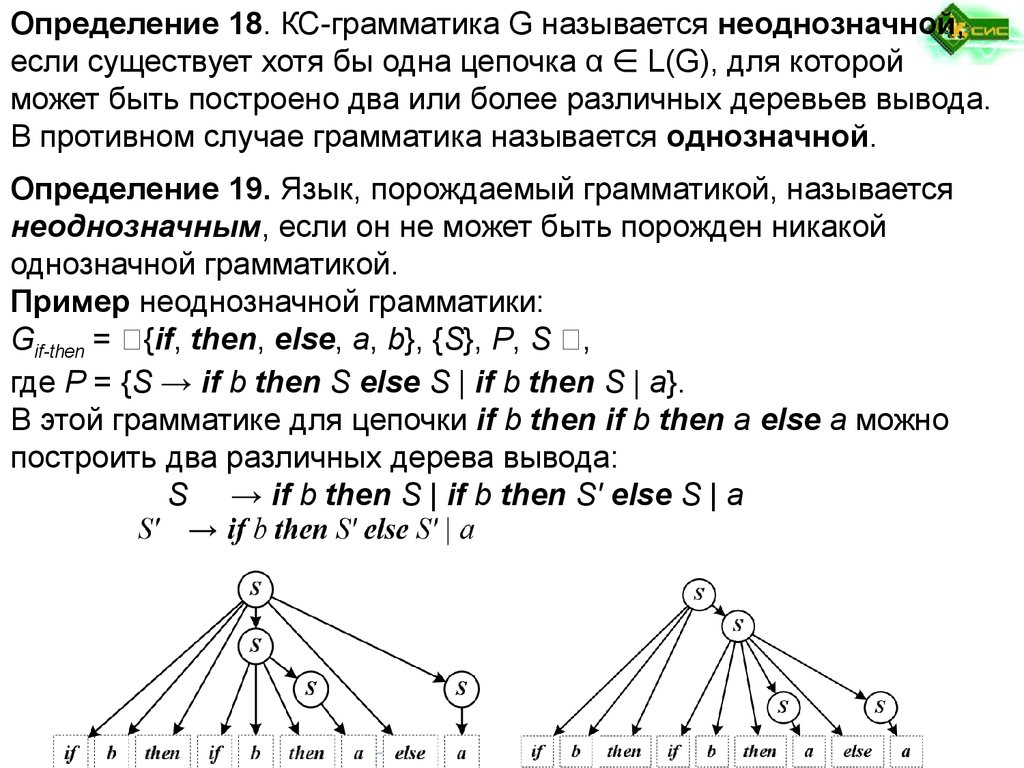
Определение 18. КС-грамматика G называется неоднозначной,если существует хотя бы одна цепочка α ∈ L(G), для которой
может быть построено два или более различных деревьев вывода.
В противном случае грамматика называется однозначной.
Определение 19. Язык, порождаемый грамматикой, называется
неоднозначным, если он не может быть порожден никакой
однозначной грамматикой.
Пример неоднозначной грамматики:
Gif-then = ✕{if, then, else, a, b}, {S}, P, S ✕,
где P = {S → if b then S else S | if b then S | a}.
В этой грамматике для цепочки if b then if b then a else a можно
построить два различных дерева вывода:
S → if b then S | if b then S' else S | a
35.
36.
Определение 20. Символ x ∈ T ∪ N называетсянедостижимым в грамматике G = 〈 T, N, P, S 〈, если он не
появляется ни в одной сентенциальной форме этой грамматики.
Алгоритм удаления недостижимых символов
Вход: КС-грамматика G = 〈 T, N, P, S 〈,
Выход: КС-грамматика G´ = 〈 T´, N´, P´, S 〈, не содержащая
недостижимых символов, для которой L(G) = L(G’).
Метод:
1. V0 = {S}; i = 1.
2. Vi = Vi − 1 ∪ {x | x ∈ T ∪ N, A → α x β ∈ P, A ∈ Vi − 1, α, β
∈ ( T ∪ N )*} .
Если Vi ≠ Vi − 1, то i = i + 1 и переходим к шагу 2, иначе N´ =
Vi ∩ N ; T´= Vi ∩ T ;
P´ состоит из правил множества P, содержащих только символы
из Vi ;
В итоге получаем G´ = 〈 T´, N´, P´, S 〈.
37.
Определение 21. Символ A ∈ N называется бесплодным вграмматике
G =〈 T, N, P, S 〈, если множество {α ∈ T* | A 〈 α} пусто.
Алгоритм удаления бесплодных символов
Вход: КС-грамматика G = 〈 T, N, P, S 〈.
Выход: КС-грамматика G´ = 〈 T´, N´, P´, S 〈, не содержащая
бесплодных символов, для которой L(G) = L(G' ).
Метод:
Строим множества N0, N1, ...
1. N0 = 〈, i = 1.
2. Ni = Ni − 1 ∪ {A | A → α ∈ P и α ∈ (Ni − 1 ∪ T*) }.
Если Ni ≠ Ni − 1, то i = i + 1 и переходим к шагу 2, иначе N´ = Ni ;
P´ состоит из правил множества P, содержащих только символы
из N´ ∪ T ;
G´ = 〈 T´, N´, P´, S 〈.
38.
Определение 22. КС-грамматика G называется приведенной,если в ней нет недостижимых и бесплодных символов.
Эквивалентные преобразования КС-грамматик
1. Обнаруживаются и удаляются все бесплодные нетерминалы.
2. Обнаруживаются и удаляются все недостижимые символы.
Удаление символов сопровождается удалением правил вывода,
содержащих эти символы.
Замечание
Если в этом алгоритме приведения поменять местами шаги (1) и
(2), то не всегда результатом будет приведенная грамматика.
Для описания синтаксиса языков программирования стараются
использовать однозначные приведенные КС-грамматики.
Некоторые применяемые на практике алгоритмы разбора по КСграмматикам требуют, чтобы в грамматиках не было правил с
пустой правой частью, т. е. чтобы КС-грамматика была
неукорочивающей. Для любой КС-грамматики существует
эквивалентная неукорачивающая.







































 informatics
informatics








