Система программирования. Основные компоненты системы программирования

1.

Система программирования —
это комплекс программных инструментов
и библиотек, который поддерживает
весь технологический цикл создания
программного продукта.
1

2. Основные компоненты системы программирования

1.
Транслятор - переводит программы с языка
программирования на машинный язык, что и позволяет
выполнить их на ЭВМ.
2.
Макрогенератор или макропроцессор - работает
непосредственно перед транслятором, используется для
получения макрорасширения исходной программы.
3.
Редактор текстов - используется для составления программ
на языке программирования.
4.
Редактор связей или компоновщик - предназначен для
связывания между собой (по внешним данным) объектных
файлов, порождаемых компилятором, а также файлов
библиотек, входящих в состав СП.
5.
Отладчик - используется для проверочных запусков
программ и исправления ошибок.
6.
Библиотеки стандартных программ - облегчают работу
программиста, используются на этапе трансляции и

3. Трансляторы

Главным компонентом систем программирования
является транслятор.
Все трансляторы подразделяются на два основных
класса:
- компиляторы,
- интерпретаторы.
3

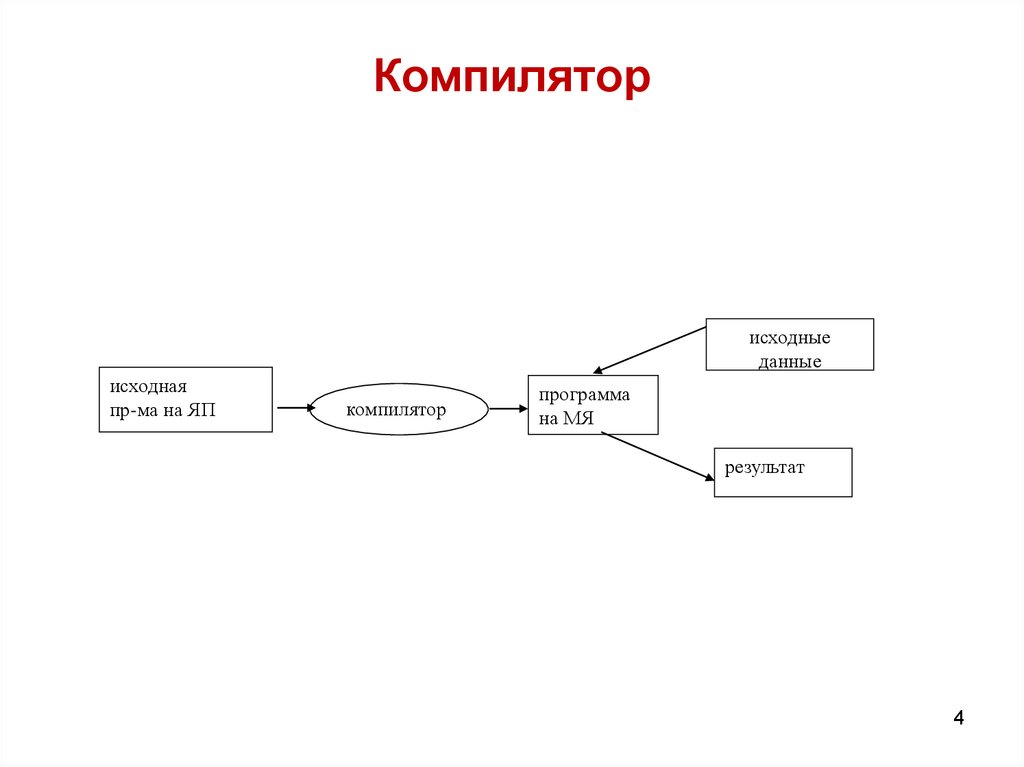
4. Компилятор

исходные
данные
исходная
пр-ма на ЯП
компилятор
программа
на МЯ
результат
4

5. Интерпретатор

исходные
данные
исходная
пр-ма на ЯП
интерпретатор
результат
5

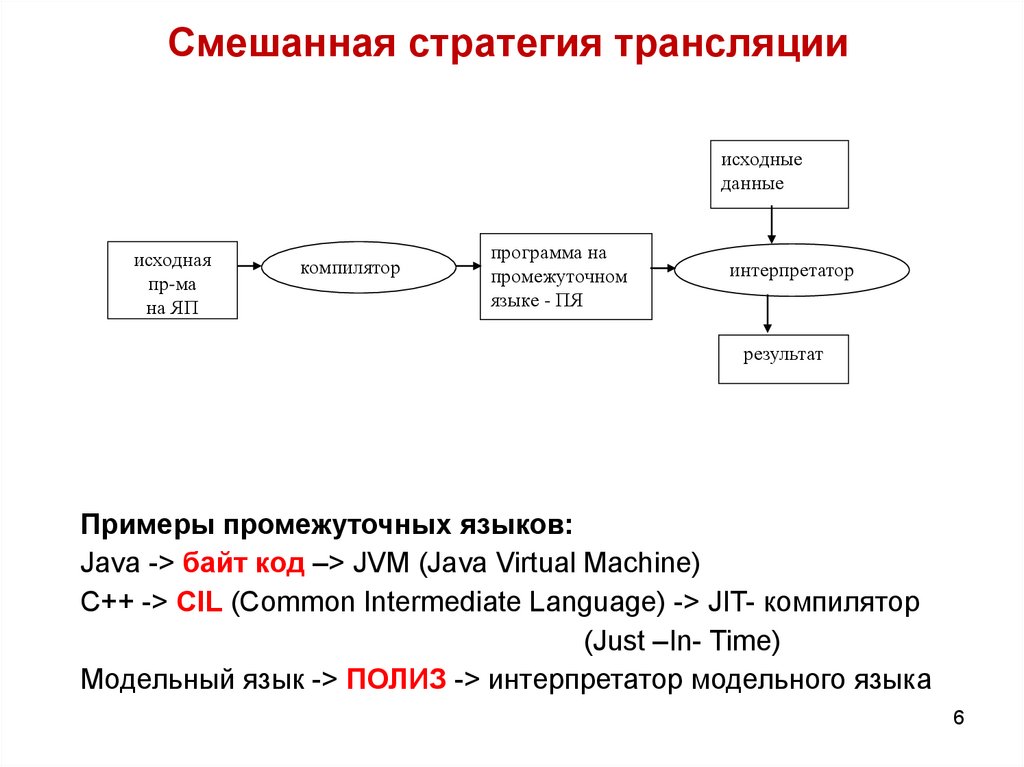
6. Смешанная стратегия трансляции

исходные
данные
исходная
пр-ма
на ЯП
компилятор
программа на
промежуточном
языке - ПЯ
интерпретатор
результат
Примеры промежуточных языков:
Java -> байт код –> JVM (Java Virtual Machine)
C++ -> CIL (Common Intermediate Language) -> JIT- компилятор
(Just –In- Time)
Модельный язык -> ПОЛИЗ -> интерпретатор модельного языка
6

7. Проход компилятора

Проход компилятора – процесс последовательного чтения
компилятором данных из внешней памяти, их обработка
и помещение результата во внешнюю память, в
частности, ОП.
Один проход включает в себя выполнение одного или
нескольких этапов компиляции.
Результат промежуточных проходов
представление исходной программы.
–
внутреннее
Результат последнего прохода – объектная программа
7

8. Схема функционирования компилятора

исходная программа на ЯП
лексический анализ
последовательность лексем
синтаксический анализ
фаза
анализа
промежуточное представление программы
семантический анализ
(контроль контекстных условий)
подготовка к генерации
объектного модуля
фаза
синтеза
генерация объектного модуля
объектный модуль
8

9. Описание формального языка

Алфавит задается перечислением символов, которые могут
использоваться для записи текстов на каком-либо языке.
Синтаксис определяется набором правил, устанавливающих, какие
комбинации символов алфавита являются правильными
текстами на определяемом языке и позволяющих связать с
каждым правильным текстом на этом языке некоторую
синтаксическую структуру.
Семантика определяет смысл синтаксически правильных
конструкций языка, то, что означает конструкция.
Семантика обычно описывается словами. Четкое и точное
описание семантики очень важно для транслятора, т.к. его цель получить эквивалентную программу на МЯ (для компилятора),
либо точно выполнить указанные действия (для интерпретатора).
Пример предложения на русском языке, допускающего 128
различных интерпретаций:
Возмущение рабочих бригад вызвало осуждение
товарища министра
9
Прагматика формального языка - аргументации того, зачем та или

10. Теория формальных языков и грамматик. Определения 1

Алфавит V - конечное непустое множество символов
Цепочка символов в алфавите V - любая конечная
последовательность символов этого алфавита.
Пустая цепочка – – цепочка, которая не содержит ни
одного символа.
Если и - цепочки, то цепочка - конкатенация
цепочек и .
Например, если
= ab
то
= abcd
и
= cd,
Для пустой цепочки: = =
10

11. Определения 2

Обращение (или реверс) цепочки - цепочка, символы
которой записаны в обратном порядке, обозначается как R.
Например, если = abcdef, то R = fedcba,
= R.
n-ая степенью цепочки ( n) – конкатенация n цепочек ;
0 = ;
n = n-1 = n-1 .
Длина цепочки - количество составляющих ее символов.
Например, если = abcdefg, то длина равна 7.
Длина цепочки обозначается | | .
| |=0
11

12. Определения 3

Язык в алфавите V - это подмножество цепочек
конечной длины в этом алфавите.
V* - множество, содержащее все цепочки конечной
длины в алфавите V, включая пустую цепочку .
Например, если V = { 0, 1 }, то
V* = { , 0, 1, 00, 11, 01, 10, 000, 001, 011, ...}.
V+ - множество, содержащее все цепочки конечной
длины в алфавите V, исключая пустую цепочку .
V* = V+ { }.
12

13. Порождающая грамматика

Порождающая грамматика G - это четверка
G = (T, N, P, S) ,
где
T – непустое множество терминальных символов
( алфавит терминалов ),
N – непустое множество нетерминальных символов
(алфавит нетерминалов), не пересекающийся с T,
P - конечное подмножество множества (T N)+ (T N)*.
Элемент ( , ) множества P называется
правилом вывода и записывается в виде → ,
причем содержит хотя бы один нетерминальный
символ.
S - начальный символ (цель) грамматики, S N.
13
Декартовым произведением A B множеств A и B называется

14. Соглашения по умолчанию

1) Большие латинские буквы будут обозначать нетерминальные
символы.
2) S - будет обозначать начальный символ (цель) грамматики.
3) Маленькие греческие буквы будут обозначать цепочки
символов.
4) Все остальные символы (маленькие латинские буквы, знаки
операций и пр.) будем считать терминальными символами.
5) для записи правил вывода с одинаковыми левыми частями
1
2
...
n
будем пользоваться сокращенной записью
1 | 2 |...| n.
Каждое i , i = 1, 2, ... ,n , будем называть альтернативой
14
правила вывода из цепочки .

15.

Понятие вывода цепочек в грамматике G = (T,N,P,S)
Цепочка (T N)* непосредственно выводима из
цепочки (T N)+ в грамматике G = (T, N, P, S) ,
обозначается: , если = 1 2, = 1 2,
где 1, 2, (T N)*, (T N)+
и правило вывода содержится в P.
Цепочка (T N)* выводима из цепочки (T N)+ в
грамматике G = (T, N, P, S), обозначается ,
если существуют цепочки 0, 1, ... , n (n >= 0), такие, что
= 0 1 ... n = .
Последовательность
выводом длины n.
0, 1, ... , n называется
15

16.

Язык, порождаемый грамматикой G = (T, N, P, S)
Язык, порождаемый грамматикой G = (T, N, P, S)
– L(G) – это множество терминальных цепочек,
выводимых из начального символа грамматики
L(G) = { T* | S }
Сентенциальная форма в грамматике G = (T, N, P, S) цепочка (T N)*, для которой S .
Язык, порождаемый грамматикой - множество
терминальных сентенциальных форм.
16

17. Примеры грамматик и порождаемых ими языков

G1 = ( {0,1}, {A,S}, P, S),
где P :
S 0A1
0A 00A1
A
L(G1) = { 0 n 1 n | n >= 1 } – формула
G2 = ( {a, b, c, d}, {A,S}, P, S),
где P :
S aAc
A b|d|
L(G2) = { abc, adc, ac } – перечисление цепочек конечного языка
G3 = ( {0,1}, {A, B, C, D, S}, P, S),
где P :
S ASB | C | D
C CA | A
D DB | B
AB BA
A 0
B 1
L(G3) = { любые цепочки из 0 и 1 с неравным количеством 0 и171} –
словесное описание

18.

Эквивалентность грамматик
Грамматики G1 и G2 эквивалентны, если L(G1) = L(G2).
Например, G1 = ({0,1}, {A,S}, P1, S)
и
G2 = ({0,1}, {S}, P2, S)
P1: S 0A1
P2: S 0S1 | 01
0A 00A1
A
эквивалентны, т.к. обе порождают один и тот же язык:
L(G1) = L(G2) = { 0 n 1 n | n > 0}.
Грамматики G1 и G2 почти эквивалентны, если
L(G1) { } = L(G2) { }.
Например, G1 = ( {0,1}, {A,S}, P1, S ) и G2 = ( {0,1}, {S}, P2, S )
P1: S 0A1
P2: S 0S1 |
0A 00A1
A
18
почти эквивалентны, так как

19. Классификация грамматик и языков по Хомскому. Типы 0 и 1

ТИП 0:
Грамматика G = (T, N, P, S) - грамматика типа 0, если на ее правила
вывода не накладывается никаких ограничений.
ТИП 1:
Грамматика G = (T, N, P, S) - неукорачивающая , если каждое правило
из P имеет вид
→ , где (T N)+, (T N)+ и | | <= | |.
Исключение - в неукорачивающей грамматике допускается наличие
правила S → , при условии, что S (начальный символ)
не встречается в правых частях правил.
Грамматика G = (T, N, P, S) - контекстно-зависимая ( КЗ ), если каждое
правило из P имеет вид
→ , где = 1 A 2; = 1 2; A N; (T N)+; 1, 2 (T N)*.
В КЗ-грамматике допускается Исключение.
19

20. Классификация грамматик и языков по Хомскому. Тип 2

ТИП 2:
Грамматика G = (T, N, P, S) - контекстно-свободная ( КС ),
если каждое правило из Р имеет вид
A → , где A N, (T N)*.
Грамматика G = (T, N, P, S) - неукорачивающая контекстносвободная (НКС), если каждое правило из Р имеет вид
A → , где A N, (T N)+.
Для неукорачивающей КС-грамматики допускается
Исключение.
Грамматику типа 2 можно определить как
контекстно-свободную, либо как
неукорачивающую контекстно-свободную.
20

21. Классификация грамматик и языков по Хомскому. Тип 3

ТИП 3:
Грамматика G = (T, N, P, S) - праволинейная, если каждое
правило из Р имеет вид имеет вид:
A → wB либо A → w, где A, B N, w T *.
Грамматика G = (T, N, P, S) - леволинейная, если каждое
правило из Р имеет вид:
A → Bw либо A → w, где A, B N, w T *.
Грамматику типа 3 (регулярную, Р-грамматику) можно
определить как праволинейную, либо как леволинейную.
Грамматика автоматная - праволинейная или леволинейная если каждое правило с непустой правой частью имеет вид:
A → a либо A → aB - для праволинейной грамматики,
A → a либо A → Ba – для леволинейной грамматики,
где A, B N, a T.
21
Грамматики типа 3 могут быть неукорачивающими, для них также

22. Соотношения между типами грамматик

неук. Р неук. КС КЗ Тип 0
(1) Любая регулярная грамматика является КС-грамматикой.
(2) Любая неукорачивающая КС-грамматика является КЗграмматикой.
(3) Любая неукорачивающая грамматика является
грамматикой типа 0.
Язык L(G) является языком типа k по Хомскому, если его
можно описать грамматикой типа k, где k - максимально
возможный номер типа грамматики по Хомскому.
22

23. Соотношения между типами языков

Р КС КЗ Тип 0
(1) Каждый регулярный язык является КС-языком, но существуют КСязыки, которые не являются регулярными
( например, L = { an bn | n > 0 }).
(2) Каждый КС-язык является КЗ-языком, но существуют КЗ-языки,
которые не являются КС-языками
( например, L = { an bn cn | n > 0 }).
,
(3) Каждый КЗ-язык является языком типа 0, но существуют языки типа
0, которые не являются КЗ-языками
(например: язык, состоящий из записей самоприменимых
алгоритмов Маркова в некотором алфавите).
(4) Кроме того, существуют языки, которые вообще нельзя описать с
помощью порождающих грамматик. Такие языки не являются
рекурсивно перечислимым множеством.
Проблема, можно ли язык, описанный грамматикой типа k, описать
грамматикой типа k + 1 (k = 0, 1, 2), является алгоритмически 23
неразрешимой.

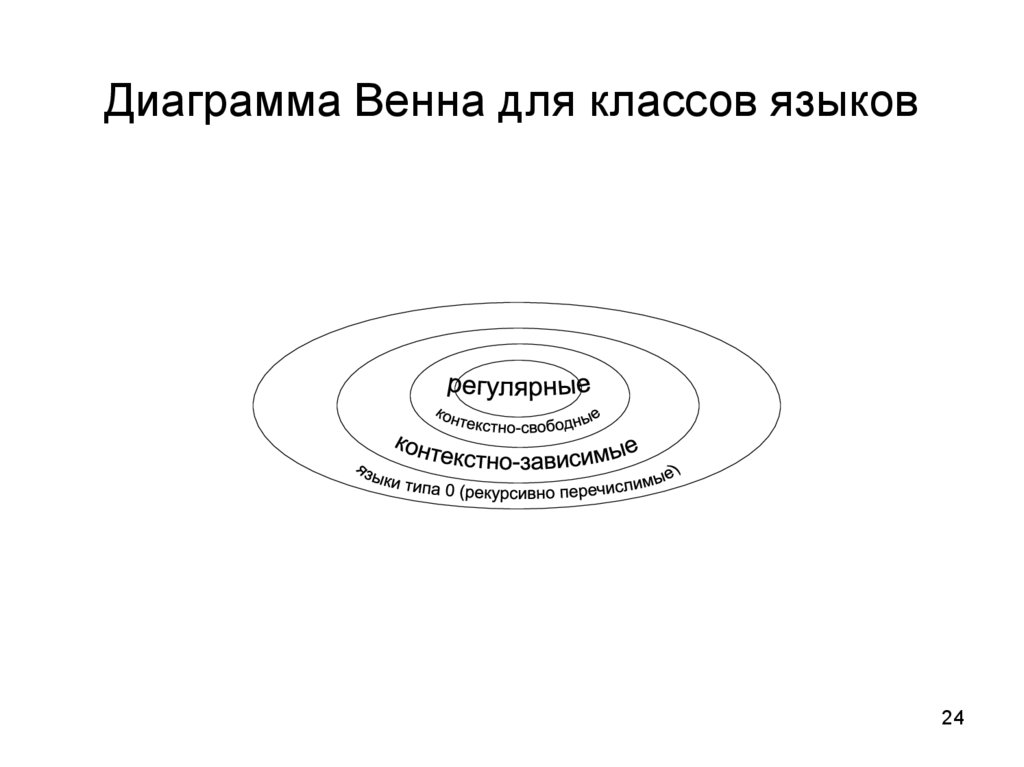
24. Диаграмма Венна для классов языков

24

25. КС-грамматики

Разбор цепочки - процесс построения вывода цепочки из цели S грамматики
G = (T, N, P, S).
Вывод цепочки T* из S N в КС-грамматике G = (T, N, P, S), называется:
- левосторонним, если в нем каждая очередная сентенциальная форма
получается из предыдущей заменой самого левого нетерминала.
- правосторонним, если в нем каждая очередная сентенциальная форма
получается из предыдущей заменой самого правого нетерминала.
Например, для цепочки a+b+a в грамматике
G = ( {a, b, +}, { S,T }, { S → T | T+S; T → a | b }, S)
можно построить выводы:
(1) S → T+S → T+T+S → T+T+T → a+T+T → a+b+T → a+b+a - произвольный
(2) S → T+S → a+S → a+T+S → a+b+S → a+b+T → a+b+a - левый
(3) S → T+S → T+T+S → T+T+T → T+T+a → T+b+a → a+b+a - правый
Выводы (1) – (3) являются эквивалентными в том смысле, что в них в одних25и
тех же местах применяются одни и те же правила вывода, но в различном порядке.

26. Дерево вывода

Дерево вывода (или дерево разбора) в КС-грамматике G = (T, N, P, S) –
дерево, для которого выполнены следующие условия:
(1) дерево ориентировано и упорядочено;
(2) каждая вершина дерева помечена символом из множества N T { },
при этом корень дерева помечен символом S; листья - символами из T { };
(3) если вершина дерева помечена символом A N, а ее непосредственные
потомки - символами a1, a2, ... , an , где каждое ai T N, то
A → a1 a2 ... an - правило вывода в этой грамматике;
(4) если вершина дерева помечена символом A N, а ее единственный
непосредственный потомок помечен символом , то A → - правило вывода в
этой грамматике.
S
Пример дерева вывода для цепочки a + b + a в грамматике G:
T
S
+
a
S
T
+
T
b
a
26

27. Неоднозначность грамматик 1

КС-грамматика G неоднозначная, если существует хотя бы одна
цепочка L(G), для которой может быть построено два или более
различных деревьев вывода.
В противном случае грамматика является однозначной.
Если грамматика однозначная, то при любом способе построения,
нисходящем или восходящем, будет получено одно и то же дерево
разбора.
Пример неоднозначной грамматики:
G_if = ( { if, then, else, a, b }, { S }, P, S),
где P = {
S → if b then S else S | if b then S | a
В этой грамматике для цепочки
if b then if b then a else a
можно построить два различных дерева вывода.
}.
27

28. Неоднозначность грамматик 2

Неоднозначность - это свойство грамматики, а не
языка.
Если грамматика используется для определения языка
программирования, то она должна быть однозначной.
Можно преобразовать грамматику G_if, устранив
неоднозначность:
S → if b then S | T
T → if b then T else S | a
Проблема определения, является ли заданная КСграмматика однозначной, является алгоритмически
неразрешимой.
28

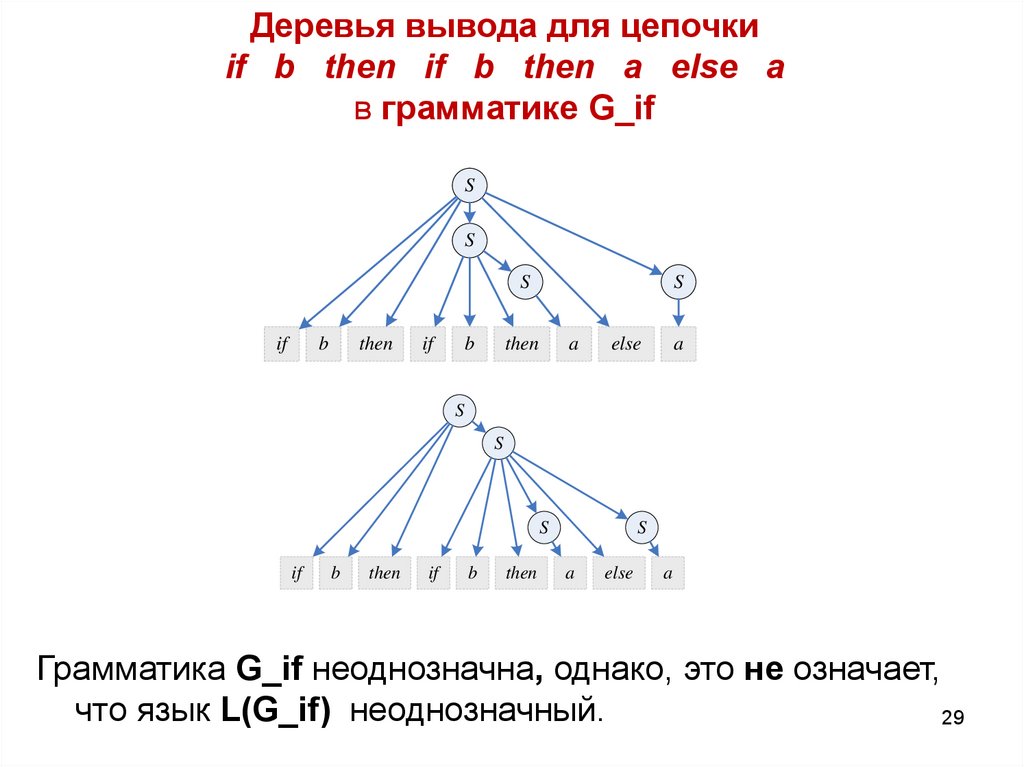
29. Деревья вывода для цепочки if b then if b then a else a в грамматике G_if

S
S
S
if
b
then
if
b
S
then
a
else
a
S
S
S
if
b
then
if
b
then
S
a
else
a
Грамматика G_if неоднозначна, однако, это не означает,
что язык L(G_if) неоднозначный.
29

30. Преобразование неоднозначных грамматик

Некоторые виды правил вывода, которые приводят к неоднозначности и
некоторые способы эквивалентных преобразований неоднозначных
грамматик к однозначным:
1. A → AA |
A → A |
(док-во для ) – порождаются подцепочки n (n >= 1);
2. A → A A |
A → A |
(док-во для ) – порождаются подцепочки ( )n (n >= 0);
3. A → A | A |
A → A | B;
B → B | , B N
(док-во для ) – порождаются подцепочки n m (n, m >= 0);
4. A → A | A A |
A → A | В;
В → В A | , B N
(док-во для ) –
порождаются подцепочки δ = n m ( δ)m (n,m
>=0)
30
Таким приемом преобразована грамматика G_if :