Similar presentations:
Функцияның туындысы нольге тең немесе туындысы болмайтын анықталу облысының ішкі нүктелері сындық нүктелер деп атайды
1. Анықтама
• Функцияның туындысы нольге тең немесетуындысы болмайтын анықталу
облысының ішкі нүктелері сындық
нүктелер деп атайды.
2. Қажетті шарты
Егер f(x) функциясының х экстремумнүктесі болып және оны осы нүктенің
аймағында f’(x ) туындысы бар болса ,
онда ол туынды х нүктесінде нөлге
тең , яғни f’(x )=0
3.
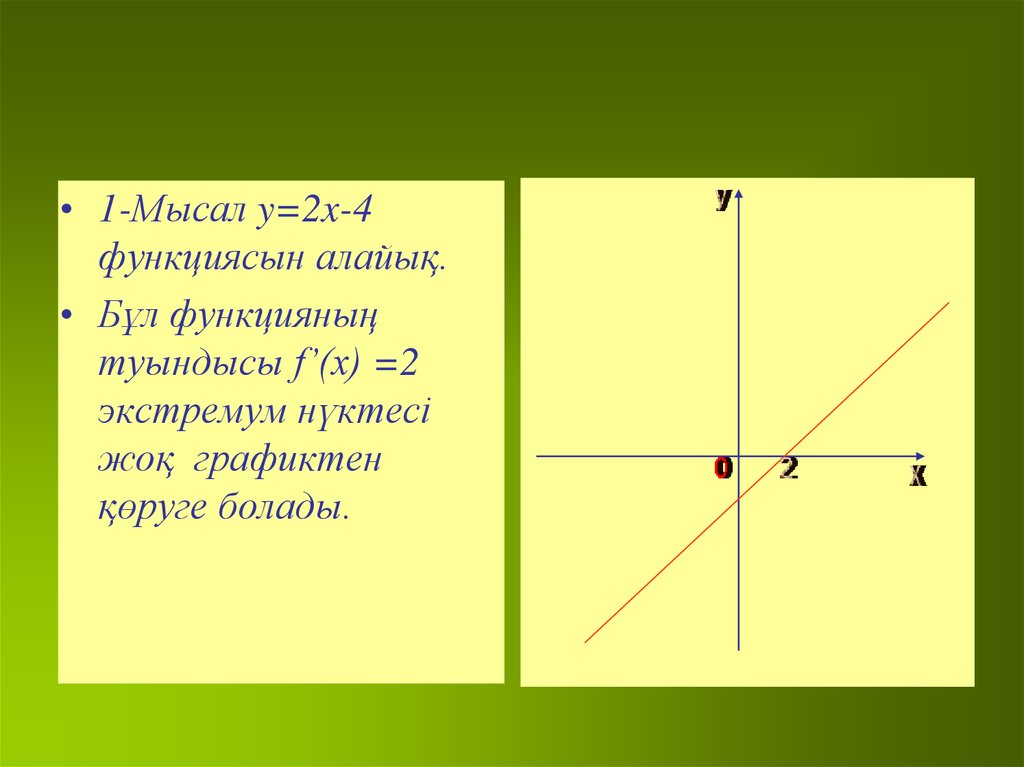
• 1-Мысал y=2x-4функциясын алайық.
• Бұл функцияның
туындысы f’(x) =2
экстремум нүктесі
жоқ графиктен
қөруге болады.
4. Жеткілікті шарты
• Егер х нүктесінде f(x) функциясыүзіліссіз, ал (а;х ) аралығында f’(x)>0
(f’(x)<0)және (х ;b) аралығында f’(x)<0
(f’(x)>0 ) болса , онда х нүктесінде f(x)
функцияның максимум (минимум)
нүктесі болады.
5. Теореманы жеңілдетілген тұжырымы
х нүктесінің аймағындатуынды таңбасы плюстен
минуске ауыстырлыса , онда х
нүктесі максимум нүтесі
болады.
х нүктесінің аймағында
туынды таңбасы минустен
плюске ауыстырлыса , онда х
нүктесі минимум нүтесі
болады.
6. Функцияның экстремум нүктелерін табу алгоритмі
• 1. функцияның туындысын табу;• 2.функцияның сындық нүктелерін табу,
яғни f’(x)=0 теңдеуін шешу;
• 3. сындық нүктелер аймағында f’(x)
тыундының таңбасын интервалдар
әдісімен анықтау;
• 4.экстремум нүтелерінің бар болуының
жеткілікті шартын ,қолданып максимум
және минимум нүктелерін табу.





 mathematics
mathematics








