Similar presentations:
Функцияның шегі. Қасиеті
1. Функцияның шегі. Қасиеті.
2. Анықтама
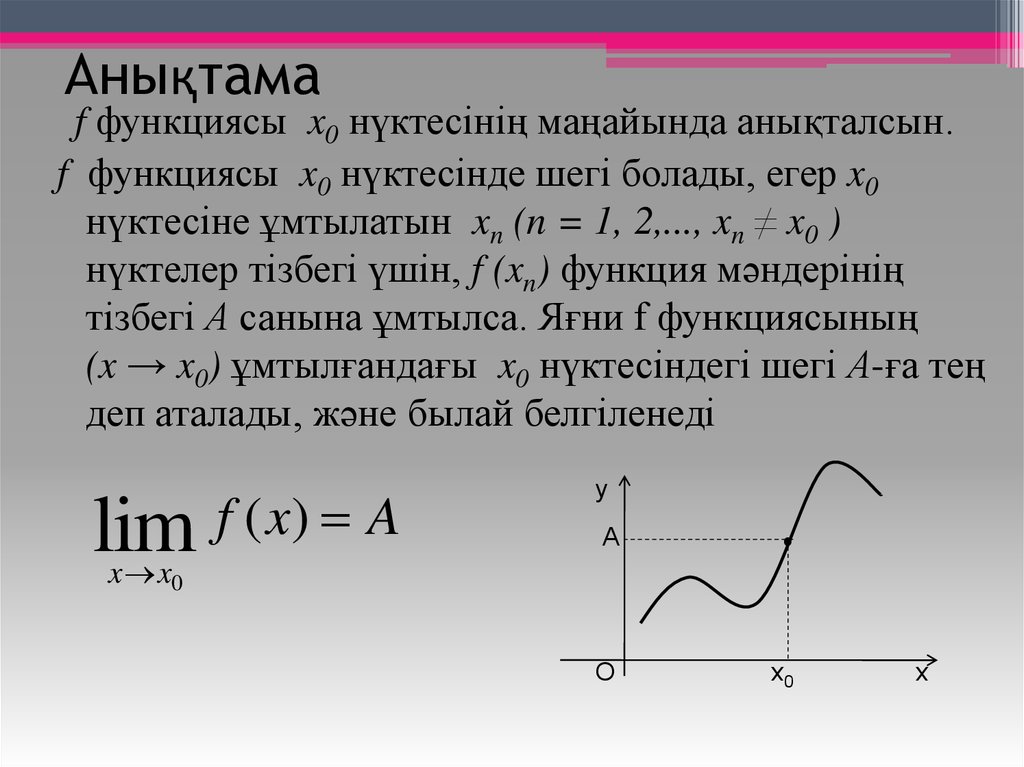
f функциясы x0 нүктесінің маңайында анықталсын.f функциясы x0 нүктесінде шегі болады, егер x0
нүктесіне ұмтылатын xn (n = 1, 2,..., xn ≠ x0 )
нүктелер тізбегі үшін, f (xn) функция мәндерінің
тізбегі А санына ұмтылса. Яғни f функциясының
(x → x0) ұмтылғандағы x0 нүктесіндегі шегі А-ға тең
деп аталады, және былай белгіленеді
lim f ( x) A
x x0
у
А
О
х0
х
3. Шектің қасиеті
егер f (x) және g (x) функциялары шегі бар болса,Онда
егер B ≠ 0 және егер g (x) ≠ 0
4. Функцияның нүктедегі шегін есептеу мысалдары
2lim
(
x
1 x 3 5x 8) 9 15 8 2
2
lim ( x 2 5 x 8)
x 5 x 8 x 3
2 1
lim 2
.
2
x 3 x x 4
lim ( x x 4) 10 5
2
x 3
3
x 2 5x 8 2
lim
.
x 3
x 3
0
5. Анықталмаған жағдайларды ашу
Шектерді есептеу барысында келесі анықталмағанжағдайлармен кездесеміз
0
0
0
,
,
(
),
(
1
),
(
0
),
(
0
)(
).
0
Осы жағдайларда шекті есептеу анықталмағандықты ашу
деп аталады. Нәтижесінде нақты сан, ноль немесе
шексіздік шығуы мүмкін
∞/∞ түріндегі анықталмағандықты ашу үшін, айнымалының
жоғарғы дәрежесіне алымы мен бөлімін бөлу жеткілікті
6.
:Жалпы ереже: егер бөлшектің алымы мен бөлімінде
көпмүшеліктер, және 0/0 түріндегі анықталмаған жағдай
болса, онда оны ашу үшін бөлшектің алымы мен бөлімін
көбейткіштерге жіктеу керек.
7.
8.
Алымы мен бөлімін түйіндес өрнекке көбейту әдісіЕгер бөлшектің алымы (бөлімінде) иррационал өрнек болса, одан
құтылу үшін бөлшектің алымы (бөлімін) түйіндес өрнекке
көбейту керек
9. Тамаша шектер
Бірінші тамаша шекsin x
lim
1;
x 0
x
Екінші тамаша шек
х
1
1
lim 1 lim (1 x) x e.
x
x 0
x








 mathematics
mathematics








