Similar presentations:
Общая идея метода статистических испытаний
1. Общая идея метода статистических испытаний
Урок № 382.
Основная идея метода статистическихиспытаний состоит в следующем:
вместо аналитического решения задачи
либо проводят эксперименты, испытания,
непосредственно рассматриваемые в
задаче, либо эти испытания заменяют другими,
имеющими с исходными одинаковую
вероятностную структуру, или, иначе говоря,
рассматриваемые в задаче случайные явления
имитируют, моделируют другими случайными
явлениями.
3.
Определенные по результатам достаточнобольшого числа испытаний характеристики
случайных явлений (относительные частоты,
средние арифметические) используют в качестве
приближенного решения задачи (в качестве оценок
вероятностей, математических ожиданий).
Допустимость этого приближения основывается на
законе больших чисел.
4.
Метод статистических испытаний применяютдля решения не только тех задач, в которых в
явном виде имеются случайные явления, но
также и для решения многих математических
задач, не содержащих таких явлений.
5.
В этом случае искусственно подбирают такоеслучайное явление, характеристики которого
связаны с результатом решения исходной
задачи.
Для определения числовых значений этих
характеристик используется метод
статистических испытаний.
6.
Так как достаточно высокая точность решенияпри использовании метода статистических
испытаний гарантируется, как правило, только
при проведении большого числа испытаний,
этот метод практически можно реализовать
только на быстродействующих ЭВМ.
По этой причине метод статистических
испытаний называют иногда «машинным».
7. Задача № 1
Система контроля качества продукциисостоит из трех приборов.
Вероятность безотказной работы
каждого из них в течении времени Т равна 5\6.
Приборы выходят из строя независимо друг от
друга.
При отказе хотя бы одного прибора вся система
перестают работать.
Найти вероятность Ротк того, что система
откажет за время Т.
8. Аналитическое решение
Событие А (выход из строя хотя бы одногоиз трех приборов за время Т) и событие А (ни
один из трех приборов не выйдет из строя за
время Т) – противоположные.
3
Вероятность Р (А) = (5/6).
Искомая вероятность
3
Р отк = Р(А) = 1 – Р(А) = 1 – (5/6) = 0,42.
9. Решение методом статических испытаний
В условиях данной задачи «натуральный»эксперимент – наблюдение за работой
системы в течении времени Т.
Многократное повторение этого
эксперимента может оказаться
трудноосуществимым или просто
невозможным.
10. Второй подход
Имитировать сложные экспериментыдругими, имеющими с исходными
одинаковую вероятностную структуру.
Заменим наблюдение за работой прибора
подбрасыванием игральной кости, так как
вероятность отказа прибора по условию
равна 1/6.
11.
Для определения того, выйдет или не выйдетиз строя за время Т отдельный прибор, будем
подбрасывать игральную кость.
Если выпадет одно очко, то будем считать, что
прибор вышел из строя; если два, три, …,
шесть очков, то будем считать, что прибор
работал безотказно.
Вероятность того, что выпадет одно очко, так
же как и вероятность выхода прибора из строя,
равна 1/6.
Вероятность того, что выпадет любое другое
число очков, как и вероятность безотказной
работы прибора, равна 5/6.
12. Работа системы
Чтобы определить, откажет или нет всясистема за время Т, будем подбрасывать
три игральные кости (или одну кость три
раза).
Если хотя бы на одной из трех костей
выпадет одно очко, то это будет означать,
что система отказала.
13.
Повторим испытание, состоящее вподбрасывании трех игральных костей,
много раз подряд и найдем отношение числа
m «отказов» системы к общему числу n
проведенных испытаний.
Вероятность отказа
Р отк ≈ m /n.
14. Задача № 2
Пусть требуется вычислить интеграл1
∫ f(x)dx.
0
Предположим, что 0 ≤ f (x) ≤ 1 при 0 ≤ x ≤ 1.
Значение этого интеграла равно площади
области G, ограниченной кривой у = f(x), осью
Ох и прямыми х = 0 и х = 1
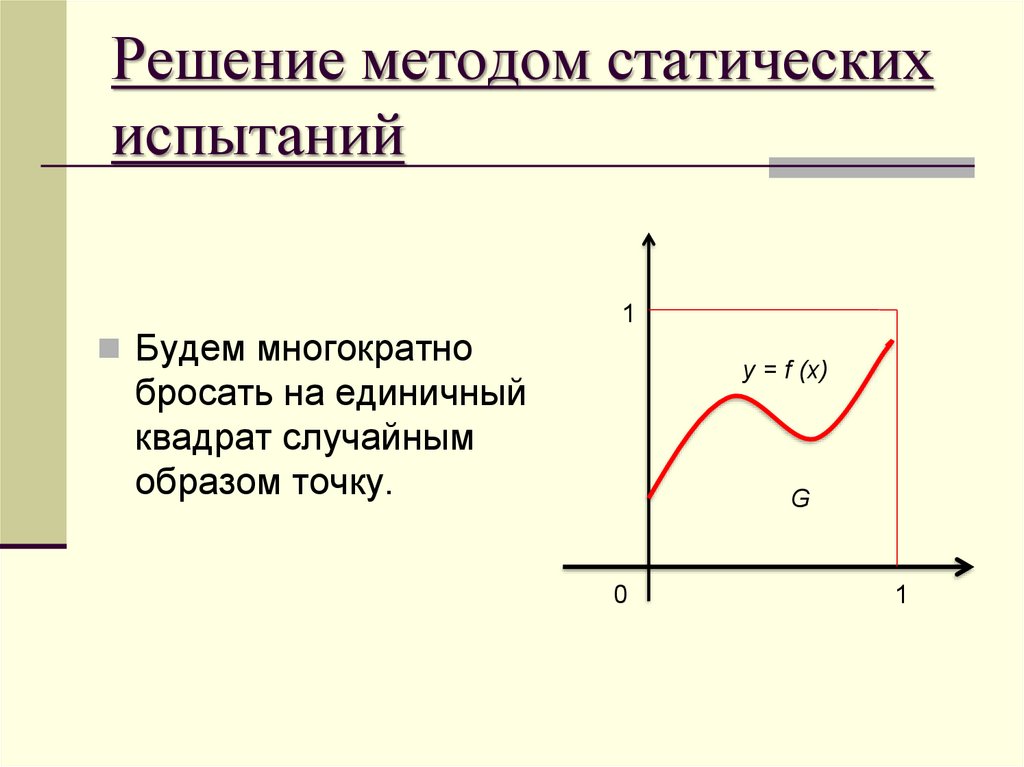
15. Решение методом статических испытаний
Будем многократно1
у = f (x)
бросать на единичный
квадрат случайным
образом точку.
G
0
1
16. Задача № 2
Подсчитаем отношение числа m бросаний, прикоторых точка попадает в область G, к общему
числу n , бросаний.
Это отношение является оценкой вероятности
pп попадания точки в область G:
pп ≈ m/ n.
17.
С другой стороны так как точка бросается вединичный квадрат наудачу, то можно
считать, что вероятность попадания ее в
область G пропорциональна площади области
и не зависит от расположения области внутри
единичного квадрата.
1
pn = SG / S11 = SG / 1 = SG =
1
∫ f(x)dx ≈ m/ n
0
∫ f(x)dx.
0
18.
В рассмотренных задачах непосредственнойцелью проведения испытаний было
определение вероятности р наступление того
или иного события.
При этом использовалось приближенное
равенство
р ≈ m/n,
где m - число наступлений события в n
испытаниях.
19.
Будем предполагать что это испытаниеБернулли, т. е. что они не зависимы и
проводятся в одинаковых условиях.
Напомним, что при выполнении этих
предположений частость m/n при достаточно
большом числе испытаний является хорошим
приближением вероятности р.
20. Это интересно!
Одним из возможных способов имитациислучайных явлений является рулетка.
Игрой в рулетку знаменит город МонтеКарло.
Именно этим объясняется другое частое
встречающееся название метода
статистических испытаний метод МонтеКарло.
21. Заключение
Таким образом, метод Монте-Карло висследовании операций есть метод
математического моделирования случайных
явлений, в котором сама случайность
непосредственно включается в процесс
моделирования и представляет собой его
существенный элемент.
Каждый раз, когда в ход операции вмешивается
тот или другой случайный фактор, его влияние
имитируется с помощью специально
организованного «розыгрыша» или «жребия».
22. Заключение
Таким образом, строится одна реализацияслучайного явления, представляющая собой как
бы результат одного «опыта».
При большом числе реализаций интересующие
нас характеристики случайного явления
(вероятности, математические ожидания)
находятся так же, как они находятся из опыта:
вероятности — как частоты событий,
математические ожидания — как средние
арифметические значений соответствующих
случайных величин.
23. Заключение
Большое число реализаций, требующееся приприменении метода Монте-Карло, делает его
вообще громоздким и трудоемким.
Прежде чем пускать в ход метод Монте-Карло,
всегда имеет смысл попытаться решить задачу
аналитически, и только если это не удается,
прибегать к статистическому моделированию.
Полезным оказывается хотя бы приближенное
предварительное аналитическое решение
задачи — это помогает выявить основные
факторы, от которых зависит результат, и
наметить план дальнейшей работы.
24. Вопросы к теме
В чем состоит основная идея методастатистических испытаний?
Перечислите методы математического
моделирования случайных явлений.
25. Домашнее задание
ЛитератураКалинина В. Н.
Глава 13.
Метод статистических испытаний.
§ 13. 1
Общая идея метода статистических
испытаний.
























 mathematics
mathematics








