Similar presentations:
Методы моделирования систем. Классификации методов. Особенности и возможности методов. Обоснование выбора методов
1. Волкова Виолетта Николаевна, д.э.н., профессор Логинова Александра Викторовна, к.э.н., доцент
• Методы моделирования систем.Классификации методов. Особенности и
возможности методов. Обоснование
выбора методов
• Методы формализованного представления
систем (МФПС): принципиальные особенности и
возможности применения
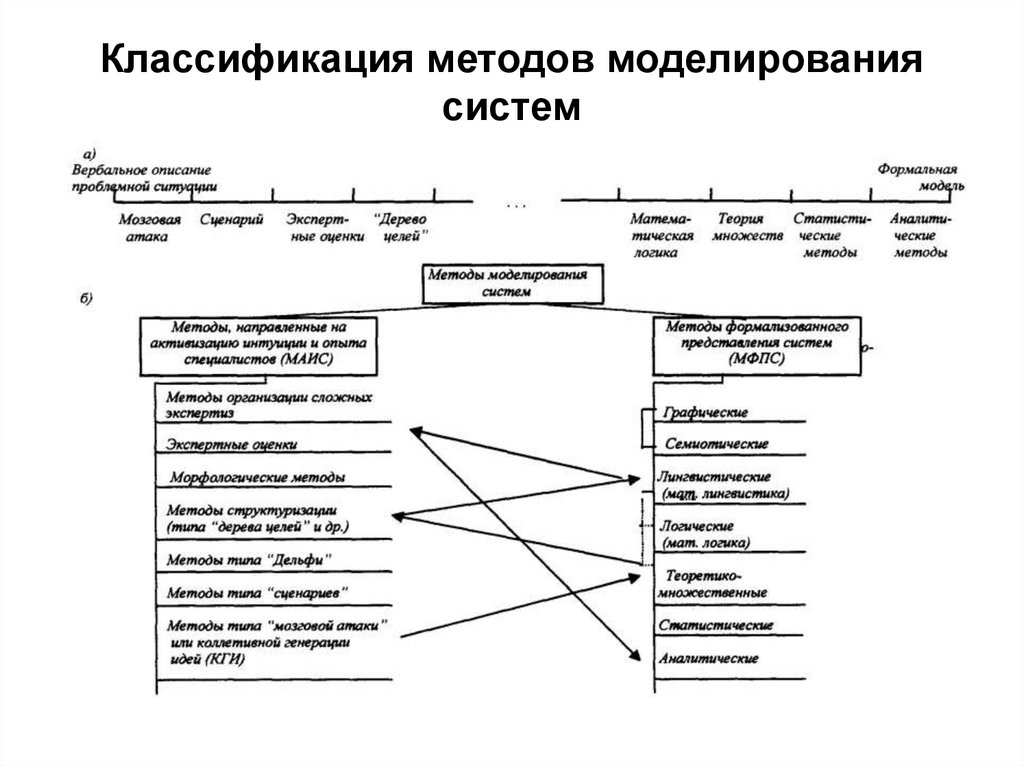
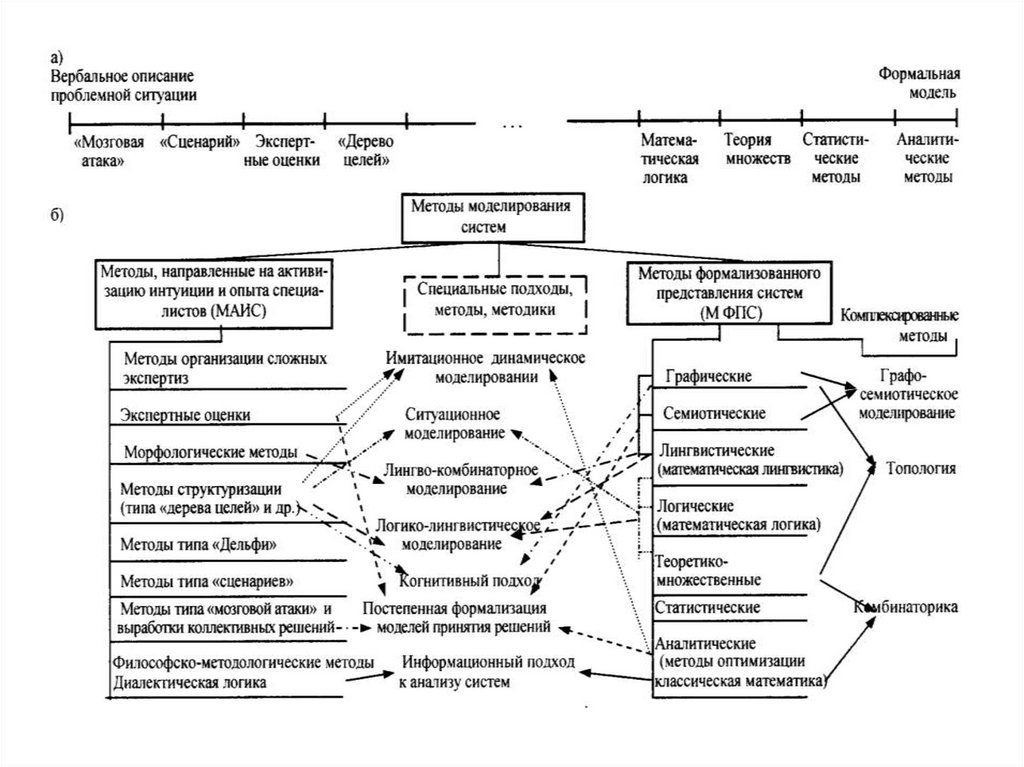
2. Классификация методов моделирования систем
3.
4. Классификация моделей по методам моделирования
5.
Классификация методов формализованного представления системВладимир
Николаевич
Козлов
Федор
Евгеньевич
Темников
6. Аналитические методы
SxФ[Sx]
• Основу понятийного (терминологического)
аппарата составляют понятия классической
математики величина, формула, функция,
уравнение, система уравнений, логарифм,
дифференциал, интеграл и т. д.).
Поведение точек, их взаимодействие описываются
строгими соотношениями, имеющими силу закона
На базе аналитических представлений возникли и
развиваются математические теории различной
сложности от аппарата классического
математического анализа (методов исследования
функций, их вида, способов представления, поиска
экстремумов функций и т.п.) до таких новых разделов
современной математики, как математическое
программирование (линейное, нелинейное,
динамическое и т. п.), теория игр (матричные игры с
чистыми стратегиями, дифференциальные игры и т. п.).
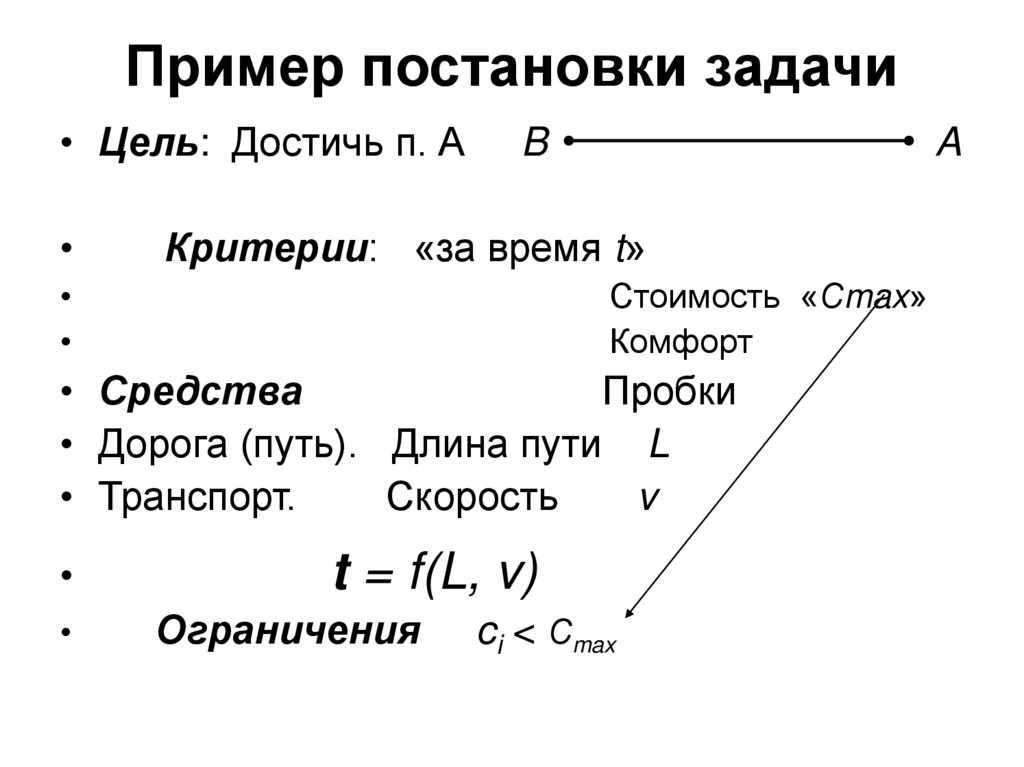
7. Пример постановки задачи
• Цель: Достичь п. АB
A
Критерии: «за время t»
Стоимость «Сmax»
Комфорт
• Средства
Пробки
• Дорога (путь). Длина пути L
• Транспорт.
Скорость
v
t = f(L, v)
Ограничения
ci < Сmax
8.
• Леони́д Вита́льевич Канторо́вич (6 (19).01.1912 —7.04.1986) —советский математик и экономист, доктор физ.-мат. наук, профессор,
академик АН СССР, один из создателей линейного программирования.
Лауреат премии по экономике памяти Альфреда Нобеля 1975 г.
• Джордж Бернард Да́нциг (англ. George Bernard Dantzig; 8.11.1914 —
13.05.2005) — американский математик, разработчик симплексметода. Считается основоположником линейного программирования,
наряду с Л. Канторовичем
• Гарольд Уильям Кун (29.07.1925 —2.07.2014 —американский
математик, Автор теоремы Куна, покера Куна, соавтор условия КунаТаккера.
• Ричард Эрнест Беллман (англ. Richard Ernest Bellman; 26.08.1920 —
19.03.1984 — американский математик, автор идеи нединейного
программирования..
9. Задача математического программирования
• Определить сколько изделий И1 и И2 (x1 и x2) нужно изготовить.Чтобы получить максимальный доход
• (сi – доход от одного изделия i-го вида; Bj – загрузка цехов)
n
• F = ci xi = 240 x1 + 320 x2 max ,
i=1
5 x1 + 4 x2 100
n
1,6 x1 + 6,4 x2 100
aij Bj .
i=1
2,9 x1 + 5,8 x2 100
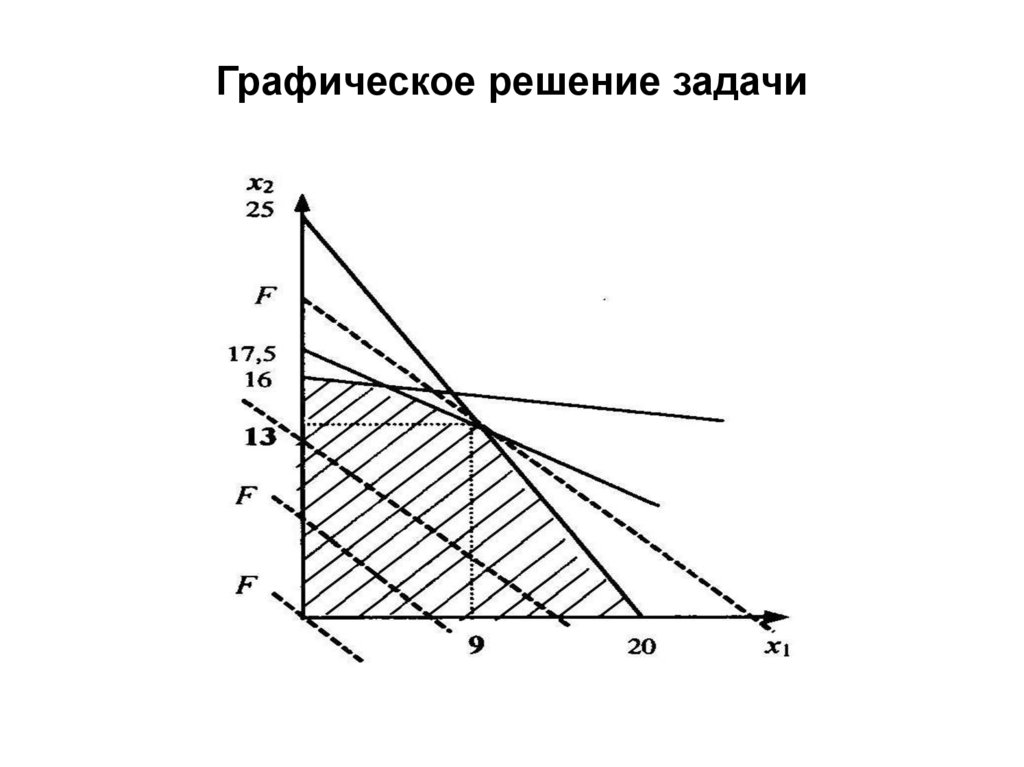
10. Графическое решение задачи
11. Постановка задаче планирования
F f i xi maxi
или
F si xi min
i
x1 – планируемый годовой выпуск изделий i-го
заказа;
Bi – количество изделий i-го вида в «портфеле
заказов»;
Di – количество изделий i-го заказа,
затребованных директивно;
pi – оптовая цена одного изделия;
P – планируемый объем реализуемой
продукции;
aij – трудоемкость изготовления i-го вида
изделия на j-м виде оборудования;
Фj – календарный фонд работы j-го вида
оборудования;
i – норматив расхода материалов на
изготовление i-го вида изделий;
Mi – фонд материалов на выпуск изделий;
zij – норматив заработной платы на
изготовление i-го вида изделий на j-м виде
оборудования;
Z – годовой фонд заработной платы;
si – себестоимость i-го вида изделий;
fi – доход от i-го изделия.
12. Пример задачи с нелинейной ЦФ
h – коэффициент загрузкиоборудования;
- коэффициент пропускной
способности оборудования
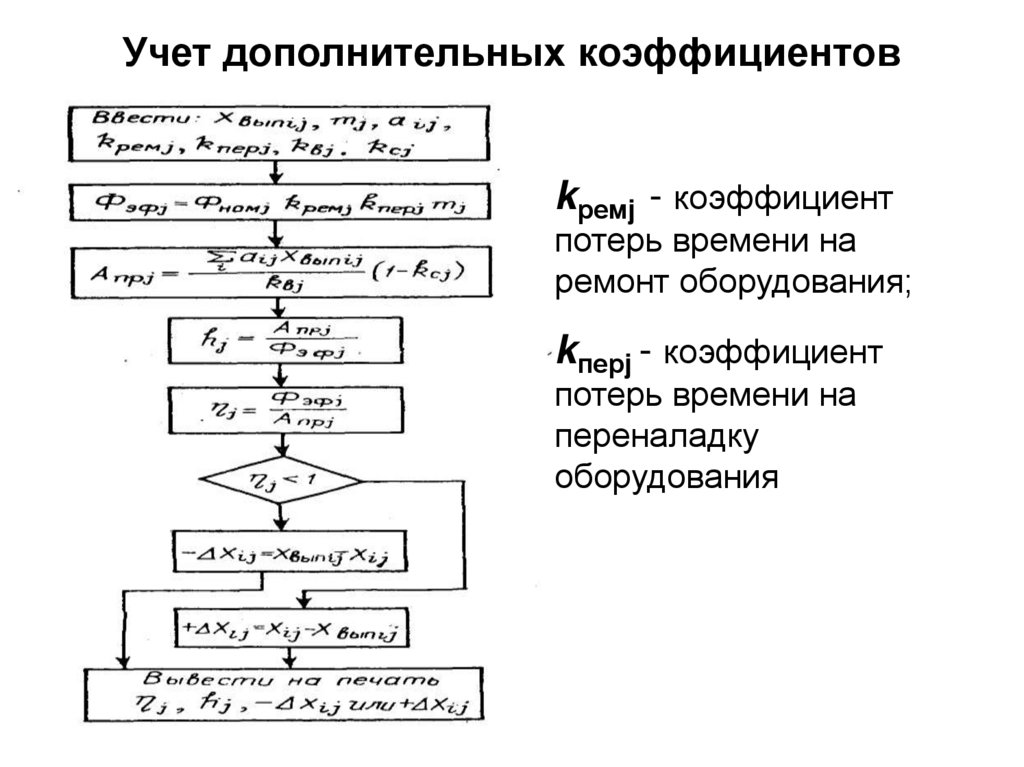
13. Учет дополнительных коэффициентов
kремj - коэффициентпотерь времени на
ремонт оборудования;
kперj - коэффициент
потерь времени на
переналадку
оборудования
14. Особенности математического программирования
введение понятий целевая функция и ограничения и ориентация на
их формирование являются и некоторыми средствами постановки
задачи; причем эти средства можно использовать даже если не удается
сформировать систему непротиворечивых ограничений или записать
целевую функцию в формальном виде, поскольку возможно в процессе
проведения исследования уточнить представление о проблемной
ситуации и, таким образом, поставить задачу хотя бы в первом
приближении; (Романовский в переписке у Купмансом)
при использовании методов математического программирования
появляется возможность объединения в единой модели
разнородных критериев (разных размерностей, предельных
значений);
модель математического программирования допускает (и даже
ориентирует на это) выход на границу области определения
переменных (в то время, как методы классической математики
требуют введения строгих начальных и граничных условий, значений
которых не может принимать переменная в процессе анализа модели);
изучение методов решения задач математического программирования
позволяет получить представление о пошаговом приближении к
решению, т. е. о пошаговом алгоритме получения результата
моделирования;
графическая интерпретация задачи дает наглядное представление об
области допустимых решений (которая на рис. 2.4 заштрихована),
что помогает в практических ситуациях даже в тех случаях, когда не
удается получить формальное отображение целевой функции и строго
решить задачу.
15. Сферы и возможности применения
• Применяются в тех случаях, когда свойства системыможно отобразить с помощью детерминированных
величин или зависимостей, т. е. когда знания о
процессах и событиях в некотором интервале
времени позволяют полностью определить
поведение их вне этого интервала. Эти методы
используются при решении задач движения и
устойчивости, оптимального размещения,
распределения работ и ресурсов, выбора
наилучшего пути, оптимальной стратегии поведения,
в том числе в конфликтных ситуациях и т. п.
• Для сложных многокомпонентных,
многокритериальных систем получить требуемые
аналитические зависимости крайне трудно. Более
того, даже если это и удается, то практически
невозможно доказать правомерность применения
таких выражений, т. е. адекватность модели
рассматриваемой задаче.
16. Статистические представления
SxФ[Sx]
a
b
Статистическим называют отображение системы
с помощью случайных (стохастических)
событий, процессов, которые описываются
вероятностными характеристиками и
статистическими закономерностями
• Статистические отображения системы можно представить как
бы в виде "размытой" точки (размытой области) в n-мерном
пространстве, в которую переводит систему (ее учитываемые в
модели свойства) оператор Ф[Sx]. "Размытую" точку следует
понимать как некоторую область, характеризующую систему;
при этом границы области заданы с некоторой вероятностью p
(p(A) = m/n, где m число появлений события A, n общее
число опытов; если при n (m/n) const.), т. е. "размыты",
и движение точки описывается некоторой случайной функцией.
• Закрепляя все параметры этой области, кроме одного, можно
получить срез по линии a b, смысл которого воздействие
данного параметра на поведение системы, что можно описать
статистическим распределением по этому параметру.
Аналогично можно получить двумерную, трехмерную и т. д.
картины статистического распределения.
17. Возникновение идей теории вероятностей
• Никко́ло Тарта́лья (итал. Niccolò Tartaglia,1499—1557) — итальянский математиксамоучка, инженер фортификационных
сооружений. Внес вклад в баллистику.
Нашел способ решения кубических
уравнений и внес вклад в развитие теории
вероятностей Одним из первых занялся
подсчетом различных комбинаций при игре в
кости («Общий трактат о числе и мере»).
• Джеро́ламо (Джироламо, Иероним)
Карда́но (лат. Hieronymus Cardanus,
итал. Girolamo Cardano, Gerolamo Cardano;
24.09.1501, Павия — 21.09.1576, Рим) —
итальянский математик, инженер, философ,
врач, астролог. Опубликовал
фундаментальные труды по алгебре, теории
вероятностей и механике )его именем
названа карданная подвеска).
18. Галилео Галилей
• Наиболее полное решениезадачи о числе всех
возможных исходов при
бросании трёх игральных
костей дал Галилео Галилей
(1564–1642) в работе «О
выходе очков при игре в
кости». Впервые она была
опубликована в 1718 году.
19. Христиан Гюйгенс
• Гюйгенс Христиан (1629–1695) –нидерландский математик, физик,
механик и астроном. Он один из
основоположников волновой оптики.
Автор одного из первых трудов по
теории вероятностей.
• В 1657 появляется труд Гюйгенса
«О расчетах при игре в кости» –
одна из первых работ по теории
вероятностей.
20. Исаак Ньютон
• Ньютон Исаак (1643–1727), английскийматематик, механик, астроном и физик,
создатель классической механики.
• С именем Ньютона связаны задачи и по
теории вероятностей, в частности, с
расчетами в азартных играх. Когда-то
Самуэль Пепайс послал Ньютону длинное и
запутанное письмо по поводу новых игр с
костями, которые он собирался опробовать.
Для выяснения, какая из них выгоднее,
Пепайсу нужен был ответ на
сформулированный в условии задачи
вопрос. Ньютон дал исчерпывающее
решение задачи, опираясь на формулу
Я.Бернулли.
21. Готфрид Вильгельм Лейбниц (1646–1716)
• В двенадцатилетнем возрастепытался во всем отыскивать
«единство и гармонию» и понять, что
наука существует для человека, а не
наоборот.
• Задача. Найти количество исходов (без повторений)
при одновременном бросании n игральных костей,
если n = 1, 2, 3, 4, 5, 6.
• Ответ. Количество исходов (без повторений) для n
костей, где n = 1, 2, 3, 4, 5, 6.
n
С n 5
22. Блез Паскаль
• Блез Паскаль (1623–1662) – французскийматематик, физик, религиозный философ и
писатель автор работ по арифметике, теории
чисел, алгебре, теории вероятностей, теории
воздушного давления; один из
основоположников гидростатики, установил
ее основной закон сформулировал одну из
основных теорем проективной геометрии;
сконструировал суммирующую машину.
• Задача. Игральная кость бросается четыре
раза. Рыцарь бился об заклад, что при этом
хотя бы один раз выпадет шесть очков.
Какова вероятность выигрыша для рыцаря?
• Решил для Шевалье де Мере.
23. Якоб Бернулли (1654 – 1705)
• Основные научные интересы Якобабыли сосредоточены на развитии и
приложении математического
анализа, а также он обнаружил
фундаментальный факт теории
вероятностей, получивший
название закон больших чисел.
• Задача. Рассмотрим некоторые события, которые
могут произойти в результате подбрасывания
игральной кости: А – выпадает «шестерка»; В –
выпадает нечетное число очков; С – выпадает
число очков, кратное трем; D – выпадает число
очков, некратное трем; Е – выпадает меньше семи
очков; F – выпадает больше шести очков. Опишите
совокупность всех исходов каждого из описанных
событий при подбрасывании игральной кости.
Найдите вероятности этих событий.
• Ответ. Вероятность случайного события может
изменяться от 0 до 1.
24.
• Елена Сергеевна Вентцель• (лит. псевдоним И. Игрекова);
Долгинцева; 8 [21].03.1907—
15.04.2002) — советский математик,
автор учебников по теории
вероятностей и исследованию
операций, русский прозаик. Развивала
исследование операций вначале на
основе статистических методов. А в
последующем – различных методов
математики, включая теорию множеств
и математическую логику.
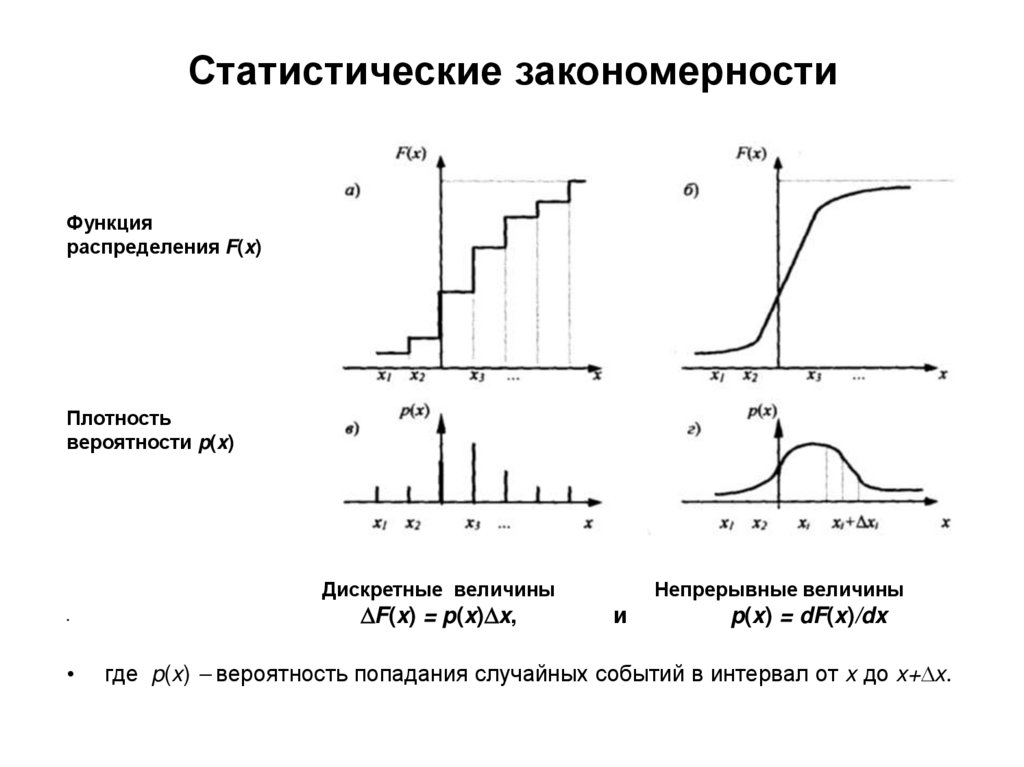
25. Статистические закономерности
Функцияраспределения F(x)
Плотность
вероятности p(x)
Дискретные величины
F(x) = p(x) x,
Непрерывные величины
и
p(x) = dF(x)/dx
где p(x) вероятность попадания случайных событий в интервал от x до x+ x.
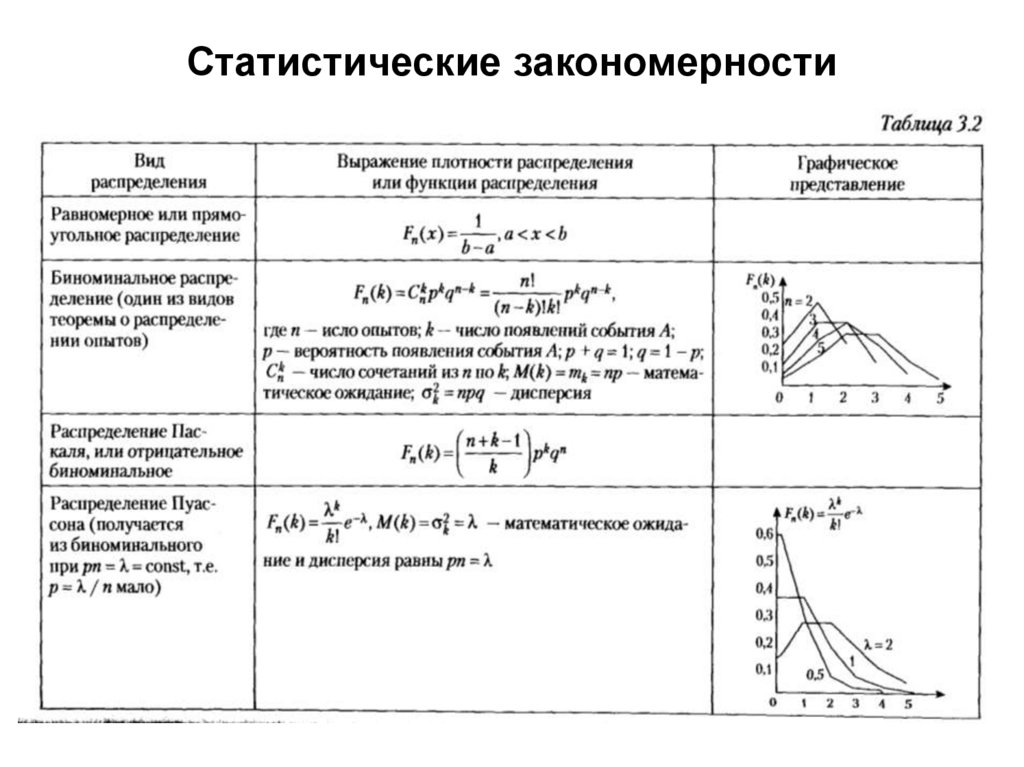
26. Статистические закономерности
27. Вероятностные характеристики
28. Условия нормирования
• Для полной группы несовместных событий имеютместо условия нормирования:
функции распределения
n
pi(xi) = 1,
i=1
и плотности вероятности
p( x)dx F ( ) F ( ) 1 0 1
29. Связь между компонентами или системами
• Связь между компонентами или системами в общемслучае характеризуется ковариацией моментом
связи; для двумерного распределения обозначаем
• cov(x, y), или mxy, или
M[(x mx)(y my)].
• Можно использовать ковариацию нормированных
отклонений коэффициент корреляции
( x m x )( y m y )
,
r cov(x ' , y ' ) M
x y
• где x = (x – mx)/ x,
y' = (y my)/ y нормированные отклонения;
x, y среднеквадратические отклонения.
30. Математические теории на базе статистических представлений
• математическая статистика, объединяющая различныеметоды статистического анализа (регрессионный,
дисперсионный, корреляционный, факторный и т. п.);
• теория статистических испытаний; основой этой теории
является метод Монте-Карло; развитием теория
статистического имитационного моделирования;
• теория выдвижения и проверки статистических
гипотез; возникла для оценки процессов передачи сигналов на
расстоянии; базируется на общей теории статистических
решающих функций А. Вальда; важным частным случаем
теории является байесовский подход к исследованию процессов
передачи информации, процессов общения, обучения и др.
ситуациях в организационных системах;
• теория потенциальной помехоустойчивости;
• обобщает последние два направления теория
статистических решений, в рамках которой, в свою очередь,
возник ряд интересных и полезных для практики направлений;
начала теории положены работами В.А.Котельникова,
проводимыми независимо от теории решающих функций;
31. Прикладные научные направления на базе статистических представлений:
• теория массового обслуживания,• статистическая радиотехника,
• статистическая теория распознавания
образов,
• стохастическое программирование,
• экономическая статистика,
• новые разделы теории игр,
• информетрия,
• и т. п.
32. Распределение Пуассона
33. Применении закона Пуассона
= mx = 2mx – математическое ожидание (среднее
значение) случайной величины;
2 – дисперсия.
=v
где v – число поступающих заказов;
– время выполнения одного
заказа.
Симео́н Дени́
Пуассо́н
(фр. Siméon
Denis Poisson;
21 июня 1781,
Франция — 25
апреля 1840,
Франция) —
французский
математик,
механик и
физик.
34. Пример задачи массового обслуживания
• Дано:• v = 120 зак/в год - число поступающих заказов на
информационно-аналитические подборки;
• = 0,5 мес. = 1/24 года – время выполнения заявки одним
сотрудником;
• Требуется определить:
• Сколько сотрудников должно одновременно находиться в
ИУК для выполнения работ, если сразу поступят все 120
заказов, чтобы обеспечивать время на выполнения заказа
0,5 мес.
• Если применить аналитические методы то нужно 120
сотрудников.
• При применении статистических методов применим закон
Пуассона
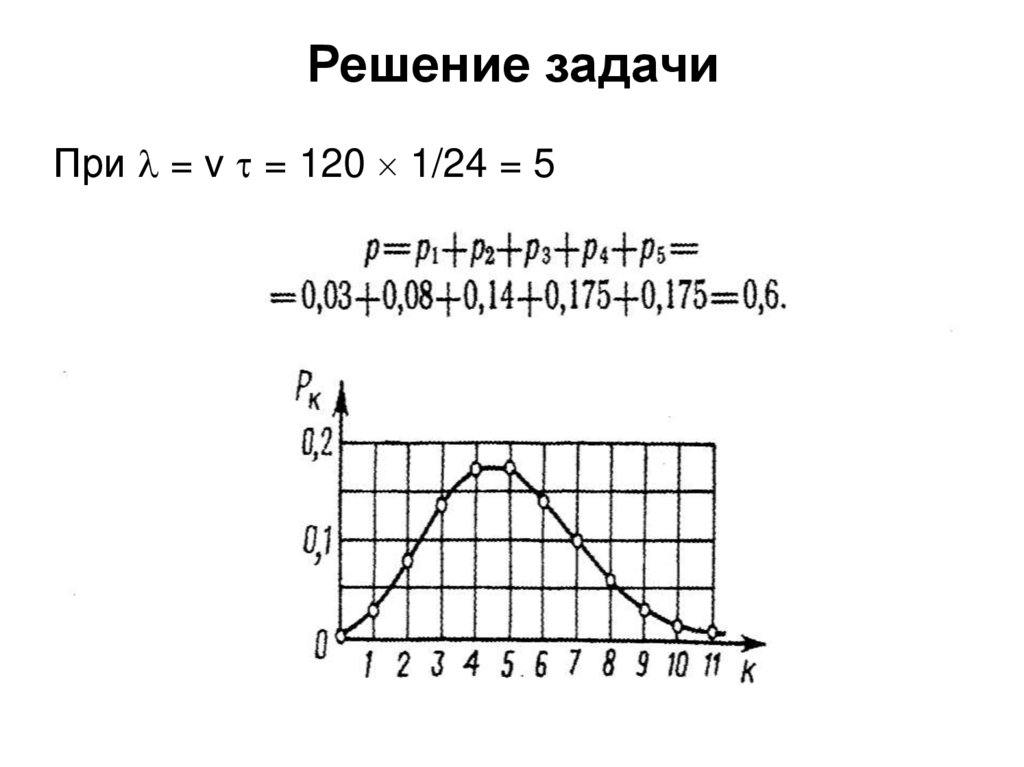
35. Решение задачи
При = v = 120 1/24 = 536. Теория статистических испытаний или статистического имитационного моделирования
• Теория статистических испытанийявляется распространением более
специфичного метода Монте-Карло [1]
на случай сложных методов и
процессов.
[1] Соболь И. М. Метод Монте-Карло / И
.М. Соболь. – М.: Наука, 1985. – 80 с.
37. Имитационное компьютерное моделирование
• Емельянов АлександрАнатольевич
• (10.06.1947 - 20.09.2020)
• Доктор экономических наук,
профессор
• Система ACTOR Pilgrim
разработана школой Александра
Анатольевича Емельянова.
• Компьютерная имитация
экономических процессов / А. А.
Емельянов, Е. А. Власова,
Р. В. Дума, Н. З. Емельянова; под
ред. А. А. Емельянова. М.: Маркет
ДС, 2010. 464 с.
38. Методы Мо́нте-Ка́рло (ММК)
• Методы Мо́нте-Ка́рло (ММК) — группа численныхметодов для изучения случайных процессов. Суть метода
заключается в следующем: процесс описывается
математической моделью с использованием генератора
случайных величин, модель многократно обсчитывается,
на основе полученных данных вычисляются
вероятностные характеристики рассматриваемого
процесса. Например, чтобы узнать методом Монте-Карло,
какое в среднем будет расстояние между двумя
случайными точками в круге, нужно взять координаты
большого числа случайных пар точек в границах заданной
окружности, для каждой пары вычислить расстояние, а
потом для них посчитать среднее арифметическое.
• Название метода происходит от района Монте-Карло,
известного своими казино.
39. Теории статистических решающих функций А. Вальда
• Абрахам Вальд (нем. AbrahamWald; 31.10.1902, АвстроВенгрия — 13.12.1950, Индия) —
венгерский математик и статистик.
В сферу его научных интересов
входили теория принятия
решений, эконометрика,
геометрия, математическая
статистика и теория вероятностей.
40. Пример выдвижения и проверки статистических гипотез
41. Критерии
шения правдоподобия и сравнение его с двумя порогами:нижним L1= /1 и верхним L2= 1 /
L(x)<L1 – отсутствие сигнала, L(x)>L2 – наличие сигнала
L1<L(x)<L2 – продолжить испытания
42. Экономическая статистика
• Экономическая статистика - разделприкладной статистики и прикладной
экономики, посвященный сбору,
обработке, обобщению,
распространению и анализу
экономических данных. Она тесно
связана со статистикой бизнеса и
эконометрикой.
• Термин ввел немецкий учёный
Готфрид Ахенвалль в 1746 году.
• Принято также называть сами данные
"экономической статистикой", но в
данном случае более
распространенным термином
являются "экономические данные".
Готфрид
Ахенвалль
(нем. Gottfried
Achenwall; 1719—
1772) — немецкий
философ,
статистик,
экономист,
педагог, историк,
юрист и один из
основоположник
ов статистики.
43. Особенности статистических представлений
• При применении статистических представленийпроцесс постановки задачи как бы частично
заменяется статистическими исследованиями,
позволяющими, не выявляя все детерминированные
связи между изучаемыми объектами (событиями) или
учитываемыми компонентами сложной системы, на
основе выборочного исследования (исследования
репрезентативной выборки) получать статистические
закономерности и распространять их на поведение
системы в целом.
• В то же время не всегда может быть определена
репрезентативная выборка, доказана правомерность
применения полученных на ее основе статистических
закономерностей. Если не удается доказать
репрезентативность выборки или для этого требуется
недопустимо большое время, то применение
статистических методов может привести к неверным
результатам.
44. Теоретико-множественные представления
• Основные понятия:• множество,
• элементы множества,
• отношения на множествах.
Sx
F[Sx]
• Множество – «многое, мыслимое нами как
единое» / Георг Кантор / [1]
1 Независимо от Георга Кантора математическую
теорию бесконечных множеств создал чешский ученый
Бернард Больцано, основной труд которого был
опубликован много лет спустя после его смерти.
45. Гео́рг Ка́нтор
• Гео́рг Ка́нтор (нем. GeorgFerdinand Ludwig Philipp Cantor;
3.03.1845, Санкт-Петербург —
6.01.1918, Галле) — немецкий
математик, ученик
Вейерштрасса. Наиболее
известен как создатель теории
множеств.
• Основатель и первый президент
Германского математического
общества, инициатор создания
Международного конгресса
математиков.
46. Бернард Больцано
• Бернард Больца́но (чеш.Bernard Placidus Johann
Nepomuk Bolzano; 5.10.1781,
Прага — 18.12.1848) —
чешский математик, философ
и теолог, автор первой строгой
теории вещественных чисел и
один из основоположников
теории множеств.
47. «Парадоксы бесконечного» Б. Больцано
• В работе «Парадоксы бесконечного»(нем. Paradoxien des Unendlichen), впервые
изданной уже посмертно в 1851 году,
сформулировал идеи, близкие к наивной
теории множеств Кантора.
• В этой работе Больцано ввёл понятие
множества и взаимно-однозначного
соответствия. Также в этой работе было
доказано утверждение о наличии предельной
точки у любого бесконечного ограниченного
множества, ставшее позднее известным как
теорема Больцано — Вейерштрасса.
48. Начала теории множеств Г. Кантора
• Основным создателем теории множеств внаивном её варианте считается немецкий
математик Георг Кантор.
• В 1880 году Кантор формулирует две ключевых
идеи теории множеств — понятие о пустом
множестве и метод трансфинитной индукции.
• Начиная с 1881 года методами Кантора начинают
пользоваться другие математики.
• В работе 1883 года Кантор даёт исторически
первое формальное определение континуума,
используя введённые им понятия совершенного
множества и плотности множества, а также в
явном виде формулирует континуум-гипотезу.
49. Сравнение произвольных множеств
• Кантор впервые определил сравнениепроизвольных множеств, включая бесконечные, по
их «мощности» (обобщению понятия количества).
Классифицировал множества по их мощности,
определил понятия кардинальных и порядковых
чисел, арифметику кардинальных и порядковых
чисел.
• В теории множеств порядковым числом, или ординалом
(лат. ordinalis — порядковый) называется порядковый тип
вполне упорядоченного множества.
• Бесконечные порядковые числа называют
трансфинитными (лат. trans — за, через + finitio — край,
предел).
50. Трансфинитные числа
• Теория Кантора о трансфинитных числахпервоначально была воспринята как нарушение
многовековых традиций, заложенных ещё
древними греками и отрицающих актуальную
бесконечность как легальный математический
объект. Со временем канторовская теория
множеств была поставлена на аксиоматическую
основу и стала краеугольным камнем в
современном построении оснований математики,
на неё опираются математический анализ,
топология, функциональный анализ, теория меры
и многие другие разделы математики.
51. Конти́нуум-гипо́теза
• Конти́нуум-гипо́теза (проблема континуума, перваяпроблема Гильберта) — выдвинутое в 1877 году
Георгом Кантором предположение о том, что любое
бесконечное подмножество континуума является
либо счётным, либо континуальным. Другими
словами, гипотеза предполагает, что мощность
континуума — наименьшая, превосходящая
мощность счётного множества, и «промежуточных»
мощностей между счетным множеством и
континуумом нет. В частности, это предположение
означает, что для любого бесконечного множества
действительных чисел всегда можно установить
взаимно-однозначное соответствие либо между
элементами этого множества и множеством целых
чисел, либо между элементами этого множества и
множеством всех действительных чисел. .
52. Никола Бурбаки
• Никола́ Бурбаки́[1] (фр. Nicolas Bourbaki) —коллективный псевдоним группы французских
математиков (позднее в неё вошли несколько
иностранцев), созданной в 1935 году.
• Целью группы являлось написание серии книг,
отражающих состояние математики того времени.
Книги Бурбаки написаны в строгой аксиоматической
манере и дают замкнутое изложение математики на
основе теории множеств Цермело — Френкеля (в
доработке Бернайса и Гёделя).
• На группу огромное влияние оказала немецкая
математическая школа — Д. Гильберт, Г. Вейль, Дж.
фон Нейман и особенно алгебраисты Э. Нётер, Э.
Артин и Б. Л. ван дер Варден
53. История группы
Шарль Дени Бурбаки, французский
генерал, фамилия которого была взята в
качестве псевдонима
• Группа Бурбаки официально называется
Association des collaborateurs de Nicolas
Bourbaki («Ассоциация сотрудников
Никола Бурбаки»). Группа была
образована выпускниками парижской
Высшей нормальной школы (École
Normale Supérieure) на базе этого же
вуза. Поскольку происхождение или
работа многих членов группы были
связаны с городом Нанси, то
псевдонимом стала фамилия известного
в этом городе генерала Шарля Дени
Бурбаки.
54. Участвовали в первой встрече
• Анри Картан (фр. Henri Cartan)• Клод Шевалле (Claude Chevalley)
• Жан Дельсарт (Jean Delsarte)
• Жан Дьёдонне (Jean Dieudonné)
• Рене де Поссель (René de Possel)
• Шолем Мандельбройт (Szolem
Mandelbrojt)
• Андре Вейль (André Weil)
55. Присоединялись в разное время
• Лоран Шварц,• Жан-Пьер Серр,
• Александр Гротендик
• Джон Тэйт
• Самуэль Эйленберг
• Серж Ленг
• Пьер Самюэль
• Арман Борель
• Пьер Картье
• Ален Конн
56. Книги группы Н. Бурбаки
– I Теория множеств (Théorie des ensembles — E ) —вышло 4 главы и сводка результатов
– II Алгебра (Algèbre — A ) — вышло 10 глав
– III Топология (Topologie générale — TG ) — вышло
10 глав, сводка результатов и словарь
– IV Функции действительного переменного
(Fonctions d’une variable réelle — FVR ) — вышло 7
глав и словарь
– V Топологические векторные пространства
(Espaces vectoriels topologiques — EVT ) — вышло
5 глав, сводка результатов и словарь
– VI Интегрирование (Intégration — INT ) — вышло 9
глав.
57. Вторая часть
– VII Коммутативная алгебра (Algèbrecommutative — AC ) — вышло 10 глав
– VIII Группы и алгебры Ли (Groupes et
algèbres de Lie — LIE ) — вышло 9 глав
– IX Спектральная теория (Théories
spectrales — TS ) — вышло 2 главы
– X Алгебраическая топология (Topologie
Algébrique — TA ) — вышло 4 главы
– (без номера) Дифференцируемые и
аналитические многообразия (Variétés
différentielles et analytiques — VAR ) —
вышла только сводка результатов.
58. В книгах Бурбаки были впервые введены
• символ для пустого множества Ø;• символы для множеств натуральных, целых,
рациональных, действительных и
комплексных чисел соответственно;
• термины инъекция, сюръекция и биекция;
• знак «опасный поворот» на полях книги,
показывающий, что данное место в
доказательстве или определении может быть
неправильно понято.
• В трактате все математические теории
описываются на основании аксиоматической
теории множеств в духе крайней абстракции.
59. Способы задания множеств
• 1) списком, перечислением – и н т е н с и о н а л ь н онапример,
{ai} , где i = 1...n ,
• или
<a1, a2, ... , ai, ... , an> ,
• где ai A , знак вхождения элементов в множество;
• 2) путем указания некоторого характеристического
свойства – э к с т е н с и о н а л ь н о.
• Например,
• «множество натуральных чисел», «множество
рабочих данного завода», «множество планет
солнечной системы», «множество А» и т. д.
60. Принцип перехода от одного способа задания множества к другому
• В основе теоретико-множественныхпреобразований лежит принцип перехода от
одного способа задания множества к другому:
A = <a1, a2, ... , ai, ... , an>,
• или
<a1, a2, ... , ai, ... , an > A.
• Переход от интенсионального способа
задания множества к экстенсиональному
называют принципом свертывания.
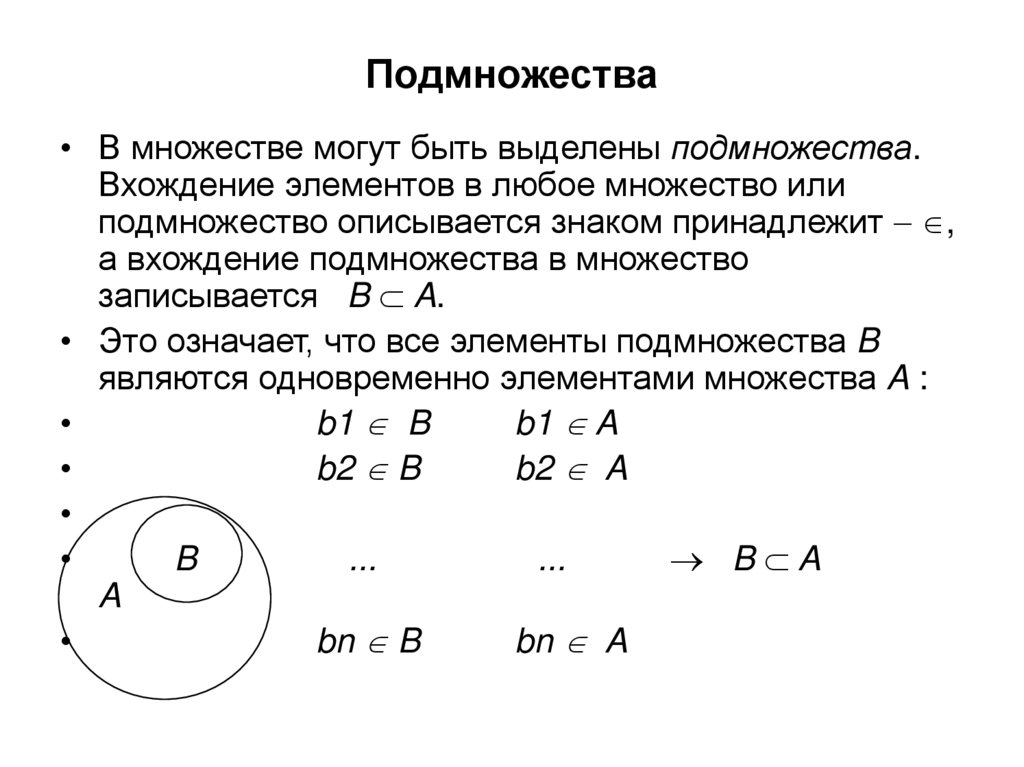
61. Подмножества
• В множестве могут быть выделены подмножества.Вхождение элементов в любое множество или
подмножество описывается знаком принадлежит ,
а вхождение подмножества в множество
записывается B A.
• Это означает, что все элементы подмножества B
являются одновременно элементами множества A :
b1 B
b1 A
b2 B
b2 A
B
...
...
B A
A
bn B
bn A
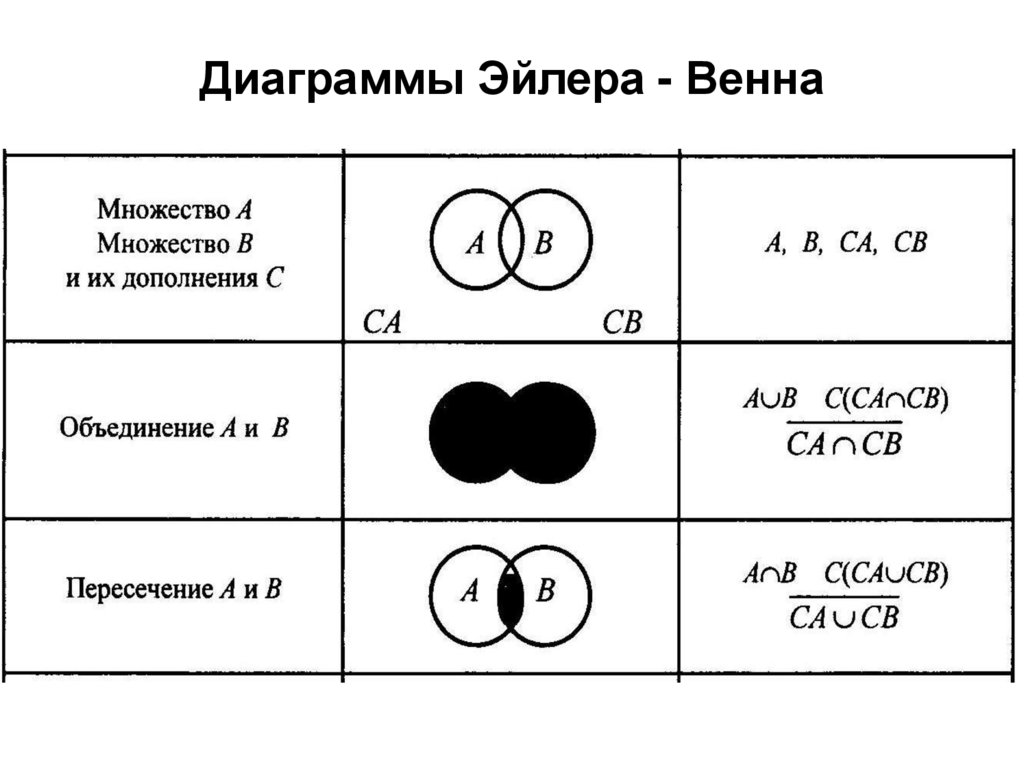
62. Отношения на множествах
• В соответствии с концепцией Г. Кантораможно вводить любые отношения. При
уточнении этих отношений применительно к
множествам удобно пользоваться
наглядными диаграммами Эйлера-Венна,
примеры которых для операции
объединения ( ), пересечения (& или ),
дополнения (отрицания, обозначаемого
знаком « » над именем множества, либо
знаком « » перед именем множества или его
элемента) приведены в таблице .
63. Диаграммы Эйлера - Венна
64. Диаграммы Эйлера - Венна
• Леона́рд Э́йлер (нем. Leonhard Euler; 15апреля 1707, Базель, Швейцария —
7 (18) сентября 1783, Санкт-Петербург,
Российская империя) — швейцарский,
прусский и российский[8] математик и
механик.
• Джон Венн (англ. John Venn; 4 августа 1834,
Халл (Йоркшир) — 4 апреля 1923,
Кембридж) — английский логик и философ.
Он известен тем, что ввёл диаграммы
Эйлера — Венна, которые используются во
многих областях, таких как теория множеств,
теория вероятностей, логика, статистика и
информатика.
65. Диаграммы Эйлера - Венна
66. Отображение эмерджентности
• Из двух или нескольких множеств можносформировать путем установления отношений
между элементами этих множеств новое множество.
Это новое множество, как правило, обладает
принципиально новыми свойствами
(эмерджентность) и может содержать
принципиально новые элементы.
• Напр., объединяя элементы из множества
«конденсаторы С» и множества «катушки
индуктивности L», получим новое множество
«колебательные контуры KK» (если объединение
проведено по соответствующим правилам).
• Аналогично из множеств «женихи Y» и «невесты G»
в ЗАГСе путем соответствующей операции
(процедуры регистрации брака) формируется
множество «Семьи С», cx = <yi rk gj >, где yi Y,
gj
G, rk Rв, Rв множество взаимоотношений
между людьми, имеющих принципиально новый
смысл для общества. При этом изменяется название
и статус элементов – «муж» и «жена».
67. «Помещение рядом» - новый смысл
• Не только установление какого-либо видаспециальных отношений, как в этих
приведенных примерах, но и формирование
элементов нового множества путем простого
«помещения рядом» (конкатенации)
элементов исходных множеств позволяет
получать эффект появления нового смысла,
т.е. возникает эффект эмерджентности
• что обеспечивается доосмыслением
взаимоотношений человеком на основе его
предшествующего опыта.
68. Ординарное и экстраординарное множество
• Если объединяемые элементы и сформированное из нихмножество относятся к одному классу объектов, его
называют ординарным
• Если в результате объединения элементов получается
множество нового класса, то такое множество называют
экстраординарным.
• Например, если множество сформировано из
геометрических фигур например, треугольников, и
принято условие, что формирование нового множества
осуществляется в той же плоскости, то полученное новое
множество будет также плоской геометрической фигурой,
а, возможно даже и треугольником. Такие множества
относят к классу ординарных.
• Аналогично можно считать ординарным колебательный
контур, поскольку он так же, как конденсаторы и катушки
индуктивности, является элементом радиотехнических
устройств.
• Однако, учитывая принципиально новые свойства
колебательного контура, можно эту же ситуацию
трактовать как формирование экстраординарного
множества с принципиально новыми свойствами.
• При формировании экстраординарного множества в
примере с семьей изменяются не только свойства
множества, но и суть и даже наименования исходных
элементов («жених» «муж», «невеста» «жена»).
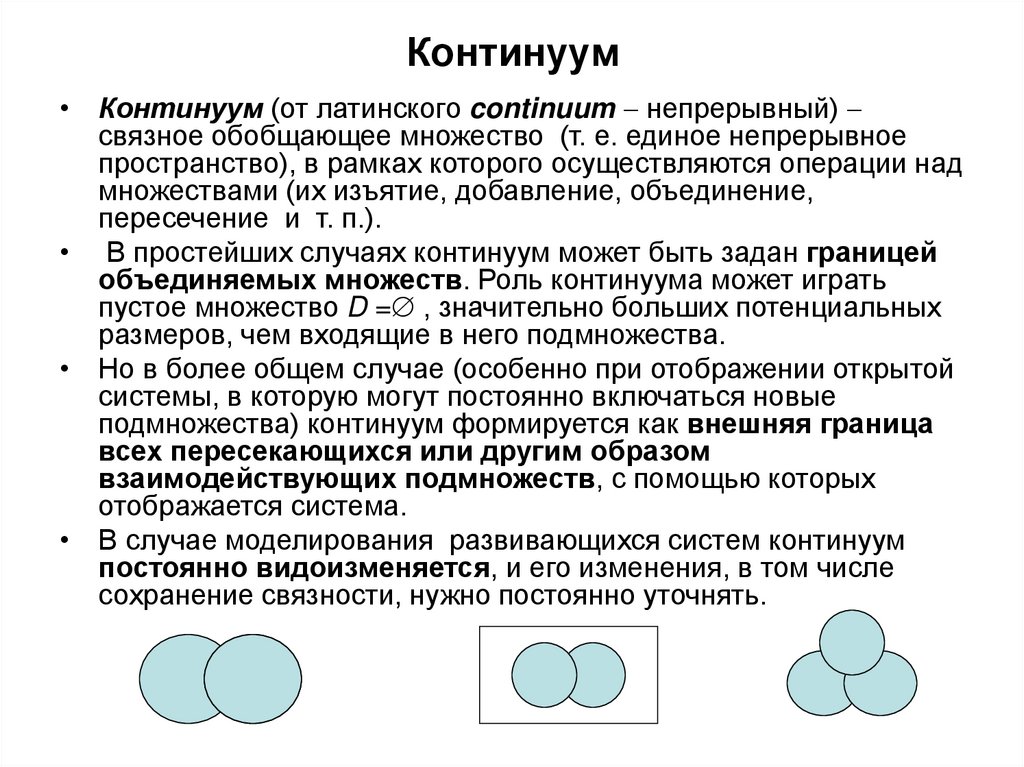
69. Континуум
• Континуум (от латинского continuum непрерывный)связное обобщающее множество (т. е. единое непрерывное
пространство), в рамках которого осуществляются операции над
множествами (их изъятие, добавление, объединение,
пересечение и т. п.).
• В простейших случаях континуум может быть задан границей
объединяемых множеств. Роль континуума может играть
пустое множество D = , значительно больших потенциальных
размеров, чем входящие в него подмножества.
• Но в более общем случае (особенно при отображении открытой
системы, в которую могут постоянно включаться новые
подмножества) континуум формируется как внешняя граница
всех пересекающихся или другим образом
взаимодействующих подмножеств, с помощью которых
отображается система.
• В случае моделирования развивающихся систем континуум
постоянно видоизменяется, и его изменения, в том числе
сохранение связности, нужно постоянно уточнять.
70. Проблема парадоксов
• При произвольных отношениях в формализованном с ихпомощью описании проблемной ситуации могут
обнаружиться неразрешимые противоречия парадоксы,
апории или антиномии, что не позволяет оперировать с
получаемыми теоретико-множественными моделями
таким же образом, как с классическими математическими
соотношениями, и доверять достоверности получаемых
результатов.
• В качестве примеров парадоксов приводят обычно:
парадокс лжеца (нельзя дать положительного ответа на
вопрос «Ты лжешь?»);
• парадокс парикмахера, который должен «брить всех
мужчин в полку, которые не бреются сами».
• Если формально записать ситуацию, то возникает
неразрешимое противоречие: парикмахер X принадлежит
множеству одновременно мужчин M1, которые не
бреются сами и которых по распоряжению он обязан
брить, и множеству тех мужчин M2, которые бреются
сами и которых согласно распоряжению он брить не
должен, и эти множества M1 и M2 не пересекаются и не
входят друг в друга, т. е. должно иметь место:
X M1, X M2, M3 = M1 U M2 = ,
• что невозможно.
71. Парадоксы или апории
• Древнегреческий философ ЗенонЭлейский жил около 490 430 гг. до н. э.
• Ученик Парменида, представитель
Элейской школы..
Знаменит своими апори́ями, которыми он
пытался доказать противоречивость концепций
движения, пространства и множества.
Научные дискуссии, вызванные этими
парадоксами, углубили понимание таких
фундаментальных понятий, как роль
дискретного и непрерывного в природе,
адекватность физического движения и его
математической модели и др.
72. "Дихотомия"
"Дихотомия"• Первая из апорий, называемая "Дихотомия" (деление на
два), утверждает, что невозможно пройти конечный отрезок
пути за конечный промежуток времени.
В самом деле, прежде чем пройти расстояние АВ = а,
надо пройти половину этого расстояния АВ1 = , а прежде
чем пройти путь АВ1, надо пройти половину этого пути АВ2
= и т.д.
• Таким образом, необходимо пройти бесконечное
количество отрезков за ограниченное время, а это
невозможно. Отсюда следует, что и движение невозможно:
73. «Ахиллес и черепаха»
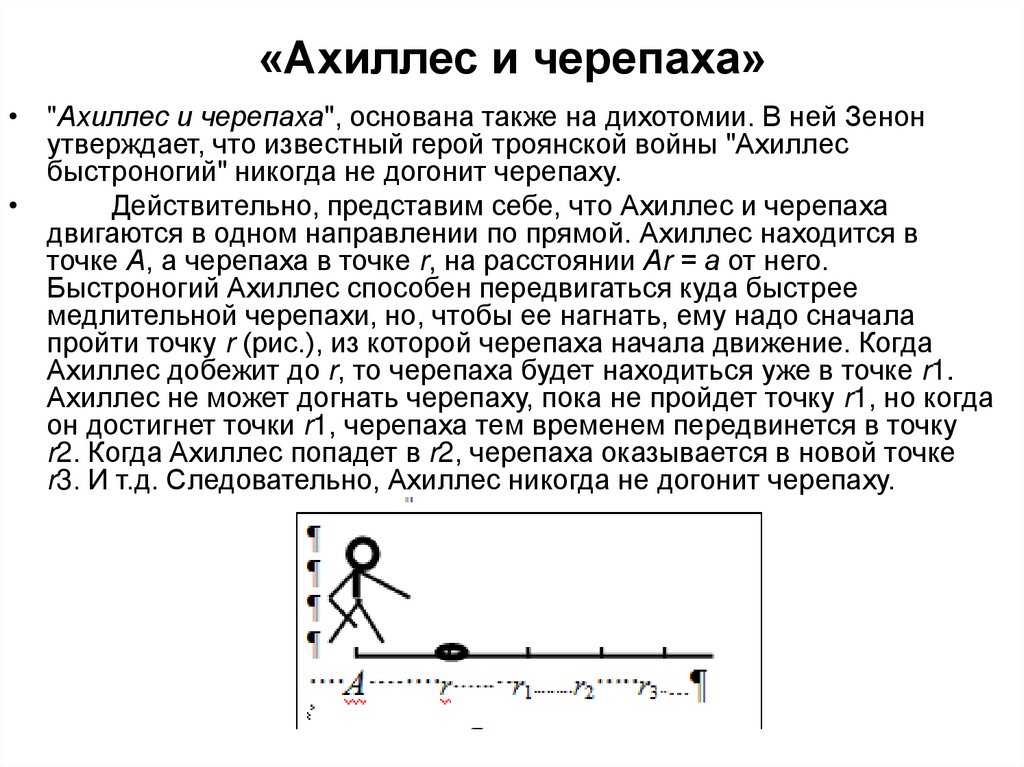
• "Ахиллес и черепаха", основана также на дихотомии. В ней Зенонутверждает, что известный герой троянской войны "Ахиллес
быстроногий" никогда не догонит черепаху.
Действительно, представим себе, что Ахиллес и черепаха
двигаются в одном направлении по прямой. Ахиллес находится в
точке А, а черепаха в точке r, на расстоянии Аr = а от него.
Быстроногий Ахиллес способен передвигаться куда быстрее
медлительной черепахи, но, чтобы ее нагнать, ему надо сначала
пройти точку r (рис.), из которой черепаха начала движение. Когда
Ахиллес добежит до r, то черепаха будет находиться уже в точке r1.
Ахиллес не может догнать черепаху, пока не пройдет точку r1, но когда
он достигнет точки r1, черепаха тем временем передвинется в точку
r2. Когда Ахиллес попадет в r2, черепаха оказывается в новой точке
r3. И т.д. Следовательно, Ахиллес никогда не догонит черепаху.
74. "Стрела"
"Стрела"Апория третья – "Стрела". Летающая стрела
покоится, утверждает Зенон, ибо в каждый
момент она занимает равное ей место, покоится
по отношению к этому месту, и, поскольку это
обстоятельство справедливо в любой момент
времени, то стрела в любой момент времени
будет покоиться и, следовательно, покоится
вообще.
Полет стрелы становится невозможным, если
время считать суммой дискретных мгновений, а
пространство суммой дискретных точек.
75. "Стадион"
"Стадион"• Пусть имеются три ряда всадников: A1A2A3A4,
B1B2B3B4 и Г1Г2Г3Г4, расположенных параллельно
друг другу так, что всадник из ряда А помещен напротив
соответствующего всадника из ряда В и всадника из
ряда Г. Ясно, что все три ряда всадников равны друг
другу. Пусть ряд А неподвижен, а ряды В и Г движутся в
разные стороны с равными скоростями. Когда в
определенный момент всадники из В и Г займут
положение, указанное на схеме, то окажется, что за один
и тот же промежуток времени всадник В4 пройдет перед
половиной ряда А и перед всем равным ему рядом Г. В
один и тот же промежуток времени всадник пройдет и
весь путь, и половину пути, т. е. 1 = 1/2 (?). Парадокс!
76. Парадокс парикмахера
• X – парикмахер;• М1 – множество мужчин которые не
бреются сами (брить должен);
• М2 – множеств мужчин, которые
бреются сами (брить не должен);
• M1 и M2 не пересекаются и не входят
друг в друга, т. е. должно иметь место:
M3 = M1 U M2 = ,
• Тогда X M1, X M2 - невозможно.
77. Парадоксы в текстах
Примеры парадоксов легко можно найти во многихвысказываниях неформализованного текста:
например,
• «Ты должен сам любить меня» (если «должен», то
«не сам»; если «сам» то «не должен», а любит без
принуждения).
• На этом свойстве текстов основаны некоторые
психологические тесты.
• «Вступили бы Вы в драку, если бы Вам пришлось
защищать девушку?» (из теста MMPI)
• Эта принципиальная особенность текстов не
позволяет однозначно отразить с их помощью
проблемные ситуации и требует перевода текстов в
формализованные описания с использованием
специализированных знаковых систем, языков, в
которых по возможности устранены парадоксы.
78. Особенности теоретико-множественных представлений
• Благодаря тому, что в соответствии с концепциейКантора при применении теории множеств
допустимо введение любых произвольных
отношений, теоретико-множественные
представления:
• а) используются как обобщающий язык при
сопоставлении различных направлений
математики и других дисциплин,
• б) явились основой для возникновения новых
научных направлений или развития
существующих.
• Использование теоретико-множественных
представлений при моделировании систем
позволяет организовать взаимодействие и
взаимопонимание между специалистами
различных областей знаний.
79. Особенности теоретико-множественных представлений (продолжение)
• Однако при произвольных отношениях вформализованном с их помощью описании
проблемной ситуации довольно быстро могут
обнаружиться неразрешимые противоречия
парадоксы, апории или антиномии, что не
позволяет оперировать с получаемыми
теоретико-множественными моделями таким
же образом, как с классическими
математическими соотношениями, и
доверять достоверности получаемых
результатов.
80. Особенности теоретико-множественных представлений (продолжение)
• Наличие парадоксов – принципиальнаяособенность текстов, что не позволяет
однозначно отразить с их помощью
проблемные ситуации и требует перевода
текстов в формализованные описания с
использованием специализированных
знаковых систем, языков, в которых по
возможности устранены парадоксы.
• Для разработки таких языков могут быть
использованы теоретико-множественные
представления, которые позволяют выявлять
и устранять парадоксы, ограничивая при этом
свободу выбора отношений, т.е., строго
говоря, огрубляя качественное описание,
уменьшая его полноту
81. Математическая логика
SxФ[Sx]
1
0
•Базовыми понятиями математической
логики являются высказывание,
предикат, логические функции
(операции)? кванторы, логический
базис, логические законы (законы
алгебры логики).
• Под высказыванием в алгебре логики понимается
повествовательное предложение (суждение),
которое характеризуется определенным значением
истинности.
• Предикат выражение, грамматически имеющее
форму высказывания, но содержащее переменные
некоторых подмножеств, на которых они определены.
82. Бинарная алгебра логики Буля
• В простейших случаях используется двазначения истинности: «истинно» «ложно»,
«да» «нет», «1» «0».
• Такая алгебра логики, в которой переменная
может принимать только два значения
истинности, называется бинарной алгеброй
логики Буля (по имени ее создателя).
• Частным случаем предиката является
пропозиционная функция функция одной
или нескольких переменных, принимающих
значения в множестве, состоящем из двух
элементов «1» «0».
83. Логические функции
• Объединение простых высказываний в сложныепроизводится без учета смысла этих высказываний
(предикатов) на основе определенных логических
правил (операций, функций).
• Число простейших логических функций в
конкретной алгебре логики зависит от количества
значений истинности n:
n
N = 22 .
• Для двузначной булевой алгебры при n = 2:
N = 16 .
• При n = 3
N = 256 логических функций.
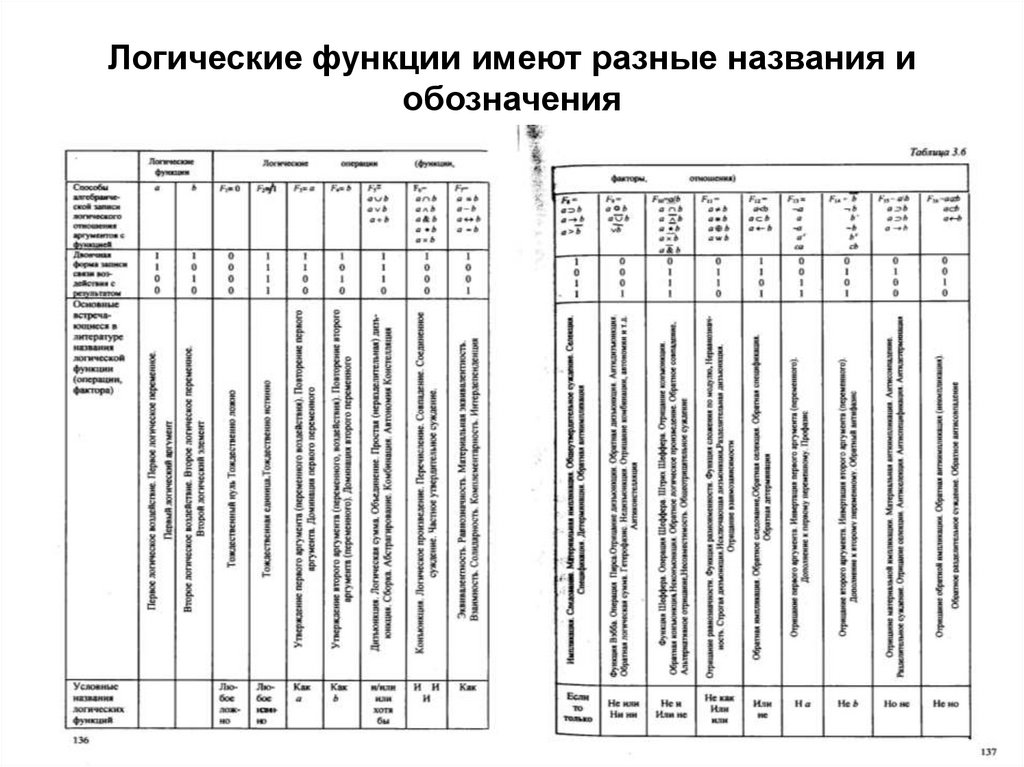
84. Логические функции имеют разные названия и обозначения
85. Кванторы
• Ква́нтор — общее название для логических операций,ограничивающих область истинности какого-либо предиката и
создающих высказывание. Чаще всего упоминают:
• Квантор всеобщности (обозначение: , читается: «для любого…»,
«для каждого…», «для всех…» или «каждый…», «любой…», «все…»).
• Квантор существования (обозначение: , читается: «существует…»
или «найдётся…»).
• В математической логике приписывание квантора к формуле
называется связыванием или квантификацией
• В многозначных логиках также вводятся и другие кванторы, например,
квантор плюральности (квантор Решера) (обозначается
перевёрнутой M, читается «для большинства «).
86. Логические законы
87. Логический базис
• Полную систему логических функций называютлогическим базисом. Для того, чтобы система функций
представляла собой базис, она должна обладать
определенными свойствами:
• необходимо и достаточно, чтобы она содержала хотя бы
одну функцию: не сохраняющую константу единица, не
сохраняющую константу ноль, нелинейную,
немонотонную, несамодвойственную.
• Полный логический базис содержит избыточное число
функций. Минимальными базисами бинарной алгебры
логики являются базисы, включающие только две функции
{ , } { , }.
• Функция отрицания не сохраняет константы ноль и
единицу и не является монотонной, функции дизъюнкции
и конъюнкции обеспечивают нелинейность и не
являются самодвойственными (в силу теорем деМоргана).
• С помощью логических алгоритмов можно описывать не
любые отношения, а только те, которые предусмотрены
законами алгебры логики и удовлетворяют требованиям
логического базиса.
88. Логический анализ и логический синтез
• Задача логического анализа состоит в описанииповедения системы с известной структурой набором
системно-логических уравнений (функций алгебры логики
ФАЛ) и исследования полученного логического
выражения с целью его минимизации, т. е. выяснения,
нельзя ли получить более простую структуру (схему), но
осуществляющую требуемые преобразования. Такие
задачи возникают при создании автоматических систем
контроля неисправностей, систем автоматического
резервирования, обеспечения надежности и т.д.
• Задача логического синтеза заключается в том, чтобы
по известному поведению системы определить ее
структуру, т. е. сопоставить системе некоторый
«автомат» «черный ящик» с известными входными и
выходными воздействиями.
• Таким образом, при логическом анализе задача сводится
к минимизации ФАЛ, т. е. к оптимизации в некотором
смысле логического алгоритма. Задача логического
синтеза сложнее, она обычно решается путем
последовательных приближений,.
• Минимизация ФАЛ осуществляется путем применения
законов алгебры логики,
89. Математическая лингвистика и семиотика
Включение их в разряд математических нельзя
считать общепризнанным.
Некоторые исследователи (например,
Ю.А.Шрейдер [1]) считают, что лингвистика в силу
специфических особенностей, позволяющих
моделировать развивающиеся системы и процессы
(что обеспечивается отсутствием закона
исключенного третьего), не является математикой в
сложившемся понимании этого термина.
В то же время французская школа математиков
считает математическую лингвистику разделом
современной математики.
[1] .Шрейдер Ю. А. Равенство, сходство, порядок. М.: Наука,
1971. 254 с.
90. Возникновение математической лингвистики
• Математическая лингвистика возникла во второйполовине XX в. как средство формализованного изучения
естественных языков и вначале развивалась как
алгебраическая лингвистика. Первые полезные
результаты алгебраической лингвистики связаны со
структуралистским (дескриптивным) подходом. Однако
в силу отсутствия в тот период концепции развития языка
эти работы привели к еще большему тупику в попытках
построения универсальной грамматики, и был период,
когда структурализм считался неперспективным
направлением развития науки о языке и даже был гоним.
• Возрождение математической лингвистики началось в
1950 1960-е гг. и связано с потребностями прикладных
технических дисциплин, усложнившиеся задачи которых
перестали удовлетворять методы классической
математики, а в ряде случаев и формальной
математической логики.
• В период уменьшения интереса к математической лингвистике
появилось статистическое направление, которое называют
статистической лингвистикой или лингвистической
статистикой.
91. Основные понятия математической лингвистики
SxФ[Sx]
TG
• Основными понятиями, на
которых базируются
лингвистические представления,
являются понятия:
• Тезаурус T,
• Грамматика G’
• Семантика
• Прагматика
92. Тезаурус
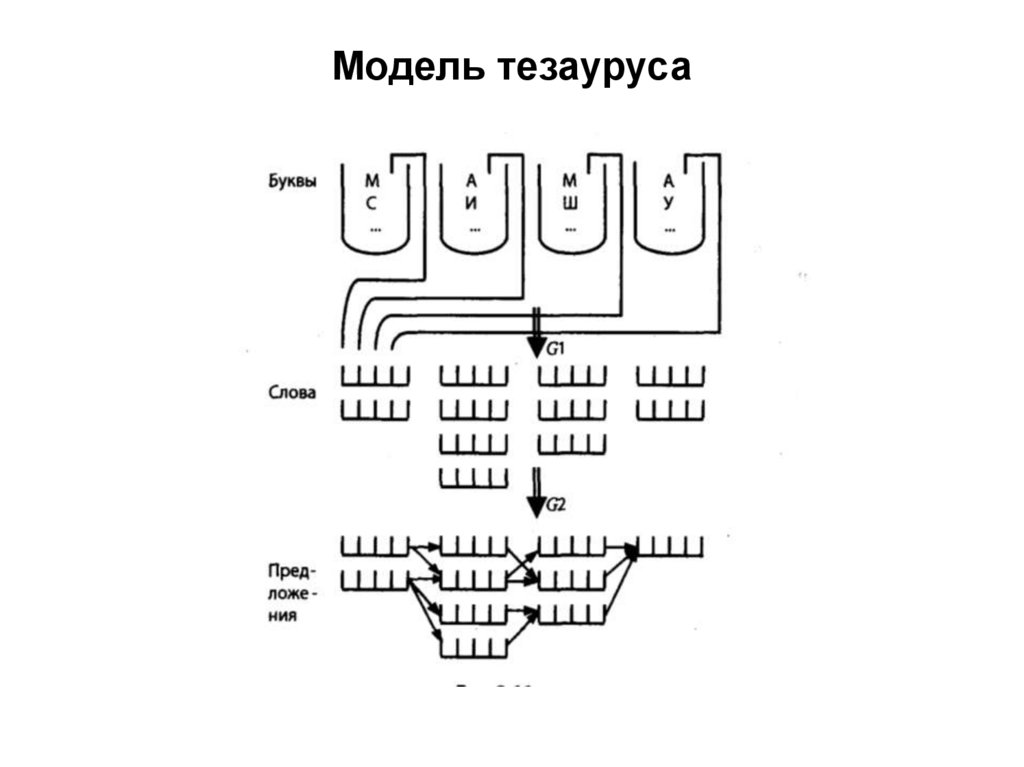
• Термин тезаурус (от греч. , thesaurosсокровищница, богатство, клад, запас и т. п.) в общем
случае характеризует совокупность научных знаний о
явлениях и законах внешнего мира и духовной
деятельности людей, накопленную всем человеческим
обществом.
• Термин был введен в современную литературу по
языкознанию и информатике в 1956 г. Кембриджской
группой по изучению языков. В то же время термин
существовал раньше: в эпоху Возрождения тезаурусами
называли энциклопедии.
• В математической лингвистике и семиотике термин
тезаурус используется в более узком смысле, для
характеристики конкретного языка, его многоуровневой
структуры.
• Тезаурус – «множества смысловыражающих элементов
языка с заданными смысловыми отношениями» 1.
1 Шрейдер Ю. А. Информация в структурах с
отношениями//Сб.: Исследования по математической
лингвистике, математической логике и информационным
языкам. М.: Наука, 1972. С. 147 159.
93. Модель тезауруса
94. Грамматика
• Под грамматикой (которую иногда называютсинтактикой, синтаксисом, что сужает понятие
грамматики, исключая из него морфологию) понимаются
правила, с помощью которых формируются
смысловыражающие элементы языка (на рис. выше G1
и G2). Пользуясь этими правилами, можно «порождать»
(формировать) грамматически (синтаксически)
правильные конструкции или распознавать их
грамматическую правильность.
• Термин грамматика употребляется в лингвистике и как
укороченная замена термина «формальная грамматика»,
который имеет иной смысл.
• Формальную грамматику определяют в виде четверки
множеств:
G = < VT, VN, R, A >,
• где VT множество основных или терминальных
символов; VN множество вспомогательных или
нетерминальных символов; R множество правил
вывода, или продукций
95. Семантика и прагматика
• Термины семантика и прагматика, трудно; обычно пояснитьразличие можно лишь при парном сопоставлении терминов:
<семантика> : : = <содержание> <смысл>
<значение>;
<прагматика>: : = <смысл>
<значение> <полезность>.
• Поэтому принято рассматривать эти понятия на примерах.
Предложение «Муха лукаво всплеснула зубами» синтаксически
правильное, но не имеет смысла в естественном русском языке в
обиходном, широком употреблении, т. е. является с точки зрения
пользователей русским языком семантически неправильным
(исключим пока гипотетическую ситуацию сказки, в которой муха может
быть наделена указанными свойствами).
Другое предложение «Маленькая девочка собирает цветы на лугу»
синтаксически и семантически правильное. Однако для директора
завода (если это луг, а не заводской газон, и учтем личный фактор
если эта девочка не его дочь) это предложение не несет никакой
информации, т. е. прагматически (с точки зрения целей руководителя)
является неправильным. Другое дело, если «Иванов (который в
данный момент должен находиться на рабочем месте) собирает цветы
на лугу». Тогда это предложение было бы прагматически правильным.
Возвратимся теперь к примеру с мухой. Приведенное предложение,
семантически неправильное, может в гипотетической ситуации сказки
оказаться прагматически правильным.
96. Порождающая и распознающая грамматика
• Под порождающей грамматикой понимаетсясовокупность правил, с помощью которых
обеспечивается возможность формирования
(порождения) из первичных элементов
(словаря) синтаксически правильных
конструкций.
• Под распознающей грамматикой правила,
с помощью которых обеспечивается
возможность распознавания синтаксической
правильности предложений, фраз или других
фрагментов языка.
• Все рассмотренные понятия в равной мере
используются как в математической
лингвистике, так и в лингвистической
семиотике.
97. Пример порождающей грамматики
Дано:
VT = <в1, в2, п, л >
VN = <S, P>
Порождающая грамматика
Распознающая грамматика
S SP
(1)
SP S
(1')
S в1S (2)
в1S S
(2')
R = S в2S (3)
в2 S S
(3')
S п
(4)
n S
(4')
P л
(5)
л P
(5')
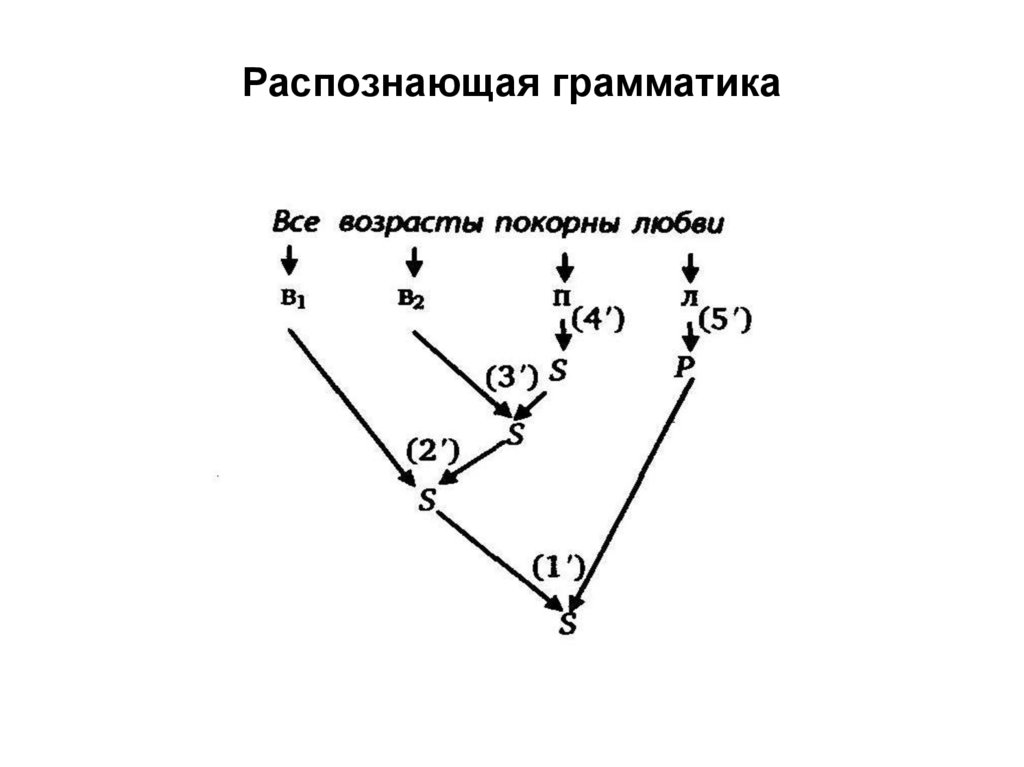
Применяя правила R левой части (2.17) в приведенной последовательности,
получим:
S S P в1 S P в1 в2 S P в1 в2 п P в1 в2 п л
(1)
(2)
(3)
(4)
(5)
Для того, чтобы получить интерпретируемое выражение, нужно расшифровать
терминальные символы, включенные в VN,
где в1 ВСЕ, в2 ВОЗРАСТЫ, п ПОКОРНЫ, л ЛЮБВИ.
Тогда полученное предложение
«в1 в2 п л» «ВСЕ ВОЗРАСТЫ ПОКОРНЫ ЛЮБВИ».
Если изменить последовательность применения правил, то будут получаться другие
предложения. Например, если применить правила в последовательности (1) (3) (2)
(4) (5), то получится «ВОЗРАСТЫ ВСЕ ПОКОРНЫ ЛЮБВИ». Если применить не все
правила: например, (1) (2) (4) (5), то получим «ВСЕ ПОКОРНЫ ЛЮБВИ».
Если же попытаться получить предложение, как у А.С. Пушкина «Любви все возрасты
покорны», то, как бы мы не меняли последовательность правил, получить эту фразу не
удается. Нужно изменить первое правило: вместо S SP включить в R правило S
PS.
98. Распознающая грамматика
99. Применение теории формальных грамматик
• В теории формальных грамматик показано, что имеетместо следующее соотношение:
А КС НС НУ .
• Иногда доказывают, что имеет место строгое
вхождение:
А КС НС НУ.
• При исследовании разных классов формальных
грамматик получены результаты, которые позволяют
сделать вывод, что по мере уменьшения числа
ограничений, накладываемых на правила вывода, т. е. по
мере продвижения слева направо, в языке увеличивается
возможность отображение смысла (повышается
смысловыражающая способность языка, т. е. возможность
выражения с помощью формальных правил
семантических особенностей проблемной ситуации):
говорят, что формальная система становится более
богатой. Однако при этом в языке растет число
алгоритмически неразрешимых проблем, т. е.
увеличивается число положений, истинность или
ложность которых не может быть доказана в рамках
формальной системы языка.
100. Семиотика
• Семиотика возникла как наука о знаках,знаковых системах.
• Однако некоторые школы, развивающие
семиотические представления, настолько
равноправно пользуются в семиотике
понятиями математической лингвистики,
такими, как тезаурус, грамматика, семантика
и т. п. (характеризуемыми далее), не выделяя
при этом в отдельное направление
лингвосемиотику, что часто трудно
определить, к какой области относится
модель математической лингвистике или
семиотике.
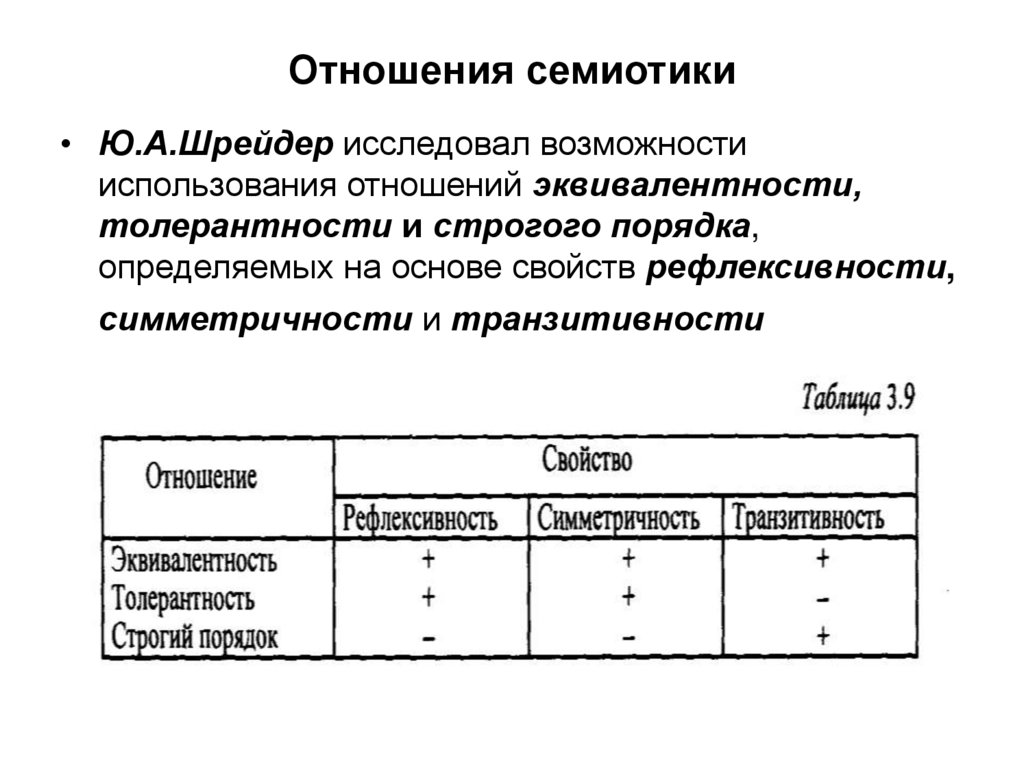
101. Отношения семиотики
• Ю.А.Шрейдер исследовал возможностииспользования отношений эквивалентности,
толерантности и строгого порядка,
определяемых на основе свойств рефлексивности,
симметричности и транзитивности
102. М.К. Эсхер «Небо и вода»
Муха – мура – тура – тара – кара – каре – кафн – кафр –каюр – каюк – крюк – крок – срок – сток – стон - слон
103. Отношение толерантности
Отношение толерантностирам-а стол
стол книг-у,
• в синтагме «рама стол» имеет место
отношение сходства с точностью до
рефлексии и симметрии,
• в синтагме «стол книгу» тоже,
• а между элементами синтагмы
• «рам-а» «книг-у» сходства нет в силу
невыполнения по определению для
рассматриваемого отношения свойства
транзитивности.
• Отражают сходство по падежу, по роду
104. Графические представления
• Геометрия, теория графов.Sx
• Понятие графа в математическом смысле
первоначально было введено Л.Эйлером F[x]
• 1. Графики, выражающие структуры и связи
(оргаграммы).
• 2. Графики, выражающие расположения предметов и
явлений во времени (хронограммы) и в пространстве
(топограммы).
• 3. Графики, выражающие количественные
отношения.
• 4. Графики расчетного характера.
• Графики Ганта PERT (Program Evaluation and
Review Technique Методика оценки и контроля
программ(.
• Теория сетевого планирования и управления (СПУ).
• Структурно-лингвистическое, графосемиотическое моделирование.
105. Темы рефератов
• Методы статистического анализа(регрессионный, дисперсионный, корреляционный,
факторный и т. п.).
• Теория статистических испытаний; основой
этой теории является метод Монте-Карло.
• Теория статистического имитационного
моделирования.
• Теория выдвижения и проверки
статистических гипотез; возникла для оценки
процессов передачи сигналов на расстоянии.
• Теория статистических решающих функций А.
Вальда; важным частным случаем теории является
байесовский подход к исследованию процессов
передачи информации, процессов общения,
обучения и др. ситуациях в организационных
системах.
106. Темы рефератов
• Теория массового обслуживания.• Статистическая радиотехника.
• Статистическая теория распознавания
образов.
• Стохастическое программирование.
• Экономическая статистика.
• Теории игр.
• Информетрия.
107. Темы рефератов
• Диаграммы Эйлера – Венна.• Законы алгебры логики.
• Логический анализ и логический синтез.
• Семиотика.
• Порождающая и распознающая грамматика.
• Отношений эквивалентности,
толерантности и строгого
порядка,
108. Список литературы
1. Волкова В. Н., Денисов А. А. Основы теории систем
и системного анализа: учебник для студентов вузов.
СПб.: Изд-во СПбГТУ, 1997. 510 с. Изд. 2-е – 1999. –
512 с. Изд. 3-е – Изд-во Политехн. ун-та, 2005. 520 с.
2. Волкова В. Н., Денисов А. А. Теория систем: учеб.
пособие для студентов вузов. М.: Высшая школа,
2006. 512 с.
3. Волкова В. Н., Денисов А. А. Теория систем и
системный анализ: учебник для академического
бакалавриата. М.: Изд-во Юрайт, 2010. – 680 с. 2-е
изд., переработанное и дополненное. М.: Изд-во
Юрайт, 2014. 616 с.
4. Системный анализ и принятие решений: Справочник /
Под ред. В.Н.Волковой и В.Н. Козлова. – М.: Высшая школа,
616 с
5. Моделирование систем. Подходы и методы: учеб. пособие
/ В. Н. Волкова, В. Н. Козлов, Ю. И. Лыпарь, А. Н. Фирсов,
Л. В. Черненькая; под ред. В. Н. Волковой, В. Н. Козлова. –
СПб.: Изд-во Политехнич.ун-та, 2012. – 440 с.
6. Моделирование систем и процессов: учебник для
академического бакалавриата / В. Н. Волкова, Г. В. Горелова,
А. А. Ефремов и др. Под ред. В. Н. Волковой. М.: Изд-во
Юрайт, 2014. 592 с. .
109. Список литературы (продолжение)
Волкова В.Н. Теория информационных процессов исистем: учебник и практикум для академического
бакалавриата. М.: Изд-во Юрайт, 2014. 502 с. Серия:
Бакалавр. Академический курс.
8. Волкова В. Н., Системный анализ информационных
комплексов: учеб. пособие. – СПб.: Изд-во Политехн.
университета, 2014. – 336 с.
9. Волкова В. Н., Темников Ф. Е. Методы
формализованного представления (отображения) систем:
Текст лекций. М.: ИПКИР, 1974. 114 с.
10. Волкова В. Н., Денисов А.А., Темников Ф. Е. Методы
формализованного представления (отображения) систем
СПб.: Изд-во СПбГТУ, 1993. 108 с.
11. Шрейдер Ю. А. Равенство, сходство, порядок. М.: Наука,
1971. 254 с.
7.




























































































 mathematics
mathematics








