Similar presentations:
Операции над графами. Примеры решения задач
1.
2.
Операции над графамиa) Дополнением графа G1 (V1 , E1 ) называется граф G1 (V1 , E1 ), множеством вершин
которого является множество V , а множеством его ребер является множество
E1 { e V1 V1 : e E1 }.
1
b) Объединением графов G1 (V1 , E1 ) и G2 (V2 , E2 ) при условии, что V1 V2 ; E1 E2 ,
называется граф G1 (V1 , E1 ) и G2 (V2 , E2 ), множеством вершин которого является
множество V1 V2 , а множеством его ребер является множество E1 E2 .
c) Пересечением графов G1 (V1 , E1 ) и G2 (V2 , E2 ) называется граф G1 (V1 , E1 ) G2 (V2 , E2 )
множеством вершин которого является множество V1 V2 , а множеством его
ребер – множество E1 E2 .
d) Суммой по модулю два графа G1 (V1 , E1 ) и G2 (V2 , E2 ) при условии, что V V ; E E ,
называется граф G1 (V1 , E1 ) G2 (V2 , E2 ), множеством вершин которого
является множество V1 V2 , а множеством его ребер – множество E1 E2 .
Другими словами, этот граф не имеет изолированных вершин и состоит только из
ребер, присутствующих либо в первом графе, либо во втором, но не в обоих
графах одновременно.
1
2
1
2
3. Примеры решения задач при помощи графов
Задача 1.Пятеро
ученых,
участвовавших
в
научной
конференции, обменялись рукопожатиями. Сколько
всего было сделано рукопожатий ?
4. Примеры решения задач при помощи графов
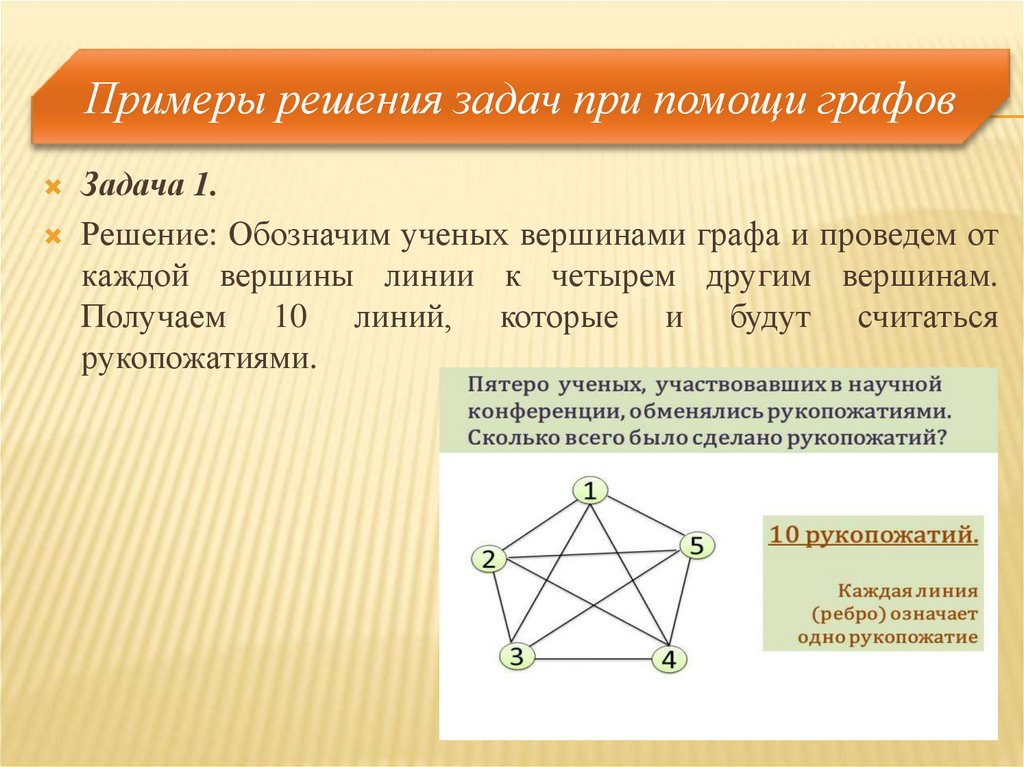
Задача 1.Решение: Обозначим ученых вершинами графа и проведем от
каждой вершины линии к четырем другим вершинам.
Получаем 10 линий, которые и будут считаться
рукопожатиями.
5. Примеры решения задач при помощи графов
Задача 2.На пришкольном участке растут 8 деревьев: яблоня,
тополь, береза, рябина, дуб, клен, лиственница и
сосна. Рябина выше лиственницы, яблоня выше
клена, дуб ниже березы, но выше сосны, сосна выше
рябины, береза ниже тополя, а лиственница выше
яблони. Расположите деревья от самого низкого к
самому высокому.
6. Примеры решения задач при помощи графов
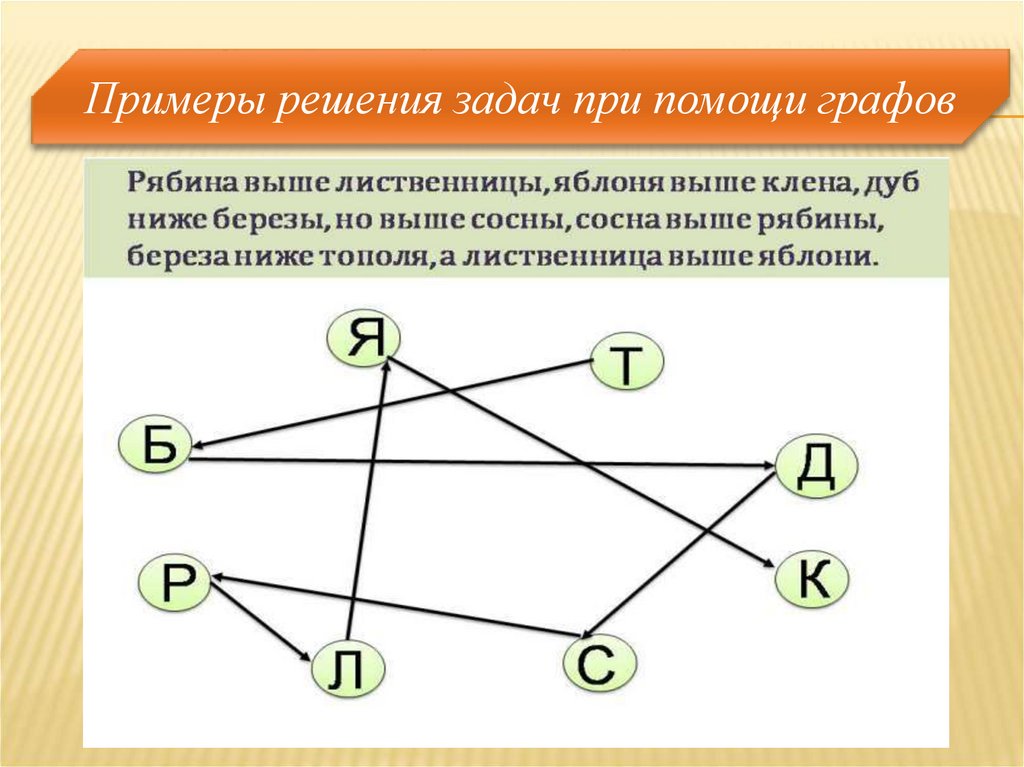
Задача 2. Решение:Вершины графа - это деревья, обозначенный первой буквой
названия дерева. В данной задача два отношения: “быть ниже” и
“быть выше”. Рассмотрим отношение “быть ниже” и проведем
стрелки от более низкого дерева к более высокому. Если в задаче
сказано, что рябина выше лиственницы, то стрелку ставим от
лиственницы к рябине и т.д. Получаем граф, на котором видно,
что самое низкое дерево – клен, затем идут яблоня, лиственница,
рябина, сосна, дуб, береза и тополь
7. Примеры решения задач при помощи графов
8. Примеры решения задач при помощи графов
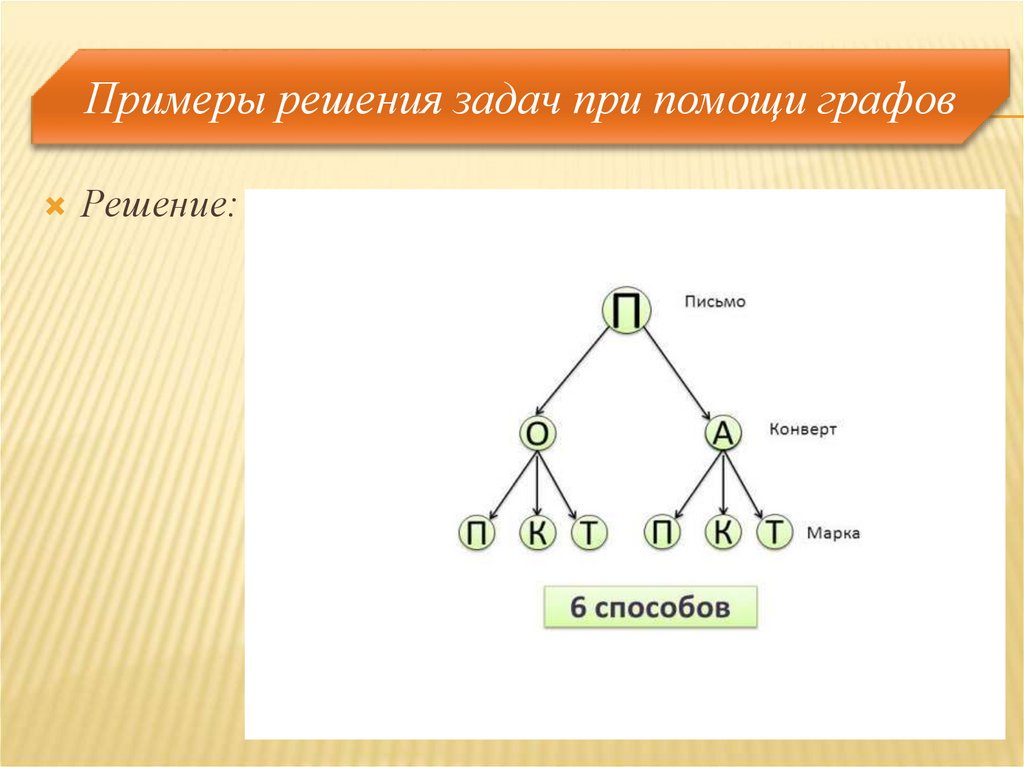
Задача 3.У
Наташи есть 2 конверта: обычный и авиа, и 3
марки: прямоугольная, квадратная и треугольная.
Сколькими способами Наташа может выбрать
конверт и марку, чтобы отправить письмо?
9. Примеры решения задач при помощи графов
Решение:10. Практическая работа
Используяматериалы Приложений 1,2,3,5
по теме «Графы», выполните практическую
работу.








 mathematics
mathematics








