Similar presentations:
Основные понятия теории графов. Виды графов: ориентированные и неориентированные графы
1.
2. повторение
ПОВТОРЕНИЕПройдите блиц-опрос по теме
«Основные понятия теории графов.
Виды графов: ориентированные и
неориентированные графы»
3. Опрос по теме
ОПРОС ПО ТЕМЕ1. Понятие маршрута.
2. Понятие графа.
3. Понятие изолированной вершины.
4. Понятие инцидентных ребра и вершины.
5. Понятие полного графа.
6. Понятие валентности вершины
7. Понятие простого цикла
8. Понятие связного графа
9. Понятие орграфа
10. Понятие мультиграфа
4. Опрос по теме
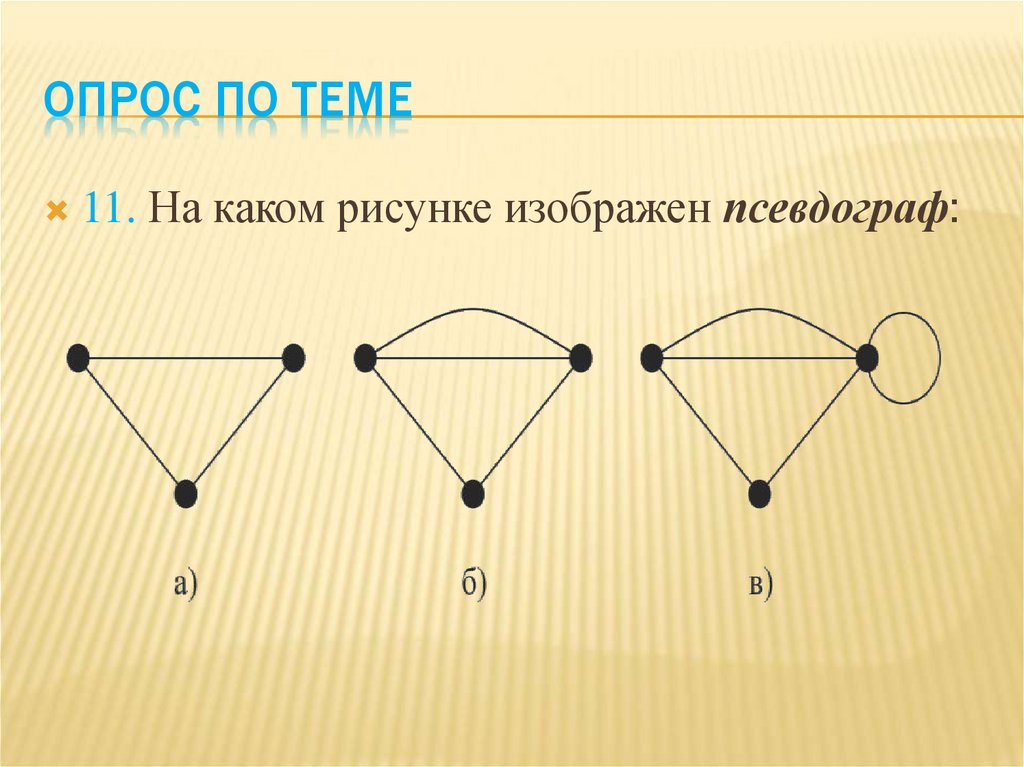
ОПРОС ПО ТЕМЕ11. На каком рисунке изображен псевдограф:
5. Опрос по теме
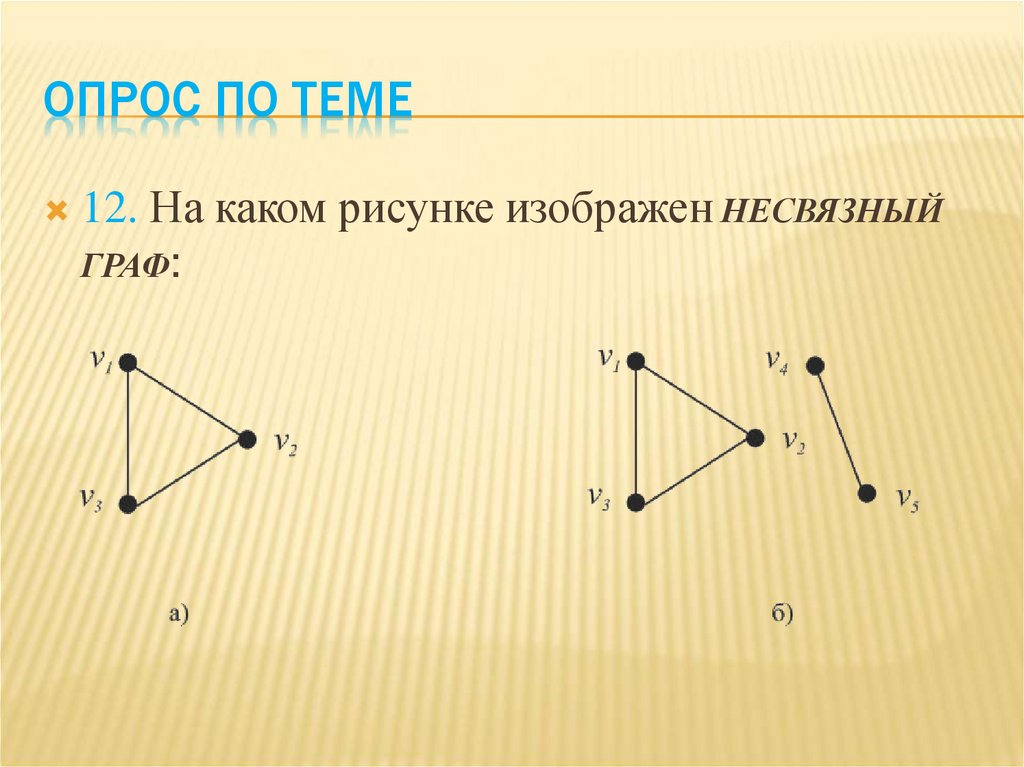
ОПРОС ПО ТЕМЕ12. На каком рисунке изображен НЕСВЯЗНЫЙ
ГРАФ:
6.
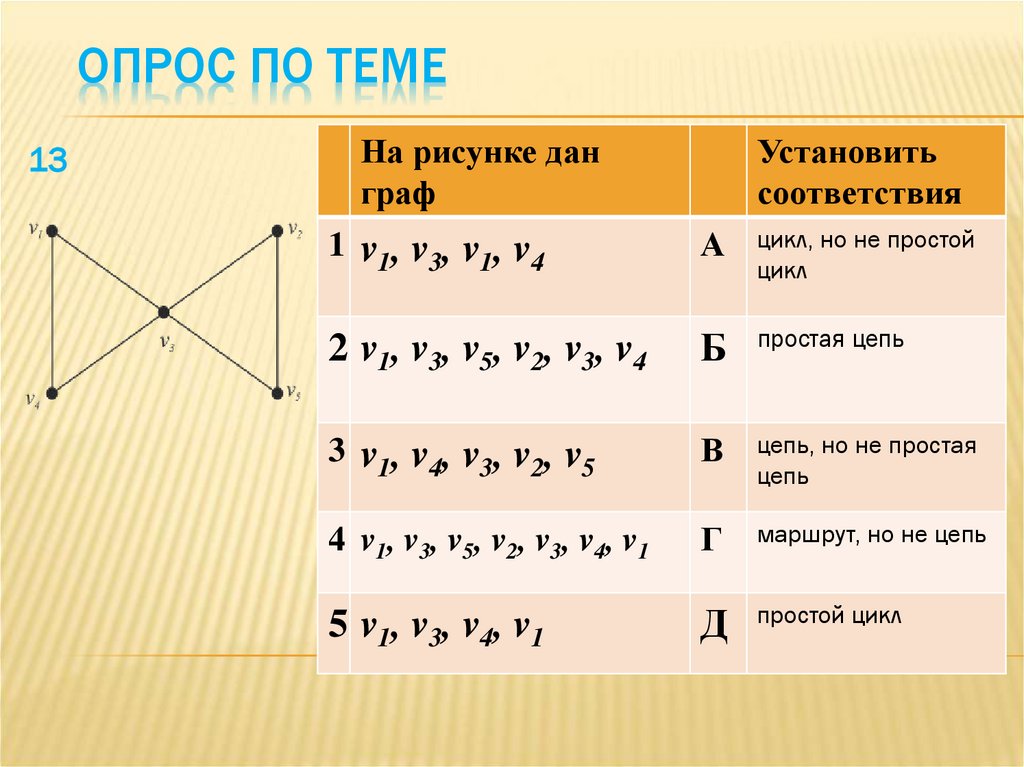
ОПРОС ПО ТЕМЕ13
На рисунке дан
граф
Установить
соответствия
1 v1, v3, v1, v4
А
цикл, но не простой
цикл
2 v1, v3, v5, v2, v3, v4
Б
простая цепь
3 v1, v4, v3, v2, v5
В
цепь, но не простая
цепь
4 v1 , v3 , v5 , v2 , v3 , v4 , v1
Г
маршрут, но не цепь
5 v1, v3, v4, v1
Д
простой цикл
7.
Некоторые типы графовЭйлеровы графы
Эйлеровым путем в графе называется путь, содержащий все ребра графа
только один раз.
Эйлеровым циклом или эйлеровой цепью называется цикл, содержащий
все ребра графа и притом по одному разу. Граф, обладающий эйлеровым
циклом, называется эйлеровым графом.
Замкнутую линию, если ее можно начертить, не отрывая карандаша от
бумаги, проходя при этом каждый участок в точности один раз, принято
называть уникурсальной. Рисунок графа, обладающего эйлеровым путем или
циклом, является уникурсальной линией.
Теорема 1. Если граф G(V,E) обладает эйлеровым циклом, то он связный
и все его вершины четные.
Теорема 2. Если граф G(V,E) связный и все его вершины четные, то он
обладает эйлеровым циклом.
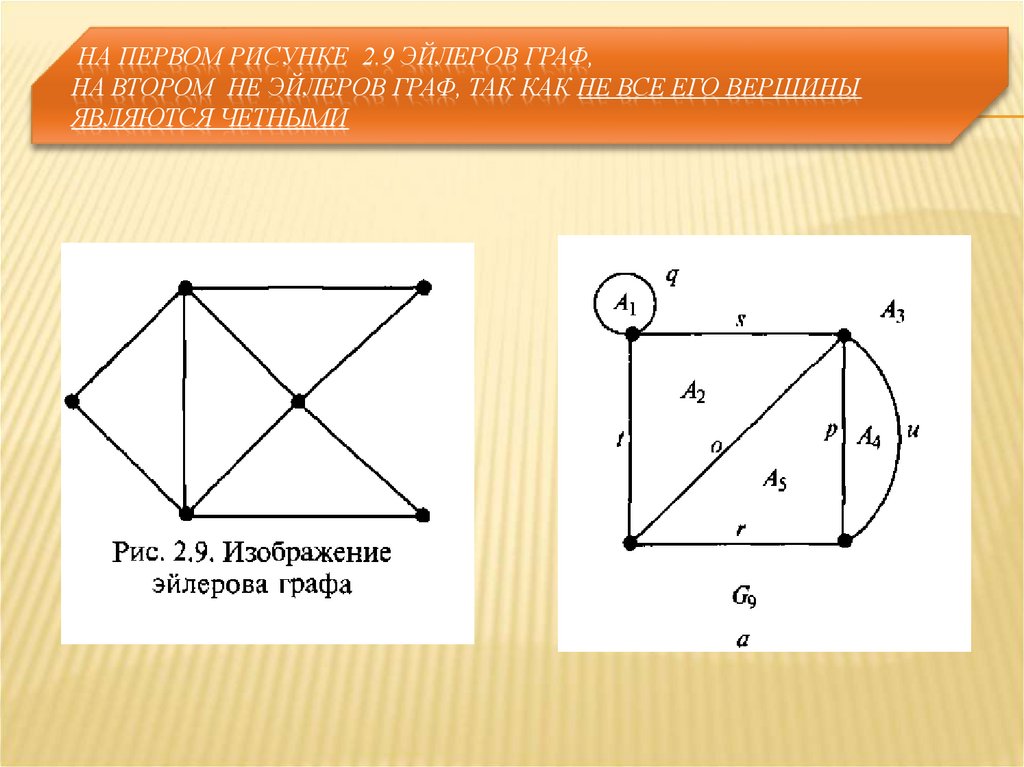
8. На первом рисунке 2.9 эйлеров граф, на втором не эйлеров граф, так как не все его вершины являются четными
НА ПЕРВОМ РИСУНКЕ 2.9 ЭЙЛЕРОВ ГРАФ,НА ВТОРОМ НЕ ЭЙЛЕРОВ ГРАФ, ТАК КАК НЕ ВСЕ ЕГО ВЕРШИНЫ
ЯВЛЯЮТСЯ ЧЕТНЫМИ
9.
Гамильтоновы графыГраф, обладающий гамильтоновым циклом, называется гамильтоновым
графом. Гамильтоновым циклом, называется цикл, или путь, проходящий
через каждую вершину графа в точности по одному разу.
Эйлеровы и гамильтоновы пути сходны по способу задания. Первые
содержат все ребра, и притом по одному разу, вторые – все вершины по
одному разу. Для решения вопроса о существовании эйлерова цикла в графе
достаточно выяснить, все ли его вершины четные.
Условия существования гамильтоновых циклов
1. Всякий полный граф является гамильтоновым, так как содержит простой
цикл, которому принадлежат все вершины данного графа.
2. Если граф, помимо простого цикла, проходящего через все его вершины,
содержит и другие ребра, то он также является гамильтоновым.
3. Если граф имеет один гамильтонов цикл, то он может иметь и другие
гамильтоновы циклы.
10.
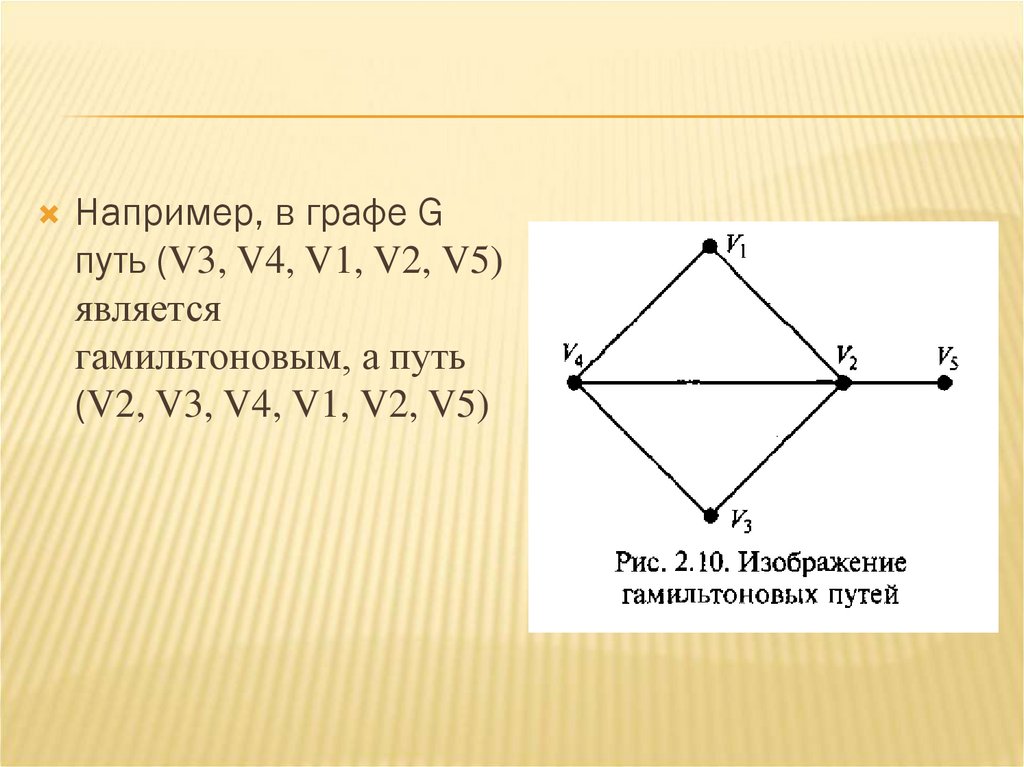
Например, в графе Gпуть (V3, V4, V1, V2, V5)
является
гамильтоновым, а путь
(V2, V3, V4, V1, V2, V5)
11.
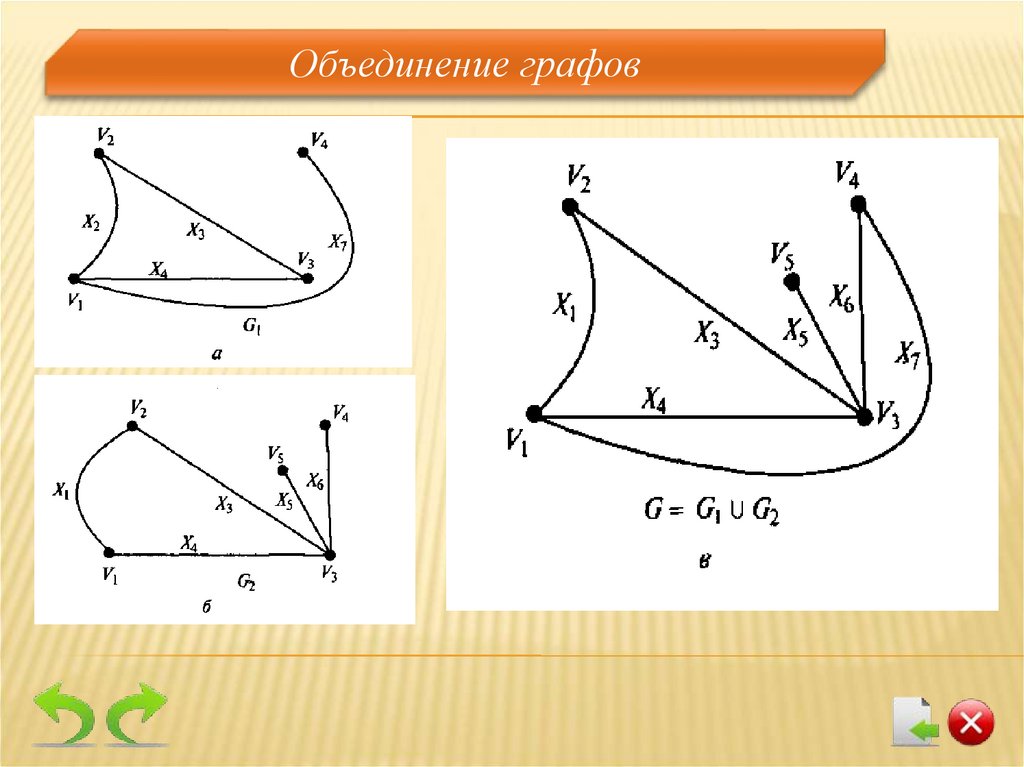
Операции над графами. Объединение графовОбъединением графов G1 (V1 , E1 ) и G2 (V2 , E2 ),
при
условии, что V1 V2 ; E1 E2 ,
называется граф V1 V2 ,
множеством вершин
которого является множество V1 V2 , а множеством
его ребер является множество E1 E2 .
12.
Объединение графов13.
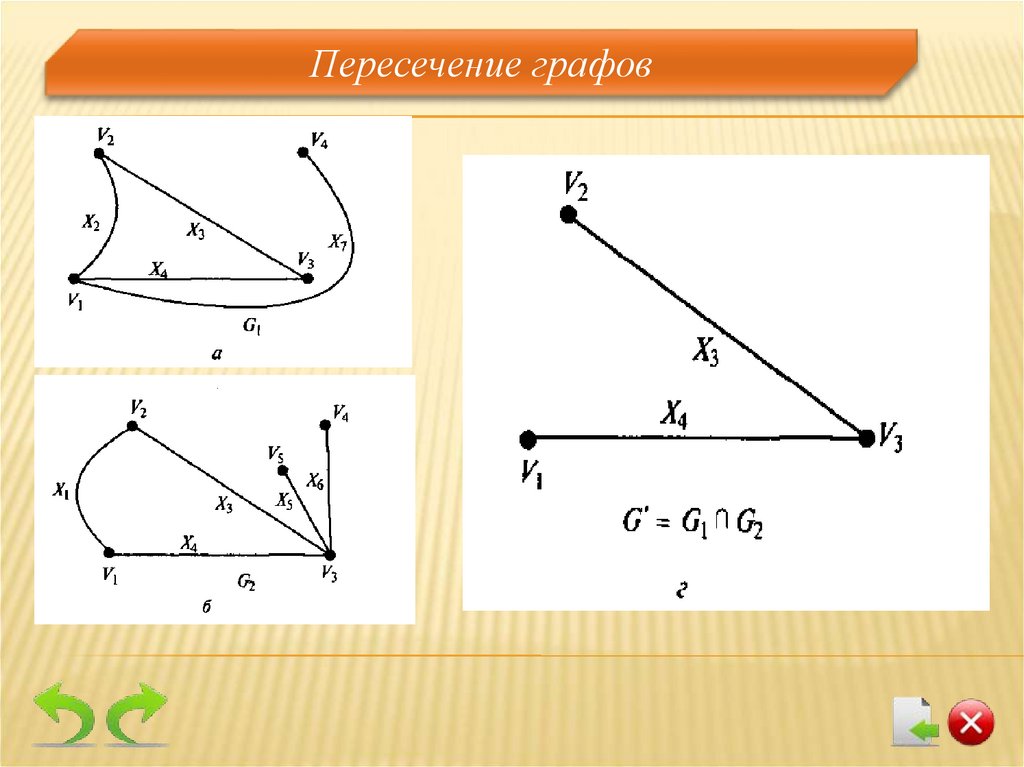
Операции над графами. Пересечение графовПересечением графов G (V , E ) и G (V , E )
называется граф G (V , E ) G (V , E )
множеством вершин которого является
множество V1 V2 ,
а множеством его ребер –
множество E1 E2 .
1
1
1
1
1
2
1
2
2
2
2
2
14.
Пересечение графов15.
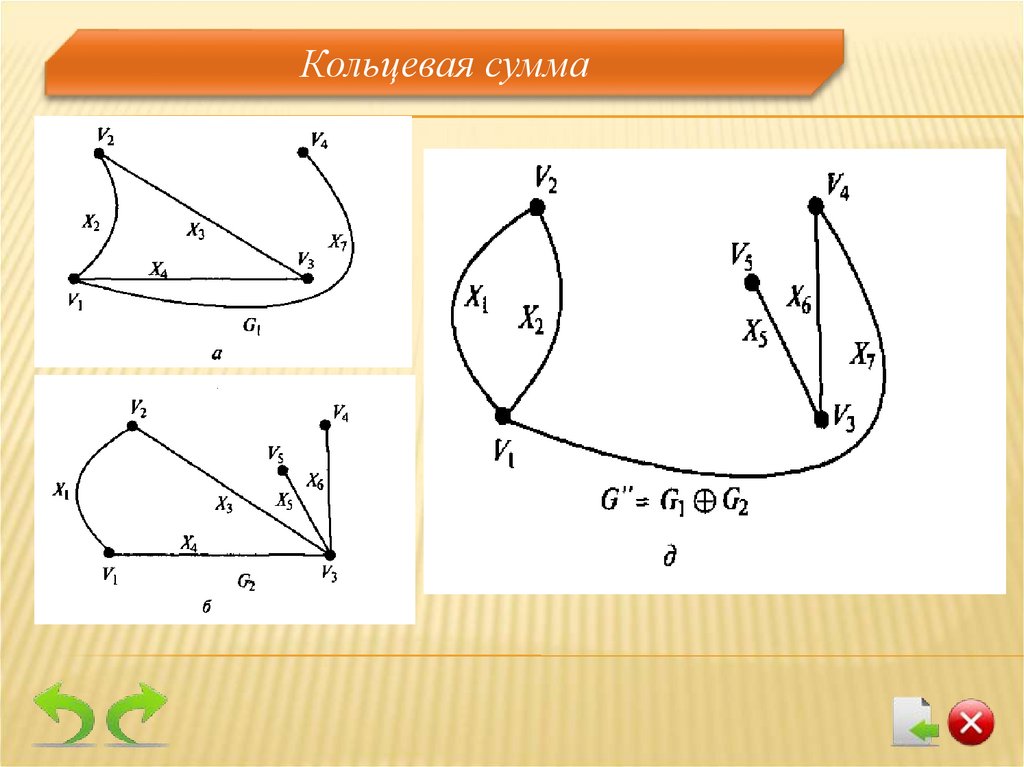
Операции над графами. Кольцевая сумма.Кольцевой суммой (суммой по модулю два) двух
графов G (V , E ) и G (V , E ) при условии, что V V ; E E ,
называется граф G G1 (V1 , E1 ) G2 (V2 , E2 ),
множеством
вершин которого является множество V1 V2 ,
а
множеством его ребер – множество
( E) E .
Другими словами, этот граф не имеет изолированных
вершин и состоит только из ребер, присутствующих
либо в первом графе, либо во втором, но не в обоих
графах одновременно.
1
1
2
1
1
2
2
2
1
2
1
2
16.
Кольцевая сумма17.
Операции над графами. Дополнение графаДополнением графа G (V , E ) называется
граф G (V , E ), множеством вершин которого
является множество V , а множеством его
ребер является множество
E1 { e V V : e E}.
1
1
1
1
1
1
1
1
1
1
18. Дополнение графа
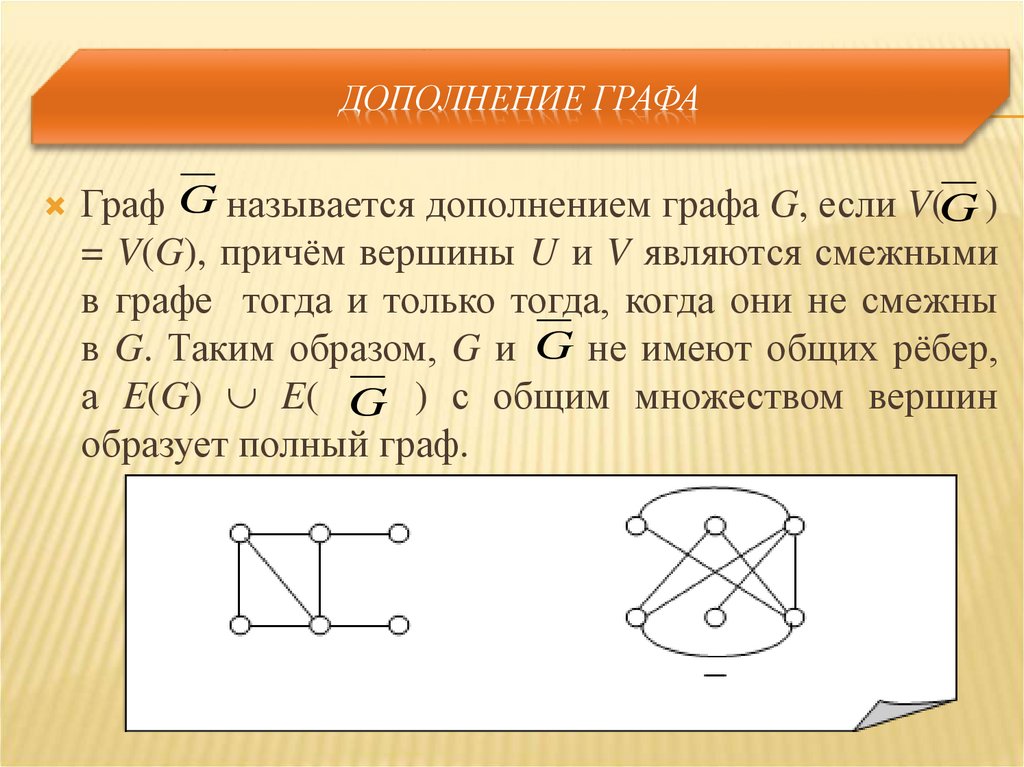
ДОПОЛНЕНИЕ ГРАФАГраф G называется дополнением графа G, если V(G )
= V(G), причём вершины U и V являются смежными
в графе тогда и только тогда, когда они не смежны
в G. Таким образом, G и G не имеют общих рёбер,
а E(G) E( G ) с общим множеством вершин
образует полный граф.
19.
Операции над графамиa) Дополнением графа G1 (V1 , E1 ) называется граф G1 (V1 , E1 ), множеством вершин
которого является множество V , а множеством его ребер является множество
E1 { e V1 V1 : e E1 }.
1
b) Объединением графов G1 (V1 , E1 ) и G2 (V2 , E2 ) при условии, что V1 V2 ; E1 E2 ,
называется граф G1 (V1 , E1 ) и G2 (V2 , E2 ), множеством вершин которого является
множество V1 V2 , а множеством его ребер является множество E1 E2 .
c) Пересечением графов G1 (V1 , E1 ) и G2 (V2 , E2 ) называется граф G1 (V1 , E1 ) G2 (V2 , E2 )
множеством вершин которого является множество V1 V2 , а множеством его
ребер – множество E1 E2 .
d) Суммой по модулю два графа G1 (V1 , E1 ) и G2 (V2 , E2 ) при условии, что V V ; E E ,
называется граф G1 (V1 , E1 ) G2 (V2 , E2 ), множеством вершин которого
является множество V1 V2 , а множеством его ребер – множество E1 E2 .
Другими словами, этот граф не имеет изолированных вершин и состоит только из
ребер, присутствующих либо в первом графе, либо во втором, но не в обоих
графах одновременно.
1
2
1
2
20. Примеры
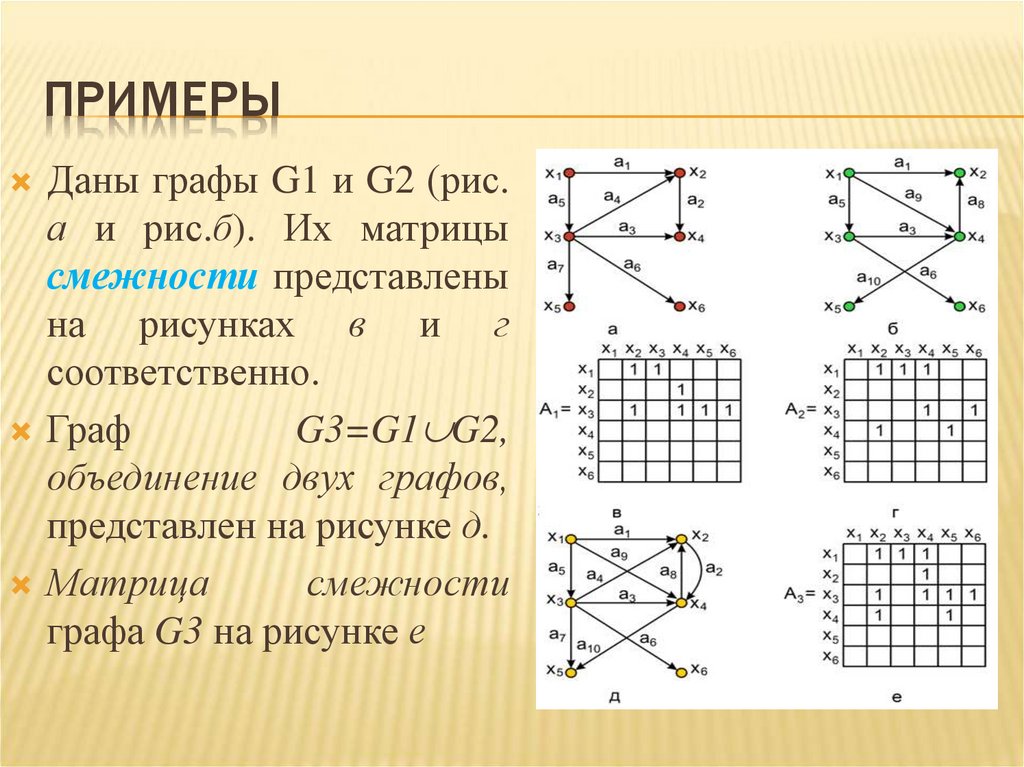
ПРИМЕРЫДаны графы G1 и G2 (рис.
а и рис.б). Их матрицы
смежности представлены
на рисунках в и г
соответственно.
Граф
G3=G1 G2,
объединение двух графов,
представлен на рисунке д.
Матрица
смежности
графа G3 на рисунке е
21.
22. Деревья
Деревом называется связный граф без циклов.Лесом называется любой неориентированный граф без циклов.
Компоненты связности леса есть деревья. Каждому дереву с m
ребрами можно поставить в соответствие двоичное слово
длины 2m, называемое кодом дерева и составленное по
правилам:
Обход дерева начинается с корня.
По каждому ребру необходимо пройти по два раза;
первому проходу по ребру ставится в соответствие 0,
второму проходу по ребру ставится в соответствие 1.
Движение по дереву производится последовательно слева
направо.
23. Деревья
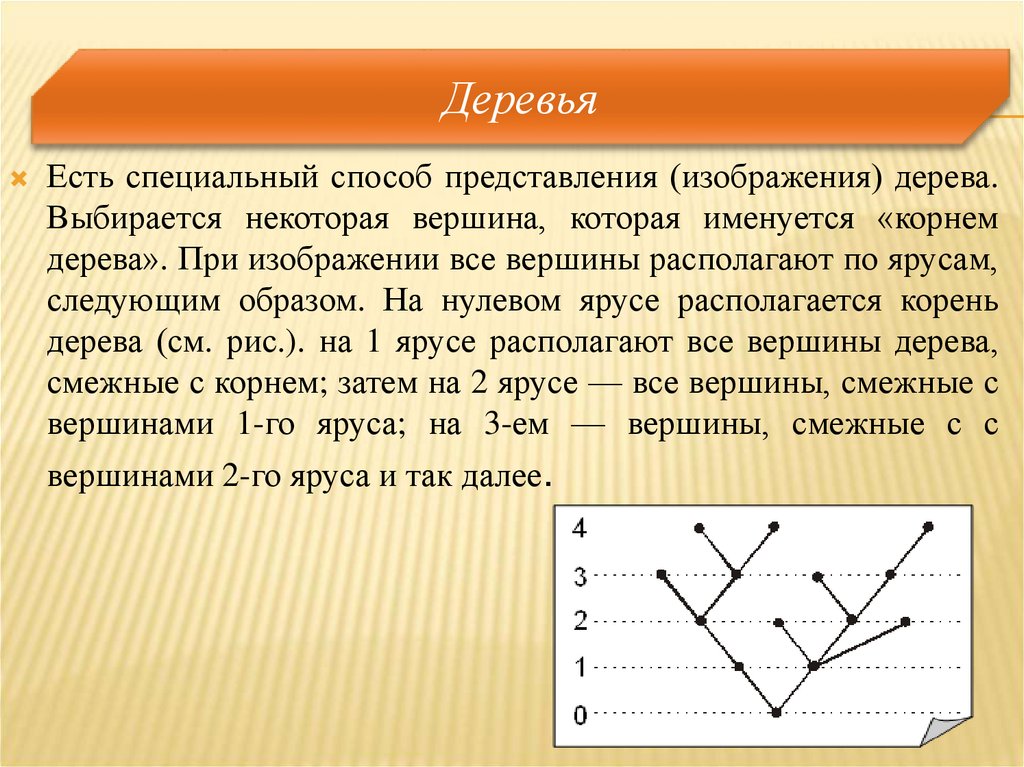
Есть специальный способ представления (изображения) дерева.Выбирается некоторая вершина, которая именуется «корнем
дерева». При изображении все вершины располагают по ярусам,
следующим образом. На нулевом ярусе располагается корень
дерева (см. рис.). на 1 ярусе располагают все вершины дерева,
смежные с корнем; затем на 2 ярусе — все вершины, смежные с
вершинами 1-го яруса; на 3-ем — вершины, смежные с с
вершинами 2-го яруса и так далее.
24. Деревья
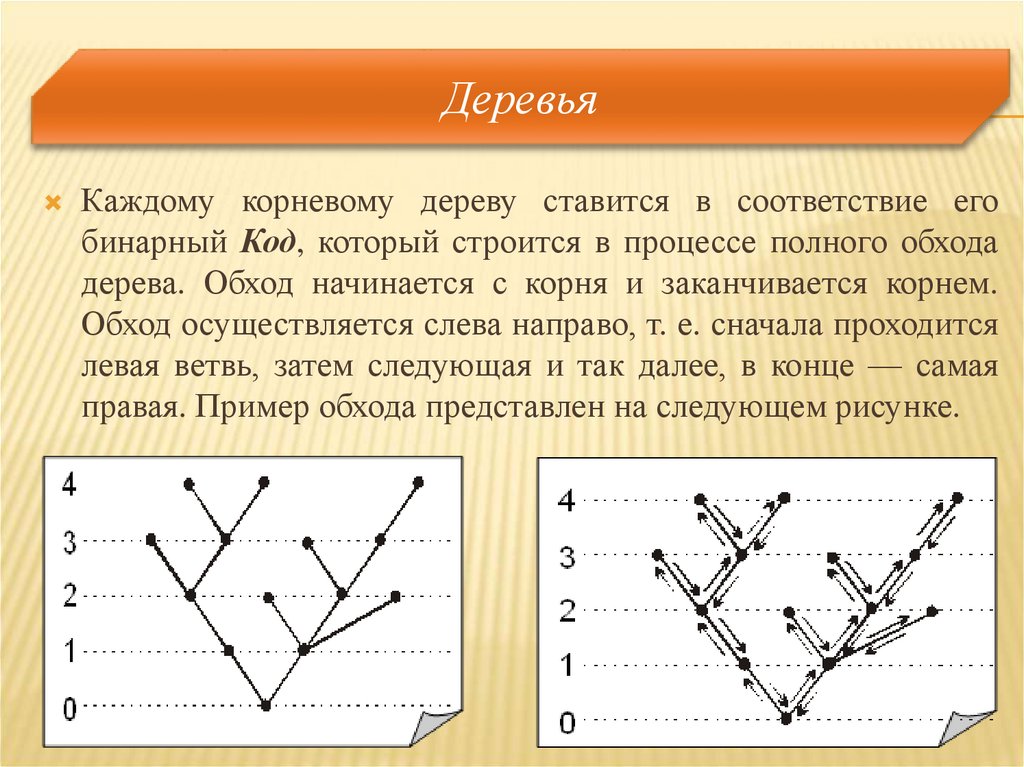
Каждому корневому дереву ставится в соответствие егобинарный Код, который строится в процессе полного обхода
дерева. Обход начинается с корня и заканчивается корнем.
Обход осуществляется слева направо, т. е. сначала проходится
левая ветвь, затем следующая и так далее, в конце — самая
правая. Пример обхода представлен на следующем рисунке.
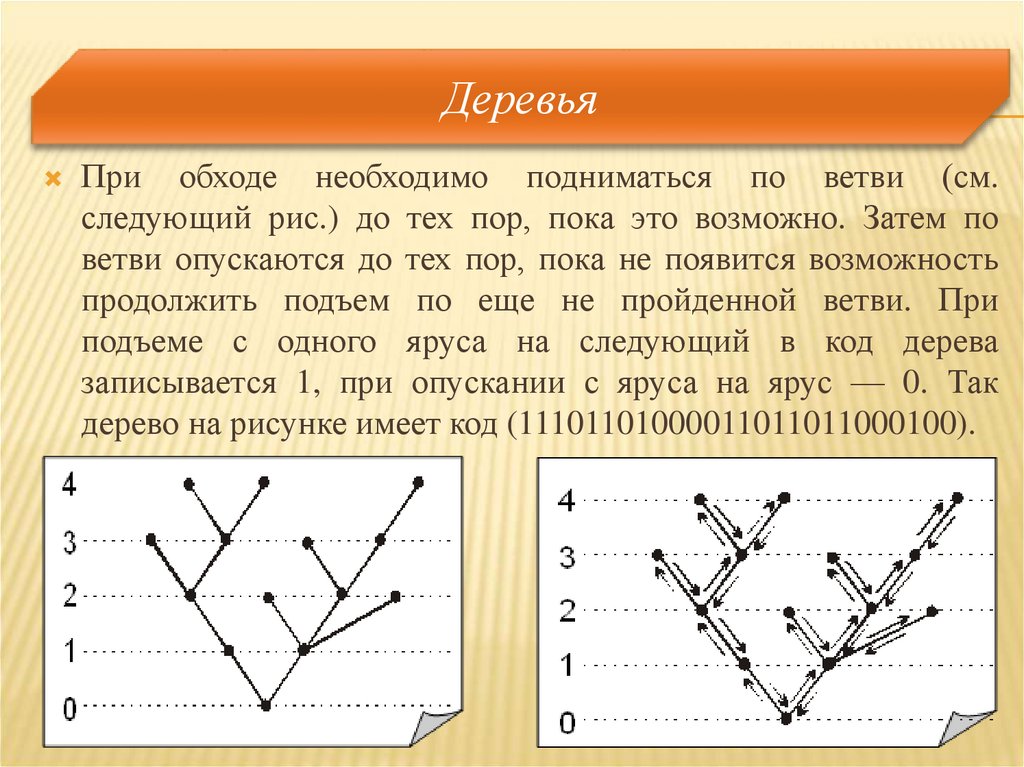
25. Деревья
При обходе необходимо подниматься по ветви (см.следующий рис.) до тех пор, пока это возможно. Затем по
ветви опускаются до тех пор, пока не появится возможность
продолжить подъем по еще не пройденной ветви. При
подъеме с одного яруса на следующий в код дерева
записывается 1, при опускании с яруса на ярус — 0. Так
дерево на рисунке имеет код (11101101000011011011000100).
26. Примеры решения задач при помощи графов
Задача 1.Пятеро
ученых,
участвовавших
в
научной
конференции, обменялись рукопожатиями. Сколько
всего было сделано рукопожатий ?
27. Примеры решения задач при помощи графов
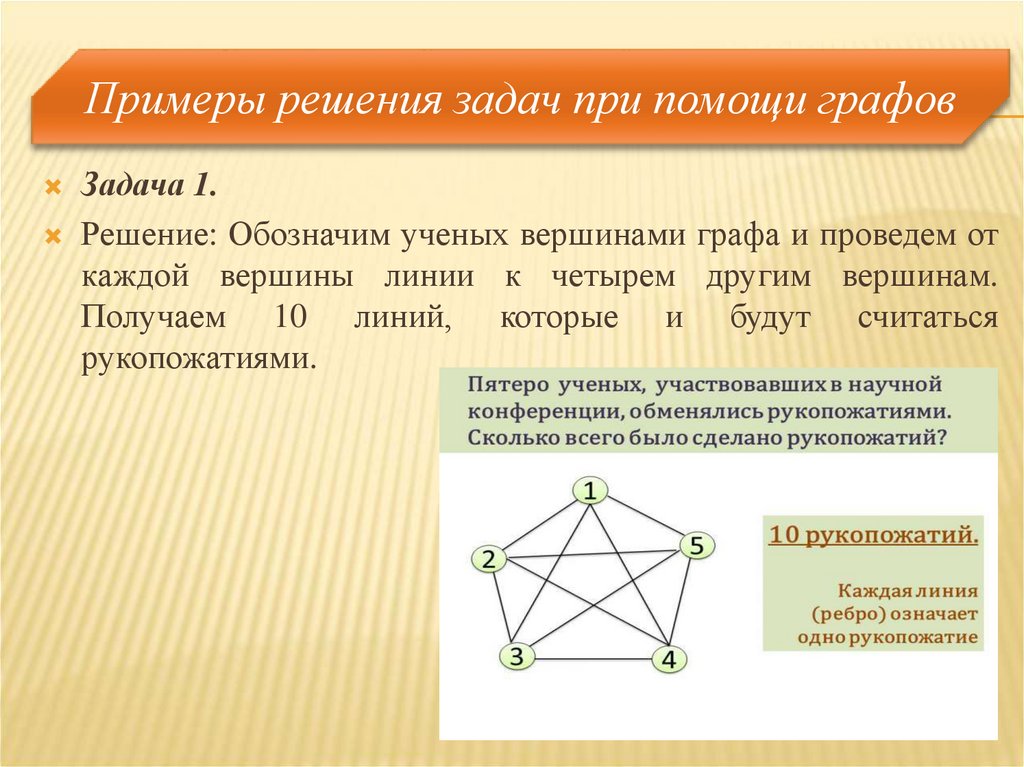
Задача 1.Решение: Обозначим ученых вершинами графа и проведем от
каждой вершины линии к четырем другим вершинам.
Получаем 10 линий, которые и будут считаться
рукопожатиями.
28. Примеры решения задач при помощи графов
Задача 2.На пришкольном участке растут 8 деревьев: яблоня,
тополь, береза, рябина, дуб, клен, лиственница и
сосна. Рябина выше лиственницы, яблоня выше
клена, дуб ниже березы, но выше сосны, сосна выше
рябины, береза ниже тополя, а лиственница выше
яблони. Расположите деревья от самого низкого к
самому высокому.
29. Примеры решения задач при помощи графов
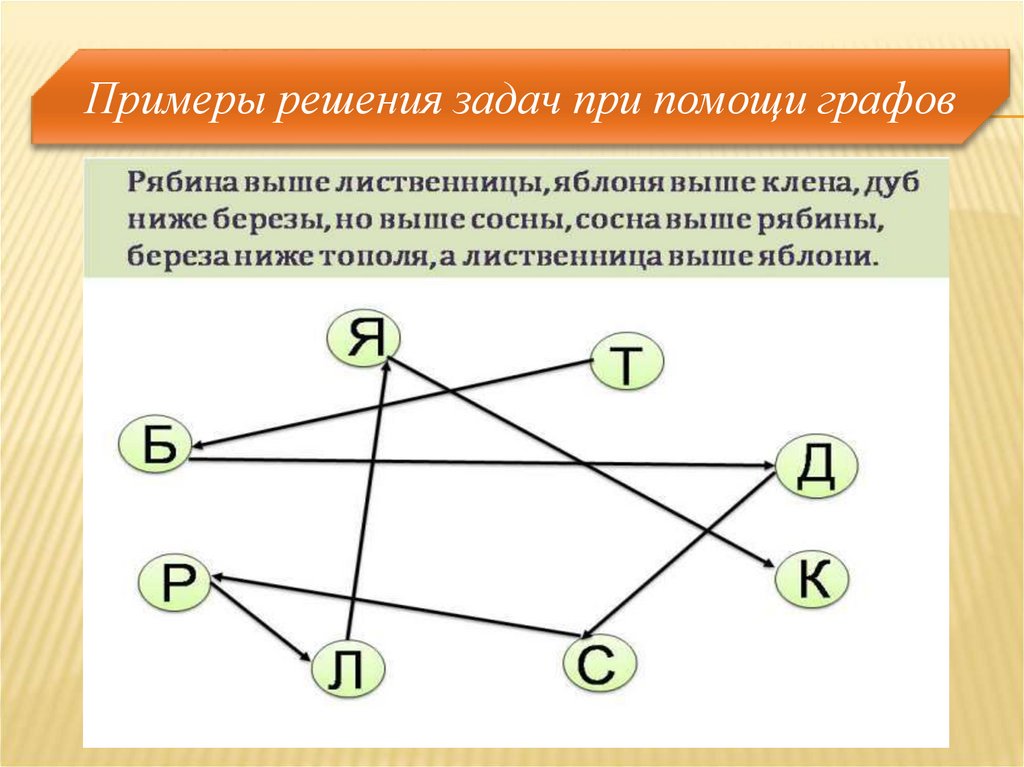
Задача 2. Решение:Вершины графа - это деревья, обозначенный первой буквой
названия дерева. В данной задача два отношения: “быть ниже” и
“быть выше”. Рассмотрим отношение “быть ниже” и проведем
стрелки от более низкого дерева к более высокому. Если в задаче
сказано, что рябина выше лиственницы, то стрелку ставим от
лиственницы к рябине и т.д. Получаем граф, на котором видно,
что самое низкое дерево – клен, затем идут яблоня, лиственница,
рябина, сосна, дуб, береза и тополь
30. Примеры решения задач при помощи графов
31. Примеры решения задач при помощи графов
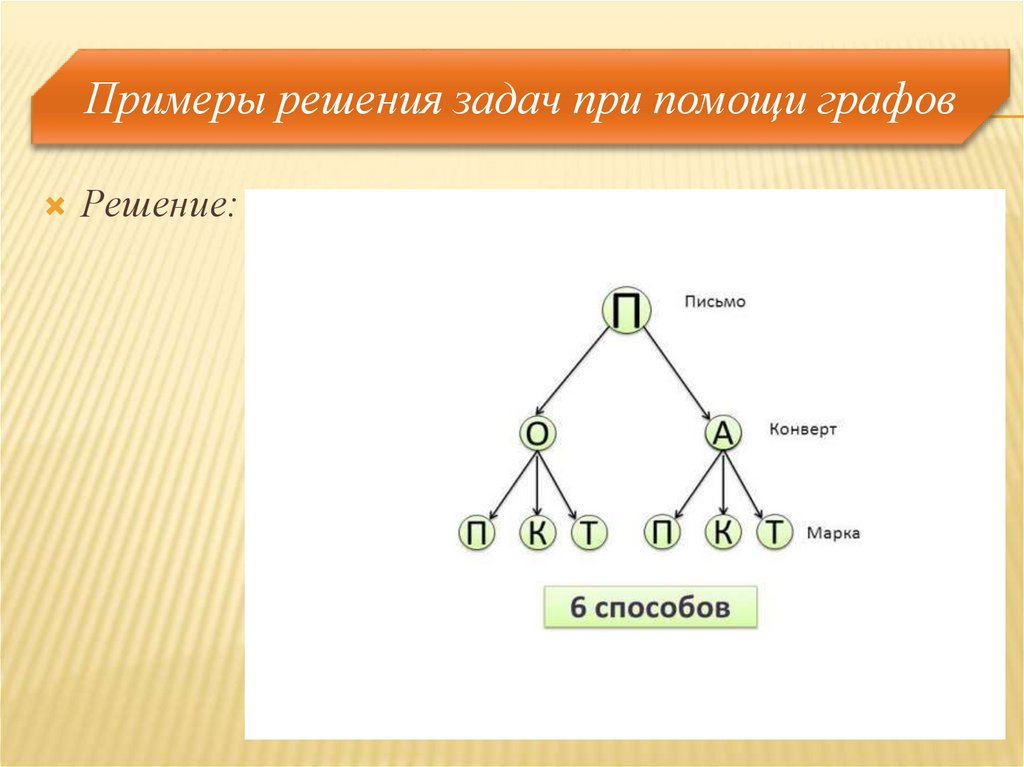
Задача 3.У
Наташи есть 2 конверта: обычный и авиа, и 3
марки: прямоугольная, квадратная и треугольная.
Сколькими способами Наташа может выбрать
конверт и марку, чтобы отправить письмо?

















 mathematics
mathematics








