Similar presentations:
Дискретные структуы. Теория графов. Основные понятия
1.
ДИСКРЕТНЫЕ СТРУКТУЫТЕОРИЯ ГРАФОВ
ОСНОВНЫЕ ПОНЯТИЯ
ЛЕКЦИЯ 13
Математический факультет. Кафедра математического
моделирования
1
2. Цель лекции – овладеть основными понятиями теории графов
ТерминыБазовые
понятия:
множество,
бинарное
отношение
Ключевые слова:
граф,
вершина,
ребро,
дуга,
смежность,
инцидентность,
степень вершины,
мультиграф,
псевдограф,
связность
2
3.
ЛитератураКристофидес Н. Теория графов. Апгоритмический
подход. М.: Мир, 1978. 432 с.
Глускин Л.М., Шор Л.А., Шварц В.Я. Задачи и
алгоритмы комбинаторики, и теории графов. Донецк,
ДПИ, 1982. 368 с.
Харари Ф. Теория графов: Пер. с англ. В.П. Козырева /
Под ред. Г.П. Гаврилова. М.: Мир, 1973. 300 с.
Новиков Ф.А. Дискретная математика длшя
программистов. С.-П., 2001. С. 263-268.
Хаханов В.І., Хаханова І.В., Кулак Е.М., Чумаченко С.В.
Методичні вказівки до практичних занять з курсу
“Дискретна математика”. Харків, ХНУРЕ. 2001. 47-62 с.
3
4.
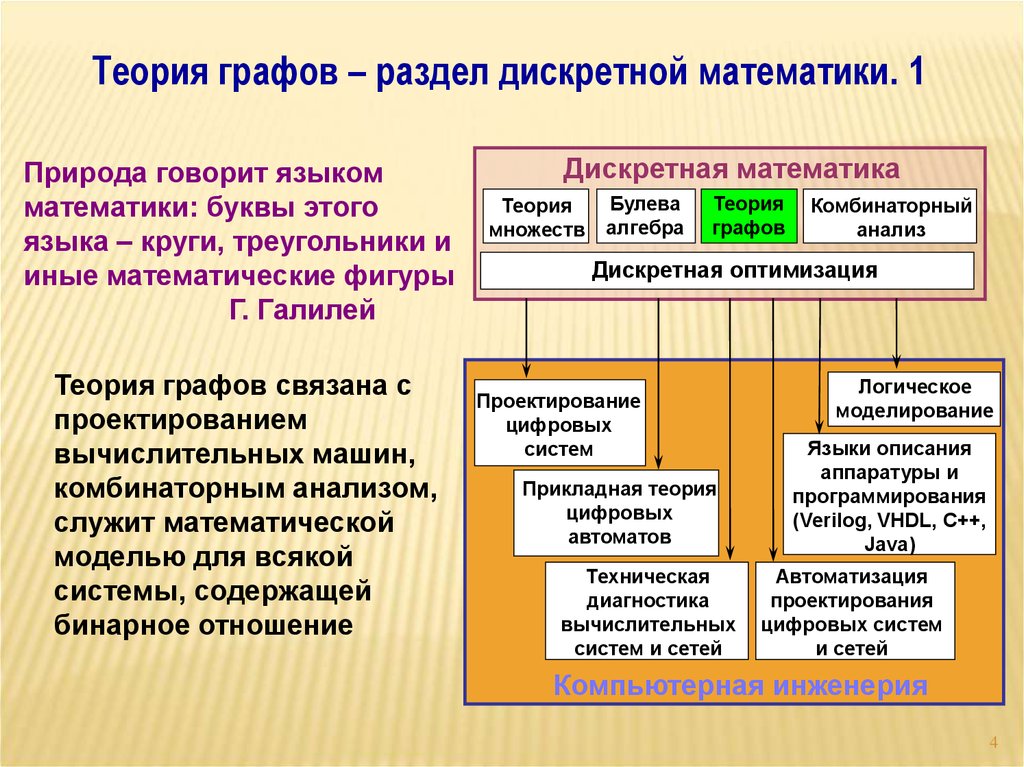
Теория графов – раздел дискретной математики. 1Природа говорит языком
математики: буквы этого
языка – круги, треугольники и
иные математические фигуры
Г. Галилей
Теория графов связана с
проектированием
вычислительных машин,
комбинаторным анализом,
служит математической
моделью для всякой
системы, содержащей
бинарное отношение
Дискретная математика
Теория
множеств
Булева
алгебра
Теория
графов
Комбинаторный
анализ
Дискретная оптимизация
Проектирование
цифровых
систем
Прикладная теория
цифровых
автоматов
Техническая
диагностика
вычислительных
систем и сетей
Логическое
моделирование
Языки описания
аппаратуры и
программирования
(Verilog, VHDL, C++,
Java)
Автоматизация
проектирования
цифровых систем
и сетей
Компьютерная инженерия
4
5.
Теория графов – раздел дискретной математики. 2В теории графов решалось много
проблем, достойных внимания самых
искушенных математиков
Основоположником теории графов
считается Леонард Эйлер, который
доказал невозможность маршрута
прохождения всех четырех частей
суши в задаче о кенигсбергских
мостах (1736)
Графы обладают эстетической
привлекательностью благодаря их
представлению в виде диаграмм
Леонард Эйлер
5
6.
Связь теории графов с теорией множествГраф имеет теоретикомножественное
представление
Граф определяется как
множество вершин и
множество ребер
Множество ребер является
бинарным отношением на
множестве вершин
Множество М
Декартово
произведение
множеств M1 M2
Декартов квадрат
множества M2
Бинарное
отношение R2 M2
Граф
G=<V,U>, U V2
6
7.
Определение графаГраф G=<V,Е > –совокупность
вершин V и ребер Е , где
множество Е представляет
собой бинарное отношение
на множестве вершин:
|V|=n, Е V (2)
Графом часто называют
диаграмму, которой он
представляется
v1
u1
v2
u2
v3
a
b
c
d
e
7
8.
Смежность и инцидентностьВершины, соединяемые некоторым ребром,
называются смежными
Ребра, имеющие общую вершину,
называются смежными
Вершина называется инцидентной ребру, если
она является его началом или концом
Ребра, инцидентные одной и той же вершине,
называются смежными
Понятие смежности относится к однородным
объектам (вершинам или ребрам)
Понятие инцидентности – к разнородным
(вершинам и ребрам)
Количество ребер, инцидентных данной
вершине, называется степенью вершины и
обозначается deg v
v2
v1
v4
v5
v3
(v5,v4)adj(v4,v3)
degv4=2
8
9.
v4Маршруты на графах
Маршрут или путь на графе –
последовательность вида v1,u1,v2,u2,…… ...
un,vn+1, где стоящие рядом ребра и вершины
инцидентны
Цепь – маршрут, в котором нет повторяющихся
ребер
Простая цепь – маршрут, в котором нет
повторяющихся вершин и ребер
Цепь, у которой первая и последняя вершины
совпадают, называется замкнутой
Замкнутая цепь называется циклом
Замкнутый маршрут называется простым
циклом, если все его n вершин различны и n 3
v1
v5
v2
v3
маршрут
v1,v2,v5,v2,v3
не является
цепью;
v1,v2,v5,v4,v2,v3 −
непростая
цепь;
v1,v2,v5,v4 −
простая цепь;
v2,v4,v5,v2 −
простой цикл
9
10.
Типы графовМультиграф – граф, в котором нет петель, но
пары вершин могут соединяться более, чем одним
ребром. Эти ребра называются кратными
Псевдограф – граф с петлями и кратными
ребрами, т.е. мультиграф с петлями
Ориентированный граф (орграф) состоит их
конечного непустого множества вершин V и
заданного набора U упорядоченных пар
различных вершин (ребер)
Дуга – ориентированное ребро
Направленный граф – это орграф, не имеющий
симметричных пар ориентированных ребер
10
11.
Связность и деревьяГраф называется
связным, если любые
две его вершины можно
соединить простой цепью
Максимальный связный
подграф графа
называется компонентой
связности
Связный граф без циклов
называется деревом
v5
v1
v4
v2
v3
v2
v5
v1
v3
v4
v6
11
12.
Деревья – примерОписать все деревья, содержащие 6 вершин
Максимальная
степень вершины 5
Максимальная
степень вершины 4
Максимальная степень вершины 3
Максимальная степень вершины 2
12
13.
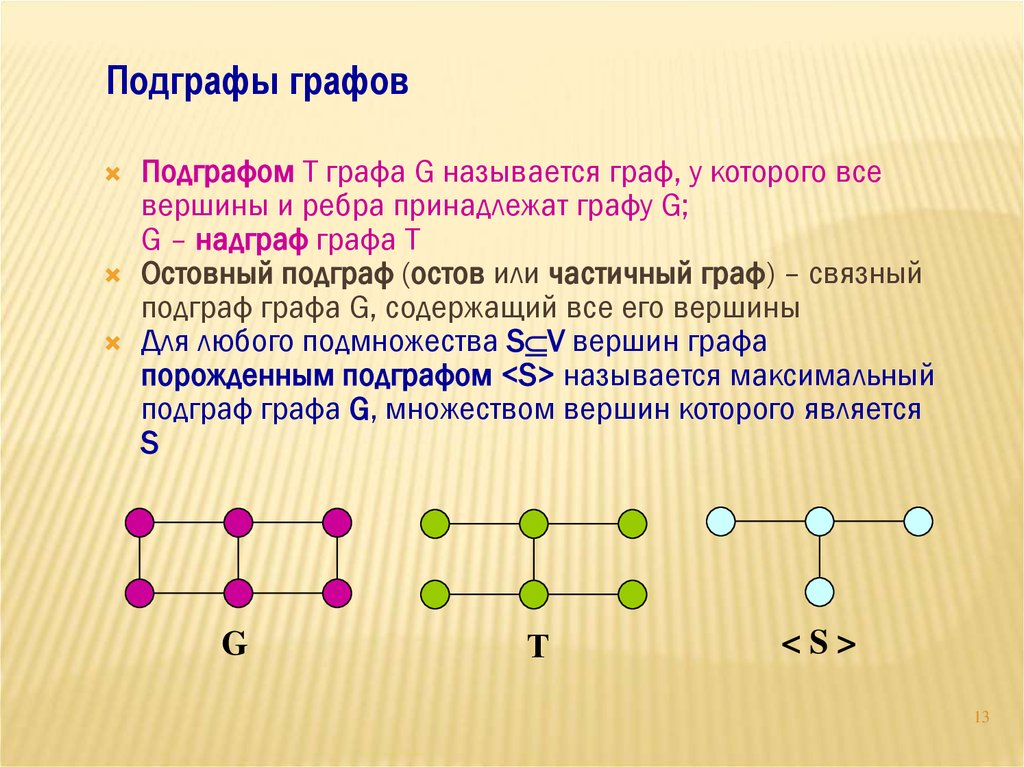
Подграфы графовПодграфом T графа G называется граф, у которого все
вершины и ребра принадлежат графу G;
G – надграф графа T
Остовный подграф (остов или частичный граф) – связный
подграф графа G, содержащий все его вершины
Для любого подмножества S V вершин графа
порожденным подграфом <S> называется максимальный
подграф графа G, множеством вершин которого является
S
G
Т
<S>
13
14. Time-Out
TIME-OUT14
15.
Изоморфизм графов. 1Изоморфизм – взаимно-однозначное
соответствие, сохраняющее свойства
объектов
Известны: изоморфизм множеств,
изоморфизм упорядоченных множеств,
изоморфизм алгебр
Изоморфизм графов – взаимнооднозначное соответствие между
множествами вершин и множествами
ребер, сохраняющее смежность
15
16.
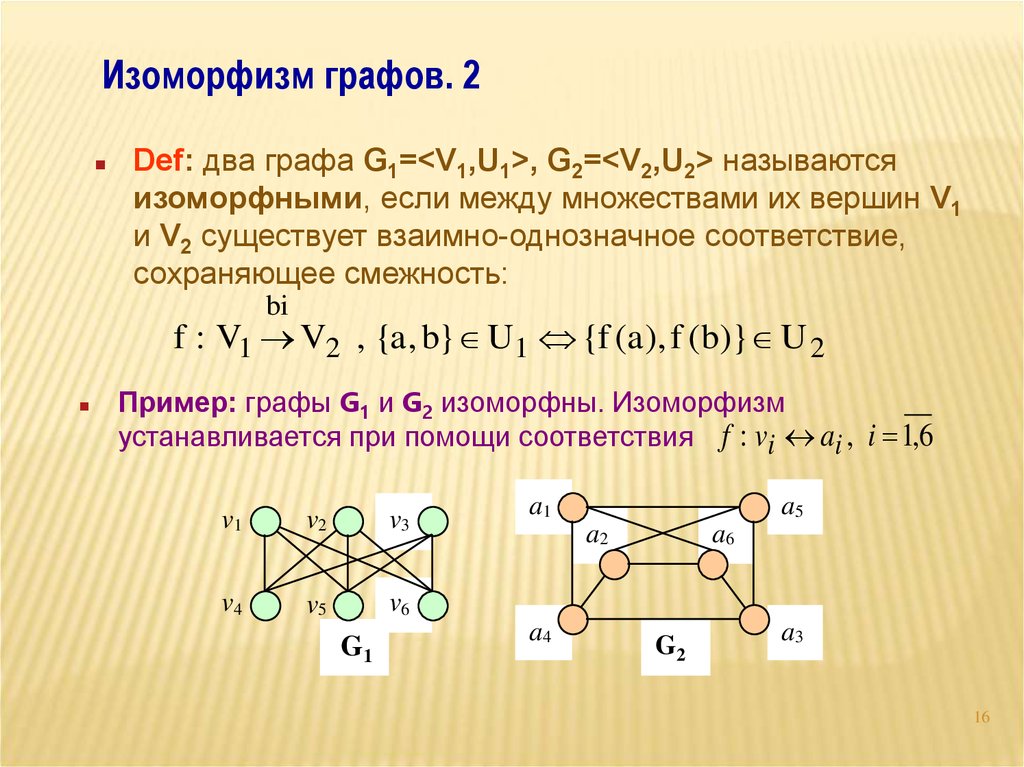
Изоморфизм графов. 2Def: два графа G1=<V1,U1>, G2=<V2,U2> называются
изоморфными, если между множествами их вершин V1
и V2 существует взаимно-однозначное соответствие,
сохраняющее смежность:
bi
f : V1 V2 , {a , b} U1 {f (a ), f (b)} U 2
Пример: графы G1 и G2 изоморфны. Изоморфизм
устанавливается при помощи соответствия f : vi ai , i 1,6
v1
v2
v3
v4
v5
v6
G1
a1
a5
a2
a4
a6
G2
a3
16
17.
Операции над графамиДля графов G1=<V1,U1>, G2=<V2,U2> с
непересекающимся множествами вершин
(носителей графов) V1∩V2= и ребер (сигнатур
графов) U1∩U2= вводятся операции:
объединение
соединение
декартово произведение
композиция
17
18.
Операции над графами: объединениеДля графов G1=<V1,U1>, G2=<V2,U2> с
непересекающимся множествами вершин
(носителей графов) V1∩V2= и ребер (сигнатур
графов) U1∩U2= операция объединение G1UG2
понимается в смысле теоретикомножественного объединения носителей и
сигнатур V1UV2 , U1UU2 :
U
G1 G2
=
G1UG2
18
19.
Операции над графами: соединениеДля графов G1=<V1,U1>, G2=<V2,U2> с
непересекающимся множествами вершин
(носителей графов) V1∩V2= и ребер (сигнатур
графов) U1∩U2= операция соединение G1+G2
заключается в объединении носителей и
сигнатур V1UV2 , U1UU2 и всех ребер,
соединяющих вершины множеств V1, V2 :
+
G1 G2
=
G1+G2
19
20.
Операции над графами: декартовопроизведение
Для графов G1=<V1,U1>, G2=<V2,U2> с непересекающимся
множествами вершин (носителей графов) V1∩V2= и
ребер (сигнатур графов) U1∩U2= операция декартово
произведение G1 G2 определяется следующим образом:
G1 G2 = <V,U>, V=V1 V2 , u=(u1,u2), v=(v1,v2) V,
u adj v ( u1=v1, u2 adj v2 ) или ( u2=v2, u1 adj v1)
u1
(u1,u2)
(u1,v2)
(u1,w2)
=
u2
v2
w2
v1
G1
G2
(v1,u2)
(v1,v2)
(v1,w2)
G1 G2
20
21.
Операции над графами: композицияДля графов G1=<V1,U1>, G2=<V2,U2> с
непересекающимся множествами вершин
(носителей графов) V1∩V2= и ребер (сигнатур
графов) U1∩U2= результат композиции G=G1[G2]
имеет в качестве множества вершин V1 V2 и
вершина u=(u1,u2) смежна с v=(v1,v2) тогда и только
тогда, когда [u1 adj v1] или [u1=v1 и u2 adj v2]:
u1
(u2,u1)
(u2,v1)
(v2,u1)
u2
v2
(v2,v1)
w2
v1
G1
G2
(w2,v1)
(w2,v1)
G1[G2]
G=G2[G1]
21
22.
Операции над графами:количество вершин и ребер
Если G1=<V1,U1>, G2=<V2,U2> – это (p1, q1)- и
(p2, q2)-графы соответственно, то для каждой из
определенных выше операций можно найти число
вершин и ребер в получающемся графе:
Операции
G1 G2
G1 G 2
G1 G 2
G1[G2 ]
Число вершин
p1 p 2
p1 p 2
p1 p 2
p1 p 2
Число ребер
q1 q 2
q1 q 2 p1 p 2
p1q 2 p 2 q1
p1q 2 p 2 q1
22
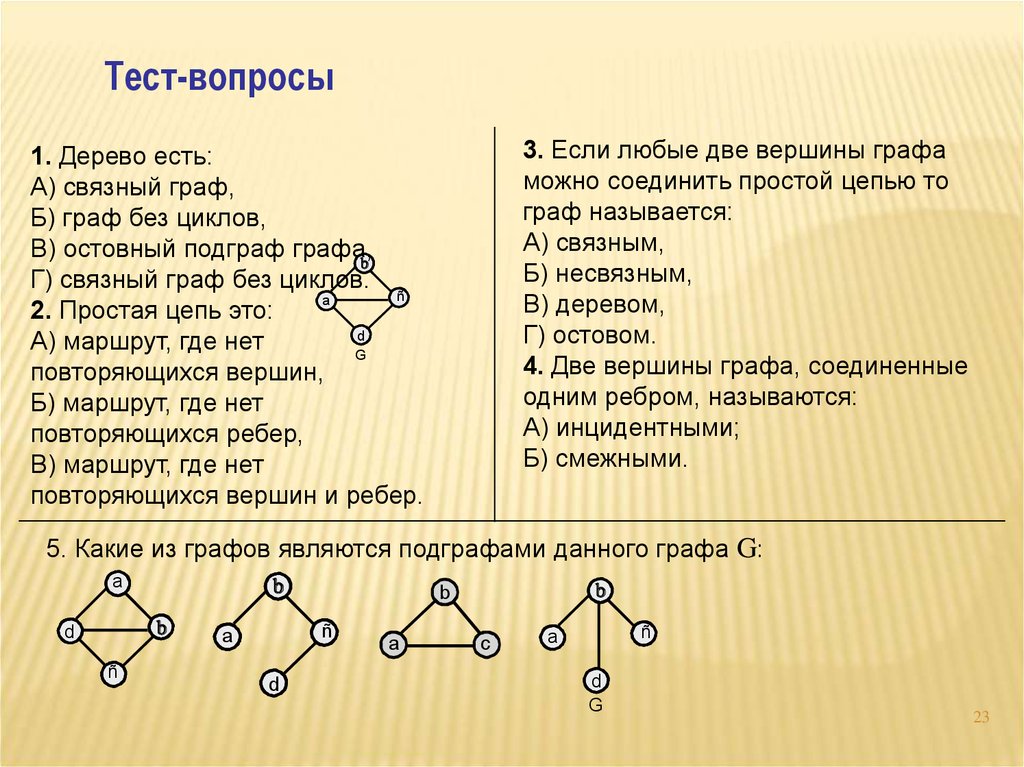
23.
Тест-вопросы3. Если любые две вершины графа
можно соединить простой цепью то
граф называется:
А) связным,
Б) несвязным,
В) деревом,
Г) остовом.
4. Две вершины графа, соединенные
одним ребром, называются:
А) инцидентными;
Б) смежными.
1. Дерево есть:
А) связный граф,
Б) граф без циклов,
В) остовный подграф графа,
Г) связный граф без циклов.
ñ
a
2. Простая цепь это:
d
А) маршрут, где нет
G
повторяющихся вершин,
Б) маршрут, где нет
повторяющихся ребер,
В) маршрут, где нет
повторяющихся вершин и ребер.
5. Какие из графов являются подграфами данного графа G:
a
d
b
ñ
a
ñ
d
a
c
ñ
a
d
G
23



















 mathematics
mathematics








