Similar presentations:
Построение графиков функций, содержащих модуль
1.
ПОСТРОЕНИЕ ГРАФИКОВФУНКЦИЙ, СОДЕРЖАЩИХ МОДУЛЬ.
10 КЛАСС.
( ЭЛЕКТИВНОЕ ЗАНЯТИЕ)
Провела учитель математики
МБОУ «Лицей №2» г. Протвино
Ларионова Г. А.
2014
2.
План занятия.1 этап. Устная работа.
2 этап. Письменная работа в группах.
3 этап. Применение графиков функций к
решению заданий с параметром.
4 этап. Заключительный. Построение графика
нестандартной функции.
3.
Цели занятия.1. Отработка умений и навыков построения
графиков функций, содержащих знак модуля:
типа f(|x|) и |f(x)|, |f(|x|)|.
2. Отработка умений и навыков построения
графиков функций с помощью геометрических
преобразований.
3. Развитие коммуникативных качеств и
коллективно-творческого мышления учащихся.
4. Развитие интереса учащихся к математике.
4.
КАК ПОСТРОИТЬ ГРАФИКИ ДАННЫХФУНКЦИЙ ?
I этап
1.
2.
3.
4.
5.
6.
у=2cosx + 0,5
у=(x + 1)2 – 4
у=4/(x-3) – 1
у=|x + 0,5| - 3
у= - |x| + 1
у=sin(x - ¼ π)
5.
Среди перечисленных функцийвыберите те, которые относятся к
типу у =| f(x)| или
у =f(|x|).
y=|x2+3x|,
y= |cos2x |,
y= |cosx –½|,
y= ½√6-|x |,
y= |x-3 | +5,
y= |x | + tg |x |,
y= x2 -6|x | +8,
y= x2 -5 |x -1| +4,
y=4/|x |- 2
6.
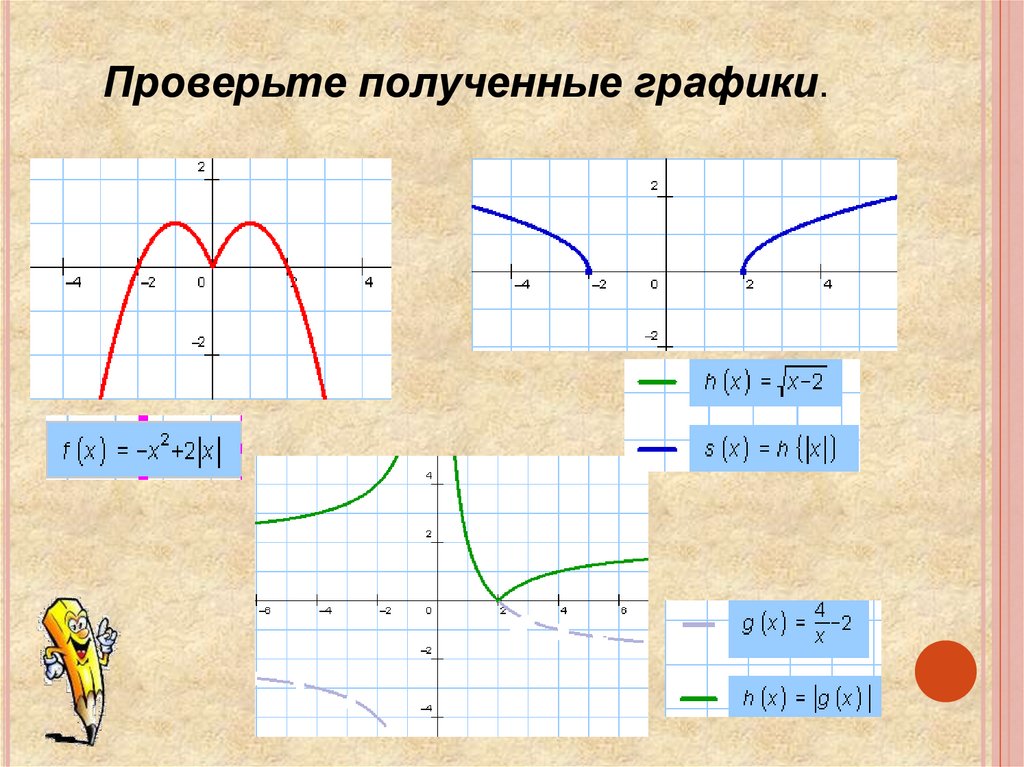
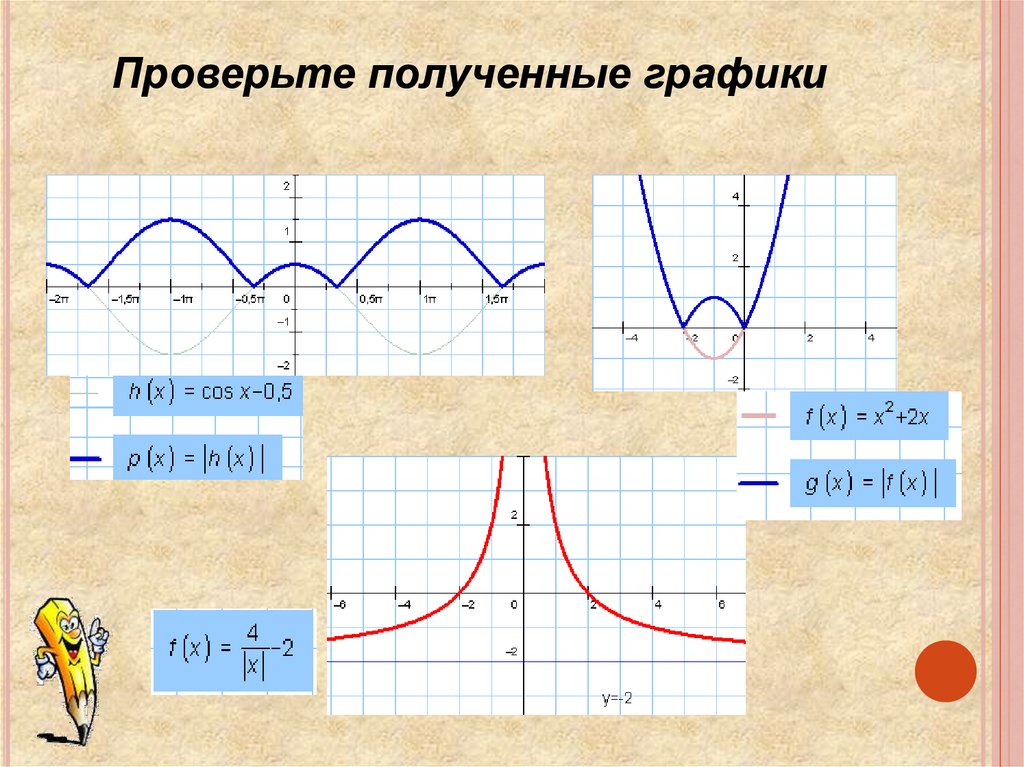
II этапПостройте графики функций.
1 группа.
у
= |cosx - ½|
y= 4:|x| -2
y= |x2 +2x|
2 группа.
y=
|4:x - 2|
y= - x2 +2|x|
y= √|x| -2
7.
Проверьте полученные графики.8.
Проверьте полученные графики9.
III этапПрименение графиков функций к
решению заданий с параметром.
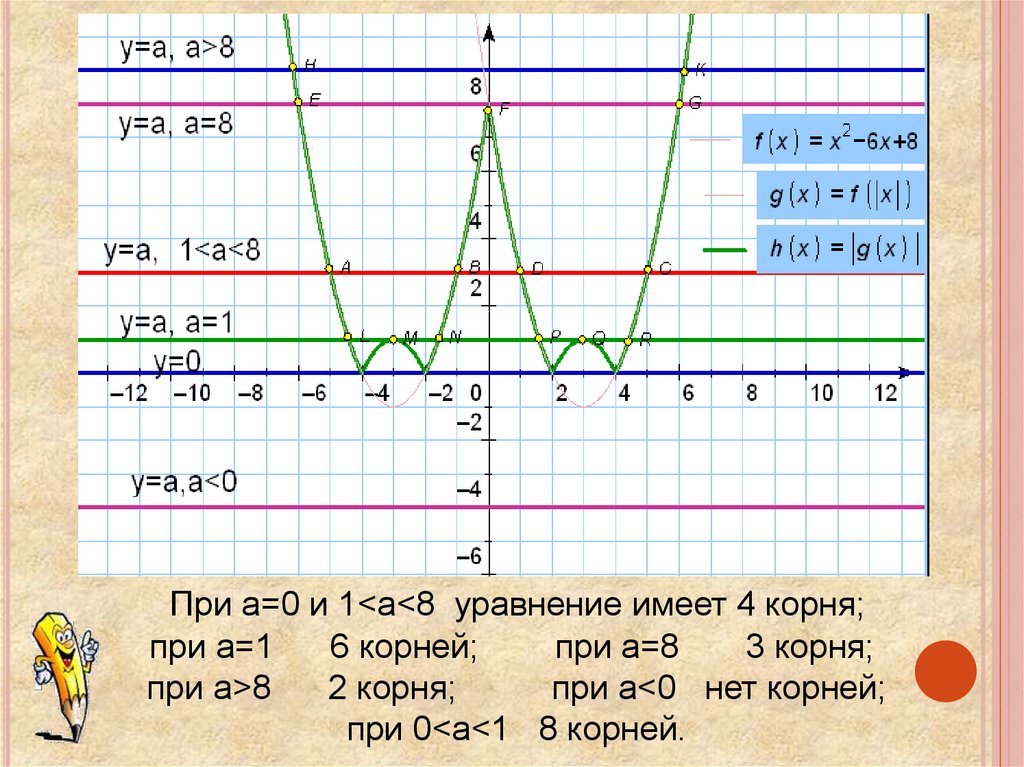
Изобразите график функции
у=|х2 -6|х|+8| и, пользуясь полученным
графиком найти: а) количество
корней уравнения |х2 -6|х|+8|= а
в зависимости от параметра а;
б)решение неравенства |х2 -6|х|+8| ≥ 3
10.
При а=0 и 1<a<8 уравнение имеет 4 корня;при а=1
6 корней;
при а=8
3 корня;
при а>8
2 корня;
при а<0 нет корней;
при 0<a<1 8 корней.
11.
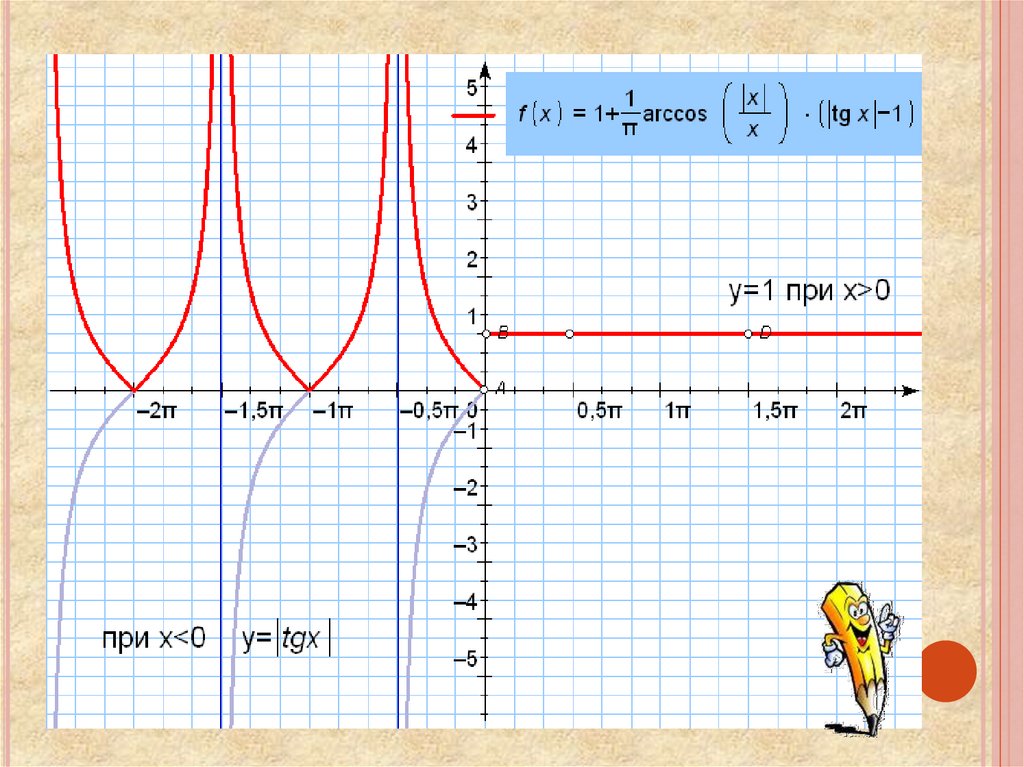
Заключительный этап.Построить график функции
у = 1+ π-1 arccos(|x|/x)*(|tgx|-1).
1. Если х >0, то у = 1 + 1/π*arccos 1*(|tgx|-1),
т. е. у=1.
2. Если х <0, то у = 1+ 1/π*arccos(- 1)*(|tgx|-1),
т. е. у =| tgx|.
D(y): x≠0, x ≠ ½π + πn, n – целое число.
12.
13.
Домашнее задание.Построить графики функций:
у= |2· |х| - х2|,
у= |(х – 4):(х +1)|,
у= х2sin((πx-π|x|):4x)+sinx·cos((πx-π|x|):4x)
14.
Используемая литература.Учебник для школ и классов с углублённым
изучением математики: «Алгебра» 9 класс. Ю. Н.
Макарычев, Н. Г. Миндюк, К. И. Нешков.
Педагогический практикум. «Нестандартные
задания по математике» 5-11 классы. В. В.
Кривоногов.
Дидактические материалы по алгебре. 9 класс. С
углублённым изучением математики. Ю. Н.
Макарычев, Н. Г. Миндюк.
Математика. Самостоятельные и контрольные
работы. Алгебра и начала анализа. 10-11 класс. А.
П. Ершова, В. В. Голобородько.











 mathematics
mathematics








