Потоки. Нахождение максимального потока

1.

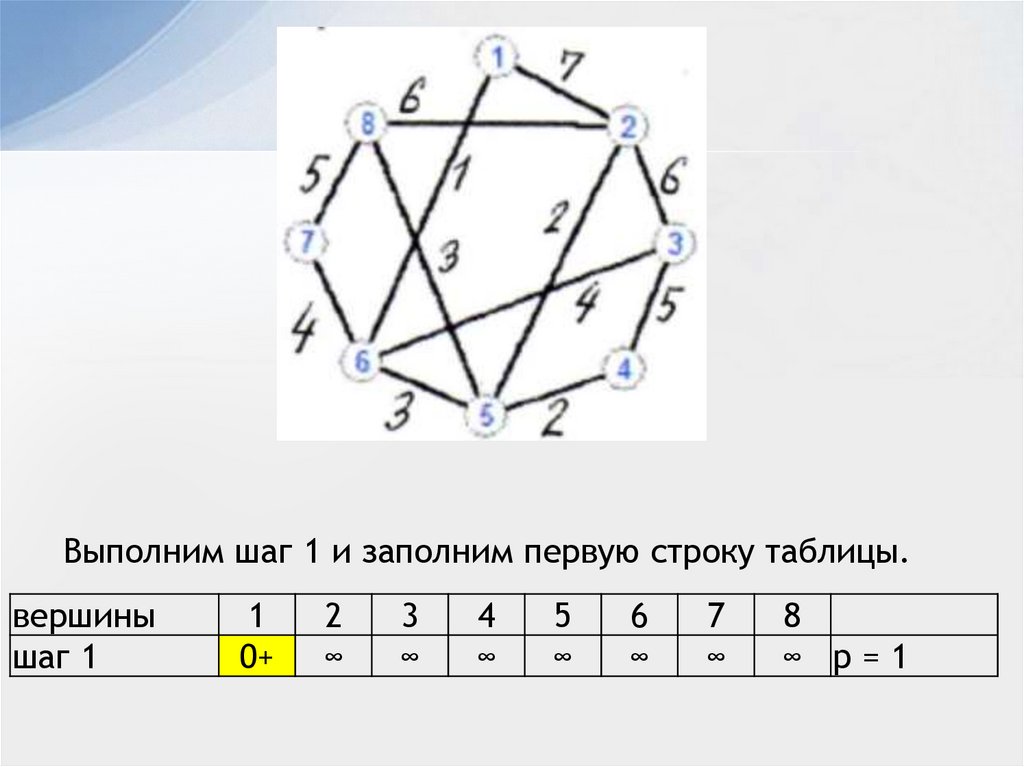
Выполним шаг 1 и заполним первую строку таблицы.
вершины
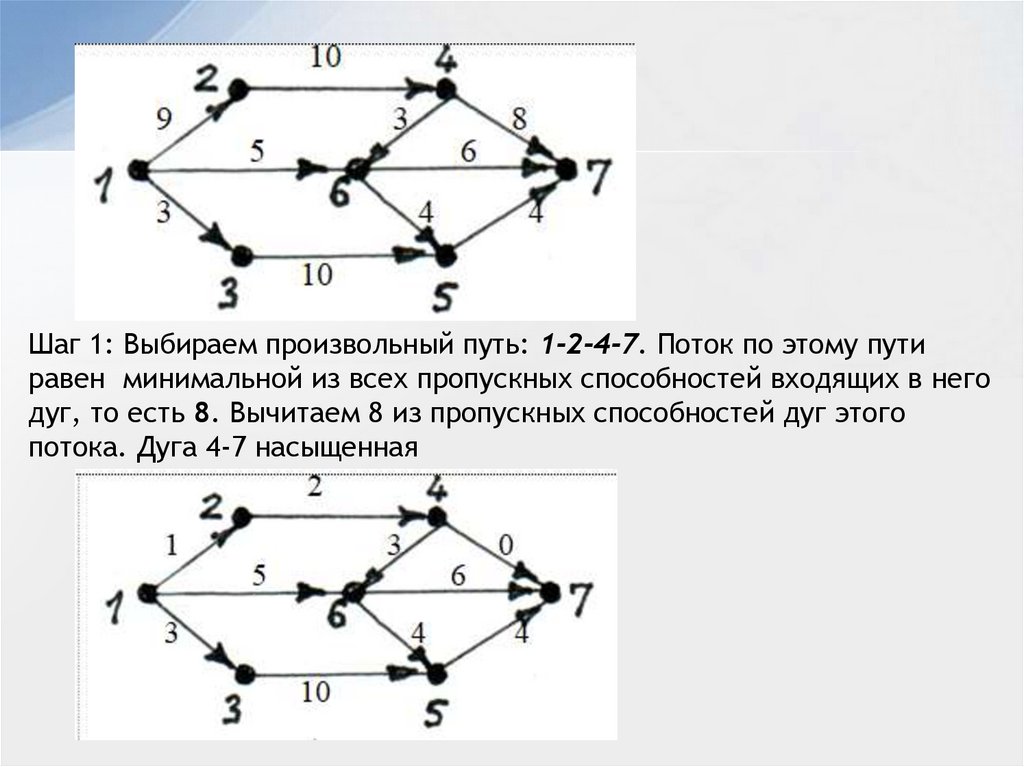
шаг 1
1
0+
2
∞
3
∞
4
∞
5
∞
6
∞
7
∞
8
∞ p=1

2.

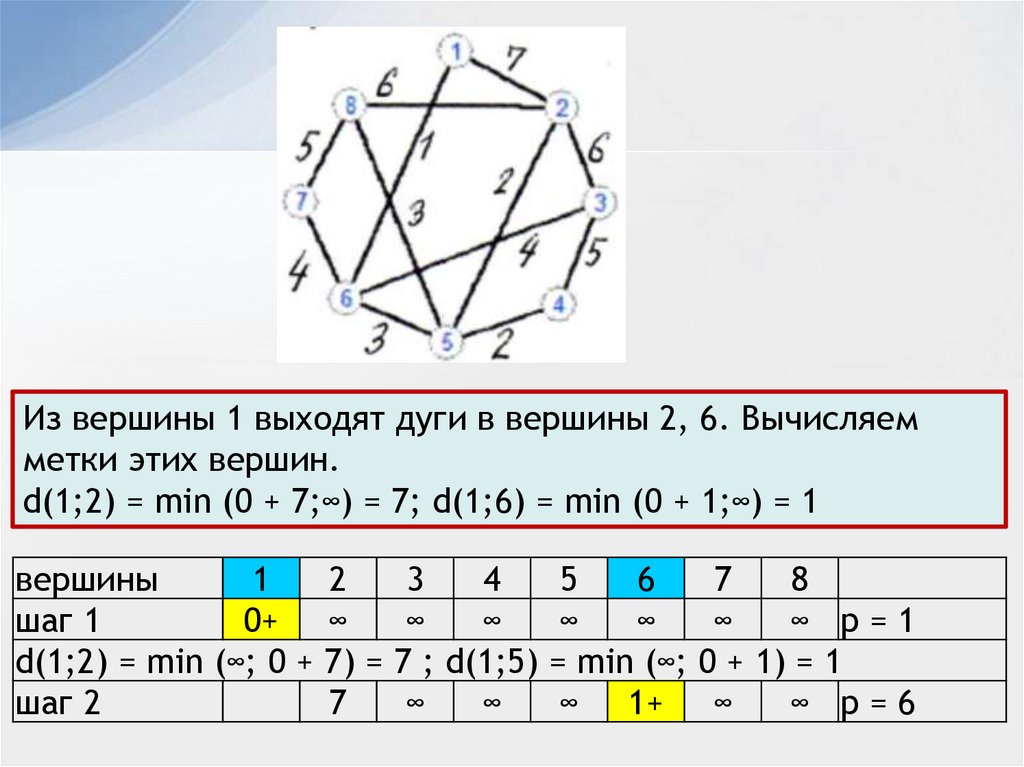
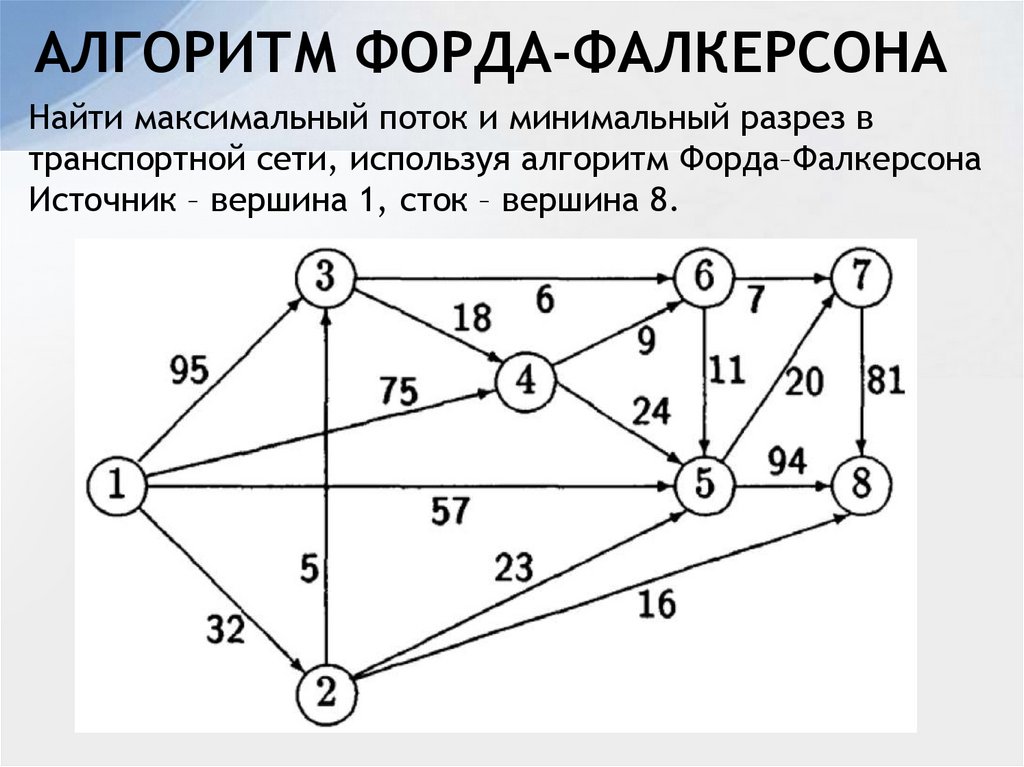
Из вершины 1 выходят дуги в вершины 2, 6. Вычисляем
метки этих вершин.
d(1;2) = min (0 + 7;∞) = 7; d(1;6) = min (0 + 1;∞) = 1
вершины
1
2
3
4
5
6
7
8
шаг 1
0+ ∞
∞
∞
∞
∞
∞
∞ p=1
d(1;2) = min (∞; 0 + 7) = 7 ; d(1;5) = min (∞; 0 + 1) = 1
шаг 2
∞ 1+ ∞
7
∞
∞
∞ p=6

3.

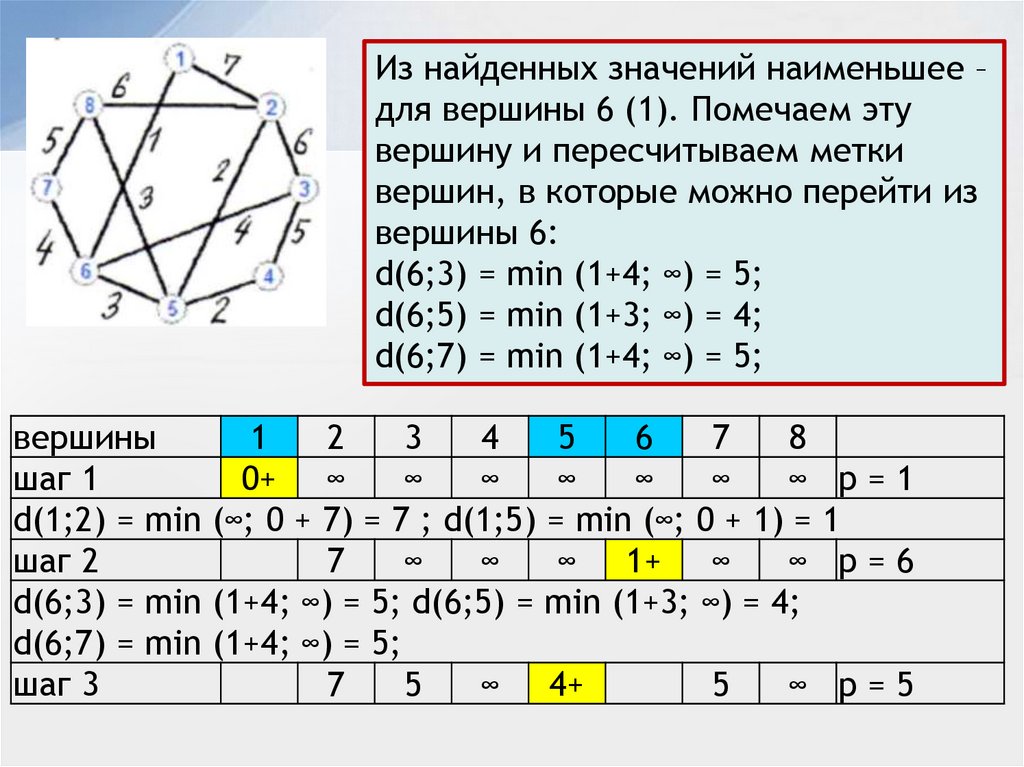
Из найденных значений наименьшее –
для вершины 6 (1). Помечаем эту
вершину и пересчитываем метки
вершин, в которые можно перейти из
вершины 6:
d(6;3) = min (1+4; ∞) = 5;
d(6;5) = min (1+3; ∞) = 4;
d(6;7) = min (1+4; ∞) = 5;
вершины
1
2
3
4
5
6
7
8
шаг 1
0+ ∞
∞
∞
∞
∞
∞
∞ p=1
d(1;2) = min (∞; 0 + 7) = 7 ; d(1;5) = min (∞; 0 + 1) = 1
шаг 2
∞ 1+ ∞
7
∞
∞
∞ p=6
d(6;3) = min (1+4; ∞) = 5; d(6;5) = min (1+3; ∞) = 4;
d(6;7) = min (1+4; ∞) = 5;
шаг 3
7
5
∞ 4+
5
∞ p=5

4.

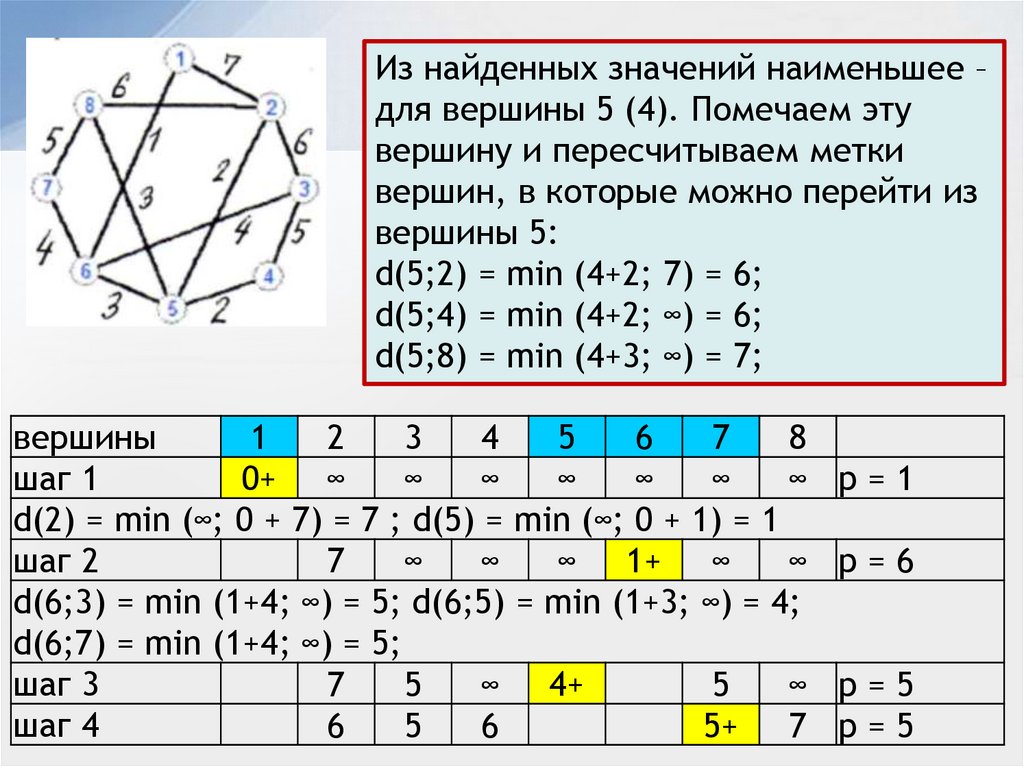
Из найденных значений наименьшее –
для вершины 5 (4). Помечаем эту
вершину и пересчитываем метки
вершин, в которые можно перейти из
вершины 5:
d(5;2) = min (4+2; 7) = 6;
d(5;4) = min (4+2; ∞) = 6;
d(5;8) = min (4+3; ∞) = 7;
вершины
1
2
3
4
5
6
7
8
шаг 1
0+ ∞
∞
∞
∞
∞
∞
∞
d(2) = min (∞; 0 + 7) = 7 ; d(5) = min (∞; 0 + 1) = 1
шаг 2
∞ 1+ ∞
7
∞
∞
∞
d(6;3) = min (1+4; ∞) = 5; d(6;5) = min (1+3; ∞) = 4;
d(6;7) = min (1+4; ∞) = 5;
шаг 3
7
5
∞ 4+
5
∞
шаг 4
6
5
6
5+ 7
p=1
p=6
p=5
p=5

5.

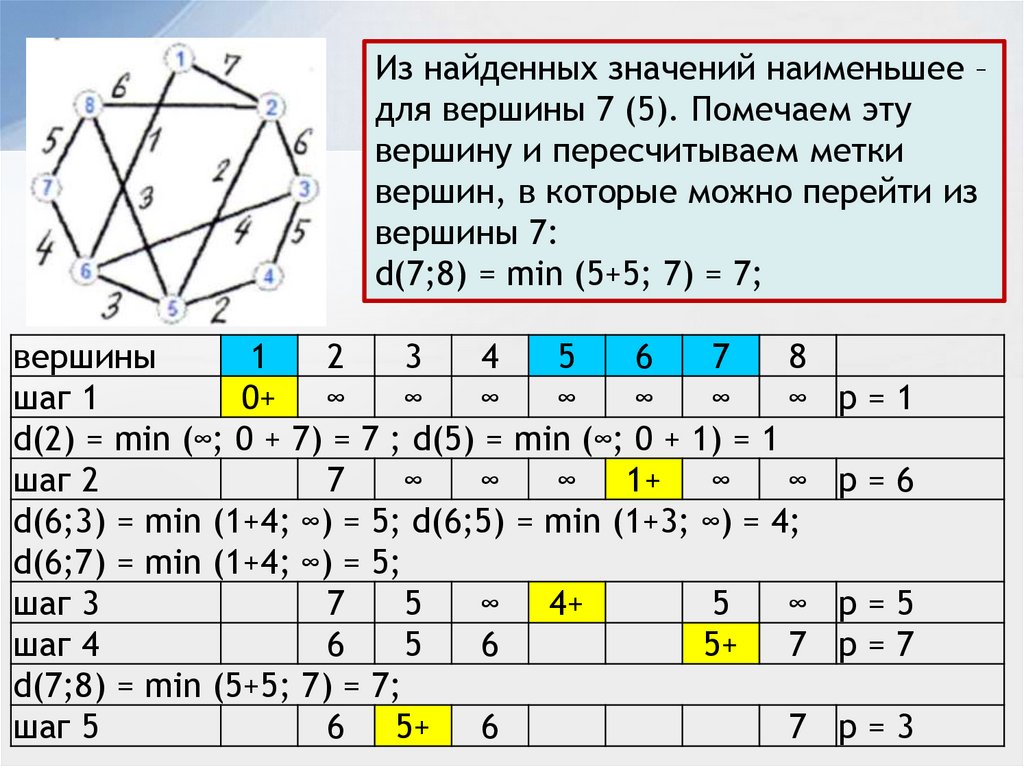
Из найденных значений наименьшее –
для вершины 7 (5). Помечаем эту
вершину и пересчитываем метки
вершин, в которые можно перейти из
вершины 7:
d(7;8) = min (5+5; 7) = 7;
вершины
1
2
3
4
5
6
7
8
шаг 1
0+ ∞
∞
∞
∞
∞
∞
∞
d(2) = min (∞; 0 + 7) = 7 ; d(5) = min (∞; 0 + 1) = 1
шаг 2
∞ 1+ ∞
7
∞
∞
∞
d(6;3) = min (1+4; ∞) = 5; d(6;5) = min (1+3; ∞) = 4;
d(6;7) = min (1+4; ∞) = 5;
шаг 3
7
5
∞ 4+
5
∞
шаг 4
6
5
6
5+ 7
d(7;8) = min (5+5; 7) = 7;
шаг 5
6 5+ 6
7
p=1
p=6
p=5
p=7
p=3

6.

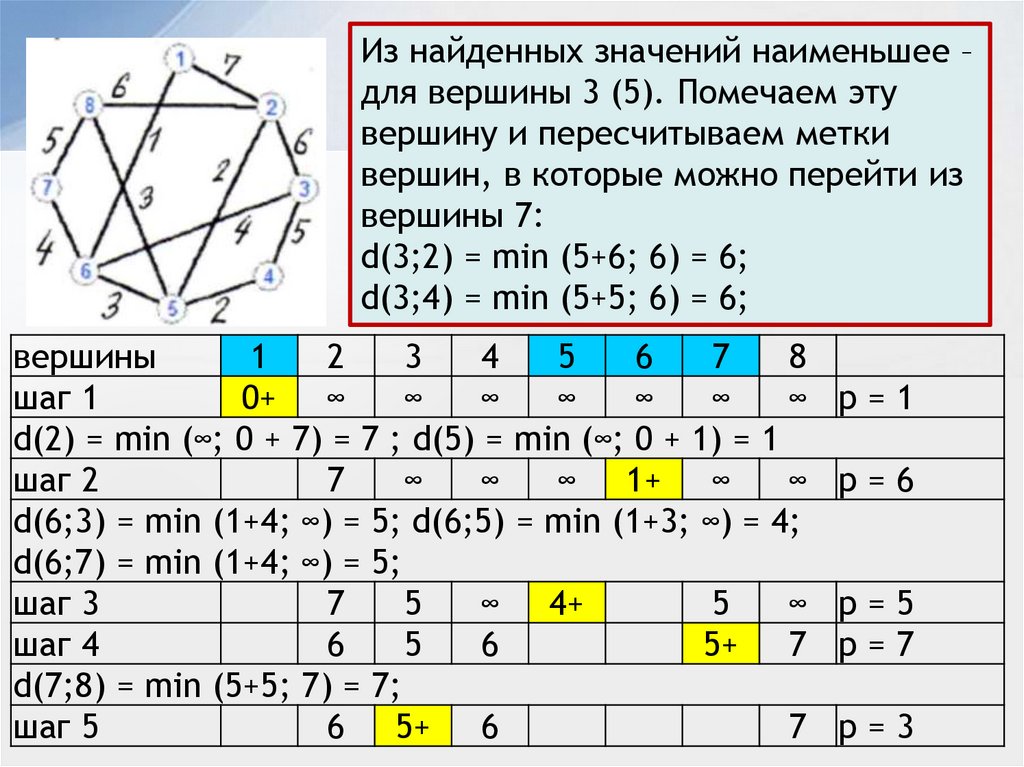
Из найденных значений наименьшее –
для вершины 3 (5). Помечаем эту
вершину и пересчитываем метки
вершин, в которые можно перейти из
вершины 7:
d(3;2) = min (5+6; 6) = 6;
d(3;4) = min (5+5; 6) = 6;
вершины
1
2
3
4
5
6
7
8
шаг 1
0+ ∞
∞
∞
∞
∞
∞
∞
d(2) = min (∞; 0 + 7) = 7 ; d(5) = min (∞; 0 + 1) = 1
шаг 2
∞ 1+ ∞
7
∞
∞
∞
d(6;3) = min (1+4; ∞) = 5; d(6;5) = min (1+3; ∞) = 4;
d(6;7) = min (1+4; ∞) = 5;
шаг 3
7
5
∞ 4+
5
∞
шаг 4
6
5
6
5+ 7
d(7;8) = min (5+5; 7) = 7;
шаг 5
6 5+ 6
7
p=1
p=6
p=5
p=7
p=3

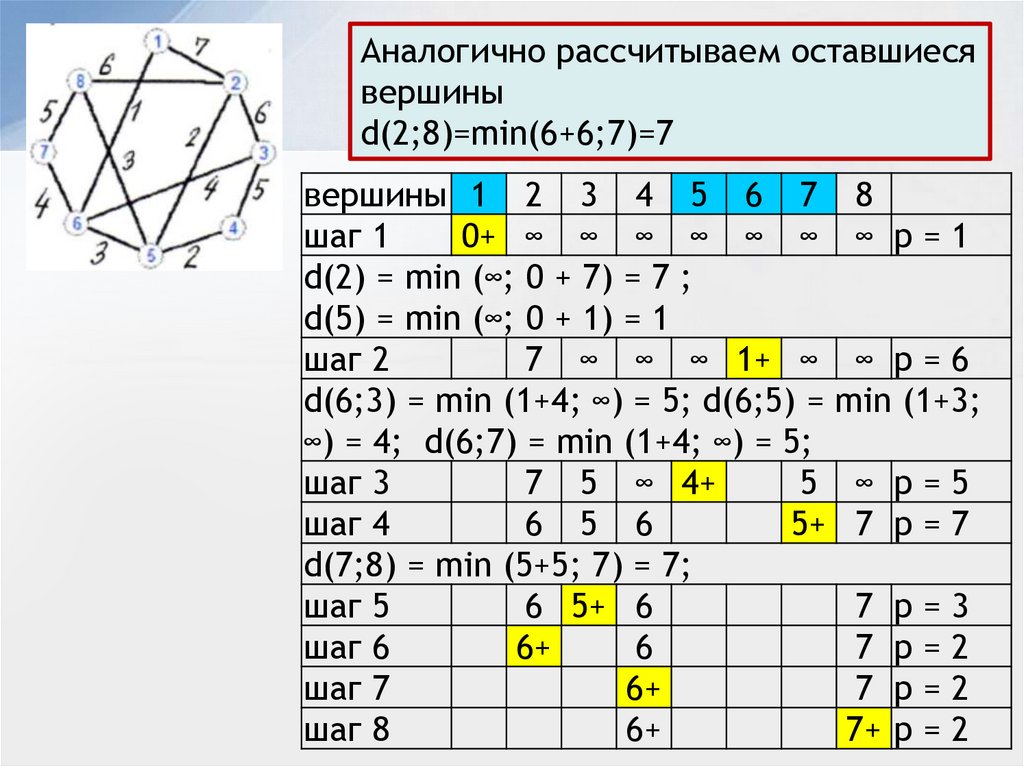
7.

Аналогично рассчитываем оставшиеся
вершины
d(2;8)=min(6+6;7)=7
вершины 1 2 3 4 5 6 7 8
шаг 1
0+ ∞ ∞ ∞ ∞ ∞ ∞ ∞ p = 1
d(2) = min (∞; 0 + 7) = 7 ;
d(5) = min (∞; 0 + 1) = 1
шаг 2
7 ∞ ∞ ∞ 1+ ∞ ∞ p = 6
d(6;3) = min (1+4; ∞) = 5; d(6;5) = min (1+3;
∞) = 4; d(6;7) = min (1+4; ∞) = 5;
шаг 3
7 5 ∞ 4+
5 ∞ p=5
шаг 4
6 5 6
5+ 7 p = 7
d(7;8) = min (5+5; 7) = 7;
шаг 5
6 5+ 6
7 p=3
шаг 6
6+
6
7 p=2
шаг 7
6+
7 p=2
шаг 8
6+
7+ p = 2

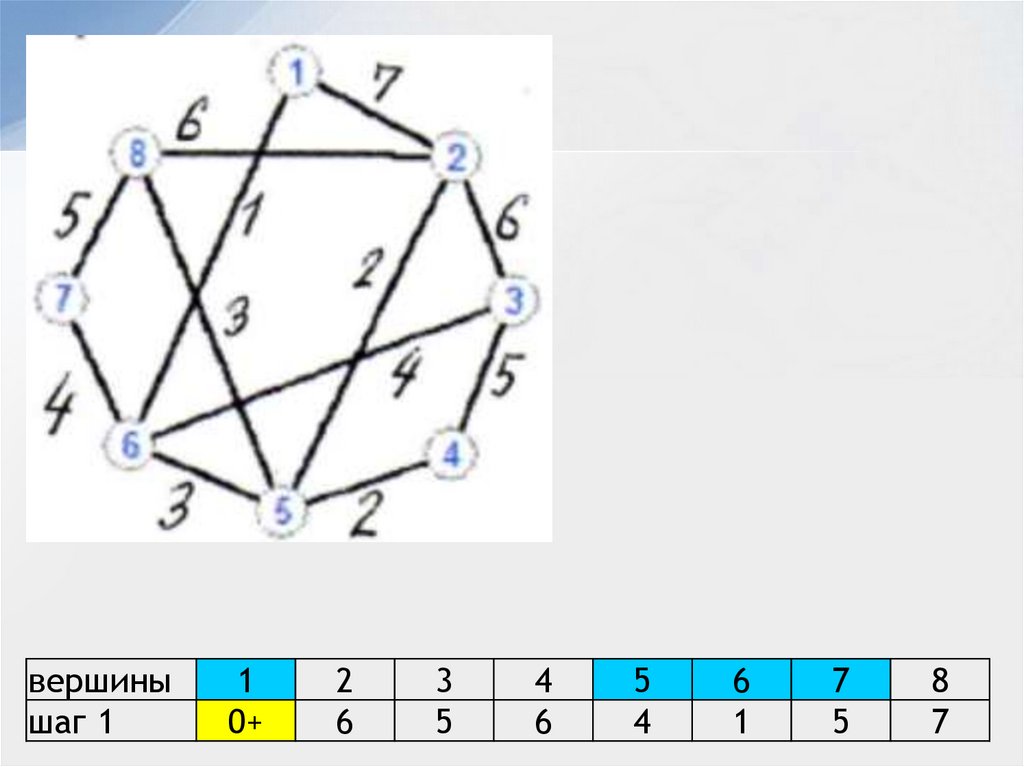
8.

вершины
шаг 1
1
0+
2
6
3
5
4
6
5
4
6
1
7
5
8
7

9.

МДК.01.02 Математический аппарат для построения компьютерных
сетей, занятие 14
Потоки в графах.
Нахождение
максимального потока
1. Понятие потока. Постановка задачи.
2. Алгоритм Форда-Фалкерсона нахождения
максимального потока.

10.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
На этом занятии будем рассматривать ориентированные
графы без петель и кратных ребер. Для вершины x
множество всех входящих в нее ребер обозначается через
E+(x), а множество выходящих – через E−(x).
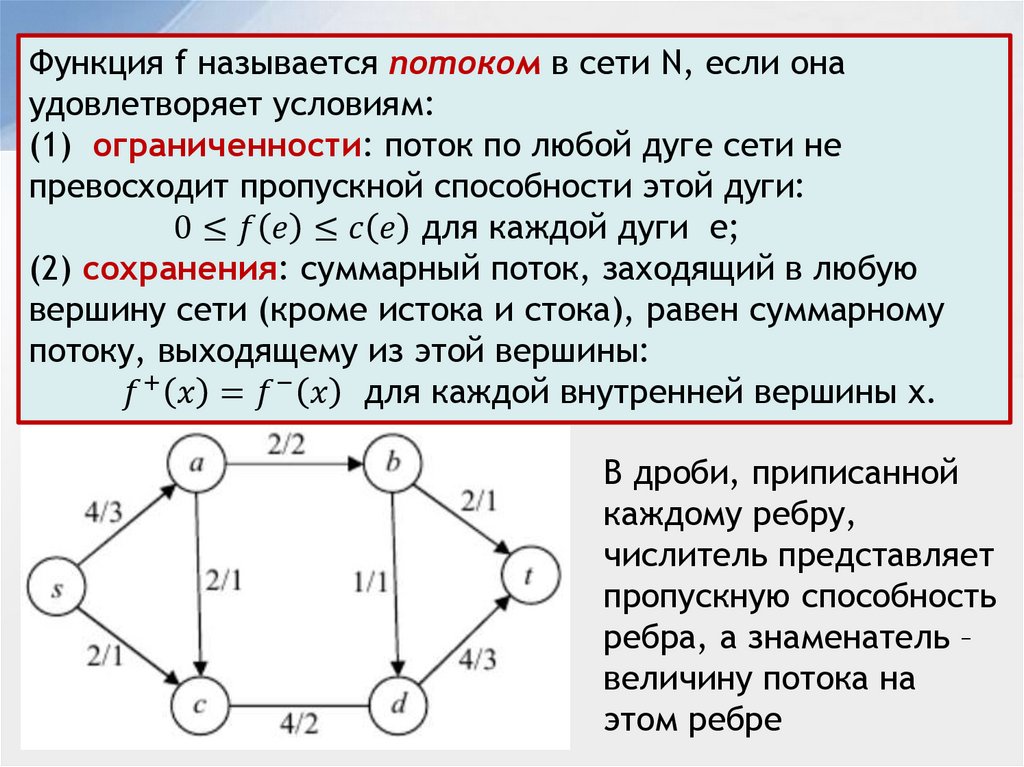
Сетью называется орграф, в котором
1) каждому ребру e приписано положительное число c(e),
называемое пропускной способностью ребра;
2) выделены две вершины s и t, называемые
соответственно источником и стоком, при этом E+(s) =
E−(t)= ∅ - то есть из источника дуги только выходят, а в сток
только входят.
В данной задаче основным параметром на дугах сети
является